Abstract
In this paper, we construct an Human immunodeficiency virus (HIV) dynamics model with impairment of B-cell functions and the general incidence rate. We incorporate three types of infected cells, (i) latently-infected cells, which contain the virus, but do not generate HIV particles, (ii) short-lived productively-infected cells, which live for a short time and generate large numbers of HIV particles, and (iii) long-lived productively-infected cells, which live for a long time and generate small numbers of HIV particles. The model considers five distributed time delays to characterize the time between the HIV contact of an uninfected CD4 T-cell and the creation of mature HIV. The nonnegativity and boundedness of the solutions are proven. The model admits two equilibria, infection-free equilibrium and endemic equilibrium . We derive the basic reproduction number , which determines the existence and stability of the two equilibria. The global stability of each equilibrium is proven by utilizing the Lyapunov function and LaSalle’s invariance principle. We prove that if , then is globally asymptotically stable, and if , then is globally asymptotically stable. These theoretical results are illustrated by numerical simulations. The effect of impairment of B-cell functions, time delays, and antiviral treatment on the HIV dynamics are studied. We show that if the functions of B-cells are impaired, then the concentration of HIV is increased in the plasma. Moreover, we observe that the time delay has a similar effect to drug efficacy. This gives some impression for developing a new class of treatments to increase the delay period and then suppress the HIV replication.
1. Introduction
Human immunodeficiency virus (HIV) infects and destroys uninfected CD4 T-cells, which play an essential role in the immune system. When the concentration of the uninfected CD4 T-cells reaches below 200 cell/mm, then the person is said to have progressed to acquired immunodeficiency syndrome (AIDS) [1]. Nowak and Bangham [2] proposed the following basic mathematical model, which describes the dynamics of the uninfected CD4 T-cells, infected CD4 T-cells producing viruses, and HIV particles:
where, U, I and P are the concentrations of the uninfected CD4 T-cells, infected CD4 T-cells, and HIV particles, respectively. is the production rate of the uninfected CD4 T-cells. is the average number of HIV particles generated in the lifetime of the infected CD4 T-cells. The death rate constants of compartments () are give by (), respectively. The term represents the incidence rate of infection. Modeling of within-host HIV dynamics has received considerable attention from mathematicians during the last few decades [1,2,3,4,5]. Mathematical modeling and analysis have been essential tools to get a better systematic and quantitative understanding of viral processes that are difficult to discern through strictly experimental approaches [6]. The global stability analysis of models (1)–(3) was first investigated in [7].
Highly-active anti-retroviral therapy (HAART) consisting of several antiretroviral drugs such as reverse transcriptase inhibitor (RTI) and protease inhibitor (PI) can suppress viral replication to a low level, but cannot eradicate the virus. An important reason is that HIV provirus can reside in latently-infected CD4 T-cells [8]. Latently-infected CD4 T-cells live long, but can be activated to produce virus by relevant antigens. Modeling the virus dynamics with latently-infected cells was presented in [9,10]. Lyapunov functions were exploited in [11,12,13,14] to establish the global stability of virus dynamics models with latently-infected cells. It was reported in [9,15,16] that there are three classes of infected CD4 T cells, (i) short-lived productively-infected cells, which live for a short time and produce large numbers of HIV, (ii) long-lived productively-infected cells, which live for a long time and produce small numbers of HIV particles, and (iii) latently-infected cells, which contain the viruses, but do not produce them until they are activated.
A major shortcoming of Models (1)–(3) is the assumption that cells produce viruses immediately after they are infected. It is commonly observed that in many biological processes, a time delay is inevitable. For HIV-1 infection, it roughly takes about one day for a newly-infected cell to become productive and then to be able to produce new virus particles [17]. Therefore, mathematicians have frequently used different types of delays to make biological models more realistic [18]. In 1996, Herz et al. [19] introduced an HIV dynamics model with intracellular delay, and they obtained the analytic expression of the viral load decline under treatment and used it to analyze the viral load decline data in patients. Nelson et al. [20] extended the analysis and showed that the time delay can affect the estimate of the death rate of infected CD4 T-cells when the effectiveness of antiviral drugs is not 100%. HIV dynamics models with an intracellular time delay were used to estimate different kinetic parameters in the presence and absence of drug therapy in [17]. The global stability of delayed virus dynamics models has been studied in several works (see, e.g., [21,22,23,24,25,26,27,28,29,30,31]). HIV dynamics models with latently-infected cells and two time delays were proposed and studied in [32,33].
One of the most important extensions of models (1)–(3) is to take into account the effect of immune response. There are two main immune responses; the first is the cytotoxic T lymphocyte (CTL) immune response. The CTL cells kill the infected CD4 T-cells. Viral infection models with CTL immune response have been presented in many papers (see, e.g., [2,34,35,36]). The B-cell immune response is considered as the second arm of the immune system. The function of B-cells is to produce antibodies that bind to virus particles and mark them as foreign structures for elimination by other cells of the immune system [4]. The antibodies can neutralize viruses and protect the body from infection [37]. The basic virus dynamics model with B-cell immune response was presented by Murase et al. [38]. To incorporate the time lag between the virus contacts with an uninfected cell and the production of new mature viruses, Wang and Zou [39] proposed the following model:
where C is the concentration of B-cells. The term represents the neutralization rate of HIV particles. The term represents the proliferation rate of the B-cells. Parameter represents the time between HIV contacts with an uninfected CD4 T-cell and the cell becoming infected. The immature virus needs time to be mature. Nowak and May [4] assumed a linear term for immune stimulation: B-cell abundance increases in response to free HIV particles at rate , and this leads to . Many delayed viral infection models have been developed with B-cell immune response (see, e.g., [40,41,42,43,44,45,46,47,48,49,50] ). The models presented in [2,34,36,40,41,42,43,44,45,46,47,48,49,50] were constructed under the assumption that the presence of the antigen can stimulate immunity and ignore the immune impairment. However, there are numerous experimental results suggesting that the HIV generates mutants, which escape from CTL immune responses [51,52]. Models with CTL immune impairment were studied several times (see, e.g., [53,54,55,56]).
On the other hand, there are some factors that affect the B-cell function and cause the impairment of the B-cells [57,58,59]. These factors include the following: malnutrition, tumors, cytotoxic drugs, irradiation, aging, trauma, some diseases (e.g., diabetes), and immunosuppression by microbes, e.g., malaria and the measles virus, but especially HIV [37] when the viral load is too high. Miao et al. [60] proposed a virus dynamics model with B-cell impairment, but they did not study the global stability analysis of the model. In a very recent works, Elaiw et al. [46] and Elaiw and Elnahary [47] studied the global stability of HIV dynamics models by including: B-cell immune response, time delays, and three types of infected cells (short-lived, long-lived, and latent). However, the B-cell immune impairment was ignored in [46,47].
Based on the discussion above, in this paper, we propose and analyze an HIV dynamics model taking into account the impairment of B-cell functions and five distributed time delays. The infected cells are divided into three classes, latently-infected, short-lived productively-infected, and long-lived productively-infected. The incidence rate is given by a general nonlinear function, which satisfies a set of conditions. The nonnegativity and boundedness of the solutions are proven. We derive the basic reproduction number, which determines the existence and stability of the equilibria. The global stability of all equilibria of the model is established by constructing Lyapunov functions. We also perform numerical simulations to support the global stability results and to explore the effect of time delays, impairment of the B-cell functions, and antiviral treatment on the HIV dynamics.
2. The Mathematical Model
We suggest an HIV infection model with B-cell impairment and distributed time delays as:
where , , and represent, respectively, the concentration of the latently-infected cells, short-lived productively-infected cells, and long-lived productively-infected cells at time t. The term represents the incidence rate, where is a general function. Latently-infected cells die with rate , and they are transmitted to short-lived productively-infected cells with rate . Parameters and are the average number of HIV particles generated in the lifetime of the short-lived productively-infected cells and long-lived productively-infected cells, respectively. Parameter is the natural death rate constant of the long-lived productively-infected cells. The B-cell impairment rate is given by . All previously described parameters are positive constants. Let over the time interval , , be the probabilities that uninfected CD4 T-cells contacted by HIV at time survive time units and become infected at time t. Otherwise, over the time interval and over the time interval represent, respectively, the probabilities that short-lived productively-infected cells and long-lived productively-infected cells produce new immature HIV particles at time , lose time units, and become mature at time t. Here, , are positive constants. The probability distribution function , satisfies and:
where . Denote and , ; thus, .
We need the following Assumptions of the function [61,62,63]:
Assumption 1.
is continuously differentiable, and for all and ,
Assumption 2.
, , and for all and ,
Assumption 3.
for all ,
Assumption 4.
is decreasing with respect to P for all .
The initial conditions of models (8)–(13) are:
where max, and , where is the Banach space of the continuous function mapping the interval into . By the standard theory of functional differential equations [64,65], we know that the system has a unique solution satisfying the initial conditions (14).
Proposition 1.
The proof of Proposition 1 is given in Appendix A.
Lemma 1.
Assume that Assumptions 1–4 are satisfied, then there exists a threshold parameter such that:
- (i)
- if , then the model has only one equilibrium point ; and
- (ii)
- if , then the model has two equilibria and .
The proof of Lemma 1 is given in Appendix A.
Global Stability of Equilibria
Define the function . Clearly, , for and .
Theorem 1.
Assume that and Assumptions 1–4 are satisfied, then the infection-free equilibrium of models (8)–(13) is globally asymptotically stable (G.A.S.).
Theorem 2.
Assume that and Assumptions 1–4 are satisfied, then the endemic equilibrium of models (8)–(13) is G.A.S.
The proofs of Theorems 1 and 2 are given in Appendix A.
3. Numerical Simulations
We conduct numerical simulations for models (8)–(13) with the Crowley–Martin incidence function:
where and are non-negative constants. We note that if then we obtain bilinear incidence, if and , then we get saturated incidence, and if and , then we obtain Holling Type-II incidence. We can easily see that is a continuously differentiable function. Moreover, satisfies the following:
, and for all and . Thus, Assumptions 1 is satisfied.
We have:
for all and . Moreover, for all , then Assumptions 2 is satisfied.
We also have:
Then, Assumptions 3 is satisfied. Finally, we have:
Then, Assumptions 4 is also satisfied. In addition, we take a particular form of the probability distributed function as:
where is the Dirac delta function. When , we have:
We have:
Moreover,
The basic reproduction number is given by:
We let , . In addition, we fix the values of parameters cells mmday, day, day, day, day, cells virusday, virus cells, virus cells, day, day, mmcellsday, mmvirusday, day, and , and the remaining parameters will be changed. We chose the parameters of the model just to perform the numerical simulations. This is because of the difficulty of getting real data from HIV-infected patients; however, if one has real data, then the parameters of the model can be estimated and the validity of the model be established.
3.1. Stability of Equilibria
For this case, we take mmvirus and mmvirus day, day, day. Let us choose the following conditions:
- IC1:
- cells mm, cells mm, cells mm, cells mm, virus mm, cells mm,
- IC2:
- , ,
- IC3:
- , , .
In Figure 1, we want to confirm our global stability results given in Theorems 1 and 2, by showing that from any initial points (any disease stage) taken from a feasible set, the trajectory of the system will tend to one of the two equilibria of the system.
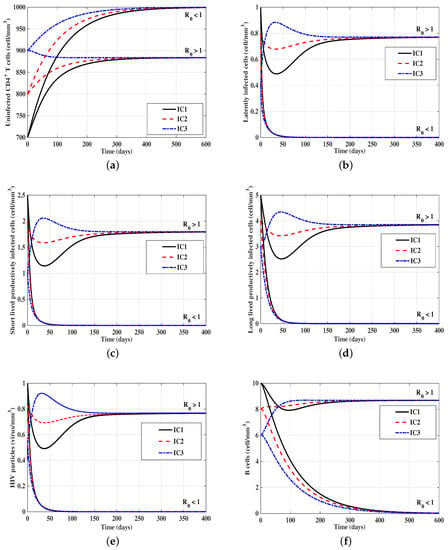
Figure 1.
Plots showing the asymptotic stability of the infection-free equilibrium when () and endemic equilibrium when () of models (15)–(20) with three initial conditions IC1–IC3. For this figure, we take , , , and . (a) Uninfected CD4 T-cells; (b) latently-infected cells; (c) short-lived productively-infected cells; (d) long-lived productively-infected cells; (e) HIV particles; (f) B-cells.
We suggest two different values of to see its effect on the solutions of the model:
- (A)
- mmcells, then . Figure 1 shows that, for all IC1–IC3, the solutions of the model tend to . This means that, is G.A.S., and the HIV is predicted to be completely cleared from the body.
- (B)
- mmcells, then we compute . Figure 1 shows that the solutions of the model converge to the equilibrium for all IC1–IC3. Then, is G.A.S., and a chronic HIV infection is attained. Moreover, we have the following:
- (i)
- is G.A.S. when , and
- (ii)
- is G.A.S. when .
Therefore, changing the parameter will change the stability properties of the equilibria. Since does not depend on the parameter , then has no effect on the stability of equilibria.
3.2. The Effect of the Time Delay on the Stability of Equilibria
In this case, we take , , , and is varied. Moreover, we consider the following initial condition IC4: , , , . Figure 2 shows that as is increased, the concentrations of latently-infected cells, short-lived productively-infected cells, long-lived productively-infected cells, HIV particles, and B-cells are decreased, while the concentration of uninfected CD4 T-cells is increased until they reach the equilibrium point . Moreover, we have the following:
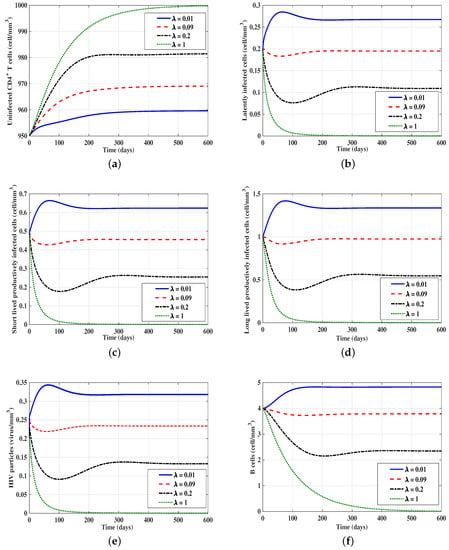
Figure 2.
Effect of the time delay parameter on the solution trajectories of models (15)–(20) with Initial Condition 4 (IC4). In this figure, we take , , and . (a) Uninfected CD4 T-cells; (b) latently-infected cells; (c) short-lived productively-infected cells; (d) long-lived productively-infected cells; (e) HIV particles; (f) B-cells.
- (i)
- is G.A.S. when .
- (ii)
- is G.A.S. when .
3.3. Effect of B-Cell Impairment Parameter on the HIV Dynamics
In this case, we take , , , and is varied. Moreover, we consider the following initial condition IC5: . Figure 3 shows that as is increased, the concentrations of latently-infected cells, short-lived productively-infected cells, long-lived productively infected cells, and HIV particles are increased, while the concentrations of uninfected CD4 T-cells and B-cells are decreased. We note that the parameter has no effect on the stability of equilibria.
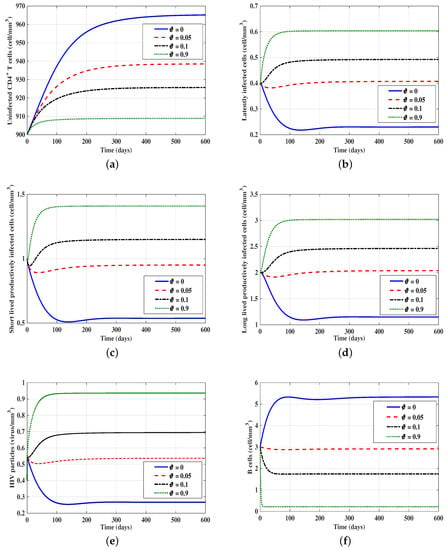
Figure 3.
Effect of the B-cell impairment parameter on the solution trajectories of models (15)–(20) with initial condition IC5. In this figure, we take , , and . (a) The behavior of uninfected CD4 T cells; (b) the behavior of latently-infected cells; (c) the behavior of short-lived productively-infected cells; (d) the behavior of long-lived productively-infected cells; (e) the behavior of HIV particles; (f) the behavior of B-cells.
3.4. Effect of Antiviral Treatment on the HIV Dynamics
Let us introduce the HIV dynamics model under the effect of highly-active antiretroviral therapies (HAART) as:
where is the efficacy of the reverse transcriptase inhibitor drug, while is the efficacy of the protease inhibitor drug. If , then the HAART has no effect, and if , the HIV growth is completely stopped. Let ; consequently, the parameter is given by:
Since the goal is to clear the HIV from the body, then we have to determine the drug efficacies that make for models (21)–(26). Then,
Since, , then for , is G.A.S. where .
We take , , , . Then, , and we have the following:
- (i)
- if , then , and is G.A.S.;
- (ii)
- if , then , and is G.A.S.
We consider the following initial condition IC6: , , to show in Figure 4 the solution trajectories of models (21)–(26) for different values of . Clearly, from the figure, the increasing of will increase the concentration of the uninfected CD4 T-cells and decrease the concentrations of latently-infected cells, short-lived productively-infected cells, long-lived productively-infected cells, HIV particles, and B-cells. One can observe that the time delay has a similar effect as drug efficacy . This gives some impression for developing a new class of treatment to increase the delay period and then suppress the HIV replication.
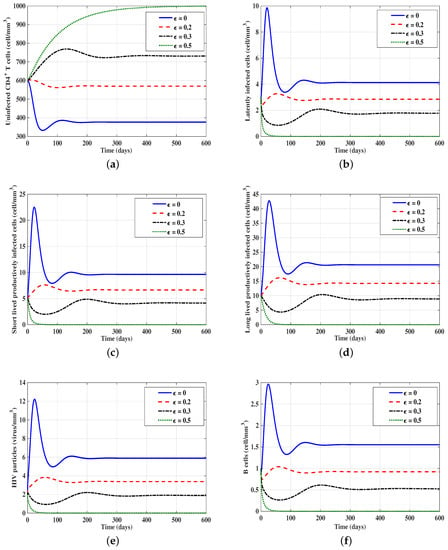
Figure 4.
Effect of the drug efficacy parameter on the solution trajectories of models (21)–(26) with initial condition IC6. For this figure, we used. We take , , and . (a) Uninfected CD4 T-cells; (b) latently-infected cells; (c) short-lived productively-infected cells; (d) long-lived productively-infected cells; (e) HIV particles; (f) B-cells.
In practice, HAART cannot completely eradicate the HIV from the body. Therefore, one can design effective antiviral drugs to reduce the concentration of the HIV particles to a lower level. Let the endemic equilibrium of models (21)–(26) as a function of be given as: . Then, the objective is to design such that:
Let us fix the parameters , , , and . We calculate and using two models:
Therefore, if we apply treatment with efficacy such that , this guarantees that for Model (I), but for Model (II). Therefore, more accurate drug efficacy, which is required to reduce the concentration of the HIV to a lower value is calculated by using Model (II). This shows the importance of considering the effect of immune impairment in the HIV dynamics model.
4. Discussion
In the literature, several mathematical models of HIV infection have considered the impairment of CTL functions. However, it has been reported in several papers that during HIV infection, the B-cell can lose its functions [57,58,59]. This article is an extension of the work discussed by Miao et al. [60], where only the local stability of the equilibria was discussed. We have shown that the solutions of our proposed model are nonnegative and bounded, which ensures the well-posedness of the model. We derived the basic reproduction number , which fully determines the existence and stability of the two equilibria of the model. We investigated the global stability of the two equilibria of the model by using the Lyapunov method and LaSalle’s invariance principle. We proved that: (i) if , then the infection-free equilibrium is globally asymptotically stable, and the HIV is predicted to be completely cleared from the HIV infected individuals; (ii) if , then the endemic equilibrium is globally asymptotically stable, and a chronic HIV infection is attained. We conducted numerical simulations and showed that both the theoretical and numerical results were consistent (see Figure 1). Moreover, we studied the effect of time delays, the impairment of the B-cell functions, and antiviral treatment on the HIV dynamics. The results show that, when the B-cells lose their functions during HIV infection, the number of antibodies produced from the B-cells is decreased, and then, the number of HIV particles is increased (Figure 3). Therefore, HAART is needed to improve the health of the HIV-infected patient. We showed that more accurate drug efficacy, which is required to reduce the concentration of the HIV to a lower value, is calculated by using our proposed HIV dynamics model with immune impairment. In addition, we observed that the time delay had a similar effect as the drug efficacy (see Figure 2 and Figure 4). This gives some impression for developing a new class of treatment to increase the delay period and then suppress the HIV replication.
Looking ahead to further developments, an interesting perspective would be introducing a stochastic internal variable, as in [66], to account for virus mutations. We mention that our HIV dynamics models assumed that HIV particles and cells are equally distributed and ignored their spatial mobility. Recently, many authors have argued that the virus moves freely in the body and follows Fickian diffusion (see, e.g., [67,68,69]). Therefore, it is more reasonable to study reaction-diffusion versions of our model.
Author Contributions
Formal analysis, S.F.A.; Investigation, A.M.E.; Methodology, A.M.E. and A.D.H.; Writing—original draft, S.F.A.
Funding
This project was funded by the Deanship of Scientific Research (DSR), King Abdulaziz University, Jeddah, Saudi Arabia under Grant No. (KEP-MSc-33-130-40).
Acknowledgments
The authors, therefore, acknowledge with thanks DSR for the technical and financial support.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
Proof of Proposition 1.
From Equation (8), we have then , for all . Furthermore, for all , we have:
Thus, by a recursive argument, we get for all . Hence, is positively invariant for models (8)–(13). The non-negativity of the model’s solution implies that where . Next, let:
Then:
where min. Hence, . Since and are all non-negative, then , and for all . Moreover, let . Then:
where min. Hence, , where . The non-negativity of and implies and , where . □
Proof of Lemma 1.
At any equilibrium , we have:
From Equation (A6), we have:
and from Equations (A2) and (A4), we obtain:
Now, from Equations (A3), (A4) and (A8), we get:
and from Equations (A5), (A7) and (A9), we have:
where . By substitution into Equations (A8) and (A9), we obtain:
Let:
Therefore, we can write U as Note that .
From Equations (A4) and (A10), we have:
Observe that is a solution of Equation (A14). Then, from Equations (A7) and (A10)–(A13), we have , , , , and . Then, we get an infection-free equilibrium . Let:
then . Let be such that , i.e.,
which gives:
We can see from Assumptions 1 that:
Moreover,
Assumptions 1 implies that then:
Therefore, if , then and such that . Let us define:
Now, let in Equation (A1), and define . Then, from Assumptions 1, we have and . Assumptions 1 implies that is a strictly decreasing function of U, and then, there exists a unique , such that . Moreover, from Equations (A7) and (A10)–(A12), we have:
Therefore, the endemic equilibrium exists if . □
Proof of Theorem 1.
Construct a Lyapunov function as:
where:
Calculating as:
Simplifying the result, we get:
From Assumptions 4, we have:
for all . Then:
This implies that:
From Assumptions 2, we have:
Therefore, if , then for all . Since , then for all , we have . Moreover, when and . Let and be the largest invariant subset of . The trajectory of models (8)–(13) tends to [64]. All the elements of satisfy and . Then, Equation (13) yields:
Furthermore, from Equation (12), we get:
The non-negativity of I and O implies that for all t. Then, from Equation (10), we have It follows that for all t. Hence, . From LaSalle’s invariance principle (L.I.P.), we derive that if , then is G.A.S. □
Proof of Theorem 2.
Define as:
We note from Equation (A6) that:
Calculating as:
Define as:
We calculate :
Define as:
Calculate as:
Construct a Lyapunov function as:
It follows that:
Now, we have:
From the equilibria conditions of , we have:
We obtain:
Note that:
Moreover, we have:
Then, will be:
Simplifying the result, we obtain:
From Assumptions 2, we have:
In addition, from Assumptions 1, 2 and 4, we have:
which gives:
Then, we get that for all , we have ; moreover, , if and only if , , , , , and . Applying L.I.P., we obtain that if , then is G.A.S. □
References
- Perelson, A.S.; Nelson, P.W. Mathematical Analysis of HIV-1 Dynamics In Vivo. SIAM Rev. 1999, 41, 3–44. [Google Scholar] [CrossRef]
- Nowak, M.A.; Bangham, C.R.M. Population dynamics of immune responses to persistent viruses. Science 1996, 272, 74–79. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Essunger, P.; Cao, Y.; Vesanen, M.; Hurley, A.; Saksela, K.; Markowitz, M.; Ho, D.D. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature 1997, 387, 188–191. [Google Scholar] [CrossRef] [PubMed]
- Nowak, M.A.; May, R.M. Virus Dynamics: Mathematical Principles of Immunology and Virology; Oxford University Press: Oxford, UK, 2000. [Google Scholar]
- Wodarz, D.; Nowak, M.A. Mathematical models of HIV pathogenesis and treatment. BioEssays 2002, 24, 1178–1187. [Google Scholar] [CrossRef] [PubMed]
- Graw, F.; Perelson, A.S. Modeling Viral Spread. Annu. Rev. Virol. 2016, 3, 555–572. [Google Scholar] [CrossRef] [PubMed]
- De Leenheer, P.; Smith, H.L. Virus dynamics: A global analysis. SIAM J. Appl. Math. 2003, 63, 1313–1327. [Google Scholar]
- Wong, J.K.; Hezareh, M.; Gunthard, H.F.; Havlir, D.V.; Ignacio, C.C.; Spina, C.A.; Richman, D.D. Recovery of replication-competent HIV despite prolonged suppression of plasma viremia. Science 1997, 278, 1291–1295. [Google Scholar] [CrossRef] [PubMed]
- Callaway, D.S.; Perelson, A.S. HIV-1 infection and low steady state viral loads. Bull. Math. Biol. 2002, 64, 29–64. [Google Scholar] [CrossRef] [PubMed]
- Perelson, A.S.; Kirschner, D.E.; Boer, R.D. Dynamics of HIV infection of CD4+ T cells. Math. Biosci. 1993, 114, 81–125. [Google Scholar] [CrossRef]
- Korobeinikov, A. Global properties of basic virus dynamics models. Bull. Math. Biol. 2004, 66, 879–883. [Google Scholar] [CrossRef]
- Elaiw, A.M. Global properties of a class of HIV models. Nonlinear Anal. Real World Appl. 2010, 11, 2253–2263. [Google Scholar] [CrossRef]
- Elaiw, A.M. Global properties of a class of virus infection models with multitarget cells. Nonlinear Dyn. 2012, 69, 423–435. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Azoz, S.A. Global properties of a class of HIV infection models with Beddington-DeAngelis functional response. Math. Methods Appl. Sci. 2013, 36, 383–394. [Google Scholar] [CrossRef]
- Hlavacek, W.S.; Stilianakis, N.I.; Perelson, A.S. Influence of follicular dendritic cells on HIV dynamics. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2000, 355, 1051–1058. [Google Scholar] [CrossRef] [PubMed]
- Rong, L.; Perelson, A.S. Modeling HIV persistence, the latent reservoir, and viral blips. J. Theor. Biol. 2009, 260, 308–331. [Google Scholar] [CrossRef] [PubMed]
- Dixit, N.M.; Markowitz, M.; Ho, D.D.; Perelson, A.S. Estimates of intracellular delay and average drug efficacy from viral load data of HIV-infected individuals under antiretroviral therapy. Antivir. Ther. 2004, 9, 237–246. [Google Scholar]
- Sahani, S.K.; Yashi. Effects of eclipse phase and delay on the dynamics of HIV infection. J. Biol. Syst. 2018, 26, 421–454. [Google Scholar] [CrossRef]
- Herz, A.; Bonhoeffer, S.; Anderson, R.M.; May, R.M.; Nowak, M.A. Viral dynamics in vivo: Limitations on estimates of intracellular delay and virus decay. Proc. Natl. Acad. Sci. USA 1996, 93, 7247–7251. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.W.; Murray, J.D.; Perelson, A.S. A model of HIV-1 pathogenesis that includes an intracellular delay. Math. Biosci. 2000, 163, 201–215. [Google Scholar] [CrossRef]
- Xu, R. Global stability of an HIV-1 infection model with saturation infection and intracellular delay. J. Math. Anal. Appl. 2011, 375, 75–81. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Stability of a general adaptive immunity virus dynamics model with multi-stages of infected cells and two routes of infection. Math. Meth. Appl. Sci. 2019. [Google Scholar] [CrossRef]
- Xu, R. Global dynamics of an HIV-1 infection model with distributed intracellular delays. Comput. Math. Appl. 2011, 61, 2799–2805. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Hassanien, I.A.; Azoz, S.A. Global stability of HIV infection models with intracellular delays. J. Korean Math. Soc. 2012, 49, 779–794. [Google Scholar] [CrossRef]
- Hattaf, K.; Yousfi, N.; Tridane, A. Stability analysis of a virus dynamics model with generalincidence rate and two delays. Appl. Math. Comput. 2013, 221, 514–521. [Google Scholar]
- Elaiw, A.M.; Almuallem, N.A. Global dynamics of delay-distributed HIV infection models with differential drug efficacy in cocirculating target cells. Math. Methods Appl. Sci. 2016, 39, 4–31. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Almuallem, N.A. Global properties of delayed-HIV dynamics models with differential drug efficacy in cocirculating target cells. Appl. Math. Comput. 2015, 265, 1067–1089. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Raezah, A.A. Stability of general virus dynamics models with both cellular and viral infections and delays. Math. Methods Appl. Sci. 2017, 40, 5863–5880. [Google Scholar] [CrossRef]
- Li, B.; Chen, Y.; Lu, X.; Liu, S. A delayed HIV-1 model with virus waning term. Math. Biosci. Eng. 2016, 13, 135–157. [Google Scholar] [CrossRef]
- Elaiw, A.M. Global dynamics of an HIV infection model with two classes of target cells and distributed delays. Discret. Dyn. Nat. Soc. 2012, 2012, 253703. [Google Scholar] [CrossRef]
- Lv, Y.; Hu, Z.; Liao, F. The stability and Hopf bifurcation for an HIV model with saturated infection rate and double delays. Int. J. Biomath. 2018, 11, 1850040. [Google Scholar] [CrossRef]
- Alshorman, A.; Wang, X.; Meyer, M.J.; Rong, L. Analysis of HIV models with two time delays. J. Biol. Dyn. 2017, 2, 40–64. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Zhang, J.-F. Dynamics of two time delays differential equation model to HIV latent infection. Phys. A 2019, 514, 384–395. [Google Scholar] [CrossRef]
- Shu, H.; Wang, L.; Watmough, J. Global stability of a nonlinear viral infection model with infinitely distributed intracellular delays and CTL imune responses. SIAM J. Appl. Math. 2013, 73, 1280–1302. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Abukwaik, R.M.; Alzahrani, E.O. Global properties of a cell mediated immunity in HIV infection model with two classes of target cells and distributed delays. Int. J. Biomath. 2014, 7, 1450055. [Google Scholar] [CrossRef]
- Wang, J.; Qin, C.; Chen, Y.; Wang, X. Hopf bifurcation in a CTL-inclusive HIV-1 infection model with two time delays. Math. Biosci. Eng. 2019, 16, 2587–2612. [Google Scholar] [PubMed]
- Lydyard, P.; Whelan, A.; Fanger, M. BIOS Instant Notes in Immunology; Taylor & Francis e-Library: London, UK, 2005. [Google Scholar]
- Murase, A.; Sasaki, T.; Kajiwara, T. Stability analysis of pathogen-immune interaction dynamics. J. Math. Biol. 2005, 51, 247–267. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Zou, D. Global stability of in-host viral models with humoral immunity and intracellular delays. Appl. Math. Model. 2012, 36, 1313–1322. [Google Scholar] [CrossRef]
- Wang, T.; Hu, Z.; Liao, F. Stability and Hopf bifurcation for a virus infection model with delayed humoral immunity response. J. Math. Anal. Appl. 2014, 411, 63–74. [Google Scholar] [CrossRef]
- Wang, T.; Hu, Z.; Liao, F.; Ma, W. Global stability analysis for delayed virus infection model with general incidence rate and humoral immunity. Math. Comput. Simul. 2013, 89, 13–22. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Stability of a general delay-distributed virus dynamics model with multi-staged infected progression and immune response. Math. Methods Appl. Sci. 2017, 40, 699–719. [Google Scholar] [CrossRef]
- Hobiny, A.D.; Elaiw, A.M.; Almatrafi, A. Stability of delayed pathogen dynamics models with latency and two routes of infection. Adv. Differ. Equ. 2018, 276. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Stability of an adaptive immunity pathogen dynamics model with latency and multiple delays. Math. Methods Appl. Sci. 2018, 41, 6645–6672. [Google Scholar] [CrossRef]
- Lin, J.; Xu, R.; Tian, X. Threshold dynamics of an HIV-1 virus model with both virus-to-cell and cell-to-cell transmissions, intracellular delay, and humoral immunity. Appl. Math. Comput. 2017, 315, 516–530. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Elnahary, E.K.; Raezah, A.A. Effect of cellular reservoirs and delays on the global dynamics of HIV. Adv. Differ. Equ. 2018, 2018, 85. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Elnahary, E.K. Analysis of general humoral immunity HIV dynamics model with HAART and distributed delays. Mathematics 2019, 7, 157. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Alshaikh, M.A. Stability analysis of a general discrete-time pathogen infection model with humoral immunity. J. Differ. Equ. Appl. 2019. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Almatrafi, A.; Hobiny, A.D.; Hattaf, K. Global properties of a general latent pathogen dynamics model with delayed pathogenic and cellular infections. Discret. Dyn. Nat. Soc. 2019, 2019, 9585497. [Google Scholar] [CrossRef]
- Miao, H.; Teng, Z.; Kang, C.; Muhammadhaji, A. Stability analysis of a virus infection model with humoral immunity response and two time delays. Math. Methods Appl. Sci. 2016, 39, 3434–3449. [Google Scholar] [CrossRef]
- Brrow, P.; Lewicki, H.; Wei, X.; Horwitz, M.S.; Peffer, N.; Meyers, H.; Nelson, J.A.; Gairin, J.E.; Beatrice, H.H.; Oldstone, M.B.A.; et al. Antiviral pressure exerted by HIV specific cytotoxic t lymphocytes (CTLs) during primary infection demonstrated by rapid selection of CTL escape virus. Nat. Med. 1997, 3, 205–211. [Google Scholar] [CrossRef]
- Goulder, P.J.R.; Phillips, R.E.; Colbert, R.A.; McAdam, S.; Ogg, G.; Nowak, M.A.; Giangrande, P.; Luzzi, G.; Morgan, B.; Edwards, A.; et al. Late escape from an immunodominant cytotoxic t-lymphocyte response associated with progression to AIDS. Nat. Med. 1997, 3, 212–217. [Google Scholar] [CrossRef]
- Hu, Z.; Zhang, J.; Wang, H.; Ma, W.; Liao, F. Dynamics analysis of a delayed viral infection model with logistic growth and immune impairment. Appl. Math. Model. 2014, 38, 524–534. [Google Scholar] [CrossRef]
- Regoes, R.; Wodarz, D.; Nowak, M.A. Virus dynamics: the effect to target cell limitation and immune responses on virus evolution. J. Theor. Biol. 1998, 191, 451–462. [Google Scholar] [CrossRef] [PubMed]
- Wang, S.; Song, X.; Ge, Z. Dynamics analysis of a delayed viral infection model with immune impairment. Appl. Math. Model. 2011, 35, 4877–4885. [Google Scholar] [CrossRef]
- Elaiw, A.M.; Raezah, A.A.; Azoz, S.A. Stability of delayed HIV dynamics models with two latent reservoirs and immune impairment. Adv. Differ. Equ. 2018, 2018, 414. [Google Scholar] [CrossRef]
- De Milito, A. B lymphocyte dysfunctions in HIV Infection. Curr. HIV Res. 2004, 2, 11–21. [Google Scholar] [CrossRef] [PubMed]
- Amu, S.; Ruffin, N.; Rethi, B.; Chiodi, F. Impairment of B-cell functions during HIV-1 infection. AIDS 2013, 27, 2323–2334. [Google Scholar] [CrossRef] [PubMed]
- Chiodi, F.; Scarlatti, G. HIV-Induced damage of B-cells and production of HIV neutralizing antibodies. Front. Immunol. 2018, 9, 297. [Google Scholar] [CrossRef] [PubMed]
- Miao, H.; Abdurahman, X.; Teng, Z.; Zhang, L. Dynamical analysis of a delayed reaction-diffusion virus infection model with logistic growth and humoral immune impairment. Chaos Solitons Fractals 2018, 110, 280–291. [Google Scholar] [CrossRef]
- Huang, G.; Takeuchi, Y.; Ma, W. Lyapunov functionals for delay differential equations model of viral infections. SIAM J. Appl. Math. 2010, 70, 2693–2708. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Global properties of nonlinear humoral immunity viral infection models. Int. J. Biomath. 2015, 8, 1550058. [Google Scholar] [CrossRef]
- Elaiw, A.M.; AlShamrani, N.H. Global stability of humoral immunity virus dynamics models with nonlinear infection rate and removal. Nonlinear Anal. Real World Appl. 2015, 26, 161–190. [Google Scholar] [CrossRef]
- Hale, J.K.; Lunel, S.V. Introduction to Functional Differential Equations; Springer: New York, NY, USA, 1993. [Google Scholar]
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Gibelli, L.; Elaiw, A.; Alghamdi, M.A.; Althiabi, A.M. Heterogeneous population dynamics of active particles: Progression, mutations, and selection dynamics. Math. Models Methods Appl. Sci. 2017, 27, 617–640. [Google Scholar] [CrossRef]
- Xu, Z.; Xu, Y. Stability of a CD4+ T-cell viral infection model with diffusion. Int. J. Biomath. 2018, 11, 1850071. [Google Scholar] [CrossRef]
- McCluskey, C.C.; Yang, Y. Global stability of a diffusive virus dynamics model with general incidence function and time delay. Nonlinear Anal. Real World Appl. 2015, 25, 64–78. [Google Scholar] [CrossRef]
- AlAgha, A.D.; Elaiw, M.A. Stability of a general reaction-diffusion HIV-1 dynamics model with humoral immunity. Eur. Phys. J. Plus 2019, 134, 390. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).