Optimal Randomness in Swarm-Based Search
Abstract
1. Introduction
2. Cuckoo Search Algorithm
2.1. Lévy Flights Random Walk
2.2. Local Random Walk
| Algorithm 1 Pseudo code of the standard CS algorithm |
| Input: Population size , fraction probability , dimensionality D, the maximum number of function evaluations Max_FEs, iteration number , objective function . Output: The best solution.
|
3. Randomness-Enhanced CS Algorithms
3.1. Commonly Used Heavy-Tailed Distributions
3.2. Improving CS with Different Heavy-Tailed Probability Distributions
4. Experimental Results
4.1. Experimental Setup
4.2. Parameter Tuning
4.3. Performance Evaluation of Randomness-Enhanced Cs Algorithms
4.4. Scalability Study
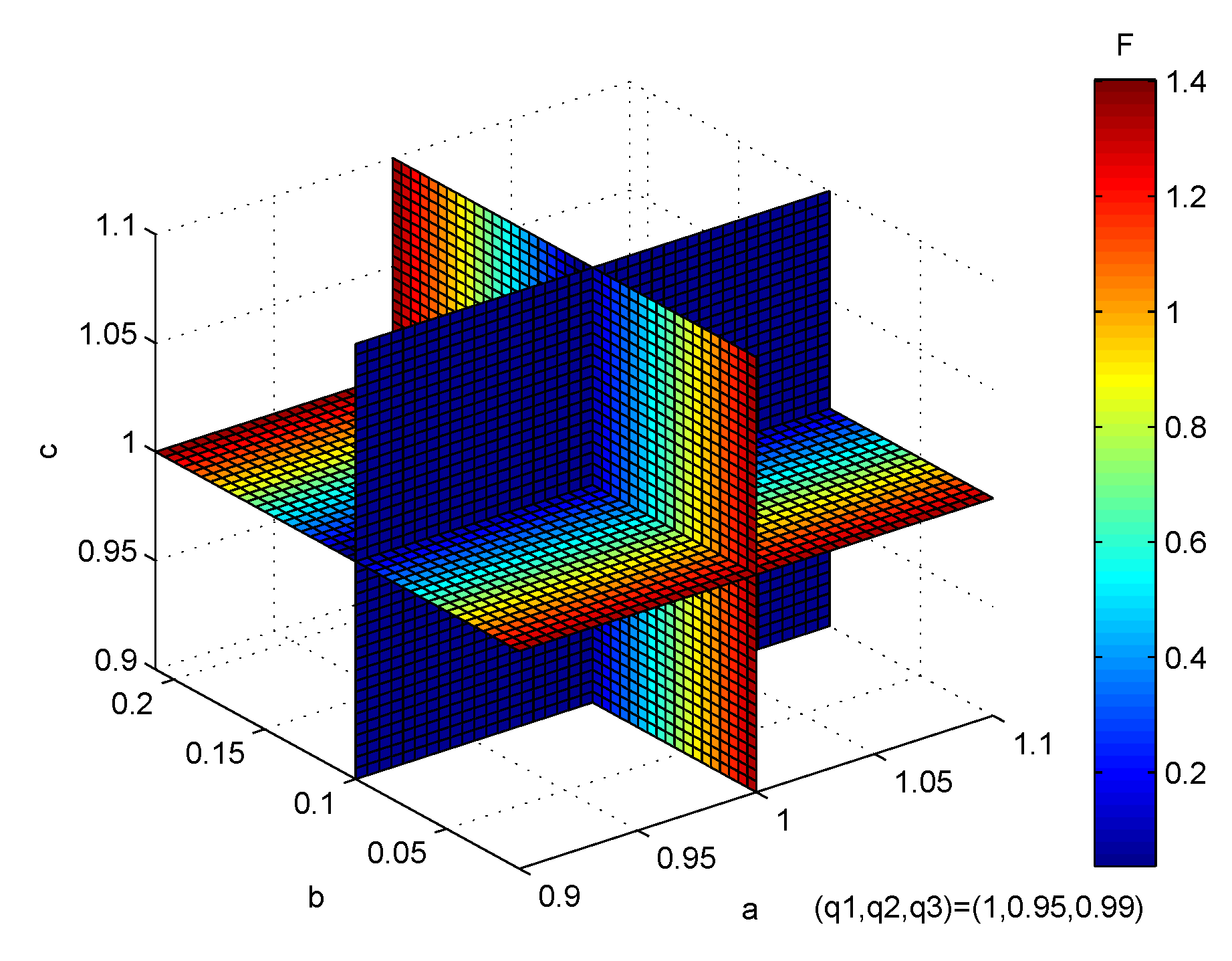
4.5. Application to Parameter Identification of Fractional-Order Chaotic Systems
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
- : Sphere’s Function.
- : Rosenbrock’s Function.
- : Ackley’s Function.
- : Griewank’s Function.
- : Rastrigin’s Function.
- : Generalized Schwefel’s Problem 2.26.
- : Salomon’s Function.
- : Whitely’s Function.
- : Generalized Penalized Function 1.
- : Generalized Penalized Function 2.
- : Shifted Sphere Function.
- : Shifted Schwefel’s Problem 1.2.
- : Shifted Rotated High Conditioned Elliptic Function.
- : Shifted Schwefel’s Problem 1.2 with Noise in Fitness.
- : Schwefel’s Problem 2.6 with global Optimum on Bounds.
- : Shifted Rosenbrock’s Function.
- : Shifted Rotated Griewank’s Function without Bounds.
- : Shifted Rotated Ackley’s Function with Global Optimum on Bounds.
- : Shifted Rastrigin’s Function.
- : Shifted Rotated Rastrigin’s Function.
| No. | Formula | Range | Optimum |
|---|---|---|---|
| 1 | 0 | ||
| 2 | 0 | ||
| 3 | 0 | ||
| 4 | 0 | ||
| 5 | 0 | ||
| 6 | 0 | ||
| 7 | 0 | ||
| 8 | 0 | ||
| 9 | , | 0 | |
| where and | |||
| 10 | 0 | ||
| 11 | , where , o: the shifted global optimum, | 0 | |
| 12 | , where , o: the shifted global optimum, | 0 | |
| 13 | , where , o: the shifted global optimum, M: orthogonal matrix, | 0 | |
| 14 | , where , o: the shifted global optimum, | 0 | |
| 15 | , where A is a matrix, are integer random numbers in the range , , | 0 | |
| is the ith row of A, , is a matrix, are random number in the range and | |||
| 16 | , where , o: the shifted global optimum, | 0 | |
| 17 | , where , o: the shifted global optimum, , | - | 0 |
| M: linear transformation matrix, condition number = 3, // initialize population in and no bounds for x | |||
| 18 | , where , | [ | 0 |
| o: the shifted global optimum, M: linear transformation matrix, condition number = 100, | |||
| 19 | , where , o: the shifted global optimum, | [ | 0 |
| 20 | , where , o: the shifted global optimum, | [ | 0 |
| M: linear transformation matrix, condition number = 2, , |
References
- Yang, X.S. Nature-Inspired Metaheuristic Algorithms; Luniver Press: Beckington, UK, 2010. [Google Scholar]
- Anandakumar, H.; Umamaheswari, K. A bio-inspired swarm intelligence technique for social aware cognitive radio handovers. Comput. Electr. Eng. 2018, 71, 925–937. [Google Scholar] [CrossRef]
- Brezočnik, L.; Fister, I.; Podgorelec, V. Swarm intelligence algorithms for feature selection: A review. Appl. Sci. 2018, 8, 1521. [Google Scholar] [CrossRef]
- Zhao, X.; Wang, C.; Su, J.; Wang, J. Research and application based on the swarm intelligence algorithm and artificial intelligence for wind farm decision system. Renew. Energy 2019, 134, 681–697. [Google Scholar] [CrossRef]
- Dulebenets, M.A. A novel memetic algorithm with a deterministic parameter control for efficient berth scheduling at marine container terminals. Marit. Bus. Rev. 2017, 2, 302–330. [Google Scholar] [CrossRef]
- Karaboga, D.; Basturk, B. A powerful and efficient algorithm for numerical function optimization: Artificial bee colony (ABC) algorithm. J. Glob. Optim. 2007, 39, 459–471. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the Nature & Biologically Inspired Computing, Coimbatore, India, 9–11 December 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 210–214. [Google Scholar]
- Yang, X.S. Firefly algorithms for multimodal optimization. In Proceedings of the International Symposium on Stochastic Algorithms, Sapporo, Japan, 26–28 October 2009; Springer: Berlin/Heidelberg, Germany, 2009; pp. 169–178. [Google Scholar]
- Kennedy, J.; Eberhart, R. Particle swarm optimization (PSO). In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; pp. 1942–1948. [Google Scholar]
- Zheng, H.; Zhou, Y. A novel cuckoo search optimization algorithm based on Gauss distribution. J. Comput. Inf. Syst. 2012, 8, 4193–4200. [Google Scholar]
- Wang, L.; Zhong, Y.; Yin, Y. Nearest neighbour cuckoo search algorithm with probabilistic mutation. Appl. Soft Comput. 2016, 49, 498–509. [Google Scholar] [CrossRef]
- Rakhshani, H.; Rahati, A. Snap-drift cuckoo search: A novel cuckoo search optimization algorithm. Appl. Soft Comput. 2017, 52, 771–794. [Google Scholar] [CrossRef]
- Cui, Z.; Sun, B.; Wang, G.; Xue, Y.; Chen, J. A novel oriented cuckoo search algorithm to improve DV-Hop performance for cyber–physical systems. J. Parallel Distrib. Comput. 2017, 103, 42–52. [Google Scholar] [CrossRef]
- Salgotra, R.; Singh, U.; Saha, S. New cuckoo search algorithms with enhanced exploration and exploitation properties. Expert Syst. Appl. 2018, 95, 384–420. [Google Scholar] [CrossRef]
- Richer, T.J.; Blackwell, T.M. The Lévy particle swarm. In Proceedings of the 2006 IEEE International Conference on Evolutionary Computation, Vancouver, BC, Canada, 16–21 July 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 808–815. [Google Scholar]
- Pavlyukevich, I. Lévy flights, non-local search and simulated annealing. J. Comput. Phys. 2007, 226, 1830–1844. [Google Scholar] [CrossRef]
- Yang, X.S. Nature-Inspired Optimization Algorithms; Elsevier: Amsterdam, The Netherlands, 2014. [Google Scholar]
- Yang, X.S.; Deb, S. Engineering optimisation by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010, 1, 330–343. [Google Scholar] [CrossRef]
- Foss, S.; Korshunov, D.; Zachary, S. An Introduction to Heavy-Tailed and Subexponential Distributions; Springer: Berlin/Heidelberg, Germany, 2011; Volume 6. [Google Scholar]
- Kozubowski, T.J.; Rachev, S.T. Univariate geometric stable laws. J. Comput. Anal. Appl. 1999, 1, 177–217. [Google Scholar]
- Noman, N.; Iba, H. Accelerating differential evolution using an adaptive local search. IEEE Trans. Evol. Comput. 2008, 12, 107–125. [Google Scholar] [CrossRef]
- Suganthan, P.N.; Hansen, N.; Liang, J.J.; Deb, K.; Chen, Y.P.; Auger, A.; Tiwari, S. Problem definitions and evaluation criteria for the CEC 2005 special session on real-parameter optimization. KanGAL Rep. 2005, 2005005, 2005. [Google Scholar]
- Gao, F.; Fei, F.X.; Lee, X.J.; Tong, H.Q.; Deng, Y.F.; Zhao, H.L. Inversion mechanism with functional extrema model for identification incommensurate and hyper fractional chaos via differential evolution. Expert Syst. Appl. 2014, 41, 1915–1927. [Google Scholar] [CrossRef]
- Chen, W.C. Nonlinear dynamics and chaos in a fractional-order financial system. Chaos Solitons Fractals 2008, 36, 1305–1314. [Google Scholar] [CrossRef]
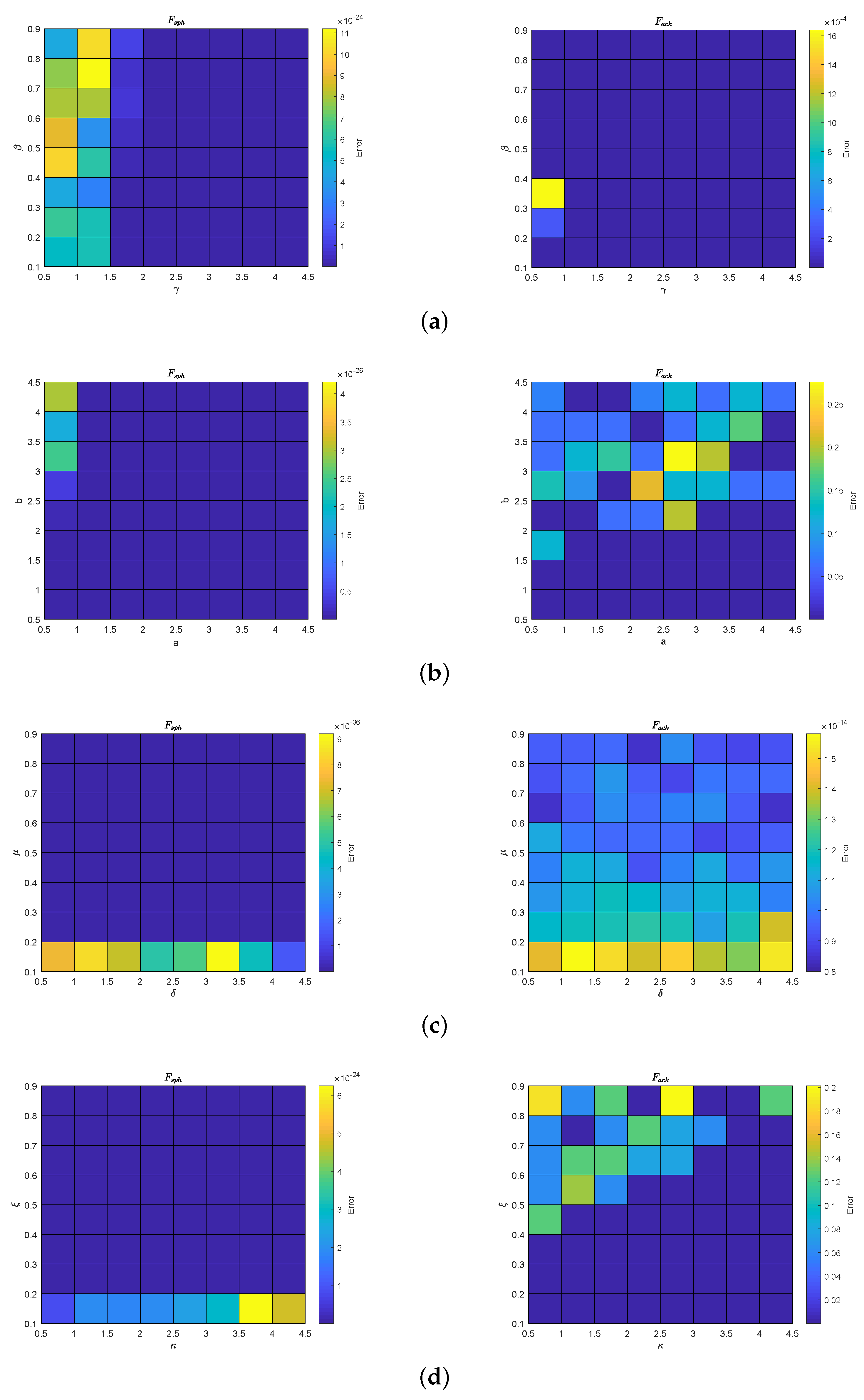



| Distribution | Algorithm | Parameters |
|---|---|---|
| Mittag-Leffler distribution | CSML | , |
| Pareto distribution | CSP | , |
| Cauchy distribution | CSC | , |
| Weibull distribution | CSW | , |
| Fun | CS | CSML | CSP | CSC | CSW |
|---|---|---|---|---|---|
| 9.58 | 4.90 | 4.74 | 1.17 | 4.40 | |
| 1.20 | 5.22 | 3.10 | 2.74 | 8.62 | |
| 7.70 | 1.06 | 1.07 | 9.56 | 8.28 | |
| 7.11 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 2.32 | 1.38 | 1.88 | 1.49 | 8.34 | |
| 1.57 | 5.37 | 1.32 | 4.80 | 3.56 | |
| 3.76 | 2.96 | 3.00 | 2.84 | 2.20 | |
| 3.73 | 2.00 | 2.49 | 2.27 | 1.93 | |
| 2.07 | 1.57 | 1.57 | 2.07 | 1.57 | |
| 4.82 | 1.35 | 1.35 | 1.35 | 1.35 | |
| 6.48 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 1.05 | 1.10 | 2.77 | 1.40 | 1.23 | |
| 2.17 | 3.04 | 2.99 | 3.25 | 3.61 | |
| 1.79 | 4.98 | 3.58 | 4.02 | 5.51 | |
| 3.17 | 2.44 | 1.98 | 2.11 | 1.94 | |
| 2.78 | 1.57 | 9.91 | 1.23 | 1.59 | |
| 1.34 | 2.22 | 5.79 | 3.73 | 2.49 | |
| 2.09 | 2.09 | 2.09 | 2.09 | 2.09 | |
| 2.84 | 1.30 | 2.74 | 1.28 | 6.81 | |
| 1.69 | 1.21 | 1.31 | 1.18 | 1.03 | |
| - | 17/1/2 | 17/1/2 | 16/2/2 | 16/1/3 | |
| p-value | - | 8.97 | 1.00 | 1.00 | 1.87 |
| Avg. rank | 4.35 | 2.78 | 2.88 | 2.58 | 2.43 |
| Fun | CS | CSML | CSP | CSC | CSW |
|---|---|---|---|---|---|
| 4.87 | 3.39 | 4.21 | 2.04 | 2.48 | |
| 9.63 | 3.02 | 1.12 | 1.75 | 2.97 | |
| 4.16 | 2.50 | 4.37 | 4.44 | 4.44 | |
| 3.44 | 0.00 | 2.22 | 2.07 | 1.44 | |
| 3.00 | 6.93 | 2.25 | 2.95 | 2.26 | |
| 6.72 | 3.80 | 1.38 | 6.91 | 1.27 | |
| 1.04 | 4.78 | 9.99 | 9.99 | 9.99 | |
| 2.40 | 9.89 | 1.54 | 1.01 | 5.72 | |
| 1.96 | 2.01 | 4.71 | 4.71 | 4.71 | |
| 4.86 | 9.17 | 1.35 | 1.35 | 1.35 | |
| 4.13 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 8.16 | 3.73 | 1.33 | 4.54 | 1.51 | |
| 2.08 | 1.70 | 7.20 | 6.78 | 8.31 | |
| 1.01 | 1.96 | 1.46 | 1.20 | 4.82 | |
| 9.30 | 6.82 | 6.13 | 5.11 | 9.27 | |
| 9.78 | 4.11 | 6.38 | 3.48 | 2.69 | |
| 5.33 | 1.07 | 5.91 | 4.72 | 4.39 | |
| 2.04 | 2.11 | 2.04 | 2.04 | 2.03 | |
| 2.75 | 7.37 | 1.80 | 1.79 | 2.35 | |
| 1.99 | 2.89 | 1.63 | 1.59 | 1.43 | |
| - | 7/0/13 | 17/1/2 | 18/1/1 | 19/1/0 | |
| Avg. rank | 4.10 | 4.28 | 2.28 | 2.25 | 2.10 |
| Fun | CS | CSML | CSP | CSC | CSW |
|---|---|---|---|---|---|
| 3.79 | 3.47 | 7.41 | 5.75 | 2.73 | |
| 4.22 | 3.07 | 2.82 | 2.99 | 3.41 | |
| 2.85 | 2.43 | 2.05 | 2.05 | 7.40 | |
| 1.93 | 0.00 | 0.00 | 0.00 | 0.00 | |
| 8.44 | 6.80 | 8.69 | 7.54 | 7.37 | |
| 4.87 | 4.14 | 6.05 | 4.38 | 2.38 | |
| 6.69 | 4.68 | 4.87 | 4.22 | 3.68 | |
| 1.36 | 9.58 | 1.21 | 1.09 | 1.13 | |
| 8.13 | 6.74 | 1.04 | 7.21 | 1.47 | |
| 3.25 | 1.02 | 1.57 | 1.44 | 2.01 | |
| 1.40 | 0.00 | 0.00 | 0.00 | 3.57 | |
| 2.34 | 3.57 | 1.86 | 4.49 | 8.59 | |
| 8.53 | 1.66 | 1.47 | 1.83 | 1.85 | |
| 2.72 | 1.99 | 1.72 | 1.91 | 1.88 | |
| 1.06 | 6.95 | 6.49 | 6.65 | 6.30 | |
| 6.38 | 3.90 | 4.15 | 3.63 | 4.43 | |
| 1.30 | 1.81 | 3.56 | 2.43 | 3.64 | |
| 2.11 | 2.11 | 2.11 | 2.11 | 2.11 | |
| 1.24 | 7.04 | 1.27 | 7.47 | 6.50 | |
| 3.87 | 2.87 | 3.13 | 2.85 | 2.69 | |
| - | 16/1/3 | 14/1/5 | 16/1/3 | 16/1/3 | |
| Avg. rank | 4.10 | 2.58 | 2.70 | 2.55 | 3.08 |
| Method | CS | CSML | CSP | CSC | CSW |
|---|---|---|---|---|---|
| a | 0.999999825481796 | 0.999999979386471 | 1.000000001165006 | 0.999999930875086 | 0.999999994619958 |
| 1.75 | 2.28 | 1.17 | 6.91 | 5.38 | |
| b | 0.100000078306700 | 0.100000006492360 | 0.099999999732393 | 0.100000038684769 | 0.100000001325757 |
| 7.83 | 1.12 | 2.68 | 3.87 | 2.06 | |
| c | 1.000000126069434 | 0.999999979588057 | 0.999999995606294 | 0.999999876500337 | 0.999999979353103 |
| 1.26 | 4.61 | 4.39 | 1.23 | 1.33 | |
| 1.07 | 4.75 | 7.46 | 1.89 | 1.03 | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wei, J.; Chen, Y.; Yu, Y.; Chen, Y. Optimal Randomness in Swarm-Based Search. Mathematics 2019, 7, 828. https://doi.org/10.3390/math7090828
Wei J, Chen Y, Yu Y, Chen Y. Optimal Randomness in Swarm-Based Search. Mathematics. 2019; 7(9):828. https://doi.org/10.3390/math7090828
Chicago/Turabian StyleWei, Jiamin, YangQuan Chen, Yongguang Yu, and Yuquan Chen. 2019. "Optimal Randomness in Swarm-Based Search" Mathematics 7, no. 9: 828. https://doi.org/10.3390/math7090828
APA StyleWei, J., Chen, Y., Yu, Y., & Chen, Y. (2019). Optimal Randomness in Swarm-Based Search. Mathematics, 7(9), 828. https://doi.org/10.3390/math7090828







