Abstract
In this paper, we define the notion of a probability function on a poset which is similar to the probability function discussed on d-algebras, and obtain three probability functions on posets. Moreover, we define a probability realizer of a poset, and we provide some examples to describe its role for the standard probability function. We apply the notion of a probability function to the ordered plane and obtain three probability functions on it.
1. Introduction
There has been some research between posets and algebraic structures. Neggers [1] proved that there is a natural isomorphism between the category of pogroupoids and the category of posets. Neggers and Kim [2] showed that a poset is -free if and only if its associated pogroupoid is modular*. Neggers and Kim [3] introduced the notion of d-algebras. It is a kind of generalization of -algebras to which they discussed some relations between d-algebras and -algebras, as well as some relations between d-algebras and oriented digraphs. Cha et al. [4] introduced the notions of a trend and probability functions on d-algebras. They obtained an equivalent condition defining a trend with condition on a standard -algebra. Loof et al. [5] discussed mutual rank probabilities in partially ordered sets. Baets et al. [6] characterized the transitivity of the mutual rank probability relation of a poset, and Lerche et al. [7] evaluated ranking probabilities for partial orders based on random linear extensions.
In this paper, we define a probability function on a poset. The idea of a probability function on a poset came from [4], and we obtained some probability functions on a poset. We defined a probability realizer on a poset, and found some examples for probability realizers of posets for the standard probability function . Moreover, we applied the notion of a probability function to the ordered plane (order geometry), and found three probability functions acting on it. Some comments have been suggested for further research.
2. Preliminaries
Some definitions and terminologies will be recalled for partially ordered sets which are necessary for reading this paper.
An ordered pair is called a partially ordered set if ≤ is a partial order, i.e., reflexive, anti-symmetric, and transitive, on the set X. A poset is said to be a chain if every two distinct elements of X are comparable, and we denote it by when the cardinality of X is equal to n. A poset is said to be an anti-chain if every two distinct elements of X are incomparable, and we denote it by when the cardinality of X is equal to n. Given two posets X and Y, a poset Z is said to be an ordinal sum of X and Y if in Z, then either and or in X, or in Y. A graph Z can be realized by placing the Hasse diagram of Y above the Hasse diagram of X, and by drawing line segments from the maximal elements of X to all the minimal elements of Y. We denote it by . A chain is said to be a linear extension of a poset if implies . A family of linear extensions of a poset is said to be a realizer of if can be realized as the intersection of R, but not as the intersection of fewer than k linear extensions. For details we refer to [8].
A non-empty set X with a constant 0 and a binary operation “*” is said to be a d-algebra [3] if it satisfies: (i) , (ii) , and (iii) and imply for all .
A mapping is said to be a trend [4] on a d-algebra if it satisfies: for any ,
- (a)
- implies ,
- (b)
- implies .
A trend is said to be a probability function [4] on a d-algebra if it satisfies: for any ,
- (c)
- implies .
It is of course possible to consider other conditions to build (different) notions of trends and probability functions and to compare the resulting classes with those obtained here. In fact, we will actually do so below. As an example of the situation above, let and let if and only if , and otherwise. Thus (a) holds if . If , then implies while means , so that (c) does not apply in that case. Condition (b) holds since implies , and yields since in that case. The groupoid is certainly a d-algebra.
3. Probability Functions on Posets
In this section we discuss probability functions on posets. We define the notion of a probability function on a poset which is a little bit different from the probability function discussed in d-algebras. Given a poset P, a map is called a probability function on P if:
- (I)
- ,
- (II)
- implies ,
- (III)
- implies ,
- (IV)
- implies ,
for any .
Theorem 1.
If π is a probability function on a poset , then:
- (IV)′
- implies ,
for any .
Proof.
Let and let . Case (i): . By (I), we have and . Hence . Case (ii): . By (III), we have . We have 3 subcases:
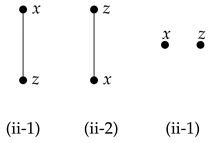

Subcase (ii-1): . By (II), we have . Now, implies and hence . Hence . Subcase (ii-2): . By (III), , since . It follows that . Hence . Subcase (ii-3): , i.e., z and x are incomparable. Subcase(ii-3-a): , i.e., 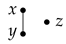 . Then . Subcase (ii-3-b): . Since , we have
. Then . Subcase (ii-3-b): . Since , we have 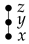 , i.e., . This is a contradiction, since . Subcase(ii-3-c): . Since , by (IV), we have . Since , we have , and , whence it follows that
, i.e., . This is a contradiction, since . Subcase(ii-3-c): . Since , by (IV), we have . Since , we have , and , whence it follows that 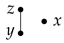 . Hence . Thus (IV) holds. □
. Hence . Thus (IV) holds. □
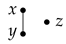 . Then . Subcase (ii-3-b): . Since , we have
. Then . Subcase (ii-3-b): . Since , we have 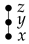 , i.e., . This is a contradiction, since . Subcase(ii-3-c): . Since , by (IV), we have . Since , we have , and , whence it follows that
, i.e., . This is a contradiction, since . Subcase(ii-3-c): . Since , by (IV), we have . Since , we have , and , whence it follows that 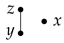 . Hence . Thus (IV) holds. □
. Hence . Thus (IV) holds. □Remark 1 (Another proof of Theorem 1).
This proof was suggested by a reviewer. It was proved axiomatically, not using the Hasse diagram of a poset. Let and let . We consider 3 cases: (i) Assume that and . Then . It follows that by using the conditions (III) and (IV). (ii) Assume . Then . (iii) Assume . Since , by (II) we obtain , proving the theorem.
Notice that if and , then if and are probability functions on a poset P, it follows that is also a probability function on P.
Let be a poset. Define a map by:
for any . We shall prove such a function is a probability function on a poset P.
Proposition 1.
The mapping is a probability function on P.
Proof.
The conditions (I), (II), and (III) hold trivially. Assume that the condition (IV) does not hold. Then there exist such that and for some . Case (i): . Then . Since , we have , a contradiction. Case (ii): . We have , which implies , which is a contradiction. Case (iii): . Then . Since , we have , which is a contradiction. □
Remark 2.
The reviewer suggested that the proof of Proposition 1 can be proved axiomatically. We omit its proof.
The mapping discussed in Proposition 1 is called a standard probability function.
Let be a finite poset and let be the collection of all linear extensions of P. Given , we denote the collection of all linear extensions satisfying the condition .
Theorem 2.
Let be a finite poset. If we define a map by:
for all , then is a probability function on P.
Proof.
(I) Given , we have . (II) Let in . Then in for any linear extension of . It follows that , and hence . (III) Let in . Then, for any linear extension of , either or . This means that there exist -number of linear extensions of and -number of linear extensions of . It follows that:
(IV) Let in and let . If is a linear extension of P with , then is also a linear extension of P with , since . It follows that . Hence:
This proves the theorem. □
Example 1. 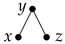 . Then it has two linear extensions:
. Then it has two linear extensions: 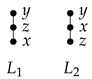
Let be a poset with the diagram:
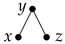 . Then it has two linear extensions:
. Then it has two linear extensions: 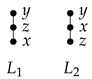
It follows that and . Hence .
Corollary 1.
If is an anti-chain, then .
Proof.
If is an anti-chain, then and hence . This shows that □.
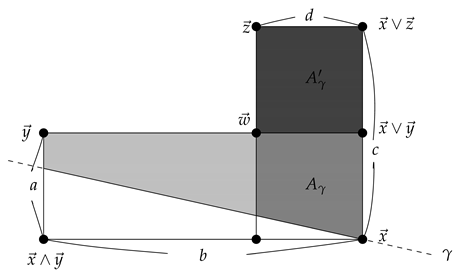
Let be a poset and let ⋀ be a linear extension of . Define a map on by:
Proposition 2.
Let be a poset and let ⋀ be a linear extension of . Then is a probability function on P.
Proof.
We show the condition (IV). Let . For any with , we have . Hence implies , which implies that . □
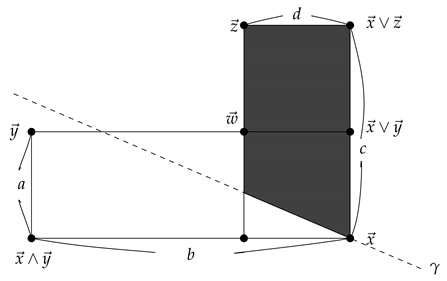
Theorem 3.
Let be a finite poset and let , say . Then .
Proof.
Given , we have 3 cases. Case 1: in . Then and hence . Since in implies in for any , we have . Case 2: in . If in , then in for any . It follows that and for any . This shows that . Case 3: in . Let such that in where . It follows that and hence . Since for any , we obtain , proving the theorem. □
4. Some Examples for Probability Realizers for π0
Let be a finite poset and let be a set of all linear extensions of . A set is said to be a probability realizer of for probability function if for some .
Example 2.
Let be a letter N-poset:

Then we have five linear extensions as follows:
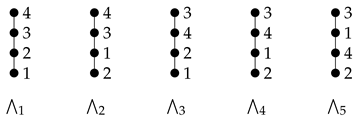

Consider in . Assume . Then . Similarly, we have . From this we obtain and . Hence , i.e., is a probability realizer of letter N-poset for the standard probability function .
Example 3.
Consider an anti-chain . It has the following six linear extensions:
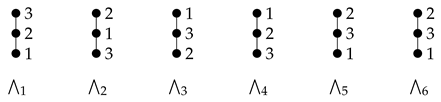

Assume for some . Then we have the following equations:
From these equations, we obtain . If we take , then . If we take , then . If we take , then . Hence are probability realizers of for .
Remark 3.
Note that, in Example 3, is a realizer of an anti-chain , but is not a probability realizer of for . In fact, assume that for some . Then we have the following equations:
It follows that , which is a contradiction.
Example 4.
Consider a poset : 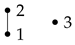 . This poset has three linear extensions as follows:
. This poset has three linear extensions as follows:
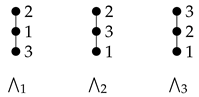
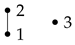 . This poset has three linear extensions as follows:
. This poset has three linear extensions as follows:
Let for some . Then we have . Similarly, we have . This shows that and . Hence , i.e., is a probability of a poset for .
5. Probability Functions on the Ordered Plane
Given a plane , we define a partial order ≤ as follows: if and only if . Such an order ≤ is called a product order on . A poset is said to be an ordered plane (or order geometry). In the book [8], the letter N-poset and the letter Y-poset were represented as follows:
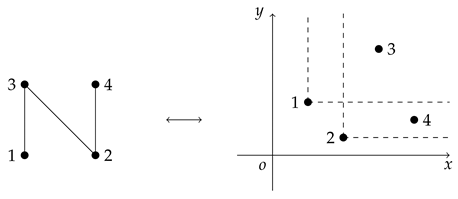
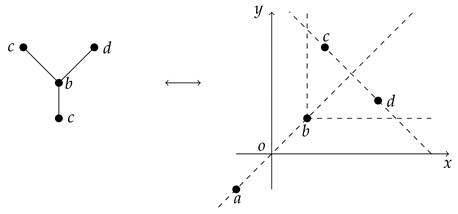


In this section, we discuss probability functions on the ordered plane. Given elements which are incomparable, i.e., , as below:
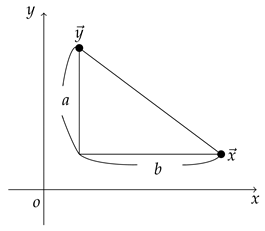

In this case, we define:
When , we define:
Theorem 4.
The mapping π defined as (1) and (2) on is a probability function.
Proof.
The proofs of (I) and (II) are trivial, and we omit it. (III) Let . Case (i): . Then we have . It follows that . Case (ii): . We let it be drawn as:
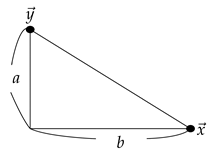

Then . (IV) Let and let . Then we have nine subdivisions where can be located in as follows:
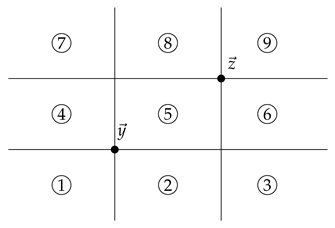

We denote its subdivision by, e.g., , when we consider a region consisting of areas ①, ②, ③. Case (i): lies in a subdivision . Then . It follows that . Case (ii): lies in a subdivision . Then and hence . Case (iii): lies in a subdivision . Consider the following figure:
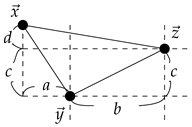

This shows that and . Since , we have . Case (iv): lies in a subdivision .

This shows that , and hence , . The following shows that .
Hence is a probability function on . □
We generalize Theorem 4 by generalizing the condition (1). Let with . Given elements which are incomparable, i.e., , as below:
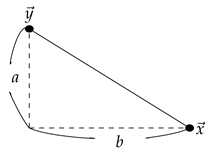

In this case, we define:
When , we define and as (2) above.
Theorem 5.
The mapping π defined as (2) and (3) on is a probability function.
Proof.
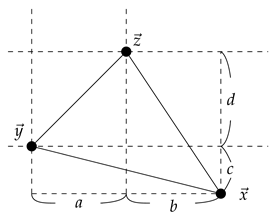
The proofs of (I)∼(III) are easy, and we omit it. Let . To show the condition (IV), we consider only two cases. Consider the following figure:
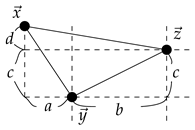

Then we have and . The following shows that .
Consider the following figure:
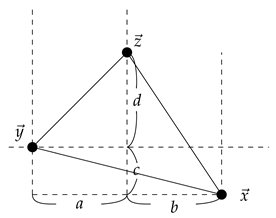

Then we have and . The following shows that .
Hence we prove that , showing that is a probability function on . □
Remark 4.
The mapping π discussed in Theorem 5 provides a two parameter family of probability functions on the ordered plane. If we let , then , i.e., we may let , i.e., 1-parameter family of probability functions determined by γ. For example, if , then . It follows that , i.e., is the slope of the lines with the property that if and only if and are on such a line.
Using previous observations, we obtain more complicated probability functions such as a convex combination:
whence yields:
for example.
Let in and we say that is below, denoted by , if is located below in the ordered plane:


Draw a line of slope through . Then this line cuts the interval into two regions, one containing and the other containing . We have two slopes, and as follows:
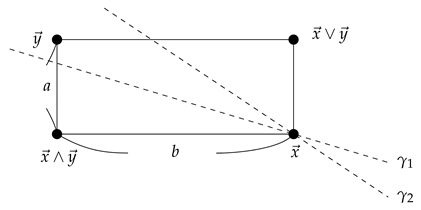

Let be the region containing the point , and let be the region containing the point .
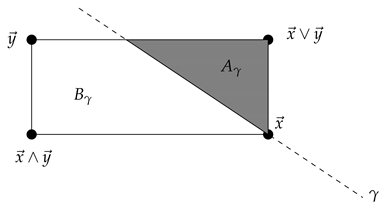

Then . Define and . Then we have two cases. Case (i): .
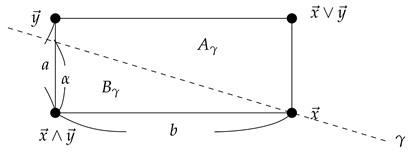

If we take so that , then and . Hence and . Notice that , which shows that . Case (ii): .
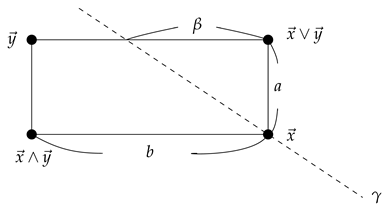

If we take so that , then and . Hence we have and . Also and . We define a map on the ordered plane as follow:
and
Moreover, we define:
when . We want to show that is a probability function on the ordered plane . The proofs of the conditions (I), (II), and (III) are easy to show, and we omit it. Assume . Given , we have nine places to put as follows:
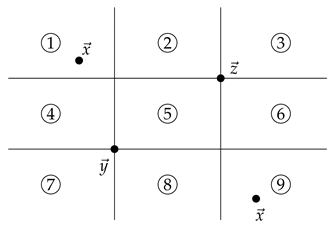

Any place except for and are easy to show condition (IV). Consider the case . The case can be shown as below:
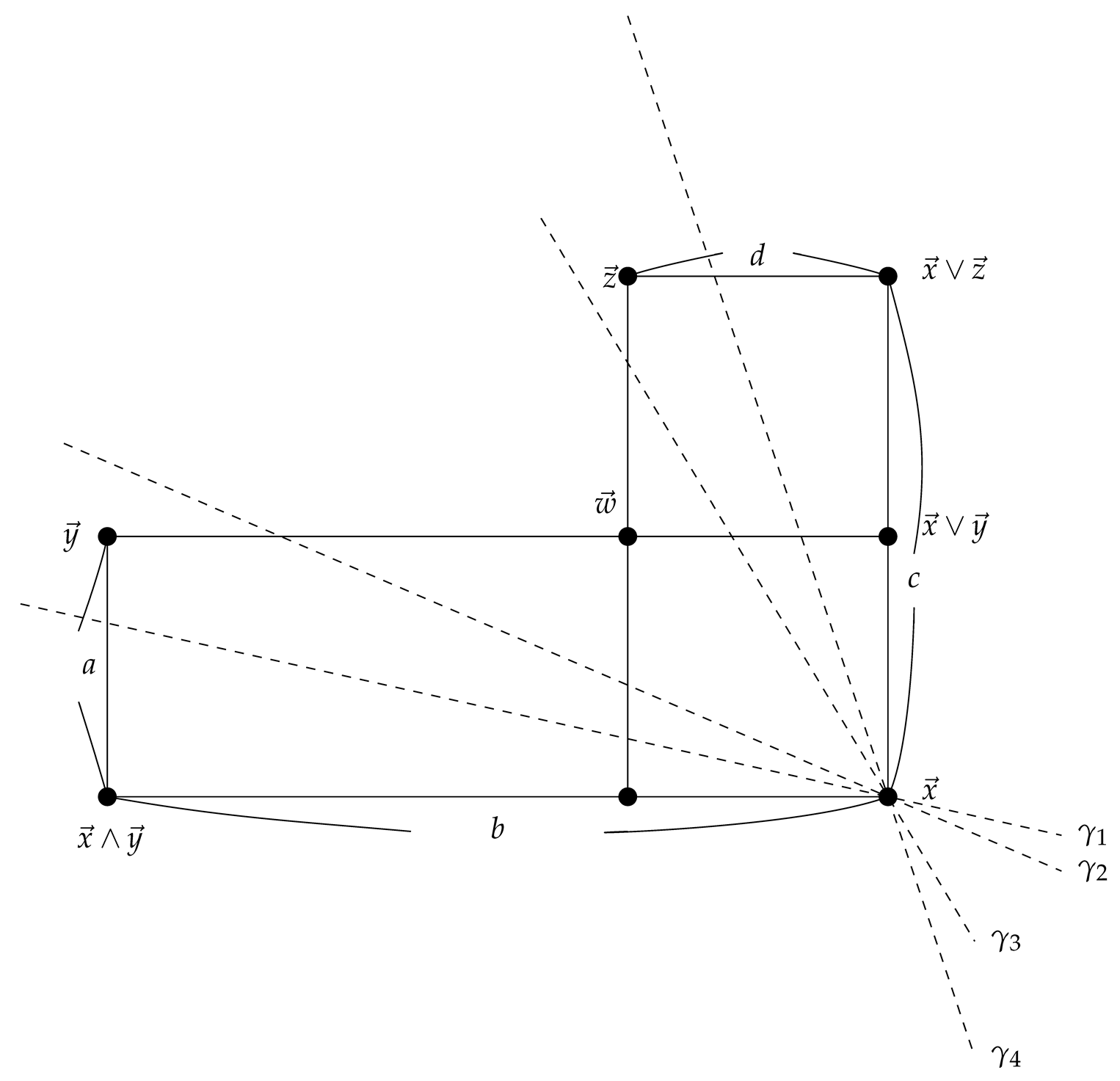

We can have four slopes between . Case (i): The slope passing through the segment as follows:

Then we have  and
and  , and and . Hence and proves the inequality as below:
, and and . Hence and proves the inequality as below:
 and
and  , and and . Hence and proves the inequality as below:
, and and . Hence and proves the inequality as below:Case (ii): The slope passing through the segment as follows:

Then we have  and
and  . Hence and proves the inequality as below:
since and .
. Hence and proves the inequality as below:
since and .
 and
and  . Hence and proves the inequality as below:
. Hence and proves the inequality as below:Case (iii): The slope passing through the segment as follows:
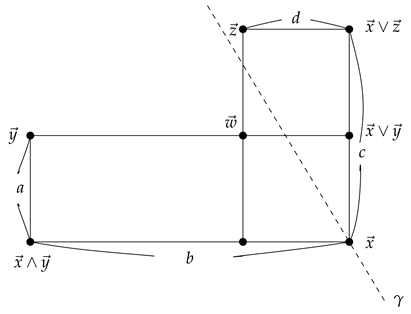

Then we have and . It follows that:
Case (iv): The slope passing through the segment as follows:
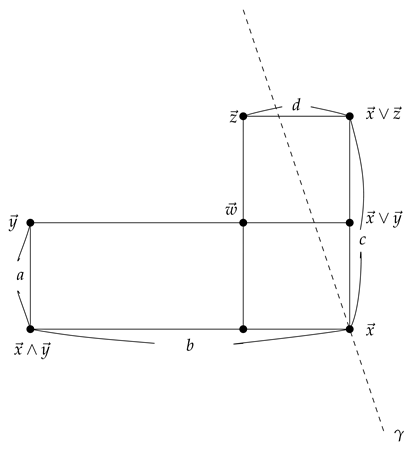

Then we have and . It follows that:
This shows that condition (IV) holds when is located at the region .
Consider the region . In the following figure, there exist four slopes passing through the point .
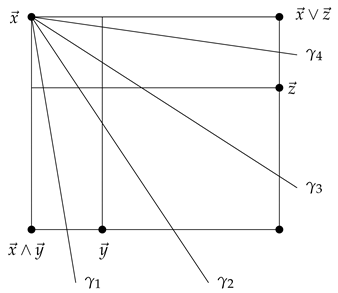

If we consider two figures below, then we find that .
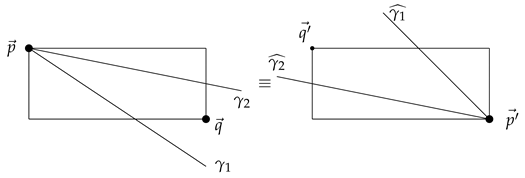

This shows that all cases for are dual of the cases for . This shows that is a probability function on the ordered plane . We summarize:
Theorem 6.
If we define a map on the ordered plane by , and , then it is a probability function on the ordered plane .
6. Conclusions
The notions of a trend and a probability function on d-algebras were developed. This kind of algebraic and axiomatic approaches gave room for the investigation on general algebraic structures in different directions. There existed algebras, e.g., -algebras, -algebras, which had poset structures. It is natural to consider some applications of probability functions to the poset structure. We defined the notion of a probability function on a poset, which is similar to the probability function discussed on d-algebras, and obtained three probability functions on posets and some basic properties. It is interesting to consider the notion of a realizer which are very useful in the study of poset theory, and so we defined a probability realizer of a poset and provided examples to describe its role for the standard probability function. We expect further investigations and theoretical results in this area. Finally, we discussed probability functions on the ordered plane and obtained probability functions acting on the ordered plane.
7. Comments for Further Research
(a) In Section 4 and Section 5, we constructed two large families of probability functions on arbitrary finite posets, each with a particular flavor and thus also with particular possible applications. Along these lines one may extend the discussion as follows. Let a poset () have n linear extensions . Then the poset is “linearly finitary” and we construct a new poset () as follows:
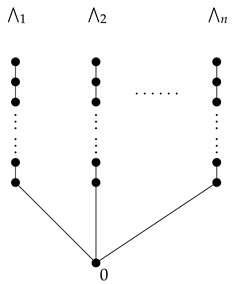

In particular, if is a chain, then
is also a chain and an ordinal sum . Then Q may be analyzed in terms of P along the line of Section 4 above.
(b) For the poset geometry, the poset with has the product order: if and only if for . If we analyze posets P embedded in () along the lines of Section 5, then we extend our ideas of () to that of n-dimensional poset geometry () and all that implies for geometry.
(c) Given a poset () having the least element 0, let mean , and (i) mean for all ; (ii) for some implies for all ; and (iii) implies . Such a mapping (or ) is said to be a soft probability function on () (or ()) more generally. If we define for all , then it is a soft probability function, but not a probability function. Thus, there are definitely differences in these concepts which may be explored further.
(d) In the setting of probability functions as studied above, the underlying model has been that of -algebras where if , is a poset with minimal element 0. Given the fact that in general the choice of 0 may be rather meaningless, we may introduce generalizations: (1) weak probability function on : , (either or analog), and (2) fuzzy weak probability function on : , . In either case implies and we may use this as an alternative to an idea, such as . For a variety of modeling in applications, the groupoid may (conveniently) not be of a usual type, so that the functions need to be of types (1) or (2) to fit any requirements. Thus, it appears that the results obtained in this paper may be further developed for various groupoids as well as developed in (1) or (2) as described above in these comments.
Author Contributions
The authors equally contributed towards the completion of this paper.
Funding
This research received no external funding.
Acknowledgments
The authors are deeply grateful to the referees for their valuable suggestions.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Neggers, J. Partially ordered sets and groupoids. Kyungpook Math. J. 1976, 16, 7–20. [Google Scholar]
- Neggers, J.; Kim, H.S. Modular posets and semigroups. Semigroup Forum 1996, 53, 57–62. [Google Scholar] [CrossRef]
- Neggers, J.; Kim, H.S. On d-algebras. Math. Slovaca 1999, 49, 19–26. [Google Scholar]
- Cha, K.J.; Kim, H.S.; Neggers, J. Trends, probability functions and fuzzy right ideals for d-algebras. Comput. Math. Appl. 2011, 62, 2988–2994. [Google Scholar] [CrossRef]
- De Loof, K.; De Baets, B.; De Meyer, H. Properties of mutual rank probabilities in partially ordered sets. In Multicirteria Ordering and Ranking: Partial Orders, Ambiguities and Applied Issues; Owsin´ski, J.W., Bru¨ggemann, R., Eds.; Systems Research Institute, Polish Academy of Sciences: Warsaw, Poland, 2008; pp. 145–165. [Google Scholar]
- De Baets, B.; De Meyer, H.; De Loof, K. On the cycle-transitivity of the mutual rank probability relation of a poset. Fuzzy Sets Syst. 2010, 161, 2695–2708. [Google Scholar] [CrossRef]
- Lerche, D.; Sørensen, P.B. Evaluation of the rank probabilities for partial orders based on random linear extensions. Chemosphere 2003, 53, 981–992. [Google Scholar] [CrossRef]
- Neggers, J.; Kim, H.S. Basic Posets; World Scientific: Singapore, 1998. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).