Multi-Attribute Multi-Perception Decision-Making Based on Generalized T-Spherical Fuzzy Weighted Aggregation Operators on Neutrosophic Sets
Abstract
1. Introduction
2. Preliminaries
- (i)
- is said to be a t-spherical fuzzy set (abbr. ) in .
- (ii)
- are respectively called the membership function, the abstinence function, and the non-membership function of .
- (iii)
- is called the degree of refusal of in .
- i)
- is said to be a single-valued neutrosophic set (abbr. ) in
- ii)
- are called the truth-membership function, the indeterminacy-membership function, and the falsity-membership function of respectively.
- (i)
- (ii)
- (iii)
- (iv)
- (i)
- (ii)
- (iii)
- (iv)
3. Monotonicity, Boundedness, Idempotency, and Commutativity of Operations
- (i)
- (ii)
- (iii)
- , for all being an
- (i)
- implies
- (ii)
- implies
- (iii)
- , for all
- (i)
- implies
- (ii)
- implies
- (iii)
- (i)
- implies
- (ii)
- implies
- (iii)
- , for all
- (i)
- implies
- (ii)
- implies
- (iii)
4. Generalized T-Spherical Fuzzy Subjectively Weighted Interaction Operators
- (i)
- (ii)
- (1)
- With being a positive real number, , and satisfying for all , it follows that:As a result,This further implies thatWe now obtainOn the other hand, it is clear that implies that .Thusand thereforeholds for all positive real numbers .
- (2)
- For each , as , so holds by taking in Lemma 2. By following the same procedure as part (1) of this lemma, with and taking place of and respectively:This further implies thatby taking in Lemma 2, again☐
- (i)
- (ii)
- (i)
- The Generalized t-Spherical Fuzzy Weighted Geometric Interaction Function, is defined as for all , wherefor all for all .In such a case,
- (a)
- is said to be the Generalized t-Spherical Fuzzy -Weighted Geometric Interaction on .
- (b)
- is said to be the weight vector of in .
- (ii)
- The Generalized t-Spherical Fuzzy Weighted Arithmetic Interaction Function, is defined as for all , wherefor all , for all .In such a case,
- (a)
- is said to be the Generalized t-Spherical Fuzzy -Weighted Arithmetic Interaction on .
- (b)
- is said to be the weight vector of in .
- (i)
- If for all , then both and
- (ii)
- If for all , then both and
- (iii)
- If for all , then both and
- (i)
- is said to be the score value of .
- (ii)
- is said to be the accuracy value of .
- (i)
- is said to be the score function of .
- (ii)
- is said to be the accuracy function of .
- (i)
- is said to be the Generalized t-Spherical score value (abbr. - score value) of .
- (ii)
- is said to be the Generalized t-Spherical accuracy value (abbr. - accuracy value) of .
- (i)
- (ii)
- but.
- (i)
- for all.
- (ii)
- Ifis such thatfor allthen.
- (i)
- for all.
- (ii)
- Ifis such thatfor all, then.
5. Algorithms for Multi-Attribute Multi-Perception Decision-Making Based on and
5.1. Prologue: The Derivation of from a Raw Dataset
5.2. Algorithm for Based Multi-Attribute Multi-Perception Decision Making
5.3. Algorithm for Based Multi-Attribute Multi-Perception Decision-Making
6. Application of the Proposed Algorithms to Air Pollution in China
6.1. An Overview of the Scenario—Air Pollution in China
6.1.1. The Two Major Smog Outbreaks in 2013
6.1.2. The Sources of Pollution
6.1.3. Actions Taken to Combat Pollution in China
6.2. The Multiple Perception of Comparing the Severity of Pollution
- (i)
- by pinpointing which city registered the highest daily PM2.5 concentrations recorded
- (ii)
- by pinpointing which city registered the lowest daily PM2.5 concentrations recorded
6.2.1. From the View of Environmental Management
6.2.2. From the View of Tourism Marketing
6.2.3. On Dealing with the Complete Absence of Data
6.3. Application of Our Proposed Method Using a Real Life Dataset
6.3.1. A Brief Description of the Dataset
6.3.2. Notations Used in the Dataset
- (a)
- Denote to be the six years of concern, where represent the years 2010, 2011, 2012, 2013, 2014 and 2015, respectively.
- (b)
- For each year :
- Denote to be the 5 cities in that year, where represents the city of Beijing, Chengdu, Guangzhou, Shanghai, and Shenyang, respectively.
- Denote to be all the hours within that year, starting with the 00:00 of 1st January, till 23:00 of 31st December. It is to be noted that , but as the year 2012 is a leap year.
- Denote all the PM2.5 readings within that year by a matrix whose elements are ordered sets of the following form:where , and for for all .
- The rows of from the 1st to the 5th represents the readings from the city of , respectively.
- The columns of from the 1st to the -th represents the readings from the hour , respectively.
- For each : if the reading exists in the dataset for the th station in the city of during the hour of , then is taken to be that reading, otherwise, is assigned to be .
- (c)
- For each in :
- Denote the set .
- Denote and to be the maximum and minimum value of .
- Denote to be the population variance of PM2.5 concentration for city during the hour of the year , which we can never know.
- Denote to be the unbiased estimate of using elements of .
6.4. The Objectives
6.5. The Chosen Method of Obtaining the SVNn
6.5.1. The Formulas
- (1)
- For the based approach used by the environment management sector, take For the based approach used by the tourism marketing sector, take . (See Section 6.2.3.)
- (2)
- (3)
- (4)
- where .
6.5.2. Motive behind the Choices of Formulas
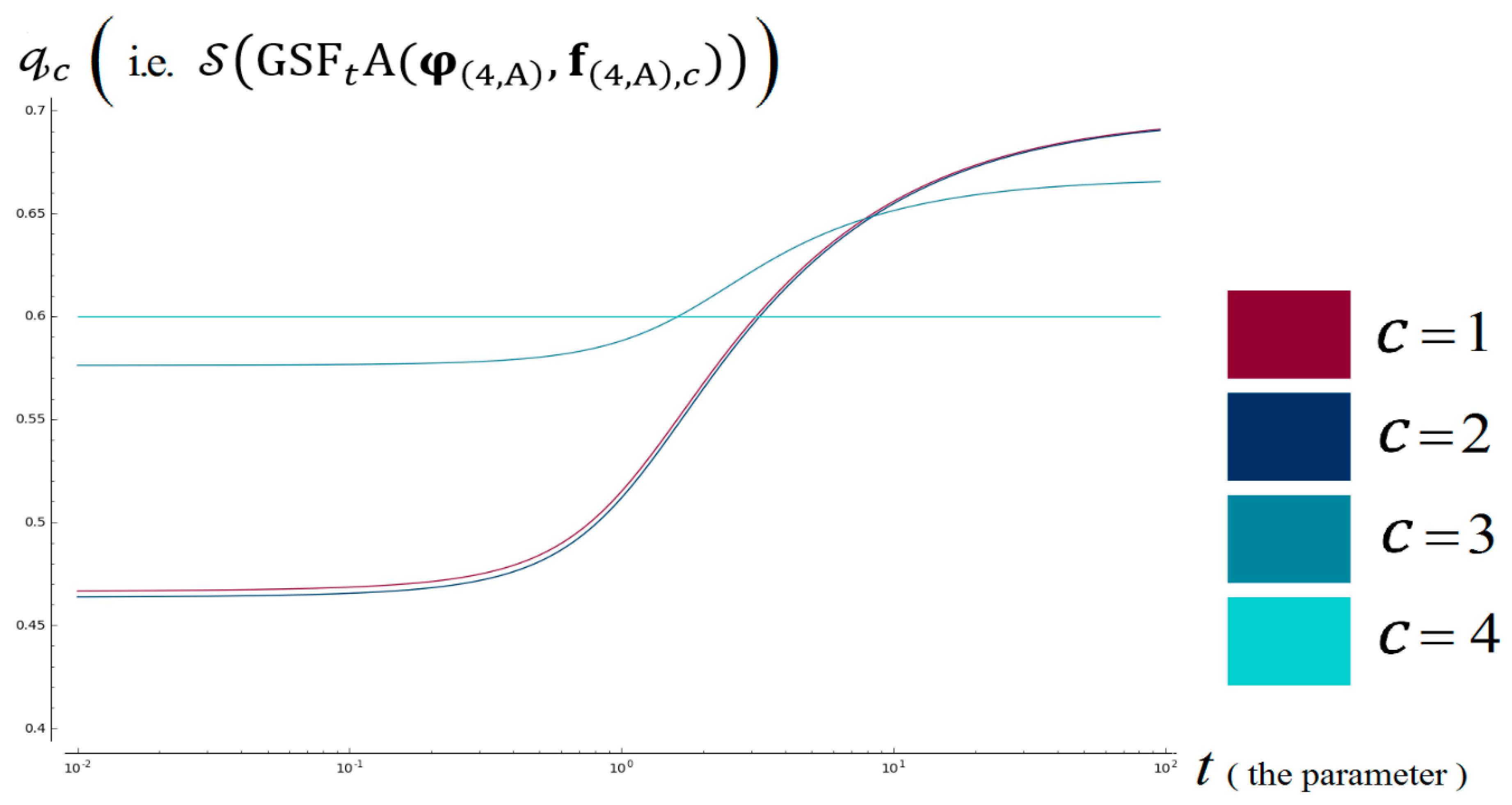
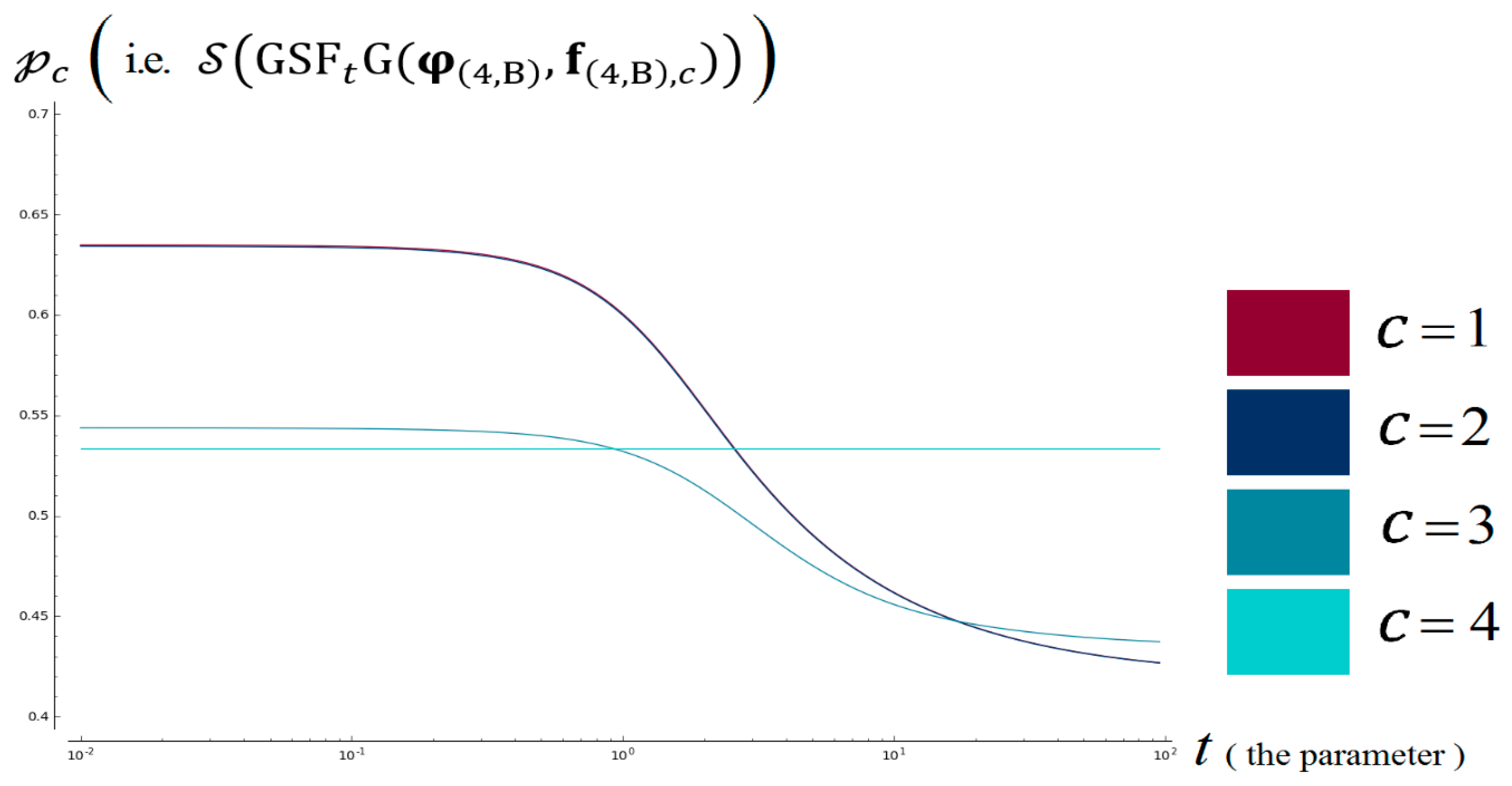
6.6. Results for Some Values of t
7. Compliance Tests to Investigate the Accuracy of our Algorithm
7.1. The Range of the Values of t to Be Investigated
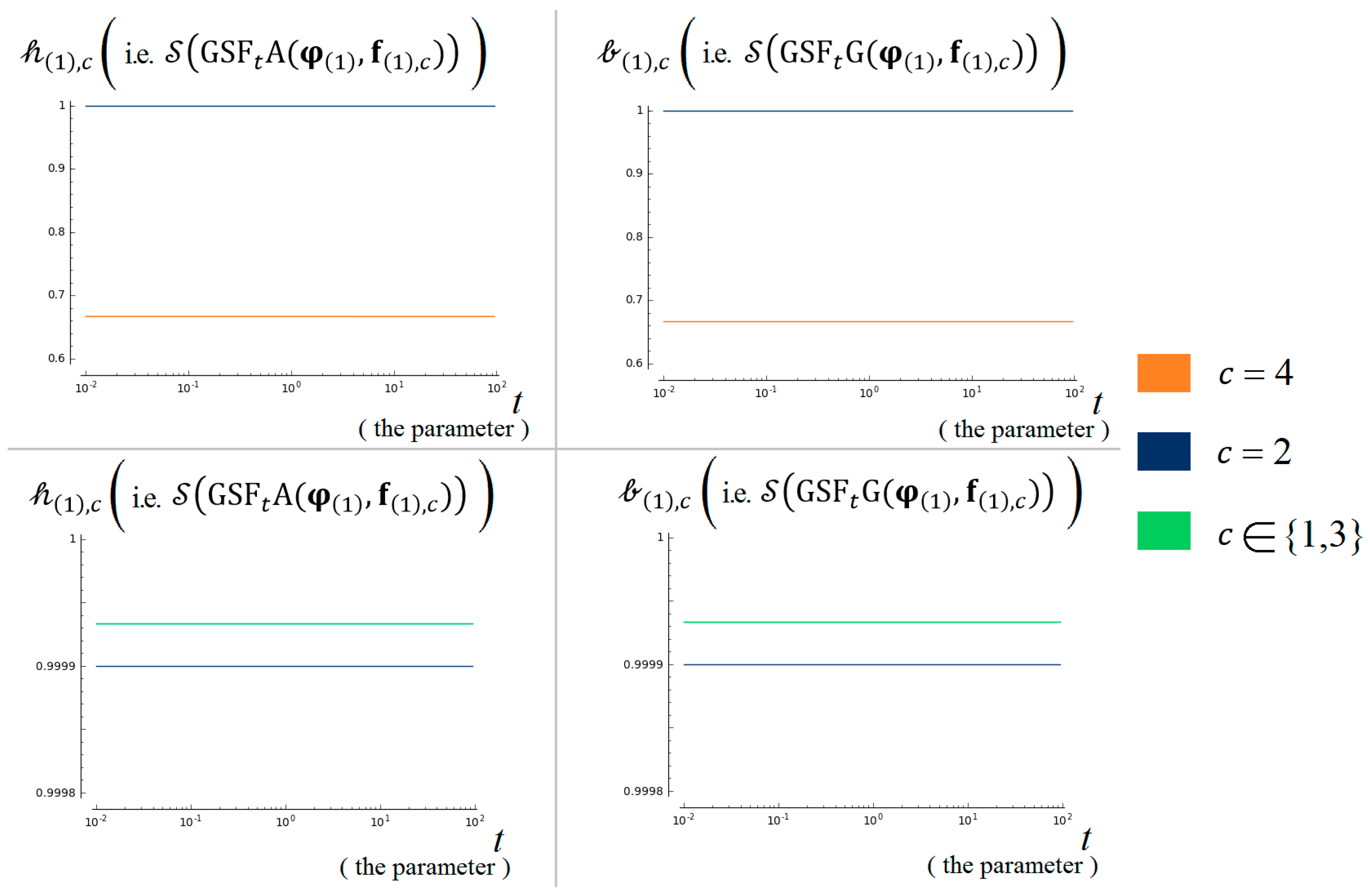
7.2. Test 1: Test for Small Values [46]
7.2.1. The Test Inputs
7.2.2. The Criteria of Compliance
7.2.3. The Results of Our Algorithm
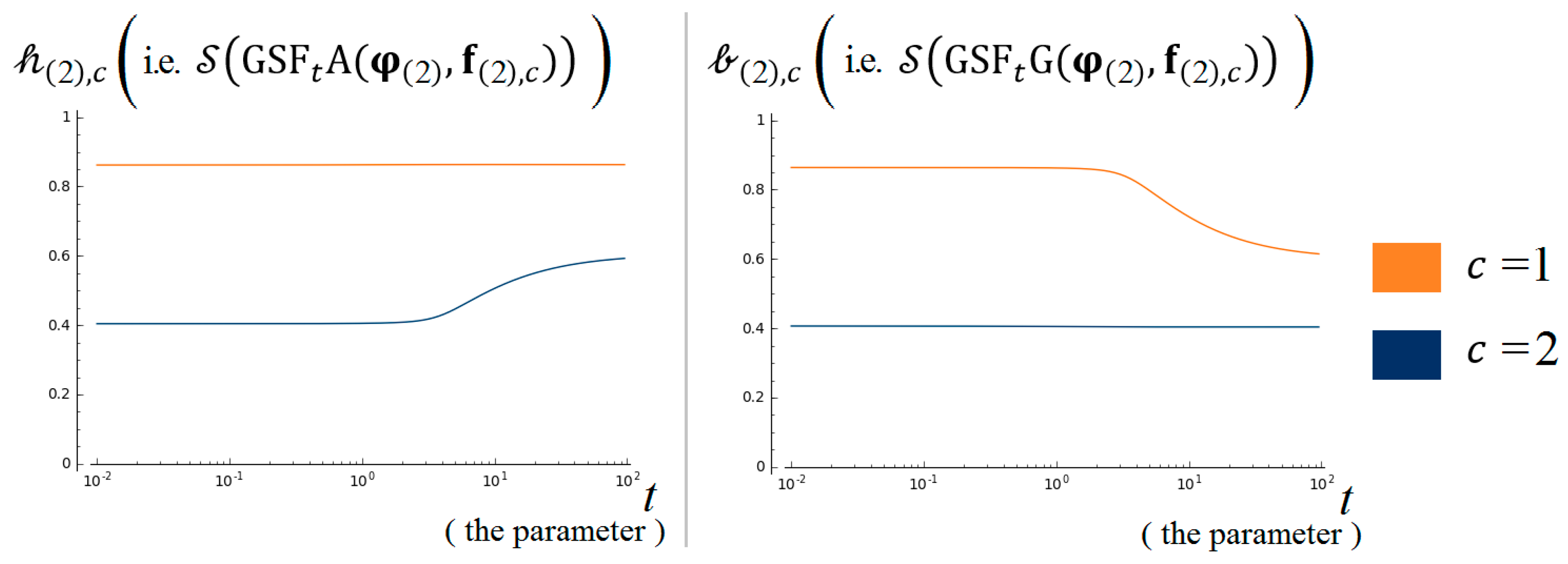
7.3. Test 2: Priority Test for Subjective Weights [46]
7.3.1. The Test Inputs
7.3.2. The Criteria of Compliance
7.3.3. The Results of Our Algorithm
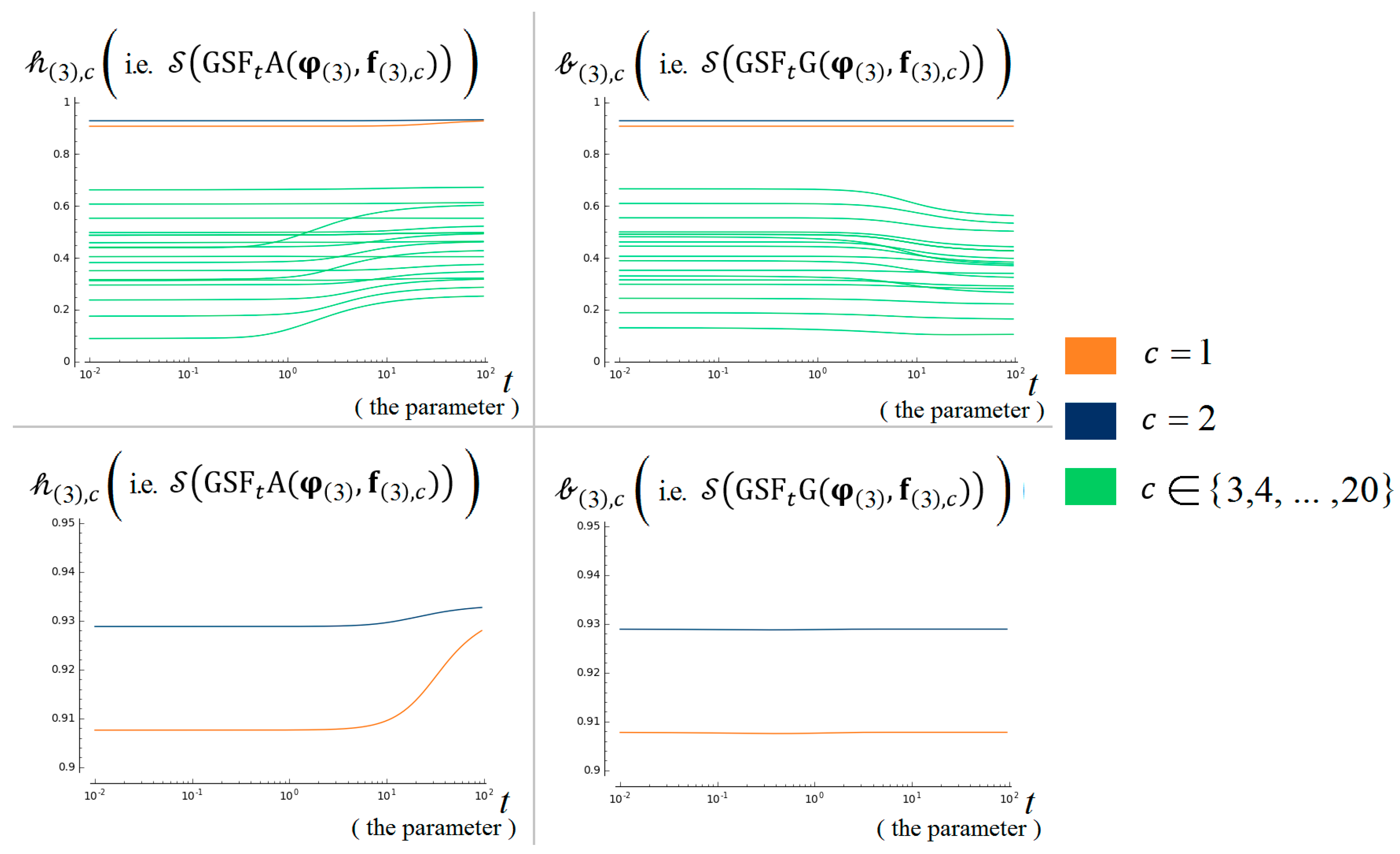
7.4. Test 3: Priority Test for Objective Weights [46]
7.4.1. The Test Inputs
7.4.2. The Criteria of Compliance
7.4.3. The Results of Our Algorithm
7.5. Test 4: t–Dependence Test
7.5.1. t-Dependence Test of Type-A: For Environmental Management
The Test Inputs
The Criteria of Compliance
- and whenever
- and whenever
- whenever
- whenever
- whenever
- whenever
- All the 10 days of City S are “slightly polluted”: . Thus, the low values of should produce an “overview” or “generalizing” perception, where a general value or trend of the degree of pollution across all the days is of primary concern. This perception consequently results in the deduction of City S as the most polluted city, for low values of .
- City P and City Q contains one day that is “severely polluted”: . Thus, the high values of should produce a “pinpointing” perception, where the highest degree of pollution recorded on a particular day is of primary concern. This perception consequently results in the deduction of City P and City Q as the two most polluted cities, for high values of .Remark 13:The most polluted city, out of City P and City Q depends on the objective weight which was already dealt by Test 3 from Section 7.4.
- City contains three days that is “medially polluted”: . Thus, the medium values of should produce a perception that is between “overview” and “pinpointing” in nature. This perception consequently results in the selection of City R as the most polluted city, for medium values of .
The Results of Our Algorithm
7.5.2. -Dependence Test of Type-B: For Tourism Marketing
The Test Inputs
The Criteria of Compliance
- and whenever .
- and whenever .
- whenever .
- whenever .
- whenever .
- whenever .
- All the 10 days of City are “slightly polluted”: . Thus, the low values of should produce an “urgent” perception, where time is at stake and therefore the photographic team must quickly take photographs of a city. This perception consequently results in the deduction of City as the least polluted city for low values of .
- City and City contain one day that is “good”: . Thus, the high values of should produce a “quality” perception, where the photographic team must wait for the clearest possible sky to produce the best possible photographs to market China tourism. This perception consequently results in the deduction of City and City as the two least polluted cities, for high values of .Remark 14:The least polluted city, out of City and City depends on the objective weight which was already dealt by Test 3 from Section 7.4.
- City contains three days that is “okay”: . Thus, the medium values of should produce a perception that is between “urgent” and “quality” in nature. This perception consequently results in the deduction of City as the least polluted city for medium values of .
The Results of Our Algorithm
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zadeh, L.A. Information and control. Fuzzy Sets 1965, 8, 338–353. [Google Scholar]
- Atanassov, K.T. Intuitionistic fuzzy sets. Fuzzy Sets Syst. 1986, 20, 87–96. [Google Scholar] [CrossRef]
- Atanassov, K.T. Intuitionistic Fuzzy Sets; Springer-Verlag: Berlin/Heidelberg, Germany, 1999. [Google Scholar]
- Yager, R.R. Pythagorean fuzzy subsets. In Proceedings of the 2013 Joint IFSA World Congress and NAFIPS Annual Meeting (IFSA/NAFIPS), Edmonton, AB, Canada, 24–28 June 2013. [Google Scholar]
- Yager, R.R. Pythagorean membership grades in multi criteria decision making. IEEE Trans. Fuzzy Syst. 2014, 22, 958–965. [Google Scholar] [CrossRef]
- Yager, R.R. Generalized orthopair fuzzy sets. IEEE Trans. Fuzzy Syst. 2017, 25, 1222–1230. [Google Scholar] [CrossRef]
- Cuong, B.C. Picture Fuzzy Sets—First Results, Part 2; Tech. Rep; Institute of Mathematics, Vietnam Academy of Science and Technology: Hanoi, Vietnam, 2013. [Google Scholar]
- Cuong, B.C. Picture Fuzzy Sets—First Results, Part 1; Institute of Mathematics, Vietnam Academy of Science and Technology: Hanoi, Vietnam, 2013. [Google Scholar]
- Mahmood, T.; Ullah, K.; Khan, Q.; Jan, N. An approach toward decision-making and medical diagnosis problems using the concept of spherical fuzzy sets. Neural Comput. Appl. 2018, 1–13. [Google Scholar] [CrossRef]
- Xu, Z.S.; Yager, R.R. Some geometric aggregation operators based on intuitionistic fuzzy sets. Int. J. Gen. Syst. 2006, 35, 417–433. [Google Scholar] [CrossRef]
- Garg, H. Generalized intuitionistic fuzzy interactive geometric interaction operators using Einstein t-norm and t-conorm and their application to decision making. Comput. Ind. Eng. 2016, 101, 53–69. [Google Scholar] [CrossRef]
- Garg, H. Novel intuitionistic fuzzy decision making method based on an improved operation laws and its application. Eng. Appl. Artif. Intell. 2017, 60, 164–174. [Google Scholar] [CrossRef]
- He, Y.; Chen, H.; Zhau, L.; Liu, J.; Tao, Z. Intuitionistic fuzzy geometric interaction averaging operators and their application to multi-criteria decision making. Inf. Sci. 2014, 259, 142–159. [Google Scholar] [CrossRef]
- Zhao, X.; Wei, G. Some intuitionistic fuzzy Einstein hybrid aggregation operators and their application to multiple attribute decision making. Knowl. Based Syst. 2013, 37, 472–479. [Google Scholar] [CrossRef]
- Liu, P. Some frank aggregation operators for interval-valued intuitionistic fuzzy numbers and their application to group decision making. J. Mult. Valued Logic Soft Comput. 2017, 29, 183–223. [Google Scholar]
- Garg, H. A new generalized Pythagorean fuzzy information aggregation using Einstein operations and its application to decision making. Int. J. Intell. Syst. 2016, 31, 886–920. [Google Scholar] [CrossRef]
- Garg, H. Generalized Pythagorean fuzzy geometric interactive aggregation operators using Einstein operations and their application to decision making. J. Exp. Theor. Artif. Intell. 2018, 1–32. [Google Scholar] [CrossRef]
- Peng, X.; Dai, J.; Garg, H. Exponential operation and aggregation operator for q-rung orthopair fuzzy set and their decision-making method with a new score function. Int. J. Intell. Syst. 2018, 33, 2255–2282. [Google Scholar] [CrossRef]
- Wei, G. Picture fuzzy aggregation operators and their application to multiple attribute decision making. J. Intell. Fuzzy Syst. 2017, 33, 713–724. [Google Scholar] [CrossRef]
- Garg, H. Some picture fuzzy aggregation operators and their applications to multicriteria decision-making. Arab. J. Sci. Eng. 2017, 42, 5275–5290. [Google Scholar] [CrossRef]
- Garg, H.; Munir, M.; Ullah, K.; Mahmood, T.; Jan, N. Algorithm for T-Spherical Fuzzy Multi-Attribute Decision Making Based on Improved Interactive Aggregation Operators. Symmetry 2018, 10, 670. [Google Scholar] [CrossRef]
- Li, Y.; Deng, Y. Generalized ordered propositions fusion based on belief entropy. Int. J. Comp. Comm. Control 2018, 13, 792–807. [Google Scholar] [CrossRef]
- Fei, L.; Wang, H.; Chen, L.; Deng, Y. A new vector valued similarity measure for intuitionistic fuzzy sets based on OWA operators. Iran. J. Fuzzy Syst. 2019, 16, 113–126. [Google Scholar]
- Wang, W.; Liu, X. Interval-valued intuitionistic fuzzy hybrid weighted averaging operator based on Einstein operation and its application to decision making. J. Intell. Fuzzy Syst. 2013, 25, 279–290. [Google Scholar]
- Wang, W.; Liu, X. The multi-attribute decision making method based on interval-valued intuitionistic fuzzy Einstein hybrid weighted geometric operator. Comput. Math. Appl. 2013, 66, 1845–1856. [Google Scholar] [CrossRef]
- Wang, W.; Liu, X.; Qin, Y. Interval-valued intuitionistic fuzzy aggregation operators. J. Syst. Eng. Electron. 2012, 23, 574–580. [Google Scholar] [CrossRef]
- Xu, Z.S.; Xia, M. Induced generalized intuitionistic fuzzy operators. Knowl. Based Syst. 2003, 24, 197–209. [Google Scholar] [CrossRef]
- Garg, H.; Kumar, K. An advanced study on the similarity measures of intuitionistic fuzzy sets based on the set pair analysis theory and their application in decision making. Soft Comput. 2018, 22, 4959–4970. [Google Scholar] [CrossRef]
- Wei, G.-W.; Xu, X.-R.; Deng, D.-X. Interval-valued dual hesitant fuzzy linguistic geometric aggregation operators in multiple attribute decision making. Int. J. Knowl. Based Intell. Eng. Syst. 2016, 20, 189–196. [Google Scholar] [CrossRef]
- Garg, H. Some robust improved geometric aggregation operators under interval-valued intuitionistic fuzzy environment for multi-criteria decision-making process. J. Ind. Manag. Optim. 2018, 14, 283–308. [Google Scholar] [CrossRef]
- Chen, S.M.; Cheng, S.H.; Tsai, W.H. Multiple attribute group decision making based on interval-valued intuitionistic fuzzy aggregation operators and transformation techniques of interval—Valued intuitionistic fuzzy values. Inf. Sci. 2016, 367–368, 418–442. [Google Scholar] [CrossRef]
- Garg, H. Some arithmetic operations on the generalized sigmoidal fuzzy numbers and its application. Granul. Comput. 2018, 3, 9–25. [Google Scholar] [CrossRef]
- Chen, S.M.; Cheng, S.H.; Chiou, C.H. Fuzzy multiattribute group decision making based on intuitionistic fuzzy sets and evidential reasoning methodology. Inf. Fusion 2016, 27, 215–227. [Google Scholar] [CrossRef]
- Wei, G.W. Interval valued hesitant fuzzy uncertain linguistic aggregation operators in multiple attribute decision making. Int. J. Mach. Learn. Cybern. 2016, 7, 1093–1114. [Google Scholar] [CrossRef]
- Kumar, K.; Garg, H. Connection number of set pair analysis based TOPSIS method on intuitionistic fuzzy sets and their application to decision making. Appl. Intell. 2018, 48, 2112–2119. [Google Scholar] [CrossRef]
- Kumar, K.; Garg, H. Prioritized linguistic interval-valued aggregation operators and their applications in group decision-making problems. Mathematics 2018, 6, 209. [Google Scholar] [CrossRef]
- Khan, M.U.; Mahmood, T.; Ullah, K.; Jan, N.; Deli, I.; Khan, Q. Some aggregation operators for bipolar-valued hesitant fuzzy information based on Einstein operational laws. J. Eng. Appl. Sci. 2017, 36, 63–72. [Google Scholar]
- Garg, H. Some methods for strategic decision-making problems with immediate probabilities in Pythagorean fuzzy environment. Int. J. Intell. Syst. 2018, 33, 687–712. [Google Scholar] [CrossRef]
- Ullah, K.; Mahmood, T.; Jan, N. Similarity measures for t-spherical fuzzy sets with applications in pattern recognition. Symmetry 2018, 10, 193. [Google Scholar] [CrossRef]
- Garg, H. Linguistic Pythagorean fuzzy sets and its applications in multi attribute decision-making process. Int. J. Intell. Syst. 2018, 33, 1234–1263. [Google Scholar] [CrossRef]
- Garg, H. New logarithmic operational laws and their aggregation operators for Pythagorean fuzzy set and their applications. Int. J. Intell. Syst. 2018. [Google Scholar] [CrossRef]
- Garg, H.; Arora, R. Generalized and group-based generalized intuitionistic fuzzy soft sets with applications in decision-making. Appl. Intell. 2018, 48, 343–356. [Google Scholar] [CrossRef]
- Garg, H. New logarithmic operational laws and their applications to multiattribute decision making for single-valued neutrosophic numbers. Cogn. Syst. Res. 2018, 52, 931–946. [Google Scholar] [CrossRef]
- Rani, D.; Garg, H. Complex intuitionistic fuzzy power aggregation operators and their applications in multi-criteria decision-making. Expert Syst. 2018, e12325. [Google Scholar] [CrossRef]
- Ullah, K.; Mahmood, T.; Jan, N.; Broumi, S.; Khan, Q. On bipolar-valued hesitant fuzzy sets and their applications in multi-attribute decision making. Nucleus 2018, 55, 93–101. [Google Scholar]
- Selvachandran, G.; Quek, S.; Smarandache, F.; Broumi, S. An Extended Technique for Order Preference by Similarity to an Ideal Solution (TOPSIS) with Maximizing Deviation Method Based on Integrated Weight Measure for Single-Valued Neutrosophic Sets. Symmetry 2018, 10, 236. [Google Scholar] [CrossRef]
- Wang, H.; Smarandache, F.; Zhang, Y.Q.; Sunderraman, R. Single valued neutrosophic sets. Multispace Multistructure 2010, 4, 410–413. [Google Scholar]
- Nirmal, N.P.; Bhatt, M.G. Selection of automated guided vehicle using single valued neutrosophic entropy based on novel multi attribute decision making technique. New Trends Neutrosophic Theory Appl. 2016, 105–114. Available online: https://www.semanticscholar.org/paper/Selection-of-Automated-Guided-Vehicle-using-Single-ANGALBoomija/985a780ec046a90d1aec2895a89db53a8ae1a6d1 (accessed on 9 May 2019).
- Jha, S.; Kumar, R.; Priyadarshini, I.; Smarandache, F.; Long, H.V. Neutrosophic Image Segmentation with Dice Coefficients. Measurement 2019, 134, 762–772. [Google Scholar] [CrossRef]
- Nguyen, G.N.; Ashour, A.S.; Dey, N. A survey of the State-of-the-arts on Neutrosophic Sets in Biomedical Diagnoses. Int. J. Mach. Learn. Cybern. 2019, 10, 1–13. [Google Scholar] [CrossRef]
- Le Hoang, S.; Fujita, H. Neural-Fuzzy with Representative Sets for Prediction of Student Performance. Appl. Intell. 2019, 49, 172–187. [Google Scholar]
- Long, H.V.; Ali, M.; Khan, M.; Tu, D.N. A novel approach for Fuzzy Clustering based on Neutrosophic Association Matrix. Comput. Ind. Eng. 2019. [Google Scholar] [CrossRef]
- Kaur, S.; Bansal, R.K.; Mittal, M.; Goyal, L.M.; Kaur, I.; Verma, A. Mixed pixel decomposition based on extended fuzzy clustering for single spectral value remote sensing images. J. Indian Soc. Remote Sens. 2019, 47, 427–437. [Google Scholar] [CrossRef]
- Tuan, T.M.; Fujita, H.; Dey, N.; Ashour, A.S.; Ngoc, V.T.N.; Chu, D.T. Dental Diagnosis from X-Ray Images: An Expert System based on Fuzzy Computing. Biomed. Signal Process. Control 2018, 39C, 64–73. [Google Scholar]
- Ali, M.; Khan, M.; Tung, N.T. Segmentation of Dental X-ray Images in Medical Imaging using Neutrosophic Orthogonal Matrices. Expert Syst. Appl. 2018, 91, 434–441. [Google Scholar] [CrossRef]
- Ngan, R.T.; Ali, M. Delta-Equality of Intuitionistic Fuzzy Sets: A New Proximity Measure and Applications in Medical Diagnosis. Appl. Intell. 2018, 48, 499–525. [Google Scholar] [CrossRef]
- Ali, M.; Dat, L.Q.; Smarandache, F. Complex Neutrosophic Set: Formulation and Applications in Decision-Making. Int. J. Fuzzy Syst. 2018, 20, 986–999. [Google Scholar] [CrossRef]
- Giap, C.N.; Son, L.H.; Chiclana, F. Dynamic Structural Neural Network. J. Intell. Fuzzy Syst. 2018, 34, 2479–2490. [Google Scholar] [CrossRef]
- Ngan, R.T.; Cuong, B.C.; Ali, M. H-max distance measure of intuitionistic fuzzy sets in decision making. Appl. Soft Comput. 2018, 69, 393–425. [Google Scholar] [CrossRef]
- Le, T.; Le Son, H.; Vo, M.; Lee, M.; Baik, S. Cluster-Based Boosting Algorithm for Bankruptcy Prediction in a Highly Imbalanced Dataset. Symmetry 2018, 10, 250. [Google Scholar] [CrossRef]
- Khan, M.; Son, L.; Ali, M.; Chau, H.; Na, N.; Smarandache, F. Systematic Review of Decision Making Algorithms in Extended Neutrosophic Sets. Symmetry 2018, 10, 314. [Google Scholar] [CrossRef]
- Hemanth, D.J.; Anitha, J.; Mittal, M. Diabetic Retinopathy Diagnosis from Retinal Images using Modified Hopfield Neural Network. J. Med. Syst. 2018, 42, 247–253. [Google Scholar] [CrossRef]
- Ngan, T.T.; Lan, L.T.H.; Ali, M.; Tamir, D.; Son, L.H.; Tuan, T.M.; Rishe, N.; Kandel, A. Logic Connectives of Complex Fuzzy Sets. Rom. J. Inf. Sci. Technol. 2018, 21, 344–358. [Google Scholar]
- Jain, R.; Jain, N.; Kapania, S.; Son, L. Degree Approximation-Based Fuzzy Partitioning Algorithm and Applications in Wheat Production Prediction. Symmetry 2018, 10, 768. [Google Scholar] [CrossRef]
- Hemanth, D.J.; Anitha, J.; Naaji, A.; Geman, O.; Popescu, D.E. Modified Deep Convolutional Neural Network for Abnormal Brain Image Classification. IEEE Access 2018, 7, 4275–4283. [Google Scholar] [CrossRef]
- Phong, P.H.; Son, L.H. Linguistic Vector Similarity Measures and Applications to Linguistic Information Classification. Int. J. Intell. Syst. 2017, 32, 67–81. [Google Scholar] [CrossRef]
- Son, L.H.; Thong, P.H. Some Novel Hybrid Forecast Methods Based On Picture Fuzzy Clustering for Weather Nowcasting from Satellite Image Sequences. Appl. Intell. 2017, 46, 1–15. [Google Scholar] [CrossRef]
- Son, L.H.; Tuan, T.M. Dental segmentation from X-ray images using semi-supervised fuzzy clustering with spatial constraints. Eng. Appl. Artif. Intell. 2017, 59, 186–195. [Google Scholar] [CrossRef]
- Hai, D.T.; Le Vinh, T. Novel Fuzzy Clustering Scheme for 3D Wireless Sensor Networks. App. Soft Comput. 2017, 54, 141–149. [Google Scholar] [CrossRef]
- Son, L.H. Measuring Analogousness in Picture Fuzzy Sets: From Picture Distance Measures to Picture Association Measures. Fuzzy Optim. Decis. Mak. 2017, 16, 359–378. [Google Scholar] [CrossRef]
- Thanh, N.D.; Ali, M.; Son, L.H. A Novel Clustering Algorithm in a Neutrosophic Recommender System for Medical Diagnosis. Cognit. Comput. 2017, 9, 526–544. [Google Scholar] [CrossRef]
- Son, L.H.; Tien, N.D. Tune up Fuzzy C-Means for Big Data: Some novel hybrid clustering algorithms based on Initial Selection and Incremental Clustering. Int. J. Fuzzy Syst. 2017, 19, 1585–1602. [Google Scholar] [CrossRef]
- Son, L.H.; Tuan, T.M. A cooperative semi-supervised fuzzy clustering framework for dental X-ray image segmentation. Expert Syst. Appl. 2016, 46, 380–393. [Google Scholar] [CrossRef]
- Wijayanto, A.W.; Purwarianti, A.; Son, L.H. Fuzzy geographically weighted clustering using artificial bee colony: An efficient geo-demographic analysis algorithm and applications to the analysis of crime behavior in population. Appl. Intell. 2016, 44, 377–398. [Google Scholar] [CrossRef]
- Thong, P.H.; Son, L.H. Picture Fuzzy Clustering: A New Computational Intelligence Method. Soft Comput. 2016, 20, 3549–3562. [Google Scholar] [CrossRef]
- Son, L.J.; Hai, P.V. A novel multiple fuzzy clustering method based on internal clustering validation measures with gradient descent. Int. J. Fuzzy Syst. 2016, 18, 894–903. [Google Scholar] [CrossRef]
- Tuan, T.M.; Ngan, T.T.; Son, L.H. A Novel Semi-Supervised Fuzzy Clustering Method based on Interactive Fuzzy Satisficing for Dental X-Ray Image Segmentation. Appl. Intell. 2016, 45, 402–428. [Google Scholar] [CrossRef]
- Son, L.H.; Phong, P.H. On the performance evaluation of intuitionistic vector similarity measures for medical diagnosis. J. Intell. Fuzzy Syst. 2016, 31, 1597–1608. [Google Scholar] [CrossRef]
- Son, L.H. Generalized Picture Distance Measure and Applications to Picture Fuzzy Clustering. Appl. Soft Comput. 2016, 46, 284–295. [Google Scholar] [CrossRef]
- Thong, P.H.; Son, L.H. A Novel Automatic Picture Fuzzy Clustering Method Based On Particle Swarm Optimization and Picture Composite Cardinality. Knowl. Based Syst. 2016, 109, 48–60. [Google Scholar] [CrossRef]
- Thong, P.H.; Son, L.H. Picture Fuzzy Clustering for Complex Data. Eng. Appl. Artif. Intell. 2016, 56, 121–130. [Google Scholar] [CrossRef]
- Ngan, T.T.; Tuan, T.M.; Minh, N.H.; Dey, N. Decision making based on fuzzy aggregation operators for medical diagnosis from dental X-ray images. J. Med. Syst. 2016, 40, 1–7. [Google Scholar] [CrossRef] [PubMed]
- Son, L.H. DPFCM: A Novel Distributed Picture Fuzzy Clustering Method on Picture Fuzzy Sets. Expert Syst. Appl. 2016, 42, 51–66. [Google Scholar] [CrossRef]


| Type of Entity in Datasets | Examples | |
|---|---|---|
| Qualitative | Nominal | Nationality (Malaysia, Singapore, China …) |
| Ordinal | Customer Feedback (Poor, Fair, Good …) | |
| Quantitative | Discrete | Number of stations (1, 2, 3, …) |
| Continuous | Measurement (12.3 kg, 34.1 m, …) | |
(Environment Management/Tourism Marketing) | ||
|---|---|---|
| 1/20 (very overviewing/very urgent) | ||
| ¼ (rather overviewing/rather urgent) | ||
| 1 (balanced) | ||
| 4 (rather pin-pointing/rather patient) | ||
| 20 (very pin-pointing/very patient) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Quek, S.G.; Selvachandran, G.; Munir, M.; Mahmood, T.; Ullah, K.; Son, L.H.; Thong, P.H.; Kumar, R.; Priyadarshini, I. Multi-Attribute Multi-Perception Decision-Making Based on Generalized T-Spherical Fuzzy Weighted Aggregation Operators on Neutrosophic Sets. Mathematics 2019, 7, 780. https://doi.org/10.3390/math7090780
Quek SG, Selvachandran G, Munir M, Mahmood T, Ullah K, Son LH, Thong PH, Kumar R, Priyadarshini I. Multi-Attribute Multi-Perception Decision-Making Based on Generalized T-Spherical Fuzzy Weighted Aggregation Operators on Neutrosophic Sets. Mathematics. 2019; 7(9):780. https://doi.org/10.3390/math7090780
Chicago/Turabian StyleQuek, Shio Gai, Ganeshsree Selvachandran, Muhammad Munir, Tahir Mahmood, Kifayat Ullah, Le Hoang Son, Pham Huy Thong, Raghvendra Kumar, and Ishaani Priyadarshini. 2019. "Multi-Attribute Multi-Perception Decision-Making Based on Generalized T-Spherical Fuzzy Weighted Aggregation Operators on Neutrosophic Sets" Mathematics 7, no. 9: 780. https://doi.org/10.3390/math7090780
APA StyleQuek, S. G., Selvachandran, G., Munir, M., Mahmood, T., Ullah, K., Son, L. H., Thong, P. H., Kumar, R., & Priyadarshini, I. (2019). Multi-Attribute Multi-Perception Decision-Making Based on Generalized T-Spherical Fuzzy Weighted Aggregation Operators on Neutrosophic Sets. Mathematics, 7(9), 780. https://doi.org/10.3390/math7090780







