On New Solutions of Time-Fractional Wave Equations Arising in Shallow Water Wave Propagation
Abstract
1. Introduction
2. Preliminaries
3. FRDTM
4. Implementation of FRDTM on the CH Equation
5. Implementation of FRDTM on the mCH Equation
6. Implementation of FRDTM on the DP Equation
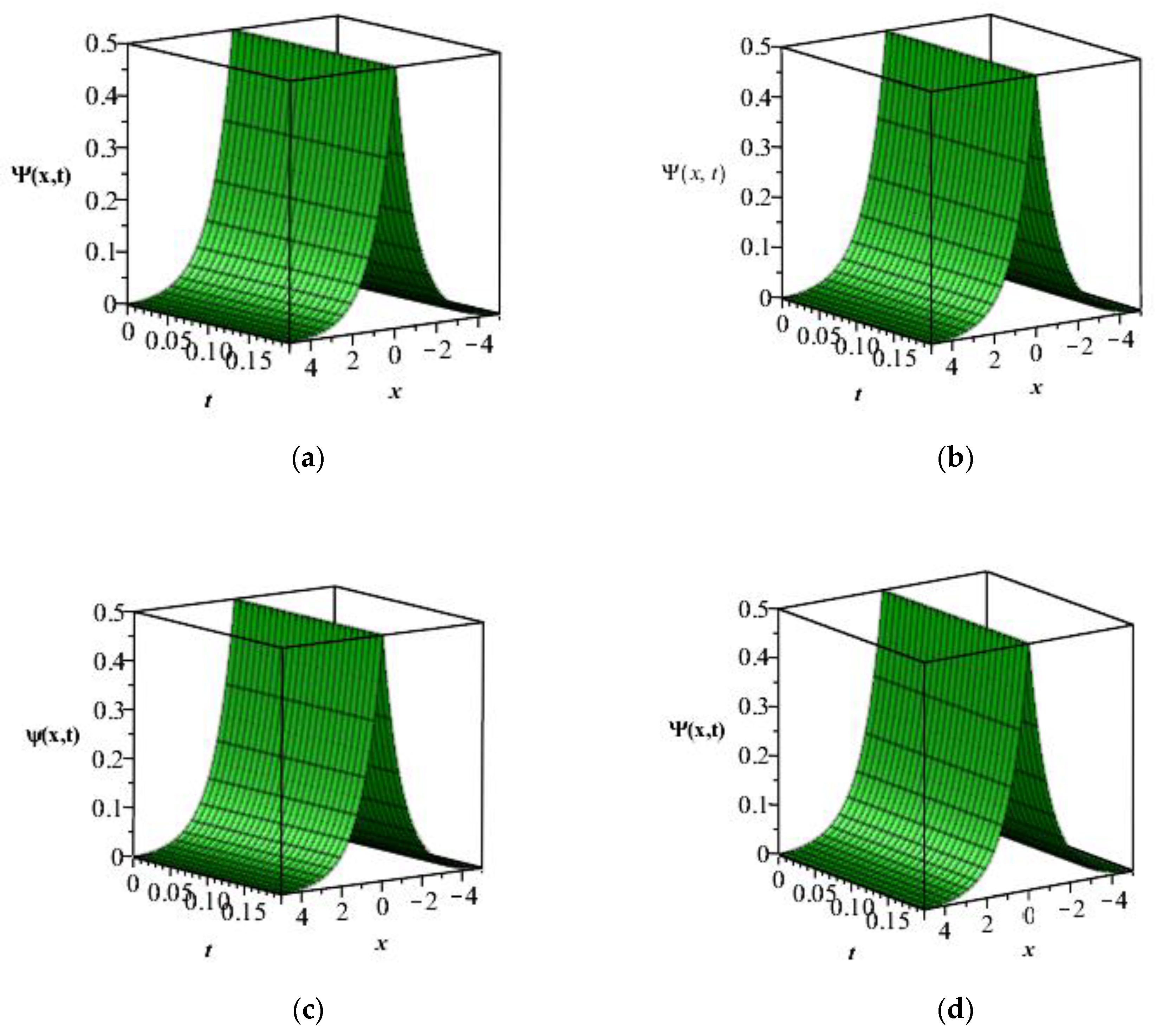
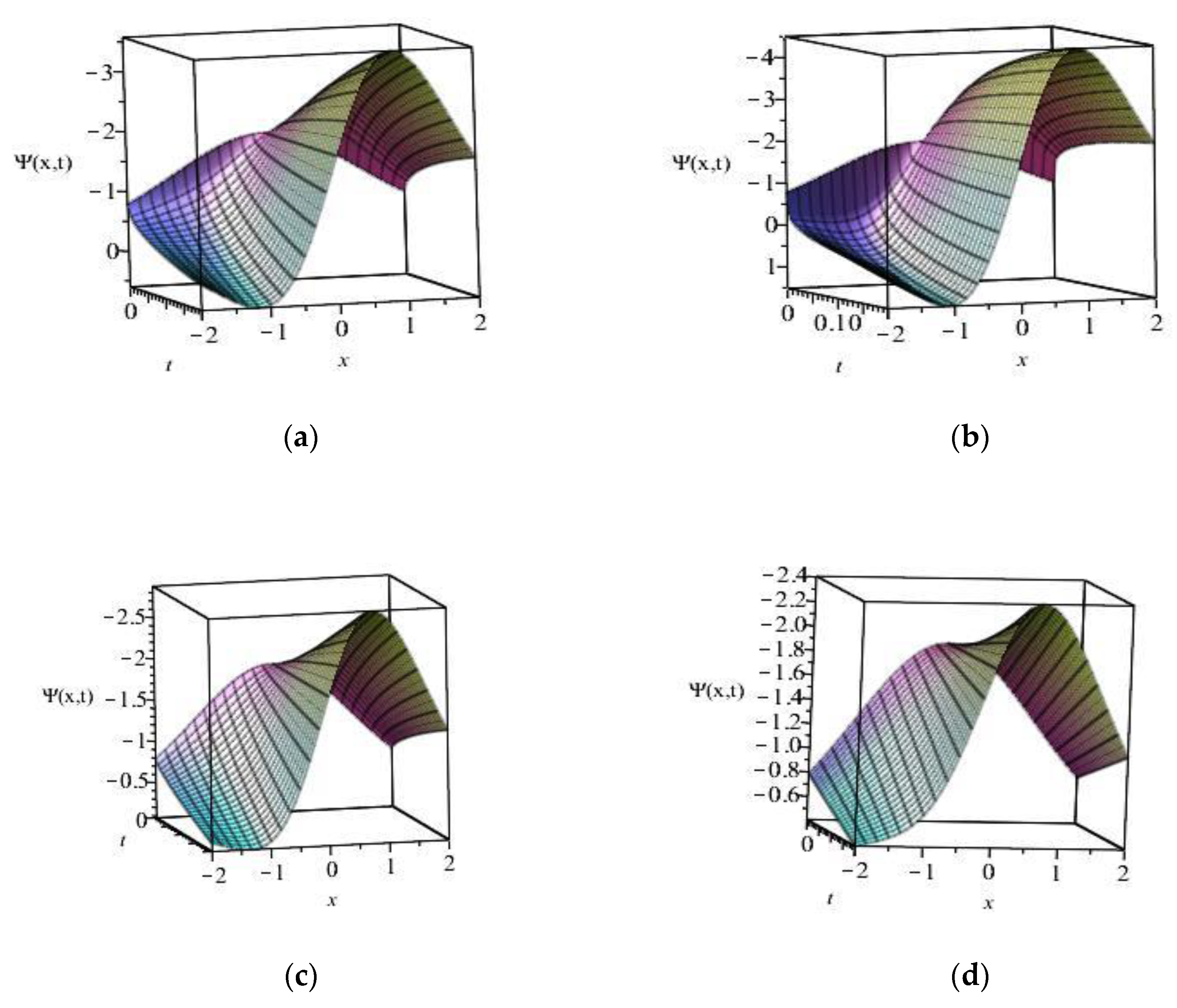
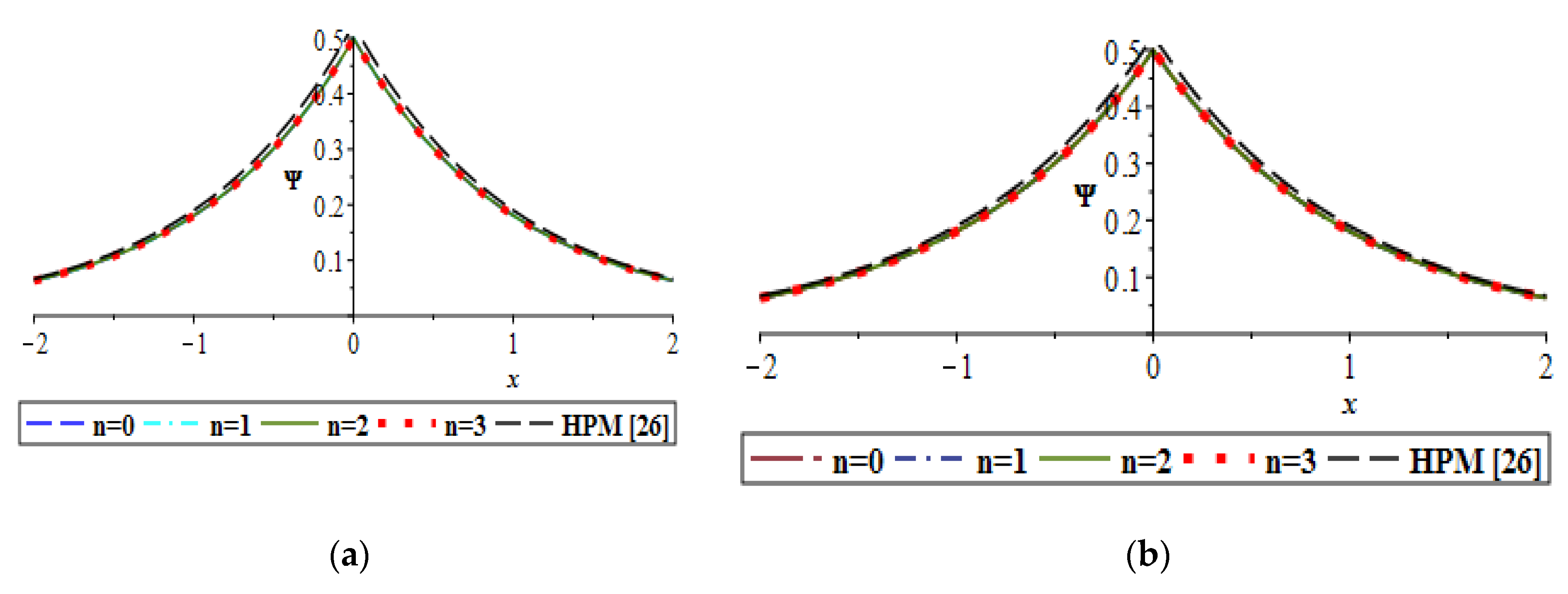
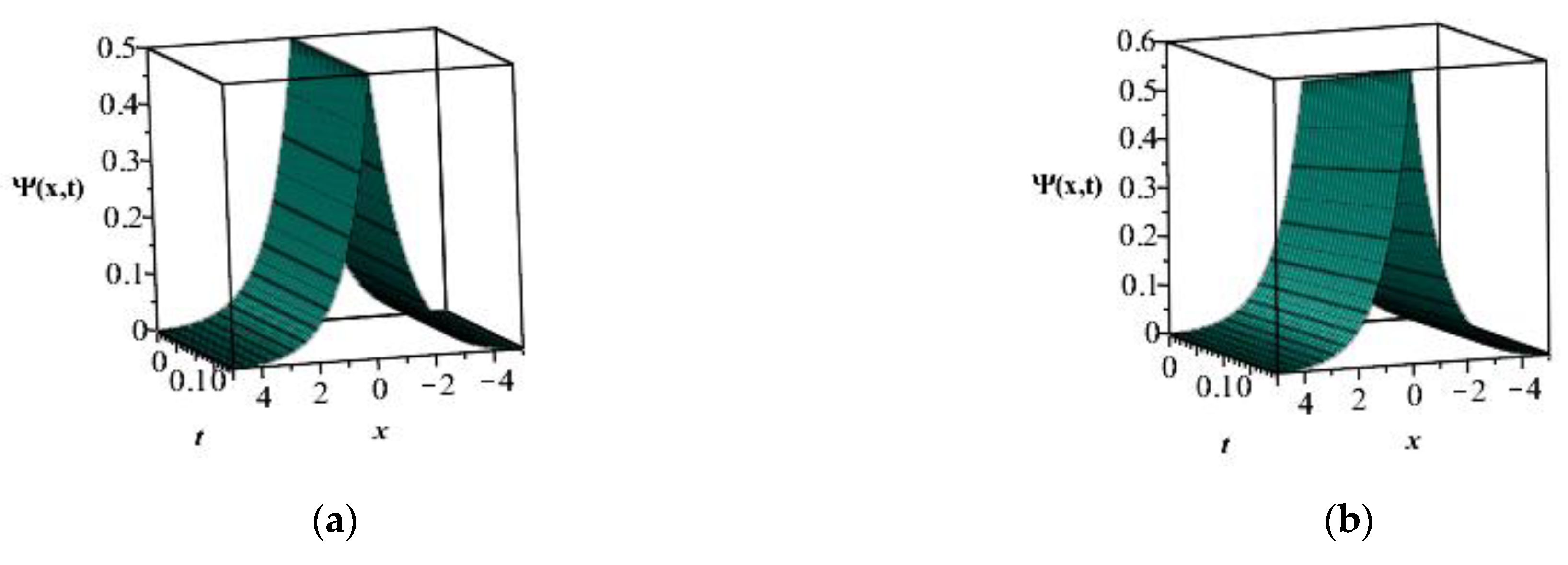
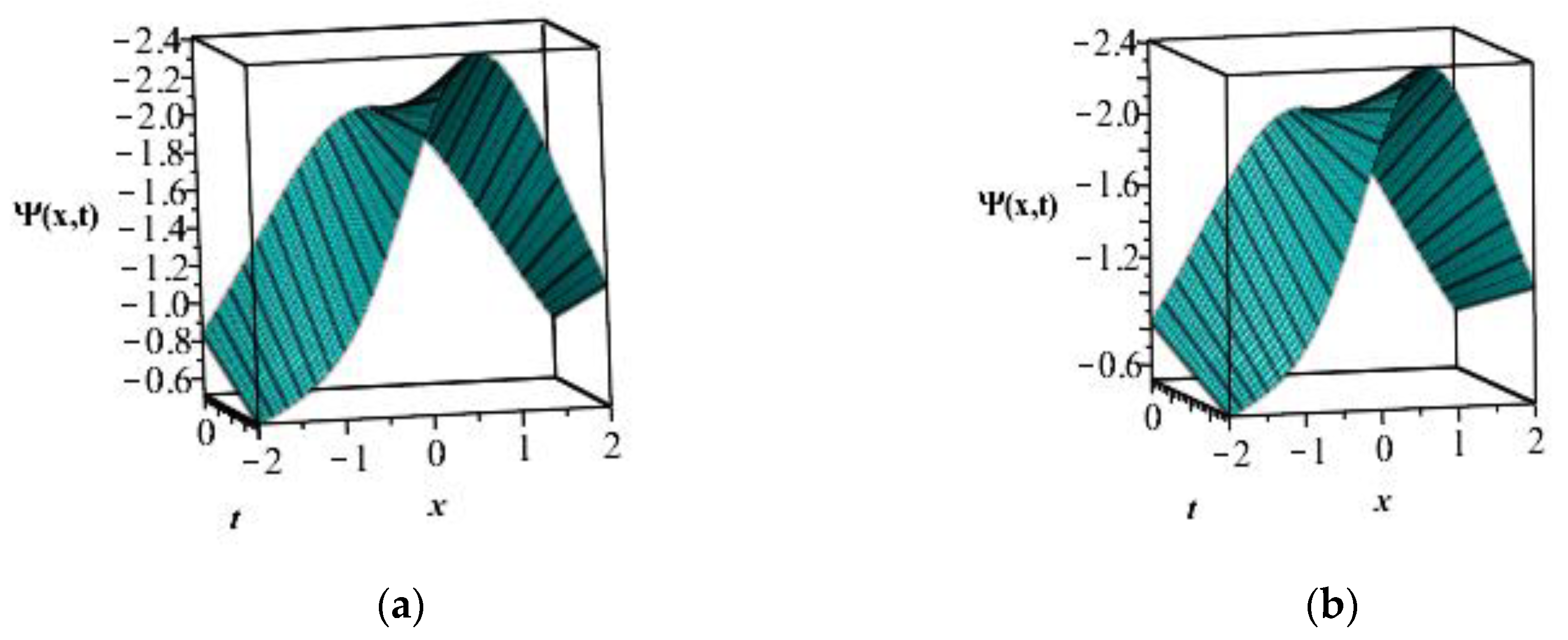
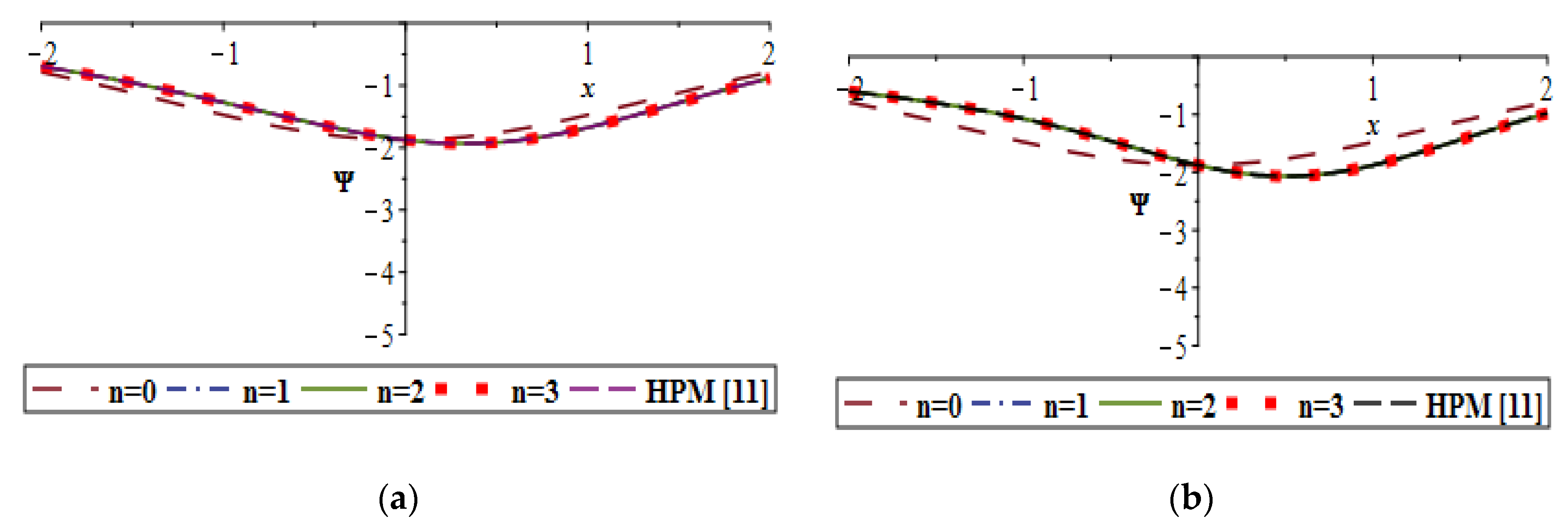
7. Results and Discussion
8. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Caputo, M.; Mainardi, F. Linear models of dissipation in an elastic solids. Riv. Nuovo Cim. 1971, 1, 161–198. [Google Scholar] [CrossRef]
- Carpinteri, A.; Mainardi, F. Fractals and Fractional Calculus in Continuum Mechanics; Springer: New York, NY, USA, 1997. [Google Scholar]
- Jena, R.M.; Chakraverty, S. A new iterative method based solution for fractional Black–Scholes option pricing equations (BSOPE). SN Appl. Sci. 2019, 1, 95. [Google Scholar] [CrossRef]
- Baleanu, D.; Diethelm, K.; Scalas, E.; Trujillo, J.J. Fractional Calculus: Models and Numerical Methods; World Scientific Publishing Company: Boston, MA, USA, 2012. [Google Scholar]
- Baleanu, D.; Machado, J.A.T.; Luo, A.C. Fractional Dynamics and Control; Springer: Berlin, Germany, 2012. [Google Scholar]
- Jena, R.M.; Chakraverty, S. Residual power series method for solving time-fractional model of vibration equation of large membranes. J. Appl. Comput. Mech. 2019, 5, 603–615. [Google Scholar]
- He, J.H. Nonlinear oscillation with fractional derivative and its applications. Int. Conf. Vib. Eng. 1998, 98, 288–291. [Google Scholar]
- Javeed, S.; Baleanu, D.; Waheed, A.; Khan, M.S.; Affan, H. Analysis of Homotopy Perturbation Method for Solving Fractional Order Differential Equations. Mathematics 2019, 7, 40. [Google Scholar] [CrossRef]
- Zhang, B.G.; Li, S.Y.; Liu, Z.R. Homotopy perturbation method for modified Camassa-Holm and Degasperis-Procesi equations. Phys. Lett. A 2008, 372, 1867–1872. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S. Solving time-fractional Navier–Stokes equations using homotopy perturbation Elzaki transform. SN Appl. Sci 2019, 1, 16. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Kilicman, A. Numerical solutions of nonlinear fractional partial differential equations arising in spatial diffusion of biological populations. Abstr. Appl. Anal. 2014, 535793. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S.; Jena, S.K. Dynamic Response Analysis of Fractionally Damped Beams Subjected to External Loads using Homotopy Analysis Method. J. Appl. Comput. Mech. 2019, 5, 355–366. [Google Scholar]
- Ganji, Z.Z.; Ganji, D.D.; Ganji, A.D.; Rostamian, M. Analytical solution of time-fractional Navier–Stokes equation in polar coordinate by homotopy perturbation method. Numer. Methods Part Differ. Equ. 2010, 26, 117–124. [Google Scholar] [CrossRef]
- Yavuz, M.; Ozdemir, N. A Quantitative Approach to Fractional Option Pricing Problems with Decomposition Series. Konuralp J. Math. 2018, 6, 102–109. [Google Scholar]
- Edeki, S.O.; Motsepa, T.; Khalique, C.M.; Akinlabi, G.O. The Greek parameters of a continuous arithmetic Asian option pricing model via Laplace Adomian decomposition method. Open Phys. 2018, 16, 780–785. [Google Scholar] [CrossRef]
- Wazwaz, A.M. Solitary wave solutions for modified forms of Degasperis-Procesi and Camassa-Holm equations. Phys. Lett. A 2006, 352, 500–504. [Google Scholar] [CrossRef]
- Jena, R.M.; Chakraverty, S. Analytical solution of Bagley-Torvik equations using Sumudu transformation method. SN Appl. Sci. 2019, 1, 246. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Kumar, S. Numerical computation of fractional multi-dimensional diffusion equations by using a modified homotopy perturbation method. J. Assoc. Arab Univ. Basic Appl. Sci 2014, 17, 20–26. [Google Scholar] [CrossRef]
- Odibat, Z.; Momani, S. Modified homotopy perturbation method application to quadratic Riccati differential equation of fractional order. Chaos Solitons Fractals 2008, 36, 167–174. [Google Scholar] [CrossRef]
- Keskin, Y.; Oturanc, G. Reduced differential transform method: a new approach to fractional partial differential equations. Nonlinear Sci. Lett. A 2010, 1, 61–72. [Google Scholar]
- Camassa, R.; Holm, D.D. An integrable shallow water equation with peaked solitons. Phys. Rev. Lett. 1993, 71, 1661–1664. [Google Scholar] [CrossRef]
- Gupta, P.K.; Singh, M.; Yildirim, A. Approximate analytical solution of the time fractional Camassa-Holm, modified Camassa-Holm, and Degasperis-Procesi equations by homotopy perturbation method. Sci. Iran. A 2016, 23, 155–165. [Google Scholar]
- Ganji, D.D.; Sadeghi, E.M.M.; Rahmat, M.G. Modified Camassa–Holm and Degasperis–Procesi Equations Solved by Adomian’s Decomposition Method and Comparison with HPM and Exact Solutions. Acta Appl. Math. 2008, 104, 303–311. [Google Scholar] [CrossRef]
- Lundmark, H.; Szmigielski, J. Multi-peakon solutions of the Degasperis–Procesi equation. Inverse Probl. 2003, 19, 1241–1245. [Google Scholar] [CrossRef]
- Degasperis, A.; Procesi, M. Asymptotic Integrability Symmetry and Perturbation Theory; World Scientific: Singapore, 2002; pp. 23–27. [Google Scholar]
- Zhang, B.G.; Li, S.Y.; Mao, J.F. Approximate explicit solution of Camassa-Holm equation by He’s homotopy perturbation method. J. Appl. Math. Comput. 2009, 31, 239–246. [Google Scholar] [CrossRef]




| Functional Form | Transformed Form |
|---|---|
| [28] | FRDTM (n = 0) | FRDTM (n = 1) | FRDTM (n = 2) | FRDTM (n = 3) | |
|---|---|---|---|---|---|
| (0.1, 0.05) | 0.47479025 | 0.45194289 | 0.45194289 | 0.45194289 | 0.45194289 |
| (0.2, 0.05) | 0.42913217 | 0.40845903 | 0.40845903 | 0.40845903 | 0.40845903 |
| (0.4, 0.05) | 0.35043736 | 0.33351162 | 0.33351162 | 0.33351162 | 0.33351162 |
| (0.8, 0.05) | 0.23325678 | 0.22191112 | 0.22191112 | 0.22191112 | 0.22191112 |
| (−0.2, 0.05) | 0.42913217 | 0.40845903 | 0.40845903 | 0.40845903 | 0.40845903 |
| (−0.4, 0.05) | 0.35043736 | 0.33351162 | 0.33351162 | 0.33351162 | 0.33351162 |
| CPU time | 0.053s | 0.063s | 0.078s | 0.124s | |
| [11] | FRDTM (n = 0) | FRDTM (n = 1) | FRDTM (n = 2) | FRDTM (n = 3) | |
|---|---|---|---|---|---|
| (8, 0.05) | −0.00268298 | −0.00268190 | −0.00268297 | −0.00268298 | −0.00268298 |
| (9, 0.05) | −0.00098718 | −0.00098703 | −0.00098718 | −0.00098718 | −0.00098718 |
| (10, 0.05) | −0.00036318 | −0.00036316 | −0.00036318 | −0.00036318 | −0.00036318 |
| (8, 0.1) | −0.00268406 | −0.00268105 | −0.00268405 | −0.00268406 | −0.00268406 |
| (9, 0.1) | −0.00098732 | −0.00098703 | −0.00098732 | −0.00098732 | −0.00098732 |
| (10, 0.1) | −0.00036320 | −0.00036316 | −0.00036320 | −0.00036320 | −0.00036320 |
| CPU time | 0.063 s | 0.093 s | 0.078 s | 0.094 s | |
| [11] | FRDTM (n = 0) | FRDTM (n = 1) | FRDTM (n = 2) | FRDTM (n = 3) | |
|---|---|---|---|---|---|
| (0, 0) | −1.875 | −1.8750 | −1.875 | −1.875 | −1.875 |
| (0.2, 0.2) | −2.1311490 | −1.8563742 | −2.1311490 | −2.1311490 | −2.1311490 |
| (0.4, 0.4) | −2.8273737 | −1.8019555 | −2.8273737 | −2.8273737 | −2.8273737 |
| (0.8, 0.8) | −4.7337056 | −4.7337056 | −4.7337056 | −4.7337056 | −4.7337056 |
| (−0.2, 0.2) | −1.5815995 | −1.8563742 | −1.5815995 | −1.5815995 | −1.5815995 |
| (−0.4, 0.4) | −0.7765374 | −1.8019555 | −0.7765374 | −0.7765374 | −0.7765374 |
| CPU time | 0.01 s | 0.016 s | 0.062 s | 0.078 s | |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jena, R.M.; Chakraverty, S.; Baleanu, D. On New Solutions of Time-Fractional Wave Equations Arising in Shallow Water Wave Propagation. Mathematics 2019, 7, 722. https://doi.org/10.3390/math7080722
Jena RM, Chakraverty S, Baleanu D. On New Solutions of Time-Fractional Wave Equations Arising in Shallow Water Wave Propagation. Mathematics. 2019; 7(8):722. https://doi.org/10.3390/math7080722
Chicago/Turabian StyleJena, Rajarama Mohan, Snehashish Chakraverty, and Dumitru Baleanu. 2019. "On New Solutions of Time-Fractional Wave Equations Arising in Shallow Water Wave Propagation" Mathematics 7, no. 8: 722. https://doi.org/10.3390/math7080722
APA StyleJena, R. M., Chakraverty, S., & Baleanu, D. (2019). On New Solutions of Time-Fractional Wave Equations Arising in Shallow Water Wave Propagation. Mathematics, 7(8), 722. https://doi.org/10.3390/math7080722







