1. Introduction
Projective Klingenberg spaces
(PKS) may be characterized as an incidence structure whose homomorphic image is a projective space over a field. Geometries over rings began to be studied systematically in the mid-20
th Century. W. Klingenberg [
1] followed the study of incidence structures of D. Barbilian [
2] and introduced
Klingenberg spaces (initially
projective spaces with homomorphisms). The definition of a PKS of general finite dimension was presented by H. H. Lück in [
3]. These topics were also developed by J. C. Ferrar and F. D. Veldkamp [
4,
5,
6] and P. Y. Bacon (e.g., [
7]). Projective geometry is also related to the theory of geodesic mappings (e.g., [
8]). F. Machala [
9] introduced projective Klingenberg spaces over local rings. The arithmetical fundament of such spaces is a free finite-dimensional
A-module over a local ring
A (
A-space in the sense of B.R. McDonald [
10]). Subspaces (points, lines, hyperplanes, etc.) of a PKS over a ring
A are subsets of points whose homomorphic images are subspaces of the respective dimension of the projective space over
mentioned above. Thus, PKS may be also treated as a projective space over a ring in the sense of Bingen. In the case of PKS over certain local rings (
plural algebras,
11]), we may study in more detail the structure of PKS, and we can find some special properties (for example, we introduce the
degree of neighborhood). By this apparatus, we may describe not only subspaces of PKS, but also such sets of points
(submodules of PKS) whose arithmetical representatives belong to a general submodule of the arithmetical fundament of PKS.
Let us consider the following local algebra
A (according to [
11]):
Definition 1. A plural algebra of order m over a field T is every linear algebra A on T having as a vector space over T a basis: Remark 1. It follows from Definition 1 that any element α of A may be uniquely expressed in the form: Evidently, A is a local ring with the maximal ideal 𝔞 = , and all proper ideals of A are just .
For the case , we obtain well-known dual numbers; for general m, we have plural numbers. Moreover, if , then A is a Weil algebra of order m and width one; therefore any A-space is also a Weil module.
Let
M be an
A-space. It is well known that all bases of
M have the same number of elements (
A-dimension of M), and from every set of generators, a basis of
M may be selected (see [
10]). Above that, in our case, the following properties of
A-space
M have been proven in [
12] (the point 3 may be considered as a criterion of transversality of two
A-subspaces; Veldkamp [
13] called two
A-subspaces
transversal if both their intersection and their sum are
A-subspaces):
Theorem 1. Let M be an A-space over a plural algebra A. Then, the following hold:
- 1.
Any linearly-independent system of elements of M may be completed to a basis of M,
- 2.
A submodule of M is a free submodule if and only if it is a direct summand of M.
- 3.
An intersection of two A-subspaces of M is an A-subspace of M if and only if the sum of them is an A-subspace of M.
Remark 2. A subspace of an A-space M (A-subspace) is usually defined as a free direct summand of M. If A is a plural algebra, it follows from Theorem 1 that A-subspaces of M are just all free submodules of M.
Through the following text, let
M denote an arbitrary, but fixed
A-space over a plural algebra
A. Let us consider an endomorphism
on
M defined by the relation:
Theorem 2. Let K be a nontrivial submodule of A-space M. Then, there exists a system of subsets on M such that:
- 1.
is a basis of M,
- 2.
is a set of generators of K.
In this case, is an integer with .
Proof. Let us denote
Since
M is a free module, it follows from [
14] that
. This implies:
Evidently, there exists a unique such that . Respecting the fact that K is a vector space over 𝔞, we have that is a nilpotent endomorphism of K, and therefore, we obtain elements
of
K such that:
form a
T-basis Ker
mod Ker
As
(see (
3)), there exist
with:
In the same way,
implies the existence of elements
with:
Let us denote
and
.
(a) Let us show the linear independence of the set
Supposing:
and denoting (according to (
1))
, where
, we obtain:
Multiplying this equality by
and using (
4) and (
5), we may write:
We have obtained a linear combination of the elements of a
T-basis of submodule
K with coefficients from
T. It gives
for
. Therefore, (
6) may be written in the form:
Multiplying this equality by
and using again (
4) and (
5), we obtain
. Then, (
6) may be written as:
Multiplying (
6) by
consecutively, we have that all
are zero and
, consequently.
Since is a set of linearly-independent elements, it may be completed by a set to an A-basis of M (according to Theorem 1).
(b) Let us show that generates (over A) the module K.
Respecting (
4) and (
5), we may write:
If an element x of M may be expressed as a linear combination of elements of a T-basis of submodule K with coefficients from T, then it may be also expressed as a linear combination of the elements of the set with coefficients from A and vice versa. ☐
2. Projective Klingenberg Spaces
Let us remind about the definition of a projective Klingenberg space (Klingenberg’s definition as modified by Lück [
3]).
Definition 2. A projective Klingenberg space of dimension n, , is an incidence structure with a homomorphism μ of onto an n-dimensional projective space such that:
- 1.
If are points in P such that are independent in , then there exists a hyperplane in H such that . This hyperplane is unique if .
- 2.
this condition is the dual of one.
- 3.
If and are such that , as well as are independent and , then:
Following [
9], we define:
Definition 3. Let A be a local ring and 𝔞 be its maximal ideal. Let us denote . Then, an incidence structure such that
- 1.
points in are just all submodules such that is a nonzero element of ,
- 2.
hyperplanes in are just all submodules such that are linearly-independent elements of ,
- 3.
the incidence relation is an inclusion,
is called an n-dimensional projective Klingenberg space over the ring A.
For any point of , an element x is called an arithmetical representative of the point X. The module M is called the arithmetical fundament of the space .
It is known that for , there is no (up to an isomorphism) other projective Klingenberg spaces except of PKS over a local ring. In the case of planes, it is true only for Desarguesian ones.
Remark 3. Let us consider the n-dimensional projective space over the field (i.e., with arithmetical fundament ). Then, is an homomorphic image of in the homomorphism μ defined by:Thus, points of are just submodules in M that are (by homomorphism μ) mapped on points of the projective space,
and hyperplanes in are just submodules in M that are mapped (by homomorphism μ) on hyperplanes of the projective space.
The following definition is natural. According to Definition 3, points and hyperplanes correspond to the cases and , respectively (it is usual to identify a hyperplane with the set of points incident with , and we will use this approach).
Definition 4. Let be an n-dimensional projective Klingenberg space and M be its arithmetical fundament. Let a submodule K of M be given. A set:is called a k-dimensional subspace in , if , and are linearly-independent elements of . The submodule K is called an arithmetical fundament of the subspace .
Define a relation “to be neighbor” on points of PKS. Thus, PKS may be also treated as Barbilian spaces.
Definition 5. Points are called neighbors, if . Otherwise, we speak of non-neighbor points.
In what follows, we study
n-dimensional PKS
over a plural algebra
A with arithmetical fundament denoted by
M (Definition 3). Obviously, the module
M is an
A-space. Using Theorem 1 (and Theorem I.2 of [
10]), we have characterized the notions
point and
hyperplane, as well as the
subspace of arbitrary dimension in PKS (cf. [
15]).
Theorem 3. Let be a projective Klingenberg space. Then, k-dimensional subspaces of , , are just all subsets (
8)
such that K is a -dimensional A-subspace in M. Theorem 3 implies that any PKS
can be also treated as a
projective space over the ring A in the sense of Bingen [
16] if we ignore the neighbor relation. Bingen has defined these projective spaces as structures formed by
A-subspaces of a free finite-dimensional
A-module.
Let us define a useful subrelation of the relation “to be neighbor”. We get a new equivalence relation on the set of points of ; a couple of points belongs to this one, if they have the same degree of neighborhood. That allows one to study new properties of PKS.
Definition 6. [
15] Let
and
be points of a projective Klingenberg space
, and let
r be a non-negative integer satisfying:
The number
r is called the
degree of neighborhood of the pointsXandY.
Clearly, for a couple of non-neighbor points, we have , for neighbor different points and for identical points .
For arbitrary point X and every integer there exists at least one point Y such that the degree of neighborhood of points is equal to r.
Definition 7. Let X be a point and be a set of points of a projective Klingenberg space. We said that r is a degree of neighborhood of X and if there exists at least one point such that the degree of the neighborhood of points is equal to r and the degree of the neighborhood of X and any point of is no greater then r.
Corollary 1. If is a subspace of and K is an arithmetical fundament of , then the degree of neighborhood of a point and subspace is equal to r if and only if
Let
be a linear form on an
h-dimensional
A-space
M such that Im
. Then, Ker
is an
-dimensional
A-subspace in
M (see [
12]), and for
, the subset (
8) forms a hyperplane in KPS
. If
is a general linear form, then its kernel need not be an
A-subspace. Then, there is a question about how to describe a set of points of
whose arithmetical representatives belong to a kernel of a general linear form.
For any linear form
on
M, there exists a linear form
with Im
and just one integer
(called an
order of linear form ) such that
(see [
17]).
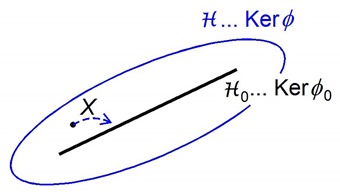
Lemma 1. Let be projective Klingenberg space. Let ϕ be an arbitrary linear form on M of order k. Then, the set:is formed by all points with the degree of neighborhood at least to a certain hyperplane of . If is a form of zero order such that , then: ![Mathematics 07 00702 i001]()
Proof. Let
, where
is a linear form of zero order. For kernels of linear forms
, it holds:
According to Theorem 3, a subset
is a hyperplane in
. Let
be a point belonging to
; thus,
. Therefore, there exists an element
with
Because
is an
A-subspace,
y may be written as
, where
z is a linearly-independent element from
(clearly,
). We get
, which means that points
X and
are neighbors with degree at least
. ☐
Now, we may present a natural generalization of the notion
subspace of Klingenberg projective space . We have seen that
subspaces in
are just all subsets of points whose arithmetical representatives belong to some
A-
subspace of
M. Let us in (
8) consider an arbitrary submodule
K of
M. In this case, the subset (
8) of points of
is appropriate, called a
submodule of KPS.
Definition 8. Let be an n-dimensional projective Klingenberg space and M be its arithmetical fundament. Let a submodule K of M be given. Then, a set:is called a submodule in (with arithmetical fundament K). The following theorem brings a pure geometric description of the submodules of PKS .
Theorem 4. Let be projective Klingenberg space and M be its arithmetical fundament. Let K be an arbitrary non-trivial submodule in M. Then, there exists a systemof sets of hyperplanes of such that the submodule of with arithmetical fundament K is equal to the intersection of:
Proof. Let us denote by
the submodule of
with arithmetical fundament
K. Due to Theorem 2, we get for a submodule
K a system of sets
. Let us denote their elements in the following way:
and construct by these sets a base
of an arithmetical fundament
M. A dual base
of a dual
A-space
may be constructed as well (cf. [
12]). Any element of
is a linear form of zero order, of course.
For any linear form
, let us denote by
a hyperplane in
with arithmetical fundament
. We obtain the following system of sets of hyperplanes:
Let us consider an arbitrary point
. Respecting the form of a set of generators of the submodule
K, as is described in Theorem 2 (2), we have that
X belongs to
(i.e.,
) if and only if:
It may be equivalently expressed by:
Finally, we have that
if and only if:
Now, using Lemma 1, we obtain the proven theorem. ☐
The notion of the “degree of neighborhood” has shown up as a key one, which allows us to describe pure geometrically point sets that form submodules of PKS. Now, we see that the structure of Klingenberg spaces is richer than the structure of subspaces of a projective space over the ring A in the sense of Bingen.