1. Introduction
Let
and
be two Hilbert spaces,
and
be two closed, convex and nonempty sets. Let operator
be bounded and linear. The split feasibility problem (SFP for short) was proposed by Censor and Elfving [
1] to solve the phase retrieval problems, and is formulated as:
Let
,
,
be the adjoint operator of
G, then SFP (1) can be reformulated as:
This class of problem has received plenty of attention due to its wide applications, such as intensity-modulated radiation therapy [
2], signal processing [
3], image reconstruction [
4], etc.
Many algorithms have been developed to solve the SFP. One of the most popular and practical algorithms is the CQ algorithm, which was proposed by Byrne [
5]:
where
is the adjoint operator of
A,
is the step size, while
and
denote the orthogonal projection onto
C and
Q, respectively.
As a quite important generalization of the CQ algorithm, López et al. [
6] introduced the following dynamic step size CQ algorithm and obtained a weak convergence result:
where
The highlight of the dynamic step size CQ algorithm is that it does not require any prior knowledge about the norm of the operator A.
Under some additional assumptions, the strong convergence property of the CQ algorithm was developed in [
7] as special cases of some generalized CQ-type algorithms. More papers about this topic are given [
8,
9] and the references therein. However, there are few results involving the rate of convergence.
In this paper, we investigate the multiple-sets split feasibility problem (MSSFP), which is to find a point such that:
where
r and
t are positive integers;
and
are closed, convex and nonempty subsets of Hilbert spaces
and
, respectively;
is a bounded linear operator. Without loss of generality, suppose that
, and choose
. Let
,
,
,
,
be the adjoint operator of
G. Then MSSFP (3) can be reformulated as:
Censor et al. [
10] proposed the following iterative formula by using the projection gradient method for solving the MSSFP:
where
is an auxiliary simple set,
,
is the spectral radius of
,
with
,
. However, this algorithm is usually difficult to calculate. Then, Censor et al. [
11] developed the following simultaneous sub-gradient projection algorithm, which is an easily calculated algorithm that uses orthogonal projection onto half-spaces, to solve the MSSFP:
Here,
,
is the spectral radius of
,
with
,
and:
where
,
, and:
where
,
. However, the above projection method with a fixed step size may be very slow. Then, motivated by the extrapolated method for solving the convex feasibility problems in [
12], Dang et al. [
13] proposed a simultaneous sub-gradient projection algorithm to solve the MSSFP by utilizing two extrapolated factors in one iterative step. We remark here that the above algorithms only converge weakly to a solution of the MSSFP. Moreover, the rate of convergence has not been explicitly estimated. Based on the above disadvantages, we propose a simultaneous sub-gradient projection algorithm with the dynamic step size (SSPA for short) for solving the MSSFP by utilizing projections onto half-spaces to replace the original convex sets, and we investigate the linear convergence of the SSPA. Furthermore, we conclude the linear convergence rate of the SSPA.
The rest of this paper is organized as follows.
Section 2 introduces the concept of bounded linear regularity for the MSSFP and presents some relevant definitions and lemmas which will be very useful for our convergence analysis.
Section 3 gives the SSPA, the proof of its linear convergence and its linear convergence rate.
Section 4 presents some numerical results to clarify the validity of our proposed algorithm.
2. Preliminaries
For convenience, we always suppose that
H is a real Hilbert space with the inner product
and the norm
.
I denotes the identity operator on
H. For a set
,
denotes the interior of
C. We denote by
and
as the unit open metric ball and unit closed metric ball with center at the origin, respectively, that is:
For a point
and a set
, the orthogonal projection of
x onto
C and the distance of
x from
C, denoted by
and
, are respectively defined by:
The following proposition is about some well-known properties of the projection operator.
Proposition 1 ([
14])
. Let be a closed, convex and nonempty set; then, for any and ,(i) ;
(ii) ;
(iii) ;
(iv) .
Throughout this paper, we denote the solution set of MSSFP (1.3) by using
S, which is defined by:
and assume that the MSSFP is consistent; thus,
S is also a closed, convex and nonempty set. Then, the following equivalence holds for any
:
The aim of this section is to construct several sufficient conditions to ensure the linear convergence of the SSPA for MSSFP (3). Recall that a sequence
in
H is said to converge linearly to its limit
(with rate
) if there exists
and a positive integer
N such that:
Next, we will introduce the concept of bounded linear regularity.
Definition 1 ([
15])
. Let be a collection of closed convex subsets in a real Hilbert space H and . The collection is said to be bounded linearly regular if for each there exists a constant such that: Lemma 1 ([
16])
. Let be a collection of closed convex subsets in a real Hilbert space H. If , then the collection is bounded linearly regular. Definition 2. The MSSFP is said to satisfy the bounded linear regularity property if for each there exists a constant such that: Let operator be bounded and linear. We use to denote the kernel of G. The orthogonal complement of is represented by . As is well known, both and are closed subspaces of H.
Lemma 2 ([
17])
. Let operator be bounded and linear. Then G is injective and has a closed range if and only if G is bounded below, namely, there exists a positive constant v such that for all . Lemma 3. Let be bounded linearly regular and the range of G be closed; then, MSSFP (4) satisfies the bounded linear regularity property.
Proof. is bounded linearly regular, so for any
there exists
such that:
Since
G restricted to
is injective and its range is closed, by Lemma 2, we know that there exists
such that:
Combining Inequations (8) and (9), we obtain:
This, together with Inequation (10), implies that:
The proof is complete. □
Now, we will provide the concept of sub-differential which is necessary to construct the iterative algorithm later.
Definition 3 ([
16])
. Let be a convex function. The sub-differential of f at x is defined as: An element of is said to be a sub-gradient.
Lemma 4 ([
16])
. Suppose that is nonempty for any ; define the half-space by:Then:
;
If , then is a half-space; otherwise, ;
;
.
Finally, the following equality and concept of the Fejér monotone sequence are also important for the convergence analysis.
Lemma 5 ([
14])
. Let be a finite family in H, and be a finite family in R with , then the following equality holds: Definition 4 ([
14])
. Let C be a nonempty subset of H and be a sequence in H. is called Fejér monotone with respect to C if: Clearly, a Fejér monotone sequence is bounded and exists.
3. Main Results
In this section, we will propose the SSPA and show that the algorithm converges linearly to a solution of MSSFP (3). Without loss of generality, the sets
and
can be represented as:
and
where
are convex functions, for all
(
t is a positive integer). Suppose that both
and
are sub-differentiable on
and
, respectively, and that
and
are bounded operators (namely, bounded on bounded sets). Define:
where
,
, and:
where
,
.
By the definition of the sub-gradient, it is clear that the half-space
contains
and the half-space
contains
. Then:
Hence, by Equation (
5), one has that:
Due to the specific form of and , from Lemma 8 we know that the orthogonal projections onto and may be computed directly.
Censor et al. [
11] defined the proximity function
of the MSSFP as follows:
where
,
for all
i and
j,
.
and
are defined by Equations (11) and (12), respectively. Hence, the function
is convex and differentiable with gradient:
and they constructed the following iterative algorithm for the MSSEP:
Here , L is the Lipschitz constant of with , is the spectral radius of , , with .
Now, we use the modification of Equation (
13) to give our simultaneous sub-gradient projection algorithm with the dynamic stepsize for the MSSFP.
Theorem 1. Suppose that MSSFP (3) satisfies the bounded linear regularity property. Let the sequence be defined by Algorithm 1. If the following conditions are met:
is linearly focusing, that is, there exists such that: ().
then, converges linearly to a solution of the MSSFP.
Proof. Without loss of generality, we suppose that is not in S for all . Otherwise, Algorithm 1 terminates in a finite number of iterations, and the conclusions are clearly true. Then, in view of Algorithm 1, one sees that is not in Q for all .
| Algorithm 1: SSPA |
For an arbitrarily initial point , the sequence is generated by:
where at each iteration n:
;
and . |
Take a point
and
. For simplicity, we write:
In fact, the first inequality is trivial, while the second one holds because, by Proposition 1 (iv) and
:
We will firstly prove that the sequence
is Fejér monotone with respect to
S. From Algorithm 1, we have:
Based on the properties of the projection operator (i.e., Proposition 1) and
, we get the following estimations:
and:
Substituting Inequations (15) and (16) into Inequation (14), we obtain:
According to (i) in Algorithm 1, it follows from Inequation (17) that:
That is, the sequence is Fejér monotone with respect to S. Hence, is bounded and exists.
Then, we will show that converges linearly to a solution of MSSFP (3).
Since
is taken arbitrarily in
S, by Inequation (17), we have:
From (i) in Algorithm 1, one deduces that:
Thus, there exists
N such that:
Then Inequation (18) reduces to:
Note that
is linearly focusing; there exists
such that:
We can know from condition (b) that
. By Lemma 1, we obtain that
is bounded linearly regular. In view of Definition 1, there exists
such that:
that is:
Substituting Inequations (20) and (21) into Inequation (19), we obtain:
where
and
and
.
Since the MSSFP satisfies the bounded linear regularity property, there exists
such that:
Substituting Inequation (23) into Inequation (22), we get:
Obviously, for each
,
is monotone decreasing for
n, hence:
Let
, then:
Since
, it follows that
is a Cauchy sequence and converges to a solution
of MSSFP (3), satisfying:
Moreover, from (i) in Algorithm 1, one knows that:
Let
, then there exists
such that
for
. It follows that:
where
. Hence,
converges linearly to
. The proof is complete. □
When , Algorithm 1 reduces to an iterative algorithm for solving SFP (2).
Definition 5. SFP (2) is said to satisfy the bounded linear regularity property if for each there exists a constant such that:where , and . Corollary 1. Let SFP (2) satisfy the bounded linear regularity property (i.e., Inequation (24) holds). For an arbitrary initial point , the sequence is defined by:where . Then, converges linearly to a solution of SFP (2). 4. Numerical Experiments
Let
,
,
and
be defined by:
then
,
. Since
and
,
,
.
and
are defined by:
respectively. Let
be defined by:
Then, , the range of G is closed and the solution set of SFP is . It is easy to know that the SFP satisfies the bounded linear regularity property by Lemma 3.
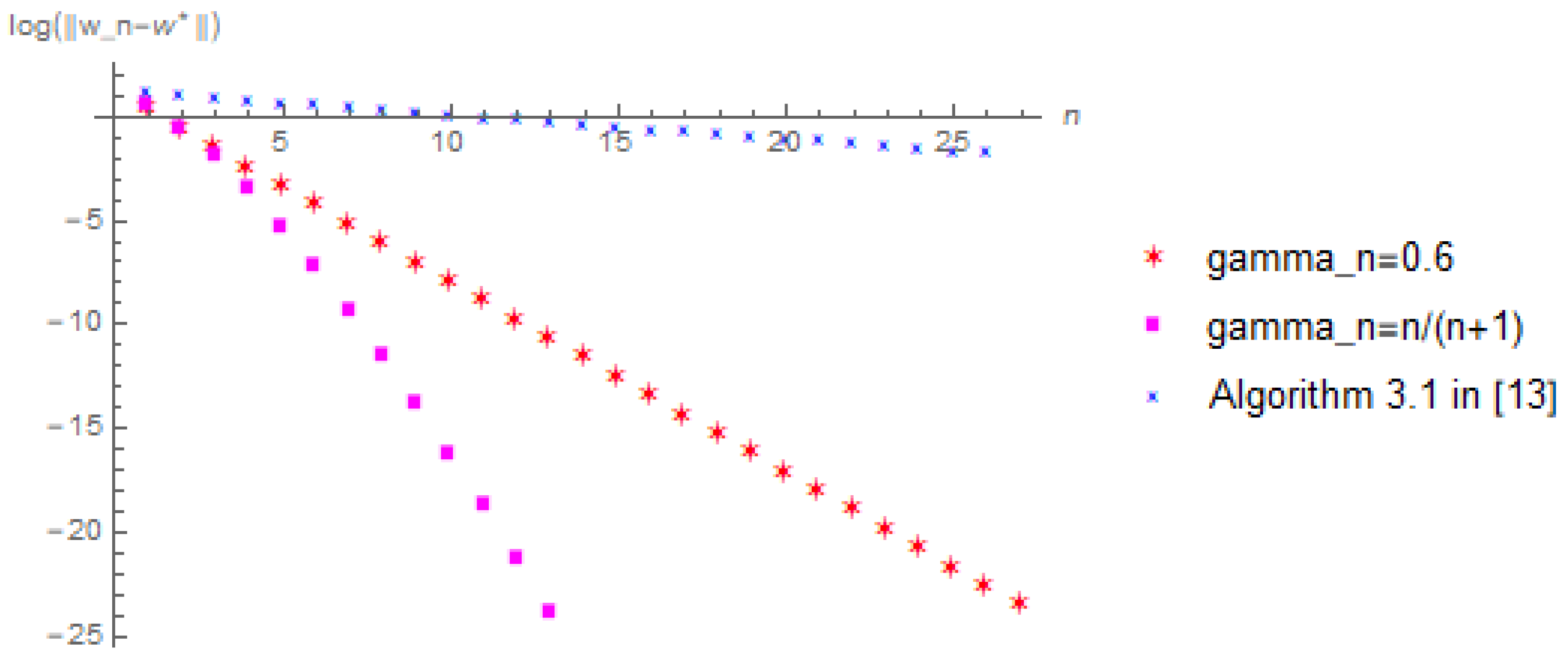
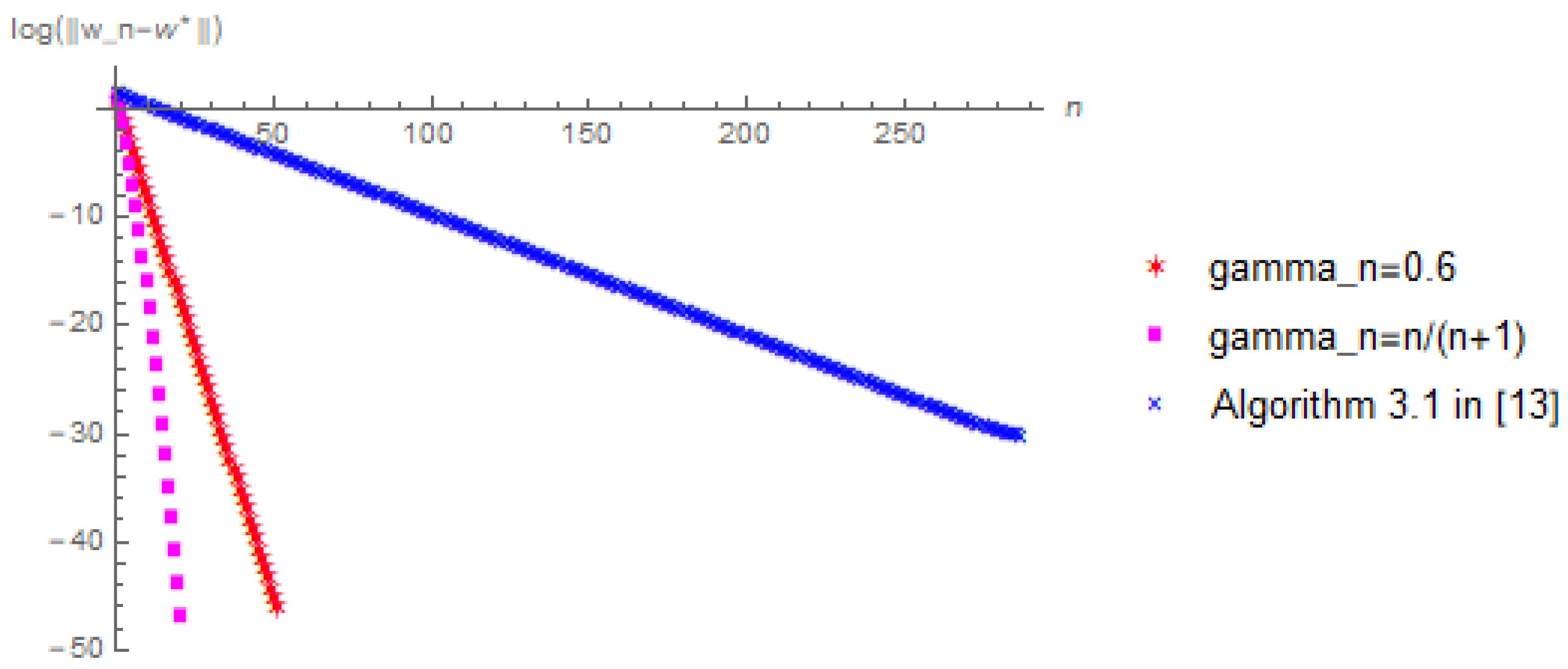
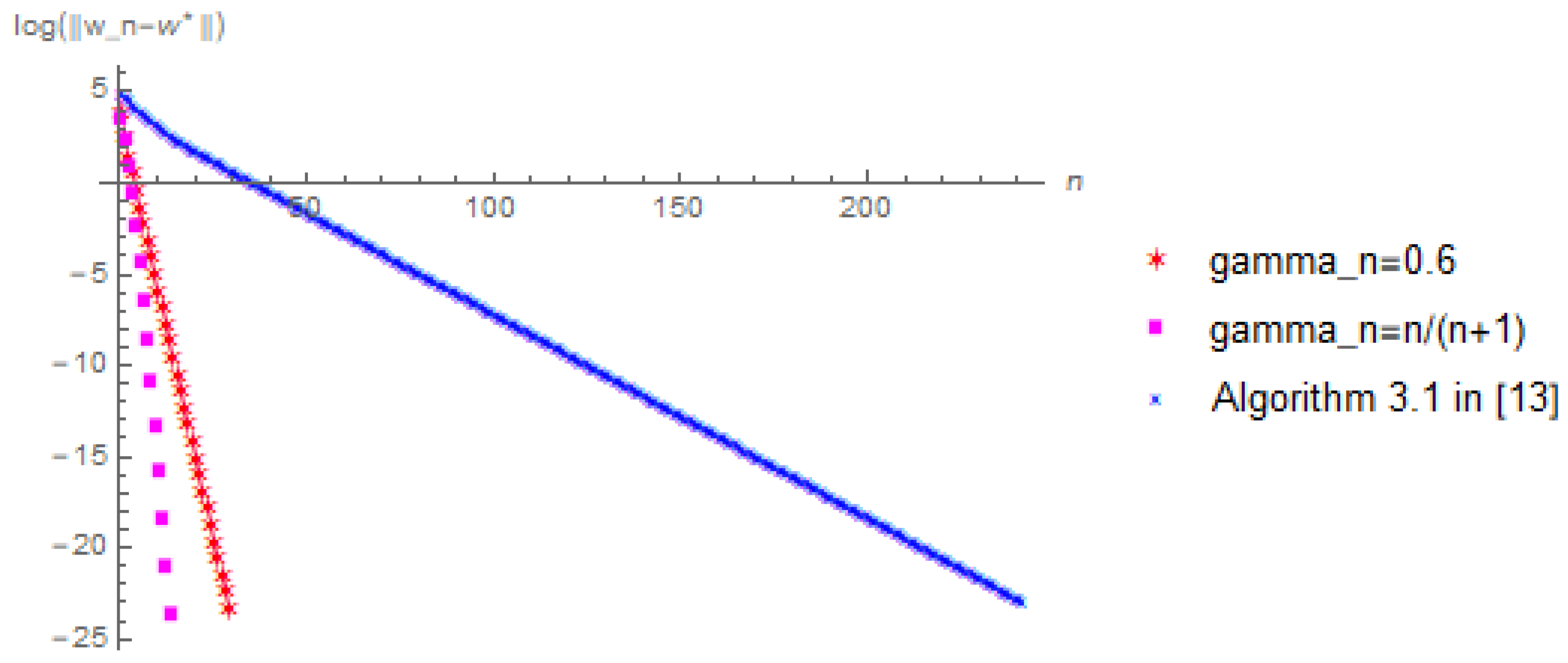
Let
. In view of Equation (
25), we have:
In algorithm (25), we take
. Moreover, we choose the error to be
and
and the initial value to be
and
, respectively. In addition, under the same conditions, we also compare with Dang’s Algorithm 3.1 in [
13] to confirm the effectiveness of our proposed algorithm. For convenience, we choose
in Dang’s Algorithm 3.1. Then we have the following numerical results displayed in
Figure 1,
Figure 2,
Figure 3 and
Figure 4. Note that we denote the number of iterations and the logarithm of the error by using the x-coordinate and the y-coordinate of the figures, respectively. We wrote all the codes in Wolfram Mathematica (version 10.3). All the numerical results were run on a personal Asus computer with AMD A9-9420 RADEON R5, 5 COMPUTE. CORES 2C+3G 3.00 GHz and RAM 8.00 GB.