Production-Inventory System for Deteriorating Items with Machine Breakdown, Inspection, and Partial Backordering

Abstract

This study considers the effects of a machine breakdown, inspection, and partial backordering for deteriorating items. Most industries try to reduce facility unavailability by implementing a regular inspection and preventive maintenance since there is a possibility that some machines will breakdown during the production process. Moreover, an emergency purchase policy can be provided for quick response to customer’s backorder. The system also produces imperfect items with different rates before and after the inspection. Rework process and post-sales warranty are launched for the defective items. Unlike previous studies, we applied a fixed-point approach and renewal reward theorem to solve the deteriorating production-inventory model while considering machine breakdown, inspection, and partial backordering. A case example and sensitivity analysis are provided. The sensitivity analysis shows the important parameters that should be considered in designing the inspection plan and the replenishment policy when facility unavailability and imperfect items exist.

1. Introduction

Inventory management is the process whereby the appropriate inventory is kept to guarantee the availability of stocks to the customers [1]. The inventory cost is one of the most dominant costs in many enterprises in managing the production-inventory system. Moreover, after a certain period, a production facility or machine used in the production process may not be available for several reasons. For example, some of the facilities may be busy with producing other items, while others may undergo random repairs. Regular maintenance is necessary for a well-performing machine. A maintenance strategy consists of inspection, overhaul, repair, and replacement. Without maintenance, defective equipment may result in losses and shortage costs.

The effect of a machine breakdown, imperfect item, quality planning, and deterioration are correlated; these factors cannot be neglected in replenishment planning (see Figure 1). For example, a regular inspection will reduce the probability of machine breakdown, which will affect the possibility of shortages and the need for an emergency purchase. Machine inspection is also correlated to its performance, which will affect the defective product rates. Wee & Widyadana [2,3] developed an economic production quantity (EPQ) model with preventive maintenance and reworked of defective units for deteriorating items, such as in semiconductor and printed circuit board (PCB) industries. Providing warranty policy is another alternative for overcoming the effect of the imperfect quality problem [4,5]. Besides, emergency purchase [6] and shortage backorder [7,8] are additional considerations in replenishment planning.

This study extends previous studies and contributes a new economic production quantity (EPQ) model while considering the effects of scheduled inspection, random machine breakdown, unpredictable repair time, and imperfect items for deterioration items. The rework process is not perfect. Therefore, a warranty is provided to compensate the customers. Moreover, a shortage is allowed, in which the manufacturer considers an emergency purchase to overcome the shortage. However, customers are impatient. Therefore, the shortage is partially backlogged. From our literature review, no models simultaneously consider the situations mentioned above. This study uses the renewal reward theorem to solve the production-inventory system. The approximate optimal solution is then derived while using a fixed point iterative approach. The objective of the proposed model is to minimize the total cost by determining the optimal production up-time period and the elapsed time of implementing inspection time. This paper consists of the following: Section 1 shows the introduction and Section 2 is the literature review. Section 3 is the notation and assumptions. An algorithm deriving the approximate optimal solution is given in Section 4. Section 5 provides a numerical example, sensitivity analysis, and some graphical illustrations. Finally, the conclusions are given in Section 6.

2. Literature Review

2.1. Economic Production Quantity with Machine Unavailability and Maintenance

Ideally, machines should restart a new production cycle when the inventory runs out. The causes of stockout are the result of a machine breakdown, unscheduled demand, and/or unscheduled corrective maintenance. Groenevelt et al. [9] investigated the effect of machine breakdown and corrective maintenance on optimal production lot size. Moinzadeh and Aggarwal [10] examined the single-stage model while considering the reorder and maximum inventory level with backorders. They assumed an exponentially distributed breakdown intervals with constant restoration times. Giri et al. [11] proposed the EPQ model while considering machine failure, repair time, and an acceptable production rate. Recently, Peymankar et al. [6] studied the effects of certain contractual agreements on the EPQ model, when considering machine breakdown. During the machine repair, the manufacturer has some options, such as purchasing the items from the free market or a predetermined supplier under contract. Their study considered revenue sharing and price discount contract.

Most industries schedule preventive maintenance to avoid or minimize the frequencies of machine breakdown. Abboud et al. [12] studied production lot-sizing, while assuming machine unavailability due to maintenance or being used for other products and customer. Lin and Gong [13] eliminated the assumption by considering random machine breakdown and a constant production rate. Aghezzaf et al. [14] provided a maintenance planning model with an integrated point of view. They investigated the inventory system with random item failure during the finite planning horizon. Chakraborty et al. [15] considered the out of control and machine breakdown condition in the EPQ model. Chakraborty et al. [16] extended their previous model by scheduling an inspection during the production run. Liao et al. [17] incorporated perfect and imperfect preventive maintenance. Chung et al. [18] considered random machine unavailability for the economic production deteriorating model to derive the optimal production uptime period. Widyadana and Wee [19] considered deterioration and random machine breakdown with stochastic repair time. Wee and Widyadana [2,3] considered stochastic preventive maintenance time and imperfect quality with different rework rules. Cheng et al. [20] extended the study by integrating the EPQ with quality control and condition-based maintenance under MTS production policy. The cost minimization model is solved while using a simulation method. Moreover, Al-Salamah [21] proposed an artificial bee colony heuristic to solve EPQ with imperfect quality and random machine breakdown. Recently, Marchi et al. [22] considered the learning effect and energy consumption in an EPQ with machine breakdown and defective items. Chiu et al. [23] studied EPQ with stochastic machine failure and random defective rate while considering a minimum service level. Chiu et al. [24] extended the model and considered a multi-shipment policy. Tsao et al. [25] incorporated the Industry 4.0 concept to support predictive maintenance.

2.2. Economic Production Quantity with Defective Item and Warranty

Perfect products are assumed in many EPQ models. However, defective items are common in most manufacturing settings. Numerous studies have investigated the inventory control problem by considering the effect of imperfect items, such as Lee and Rosenblatt [26], who considered process deterioration results in defective products; they determined the optimal production cycle times and the number of inspections. Hayek and Salameh [27] examined an optimal replenishment policy to minimize the overall inventory cost while considering imperfect quality, shortage, and backorder for a finite production model. Huang [28] studied an optimal integrated inventor model while considering defective items in a small lot size. Goyal et al. [29] developed an approach to determine an optimally integrated vendor-buyer inventory with imperfect quality.

Industries may offer warranties for the non-conforming items within a warranty period to reduce the customer’s complaint. Yeh et al. [4] considered free minimal repair warranty and optimized the production run length. An optimal production run length will keep the system in its in-control state, hence reducing the defects and warranty cost. Wang and Sheu [5] considered the tradeoff between manufacturing and warranty costs for products sold under free-repair warranty to find the optimal lot size. Wang [30] extended the EPQ with free-repair warranty model assuming an increasing production failure rate. Chen et al. [31] studied three different manufacturer’s pricing strategy in a single-manufacturer dual-competing retailer supply chain with warranty period-dependent demand. Sana [32] simultaneously considered rework, warranty, and preventive maintenance and determined the optimal buffer inventory. Chiu et al. [33] considered abort/resume policy in EPQ system with machine breakdown and imperfect items. Taleizadeh and Wee [34] examined a manufacturing system with immediate rework and partial backordering. Sarkar and Saren [35] developed EPQ models that considered warranty cost and the possibility of inspection errors due to product inspection policy. Sett et al. [36] investigated an imperfect production system with preventive maintenance to obtain the optimal buffer inventory and inspection policy. Recently, Cunha et al. [37] developed an EPQ model considering a discount price for imperfect quality items to reduce the total production cost. Taleizadeh et al. [38] considered repair failure, partial backordering, and delayed payment policy in a multi-item EPQ model. Nobil et al. [39] considered non-zero rework setup times in a multi-item EPQ. Taheri-Tolgari et al. [40] considered two types of human inspection error in the EPQ model under fuzzy environment.

2.3. Deterioration Factor

Deteriorating items experience damage, decay, obsolescence, pilferage, and loss of marginal value, which cause reduced usefulness [7]. Misra [41] started the study on EPQ for deteriorating items with some assumptions, such as constant demand, no shortages, and no constraint in space, production lot size, and production setups. Further, the machine is assumed to always be in good condition. Goyal and Gunasekaran [42] studied a deteriorating model by introducing the effects of some marketing policies on the EPQ model. Skouri and Papachristos [43] modeled a deteriorating items EOQ model with time-dependent partial backordering and proposed an algorithm to derive the optimal stopping and restarting production times. Teng and Chang [44] modeled deteriorating items EPQ models while assuming price and stock dependent demand. Law and Wee [45] discussed an integrated supply chain model for both ameliorating and deteriorating items, following Weibull distribution. The model incorporated partial backordering, multiple deliveries, and time discounting.

Chung et al. [18] formulated a production inventory deteriorating item model with random machine unavailability to gain insight into the effect of optimal production uptime period. Palanivel and Uthayakumar [46] developed an economic production quantity model for deteriorating items with price dependent demand, time-dependent holding cost, and partial backordering under inflation. Chen [47] investigated an imperfect manufacturing system to obtain the optimal retail price, replenishment cycle, and the number of shipments. Recently, Daryanto et al. [48] studied the environmental impact of an integrated inventory model while considering carbon emission, imperfect quality, and deterioration.

This research contributes a new EPQ model for deteriorating items under an imperfect production system with random machine breakdown and a certain amount of imperfect quality products. Regular inspection and preventive maintenance are scheduled. However, machine breakdown still occurs and it needs a corrective repair. The rework process is not perfect. Therefore, a warranty is provided to compensate the customers. Moreover, a shortage is allowed, in which the manufacturer considers an emergency purchase to overcome the shortage. However, customers are impatient. Therefore, the shortage is partially backlogged. From our literature review, although the study on EPQ model with machine breakdown and imperfect quality items are a lot, no models simultaneously consider the situations mentioned above.

Table 1. Contribution of selected authors.

Author(s)	EPQ	Machine Breakdown	Preventive Maintenance	Rework	Warranty	Emergency Purchase	Partial Backorder	Deteriorating Items
Misra (1975)	√							√
Groenevelt et al. (1992)	√	√
Wee (1993)	√						√	√
Yan & Cheng (1998)	√						√	√
Abboud et al. (2000)	√	√	√
Yeh et al. (2000)	√				√
Wang & Sheu (2003)	√			√	√
Skouri & Papachristos (2003)	√						√	√
Giri et al. (2005)	√	√
Lin & Gong (2006)	√	√						√
Aghezzaf et al. (2007)	√	√	√
Chakraborty et al. (2008)	√	√	√
Chakraborty et al. (2009)	√	√	√
Liao et al. (2009)	√	√	√	√
Chung et al. (2011)	√	√						√
Widyadana & Wee (2011)	√	√						√
Wee & Widyadana (2012)	√		√	√				√
Sana (2012)	√		√	√	√
Wee & Widyadana (2013)	√		√	√				√
Chiu et al. (2013)	√	√
Palanivel & Uthayakumar (2015)	√						√	√
Taleizadeh & Wee (2015)	√			√			√
Sarkar & Saren (2016)	√				√
Sett et al. (2017)	√		√		√
Peymankar et al. (2018)	√	√				√
Cheng et al. (2018)	√	√	√
Al-Salamah (2018)	√	√		√
Cunha et al. (2018)	√						√
Marchi et al. (2019)	√	√		√
Chiu et al. (2019a)	√	√		√
Chiu et al. (2019b)	√	√
Tsao et al. (2019)	√	√	√	√
Taleizadeh et al. (2019)	√			√			√
Nobil et al. (2019)	√			√
Taheri-Tolgari et al. (2019)	√		√		√		√
This paper	√	√	√	√	√	√	√	√

presents the contribution of this research and other authors.

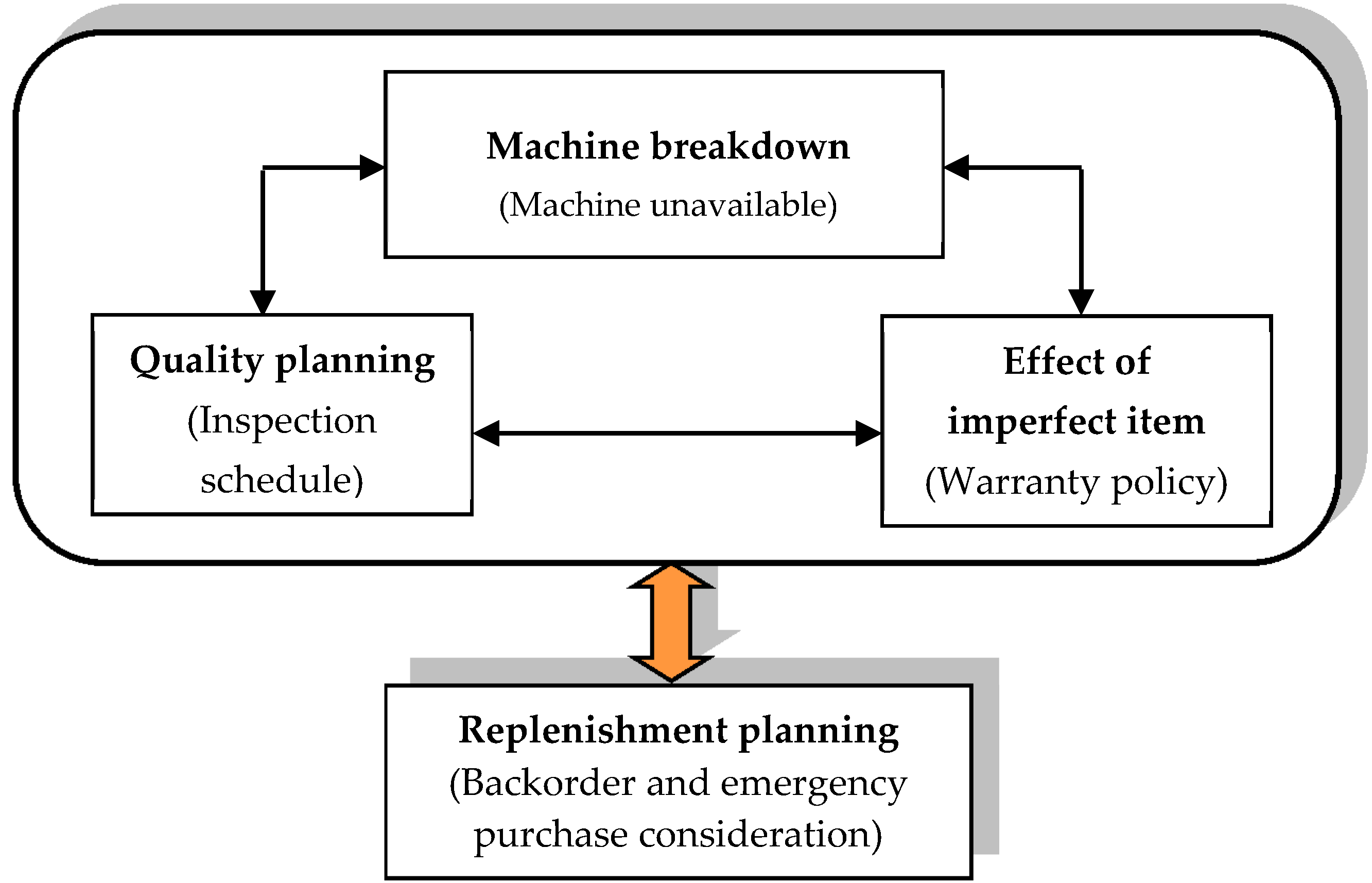
3. Notation and Assumptions

The proposed model is an EPQ model where a machine inspection is scheduled. However, a machine breakdown still possibly occurs during the production up-time. Hence, it requires corrective repair, and then a shortage may occur. In this case, partial backordering takes place and an emergency purchase may be required. The system also produces imperfect items with different rates before and after the inspection. Rework process and post-sales warranty are launched for the defective items. The inventory also considers the effect of item deterioration. The objective of the model is to minimize the total cost by determining the production up-time period and the elapsed time of implementing the inspection time. The following notations and assumptions are used to develop the model.

3.1. Notation

p = production rate

d = demand rate

θ = deteriorating rate

C_s = setup cost

H_s = holding cost per unit

S_d = lost sales cost per unit

C_d = deteriorating cost per unit

I_h = inventory level

I_m = maximum inventory level

I₁ = inventory level in production up-time period

I₂ = inventory level in production down-time period

s = the elapsed time of implementing inspection time

V_sk = cost ratio of setup cost during inspection plan which is inversely proportional to s

R_rsk = variable risk cost per unit time which is proportional to s

C_M = machine breakdown corrective cost

T₁ = production up-time period

T₂ = production down-time period

T₃ = shortage period

T_p = machine breakdown period

T = total replenishment cycle length

θ₁ = Defective rate before predetermined inspection time

θ₂ = Defective rate after predetermined inspection time

C_R = Rework cost per unit

h₁ = Hazard rate of product produced before predetermined inspection time

h₂ = Hazard rate of product produced after predetermined inspection time

C_w = Post-sale warranty cost per unit

C_Ep = Emergency purchase cost per unit from outside supplier

A_Ep = Setup cost per unit per unit time for emergency purchase

γ = backordering rate

μ = The arrival rate of machine breakdown

λ = The maintenance rate

3.2. Assumption

• A single item with a constant rate of production, demand, and deteriorating is considered.
• Production rate is greater than the demand rate.
• The deteriorated items are not replaced.
• Machine repair time is not dependent on the machine breakdown.
• The probability of machine breakdown is exponentially distributed [3,10].

4. Model Development

Figure 2 provides the behavior of the inventory with machine breakdown, inspection, and partial backordering. The production ends at T₁, in which the machine does not breakdown and it reaches the maximum inventory level (I_m). The inventory decreases and reaches zero units due to demand and deterioration at the time (T₁ + T₂). Hence, the machine starts the new cycle. T_p is the elapsed time until breakdown state since there is a machine breakdown possibility during production up-time period T₁. It will require time to repair and reset the machine. During the repair and reset period, the inventory also decreases. The shortage may occur at period T₃, and partial backordering take place because the repair time is stochastic in (T₂ + T₃) period. An emergency purchase may be required to fulfill the backorder quantity from an outside supplier.

From Figure 2, the inventory levels are as follows:

$$\frac{d{I}_1(t_1)}{d{t}_1}+\theta I_1(t_1)=p-d0\le t_1\le T_1$$

(1)

And

$$\frac{d{I}_2(t_2)}{d{t}_2}+\theta I_2(t_2)=-d0\le t_2\le T_2$$

(2)

From the boundary condition of I₁ (0) = 0 and I₂ (T₂) = 0, Equations (1) and (2) can be solved as:

$$I_1(t_1)=\frac{p-d}{\theta }\left\{1-\exp \left(-\theta t_1\right)\right\}0\le t_1\le T_1$$

(3)

$$I_2(t_2)=\frac{d}{\theta }\left\{\exp \left[\theta \left(T_2-t_2\right)\right]-1\right\}0\le t_2\le T_2$$

(4)

Since I₁ (T₁) = I₂ (0), then one has the relationship between T₁ and T₂:

$$I_1(T_1)=\frac{p-d}{\theta }\left\{1-\exp \left(-\theta T_1\right)\right\}=I_2(0)=\frac{d}{\theta }\left\{\exp \left[\theta \left(T_2\right)\right]-1\right\}$$

(5)

Using the Taylor series approximation (Misra, [41]), Equation (5) is rewritten as:

$$(p-d)(T_1-\frac{1}{2}\theta T_1^2)\cong d(T_2+\frac{1}{2}\theta T_2{}^2)$$

(6)

Since θT₂ is a small value, T₂ in terms of T₁ can be approximated as:

$$T_2\cong \frac{(p-d)T_1(1-\frac{1}{2}\theta T_1)}{d}$$

(7)

Most studies in deteriorating production-inventory system assume similar approximation.

4.1. Relevant Cost Functions for Deteriorating Production-Inventory System

4.1.1. Holding Cost Function

The amount of inventory holding, I_h, is illustrated by the following equation:

$$I_h={\displaystyle \underset{t_1=0}{\overset{T_1}{\int }}\frac{p-d}{\theta }\left\{1-\exp \left(-\theta t_1\right)\right\}d{t}_1+{\displaystyle \underset{t_2=0}{\overset{T_2}{\int }}\frac{d}{\theta }\left\{\exp \left[\theta \left(T_2-t_2\right)\right]-1\right\}d{t}_2}}$$

(8)

Assuming that ${\theta }^2{T}_1^2$ is very small, Equation (8) becomes

$$I_h=(p-d)\left(\frac{T_1{}^2}{2}\left(1-\frac{\theta T_1}{3}\right)\right)+d\left(\frac{T_2{}^2}{2}\right)\left(1+\frac{\theta T_2}{3}\right)$$

(9)

By substituting Equation (7) to Equation (9), one has

$$I_h=\left(p-d\right)\left(\frac{T_1{}^2}{2}\left(1-\frac{\theta T_1}{3}\right)\right)+\frac{d}{2}{\left(\frac{(p-d)T_1(1-\frac{1}{2}\theta T_1)}{d}\right)}^2\left(1+\frac{\theta (p-d)T_1(1-\frac{1}{2}\theta T_1)}{3}\right)$$

(10)

Assuming that ${\theta }^2{T}_1^2$ is very small, Equation (10) can be simplified as:

$$I_h=\frac{p^2}{2d}{T}_1^2\left\{\left(1-\frac{d}{p}\right)+\frac{2\theta T_1}{d}\left\{\left[\frac{p}{6}-d\left(1+\frac{d}{p}\left(\frac{d}{2p}+\frac{4}{3}\right)\right)\right]\right\}\right\}$$

(11)

Since there are possibilities of machine unavailable, based on the time point of a machine breakdown, then Equation (11) can be formulated as:

$$I_h=\{\begin{array}{c}\frac{p^2}{2d}{T}_p^2\left\{\left(1-\frac{d}{p}\right)+\frac{2\theta T_p}{d}\left\{\left[\frac{p}{6}-d\left(1+\frac{d}{p}\left(\frac{d}{2p}+\frac{4}{3}\right)\right)\right]\right\}\right\},\begin{array}{ccc}& & for\begin{array}{cc}& T_p\le T_1\end{array}\end{array}\\ \frac{p^2}{2d}{T}_1^2\left\{\left(1-\frac{d}{p}\right)+\frac{2\theta T_1}{d}\left\{\left[\frac{p}{6}-d\left(1+\frac{d}{p}\left(\frac{d}{2p}+\frac{4}{3}\right)\right)\right]\right\}\right\},\begin{array}{ccc}& & for\begin{array}{cc}& T_p>T_1\end{array}\end{array}\end{array}$$

(12)

Here, assuming that f(T_p) is the probability density function (p.d.f.) of the machine breakdown T_p and is exponentially distributed, i.e., f(T_p) = μe^−μT_p for T_p > 0. Therefore, the expected holding cost becomes

$$\begin{array}{l}{H}_S\times E\left[I_h\right]=H_S{\displaystyle \underset{T_p=0}{\overset{T_1}{\int }}\left[\frac{p^2}{2d}{T}_p^2\left\{\left(1-\frac{d}{p}\right)+\frac{2\theta T_p}{d}\left\{\left[\frac{p}{6}-d\left(1+\frac{d}{p}\left(\frac{d}{2p}+\frac{4}{3}\right)\right)\right]\right\}\right\}\right]}\mu e^{-\mu T_p}d{T}_p\\ +H_S{\displaystyle \underset{T_p=T_1}{\overset{\infty }{\int }}\left[\frac{p^2}{2d}{T}_1^2\left\{\left(1-\frac{d}{p}\right)+\frac{2\theta T_1}{d}\left\{\left[\frac{p}{6}-d\left(1+\frac{d}{p}\left(\frac{d}{2p}+\frac{4}{3}\right)\right)\right]\right\}\right\}\right]}\mu e^{-\mu T_p}d{T}_p\end{array}$$

(13)

4.1.2. Deterioration Cost

The deteriorated item is calculated by subtracting the production quantity by the demand during T₁ + T₂, as follows:

$$Det=\mathrm{Quantities}\mathrm{produced}–\mathrm{the}\mathrm{demand}\mathrm{during}(T_1+T_2)=p{T}_1-d(T_1+T_2)$$

(14)

Substitute T₂ derived from Equation (7) into Equation (14), it can be simplified as:

$$Det\cong \{\begin{array}{c}\frac{p}{2}(1-\frac{d}{p})\theta T_p^{2}for{T}_p\le T_1\\ \frac{p}{2}(1-\frac{d}{p})\theta T_1^{2}for{T}_p>T_1\end{array}$$

(15)

By using similar f(T_p), the expected deterioration cost becomes

$$C_d\times E\left[Det\right]=C_d\left\{{\displaystyle \underset{T_p=0}{\overset{T_1}{\int }}\left[\frac{p}{2}(1-\frac{d}{p})\theta T_p^2\right]}\mu e^{-\mu T_p}d{T}_p+{\displaystyle \underset{T_p=T_1}{\overset{\infty }{\int }}\left[\frac{p}{2}(1-\frac{d}{p})\theta T_1^2\right]}\mu e^{-\mu T_p}d{T}_p\right\}$$

(16)

4.1.3. Inspection Cost, Risk Cost and Corrective Cost of the Machine

The setup cost and risk cost occur during inspection planning. The inspection setup cost will increase when the inspection interval (s) decreases. However, the risk cost for inspection actions will decrease due to early fault detection (Chung and Wee [49]). There is a trade-off between the setup cost and the risk cost for inspection schedule when the inspection interval, s, is considered. Generally, the inspection setup cost, which is defined as V_sk/s, is inversely proportional to the fraction of the elapsed time, s, and the variable risk cost, defined as R_rsks, is proportional to s. The total inspection cost C_bs is

$$C_{bs}(s)=\left(\frac{V_{sk}}{s}+R_{rsk}s\right)$$

(17a)

When the production process shifts from the in-control state to out-of-control state, there is a need to restore the production system. The expected corrective cost for machine breakdown during interval of [0, T₁] can be formulated as:

$$E\left[C_{ret}\right]=C_M{\displaystyle \underset{t_p=0}{\overset{T_1}{\int }}\mu \exp \left(-\mu t_p\right)}d{t}_p=C_M\left[1-\exp \left(-\mu T_1\right)\right]$$

(17b)

4.1.4. Rework Cost

T_p is the elapse time when the facility shifts from in-control state to breakdown stat since there is a possibility of machine breakdown during production up-time period T₁. When the predetermined inspection time s is considered, the amount of nonconforming item is Z, one has:

$$Z\cong \{\begin{array}{c}\begin{array}{ll}{\theta }_{1}p{T}_p& ,for0<T_p\le s\\ {\theta }_{1}ps+{\theta }_{2}p\left(T_p-s\right)& ,fors<T_p\le T_1\end{array}\\ {\theta }_{1}ps+{\theta }_{2}p\left(T_1-s\right)& ,for{T}_p>T_1\end{array}$$

(18)

Where s is the time interval of predetermined inspection and θ₁ and θ₂ are the defective rates before and after the inspection is conducted. From Equation (18), the expected rework cost can be derived as E[RW] = C_RE[Z]. While considering the machine breakdown, one has the expected rework cost as:

$$\begin{gathered} E\left[RW\right]={\displaystyle \underset{T_p=0}{\overset{s}{\int }}{C}_R\left[{\theta }_{1}p{T}_p\right]}\mu \exp \left(-\mu T_p\right)d{T}_p \\ +{\displaystyle \underset{T_p=s}{\overset{T_1}{\int }}{C}_R\left[{\theta }_{1}ps+{\theta }_{2}p\left(T_p-s\right)\right]}\mu \exp \left(-\mu T_p\right)d{T}_p \\ +{\displaystyle \underset{T_p=T_1}{\overset{\infty }{\int }}{C}_R\left[{\theta }_{1}ps+{\theta }_{2}p\left(T_1-s\right)\right]}\mu \exp \left(-\mu T_p\right)d{T}_p \end{gathered}$$

(19)

4.1.5. Post-sale Warranty Cost

The product may become unusable after sales. Therefore, this study considers the post-sale warranty policy. Post-sale warranty policy is not only cost-effectiveness, but it can also improve customer satisfaction. For the warrant period τ, the failure rates of the conforming items and the nonconforming items with and without inspection are v₁(τ) and v₂(τ), respectively. The calculated failure rates with a warranty period of K for which the conforming items and the nonconforming items are $h_1={\displaystyle {\int }_0^K{v}_1\left(\tau \right)d\tau }$ and $h_2={\int }_0^K{v}_2\left(\tau \right)d\tau$, respectively. If the calculated failure rates of the conforming and nonconforming items follow Weibull distribution, and they are independent of the elapsed time Tp, the hazard rates are:

$$\begin{array}{c}{h}_1={\displaystyle \underset{0}{\overset{K}{\int }}{v}_1\left(\tau \right)d\tau }={\displaystyle \underset{0}{\overset{K}{\int }}({\lambda }_1^{{\rho }_1}{\rho }_1}{\tau }^{{\rho }_1-1})d\tau ={\left({\lambda }_{1}K\right)}^{{\rho }_1}\mathrm{and}\\ h_2={\displaystyle \underset{0}{\overset{K}{\int }}{v}_2\left(\tau \right)d\tau }={\displaystyle \underset{0}{\overset{K}{\int }}({\lambda }_2^{{\rho }_2}{\rho }_2}{\tau }^{{\rho }_2-1})d\tau ={\left({\lambda }_{2}K\right)}^{{\rho }_2},\mathrm{respectively}.\end{array}$$

(20)

where λ_i,i = 1,2 represent arrival rates and ρ_i,i = 1,2 are the shape parameters for the conforming items and the nonconforming items during the warranty period K. Taking the nonconforming item, Z, which include the quantities of the conforming and nonconforming items into account, the amount of unusable defective item resulting in free-repair warranty cost is

$$Z_h\cong \{\begin{array}{c}\begin{array}{ll}p{T}_p((1-{\theta }_1)h_1+{\theta }_1{h}_2)& ,\mathrm{for}0<T_p\le s\\ ps((1-{\theta }_1)h_1+{\theta }_1{h}_2)+p(T_p-s)((1-{\theta }_2)h_1+{\theta }_2{h}_2)& ,\mathrm{for}s<T_p\le T_1\end{array}\\ ps((1-{\theta }_1)h_1+{\theta }_1{h}_2)+p(T_1-s)((1-{\theta }_2)h_1+{\theta }_2{h}_2)& ,\mathrm{for}{T}_p>T_1\end{array}$$

(21)

Consequently, referring to Equations (20) and (21), the expected post-sale warranty cost is as follows.

$$\begin{array}{c}E[PO]=C_{w}E[Z_h]=C_w{\displaystyle \underset{T_p=0}{\overset{s}{\int }}\left[p{T}_p((1-{\theta }_1)h_1+{\theta }_1{h}_2)\right]}\mu \exp \left(-\mu T_p\right)d{T}_p\\ +C_w{\displaystyle \underset{T_p=s}{\overset{T_1}{\int }}\left[ps((1-{\theta }_1)h_1+{\theta }_1{h}_2)+p(T_p-s)((1-{\theta }_2)h_1+{\theta }_2{h}_2)\right]}\mu \exp \left(-\mu T_p\right)d{T}_p\\ +C_w{\displaystyle \underset{T_p=T_1}{\overset{\infty }{\int }}\left[ps((1-{\theta }_1)h_1+{\theta }_1{h}_2)+p(T_1-s)((1-{\theta }_2)h_1+{\theta }_2{h}_2)\right]}\mu \exp \left(-\mu T_p\right)d{T}_p\end{array}$$

(22)

4.1.6. Emergency Purchasing Cost for Partial Backorder and Lost Sale Cost

Figure 2 shows the inventory level with a partial backorder, because lost sales may occur due to impatient customers after the production down-time period. The backorder demand will be met by emergency purchasing and the number of partial backorder demands will be replenished at the end of T₃. The amount of emergency purchases is counted on the shortage period. Assuming the backordering rate is γ, the expected emergent purchasing cost for partial backorder can be defined as:

$$E[E_C]=C_{Ep}\gamma dE[T_3]=\gamma C_{Ep}d\left({\displaystyle \underset{T_p=0}{\overset{T_1}{\int }}\left[{\displaystyle \underset{t=T_2}{\overset{\infty }{\int }}(t-T_2)}f(t)dt\right]\mu e^{-\mu T_p}d{T}_p}\right)$$

(23a)

Taking into consideration the machine breakdown and the repair time in which the lost sale rate is 1-γ, the expected lost sale cost is

$$E[L_C]=\left(1-\gamma \right)S_{d}dE[T_3]=\left(1-\gamma \right)S_{d}d\left({\displaystyle \underset{T_p=0}{\overset{T_1}{\int }}\left[{\displaystyle \underset{t=T_2}{\overset{\infty }{\int }}(t-T_2)}f(t)dt\right]\mu e^{-\mu T_p}d{T}_p}\right)$$

(23b)

The setup cost of an emergency purchase from an outside supplier depends upon the demand and shortage period. Consequently, the expected time-dependent setup cost for emergency purchases can be derived as

$$E[S_{Ep}]=A_{Ep}dE[T_3]=A_{Ep}d\left({\displaystyle \underset{T_p=0}{\overset{T_1}{\int }}\left[{\displaystyle \underset{t=T_2}{\overset{\infty }{\int }}(t-T_2)}f(t)dt\right]\mu e^{-\mu T_p}d{T}_p}\right)$$

(23c)

4.1.7. Expected Deteriorating Economic Production Quantity Total Cost

The total cost of the EPQ model includes expected total setup cost C_s, holding cost H_sE[I_h], deteriorating cost C_dE[Det], inspection cost C_bs(s), corrective cost E[C_ret], rework cost E[RW], post-sale warranty cost E[PO], partial emergency purchase E[E_c], setup cost E[S_Ep], and lost-sale cost E[L_c]. Therefore, the expected total cost, E[TC], can be expressed as:

$$\begin{array}{c}E[TC]=C_s+H_{s}E\left[I_h\right]+C_{d}E\left[Det\right]+C_{bs}(s)+E\left[C_{ret}\right]+E\left[RW\right]\\ +E[PO]+E[E_C]+E[L_C]+E[S_{Ep}]\end{array}$$

(24)

4.2. Expected Replenishment Time for the Proposed Model Considering Random Machine Unavailability

The replenishment time is changeable and is not a constant because the machine breakdown and repair time is unpredictable. The total replenishment time (T) consists of the production up-time period, the production down-time period, and the possible breakdown-repair time. Therefore, T for different conditions can be written as:

$$T=\{\begin{array}{cc}{T}_p+T_2+{\displaystyle \underset{t=T_2}{\overset{\infty }{\int }}}(t-T_2)f(t)dt,& T_p\le T_1\\ T_1+T_2+{\displaystyle \underset{t=T_2}{\overset{\infty }{\int }}}(t-T_2)f(t)dt,& T_p>T_1\end{array}$$

(25a)

From Equation (25a), with the probability of machine breakdown, the expected T is

$$E\left[T\right]={\displaystyle \underset{T_p=0}{\overset{T_1}{\int }}\left[T_p+T_2+{\displaystyle \underset{t=T_2}{\overset{\infty }{\int }}(t-T_2)f(t)dt}\right]\mu e^{-\mu T_p}d{T}_p+{\displaystyle \underset{T_p=T_1}{\overset{\infty }{\int }}\left[T_1+T_2+{\displaystyle \underset{t=T_2}{\overset{\infty }{\int }}(t-T_2)f(t)dt}\right]\mu e^{-\mu T_p}d{T}_p}}$$

(25b)

However, when T_p ≦ T_1, backorder or lost sale may occur during the production down-time. The longer expected repair time can be represented, as follows:

$$E[T_3]={\displaystyle \underset{T_p=0}{\overset{T_1}{\int }}\left[{\displaystyle \underset{t=T_2}{\overset{\infty }{\int }}(t-T_2)}f(t)dt\right]\mu e^{-\mu T_p}d{T}_p}$$

(25c)

With the relationships among T_p, T₁, and T₂ in Equation (7), the expected T₁ and T₂ period can be obtained as:

$$\begin{array}{c}E\left[T_1+T_2\right]={\displaystyle \underset{T_p=0}{\overset{T_1}{\int }}\left(1+(p-d)\frac{(1-\theta T_p/2)}{d}\right)T_p}\mu e^{-\mu T_p}d{T}_p+{\displaystyle \underset{T_p=T_1}{\overset{\infty }{\int }}\left(1+(p-d)\frac{(1-\theta T_1/2)}{d}\right)T_1}\mu e^{-\mu T_p}d{T}_p\\ \cong \frac{p\left[1-\exp \left(-\mu T_1\right)\right]}{d\mu }\end{array}$$

(26)

Referring to Equations (25b), (25c), and (26), one has the expected T:

$$E\left[T\right]\cong \frac{p\left[1-\exp \left(-\mu T_1\right)\right]}{d\mu }+{\displaystyle \underset{T_p=0}{\overset{T_1}{\int }}\left[{\displaystyle \underset{t=T_2}{\overset{\infty }{\int }}(t-T_2)}f(t)dt\right]\mu e^{-\mu T_p}d{T}_p}$$

(27)

The replenishment cycle length of T is a variable since machine breakdown is likely. We can use renewal reward theorem to solve the variable replenishment cycle length. From Equations (24) and (27), we can derive the expected total cost per unit time. One has:

$$E\left[TEC\right]=\frac{E\left[TC\right]}{E\left[T\right]}$$

(28)

Moreover, the following properties can be utilized to optimize the expected total cost of the proposed deteriorating economic production quantity model.

Property 1

For a function f: S →R₁ defined by f(x) = g(x)/h(x) where g: S → R₁ and h: S → R₁, and S is a nonempty convex set in E_n.

The following theme form literature shows the conditions for convexity and concavity:

(1) g is convex on S and g (x) ≥ 0 for each x ∈S,

(2) h is concave on S, and h(x) ≥ 0 for each x ∈ S, and

(3) Both g and h are differentiable.

4.2.1. Machine Breakdown with an Exponentially Distributed Repair Time

In this case, the machine repair time is an exponentially distributed random variable. The exponential p.d.f. with mean 1/λ is given as:

$$f(t)=\lambda e^{-\lambda t}\mathrm{for}\lambda >0$$

The expected period of the shortage is derived from Equation (25c):

$$E[T_3]={\displaystyle \underset{T_p=0}{\overset{T_1}{\int }}\left[{\displaystyle \underset{t=T_2}{\overset{\infty }{\int }}(t-T_2)}\lambda e^{-\lambda t}dt\right]\mu e^{-\mu T_p}d{T}_p}$$

(29a)

$$E[T_3]=\frac{\exp \left[T_1\left(\frac{\lambda (p-d)}{2d}(-2+\theta T_1)+\frac{\lambda p}{d}+\mu \right)\right]-\exp \left[\lambda T_1\left(\frac{T_{1}p\theta }{2d}+1-\frac{\theta T_1}{2}\right)\right]}{\exp \left[T_1\left(\frac{\lambda p}{d}+\mu \right)\right]}$$

(29b)

From Equations (26) and (29a,b), the expected value of total replenishment time with the exponential distribution of machine repair time can be expressed as:

$$E[T]=E[T_1+T_2]+E[T_3]$$

(30a)

$$\begin{array}{l}E[T]=\frac{p\left[1-\exp \left(-\mu T_1\right)\right]}{d\mu }\\ +\frac{\exp \left[T_1\left(\frac{\lambda (p-d)}{2d}(-2+\theta T_1)+\frac{\lambda p}{d}+\mu \right)\right]-\exp \left[\lambda T_1\left(\frac{T_{1}p\theta }{2d}+1-\frac{\theta T_1}{2}\right)\right]}{\exp \left[T_1\left(\frac{\lambda p}{d}+\mu \right)\right]}\end{array}$$

(30b)

Consequently, neglecting the terms higher than $\lambda T_1^2$, $\mu T_1^2$, and $\theta T_1^2$ due to small values of λ, μ, and θ, the value of the total replenishment cycle time is:

$$E[T]\cong \left[\frac{{\lambda }^2}{2}-p\mu \left(\frac{\mu +0.5}{d}\right)+\frac{\theta }{2}\right]T_1^2+\left(\frac{p}{d}+\mu \right)T_1$$

(30c)

The lost sale and efficiency of machine utilization have been critical issues in the management of production and inventory control due to the unpredictable conditions of repair. This paper discusses the effects of repair time on production: the up-time period and the replenishment time length. Two circumstances are studied when considering the replenishment time with or without the repair time.

Scenario A: Without repair time

Replenishment time considering machine breakdown with a negligible repair time

The total replenishment time can be represented in term of T_p, since there is a possibility of a machine breakdown at the time of T_p and when the repair time is negligible, by Equation (7), as follows:

$$\begin{array}{l}{T}_{brk}=T_p+T_2\\ =T_p+(p-d)T_p(1-\frac{1}{2}\theta T_p)/d\approx \frac{p{T}_p}{d}-\frac{(p-d)\theta T_p^2}{2d}\end{array}$$

(31a)

T_brk is the replenishment time when the machine breakdown occurs. From Equation (31a), the replenishment time length is of T_brk and is equal to T_p + T₂. Consequently, the expected value of total replenishment time with respect to T_p is

$$E\left[T_{brk}\right]\approx \frac{pE\left[T_p\right]}{d}-\frac{(p-d)\theta E\left[T_p^2\right]}{2d}\begin{array}{c}\\ \\ \end{array}$$

(31b)

By utilizing the algebraic calculation, the expected replenishment time without considering the repair time is

$$E\left[T_{brk}\right]\approx \frac{pE[T_p]}{d}-\frac{(p-d)\theta }{2d}\left({\sigma }_{Tp}^2+{\overline{\psi }}^2\right)$$

(31c)

where $\overline{\psi }$ and ${\sigma }_{Tp}^2$, respectively, represent the expected value and variance of the machine breakdown elapsed time, T_p, i.e., $\overline{\psi }=E\left[T_p\right]={\displaystyle \int T_{p}f(T_p)}d{T}_p$ = $1/\mu$ and $E[T_p^2]=\left({\sigma }_{Tp}^2+{\overline{\psi }}^2\right)=\left({\sigma }_{Tp}^2+{\left(E[T_p]\right)}^2\right)$.

The variance and the mean value of machine breakdown probability influence the optimal expected replenishment time. From the (31c), the optimally expected production up-time can be derived by solving the quadratic equation as

$$E{\left[T_p\right]}^{\left(1\right)*}=\left\{\tilde{D}-\sqrt{{(\tilde{D})}^2-\frac{\left[2d\right]}{p}\tilde{D}\cdot \left(\frac{(p-d)\theta }{2d}{\sigma }_{Tp}^2+E[T_{brk}]\right)}\right\}$$

(32a)

$$E{\left[T_p\right]}^{\left(2\right)*}=\left\{\tilde{D}+\sqrt{{(\tilde{D})}^2-\frac{\left[2d\right]}{p}\tilde{D}\cdot \left(\frac{(p-d)\theta }{2d}{\sigma }_{Tp}^2+E[T_{brk}]\right)}\right\}$$

(32b)

where $\tilde{D}={\left[\left(1-\frac{d}{p}\right)\theta \right]}^{-1}$.

The Taylor’s series expansion is used to simplify E[T_p] in terms of E[T_brk] due to the complexity of Equation (32a), as following

$$\begin{array}{l}E[T_p]=\frac{d}{p}{\left[1-{\left(\left(1-\frac{d}{p}\right)\theta \right)}^2{\sigma }_{Tp}^2\right]}^{\frac{-1}{2}}E[T_{brk}]\\ +\frac{1}{2}{\left(\frac{d}{p}\right)}^2\left(1-\frac{d}{p}\right)\theta {\left[1-{\left(\left(1-\frac{d}{p}\right)\theta \right)}^2{\sigma }_{Tp}^2\right]}^{\frac{-3}{2}}{\left(E[T_{brk}]\right)}^2\end{array}$$

(33a)

In scenario A, for the given f (T_p), when λ, θ, and μ approach 0, then E[T_p] → T₁ and both roots of the expected replenishment time can be derived by using L’Hospital’s rule:

Property 2

$$\underset{\begin{array}{l}\lambda \to 0\\ \mu \to 0\\ \theta \to 0\end{array}}{\lim }E{[T_p]}^{(1)}\to T_1=\frac{d}{p}T\mathrm{and}\underset{\begin{array}{l}\lambda \to 0\\ \mu \to 0\\ \theta \to 0\end{array}}{\lim }E{[T_p]}^{(2)}\to T_1=-\frac{d}{p}T$$

(33b)

Hence, we should choose the first root. From Equation (33b), this result is the same as the property of the deterministic EPQ model. Note that, for Equation (32a) to exit, we must have

$$E[T_{brk}]\le \left\{{\left[\frac{2d}{p}\left(1-\frac{d}{p}\right)\theta \right]}^{-1}-\frac{(p-d)\theta }{2d}{\sigma }_{Tp}^2\right\}$$

(33c)

The above equation shows that product deterioration and the variance of f(T_p) are significant. When the probability of a machine breakdown is tiny, i.e., μ approaches 0, then ${\sigma }_{Tp}^2\to 0$, $E[T_{brk}]\to T$, and one has an upper bound for the replenishment time length is as follows:

$$E[T_{brk}]\to T\le \left\{{\left[\frac{2d}{p}\left(1-\frac{d}{p}\right)\theta \right]}^{-1}\right\}$$

(33d)

Equation (33d) reduces it to be the replenishment cycle time length of the traditional deteriorating production inventory model.

Scenario B: With repair time

General form: Replenishment time considering machine breakdown and repair time

Referred to Equation (30c), as shown below,

$$E\left[T\right]\cong [\frac{{\lambda }^2}{2}-p\mu \left(\frac{\mu +0.5}{d}\right)+\frac{\theta }{2}]T_1^2+\left(\frac{p}{d}+\mu \right)T_1$$

Note that, Equation (30c) is a quadratic equation of T₁. We solve Equation (30c) for T₁ in order to express T₁ in term of E[T], which leads to the following two roots:

$$T_1^{(1)}=-A(\mu ,\lambda ,\theta )-\sqrt{A^2(\mu ,\lambda ,\theta )+\frac{2dA(\mu ,\lambda ,\theta )}{\left(p+\mu d\right)}E[T]}$$

and

$$T_1^{(2)}=-A(\mu ,\lambda ,\theta )+\sqrt{A^2(\mu ,\lambda ,\theta )+\frac{2dA(\mu ,\lambda ,\theta )}{\left(p+\mu d\right)}E[T]}$$

(34)

where

$$A(\mu ,\lambda ,\theta )=\frac{-\left(p+\mu d\right)}{(-d{\lambda }^2-d\theta +2{\mu }^{2}p+\mu p)}$$

From the proposed model with repair time, Equation (34) is true when the following condition exists:

$$E[T]\le \frac{A(\mu ,\lambda ,\theta )\left(p+\mu d\right)}{-2d}=\frac{{\left(p+\mu d\right)}^2}{2\left[\mu pd\left(1+2\mu \right)-d^2\left({\lambda }^2+\theta \right)\right]\begin{array}{c}\\ \end{array}}$$

(35)

Replenishment time without considering machine breakdown:

From Equations (30a–c) and (34), when the probability of machine breakdown is extremely small, i.e., μ → 0, the following rules are implemented to obtain both of the roots. The machine is assumed to be in an excellent condition of performance. When μ approaches to 0, by using L’Hospital’s rule and rearranging Equation (34), property 3 exists:

Property 3

For a given mean, $\overline{\psi }$, variance, ${\sigma }_{T_p}^2$, and maintenance rate λ, when the probability of machine breakdown approximates to zero, the production up-time period of the inventory system is:

$$\begin{array}{c}\underset{\mu \to 0}{\lim }{T}_1^{(1)}=\frac{d}{p}-\left[d\left(1-E[T]\right)/\sqrt{\left(p^2+2d^2{\lambda }^{2}E[T]+2d^2\theta E[T]\right)}\right]\\ \mathrm{and}\underset{\mu \to 0}{\lim }{T}_1^{(2)}=-\frac{d}{p}+\left[d\left(1-E[T]\right)/\sqrt{\left(p^2+2d^2{\lambda }^{2}E[T]+2d^2\theta E[T]\right)}\right]\end{array}$$

(36a)

Replenishment time without considering machine breakdown and repair time:

If the defective factor can be quickly eradicated, the repair time can be neglected (property 3); the production up-time period of inventory system reduces to be

$$\begin{array}{c}\underset{\begin{array}{l}\mu \to 0\\ \lambda \to 0\end{array}}{\lim }{T}_1^{(1)}=\frac{d}{p}-\left[d\left(1-E[T]\right)/\sqrt{\left(p^2+2d^2\theta E[T]\right)}\right]\\ \mathrm{and}\underset{\begin{array}{l}\mu \to 0\\ \lambda \to 0\end{array}}{\lim }{T}_1^{(2)}=-\frac{d}{p}+\left[d\left(1-E[T]\right)/\sqrt{\left(p^2+2d^2\theta E[T]\right)}\right]\end{array}$$

(36b)

Note that when the probability of machine breakdown approximates to zero, Equation (33a) reduces to be same as Equation (36b).

Replenishment time without considering machine breakdown, repair time, and deterioration:

From Equations (33a) and (36b), when the probability of machine breakdown approximates to zero, T_p approaches to T₁, and E[T_brk] approximates to predetermined replenishment time T. With negligible repair time and deterioration (from property 3), the production up-time of the above roots reduce to:

Property 4

$$\underset{\begin{array}{l}\mu \to 0\\ \lambda \to 0\\ \theta \to 0\end{array}}{\lim }{T}_1^{(1)}=\frac{d}{p}T\mathrm{and}\underset{\begin{array}{l}\mu \to 0\\ \lambda \to 0\\ \theta \to 0\end{array}}{\lim }{T}_1^{(2)}=-\frac{d}{p}T$$

(36c)

Hence, we should choose the first root as the solution of T₁:

$$T_1^{*}=-A(\mu ,\lambda ,\theta )-\sqrt{A^2(\mu ,\lambda ,\theta )+\frac{2dA(\mu ,\lambda ,\theta )}{\left(p+\mu d\right)}E[T]}$$

(37)

where $A(\mu ,\lambda ,\theta )=\frac{-\left(p+\mu d\right)}{(-d{\lambda }^2-d\theta +2{\mu }^{2}p+\mu p)}$ < 0.

4.3. Optimization of the Deteriorating Economic Production Quantity Model

The expected total system cost per unit time for the case with exponential distribution can be formulated by substituting Equations (24) and (30a–c) into Equation (28).

Assuming that $\lambda T_1^3$, ${\theta }_1{T}_1^3$, ${\theta }_2{T}_1^3$, and $\theta T_1^3$ approach to zero and when considering property 1, Equation (28) can be rearranged as:

$$E\left[TEC\right]=\frac{k_1{T}_1^2+k_2{T}_1+C_k}{k_3{T}_1^2+k_4{T}_1}$$

(38a)

Where

• $\begin{array}{l}{k}_1=\frac{\lambda \left(1-\gamma \right)S_{d}d}{2}\left(\theta -\mu \right)\left(\frac{p}{d}+1\right)+H_S\left(\frac{-3\theta d}{2\mu }+\frac{4\theta p}{\mu }\right)\\ -\left(1-\gamma \right)S_{d}dp\mu \left(\frac{\mu +0.5}{d}+\frac{\mu \left(1+C_M/\left(\left(1-\gamma \right)S_{d}d\right)\right)}{p}\right)\\ +d\left[\gamma \left(A_{Ep}+C_{Ep}\right)\right]\cdot \left[p\mu \left(\frac{0.5-\mu }{d}\right)+\frac{\theta }{2}\right]\\ +\frac{p\mu }{2}\left[{\theta }_2\left(C_R+h_2{C}_w\right)\left(s\mu -1\right)-{\theta }_1\mu s\left(C_R+h_1{C}_w\right)\right]>0,\end{array}$
• $k_2=\lambda \left(1-\gamma \right)S_{d}d+{\theta }_{2}p\left(C_R+h_2{C}_w\right)+\mu \left(C_M+\left(1-\gamma \right)S_{d}d\right)+d\mu \left[\gamma \left(A_{Ep}+C_{Ep}\right)\right]>0,$
• $k_3=\frac{{\lambda }^2}{2}-p\mu \left(\frac{\mu +0.5}{d}\right)+\frac{\theta }{2}<0,$
• $k_4=\left(\frac{p}{d}+\lambda \right)>0$,
• $a_1=\frac{\mu p}{2}\left[C_R\left({\theta }_2-{\theta }_1\right)+C_w\left({\theta }_2{h}_2-{\theta }_1{h}_1\right)\right]$,
• $a_2=\left[R_{rsk}+C_{R}p\left({\theta }_2-{\theta }_1\right)-p{C}_w\left({\theta }_2{h}_2-{\theta }_1{h}_1\right)\right]$,

$$\mathrm{and}{C}_k=a_1{s}^2+a_{2}s+C_S+\frac{V_{sk}}{s}$$

(38b)

4.3.1. Optimal Conditions for Deriving the Optimal Solution of the Proposed Model

While considering Property 1, the following conditions are essential in deriving the optimal solution.

Optimal condition (1):

Considering Equations (24) and (38a), taking the second derivative of E[TC] with respect to T₁, one has:

$$\begin{array}{c}\frac{d^{2}E[TC]}{d{T}_1^2}=2k_1=2\{\frac{\lambda \left(1-\gamma \right)S_{d}d}{2}\left(\theta -\mu \right)\left(\frac{p}{d}+1\right)+H_S\left(\frac{-3\theta d}{2\mu }+\frac{4\theta p}{\mu }\right)\\ -\left(1-\gamma \right)S_{d}dp\mu \left(\frac{\mu +0.5}{d}+\frac{\mu \left(1+C_M/\left(\left(1-\gamma \right)S_{d}d\right)\right)}{p}\right)\\ +d\left[\gamma \left(A_{Ep}+C_{Ep}\right)\right]\cdot \left[p\mu \left(\frac{0.5-\mu }{d}\right)+\frac{\theta }{2}\right]\\ +\frac{p\mu }{2}\left[{\theta }_2\left(C_R+h_2{C}_w\right)\left(s\mu -1\right)-{\theta }_1\mu s\left(C_R+h_1{C}_w\right)\right]\begin{array}{c}\\ \end{array}\}\text{>}0\end{array}$$

(39a)

Hence, E[TC] is a convex function of T₁.

Optimal condition (2):

Referring to Equation (30c), taking the second derivative of E[T] with respect to T₁, one has:

$$\frac{d^{2}E[T]}{d{T}_1^2}=2k_3=2\left\{\frac{(\theta +{\lambda }^2)}{2}-p\mu \left(\frac{\mu +0.5}{d}\right)\right\}<0$$

(39b)

Therefore, E[T] is a concave function of T₁.

As shown in the optimal conditions (1) and (2), the optimal T₁ can be derived, since the expected total cost function $E\left[TEC\right]=E\left[TC\right]/E\left[T\right]$ is convex for small value of λ, µ, and T₁, as well as satisfying the following condition:

$$0<\lambda <\sqrt{\frac{2p\mu }{d}\left(0.5+\mu \right)-\theta }$$

(39c)

(The proof is shown in Appendix A)

4.3.2. Derivation of Iterative Solutions to the Deteriorating Economic Production Quantity Model

The objective of the proposed model is to solve the optimal production up-time period, T₁ and the optimal elapsed time, s for the inspection plan. If E[TEC] can satisfy the property 1, taking the first derivative of E[TEC] with respect to T₁ and setting the result to zero, the solution of production up-time T₁ is derived

$$T_1^{*}=\frac{C_k{k}_3+\sqrt{C_k^2{k}_3^2+C_k{k}_4^2{k}_1-C_k{k}_4{k}_2{k}_3}}{k_1{k}_4-k_2{k}_3}$$

(40a)

For the optimal elapsed time, s of implementing an inspection plan, one has

$$\frac{\partial E[TEC]}{\partial s}=\frac{\frac{p{\mu }^2\left({\theta }_2\left(C_R+h_2{C}_w\right)-{\theta }_1\left(C_R+h_1{C}_w\right)\right)T_1^2}{2}+2a_{1}s+a_2-\frac{Vsk}{s^2}}{K_3{T}_1^2+K_4{T}_1}$$

(40b)

Since μ²θ₁ and μ²θ₂ are very small, by setting the above result to zero and using the fixed-point methodology, an iterative solution of s that considers T₁ can be obtained as

$$s_n=\sqrt{\frac{V_{sk}^{}}{{\tilde{U}}_{n-1}+2a_1{s}_{n-1}+a_2}}$$

(40c)

where ${\tilde{U}}_{n-1}=\frac{p}{2}{\mu }^2\left[{\theta }_2\left(C_R+h_2{C}_w\right)-{\theta }_1\left(C_R+h_1{C}_w\right)\right]\cdot T_{1,n-1}^2$ < 0.

Taking first derivative of s_n with respect to T₁, one has:

$$\frac{d{s}_n}{d{T}_1}={\left(\sqrt{\frac{V_{sk}}{{\tilde{U}}_{n-1}+2a_1{s}_{n-1}+a_2}}\right)}^{-1}\cdot \frac{\left(-V_{sk}\cdot {\tilde{U}}_{n-1}\right)}{T_1{\left({\tilde{U}}_{n-1}+2a_1{s}_{n-1}+a_2\right)}^2}<0$$

(40d)

Since $a_2>0$, $\mu \to 0$, $s_{n-1}$, θ₁, and θ₂ are very small, then the terms of $2a_1{s}_{n-1}$ and ${\tilde{U}}_{n-1}$ approach to zero and Equation (40d) is negative. When the effect of production up-time length (T₁) on the elapsed time of inspection (s) is negative, indicating that the T₁ increases as the s decreases. This indicates that, when the elapsed time interval of implementing inspection increases, the production up-time length (T₁) is shortened, which results in a more frequent production replenishment policy.

Moreover, the estimated range of elapsed time for performing an inspection $s_J^{est}$ can be obtained by setting the terms of $2a_1{s}_{n-1}$ and ${\tilde{U}}_{n-1}$ in Equation (40c) to zero:

$$s_n^{*}>s_J^{est}=\sqrt{\frac{Vsk}{a_2}}\mathrm{or}{s}_n^{*}<s_J^{est}=-\sqrt{\frac{Vsk}{a_2}}$$

(41)

where $a_2=R_{rsk}+p\left[C_R\left({\theta }_1-{\theta }_2\right)-C_w\left({\theta }_2{h}_2-{\theta }_1{h}_1\right)\right]$

A starting point of s can be derived from Equation (41).

Remarks: 

One of the optimal conditions is obtained by letting the function in the square root of T₁ larger than zero since the square root value of the optimal T₁ is positive. i.e., C_K > 0.

4.4. Solution Procedure

We developed a solution procedure with a fixed point iterative method for obtaining the approximate optimal solution, as shown in Equations (40a–d) and (41) of Section 4.3.2, since solving the symbolic solutions of the planned production up-time T₁ and the elapsed time of implementing inspection time s is complex, as shown in Equations (38a,b) and (39a–c). This is due to the fact that the objective function Equations (38a,b) of the proposed model is a nonlinear optimization problem and is difficult to optimize through direct differentiation.

Step 1:

If input parameteris λ not in the range of Equation (39c), the solution is infeasible.

Step 2:

Initiate an integer value of n. Let n = 1, s_n-1 = 0 and T_{1, n-1} = 0 at n = 1.

Step 3:

Compute the parameter values of a₁, a₂, k₁, k₂, k₃, k₄, and C_{k, n-1} using Equations (38a) and (38b).

Step 4:

Derive ${\tilde{U}}_{n-1}=0.5p{\mu }^2\left[{\theta }_2\left(C_R+h_2{C}_w\right)-{\theta }_1\left(C_R+h_1{C}_w\right)\right]\cdot T_{1,n-1}^2$ in Equation (40c).

Step (4-1):

From Equation (40c), calculate $s_n=\sqrt{V_{sk}/({\tilde{U}}_{n-1}+2a_1{s}_{n-1}+a_2)}$ using s_n-1, ${\tilde{U}}_{n-1}$ and T_{1, n-1}.

Step (4-2):

Determine if s_n = s_n-1, let s* = s_n; then, go to step 5. Otherwise, let n = n + 1 and compute C_{k, n-1} and T_{1, n-1} using Equations (38b) and (40a); then return to Step 4.

Step 5:

Calculate $C_k^{*}$ and $T_1^{*}$ using Equations (38b) and (40a) and the optimal elapsed time of inspection plan, s*. Finally, determine $T_2^{*}$ using Equation (7), then solve Q* using pT₁^* and derive the optimal total system cost per unit time, E[TEC].

5. Case Example and Sensitivity Analysis

A Taiwan thin-film manufacturer (UNMC) produces various products of thin-film that is used in automotive, printing, and electronic industries. A predetermined production up-time is scheduled. The product is manufactured with a defective rate of θ₁ before the inspection and with a defective rate of θ₂ after inspection. The defective rates can be reduced after the inspection is implemented. There is a probability of machine breakdown in the factory. Shortages will occur when the machine is unavailable after the production down-time due to preventive maintenance or unpredicted repair time. Defective items are detected and reworked during production. Moreover, products during storage incur deterioration loss due to manufacturing faulty, the nature of the material, and the storage environment.

We modified the parameters from a thin film manufacturer to avoid copyright issues and simplify the modeling. The resulting parameters are as follows:

θ= 0.01 P = 14,000 units d = 8500 units CS = $120 HS =$1.5 Cm = $10

Rrsk = $4500 Vsk = $20 Sd = $30 CR = $19 h1 = 0.003 h2 = 0.0025

θ1 = 0.0025 θ2 = 0.002 µ = 0.006 Cw = 35 AEp =120 λ = 0.009

Based on the stated solution procedures, the approximate optimal solutions while considering deterioration are derived as (T₁*, s*, ETC*) = (0.082084 year, 0.06569 year, and $11,066.99), respectively. If deterioration approximates to zero, the solution is derived as in

Table 2. Sensitivity analysis when the deteriorating rate changes.

{θ}	0.008	0.009	{0.01}	0.011	0.012
T1	0.09177	0.086523	0.082084	0.078265	0.074934
s	0.065694	0.065694	0.065694	0.065694	0.065694
Q	505	476	451	430	412
T2	0.05936	0.055964	0.053091	0.05062	0.04846
ETC	9933.06	10,515.81	11,066.99	11,591.23	12,092.13
PTCD(%)	−10.25%	−4.98%	0.00%	4.74%	9.26%

. This study uses the percentage of total cost difference (PTCD) to analyze the sensitivity of the key parameters. The percentage of total cost difference is defined as PTCD = (TC − TC*)/TC*.

Referring to Equation (40d), the production up-time length decreases as the elapsed time of implementing inspection increases. It indicates that the manager should carry out a frequent production replenishment strategy to optimize the expected total inventory system cost. The parameters are increased and decreased by 10% and 20%. The results are given in Table 2,

Table 3. Sensitivity analysis when defective rate before inspection changes.

{θ1}	0.002	0.00225	{0.0025}	0.00275	0.003
T1	0.08158	0.08184	0.082084	0.08233	0.08257
s	0.066663	0.066173	0.065694	0.065225	0.064766
Q	449	450	451	453	454
T2	0.05277	0.05293	0.053091	0.05325	0.05341
ETC	11,001.57	11,034.45	11,066.99	11,099.20	11,131.09
PTCD(%)	−0.59%	−0.29%	0.00%	0.29%	0.58%

,

Table 4. Sensitivity analysis when defective rate after inspection changes.

{θ2}	0.0016	0.0018	{0.002}	0.0022	0.0024
T1	0.08248	0.08228	0.082084	0.08189	0.08169
s	0.064949	0.065319	0.065694	0.066076	0.066465
Q	453	452	451	450	449
T2	0.05334	0.05322	0.053091	0.05296	0.05283
ETC	11,053.66	11,060.43	11,066.99	11,073.34	11,079.47
PTCD(%)	−0.12%	−0.06%	0.00%	0.06%	0.11%

,

Table 5. Sensitivity analysis when the hazard rate of sold product before inspection changes.

{h1}	0.0024	0.0027	{0.003}	0.0033	0.0036
T1	0.082081	0.082082	0.082084	0.082085	0.082086
s	0.065699	0.065697	0.065694	0.065691	0.065689
Q	451	451	451	451	451
T2	0.05309	0.053090	0.053091	0.053092	0.053093
ETC	11,066.63	11,0066.81	11,066.99	11,067.17	11,067.35
PTCD(%)	0.00%	−0.54%	0.00%	0.00%	0.00%

,

Table 6. Sensitivity analysis when the hazard rate of sold product after inspection changes.

{h2}	0.002	0.00225	{0.0025}	0.00275	0.003
T1	0.082086	0.082085	0.082084	0.082083	0.082082
s	0.065691	0.065692	0.065694	0.065695	0.065697
Q	451	451	451	451	451
T2	0.053092	0.053092	0.053091	0.053091	0.053090
ETC	11,066.93	11,066.96	11,066.99	11,067.02	11,067.05
PTCD(%)	0.00%	0.00%	0.00%	0.00%	0.00%

,

Table 7. Sensitivity analysis when the arrival rate changes.

{μ}	0.0048	0.0054	{0.006}	0.0066	0.0072
T1	0.073423	0.077874	0.082084	0.086087	0.089911
s	0.065694	0.065694	0.065694	0.065694	0.065694
Q	404	428	451	473	494
T2	0.047492	0.05037	0.053091	0.055679	0.058152
ETC	12,343.16	11,651.93	11,066.99	10,563.59	10,124.38
PTCD(%)	11.53%	5.29%	0.00%	−4.55%	−8.52%

,

Table 8. Sensitivity analysis when the demand rate changes.

{d}	6800	7650	{8500}	9350	10200
T1	0.079767	0.08090	0.082084	0.083321	0.084616
s	0.065694	0.065694	0.065694	0.065694	0.065694
Q	574	514	451	387	321
T2	0.08443	0.067125	0.053091	0.04142	0.03151
ETC	9109.88	10,105.41	11,066.99	11,993.88	12,885.30
PTCD(%)	−17.68%	−8.69%	0.00%	8.38%	16.43%

,

Table 9. Sensitivity analysis when the production rate changes.

{P}	11,200	12,600	{14,000}	15,400	16,800
T1	0.095234	0.087922	0.082084	0.077284	0.073247
s	0.065885	0.065789	0.065694	0.065599	0.065506
Q	275	360	451	533	608
T2	0.030236	0.04239	0.053091	0.062712	0.071497
ETC	11,859.74	11,449.98	11,066.99	10,713.00	10,387.06
PTCD(%)	7.16%	3.46%	0.00%	−3.20%	−6.14%

,

Table 10. Sensitivity analysis when the fixed risk cost changes.

{Rrsk}	3600	4050	{4500}	4950	5400
T1	0.078498	0.080359	0.082084	0.083694	0.085205
s	0.073184	0.069136	0.065694	0.062719	0.0601157
Q	432	442	451	460	468
T2	0.050773	0.051976	0.053091	0.054132	0.055109
ETC	10,597.38	10,841.13	11,066.99	11,277.80	11,475.74
PTCD(%)	−4.24%	−2.04%	0.00%	1.90%	3.69%

,

Table 11. Sensitivity analysis when the variable risk cost changes.

{Vsk}	16	18	{20}	22	24
T1	0.078382	0.080306	0.082084	0.083740	0.085296
s	0.058758	0.062323	0.065694	0.068900	0.071964
Q	431	442	451	460	496
T2	0.0506977	0.051942	0.053091	0.04142	0.03151
ETC	10,582.21	10,834.14	11,066.99	11,283.88	11,487.18
PTCD(%)	−4.38%	−2.10%	0.00%	1.96%	3.80%

,

Table 12. Sensitivity analysis when the rework cost changes.

{CR}	15.2	17.1	{19}	20.9	22.8
T1	0.081985	0.082035	0.082084	0.082133	0.082133
s	0.065883	0.065788	0.065694	0.065600	0.065506
Q	451	451	451	452	452
T2	0.053028	0.053059	0.053091	0.053123	0.053155
ETC	10,989.72	11,028.36	11,066.99	11,105.61	11,144.22
PTCD(%)	−0.70%	−0.35%	0.00%	0.35%	0.70%

and

Table 13. Sensitivity analysis when the unit holding cost changes.

{HS}	1.2	1.35	{1.5}	1.65	1.8
T1	0.091799	0.08655	0.082084	0.078289	0.074957
S	0.065643	0.065644	0.065694	0.065695	0.065696
Q	505	476	451	430	412
T2	0.059372	0.055979	0.053091	0.050638	0.048484
ETC	9953.03	10,535.96	11,066.99	11,611.72	12,112.79
PTCD(%)	−10.07%	−4.80%	0.00%	4.92%	9.45%

and Figure 3, Figure 4, Figure 5, Figure 6 and Figure 7. “*” is the minimum total cost and “{•}” is the base column. There are some findings, as follows:

(a)

For increasing {θ }, a lesser production-lot-size should be implemented to optimize the inventory system (Table 2 or Figure 7). The achievement in the deterioration rate reduction will benefit the economic production inventory system.

(b)

For decreasing {θ₁} and increasing {θ₂}, the total sum of the production the up-time period and down-time period tends to decrease. That investment on the defective rate reduction will influence the production and delivery policies. In practice, when the defective rate decreases, a frequent delivery policy should be implemented (Table 3 and Table 4 or Figure 4 and Figure 5).

(c)

When the variable risk cost tends to increase, the predetermined inspection period {s} also tends to increase. (See Table 11 or Figure 3)

(d)

The total cost is positively sensitive to {d}, {θ} and {H_s} (Table 2, Table 8, Table 13, and Figure 6). When the unit holding cost increases, the production up-time period and down-time period tend to decrease. That is, a manager may use a frequent and small lot-size policy when the unit holding cost increases (Figure 4 and Figure 5). The results are similar to the parameter of the deterioration rate {θ}.

(e)

The total cost is negatively sensitive to {p} and {μ} (Table 7 and Table 9 and Figure 6). When the mean time between breakdown {1/μ} increases, a frequent production policy is encouraged to be carried out (Figure 7).

(f)

When {H_s} increases, the manager should consider a smaller production-lot-size and shorter cycle-time policies to lower the production inventory level (Table 13 and Figure 4, Figure 5, and Figure 7).

(g)

The production lot size, Q, is positively sensitive to {p}, the arrival rate of machine breakdown {μ} and variable risk cost {V_sk}, and it is negatively sensitive to {d}, {H_s} and the deterioration rate {θ}. In practice, when {d} increases and {p} decreases, the total sum of the production up-time period and down-time period should be shortened (Table 2, Table 7, Table 8, Table 9, Table 10, and Table 13, and Figure 7).

6. Conclusions

The inventory models applying differential calculus are commonly used in existing research. A renewal reward approach is an alternate method for solving the inventory control of deteriorating items with a random breakdown or machine unavailability. This paper develops an EPQ model that considers facility unavailability and the imperfect items. The study assumed that a predetermined inspection scheduled. Shortages are allowed during facility unavailability due to preventive maintenance or unpredicted repair time. Imperfect quality rework, warranty, emergency purchase, and partial backorder are incorporated. Our study uses the renewal reward method and the fixed-point approach to solve the replenishment and inventory model. The approximate optimal solution is derived while using a fixed point iterative approach. The sensitivity analysis shows that the deteriorating rate, unit holding cost, and demand rate should be considered in designing the inspection plan and the replenishment policy when facility unavailability and imperfect items exist.

Further research can be extended to consider the different partnership contract with supply chain members. Revenue sharing or price discount contract with supplier and trade credit can be incorporated. Furthermore, when considering the environmental aspect, such as from the production, maintenance, rework, and inventory, another interesting future work is to develop a green production system.