Linear Maps in Minimal Free Resolutions of Stanley-Reisner Rings
Abstract
:1. Introduction
2. Notation and Preliminaries
2.1. The Linear Part
2.2. Simplicial Chains and Cochains
3. Proof of the Main Result
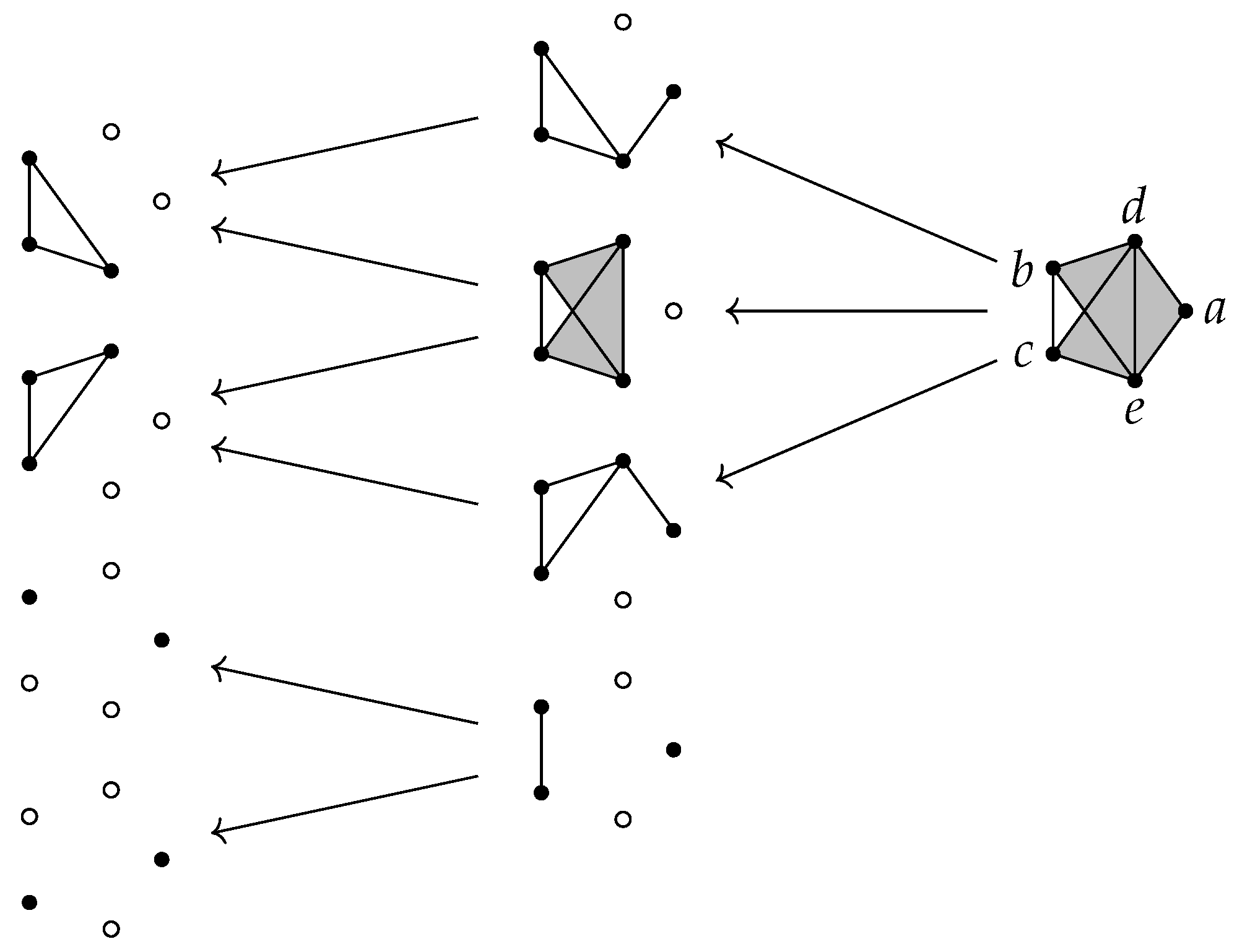
- for some ,
- ,
- splits into several connected components of with ,
- same as (3), with ,
- is the isolated vertex u.
4. Questions and Open Problems
4.1. Affine Monoid Algebras
4.2. Approximations of Resolutions
4.3. Coefficients in Resolutions
Funding
Acknowledgments
Conflicts of Interest
References
- Eisenbud, D.; Fløystad, G.; Schreyer, F.O. Sheaf cohomology and free resolutions over exterior algebras. Trans. Am. Math. Soc. 2003, 355, 4397–4426. [Google Scholar] [CrossRef]
- Reiner, V.; Welker, V. Linear syzygies of Stanley-Reisner ideals. Math. Scand. 2001, 89, 117–132. [Google Scholar] [CrossRef] [Green Version]
- Yanagawa, K. Alexander Duality for Stanley–Reisner rings and squarefree n-graded modules. J. Algebra 2000, 225, 630–645. [Google Scholar] [CrossRef]
- Horwitz, N. Linear resolutions of quadratic monomial ideals. J. Algebra 2007, 318, 981–1001. [Google Scholar] [CrossRef] [Green Version]
- Chen, R.X. Minimal free resolutions of linear edge ideals. J. Algebra 2010, 324, 3591–3613. [Google Scholar] [CrossRef]
- Herzog, J.; Simis, A.; Vasconcelos, W.V. Approximation complexes of blowing-up rings, II. J. Algebra 1983, 82, 53–83. [Google Scholar] [CrossRef] [Green Version]
- Miller, E.; Sturmfels, B. Combinatorial Commutative Algebra; Springer: New York, NY, USA, 2005. [Google Scholar]
- Hochster, M. Cohen-Macaulay rings, combinatorics, and simplicial complexes. In Ring Theory II; Dekker: New York, NY, USA, 1977; pp. 171–223. [Google Scholar]
- Bruns, W.; Herzog, J. Cohen-Macaulay Rings; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Katthän, L. Linear Maps in Minimal Free Resolutions of Stanley-Reisner Rings. Mathematics 2019, 7, 605. https://doi.org/10.3390/math7070605
Katthän L. Linear Maps in Minimal Free Resolutions of Stanley-Reisner Rings. Mathematics. 2019; 7(7):605. https://doi.org/10.3390/math7070605
Chicago/Turabian StyleKatthän, Lukas. 2019. "Linear Maps in Minimal Free Resolutions of Stanley-Reisner Rings" Mathematics 7, no. 7: 605. https://doi.org/10.3390/math7070605
APA StyleKatthän, L. (2019). Linear Maps in Minimal Free Resolutions of Stanley-Reisner Rings. Mathematics, 7(7), 605. https://doi.org/10.3390/math7070605



