Semi Square Stable Graphs

Abstract

The independent number of a graph G is the cardinality of the maximum independent set of G, denoted by $\alpha (G)$. The independent dominating number is the cardinality of the smallest independent set that dominates all vertices of G. In this paper, we introduce a new class of graphs called semi-square stable for which $\alpha (G^2)=i(G)$. We give a necessary and sufficient condition for a graph to be semi-square stable, and we study when interval graphs are semi-square stable.

1. Introduction

In a graph G, a set of vertices S is called a dominating set in G if every vertex of G, that is not in S, is adjacent to a vertex in S; a minimum size of such a set is called the dominating number of G and denoted by $\gamma (G)$. An independent set of the graph G (or stable set) is a set of vertices where no two vertices are adjacent. A set that admits both independent and dominating properties is called an independent dominating set; the minimum size of such a set (independent dominating set) is called the independent dominating number denoted by $i(G)$. On the other hand, the maximum size of sets that admit the independence property is called the independent number of G, denoted by $\alpha (G)$. Immediately from the above definition, for any graph G, the following inequality holds:

$$\gamma (G)\le i(G)\le \alpha (G).$$

A $\gamma$-set of the graph G is a dominating set of G of size $\gamma (G)$, while an i-set ($\alpha$-set) of G is any independent dominating set (independent set) of size $i(G)$($\alpha (G)$).

A complete subgraph of a graph G is called clique; it is called maximal if it is not a proper subgraph of a clique in G. The maximum size of cliques in a graph G is called the clique number of G, denoted by $\omega (G)$. A collection of subgraphs of a graph G is called a cover of G if the union of its vertices is $V(G)$; also, the minimum number of cliques that cover $V(G)$ is called the clique covering number, denoted by $\theta (G)$.

Given a graph G and a positive integer d, a new graph $G^d$, called the $d^{\mathrm{th}}$ power of G, is defined as the graph whose vertex set is $V(G^d)=V(G)$, and two distinct vertices x and y are adjacent in $G^d$ if the distance between x and y in G, $d_G(x,y)$, is at most d.

A graph G is a well-covered graph if $i(G)=\alpha (G)$. A graph G is called a square stable graph if $\alpha (G)=\alpha (G^2)$. This class of graphs has been proven to be an interesting class of graphs. Levit and Mandrescu in [1] proved that every square stable graph is a well-covered graph. Well-covered graphs have been intensively studied in the literature; see [1,2,3,4].

Our aim is to initiate a study of a larger class of graphs called semi-square stable graphs. Levit and Mandrescu in [1] mentioned the following inequality:

$$\alpha (G^2)\le \theta (G^2)\le \gamma (G)\le i(G)\le \alpha (G)\le \theta (G).$$

The equality $\alpha (G^2)=\alpha (G)$ is equivalent to:

$$\alpha (G^2)=\theta (G^2)=\gamma (G)=i(G)=\alpha (G).$$

They defined and studied the square stable graphs.

In the literature, there are many papers that have studied when certain independent sets for certain graphs are equal. Alomari et al. in [5] showed that the independent number of a square of a graph is equal to the independent number of its complement, and it is obvious that every square complementary graph [6,7,8] will satisfy this condition. Such a property may be extended to a wide class of graphs such as the $k^{\mathrm{th}}$ complementary graph as in [9]. Motivated by [5] and Levit’s work, we define the graph G to be semi-square stable (SSS-graph) if the equality $i(G)=\alpha (G^2)$ holds. According to Levit’s inequality, we have $\alpha (G^2)=\gamma (G)=i(G)$. Therefore, every square stable graph is a semi-square stable graph.

Unless stated otherwise, all graphs considered in this paper will be connected, finite, simple, and undirected.

Definition 1.

A graph G is called semi-square stable, an SSS-graph for short, if $i(G)=\alpha (G^2)$.

Semi-square stable graphs are a generalization of square stable graphs. Levit and Mandrescu [1] proved that every square stable graph is well covered, while the converse need not be true. The following result shows when the converse is true.

Corollary 1.

A graph G is a square stable graph if and only if it is a well-covered semi-square stable graph.

The proof is straightforward from the definitions and the fact that every square stable graph is a well-covered graph.

2. Constructions and Examples

In this section, after characterizing when the cycle $C_n$ and the path $P_n$ are semi-square stable, we give two constructions giving ways of constructing new semi-square stable graphs out of known ones.

Theorem 1.

1. 

$i(C_n)=\alpha (C_n^2)$ if and only if $n\equiv 0(mod3)$.

2. 

$i(P_n)=\alpha (P_n^2)$ for all n.

Proof. 

• Consider the set $I=\{0,3,6,\cdots ,3(\lfloor \frac{n}{3}\rfloor -1)\}\subset V(C_n))$; I is an independent set of vertices with the property that for any vertex i of $C_n$, there is at most one vertex in I that dominates i; so, if $n\equiv 0(mod3)$, then I forms the minimum independent set in $C_n$, and if $n\neg \equiv 0(mod3)$, then $I\cup \{3\lfloor \frac{n}{3}\rfloor +2\}$ forms the minimum independent set in $C_n$; therefore,

  $$i(C_n)=\left\{\begin{array}{ll}\frac{n}{3}& \mathrm{if}n\equiv 0(mod3),\\ \lfloor \frac{n}{3}\rfloor +1& \mathrm{if}n\neg \equiv 0(mod3),\end{array}\right.=\lceil \frac{n}{3}\rceil .$$
  On the other hand, I forms a maximum independent set in $C_n^2$; therefore, $\alpha (C_n^2)=\lfloor \frac{n}{3}\rfloor$. Therefore, $C_n$ is a semi-square stable graph if and only if $\lceil \frac{n}{3}\rceil =\lfloor \frac{n}{3}\rfloor$; therefore, $n\equiv 0(mod3)$.
• $i(P_n)=\lceil \frac{n}{3}\rceil =\alpha (P_n^2)$. □

For the set of integers $R={\left\{r_i\right\}}_{i=1}^n$ and a graph G of order n with vertices of $V(G)=\{v_1,v_2,\cdots ,v_n\}$, the graph $exp(G,R)$ is the graph obtained from G as follows:

• For each $1\le i\le n$, replace the vertex $v_i\in V(G)$ with the independent set $I_{v_i}={\left\{v_{(i,m)}\right\}}_{m=1}^{r_i}$ of size $r_i$,
• For each $1\le i,j\le n$, if $v_i{v}_j\in E(G)$, then ${\left\{v_{(i,m)}{v}_{(j,k)}\right\}}_{m=1,j=1}^{r_i,r_j}\subseteq E(exp(G,R))$, so we just replace the old edges of G by the complete bipartite graph with partite sets $I_{v_i}$ and $I_{v_j}$ in the graph $exp(G,R)$.

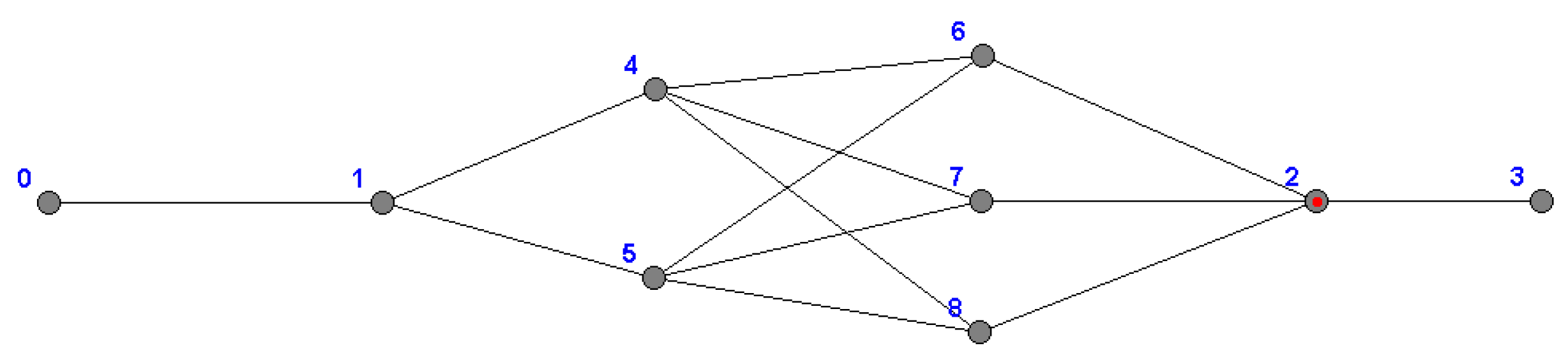
In Figure 1 we illustrate the graph $exp(P_5,1,1,2,3,1,1).$

Theorem 2.

Let G be a semi-square stable graph of order n and $R={\left\{r_i\right\}}_{i=1}^n$ be a set of integers; if $I=\{v_i\in V(G):r_i=1\}$ contains an i-set of G, then $exp(G,R)$ is a semi-square stable graph.

Proof. 

Let $I^{\prime }\subset I$ be an $i-set$ of G and $S={\left\{a_j\right\}}_{j=1}^{i(G)}$ be an $\alpha -set$ of G; then, by the definition of $exp(G,R)$, $I^{\prime }$ is an $i-set$ of $exp(G,R)$; on the other hand, since for $1\le k\le i(G)$, $d_{exp(G,R)}(a_{(i,k)},a_{(i,m)})=2$, we have $a_{(i,k)}{a}_{(i,m)}\in exp{(G,R)}^2$, therefore, $S^{\prime }={\left\{a_{(j,1)}\right\}}_{j=1}^{i(G)}$ will dominate all vertices of the graph $exp{(G,R)}^2$; also, since S is maximum independent set in G, $S^{\prime }$ is a maximum independent set in $exp{(G,R)}^2$. Using the fact $|S^{\prime }|=|I^{\prime }|=i(G)$, we have that $exp(G,R)$ is a semi-square stable graph. □

For any given graphs G and a family of graphs $\mathcal{H}={\left\{H_i\right\}}_{i=1}^n$, define the corona product between G and $\mathcal{H}$, denoted by $coro(G,\mathcal{H})$, as the graph obtained from G and $\mathcal{H}$ by joining the $i^{\mathrm{th}}$ vertex of G with each vertex of $H_i$. Therefore, if $V(G)=\{v_1,v_2,\cdots ,v_n\}$ and $V(H_i)=\{a_{(i,1)},a_{(i,2)},\cdots ,a_{(i,m_i)}\}$, then $Coro(G,\mathcal{H})=V(G)\cup V(H_1)\cup V(H_2)\cup \cdots \cup V(H_n)$, where $V(H_i)=\left\{a_{(i,j)}\right|1\le j\le m_i\}$ is the vertex-set of $H_i$, and $E(coro(G,\mathcal{H}))=E(G)\cup \left\{v_i{a}_{(i,j)}\right|1\le j\le m_i,1\le i\le n\}{\cup }_{i=1}^{n}E(H_i)$, see Figure 2.

Theorem 3.

Let G be a semi-square stable graph and ${\left\{v_{k_j}\right\}}_{j=1}^{i(G)}\subset V(G)$ be an i-set in G; for any $\mathcal{H}={\left\{H_i\right\}}_{i=1}^n$ collection of graphs, the graph $coro(G,\mathcal{H})$ is a semi-square stable graph if the following conditions hold:

1. $H_i$ is a non-empty graph if $i=k_j$ for some $1\le j\le i(G)$.

2. $H_i$ is an empty graph if $i\ne k_j$ for all $1\le j\le i(G)$.

Proof. 

Let $I={\left\{v_{k_j}\right\}}_{j=1}^{i(G)}$ be an i-set in G and ${\left\{b_j\right\}}_{j=1}^{i(G)}$ be an $\alpha$-set in $G^2$. I is an i-set in $coro(G,\mathcal{H})$; moreover, since $d_{coro(G,\mathcal{H})}(a_{(i,m)},a_{(i,k)})\le 2$ for each $a_{(i,m)}$ and $a_{(i,k)}$ in $H_i$, we have that ${\left\{b_j\right\}}_{j=1}^{i(G)}$ is an $\alpha$-set in $coro(G,\mathcal{H})$; therefore, $coro(G,\mathcal{H})$ is a semi-square stable graph. □

3. Efficient Dominating Set

Given a group A and a subset S of A, the Cayley graph, $Cay(A:S)$, is the undirected graph with:

• the vertex set represented by elements of A,
• the edge set that connects the vertex a with the vertices $sa$ and $s^{-1}a$ for each $s\in S$.

A vertex set A and edge set contain an edge from a to $sa$ and from a to $s^{-1}a$ whenever $a\in G$ and $s\in S$. A special case of Cayley graphs is the circulant graphs, which can be defined as follows:

For any two integers $n,m$ and set of positive integers $\{a_1,a_2,...,a_m\}$ where $1\le a_i\le \lfloor \frac{n}{2}\rfloor$, the circulant graph, denoted by $C(n;a_1,a_2,\cdots ,a_m)$ is defined to be the undirected graph with vertex set $V=\{v_1,v_2,\cdots ,v_n\}$ and the edge set $E=\{v_i{v}_{i+a_j}:1\le i\le n,1\le j\le m\}$, where the indices are considered to be taken modulo n. The graphs of $C(6;1)$ and $C(12;1,5,6,7)$ are shown in Figure 3.

Cayley graphs have been proven useful in various sciences especially in computer science fields such as computer architecture, theoretical computer science, routing problem, coding theory, and networking. In coding theory, regular graphs, distance transitive graphs, and vertex transitive graphs play a central role. Error-correcting codes were introduced by Biggs [10], in particular perfect one-codes, that is one error can be corrected.

A dominating set D is efficient (perfect codes) if it is independent and each vertex $v\notin D$ has exactly one neighbor in D. Kumar and MacGillivray in [11] investigated when certain circulant graphs admit an efficient dominating set; they used the lexicographic product to construct infinitely many circulant graphs that admit an efficient dominating set. In this section, we give a sufficient and necessary condition for regular graphs to admit an efficient dominating set.

Theorem 4.

A regular graph G admits an efficient dominating set if and only if G is a semi-square stable graph.

Proof. 

Suppose that D is an efficient dominating set, then $\left|D\right|=i(G)$ and for each $u,v\in D,d_G(u,v)\ge 3$. Therefore, D is an independent set in $G^2$ and:

$$\alpha (G^2)\le i(G)=\left|D\right|\le \alpha (G^2),$$

thus

$$\alpha (G^2)=i(G),$$

and so, G is a semi-square stable graph.

Suppose that G is a semi-square stable graph. Let D be a maximum independent set in $G^2$, then ${\left\{N_G(u)\right\}}_{u\in D}$ are mutually disjoint sets. Therefore,

$$\alpha (G^2)(\delta +1)\le \left|V(G)\right|,$$

where $\delta$ is the vertex degree. On the other hand, if $D^{*}$ is an independent set in G, then:

$$|D^{*}|(\delta +1)\ge |V(G)|,$$

so:

$$i(G)(\delta +1)\ge |V(G)|;$$

therefore,

$$\alpha (G^2)(\delta +1)\le \left|V(G)\right|\le i(G)(\delta +1).$$

Since G is a semi-square stable graph, we have $\alpha (G^2)(\delta +1)=\left|V(G)\right|$. Therefore, ${\left\{N_G(u)\right\}}_{u\in G}$ form a partition of $V(G)$. Therefore, D is an efficient dominating set of G. □

The above theorem not only characterizes an efficient dominating set in regular graphs, it also determines the efficient dominating set.

Corollary 2.

If G is a regular semi-square stable graph and D is a maximum dominating set of $G^2$, then D is an efficient dominating set of G.

Corollary 3.

If G is a regular graph that admits an efficient dominating set, then:

$$\alpha (G^2)=\theta (G^2)=\gamma (G)=i(G).$$

The following theorem was proven by Kumar and MacGillivray in [11]. We provide a new and simpler proof using the above theorem.

Theorem 5

([11]). Let $F=Circ(mn,T)$, and suppose $T\cup \left\{0\right\}$ is a union of cosets of $〈n〉$. Let S be any set of representatives of the cosets $〈n〉+t,t\in T-〈n〉$. Then, F has an efficient dominating set if and only if $G=Circ(n,S)$ has an efficient dominating set.

Proof. 

Consider the natural homomorphism:

$$\psi :{\mathbb{Z}}_{nm}\to \mathbb{Z}{{}_{nm}}_{/〈n〉}\cong {\mathbb{Z}}_n$$

defined by:

$$\psi (x)=x+〈n〉.$$

Now, x and y are independent in $Circ(mn,T)$:

$$\begin{array}{c}\iff x-y\notin T\hfill \\ \iff \psi (x+y)\notin S.\hfill \end{array}$$

Therefore,

$$\begin{array}{c}D\mathrm{is}\mathrm{an}\mathrm{independent}\mathrm{dominating}\mathrm{set}\mathrm{in}Circ(nm,T)\hfill \\ \iff \hfill \\ \psi (D)\mathrm{is}\mathrm{an}\mathrm{independent}\mathrm{dominating}\mathrm{set}\mathrm{in}Circ(n,S),\hfill \end{array}$$

so,

$$i(Circ(nm,T))=i(Circ(n,S)),$$

and:

$$\begin{array}{cc}\hfill \alpha ({(Circ(nm,T))}^2)& =\alpha (Circ(nm,\cup \{s_1+s_2+〈n〉:s_1,s_2\in S\}))\hfill \\ & =\alpha (Circ(n,\{s_1+s_2:s_1,s_2\in S\}))\hfill \\ & =\alpha ({(Circ(n,S))}^2).\hfill \end{array}$$

Therefore, $Circ(nm,(T))$, admits an efficient dominating set if and only if $Circ(n,S)$ admits an efficient dominating set. □

Theorem 6.

The circulant graph $Circ(n,\{1,2,3,\cdots ,k\})$ has an efficient dominating set if and only if $n=r(2k+1)$ for some integer r.

Proof. 

Let $G=Circ(n,\{1,2,3,\cdots ,k\})$. Since $G^2=Circ(n,\{1,2,3,\cdots ,2k\})$, we have that $D={\{2rk+r\}}_{r=1}^{\lfloor \frac{n}{2k+1}\rfloor }$ is a maximum independent set in $G^2$, and it forms an independent set in G.

Therefore, if $n=r(2k+1)$ for some integer r, then D is an independent dominating set in G; therefore, $\alpha (G^2)=i(G)$. Therefore, G admits an efficient dominating set.

If $n\ne r(2k+1)$, then D will not dominate all vertices in G; therefore, $\alpha (G^2)<i(G)$, and therefore it does not admit an efficient dominating set. □

4. Proper Interval Graphs

An interval graph is any graph whose vertices can be represented as a set of intervals and an edge set that connects vertices corresponding to intervals with a non-empty intersection. An interval graph with assigned intervals has the property that no interval contains any other interval and is properly called a proper interval graph. The applications of these classes of graphs are important; their applications can be found in biology, scheduling problems, social science, circuit design, and psychology. An interval graph is called a unit interval graph, if the assigned intervals are of the same length.

As seen before, all paths, $P_n$, are semi-square stable graphs. Therefore, one might raise the question, “Is every interval graph a semi-square stable graph?”. In fact, the answer is no, as one can see that a double star graph with $n\ge 2$ leaves on every side is an interval graph that is not a semi-square stable graph.

In this section, we study the independent number and independent dominating number of proper interval graphs. In [12], Bogart and West showed that proper interval graphs, claw-free interval graphs, and unit interval graphs are equivalent. It turns out that all proper interval graphs are semi-square stable graphs.

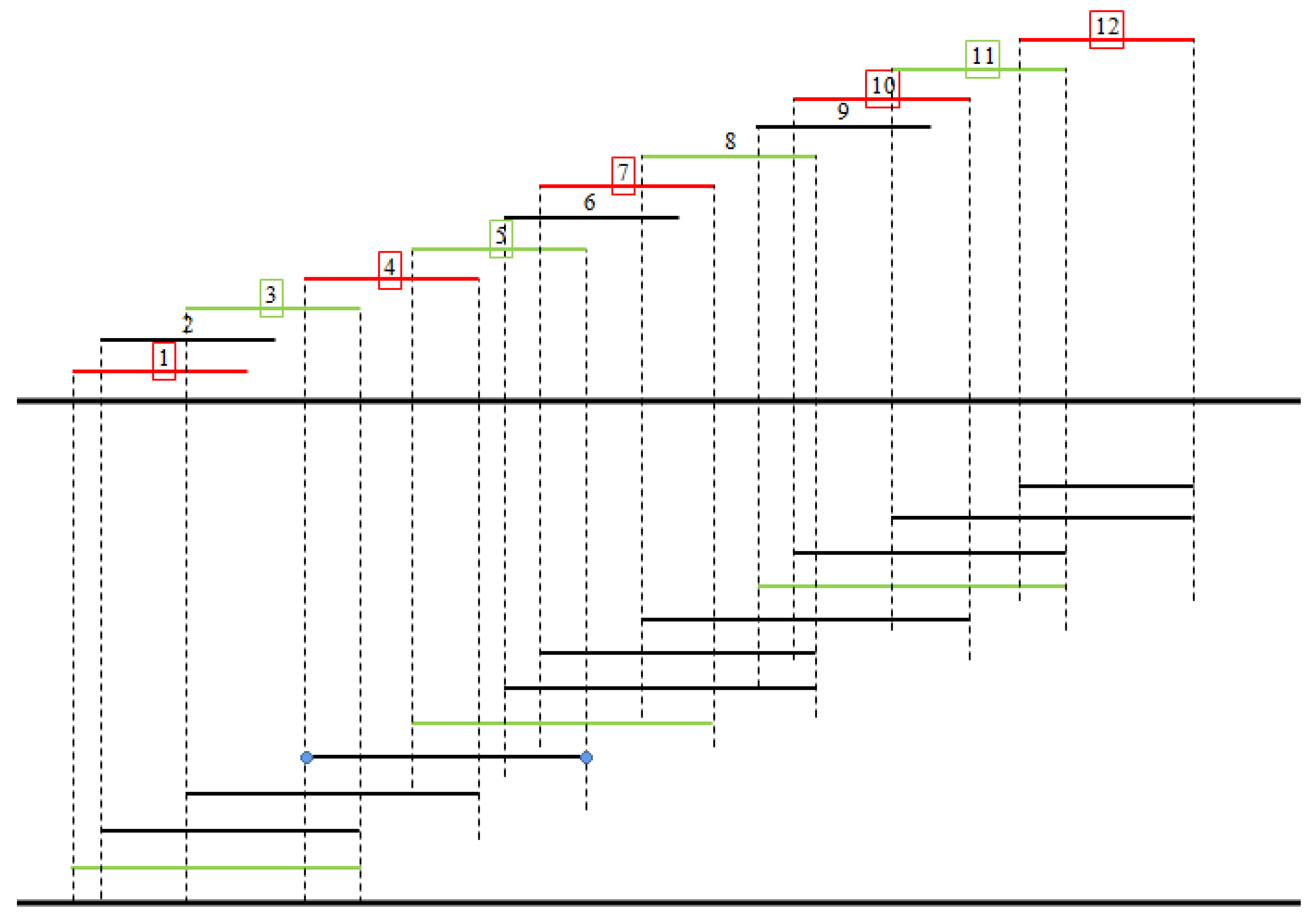
Definition 2.

For an interval graph G of order n, G has a normal interval representation (NIR) if the vertices can be represented by intervals satisfying the conditions:

1. 

All intervals are semi-open and of the form $[i,j)$, where $0\le i<j\le n$.

2. 

No two intervals start at the same number.

Lemma 1

([13]). An arbitrary graph is an interval graph if and only if it can be represented by the NIR form.

Now, consider the case where G is a proper interval graph, that is no interval is contained properly in another interval. Since G is also an interval graph, G has the NIR form. In fact, G has a special type of NIR form as described in the following definition:

Definition 3.

For a proper interval graph G, an NIR form of the graph G is called a stair normal interval representation (SNIR) if it has the following additional property:

For any two intervals $[a,b)$ and $[c,d)$, whenever $a<c$ holds, we have that $b<d$ holds.

Lemma 2

([13]). An arbitrary graph is a proper interval graph if and only if it can be represented by the SNIR form.

Let G be a proper graph with the $S={\{I_i=[a_i,b_i)\}}_{i=1}^n$ SNIR form. Define the function f by:

$$f(1)=1,\mathrm{and},f(k+1)=max\{i:a_i<b_{f(k)}\}.$$

Figure 4 illustrates the idea of the function f defined above.

Theorem 7.

If G is a connected proper interval graph with the $S={\{I_i=[a_i,b_i)\}}_{i=1}^n$ SNIR form, then the vertices corresponding to the intervals $\{I_{f(2)},I_{f(4),\cdots }\}$ form an i-set in G.

Proof. 

Using the definition of f, we have, for any i,

$$a_{f(2i+1)}<b_{f(2i)}<a_{f(2i+2)}<b_{f(2i+1)}.$$

Therefore, whenever $i\ne j$, $I_{f(2i)}\cap I_{f(2j)}=\varphi$, and therefore, the vertices corresponding to $\{I_{f(2)},I_{f(4)},\cdots \}$ form an independent set.

Now, let $I_j\in S$; if $j=f(k)$ for some k, then $I_{f(k)}\cap I_{f(k+1)}\ne \varphi$.

If $j\ne f(k)$, then for $k^{*}=min\{r:a_j<b_{f(r)}\}$, we have,

$$a_j<a_{f(k^{*}+1)}<b_{f(k^{*})}<b_j;$$

therefore, $I_j\cap I_{f(k^{*})}\ne \varphi$ and $I_j\cap I_{f(k^{*}+1)}\ne \varphi$.

Since either k or $k+1$ is even, we have that $\{I_{f(2)},I_{f(4)},\cdots ,\}$ form an i-set. □

Now, let G be an interval graph with the NIR form and $S={\{I_i=[a_i,b_i)\}}_{i=1}^n$ satisfying the property $a_i<a_j⟹b_i\le b_j$. Define the function g by:

$$g(1)=1,\mathrm{and},g(k+1)=min\{i:b_{g(k)}\le a_i\}$$

Theorem 8.

If G is an interval graph with the $S={\{I_i=[a_i,b_i)\}}_{i=1}^n$ NIR form satisfying the property whenever $a_i<a_j$, we have $b_i\le b_j$, then the vertices corresponding to the intervals $\{I_{g(1)},I_{g(2)},\cdots \}$ form an α-set in G.

Proof. 

Since G is a connected graph, for any i, $b_{g(i)}<a_{g(i+1)}$, the vertices corresponding to the intervals $\{I_{g(1)},I_{g(2)},I_{g(3)},\cdots ,\}$ form an independent set in G.

Now, suppose that D is an $\alpha$-set in G, then using the definition of g and since D is the maximum independent set, we have:

$$\begin{array}{cc}\hfill a_{g(1)}& \le a_{i_1}<b_{g(1)}<b_{i_1}<b_{g(2)}\hfill \\ \hfill a_{g(2)}& \le a_{i_2}<b_{g(2)}<b_{i_2}<b_{g(3)}\hfill \\ & ⋮\hfill \end{array}$$

Therefore,

$$\left|D\right|=\left|\right\{I_{g(1)},I_{g(2)},I_{g(3)},\cdots ,\left\}\right|$$

 □

Theorem 9.

If G is a proper interval graph with the $S={\{I_i=[a_i,b_i)\}}_{i=1}^n$ SNIR form, then $G^2$ is an interval graph with the $S^{\prime }=\{[a_j,b_{k_j}):k_j=max\{i:a_i<b_j\}\}$ NIR form.

Proof. 

First, it is obvious that if $I_i\cap I_j\ne \varphi$, then, $[a_j,b_{k_j})\cap [a_i,b_{k_i})\ne \varphi$, and so, $E(G)\subset E(G^2)$.

Now, let $I_m,I_r$ and $I_s\in S$ with $a_m<a_r<a_s$, $I_m\cap I_r\ne \varphi$ and $I_r\cap I_s\ne \varphi$, then $b_m>a_r$ and $b_r>a_s$; this means that $b_{k_m}\ge b_r>a_s$. Therefore, $[a_m,b_{k_m})\cap [a_s,b_{k_s})\ne \varphi$. This proves that if $d_G(u,v)\le 2$, then, $uv\in E(G^2)$.

Finally, suppose that $I_m,I_s\in S$ with $a_m<a_s$ and $d_G(I_m,I_s)\ge 3$, then if there is $I_r$ such that $a_m<a_r<b_m<a_s<b_r$, then $d_G(I_m,I_s)=2$. Therefore, for any $I_r\in S$, if $a_r<b_m$, then $b_r<a_s$; therefore, $b_{k_m}<a_s$. This proves that if $d_G(u,v)\ge 3$, then $uv\notin E(G^2)$. □

Finally, we give the proof of our main result.

Theorem 10.

Any proper interval graph is a semi-square stable graph.

Proof. 

Let G be a proper interval graph with the $S={\{I_i=[a_i,b_i)\}}_{i=1}^n$ SNIR form and $S^{\prime }={\{I_i=[a_j,b_{k_j}):k_j=max\{i:a_i<b_j\}\}}_{i=1}^n$ be the SNIR form of $G^2$, then using Theorems 7 and 8, we have:

$D=\{[a_1,b_{k_1}),[a_{g(2)},b_{g(k_2)}),\cdots \}$ is the independent set of $G^2$, and $D^{\prime }=\{[a_{f(2)},b_{f(2)}),[a_{f(4)},b_{f(4)}),\cdots \}$ is the dominating set of G.

Since $b_{f(2r)}=b_{g(k_r)}$, we have $\left|D\right|=|D^{\prime }|$, and so, G is a semi-square stable graph. □