Audio Signal Processing Using Fractional Linear Prediction
Abstract
:1. Introduction
2. Linear Prediction
2.1. Conventional Linear Prediction
2.2. Fractional Linear Prediction with “Restricted Memory”
3. Datasets
3.1. MAPS Dataset
3.2. Orchset Dataset
3.3. Signal Preprocessing
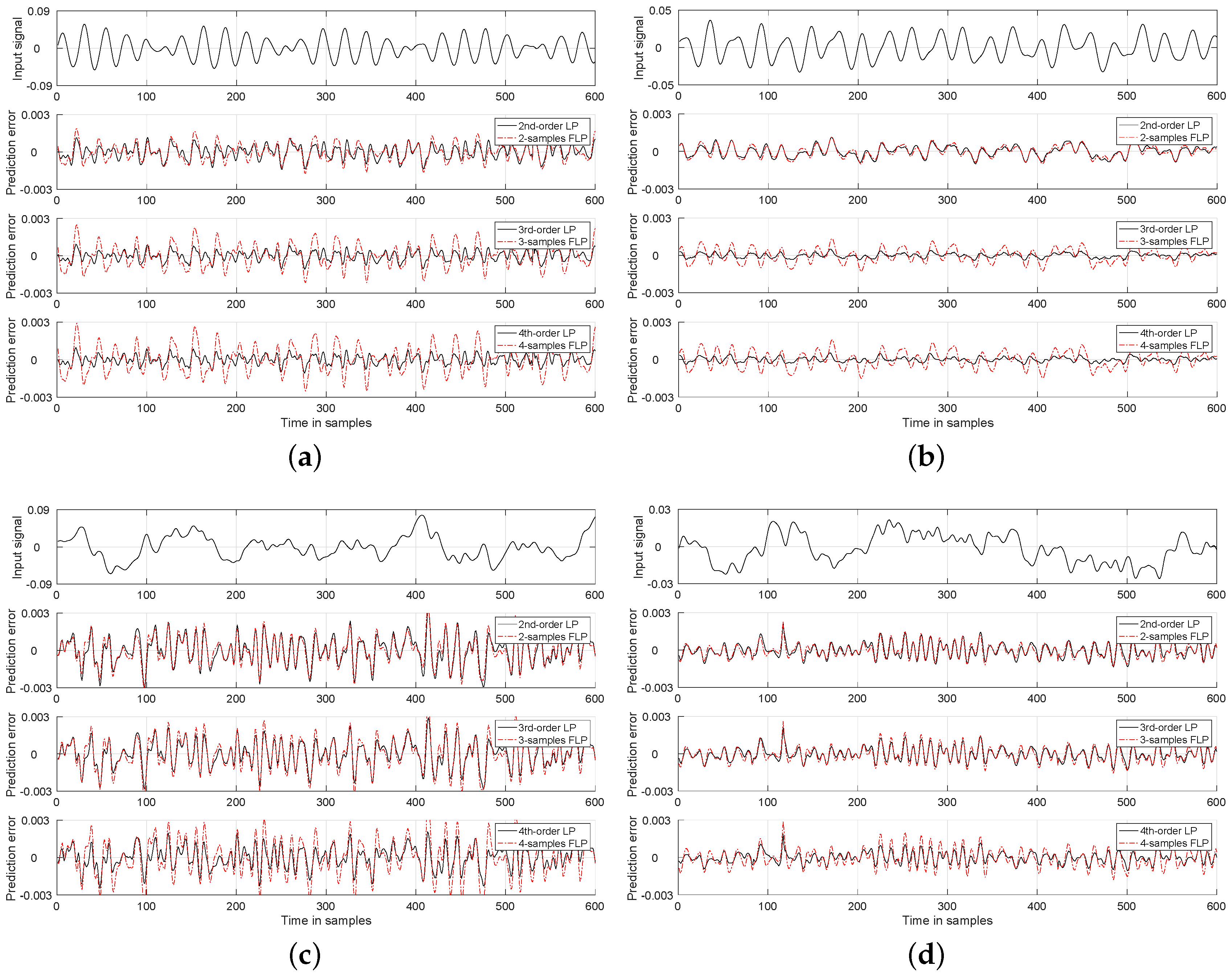
4. Numerical Results and Discussion
Experiments
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Purnhagen, H.; Meine, N. HILN–The MPEG-4 Parametric Audio Coding Tools. In Proceedings of the 2000 IEEE International Symposium on Circuits and Systems. Emerging Technologies for the 21st Century, Geneva, Switzerland, 28–31 May 2000; Volume 3, pp. 201–204. [Google Scholar]
- Marchand, S.; Strandh, R. InSpect and ReSpect: Spectral Modeling, Analysis and Real-Time Synthesis Software Tools for Researchers and Composers. In Proceedings of the Int. Computer Music Conference (ICMC 1999), Beijing, China, 22–27 October 1999; pp. 341–344. [Google Scholar]
- Lagrange, M.; Marchand, S. Long Interpolation of Audio Signals Using Linear Prediction in Sinusoidal Modeling. J. Audio Eng. Soc. 2005, 53, 891–905. [Google Scholar]
- Thompson, W.F. Music, Thought, and Feeling: Understanding the Psychology of Music; Oxford University Press: Oxford, UK; New York, NY, USA, 2008. [Google Scholar]
- Atal, B.S. The History of Linear Prediction. IEEE Signal Process. Mag. 2006, 23, 154–161. [Google Scholar] [CrossRef]
- Benesty, J.; Chen, J.; Huang, Y. Linear Prediction. In Springer Handbook of Speech Processing; Benesty, J., Sondhi, M.M., Huang, Y., Eds.; Springer: Berlin, Germany, 2007; Chapter 7; pp. 121–133. [Google Scholar]
- Vaidyanathan, P.P. The Theory of Linear Prediction; Synthesis Lectures on Signal Processing; Morgan & Claypool: San Rafael, CA, USA, 2008. [Google Scholar]
- van Waterschoot, T.; Moonen, M. Comparison of linear prediction models for audio signals. EURASIP J. Audio Speech Music Process. 2009, 2008. [Google Scholar] [CrossRef]
- Harma, A.; Laine, U.K. A comparison of warped and conventional linear predictive coding. IEEE Trans. Speech Audio Process. 2001, 9, 579–588. [Google Scholar] [CrossRef]
- Deriche, M.; Ning, D. A novel audio coding scheme using warped linear prediction model and the discrete wavelet transform. IEEE Trans. Audio Speech Lang. Process. 2006, 14, 2039–2048. [Google Scholar] [CrossRef]
- Van Waterschoot, T.; Rombouts, G.; Verhoeve, P.; Moonen, M. Double-talk-robust prediction error identification algorithms for acoustic echo cancellation. IEEE Trans. Signal Process. 2007, 55, 846–858. [Google Scholar] [CrossRef]
- Mahkonen, K.; Eronen, A.; Virtanen, T.; Helander, E.; Popa, V.; Leppanen, J.; Curcio, I.D. Music dereverberation by spectral linear prediction in live recordings. In Proceedings of the 16th Int. Conference on Digital Audio Effects (DAFx-13), Maynooth, Ireland, 2–6 September 2013; pp. 1–4. [Google Scholar]
- Grama, L.; Rusu, C. Audio signal classification using Linear Predictive Coding and Random Forests, Bucharest, Romania. In Proceedings of the International Conference on Speech Technology and Human-Computer Dialogue (SpeD 2017), Bucharest, Romania, 6–9 July 2017. [Google Scholar]
- Glover, J.; Lazzarini, V.; Timoney, J. Real-time detection of musical onsets with linear prediction and sinusoidal modeling. EURASIP J. Adv. Signal Process. 2011, 2011, 68. [Google Scholar] [CrossRef] [Green Version]
- Marchi, E.; Ferroni, G.; Eyben, F.; Gabrielli, L.; Squartini, S.; Schuller, B. Multi-resolution linear prediction based features for audio onset detection with bidirectional LSTM neural networks. In Proceedings of the IEEE International Conference on Acoustic, Speech and Signal Processing (ICASSP 2014), Florence, Italy, 4–9 May 2014; pp. 2183–2187. [Google Scholar]
- Skovranek, T.; Despotovic, V. Signal Prediction using Fractional Derivative Models. In Handbook of Fractional Calculus with Applications; Baleanu, D., Lopes, A.M., Eds.; Walter de Gruyter GmbH: Berlin/Munich, Germany; Boston, MA, USA, 2019; Volume 8, Chapter 7; pp. 179–206. [Google Scholar]
- Joshia, V.; Pachori, R.B.; Vijesh, A. Classification of ictal and seizure-free EEG signals using fractional linear prediction. Biomed. Signal Process. Control 2014, 9, 1–5. [Google Scholar] [CrossRef]
- Talbi, M.L.; Ravier, P. Detection of PVC in ECG Signals Using Fractional Linear Prediction. Biomed. Signal Process. Control 2016, 23, 42–51. [Google Scholar] [CrossRef]
- Assaleh, K.; Ahmad, W.M. Modeling of Speech Signals Using Fractional Calculus. In Proceedings of the 9th International Symposium on Signal Processing and Its Applications (ISSPA’07), Sharjah, UAE, 12–15 February 2007; pp. 1–4. [Google Scholar]
- Despotovic, V.; Skovranek, T. Fractional-order Speech Prediction. In Proceedings of the International Conference on Fractional Differentiation and its Applications (ICFDA’16), Novi Sad, Serbia, 18–20 July 2016; pp. 124–127. [Google Scholar]
- Despotovic, V.; Skovranek, T.; Peric, Z. One-parameter fractional linear prediction. Comput. Electr. Eng. Spec. Issue Signal Process. 2018, 69, 158–170. [Google Scholar] [CrossRef]
- Skovranek, T.; Despotovic, V.; Peric, Z. Optimal Fractional Linear Prediction With Restricted Memory. IEEE Signal Process. Lett. 2019, 26, 760–764. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic Press: San Diego, CA, USA, 1999. [Google Scholar]
- Emiya, V.; Badeau, R.; David, B. Multipitch estimation of piano sounds using a new probabilistic spectral smoothness principle. IEEE Trans. Audio Speech Lang. Process. 2010, 18, 1643–1654. [Google Scholar] [CrossRef]
- Emiya, V. Transcription Automatique de la Musique de Piano. Ph.D. Thesis, Telecom ParisTech, Paris, France, October 2008. [Google Scholar]
- Bosch, J.; Marxer, R.; Gomez, E. Evaluation and Combination of Pitch Estimation Methods for Melody Extraction in Symphonic Classical Music. J. New Music Res. 2016, 45, 101–117. [Google Scholar] [CrossRef]
- Driedger, J.; Mueller, M. A Review of Time-Scale Modification of Music Signals. Appl. Sci. 2016, 6, 57. [Google Scholar] [CrossRef]
- Theodoridis, S.; Koutroumbas, K. Pattern Recognition, 4th ed.; Academic Press: San Diego, CA, USA, 2008. [Google Scholar]
- Chu, W.C. Speech Coding Algorithms: Foundation and Evolution of Standardized Coders; John Wiley & Sons: Hoboken, NJ, USA, 2003. [Google Scholar]



| MAPS–RAND | ||||||
|---|---|---|---|---|---|---|
| Studio | Jazz | Church | Concert | |||
| 120 ms | LP | First-order | 17.41 | 17.53 | 19.10 | 15.48 |
| Second-order | 23.94 | 23.91 | 26.25 | 22.51 | ||
| Third-order | 24.85 | 24.52 | 26.89 | 23.55 | ||
| Fourth-order | 25.25 | 24.79 | 27.15 | 23.96 | ||
| FLP | Two-sample memory | 23.40 | 23.36 | 25.82 | 22.14 | |
| Three-sample memory | 23.41 | 23.68 | 26.02 | 22.01 | ||
| Four-sample memory | 23.11 | 25.06 | 25.88 | 21.63 | ||
| 60 ms | LP | First-order | 17.15 | 17.35 | 18.90 | 15.23 |
| Second-order | 22.90 | 22.82 | 25.15 | 21.43 | ||
| Third-order | 23.51 | 23.42 | 25.70 | 22.14 | ||
| Fourth-order | 23.85 | 23.66 | 25.93 | 22.51 | ||
| FLP | Two-sample memory | 22.32 | 22.25 | 24.71 | 21.07 | |
| Three-sample memory | 22.47 | 22.66 | 25.01 | 21.08 | ||
| Four-sample memory | 22.28 | 22.73 | 24.96 | 20.81 | ||
| 10 ms | LP | First-order | 16.35 | 16.58 | 18.13 | 14.65 |
| Second-order | 19.82 | 19.95 | 21.65 | 18.86 | ||
| Third-order | 20.28 | 20.48 | 22.19 | 19.29 | ||
| Fourth-order | 20.46 | 20.68 | 22.38 | 19.50 | ||
| FLP | Two-sample memory | 19.30 | 19.37 | 21.22 | 18.50 | |
| Three-sample memory | 19.74 | 19.96 | 21.78 | 18.80 | ||
| Four-sample memory | 19.81 | 20.17 | 21.94 | 18.76 | ||
| MAPS–UCHO | ||||||
|---|---|---|---|---|---|---|
| Studio | Jazz | Church | Concert | |||
| 120 ms | LP | First-order | 17.03 | 18.54 | 18.74 | 17.44 |
| Second-order | 24.51 | 25.75 | 26.62 | 25.22 | ||
| Third-order | 25.25 | 26.29 | 27.12 | 26.02 | ||
| Fourth-order | 25.61 | 26.52 | 27.34 | 26.39 | ||
| FLP | Two-sample memory | 23.95 | 25.08 | 26.29 | 24.92 | |
| Three-sample memory | 23.90 | 25.44 | 26.46 | 24.78 | ||
| Four-sample memory | 23.57 | 25.47 | 26.29 | 24.37 | ||
| 60 ms | LP | First-order | 16.83 | 18.37 | 18.53 | 17.15 |
| Second-order | 23.53 | 24.58 | 25.42 | 24.07 | ||
| Third-order | 24.04 | 25.10 | 25.91 | 24.62 | ||
| Fourth-order | 24.32 | 25.29 | 26.08 | 24.93 | ||
| FLP | Two-sample memory | 22.97 | 23.89 | 25.07 | 23.76 | |
| Three-sample memory | 23.05 | 24.36 | 25.36 | 23.76 | ||
| Four-sample memory | 22.82 | 24.47 | 25.30 | 23.46 | ||
| 10 ms | LP | First-order | 16.07 | 17.46 | 17.71 | 16.38 |
| Second-order | 20.44 | 21.15 | 21.77 | 20.85 | ||
| Third-order | 20.87 | 21.74 | 22.32 | 21.29 | ||
| Fourth-order | 21.01 | 21.93 | 22.49 | 21.45 | ||
| FLP | Two-sample memory | 19.95 | 20.51 | 21.45 | 20.57 | |
| Three-sample memory | 20.34 | 21.15 | 21.99 | 20.90 | ||
| Four-sample memory | 20.37 | 21.42 | 22.14 | 20.88 | ||
| MAPS–MUS | Orchset | ||||||
|---|---|---|---|---|---|---|---|
| Studio | Jazz | Church | Concert | ||||
| 120 ms | LP | First-order | 20.54 | 22.13 | 21.90 | 19.60 | 18.12 |
| Second-order | 31.60 | 34.04 | 32.95 | 30.21 | 26.82 | ||
| Third-order | 32.36 | 34.52 | 33.51 | 31.24 | 27.94 | ||
| Fourth-order | 32.86 | 34.75 | 33.78 | 31.74 | 28.15 | ||
| FLP | Two-sample memory | 31.59 | 34.02 | 32.94 | 30.18 | 26.70 | |
| Three-sample memory | 31.20 | 34.25 | 32.98 | 29.69 | 26.03 | ||
| Four-sample memory | 30.55 | 33.98 | 32.65 | 28.96 | 25.29 | ||
| 60 ms | LP | First-order | 20.49 | 22.00 | 21.79 | 19.58 | 18.08 |
| Second-order | 30.27 | 32.05 | 31.28 | 29.10 | 26.18 | ||
| Third-order | 30.81 | 32.63 | 31.87 | 29.82 | 26.99 | ||
| Fourth-order | 31.17 | 32.80 | 32.07 | 30.22 | 27.18 | ||
| FLP | Two-sample memory | 30.25 | 32.04 | 31.26 | 29.08 | 26.09 | |
| Three-sample memory | 30.14 | 32.56 | 31.57 | 28.83 | 25.56 | ||
| Four-sample memory | 29.66 | 32.44 | 31.39 | 28.25 | 24.91 | ||
| 10 ms | LP | First-order | 19.68 | 20.94 | 20.77 | 18.90 | 17.53 |
| Second-order | 25.18 | 25.92 | 25.66 | 24.60 | 23.01 | ||
| Third-order | 25.75 | 26.75 | 26.40 | 25.15 | 23.37 | ||
| Fourth-order | 25.92 | 27.01 | 26.62 | 25.35 | 23.49 | ||
| FLP | Two-sample memory | 25.17 | 25.92 | 25.66 | 24.57 | 23.00 | |
| Three-sample memory | 25.70 | 26.74 | 26.39 | 24.97 | 22.93 | ||
| Four-sample memory | 25.64 | 27.00 | 26.52 | 24.81 | 22.62 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Skovranek, T.; Despotovic, V. Audio Signal Processing Using Fractional Linear Prediction. Mathematics 2019, 7, 580. https://doi.org/10.3390/math7070580
Skovranek T, Despotovic V. Audio Signal Processing Using Fractional Linear Prediction. Mathematics. 2019; 7(7):580. https://doi.org/10.3390/math7070580
Chicago/Turabian StyleSkovranek, Tomas, and Vladimir Despotovic. 2019. "Audio Signal Processing Using Fractional Linear Prediction" Mathematics 7, no. 7: 580. https://doi.org/10.3390/math7070580
APA StyleSkovranek, T., & Despotovic, V. (2019). Audio Signal Processing Using Fractional Linear Prediction. Mathematics, 7(7), 580. https://doi.org/10.3390/math7070580






