Abstract
Connectivity is a critical parameter that can measure the reliability of networks. Let be a vertex set. If is disconnected and every component of contains at least vertices, then Q is an extra-cut. The number of vertices in the smallest extra-cut is the extraconnectivity . Suppose is the number of components of G and ; if , then w is a t-component cut of G. The number of vertices in the least t-component cut is the t-component connectivity of G. The t-component edge connectivity is defined similarly. In this note, we study the BC networks and obtain the t-component (edge) connectivity of bijective connection networks for some t.
1. Introduction
Multiprocessor systems have many advantages over their uniprocessor counterparts, such as high performance and reliability, better reconfigurability, and scalability. With the development of VLSItechnology and software technology, multiprocessor systems with hundreds of thousands of processors have become available. With the continuous increase in the size of multiprocessor systems, the complexity of a system can adversely affect its fault tolerance and reliability. For the design and maintenance purpose of multiprocessor systems, appropriate measures of reliability should be found.
A graph can simulate a network. The edges can represent links between the nodes, and the vertices can represent nodes that are processors or stations. Reliability is the essential consideration in network design [1,2]. For a connected graph G, the connectivity is defined as the minimum number k of vertices that can be removed to reduce the graph connectivity or leave only one vertex. For the reliability of networks, connectivity is worst for most measures. To compensate for this shortcoming, it seems reasonable to generalize the notion of classical connectivity by imposing some conditions or restrictions on the components of , where F denotes faulty processors/links. Hence, many parameters that can measure the reliability of multiprocessor systems have been proposed. Suppose ; if , then is a t-component cut of G. The number of vertices in the least t-component cut is the t-component connectivity of G. Correspondingly, the t-component edge connectivity is obtained. The t-component (edge) connectivity was proposed in [3,4] independently. Fábrega et al. proposed extraconnectivity in [5]. Let be a vertex set. If is disconnected and every component of contains at least vertices, then is an extra-cut. The number of vertices in the smallest extra-cut is the extraconnectivity .
Suppose is a connected graph, (simply ), e is an edge, and w is an end of e}.
Q is a subset of V; is the subgraph induced by the vertices in Q, ; is the subgraph of G that is induced by the vertices of . If , then is the number of edges of the shortest -path. For , the edge set . We follow [6] for terminology and notation. We only consider simple, finite, and undirected graphs.
Definition 1.
BC networks:The one-dimensional bijective connection network is the complete graph . Let and G be an n-dimensional BC graph. Suppose is an n-dimensional bijective connection graph}. An n-dimensional BC graph G can be defined recursively:
- (1)
- For two non-empty subsets , ;
- (2)
- An edge set , Q is a perfect matching between and , .
In the following, we denote an n-dimensional BC network. The n-dimensional BC network with vertices and edges was introduced by Fan et al. [7]. An n-dimensional BC graph is n regular Hamilton-connected. BC graphs contain most of the variants of the hypercube: hypercube, crossed cube, twisted cube, locally-twisted cube, and so on. We can see that , , , where is a four-cycle, is a three-dimensional hypercube, is a three-dimensional crossed cube, is a three-dimensional twisted cube, and is a three-dimensional locally-twisted cube. and are isomorphs of .
According to the definition, every vertex of has only one neighbor in , and every vertex of also has only one neighbor in . Because can be obtained by putting a perfect matching W between and , can be viewed as or . Suppose is the edge incident to w in W.
The BC graphs are an attractive alternative to hypercubes . For more references about BC networks, see [8,9,10,11,12,13]. For more references about component connectivity, see [14,15,16].
In this work, we get that:
- (1)
- Suppose ; .
- (2)
- Suppose ; .
- (3)
- Suppose ; .
- (4)
- Suppose ; .
- (5)
- Suppose ; .
2. Properties of BC Networks
The BC networks has an important property as follows.
Lemma 1
([11]). Let be any two vertices. Then, .
Corollary 1.
Suppose that are any two vertices. Then,
- (1)
- if is two, then ;
- (2)
- if , then .
From Lemma 1, we can see that the girth of is . By the definition of , we obtain:
Lemma 2.
Suppose that are any two vertices such that .
- (1)
- If , then and .
- (2)
- If or , then or .
Lemma 3
([7]). If , then .
Theorem 1.
If , .
Theorem 2.
Suppose , .
Proof.
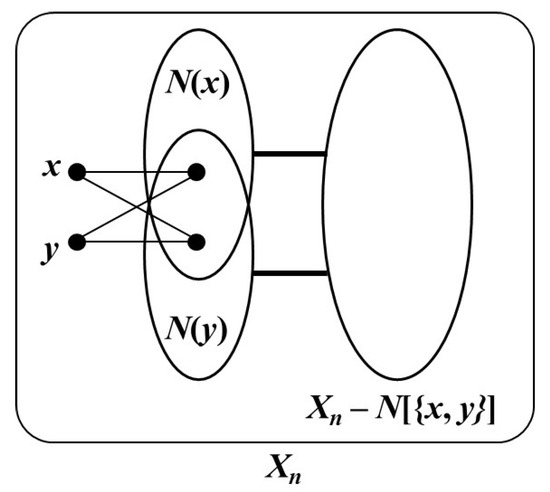
In a cycle , take with . Then, (see Figure 1) and . Hence, .

Figure 1.
Illustration of .
We will show by induction; this is right for . Hence, let . Suppose that the case of is true. Set .
By contradiction, suppose and . Furthermore, , say and . We have or . We set by symmetry. Hence, must be connected.
If , then by the inductive hypothesis, and . Since every vertex of has one neighbor in , at most one vertex of does not have neighbors in . Hence, , a contradiction.
Hence, . At most one connected component of is not connected to . Then, , a contradiction again. □
Lemma 4.
Let be an any vertex. The connectivity is .
Proof.
Since , . We need to prove . The case of is true. Set and .
By contradiction, suppose with . Next, it will be proven that is connected. Since , is connected. By Theorem 4, , then : one component is the vertex w, and the other component is . However, for , and at least one vertex of is connected to . Then, is connected, and this contradicts the hypothesis. □
Lemma 5.
Suppose , then .
Proof.
Pick an edge . Therefore, is disconnected, and at least two vertices are contained in every connected component. That is .
It suffices to show by induction. The case of is true. Assume that , and this is right when . This will be proven for .
By contradiction, suppose with . We will show that is connected or contains an isolated vertex. We suppose by symmetry. Then, is connected.
If each connected component of contains more than one vertex, according to the inductive hypothesis, and . At most one vertex of does not have neighbors in . Hence, is connected.
Suppose is the isolated vertex of . Note that , and by Lemma 4, . If , then . Then, has an isolated vertex , or has an isolated vertex whose degree is in , or is connected to , a contradiction.
Assume . Since , and , is connected by Lemma 4. However, , is connected to or has an isolated vertex , and this contradicts the hypothesis. □
Theorem 3.
Suppose , .
Theorem 4.
Suppose , .
Proof.
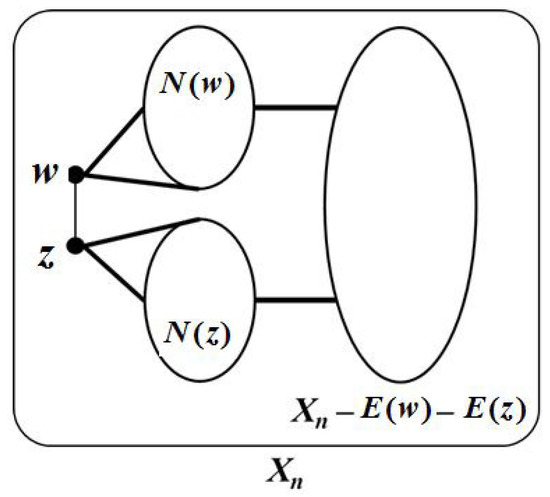
Pick an edge , then . (see Figure 2). That is, .

Figure 2.
Illustration of .
Next, we will show that by induction. The cases of are true. Therefore, we set , and this is right for . Next, for , it will be proven that this is right.
By contradiction, suppose , , and has at least three components. Since , we have or , say . Note that .
Case 1.
is disconnected.
We obtain and .
If is disconnected, then . That is . However, every vertex of has a path to one component of . Hence, has at most two components, and this is a contradiction.
Since , if is connected, then has a path to one component of . Hence, , and this is a contradiction.
Case 2.
is connected.
If is connected, then it holds. Assume that is not connected. At most one isolated vertex is in since .
If , then by the inductive hypothesis. Then, at most one of the components of is not connected to , , a contradiction.
Therefore, we suppose that . However, , , a contradiction. □
Theorem 5.
Suppose , then .
Proof.
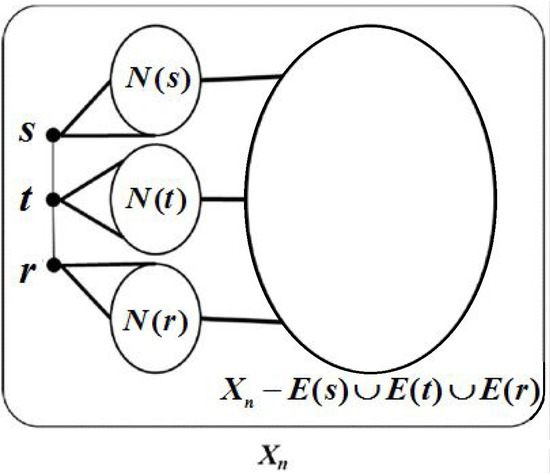
Pick a path . Then, . Then, (see Figure 3). That is, .

Figure 3.
Illustration of .
Next, we will show that by induction. The cases of are true. Therefore, we suppose and assume all the cases of are true. We will prove that the case of holds.
By contradiction, assume that , , and . Since , we have or , say . Since , .
Case 1.
is connected.
If , then according to the inductive hypothesis. At most two edges need to be deleted again. Because every vertex of has a neighbor in and , , a contradiction.
Suppose . If , then . Assume that . At most one edge needs to be delete again. Note that , and and are connected. Hence, , a contradiction. Then, . At least one component of is connected to . Then, , a contradiction again.
Then, let . Because of , , a contradiction.
Case 2.
.
Then, and . Note that .
If , then and . However, and , , a contradiction.
Hence, . We have , and , a contradiction. □
Author Contributions
These authors contributed equally to this work.
Funding
The project is supported by Natural Science Foundation of Fujian Province, China (No. 2019J01857), and Fujian Scholarship for Study Abroad.
Acknowledgments
We would like to thank the referees for their kind help and valuable suggestions.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Cheng, E.; Lesniak, L.; Lipman, M.; Lipták, L. Conditional matching preclusion sets. Inf. Sci. 2009, 179, 1092–1101. [Google Scholar] [CrossRef]
- Lin, M.; Chang, M.; Chen, D. Efficient algorithms for reliability analysis of distributed computing systems. Inf. Sci. 1999, 117, 89–106. [Google Scholar] [CrossRef]
- Chartrand, G.; Kapoor, S.; Lesniak, L.; Lick, D. Generalized connectivity in graphs. Bull. Bombay Math. Colloq. 1984, 2, 1–6. [Google Scholar]
- Sampathkumar, E. Connectivity of a graph—A generalization. J. Combin. Inform. Syst. Sci. 1984, 9, 71–78. [Google Scholar]
- Fábrega, J.; Fiol, M. On the extraconnectivity of graphs. Dis. Math. 1996, 155, 49–57. [Google Scholar] [CrossRef]
- Bondy, J.; Murty, U. Graph Theory and Its Application; Academic Press: Cambridge, MA, USA, 1976. [Google Scholar]
- Fan, J.; He, L. BC interconnection networks and their properties. China J. Comput. 2003, 26, 84–90. [Google Scholar]
- Chang, N.; Hsieh, S. {2,3}-Extraconnectivities of hypercube-like networks. J. Comput. Syst. Sci. 2013, 79, 669–688. [Google Scholar] [CrossRef]
- Hsieh, S. Extra edge connectivity of hypercube-like networks. Int. J. Parallel Emergent Distrib. Syst. 2013, 28, 123–133. [Google Scholar]
- Fan, J.; Lin, X. The t/k-diagnosability of the BC graphs. IEEE Trans. Comput. 2005, 54, 176–185. [Google Scholar]
- Zhu, Q. On conditional diagnosability and reliability of the BC networks. J. Supercomput. 2008, 45, 173–184. [Google Scholar] [CrossRef]
- Zhu, Q.; Wang, X.; Cheng, G. Reliability evaluation of BC networks. IEEE Trans. Comput. 2013, 62, 2337–2340. [Google Scholar] [CrossRef]
- Zhou, J. On g-extra connectivity of hypercube-like networks. J. Comput. Syst. Sci. 2017, 88, 208–219. [Google Scholar] [CrossRef]
- Guo, L. Reliability analysis of twisted cubes. Theor. Comput. Sci. 2018, 707, 96–101. [Google Scholar] [CrossRef]
- Hsu, L.; Cheng, E.; Lipták, L.; Tan, J.; Lin, C.; Ho, T. Component connectivity of the hypercubes. Int. J. Comput. Math. 2012, 89, 137–145. [Google Scholar] [CrossRef]
- Zhao, S.; Yang, W.; Zhang, S. Component connectivity of hypercubes. Theor. Comput. Sci. 2016, 640, 115–118. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).