Natural Transform Decomposition Method for Solving Fractional-Order Partial Differential Equations with Proportional Delay
Abstract
1. Introduction
2. Preliminaries
3. Idea of Fractional Natural Transform Decomposition Method
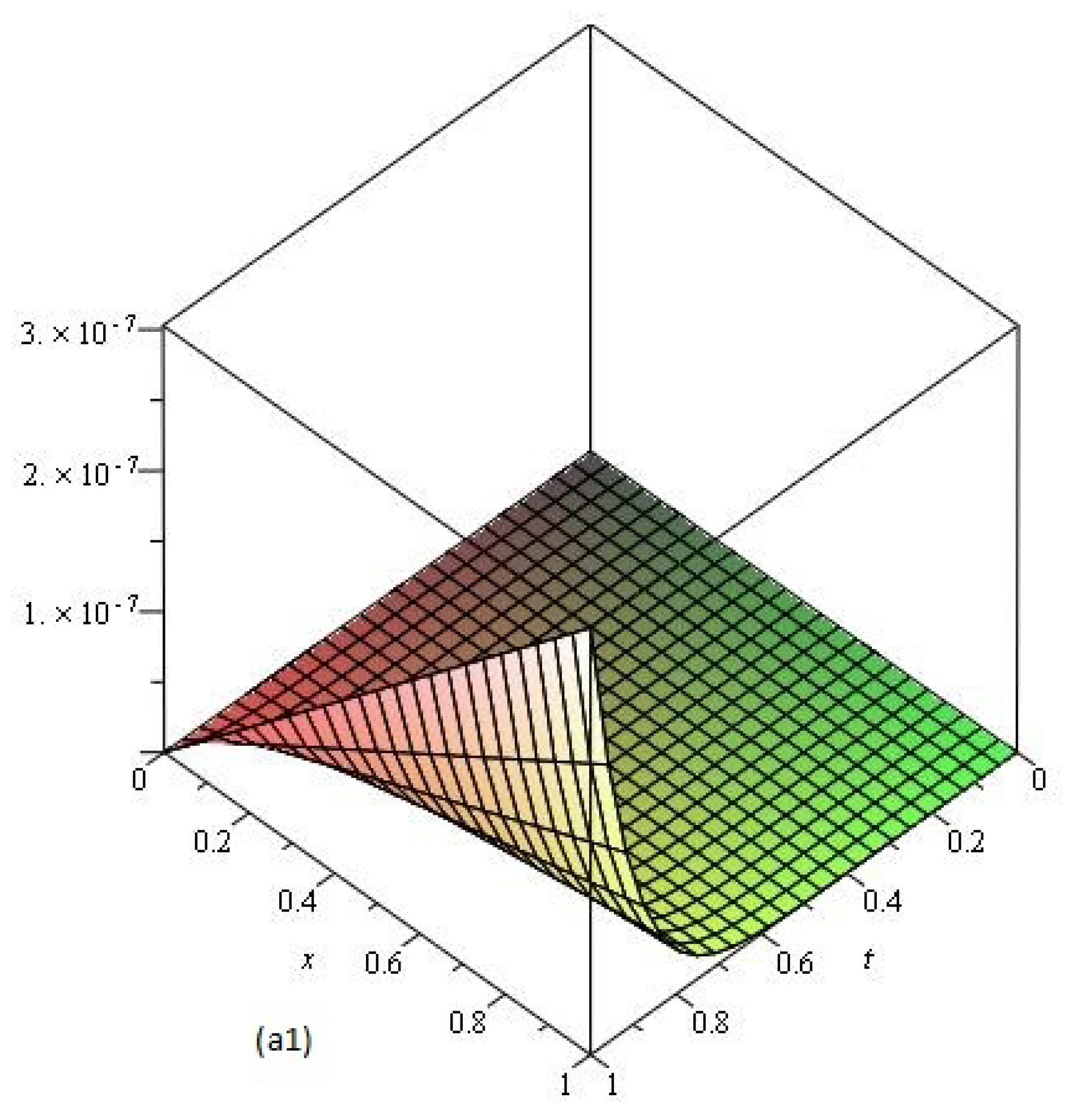
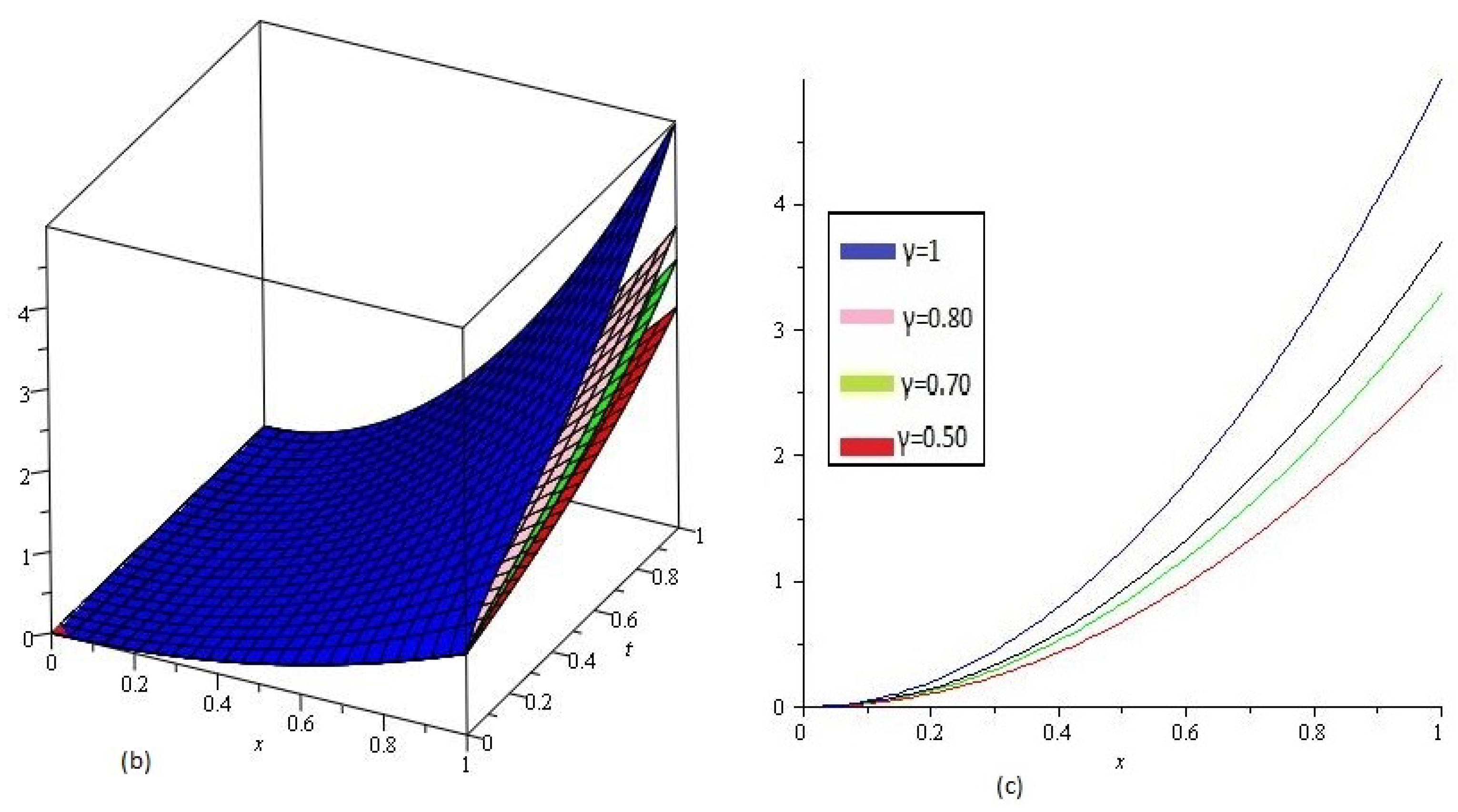
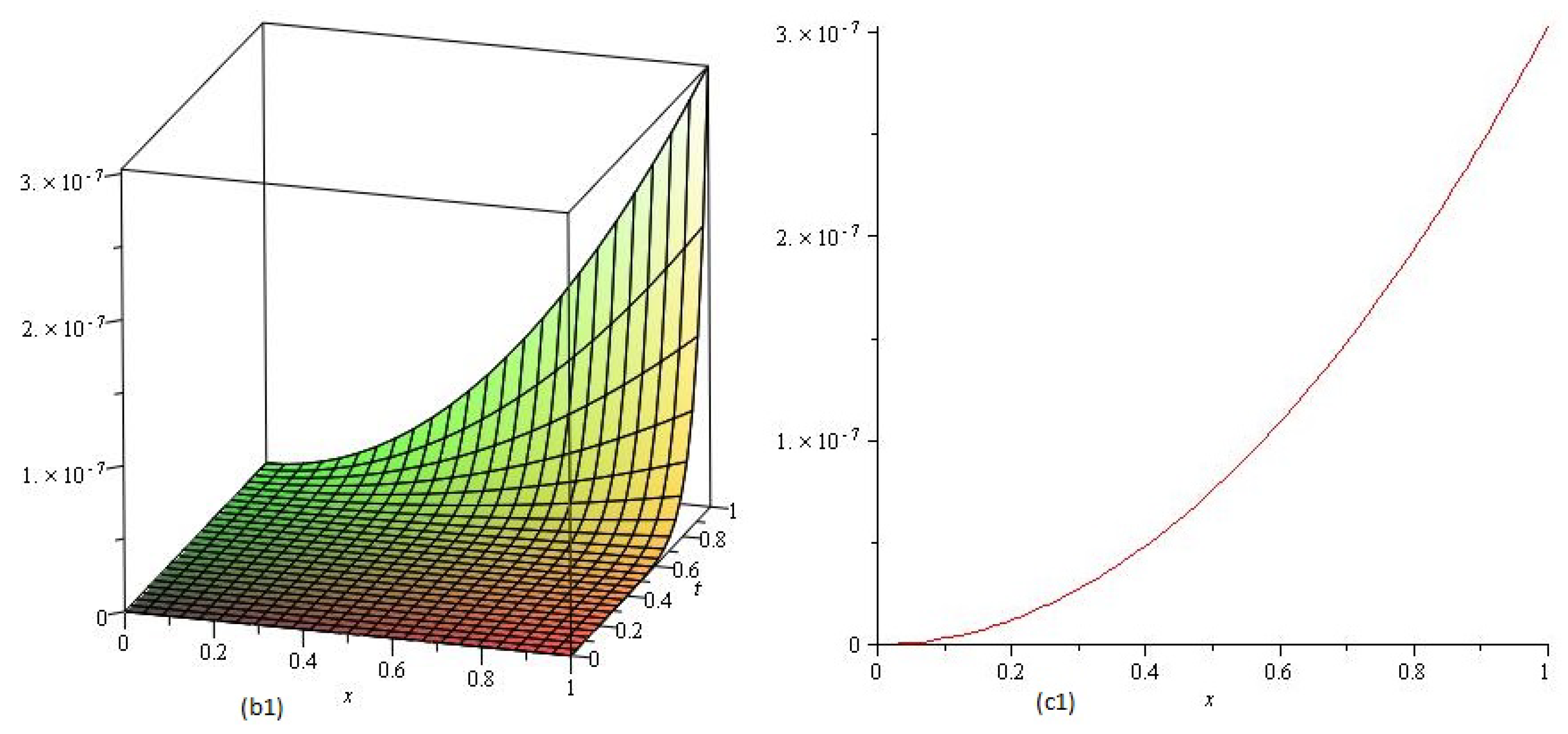
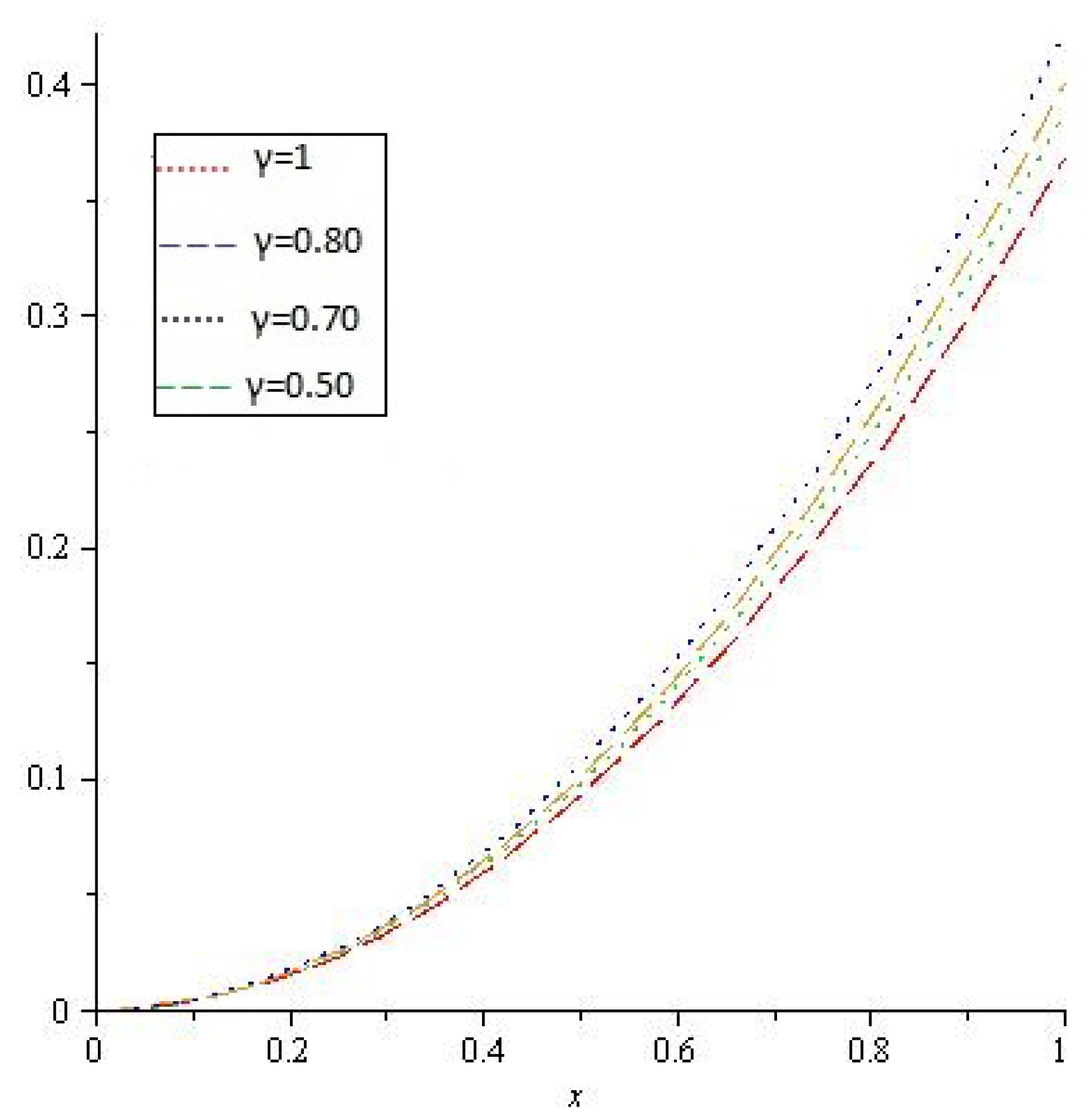
4. Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Kuang, Y. Delay Differential Equations with Applications in Population Dynamics; Academic Press, Inc.: New York, NY, USA, 1993. [Google Scholar]
- Dugard, L.; Verriest, E.I. Stability and control of time-delay systems. In Lecture Notes in Control and Information Sciences; Springer: Berlin, Germany, 1997; Volume 228. [Google Scholar]
- Fridman, E.; Fridman, L.; Shustin, E. Steady modes in relay control systems with time delay and periodic disturbances. J. Dyn. Syst. Measur. Control 2000, 122, 732–737. [Google Scholar] [CrossRef]
- Shakeri, F.; Dehghan, M. Solution of delay differential equations via a homotopy perturbation method. Math. Comput. Model. 2008, 48, 486–498. [Google Scholar] [CrossRef]
- Polyanin, A.D.; Zhurov, A.I. Functional constraints method for constructing exact solutions to delay reaction-diffusion equations and more complex nonlinear equations. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 417–430. [Google Scholar] [CrossRef]
- Mead, J.; Zubik-Kowal, B. An iterated pseudospectral method for delay partial differential equations. Appl. Numer. Math. 2005, 55, 227–250. [Google Scholar] [CrossRef]
- Abazari, A. Kilicman, Application of differential transform method on nonlinear integro-differential equations with proportional delay. Neural Comput. Appl. 2014, 24, 391–397. [Google Scholar] [CrossRef]
- Sakar, M.G.; Uludag, F.; Erdogan, F. Numerical solution of time-fractional nonlinear PDEs with proportional delays by homotopy perturbation method. Appl. Math. Model. 2016, 40, 6639–6649. [Google Scholar] [CrossRef]
- Chen, X.; Wang, L. The variational iteration method for solving a neutral functional-differential equation with proportional delays. Comput. Math. Appl. 2010, 59, 2696–2702. [Google Scholar] [CrossRef]
- Bhalekar, S.A.C.H.I.N.; Daftardar-Gejji, V.A.R.S.H.A. A predictor-corrector scheme for solving nonlinear delay differential equations of fractional order. J. Fract. Calcul. Appl. 2011, 5, 1–9. [Google Scholar]
- Wang, Z. A numerical method for delayed fractional-order differential equations. J. Appl. Math. 2013. [Google Scholar] [CrossRef]
- Wang, Z.; Huang, X.; Zhou, J. A numerical method for delayed fractional-order differential equations: Based on GL definition. Appl. Math. Inf. Sci. 2013, 7, 525–529. [Google Scholar]
- Moghaddam, B.P.; Yaghoobi, S.; Machado, J.T. An extended predictor–corrector algorithm for variable-order fractional delay differential equations. J. Comput. Nonlinear Dyn. 2016, 11, 061001. [Google Scholar]
- Dabiri, A.; Butcher, E.A.; Poursina, M.; Nazari, M. Optimal periodic-gain fractional delayed state feedback control for linear fractional periodic time-delayed systems. IEEE Trans. Autom. Control 2017, 63, 989–1002. [Google Scholar] [CrossRef]
- Dabiri, A.; Butcher, E.A. Numerical solution of multi-order fractional differential equations with multiple delays via spectral collocation methods. Appl. Math. Model. 2018, 56, 424–448. [Google Scholar] [CrossRef]
- Tanthanuch, J. Symmetry analysis of the nonhomogeneous inviscid burgers equation with delay. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4978–4987. [Google Scholar] [CrossRef]
- Abazari, R.; Masoud, G. Extended two-dimensional DTM and its application on nonlinear PDEs with proportional delay. Int. J. Comp. Math. 2011, 88, 1749–1762. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Solving coupled system of nonlinear PDE’s using the natural decomposition method. Int. J. Pure Appl. Math. 2014, 92, 757–776. [Google Scholar] [CrossRef]
- Rawashdeh, M.S.; Maitama, S. Solving nonlinear ordinary differential equations using the NDM. J. Appl. Anal. Comput. 2015, 5, 77–88. [Google Scholar]
- Rawashdeh, M.; Maitama, S. Finding exact solutions of nonlinear PDEs using the natural decomposition method. Math. Methods Appl. Sci. 2017, 40, 223–236. [Google Scholar] [CrossRef]
- Cherif, M.H.; Ziane, D.; Belghaba, K. Fractional natural decomposition method for solving fractional system of nonlinear equations of unsteady flow of a polytropic gas. Nonlinear Stud. 2018, 25, 753–764. [Google Scholar]
- Eltayeb, H.; Abdalla, Y.T.; Bachar, I.; Khabir, M.H. Fractional telegraph equation and its solution by natural transform decomposition method. Symmetry 2019, 11, 334. [Google Scholar] [CrossRef]
- Abdel-Rady, A.S.; Rida, S.Z.; Arafa, A.A.M.; Abedl-Rahim, H.R. Natural transform for solving fractional models. J. Appl. Math. Phys. 2015, 3, 1633. [Google Scholar] [CrossRef]
- Belgacem, F.B.M.; Silambarasan, R. November. Advances in the natural transform. AIP Conf. Proc. 2012, 1493, 106–110. [Google Scholar]
- Khan, Z.H.; Khan, W.A. N-transform properties and applications. NUST J. Eng. Sci. 2008, 1, 127–133. [Google Scholar]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Science Publishing: River Edge, NJ, USA, 2000. [Google Scholar]
- Podlubny, I. Fractional Differential Equations: An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of Their Solution and Some of Their Applications; Elsevier: Amsterdam, The Netherlands, 1998; Volume 198. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus AND Fractional Differential Equations, 1st ed.; Wiley: London, UK, 1993; p. 384. [Google Scholar]
- Naghipour, A.; Manafian, J. Application of the Laplace Adomian decomposition and implicit methods for solving Burgers’ equation. TWMS J. Pure Appl. Math. 2015, 6, 68–77. [Google Scholar]
- Singh, B.K.; Pramod, K. Homotopy perturbation transform method for solving fractional partial differential equations with proportional delay. SeMA J. 2018, 75, 111–125. [Google Scholar] [CrossRef]


| NTDM () | HPM [8] | Exact | AE | |||
|---|---|---|---|---|---|---|
| 0.25 | 0.25 | 0.390443474 | 0.321004230 | 0.321004232 | 0.3210063542 | 2.12240 × 10 |
| 0.50 | 0.529812605 | 0.412109374 | 0.412109375 | 0.4121803178 | 7.09428 × 10 | |
| 0.75 | 0.695464609 | 0.528686521 | 0.528686522 | 0.5292500042 | 5.63480 × 10 | |
| 1.00 | 0.893414574 | 0.677083333 | 0.677083335 | 0.6795704570 | 2.48712 × 10 | |
| 0.50 | 0.25 | 0.780886948 | 0.642008463 | 0.642008465 | 0.6420127085 | 4.24500 × 10 |
| 0.50 | 1.059625210 | 0.824218749 | 0.824218750 | 0.8243606355 | 1.41885 × 10 | |
| 0.75 | 1.390929217 | 1.057373039 | 1.057373040 | 1.0585000080 | 1.12696 × 10 | |
| 1.00 | 1.786829148 | 1.354166666 | 1.354166670 | 1.3591409140 | 4.97424 × 10 | |
| 0.75 | 0.25 | 1.171330424 | 0.963012695 | 0.963012698 | 0.9630190628 | 6.36750 × 10 |
| 0.50 | 1.589437815 | 1.236328118 | 1.236328120 | 1.2365409530 | 2.12828 × 10 | |
| 0.75 | 2.086393828 | 1.586059568 | 1.586059570 | 1.5877500130 | 1.69044 × 10 | |
| 1.00 | 2.680243723 | 2.031248999 | 2.031250000 | 2.0387113710 | 7.46137 × 10 |
| Exact | Absolute Error | ||||
|---|---|---|---|---|---|
| 0.25 | 0.25 | 0.0976593036 | 0.08025158853 | 0.08025158856 | 3.00000 × 10 |
| 0.50 | 0.1330574978 | 0.10304507290 | 0.10304507940 | 6.50000 × 10 | |
| 0.75 | 0.1765973237 | 0.13231233190 | 0.13231250110 | 1.69200 × 10 | |
| 1.00 | 0.2314929791 | 0.16989087310 | 0.16989261420 | 1.74110 × 10 | |
| 0.50 | 0.25 | 0.3906372147 | 0.32100635410 | 0.32100635420 | 1.00000 × 10 |
| 0.50 | 0.5322299913 | 0.41218029200 | 0.41218031780 | 2.58000 × 10 | |
| 0.75 | 0.7063892947 | 0.52924932750 | 0.52925000420 | 6.76700 × 10 | |
| 1.00 | 0.9259719163 | 0.67956349210 | 0.67957045700 | 6.96490 × 10 | |
| 1 | 0.25 | 1.5625488590 | 1.28402541600 | 1.28402541700 | 1.00000 × 10 |
| 0.50 | 2.1289199640 | 1.64872116800 | 1.64872127100 | 1.03000 × 10 | |
| 0.75 | 2.8255571770 | 2.11699731000 | 2.11700001700 | 2.70700 × 10 | |
| 1.00 | 3.7038876660 | 2.71825396900 | 2.71828182800 | 2.78590 × 10 |
| x | t | Exact | Absolute Error | ||
|---|---|---|---|---|---|
| 0.25 | 0.25 | 0.0976593036 | 0.04867504891 | 0.04867504894 | 3.00000 × 10 |
| 0.50 | 0.1330574978 | 0.03790816051 | 0.03790816623 | 5.72000 × 10 | |
| 0.75 | 0.1765973237 | 0.02952276638 | 0.02952290954 | 1.43160 × 10 | |
| 1.00 | 0.2314929791 | 0.02299107144 | 0.02299246508 | 1.39364 × 10 | |
| 0.50 | 0.25 | 0.3906372147 | 0.19470019570 | 0.19470019580 | 1.00000 × 10 |
| 0.50 | 0.5322299913 | 0.15163264200 | 0.15163266490 | 2.29000 × 10 | |
| 0.75 | 0.7063892947 | 0.11809106550 | 0.11809163820 | 5.72700 × 10 | |
| 1.00 | 0.9259719163 | 0.09196428572 | 0.09196986030 | 5.57458 × 10 | |
| 1 | 0.25 | 1.5625488590 | 0.77880078270 | 0.77880078310 | 4.00000 × 10 |
| 0.50 | 2.1289199640 | 0.60653056800 | 0.60653065970 | 9.17000 × 10 | |
| 0.75 | 2.8255571770 | 0.47236426220 | 0.47236655270 | 2.29050 × 10 | |
| 1.00 | 3.7038876660 | 0.36785714290 | 0.36787944120 | 2.22983 × 10 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shah, R.; Khan, H.; Kumam, P.; Arif, M.; Baleanu, D. Natural Transform Decomposition Method for Solving Fractional-Order Partial Differential Equations with Proportional Delay. Mathematics 2019, 7, 532. https://doi.org/10.3390/math7060532
Shah R, Khan H, Kumam P, Arif M, Baleanu D. Natural Transform Decomposition Method for Solving Fractional-Order Partial Differential Equations with Proportional Delay. Mathematics. 2019; 7(6):532. https://doi.org/10.3390/math7060532
Chicago/Turabian StyleShah, Rasool, Hassan Khan, Poom Kumam, Muhammad Arif, and Dumitru Baleanu. 2019. "Natural Transform Decomposition Method for Solving Fractional-Order Partial Differential Equations with Proportional Delay" Mathematics 7, no. 6: 532. https://doi.org/10.3390/math7060532
APA StyleShah, R., Khan, H., Kumam, P., Arif, M., & Baleanu, D. (2019). Natural Transform Decomposition Method for Solving Fractional-Order Partial Differential Equations with Proportional Delay. Mathematics, 7(6), 532. https://doi.org/10.3390/math7060532








