The Gegenbauer Wavelets-Based Computational Methods for the Coupled System of Burgers’ Equations with Time-Fractional Derivative
Abstract
1. Introduction
2. Mathematical Preliminaries of Fractional Calculus
- (i)
- (ii)
- (iii)
3. Gegenbauer Polynomials and Gegenbauer Wavelets
4. Function Approximation by Gegenbauer Wavelets
5. Operational Matrix of Fractional Integration
6. Description of the Presented Methods
6.1. Gegenbauer Wavelets Collocation Method (GWCM)
6.2. Gegenbauer Wavelets Galerkin Method (GWGM)
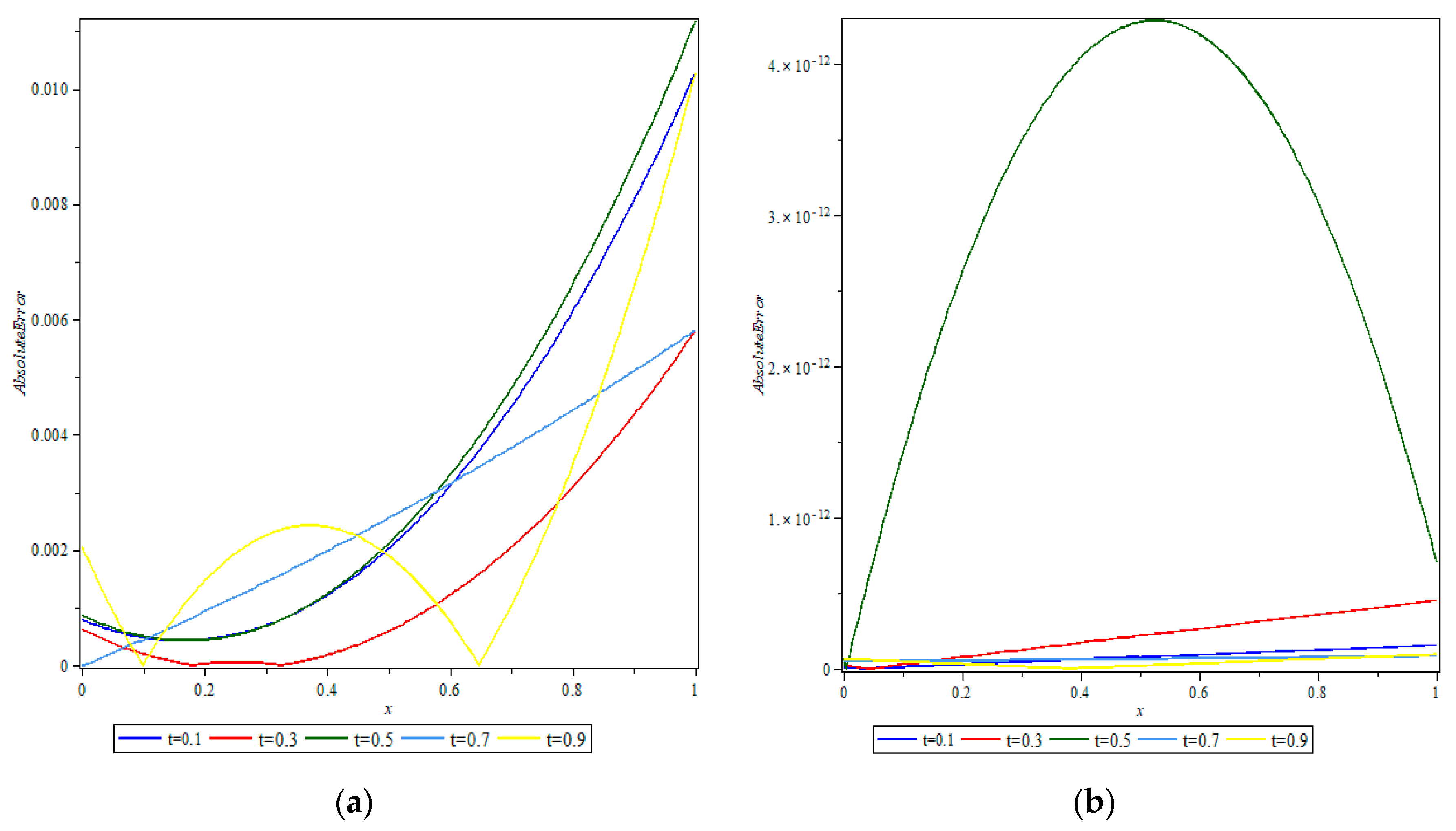
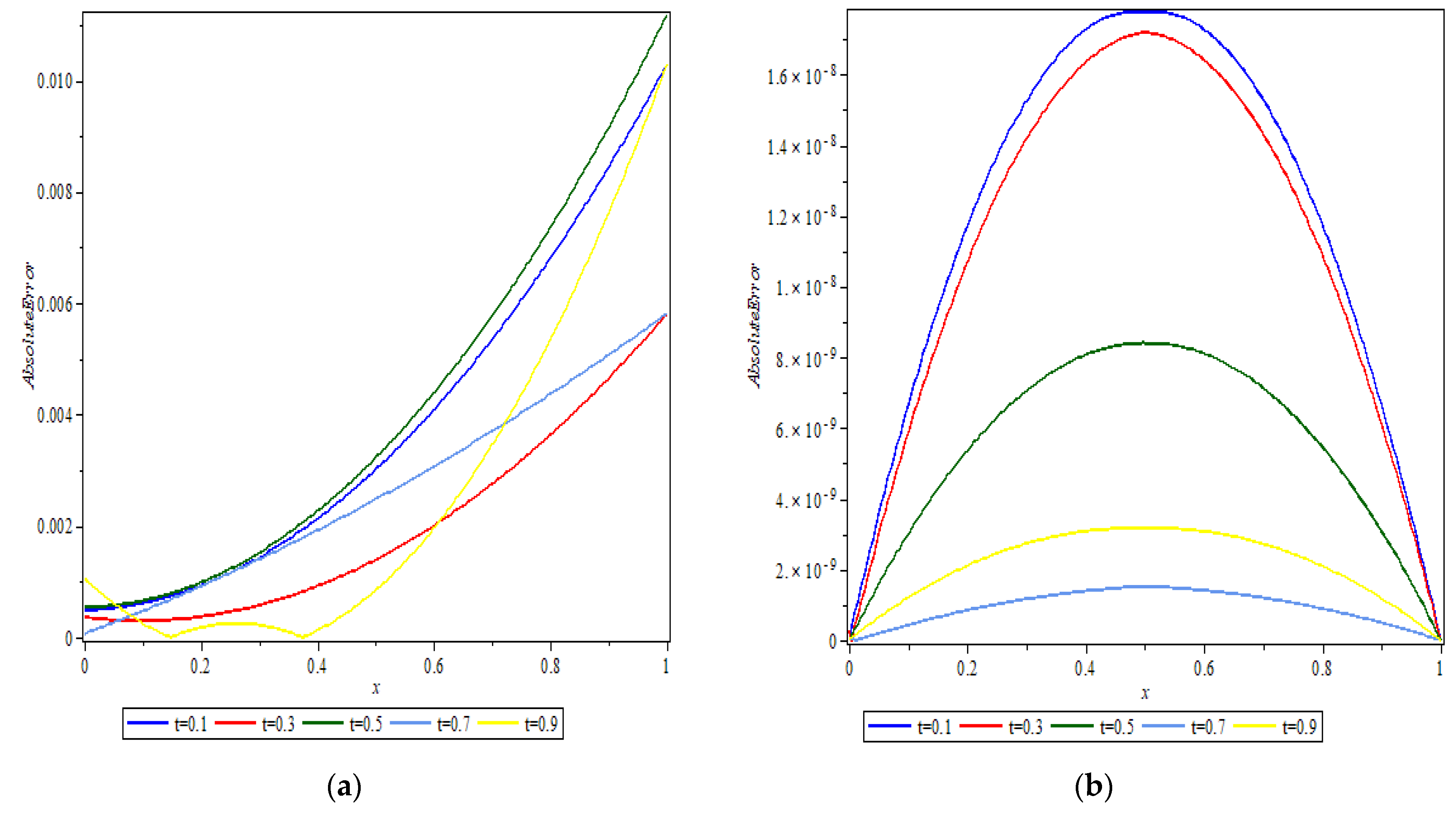
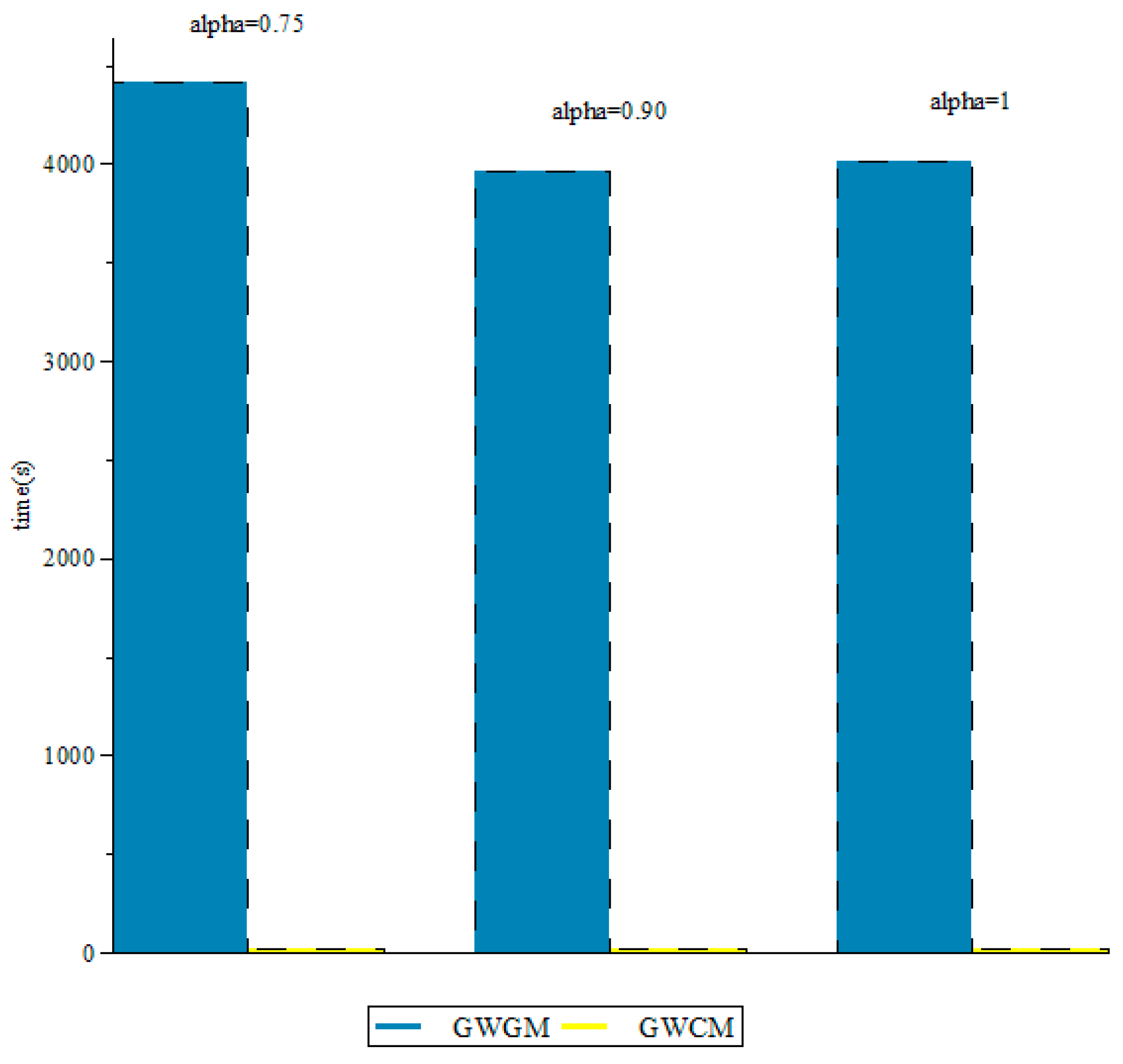
7. Test Problem
8. Conclusions
Authors Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Albuohimad, B.; Hojatollah, A. The Chebyshev collocation solution of the time fractional coupled Burgers’ equation. J. Math. Comput. Sci. 2017, 17, 179–193. [Google Scholar] [CrossRef]
- Nee, J.; Jinqiao, D. Limit set of trajectories of the coupled viscous Burgers’ equations. Appl. Math. Lett. 1998, 11, 57–61. [Google Scholar] [CrossRef]
- Esipov, S.E. Coupled Burgers equations: A model of polydispersive sedimentation. Phys. Rev. E 1995, 52, 3711. [Google Scholar] [CrossRef]
- Burgers, J.M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech. 1948, 1, 171–199. [Google Scholar]
- Fletcher, C.A. Generating exact solutions of the two-dimensional Burgers’ equations. Int. J. Numer. Methods Fluids 1983, 3, 213–216. [Google Scholar] [CrossRef]
- Albuohimad, B.; Hojatollah, A. On a hybrid spectral exponential Chebyshev method for time-fractional coupled Burgers equations on a semi-infinite domain. Adv. Differ. Equ. 2017, 2017, 85. [Google Scholar] [CrossRef]
- Saha Ray, S. Numerical solutions of (1 + 1) dimensional time fractional coupled Burger equations using new coupled fractional reduced differential transform method. Int. J. Comput. Sci. Math. 2013, 4, 1–15. [Google Scholar]
- Alam, K.; Najeeb, A.A.; Amir, M. Numerical solutions of time-fractional Burgers equations: A comparison between generalized differential transformation technique and homotopy perturbation method. Int. J. Numer. Methods Heat Fluid Flow 2012, 22, 175–193. [Google Scholar] [CrossRef]
- Prakash, A.; Manoj, K.; Kapil, K.S. Numerical method for solving fractional coupled Burgers equations. Appl. Math. Comput. 2015, 260, 314–320. [Google Scholar] [CrossRef]
- Singh, J.; Devendra, K.; Ram, S. Numerical solution of time-and space-fractional coupled Burgers’ equations via homotopy algorithm. Alex. Eng. J. 2016, 55, 1753–1763. [Google Scholar] [CrossRef]
- Hassan, E.; Bachar, I.; Adem, K. On Conformable Double Laplace Transform and One Dimensional Fractional Coupled Burgers’ Equation. Symmetry 2019, 11, 417. [Google Scholar]
- Al-luhaibi, M.S. New iterative method for fractional gas dynamics and coupled burger’s equations. Sci. World J. 2015, 2015, 153124. [Google Scholar] [CrossRef] [PubMed]
- Chen, Y.; Hong-Li, A. Numerical solutions of coupled Burgers equations with time-and space-fractional derivatives. Appl. Math. Comput. 2008, 200, 87–95. [Google Scholar] [CrossRef]
- Zayed, E.M.; Amer, Y.A.; Shohib, R.M. The fractional complex transformation for nonlinear fractional partial differential equations in the mathematical physics. J. Assoc. Arab Univ. Basic Appl. Sci. 2016, 19, 59–69. [Google Scholar] [CrossRef]
- Liu, J.; Guolin, H. Numerical solutions of the space-and time-fractional coupled Burgers equations by generalized differential transform method. Appl. Math. Comput. 2011, 217, 7001–7008. [Google Scholar] [CrossRef]
- Kaplan, M.; Bekir, A.; Akbulut, A.; Aksoy, E. The modified simple equation method for nonlinear fractional differential equations. Rom. J. Phys. 2015, 60, 1374–1383. [Google Scholar]
- Zhao, J.; Tang, B.; Kumar, S.; Hou, Y. The extended fractional subequation method for nonlinear fractional differential equations. Math. Probl. Eng. 2012, 2012, 924956. [Google Scholar] [CrossRef]
- Abazari, R.; Borhanifar, A. Numerical study of the solution of the Burgers and coupled Burgers equations by a differential transformation method. Comput. Math. Appl. 2010, 59, 2711–2722. [Google Scholar] [CrossRef]
- Srivastava, V.K.; Tamsir, M.; Awasthi, M.K.; Singh, S. One-dimensional coupled Burgers’ equation and its numerical solution by an implicit logarithmic finite-difference method. AIP Adv. 2014, 4, 037119. [Google Scholar] [CrossRef]
- Kaya, D. An explicit solution of coupled viscous Burgers’ equation by the decomposition method. Int. J. Math. Math. Sci. 2011, 27, 675–680. [Google Scholar] [CrossRef]
- Khater, A.H.; Temsah, R.S.; Hassan, M.M. A Chebyshev spectral collocation method for solving Burgers’-type equations. J. Comput. Appl. Math. 2008, 222, 333–350. [Google Scholar] [CrossRef]
- Masho, J.; Alemayehu, S.; Ali, T. Numerical Solution of the Coupled Viscous Burgers’ Equation Using Differential Quadrature Method Based on Fourier Expansion Basis. Appl. Math. 2018, 9, 821–835. [Google Scholar]
- Islam, M.N.; Akbar, M.A. New exact wave solutions to the space-time fractional-coupled Burgers equations and the space-time fractional foam drainage equation. Cogent Phys. 2018, 5, 1422957. [Google Scholar] [CrossRef]
- Elzaki, S.M. Exact solutions of coupled burgers equation with time-and space-fractional derivative. Int. J. Appl. Math. Res. 2015, 4, 99–105. [Google Scholar] [CrossRef]
- Secer, A.; Altun, S. A New Operational Matrix of Fractional Derivatives to Solve Systems of Fractional Differential Equations via Legendre Wavelets. Mathematics 2018, 6, 238. [Google Scholar] [CrossRef]
- Yin, F.; Tian, T.; Song, J.; Zhu, M. Spectral methods using Legendre wavelets for nonlinear Klein Sine-Gordon equations. J. Comput. Appl. Math. 2015, 275, 321–334. [Google Scholar] [CrossRef]
- Oruç, Ö.; Bulut, F.; Esen, A. Chebyshev Wavelet Method for Numerical Solutions of Coupled Burgers’ Equation. Hacet. J. Math. Stat. 2019, 48, 1–16. [Google Scholar] [CrossRef]
- Oruç, Ö.; Bulut, F.; Esen, A. Numerical solutions of regularized long wave equation by Haar wavelet method. Mediterr. J. Math. 2016, 13, 3235–3253. [Google Scholar] [CrossRef]
- Oruç, Ö.; Bulut, F.; Esen, A. A Haar wavelet-finite difference hybrid method for the numerical solution of the modified Burgers’ equation. J. Math. Chem. 2015, 53, 1592–1607. [Google Scholar] [CrossRef]
- Saeed, U. Hermite wavelet method for fractional delay differential equations. J. Differ. Equ. 2014, 2014, 359093. [Google Scholar] [CrossRef]
- Cattani, C.; Kudreyko, A. Harmonic wavelet method towards solution of the Fredholm type integral equations of the second kind. Appl. Math. Comput. 2010, 215, 4164–4171. [Google Scholar] [CrossRef]
- Heydari, M.H.; Hooshmandasl, M.R.; Barid Loghmani, G.; Cattani, C. Wavelets Galerkin method for solving stochastic heat equation. Int. J. Comput. Math. 2016, 93, 1579–1596. [Google Scholar] [CrossRef]
- Heydari, M.H.; Maalek Ghaini, F.M.; Hooshmandasl, M.R. Legendre wavelets method for numerical solution of time-fractional heat equation. Wavelet Linear Algebra 2014, 1, 19–31. [Google Scholar]
- Heydari, M.H.; Hooshmandasl, M.R.; Ghaini, F.M. A new approach of the Chebyshev wavelets method for partial differential equations with boundary conditions of the telegraph type. Appl. Math. Model. 2014, 38, 1597–1606. [Google Scholar] [CrossRef]
- Singh, S.; Patel, V.K.; Singh, V.K. Application of wavelet collocation method for hyperbolic partial differential equations via matrices. Appl. Math. Comput. 2018, 320, 407–424. [Google Scholar] [CrossRef]
- Podlubny, I. Fractional Differential Equations; Academic: New York, NY, USA, 1999. [Google Scholar]
- Samko, S.G.; Kilbas, A.A.; Marichev, O.I. Fractional Integrals and Derivatives: Theory and Applications; Taylor and Francis: London, UK, 1993. [Google Scholar]
- Szegö, G. Orthogonal Polynomials, 4th ed.; American Mathematical Society: Providence, RI, USA, 1975. [Google Scholar]
- Shen, J.; Tang, T.; Wang, L.L. Spectral Methods: Algorithms, Analysis and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 41, p. 23. [Google Scholar]
- Celik, I. Generalization of Gegenbauer Wavelet Collocation Method to the Generalized Kuramoto–Sivashinsky Equation. Int. J. Appl. Comput. Math. 2018, 4, 111. [Google Scholar] [CrossRef]
- Adem, K.; Al Zhour, Z.A. Kronecker operational matrices for fractional calculus and some applications. Appl. Math. Comput. 2007, 187, 250–265. [Google Scholar]
- Canuto, C.; Hussaini, M.Y.; Quarteroni, A.; Thomas, A., Jr. Spectral Methods in Fluid Dynamics; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ozdemir, N.; Secer, A.; Bayram, M. The Gegenbauer Wavelets-Based Computational Methods for the Coupled System of Burgers’ Equations with Time-Fractional Derivative. Mathematics 2019, 7, 486. https://doi.org/10.3390/math7060486
Ozdemir N, Secer A, Bayram M. The Gegenbauer Wavelets-Based Computational Methods for the Coupled System of Burgers’ Equations with Time-Fractional Derivative. Mathematics. 2019; 7(6):486. https://doi.org/10.3390/math7060486
Chicago/Turabian StyleOzdemir, Neslihan, Aydin Secer, and Mustafa Bayram. 2019. "The Gegenbauer Wavelets-Based Computational Methods for the Coupled System of Burgers’ Equations with Time-Fractional Derivative" Mathematics 7, no. 6: 486. https://doi.org/10.3390/math7060486
APA StyleOzdemir, N., Secer, A., & Bayram, M. (2019). The Gegenbauer Wavelets-Based Computational Methods for the Coupled System of Burgers’ Equations with Time-Fractional Derivative. Mathematics, 7(6), 486. https://doi.org/10.3390/math7060486





