Coordinating Supply-Chain Management under Stochastic Fuzzy Environment and Lead-Time Reduction

Abstract

In this paper, a supply-chain (SC) coordination method based on the lead-time crashing is proposed for a seller–buyer system. By considering different transportation modes, we control the lead-time (LT) variability. For the first time, we have attempted to determine the impact of the reliable and unreliable seller in a continuous-review supply-chain model under the stochastic environment. The authors discussed two reliability cases for the seller. First, we consider the seller is unreliable and in the second case, the seller is reliable. In addition, the demand during the lead time is stochastic with the known mean and variance. The proposed approach tries to find an optimal solution that performs well without a specific probability distribution. Besides, a discrete investment is made to reduce the setup cost, which will indirectly help supply-chain members to increase the total profit of the system. In the proposed model, the seller motivates the buyer by reducing lead time to take part in coordinating decision-making for the system’s profit optimization. We derive the coordination conditions for both members, the seller and the buyer, under which they are convinced to take part in the cooperative decision-making plan. Therefore, lead-time crashing is the proposed incentive mechanism for collaborative supply-chain management. We use a fixed-charge step function to calculate the lead-time crashing cost for slow and fast shipping mode. We give two numerical examples to validate the proposed models and demonstrate the service-level enhancement under the collaborative supply-chain management in case of an unreliable seller. Concluding remarks and future extensions are discussed at the end.

1. Introduction

In recent years, the supply-chain coordination mechanism between supply-chain players has gained the enormous interest of researchers. Each player’s decisions in the supply chain not only affect his/her profit but also have a substantial impact on the other player’s profitability. However, it is common that in the decentralized decision-making system the seller’s optimal values are unacceptable for the buyer and buyer’s optimal solutions are undesirable to the seller. Usually, this problem happens due to more profit or benefits to the more powerful party. Both parties can resolve this problem by negotiating over the optimal policy [1], which is acceptable to both and it is dependent on the vendor–buyer relationships.

Researchers are developing different coordination techniques and mechanisms to convince supply-chain members for combined or coordinated decision-making to optimize the overall profit of the supply-chain system. Usually, different transportation modes are available for order shipment between supply-chain parties. For each transportation mode, transportation lead time and cost is different. Use of slow shipping mode is cheaper compared to the fast mode which requires significantly higher transportation cost. However, slower shipping mode requires a long transportation lead time which results in late deliveries for customers or buyers. On the buyer’s side, overstocking is caused by uncertainties in demand and uncertain transportation lead time. To avoid this risk of overstocking, the buyer can reduce its service level, but the problem gets worse because the service level directly affects the profitability of the buyer and the whole supply chain. On the other side, the seller can increase the service level to mitigate stockout, but the inventory cost increases with the increase in service level. Therefore, the buyer will not agree to amplify service level because of the profit loss.

Recently, Heydari et al. [2] considered transportation lead-time reduction at the seller’s end as an incentive mechanism to convince the buyer to undertake cooperative decision-making within the supply chain. They considered normally distributed stochastic demand and the fixed setup cost for the seller. However, in real-life problems, it is difficult to get complete information about the demand distribution precisely. The unknown distribution also creates another major issue for the buyer to find the near-optimal value of demand during the lead time. Therefore, researchers adopted a distribution-free approach to solve these types of problems, which is a more realistic approach [3,4,5]. It is proved from the literature that additional investments can reduce the setup cost for the production system [6,7,8,9]. Mostly, researchers consider continuous investments for controlling the setup cost; however, the discrete investment can be more realistic as the industry may not prefer continuous investment; thus, this is another research gap in the literature. The proposed study is the first in supply-chain coordination with multiple transportation modes and stochastic fuzzy demand.

The significant contributions of this study are: it uses a reduction in transportation lead time as coordination scheme between supply-chain members. We consider setup cost as a variable and use a discrete investment function to reduce the setup cost. To make this model a realistic one, we considered lead-time demand to be stochastic with unknown distribution function and limited known information, i.e., mean and standard deviation. Therefore, the authors used a distribution-free approach to solve this problem. In addition, we developed two scenarios based on the seller’s reliability for this model: (1) reliable seller; and (2) unreliable seller. To the best of the authors’ knowledge, this model is the first time we consider reliable and unreliable sellers, variable setup cost, uncertainties in demand, and shipping mode enhancement with the distribution-free approach for lead-time demand. We hope this model will open a new direction in lead-time (LT) reduction by transportation mode selection, stochastic fuzzy demand, and supply-chain coordination.

2. Literature Review

In the supply chain, researchers and practitioners develop different coordinating mechanisms for enhancing profitability. Researchers published research with different coordination techniques for the supply chain. Sana [1] developed an imperfect production model for collaborating the supply chain with the production rate, the number of shipments, and order quantity as decision variables. They introduced a three-member supply-chain coordination scheme centralized decision-making with the buy-back policy for defective items. Panda [10] introduced manufacturer-retailer supply chain with cost-sharing mutual contract as a coordinating scheme between manufacturer-retailer under time- and price-dependent demand rate. Panda et al. [11] studied a perishable product’s three-echelon SC model with bargaining over disposal cost-sharing between vendor and buyer. Roy et al. [12] introduced a cooperative advertising policy for a two-layer supply-chain pricing problem. They consider the demand as partly dependent on the promotional effort and uncertain factors with buy-back policy for unsold items by the retailer.

Furthermore, a two-echelon SC for different demand patterns with revenue sharing was studied by Panda et al. [13]. Giri and Sharma [14] studied wholesale pricing strategies in a Stackelberg game approach with advertising cost-sharing contract between players in a two-player supply chain. They developed two different models and irrespective of sales cost differences for retailers they set the same wholesale price. Saha et al. [15] developed a coordination supply-chain model by considering two different promotional policies: (i) downward direct discounts, and (ii) mail-in-rebate. Furthermore, Saha and Goyal [16] studied a multi-echelon supply-chain model with three different coordination mechanisms, i.e., wholesale price discount, contract for cost-sharing, and contract of a joint rebate. Recently, Heydari et al. [2] introduced a stochastic supply-chain model with lead-time crashing by different transportation modes as the cooperative scheme. An agro-industry-based supply-chain model was developed for revenue sharing within players by Sana et al. [17]. For further in-depth study, readers can see Basiri and Heydari [18], Pal, Sana, and Chaudhuri [19], Johari and Hosseini-Motlagh [20] and Venegas and Ventura [21].

In the supply chain, controlling lead time has gained the attention of several researchers and practitioners over the past decade. For the first time, Liao and Shyu [22] introduced lead-time crashing cost for controlling lead time within different inventory models. Arkan and Hejazi [23] studied a two-echelon coordinating supply chain by using the credit period as coordination contract with controllable lead time and reduction in ordering cost. Glock [24] developed a single-vendor single-buyer integrated model for different lead-time reduction strategies with stochastic demand and lead times as a function of lot-size. Furthermore, Jha and Shanker [25] extended it to single-vendor multi-buyer model. Soni et al. [26] studied an imperfect production-inventory model with fuzzy costs, controllable lead time, and investment for lost sales reduction and quality improvement.

Several authors used LT variation control as a coordination mechanism to convince the vendor and buyer to undertake collaborative decision-making. Chaharsooghi and Heydari [27] considered the importance of variation reduction in lead-time variance and lead-time mean to enhance the supply-chain profit. Ye and Xu [28] analyzed a cost allocation model with different bargaining powers for retailer and supplier. They considered one member as more powerful and paid a lower crashing cost compared to the weaker member. Li et al. [29] investigated a supplier-buyer model with service-level (SL) constraint for the supplier, lead-time crashing cost for the buyer, and suggested a price discount policy for coordination and information sharing. Heydari [30] studied a supply-chain model with controllable lead-time variations for coordination between vendor and buyer to maximize the whole system profit. Recently, Heydari et al. [2] suggested a lead-time reduction problem with stochastic lead-time demand. They introduced the fixed-charge transportation model with different shipment modes and coordination scheme over transportation cost. They considered that the limited lead-time reduction is possible with the same shipment mode and it can be reduced more by enhancing the mode from a slower to a faster one with an extra fixed cost.

In the literature, researchers consider lead-time demand as normally distributed, but in real-world problems it is nearly impossible to get complete information and an exact distribution function of lead-time demand. Therefore, Scarf [31] introduced a distribution-free approach for stochastic demand with limited information. Gallego and Moon [32] simplified the proof of the Scarf’s distribution-free approach where only the mean and standard deviation of the lead-time demand is known. Moon and Choi [33] studied a distribution-free approach with the controllable lead time for different continuous-review inventory models. Recently, Sarkar et al. [34] introduced an inventory model with controllable lead time, quality improvement, and discounted price for backordered quantity. They considered lead-time demand to be stochastic and used a min-max distribution-free approach to solve the problem with an unknown distribution. Udayakumar and Geeta [35] studied a supply-chain coordination model with variable lead-time and permissible delay in payments. They assumed lead time, the number of shipments, and order quantity as decision variables. They adopted normal distribution and distribution-free approaches to solve the stochastic lead-time demand problem. Furthermore, Malik and Sarkar [8] studied a continuous-review policy for multiple products with uncertain demand, investments for quality improvements and setup cost reduction, and lead-time control with unknown lead-time demand distribution. Malik and Sarkar [9] recently presented a backorder price discount model with controllable lead time and unknown distribution for lead-time demands. A recent study in a similar direction can be found in Dey et al. [4].

The setup cost is usually taken as a fixed or constant parameter in supply-chain models. However, it can be reduced with some initial investments to the system. For the first time, Porteus [36] introduced investment functions for quality improvement and setup cost reduction within inventory models. Sarker and Coates [37] analyzed the EOQ model for variable lead times and limited opportunities for investments in setup cost reduction. Huang et al. [38] suggested a cooperative vendor–buyer model for optimal inventory policy with variable setup cost by using the discontinuous investment function. Sarkar and Majumder [6] investigated a supply-chain model with the vendor’s setup cost reduction by using a continuous investment function and, based on the probability distribution of lead-time demand, they constructed two models. First, they consider lead-time demand as normally distributed and in the second model, limited information, i.e., mean and standard deviation, is known. Sarkar et al. [7] developed an imperfect vendor–buyer supply-chain model with continuous investments for setup cost reduction manufacturing quality improvement. Recently, Dey et al. [4] studied vendor–buyer supply-chain model with ordering cost and setup cost reduction model with discrete investments and flexible production rate.

In supply-chain management (SCM), unreliable (random yield) and reliable supply is a topic that has attracted researchers and managers in the last decade or two. Özekici and Parlar [39] studied a periodic review model with an unreliable suppliers problem in a random environment. Li et al. [29] investigated a production yield uncertainty problem in the supply chain with optimal order quantity and examined the profit loss of supply-chain members because of random yield. Recently, Park and Lee [40] introduced a single-period supply-chain model with multiple unreliable suppliers and distribution-free approach. They considered that the standard deviation is zero for a perfectly reliable supplier. Furthermore, Na et al. [41] considered the unreliable supplier problem with different customers, random demand, and multiple service levels. Giri and Chakarborty [42] analyzed a supply-chain model for stochastic demand and uncertain yield with the optimal shipment policy. The model considered two types of supplies, instantaneous and non-instantaneous, and revenue sharing as a coordination scheme. Pal, Sana, and Chaudhuri [19] investigated the supply-chain coordination model with random yield in the supplier’s manufacturing and analyzed the model under vertical Nash approach. They introduced revenue sharing and penalty as a coordination scheme between two players.

Furthermore, several studies on the relationship between artificial neural network, wavelet analysis, probability, fractal geometry, and stochastic fuzzy models can be found in the literature. On this topic, Hutchinson [43] studied the fractals and statistical self-similarity to model various physical phenomena. Melin and Castillo [44] studied the application of fractal theory and fuzzy logic for the industrial quality control with neural networks. Shah and Debnath [45] studied a hybrid method for yield based on coupling artificial neural network and discrete wavelet transforms. Guido et al. [46] studied a time-frequency analysis with wavelet transform for the biomedical signal processing. Guariglia [47] analyzed the entropy of fractal antennas and linked it to the physical performance and fractal geometrical shape. Guido [48] did some analyses to efficiently interpret the discrete wavelet-transformed signals. Roberto et al. [49] analyzed a multi-dimensional stochastic fuzzy system with training patterns for an artificial neural network and its applications to a neuro-fuzzy fabric evaluation system. Guariglia [50] investigated the generalization of the Sierpinski gasket through harmonic metric and its applications. In addition, the study on primality, image analysis, and fractality can be found in Guariglia [51]. They dealt with the hidden structure of prime numbers.

3. Problem Definition, Notation, and Assumptions

In this section, the problem is defined along with the basic assumptions and notations.

3.1. Problem Definition

From the existing literature, one can see that only a few pieces of research studies have considered lead time as a coordination mechanism between seller and buyer. This article contains different shipping modes for order shipments. Reliability of the seller is another essential factor to be considered while analyzing coordination between supply-chain members because the uncertainty in the seller’s supply creates stockouts which increase the chance of losing a good amount of profit. Furthermore, in stochastic cases mostly researchers have focused on lead-time demand following the normal distribution; a related article is Heydari et al. [2]. However, in real cases, it is challenging to make sure that the demand is following normal or any probability distribution. Previously, authors were considering setup cost as a fixed or constant parameter. There is a chance of saving a good amount of cost by investing once in setup to reduce the setup cost. By keeping these real-life factors in mind, this study is an attempt to make a coordination supply-chain model with stochastic fuzzy demand, which does not follow any distribution and investment with the discrete function reducing the setup cost for the system’s total profit maximization. This study discusses the centralized and decentralized decision-making models in detail. Moreover, we propose a coordination mechanism based on LT crashing with different shipping mode.

3.2. Notation

The following notations were used in this paper for mathematical model formulation.

D	demand per year (units/year)
p	retail price of the item ($/unit)
w	wholesale price of the item ($/unit)
m	raw material price of the item ($/unit)
$S_0$	initial setup cost per setup ($/setup)
$A_s$	ordering cost for seller per order ($/order)
$A_b$	ordering cost for buyer per order ($/order)
$h_s$	holding cost for seller per unit per year ($/unit/year)
$h_b$	holding cost for buyer per unit per year ($/unit/year)
$B_b$	shortages cost per unit ($/unit/unit time)
$C_{ST}$	transportation cost for slow mode
$C_{FT}$	transportation cost for fast mode
F	maximum point at which more reduction in lead-time requires switching to fast shipping mode
M	maximum possible crashing in lead-time
T	fixed cost for switching shipping mode
$\sigma$	standard deviation for demand
L	lead-time duration, it is controllable by seller
Q	buyer’s order quantity per order (units/order) (a decision variable)
n	seller’s replenishment multiplier (a decision variable)
k	inventory safety factor (a decision variable)

3.3. Assumptions

• The coordination for integrated inventory model with single buyer and single seller is considered. The seller produces a single type of product. The buyer’s order quantity is produced in single stages. However, the seller delivers it in multiple shipments.
• The buyer adopts a continuous-review inventory management policy. The buyer continuously keeps reviewing his inventory level and whenever the inventory level reaches the reorder point r the buyer immediately orders the quantity Q.
• The reorder point is determined by $r=DL+k\sigma \sqrt{L}$, where $DL=$ is expected demand during the lead time, and is $k\sigma \sqrt{L}=$ safety stock.
• Lead-time demand is stochastic, and distribution is unknown. Only the mean and standard deviation are known.
• To reduce the setup cost, an additional discrete investment is needed. Thus, the model assumes a discrete investment function $S(J_i)=S_0{e}^{-r{J}_i}$, where r is the known shape parameter, which is estimated using the previous data, and J is the setup cost for the seller. $i=0,1,\dots ,n$ and $J_0=0$.
• Shortages lead to lost sales.

The information about the form of the probability distribution of the lead time is often limited in practice. In this model, the assumption about the distribution of the protection interval demand is relaxed, and it is only assumed that the density function of the lead-time demand belongs to the $\mathsf{\Omega }$ with finite mean $DL$ and standard deviation $\sigma \sqrt{L}$. As the distributional form of lead-time demand X is unknown, the exact value of $E{(X-r)}^{+}$ cannot be determined. Therefore, the min-max distribution-free approach is considered to solve this problem (Gallego and Moon [32]).

$$\begin{array}{c}\hfill {\mathrm{Min}-\mathrm{Max}}_{F\in \mathsf{\Omega }}TEP\\ \hfill \mathrm{subject}\mathrm{to}0<J\le S_0\end{array}$$

(1)

The following proposition is used to approximate the value of $E{(X-r)}^{+}$ which was proposed by Gallego and Moon [32].

Proposition 1.

For any $F\in \mathsf{\Omega }$,

$$\begin{array}{c}\hfill E{(X-r)}^{+}\le \frac{1}{2}\left\{\sqrt{{\sigma }^{2}L+{(r-DL)}^2-(r-DL)}\right\}\end{array}$$

(2)

According to Gallego and Moon [32], the upper bound is tight

Replacing r with $DL+k\sigma \sqrt{L}$ into above equation, one can obtain

$$\begin{array}{c}\hfill E{(X-r)}^{+}\le \frac{1}{2}\sigma \sqrt{L}(\sqrt{1+k^2}-k)\end{array}$$

(3)

4. Mathematical Model

In this section, three mathematical models are presented. First, a decentralized decision-making scenario is considered for seller and buyer. In the second model, a centralized system is analyzed for the combined decision-making for seller and buyer. In the end, a coordinating supply-chain model is developed, and lead-time reduction is used as a coordination scheme between seller and buyer for profit maximization.

4.1. Decentralized Decision-Making

In the decentralized supply-chain system, the buyer optimizes his decisions alone to maximize his profit. In reality, each supply-chain member tries to optimize his profit in the decentralized system without taking care of other members. In this study, the two decision variables, as service level (SL) and order quantity, are under the control of the buyer. The service level is determined by the inventory safety factor (k) and it has a notable impact on sales volume and profitability of buyer. In this model, the buyer acts as the supply-chain leader and the seller reacts as a follower to the buyer’s decisions.

This model uses the inventory model established by Silver et al. [52]. The buyer continuously keeps reviewing his inventory level and whenever the inventory in hand reaches the reorder point, the buyer immediately orders the quantity Q. In this paper, we examine a continuous-review model with shortages and distribution-free approach for lead-time demand. Therefore, the expected total profit for the buyer with a distribution-free approach and is defined as

$$\begin{array}{ccc}\hfill E{P}_b(Q,k)& =& (p-w)D-\frac{A_{b}D}{Q}-h_b\left[\frac{Q}{2}+k\sigma \sqrt{L}+\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\right]\hfill \\ & -& (B_b+p-w)\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\frac{D}{Q}\hfill \end{array}$$

(4)

In the above equation, the first term is the revenue for the buyer and the second term is holding cost for the buyer. The third term represents shortages in cost caused by the expected shortages during the cycle.

Setup cost

The seller has a fixed setup cost of $S_0$ per cycle, initially. The seller must fulfill the demand D per cycle, and he ships $nQ$ quantity in each shipment. The numbers of cycles per year are $\frac{D}{nQ}$. Therefore, one can express the seller’s setup cost per manufacturing setup as:

$$\begin{array}{ccc}\hfill STC& =& \frac{S(J_i)D}{nQ};\mathrm{where},S(J_i)=S_0{e}^{-r{J}_i},\hfill \\ \hfill STC& =& \frac{S_0{e}^{-r{J}_i}D}{nQ}.\hfill \end{array}$$

(5)

where r = known parameter and it is estimated by using the historical data, and $J=$ investment required to achieve setup cost S per production cycle.

Investment for setup cost reduction

For the setup cost reduction, this model assumes an additional discrete investment J (Huang et al., 2011)

$$\begin{array}{c}\hfill \mathrm{Investment}\mathrm{for}\mathrm{setup}\cos \mathrm{t}\mathrm{reduction}=\frac{JD}{Q}\end{array}$$

Hence, the expected total profit for seller is defined

$$\begin{array}{ccc}\hfill E{P}_s(J,n)& =& (w-m)D\left(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q}\right)-A_s\left[\frac{D(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{nQ}\right]\hfill \\ & -& \frac{S_0{e}^{-r{J}_i}D(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{nQ}-\frac{JD(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{Q}-h_s\frac{(n-1)Q}{2}.\hfill \end{array}$$

(6)

Fuzzification

In reality, it is difficult to predict the exact demand of a product. Mostly, the researchers considered constant demand by considering a distribution-free approach for lead-time demand. However, several researchers consider fuzzy demand (see for reference Sarkar and Mahapatra [53], Kumar and Goswami [54], Soni et al. [55], and Tayyab et al. [56]) with the distribution-free approach. Demand in existing literature is considered to be a triangular fuzzy number, so for this we are assuming it is a triangular number [57,58,59]. The main advantage of triangular member function is simplicity. A triangular membership function is used unless there is a good reason to do otherwise [59]. Furthermore, Taleizadeh et al. [60] presented a market investigation on the products and showed that product demand does not follow a specific pattern such that it can neither be considered fixed nor to have a certain probability distribution, justifying the usage of fuzzy triangular demand. Thus, the presented model also considers fuzzy triangular demand to make it realistic.

In the model, considered fuzzy demand $\tilde{D}=(D-{\delta }_1,D,D+{\delta }_2)$ is a non-negative triangular fuzzy number. One can obtain the expected profit function for buyer and seller by substituting the non-negative triangular fuzzy number in the above equation. Hence, the expected total profit for a buyer with a fuzzy demand

$$\begin{array}{ccc}\hfill \widetilde{E{P}_b}(Q,k)& =& (p-w)\tilde{D}-A_b\frac{\tilde{D}}{Q}-h_b\left[\frac{Q}{2}+k\sigma \sqrt{L}+\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\right]\hfill \\ & -& (B_b+p-w)\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\frac{\tilde{D}}{Q},\hfill \end{array}$$

(7)

In addition, the expected total profit for seller with fuzzy demand

$$\begin{array}{ccc}\hfill \widetilde{E{P}_s}(J,n)& =& (w-m)\tilde{D}\left(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q}\right)-A_s\left[\frac{\tilde{D}(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{nQ}\right]\hfill \\ & -& \frac{S_0{e}^{-r{J}_i}\tilde{D}(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{nQ}-\frac{J\tilde{D}(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{Q}-h_s\frac{(n-1)Q}{2}.\hfill \end{array}$$

(8)

Defuzzification

To get ultimate conclusions and decision-making, the fuzzy numbers are mostly converted to crisp values. The method used here for converting fuzzy results to the crisp models is commonly known among researchers as signed distance method. Hence, the expected profit for seller and buyer in a decentralized inventory model is given by:

$$\begin{array}{ccc}\hfill E{P}_b(Q,k)& =& (p-w)\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]-A_b\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q}\hfill \\ & -& h_b\left[\frac{Q}{2}+k\sigma \sqrt{L}+\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\right]\hfill \\ & -& (B_b+p-w)\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q},\hfill \end{array}$$

(9)

$$\begin{array}{ccc}\hfill E{P}_s(J,n)& =& (w-m)\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]\left(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q}\right)\hfill \\ & -& A_s\left[\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right](1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{nQ}\right]\hfill \\ & -& \frac{S_0{e}^{-r{J}_i}\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right](1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{nQ}\hfill \\ & -& \frac{J\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right](1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{Q}-h_s\frac{(n-1)Q}{2}.\hfill \end{array}$$

(10)

In the decentralized supply chain, the seller and buyer do not cooperate in decision-making and they only decide their optimal policies for individual profit maximization. First, the buyer decides his optimal order quantity Q and inventory safety factor k to maximize own expected annual profit. Then, the seller considers the buyer’s optimal values as an input to decide the optimal number of shipments n and possible investment for setup cost reduction and maximize his expected annual profit. In the decentralized case, the buyer is a leader and the seller is a follower in the decision-making sequence.

$$\begin{array}{ccc}\hfill \frac{\partial E{P}_b(Q,k)}{\partial Q}& =& A_b\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q^2}-h_b\left[\frac{1}{2}\right]\hfill \\ & +& (B_b+p-w)\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q^2},\hfill \end{array}$$

(11)

$$\begin{array}{ccc}\hfill \frac{\partial E{P}_b(Q,k)}{\partial k}& =& -h_b\left[\sigma \sqrt{L}+\frac{1}{2}\sigma \sqrt{L}\left(\frac{k}{\sqrt{(1+k^2)}}-1\right)\right]\hfill \\ & -& (B_b+p-w)\frac{1}{2}\sigma \sqrt{L}\left(\frac{k}{\sqrt{(1+k^2)}}-1\right)\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q}.\hfill \end{array}$$

(12)

By using the necessary conditions for the multiple variables problem, one can easily obtain the optimal order quantity $Q^{*}$ for the decentralized system as

$$\begin{array}{ccc}\hfill Q^{*}& =& \sqrt{\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]\left[2A_b+(B_b+p-w)\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\right]}{h_b}},\hfill \end{array}$$

(13)

and

$$\begin{array}{c}\hfill \frac{k^{*}}{\sqrt{1+k^{*2}}}=1-\frac{2h_{b}Q}{\left[Q{h}_b+(B_b+p-w)\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]\right]}.\end{array}$$

(14)

To prove the concavity of the buyer’s expected profit regarding k and Q, the Hessian matrix is calculated. A negative definite Hessian matrix proves the concavity of the buyer’s profit for decision variables safety factor k and order quantity Q. The proof of the Hessian matrix is provided in Appendix A. To get the optimal values of the decision variables and profit for the buyer, the below Algorithm 1 is given.

Algorithm 1 Solution algorithm to find optimal results for decentralized SCM.

Step I:     Assign value for $n=1$, and set $ETP(Q,J,n,k)=0$; Step II:    Set value of $s(k)=0$; Step III:  Evaluate the value of Q from Equation (13); Step IV:  Evaluate value of k and $s(k)$ by using Equation (14); Step V:   Repeat Step 2 to 4 with the obtained value of $s(k)$ until the variation is negligible.

Similarly, one can obtain the optimal number of shipments for seller as

$$\begin{array}{c}\hfill \frac{\partial E{P}_s(J,n)}{\partial n}=A_s\left[\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right](1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{n^{2}Q}\right]\\ \hfill +\frac{S_0{e}^{-r{J}_i}\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right](1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{n^{2}Q}-h_s\frac{Q}{2}.\end{array}$$

(15)

The seller decides his optimal number of shipments $n^{*}$ by predicting the buyer’s optimal order quantity $Q^{*}$. Expected profit for the seller is convex for n when all the other parameters are fixed, hence

$$\begin{array}{c}\hfill \frac{{\partial }^{2}E{P}_s(J,n)}{\partial n^2}=-\frac{2A_s}{n^{3}Q}\left[\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]\left(1-\frac{\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{2Q}\right)\right].\end{array}$$

(16)

Here, $\frac{\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{2Q}$ is always less than 1. Hence, the second derivative of the expected profit for the seller with respect to n is negative. Therefore, expected profit function for the seller is concave for n.

The seller’s optimal value of $n=n^{*}$ is obtained, only when

$$\begin{array}{c}\hfill \left\{\begin{array}{c}E{P}_s(n^{*})\ge E{P}_s(n^{*}+1)\hfill \\ E{P}_s(n^{*})\ge E{P}_s(n^{*}-1).\hfill \end{array}\right.\end{array}$$

4.2. Centralized Decision-Making

In the centralized system, there is one supply-chain planner who makes all the globally optimal decisions by ensuring that the whole system’s profitability is maximized. In centralized decision-making in this model, the supply-chain planner considers only the original “slow” shipping mode and makes the decisions over variables Q, n, and k. The planner does not consider the lead-time crashing while optimizing these decision variables. The integrated seller–buyer inventory model under the centralized model and the expected total profit function of the supply chain is given by

$$\begin{array}{ccc}\hfill ETP(Q,k,J,n)& =& E{P}_b(Q,k)+E{P}_s(J,n)\hfill \\ & =& (p-w)D-A_b\frac{D}{Q}-h_b\left[\frac{Q}{2}+k\sigma \sqrt{L}+\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\right]\hfill \\ & -& (B_b+p-w)\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\frac{D}{Q}\hfill \\ & +& (w-m)D\left(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q}\right)-A_s\left[\frac{D(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{nQ}\right]\hfill \\ & -& \frac{S_0{e}^{-r{J}_i}D(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{nQ}-\frac{JD(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{Q}\hfill \\ & -& h_s\frac{(n-1)Q}{2}.\hfill \end{array}$$

(17)

After some mathematical calculations, one can obtain the simplified profit function as

$$\begin{array}{ccc}\hfill ETP(Q,k,J,n)& =& (p-m)D-\left(A_b+\frac{A_s}{n}\right)\frac{D}{Q}-((n-1)h_s+h_b)\frac{Q}{2}\hfill \\ & -& h_b\left(k\sigma \sqrt{L}+\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\right)\hfill \\ & -& (B_b+p-m-\frac{A_s}{nQ})\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\frac{D}{Q}-\frac{S_0{e}^{-r{J}_i}D(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{nQ}\hfill \\ & -& \frac{JD(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{Q}.\hfill \end{array}$$

(18)

Fuzzification

Fuzzifiaction is done similarly to in the previous decentralized model and the expected profit function is

$$\begin{array}{ccc}\hfill \widetilde{ETP}(Q,k,J,n)& =& (p-m)\tilde{D}-\left(A_b+\frac{A_s}{n}\right)\frac{\tilde{D}}{Q}-((n-1)h_s+h_b)\frac{Q}{2}\hfill \\ & -& h_b\left(k\sigma \sqrt{L}+\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\right)\hfill \\ & -& (B_b+p-m-\frac{A_s}{nQ})\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\frac{\tilde{D}}{Q}-\frac{S_0{e}^{-r{J}_i}\tilde{D}(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{nQ}\hfill \\ & -& \frac{J\tilde{D}(1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{Q}.\hfill \end{array}$$

(19)

Defuzzification

The defuzzification is done similarly to in the previous decentralized model and the expected profit function is written as

$$\begin{array}{ccc}\hfill ETP(Q,k,J,n)& =& (p-m)\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]-\left(A_b+\frac{A_s}{n}\right)\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q}\hfill \\ & -& ((n-1)h_s+h_b)\frac{Q}{2}-h_b\left(k\sigma \sqrt{L}+\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\right)\hfill \\ & -& (B_b+p-m-\frac{A_s}{nQ})\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q}\hfill \\ & -& \frac{S_0{e}^{-r{J}_i}\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right](1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{nQ}\hfill \\ & -& \frac{J\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right](1-\frac{\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q})}{Q}.\hfill \end{array}$$

(20)

From the necessary condition of the global optimality, we can write

$$\begin{array}{ccc}\hfill \frac{\partial ETP(Q,k,J,n)}{\partial Q}& =& \left(A_b+\frac{A_s}{n}\right)\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q^2}-\left((n-1)h_s+h_b\right)\frac{1}{2}\hfill \\ & +& \left(B_b+p-m-\frac{2A_s}{nQ}\right)\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q^2}\hfill \\ & +& \frac{S_0{e}^{-r{J}_i}\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{n{Q}^2}\left(1-\frac{\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q}\right)\hfill \\ & +& \frac{J\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q^2}\left(1-\frac{\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)}{Q}\right)=0,\hfill \end{array}$$

(21)

$$\begin{array}{ccc}{Q}^{*}\hfill & =\hfill & \sqrt{\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]\left[\left(A_b+\frac{A_s}{n}\right)+\frac{{\mathsf{\Phi }}_1}{2}(B_b+p-m-\frac{2A_s}{nQ})+\left(\frac{S_0{e}^{-r{J}_i}}{n}+J\right)(1-\frac{{\mathsf{\Phi }}_1}{Q})\right]}{\frac{1}{2}((n-1)h_s+h_b)}}\hfill \end{array}$$

(22)

$$\begin{array}{c}\hfill {\mathsf{\Phi }}_1=\sigma \sqrt{L}(\sqrt{(1+k^2)}-k)\end{array}$$

(23)

$$\begin{array}{ccc}\hfill \frac{\partial ETP(Q,k,J,n)}{\partial k}& =& -h_b\left(\sigma \sqrt{L}+\frac{1}{2}\sigma \sqrt{L}\left(\frac{k}{\sqrt{(1+k^2)}}-1\right)\right)\hfill \\ & -& (B_b+p-m-\frac{A_s}{nQ})\frac{1}{2}\sigma \sqrt{L}\left(\frac{k}{\sqrt{(1+k^2)}}-1\right)\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q}\hfill \\ & +& \frac{S_0{e}^{-r{J}_i}\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{n{Q}^2}\frac{1}{2}\sigma \sqrt{L}\left(\frac{k}{\sqrt{(1+k^2)}}-1\right)\hfill \\ & +& \frac{J\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q^2}\frac{1}{2}\sigma \sqrt{L}\left(\frac{k}{\sqrt{(1+k^2)}}-1\right)\hfill \end{array}$$

(24)

$$\begin{array}{ccc}\hfill \frac{k}{\sqrt{(1+k^2)}}& =& 1-\frac{2h_b{Q}^2}{Q^2{h}_b-\left((B_b+p-m-\frac{A_s}{nQ})Q-\frac{S_0{e}^{-r{J}_i}}{n}-J\right)\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}\hfill \end{array}$$

(25)

The expected profit for seller and the optimal values of the decision variables have been obtained by using Algorithm 2.

Algorithm 2 Solution algorithm to find optimal results for centralized SCM.

Step I:    Assign value for $n=1$ and set $ETP(Q,J,n,k)=0$; Step II:    Set value of $s(k)=0$; Step III:    Evaluate the value of Q from Equation (22); Step IV:    Evaluate value of k from Equation (25); Step V:    Repeat calculations for (22) and (25) until the difference between two values is negligible; Step VI:    The calculated values for decision variables are optimal for the fixed n; Step VII:    Set $n=n+1$; run from Step II to Step VI; Step VIII:    The values that gives the maximum profit $ETP(Q,J,k,n)$ are the optimal values for decision variables.

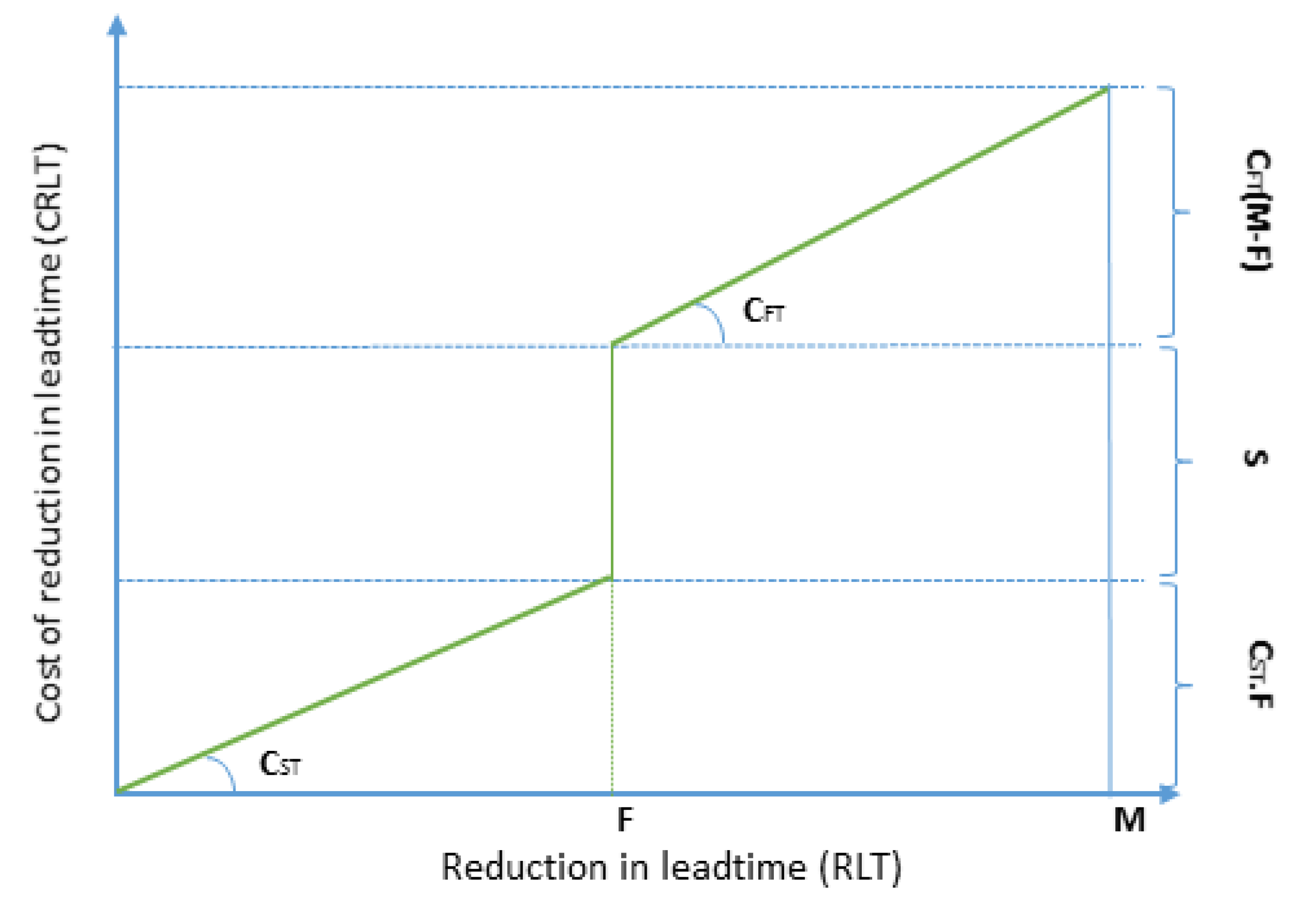
4.3. Coordination Mechanism between Seller and Buyer: Lead-Time Reduction

The expected profit function for buyer, as he commits to $Q^{**}$, $J^{**}$, $k^{**}$ and exploiting from the reduced lead time $(LT)$, is:

$$\begin{array}{ccc}\hfill E{P}_b(Q^{**},k^{**},L_{new})& =& (p-w)\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]-A_b\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q^{**}}-h_b[\frac{Q^{**}}{2}+k^{**}\sigma \sqrt{L_{new}}\hfill \\ & +& \frac{1}{2}\sigma \sqrt{L_{new}}(\sqrt{(1+{k^2}^{**})}-k^{**})]-(B_b+p-w)\frac{1}{2}\sigma \sqrt{L_{new}}(\sqrt{(1+{k^2}^{**})}\hfill \\ & -& k^{**})\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q^{**}}\hfill \end{array}$$

(26)

here, $L_{new}$ is the reduced lead time and it is obtained by applying the reduction coefficient $(1-RLT)$ to the original lead time L i.e.,: $L_{new}=(1-RLT)L$

$$\begin{array}{ccc}\hfill E{P}_s(J^{**},n^{**},L_{new})& =& (w-m)\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]\left(1-\frac{\frac{1}{2}\sigma \sqrt{L_{new}}(\sqrt{(1+{k^2}^{**})}-k^{**})}{Q^{**}}\right)\hfill \\ & -& A_s\left[\frac{\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right](1-\frac{\frac{1}{2}\sigma \sqrt{L_{new}}(\sqrt{(1+{k^2}^{**})}-k^{**})}{Q^{**}})}{n^{**}{Q}^{**}}\right]\hfill \\ & -& \frac{S_0{e}^{-r{J}_i^{**}}\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{n^{**}{Q}^{**}}-\frac{J^{**}\left[D+\frac{1}{4}({\delta }_2-{\delta }_1)\right]}{Q^{**}}-h_s\frac{(n^{**}-1)Q^{**}}{2}\hfill \\ & -& \frac{(CRLT)D}{Q^{**}}\hfill \end{array}$$

(27)

The cost for reduction in lead time is added at the end in the above equation; “CRLT” is the cost for reduction in lead time per replenishment cycle.

Kowalski and Lev [61] proposed an SFCTP (step-fixed-charge-transportation problem) and planned the transportation cost as a function of shipped units. Similarly, this study considers the CRLT as a function of the lead-time volume reduced. In the same way, this study proposes a function for CRLT which is based on SFCTP, see Figure 1 for graphical representation. The idea has a basis in the fact that in one shipping mode (e.g., train) the lead time can be reduced up to a limit and reduction beyond this limit is only by replacing this mode with the faster one (e.g., truck). The lead time considered here is not a function of order quantity because this model only considers the shipping lead time and ignores production or loading and unloading lead times. Therefore, it is assumed that the lead-time reduction cost is the function of the lead-time reduction and shipping mode. In a major transaction, lead-time reduction is in two ways:

• Limited reduction is possible within the same shipping mode and CRLT increases linearly. The described type of reduction within the same shipping mode is limited to a level.
• Extra reduction is achievable by switching the shipping model from slow to fast, and it adds an extra fixed cost to the seller.

The maximum lead-time (MLT) crashing can be defined as

$$\begin{array}{c}\hfill MLT=\frac{\mathrm{Normal}\mathrm{Lead}-\mathrm{time}-\mathrm{Fully}\mathrm{Crashed}\mathrm{Lead}-\mathrm{time}}{\mathrm{Normal}\mathrm{Lead}-\mathrm{time}}\end{array}$$

(28)

The value of $MLT$ should always be less than 1 and the interval for lead-time reduction ($LTR$) is clear to be between 0 and $MLT$$(0,MLT)$. The lead-time reduction cost ($CRLT$) is given by

$$\begin{array}{c}\hfill CRLT=\left\{\begin{array}{c}{C}_{ST}.LTR0<LTR\le F\hfill \\ C_{FT}(LTR-F)+T+C_{ST}.FF<LTR\le MLT\hfill \end{array}\right.\end{array}$$

(29)

We consider two different shipping modes for this model, slow shipping mode and fast shipping mode. As described in assumptions, without shifting shipping mode only F (%) reduction in lead time is possible. Selection of shipping mode depends on the lead-time reduction coefficient; if it lies within interval $[0,F]$ then slow shipping mode is suitable for the system. For the lead-time reduction coefficient beyond F and less than MLT (interval $[F,MLT]$), then the fast shipping mode is appropriate for the seller.

4.3.1. Buyer’s Conditions for Participation in Joint Decision-Making

To make sure the buyer’s participation in decision-making with coordination is possible when his profit is more than the decentralized system, the participation constraint for the buyer is

$$\begin{array}{c}\hfill E{P}_b(Q^{**},k^{**},L_{new})\ge E{P}_b(Q^{*},k^{*})\end{array}$$

(30)

$$\begin{array}{c}\hfill RL{T}_{min}=1-\frac{1}{L}{\left[\frac{Z}{Y}\right]}^2\end{array}$$

(31)

here,

$$\begin{array}{ccc}\hfill Z& =& A_{b}D\left(\frac{1}{Q^{**}}-\frac{1}{Q^{*}}\right)+\frac{h_b}{2}(Q^{**}-Q^{*})-h_b\left[k^{*}\sigma \sqrt{L}+\frac{1}{2}\sigma \sqrt{L}(\sqrt{(1+{k^{*}}^2)}-k^{*})\right]\hfill \\ & -& \frac{\sigma \sqrt{L}(\sqrt{(1+{k^{*}}^2)}-k^{*})D}{2Q^{*}}(B_b+p-w)\hfill \end{array}$$

(32)

$$\begin{array}{c}\hfill Y=-h_b\left[k^{**}\sigma +\frac{1}{2}\sigma (\sqrt{(1+{k^{**}}^2)}-k^{**})\right]-\frac{\sigma (\sqrt{(1+{k^{**}}^2)}-k^{**})D}{2Q^{**}}(B_b+p-w)\end{array}$$

(33)

4.3.2. Seller’s Conditions for Participation in Joint Decision-Making

$$\begin{array}{c}\hfill E{P}_s(Q^{**},k^{**},n^{**},L_{new})\ge E{P}_s(Q^{*},k^{*},n^{*})\end{array}$$

(34)

Because of the complexity of the coordination model for the seller, it is not possible to find the closed-form formula for the maximum value of lead-time reduction $(RL{T}_{max})$. Therefore, the Algorithm 3 is given below to calculate the maximum value for the seller $(RL{T}_{max})$ which is to make sure the participation in coordination.

Algorithm 3 Solution algorithm to find optimal ‘RLT’.

Step I:    Assign value for $LR=M$; Step II:    Evaluate Equation (17) for the coordination model and calculate seller’s profit; Step III:    Check Equation (34) the participation constraint for seller; Step IV:    In case the participation condition for the seller in Equation (34) is not satisfied, then set the value $RLT=RLT-a$, where a is a very small positive quantity, and repeat Step V; otherwise, the obtained value for $RLT$ is $RL{T}_{max}$.

Lastly, after obtaining $RL{T}_{max}$ and $RL{T}_{min}$, all values of $RLT$ in the interval $[RL{T}_{min}$, $RL{T}_{max}]$ are acceptable for the channel coordination. However, based on the relative bargaining power of supply-chain members, an appropriate value of $RLT$ is chosen from interval $[RL{T}_{min}$, $RL{T}_{max}]$. To obtain the acceptable value of $RLT$ within interval [$RL{T}_{min}$, $L{R}_{max}$], one can apply a linear model with bargaining powers of supply-chain members. Based on a linear model, one can write $LR=\eta L{R}_{min}+(1-\eta )L{R}_{max}$, where $\eta$ is a positive real number in an interval $[0,1]$, and it represents the bargaining power for the seller in comparison to the buyer. The larger value of $\eta$ (near to 1) makes $RLT$ closer to the lower bound ($RL{T}_{min}$), which creates more savings for the seller. Meanwhile, the lower value of $\alpha$ (near to zero) makes $RLT$ near to the upper bound ($L{R}_{max}$). It means more profit for the buyer. Here, the below Theorem 1 outlines the major insight from the proposed supply-chain coordination policy.

Theorem 1.

All values of $RLT$ in given interval $[RL{T}_{min}$, $RL{T}_{max}]$ can synchronize the inventory and pricing decisions between supply-chain members. If $RL{T}^{*}=RL{T}_{min}$ then the seller will enjoy all the benefits of the coordinated decisions, which means more savings for the seller. If $RL{T}^{*}=RL{T}_{max}$ then the buyer will enjoy all the benefits of coordinated decisions.

Proof. 

From a linear model with relative bargaining powers one can write

$$LR=\eta L{R}_{min}+(1-\eta )L{R}_{max},$$

where $\eta$ is a real positive number in an interval $[0,1]$. One can obtain,

$$LR=L{R}_{min},\mathrm{when}\eta \mathrm{is}1,$$

and, one gets

$$LR=L{R}_{max},\mathrm{when}\eta \mathrm{is}0.$$

 □

5. Numerical Example

To validate the proposed model, we conducted a set of numerical examples. The input data is taken from Heydari et al. [2] and it is given in

Table 1. Input data for numerical example.

Parameter	Problem 1	Problem 2	Parameter	Problem 1	Problem 2
D (units/year)	20,000	20,000	L	30	80
p ($/unit)	20	15	$\sigma$	5	9
w ($/unit)	17	13	F	$0.3$	$0.6$
m ($/unit)	12	7	T	20	100
$S_0$ ($/setup)	600	900	M	$0.9$	$0.8$
$A_s$ ($/order)	100	100	$\eta$	$0.5$	$0.5$
$A_b$ ($/order)	200	160	r	$0.3$	$0.2$
$h_s$ ($/unit/year)	5	3	${\delta }_1$	150	180
$h_b$ ($/unit/year)	10	6	${\delta }_2$	130	100
$B_b$ ($/unit/unit time)	6	6	$C_{FT}$ ($/shipment)	30	15
$C_{ST}$ ($/shipment)	20	8

. Results for numerical examples are given in

Table 2. Output data for numerical problem 1, in case of unreliable seller.

Decision Variable	Decentralized System	Centralized System	Coordinating System
Q (units)	925	$1104.8$	$920.6$
$SL$	$95.11\%$	$94.21\%$	$95.13\%$
n	1	1	1
$s(k)$	$1.56$	$1.75$	$1.32$
J ($)	17	17	17
$E{P}_b$ ($)	50,108.79	50,411.93	50,177.23
$E{P}_s$ ($)	97,817.32	97,636.19	97,489.72
$ETP$ ($)	147,926.12	147,953.27	147,666.95

,

Table 3. Output data for numerical problem 2, in case of unreliable Seller.

Decision Variable	Decentralized System	Centralized System	Coordinating System
Q (units)	1132	1305	$1050.2$
$SL$	$95.92\%$	$95.3\%$	$96.2\%$
n	1	1	1
$s(k)$	$4.07$	$4.4$	$1.23$
J ($)	26	26	17
$E{P}_b$ ($)	32,239.1	32,719.6	33,209.08
$E{P}_s$ ($)	118,122.2	117,473.5	118,052.03
$ETP$ ($)	150,361.2	150,057.1	151,187.42

,

Table 4. Output data for numerical problem 1, in case of reliable Seller.

Decision Variable	Decentralized System	Centralized System	Coordinating System
Q (units)	894	1132	1132
$SL$	$95.3\%$	$94.1\%$	$94.1\%$
n	1	1	1
J ($)	17	17	17
$E{P}_b$ ($)	50,580.0	50,791.6	50,633.3
$E{P}_s$ ($)	97,739.2	97,844.5	97,684.8
$ETP$ ($)	148,319.2	148,636.1	148,318.1

and

Table 5. Output data for numerical problem 2, in the case of a reliable Seller.

Decision Variable	Decentralized System	Centralized System	Coordinating System
Q (units)	1032	1392	1392
$SL$	$96.3\%$	$95.3\%$	$95.0\%$
n	1	1	1
J ($)	26	26	26
$E{P}_b$ ($)	33,167.0	33,487.4	33,443.8
$E{P}_s$ ($)	117,944.5	118,000.3	117,956.6
$ETP$ ($)	151,111.5	151,487.6	151,400.04

.

As one can see from Table 2, there is a significant increase in profit for the whole SCM under centralized decision-making as compared to decentralized decision-making, which means the join decision-making on decision variables creates more advantages in terms of profit if the SCM is designed properly.

The SCM managers can enhance the service level with the proposed coordination scheme, and it is shown in Table 3. One can see the increase in profit for the coordinating system for Example 2 when the seller is unreliable. This profitability enhancement is mainly because of the service-level improvement under coordinated decision-making.

We see from Table 4 and Table 5 that the increase in profit under centralized decision-making is more in the case of a reliable seller than an unreliable seller. This performance improvement shows the importance of the reliability of SCM members for the profitability of the entire system.

The centralized decision policy is making more profit than the decentralized decision-making for the whole supply-chain management in Problem 1 for both the reliable seller and unreliable seller case. However, the service level to the customers is under the decentralized strategy in both cases for Problem 1. Meanwhile, for Problem 2, the profit is more under the coordinating strategy when the seller is unreliable and for the reliable seller case profit is slightly higher under the centralized strategy. This comparison shows that the centralized SCM for decision-making regarding order quantities and other decision variables makes more profit for SCM players in all cases. Besides this, it reduces the expected shortages for the buyer. Hence, it increases the service level for the supply chain and is effective for enhancing profitability.

6. Sensitivity Analysis

This section presents sensitivity analyses for major parameters to show the overall effect of value changes on the total profit in both cases, i.e., reliable and unreliable seller. This sensitivity analysis is performed by changing the parameter values to $-50\%$, $-25\%$$+25\%$ and $+50\%$ and keeping other parameters unchanged.

Table 6. Sensitivity analysis for numerical problem 1, in case of unreliable seller.

Parameter	Percentage Changes (%)	Change in Total Profit (%)
		Decentralized System	Centralized System
	$-50\%$	$-0.0267$	$0.0211$
	$-25\%$	$-0.0134$	$0.0106$
$S_0$	$0\%$	0	0
	$+25\%$	$0.0134$	$-0.0105$
	$+50\%$	$0.0267$	$-0.0211$
	$-50\%$	$-0.0556$	$0.017$
	$-25\%$	$-0.0292$	$0.0122$
$B_b$	$0\%$	0	0
	$+25\%$	$0.0323$	$-0.0151$
	$+50\%$	$0.0709$	$-0.0313$
	$-50\%$	$-0.7293$	$0.5982$
	$-25\%$	$-0.3646$	$0.2932$
$A_s$	$0\%$	0	0
	$+25\%$	$0.3646$	$-0.2826$
	$+50\%$	$0.7293$	$-0.5557$
	$-50\%$	$-1.0079$	$1.2535$
	$-25\%$	$-0.5132$	$0.5995$
$A_b$	$0\%$	0	0
	$+25\%$	$0.5229$	$-0.55667$
	$+50\%$	$1.0186$	$-1.0787$

and

Table 7. Sensitivity analysis for numerical Problem 1, in case of reliable seller.

Parameter	Percentage Changes (%)	Change in Total Profit (%)
		Decentralized System	Centralized System
	$-50\%$	$0.027575665$	$0.0218$
	$-25\%$	$0.013787832$	$0.0109$
$S_0$	$0\%$	0	0
	$+25\%$	$-0.01378109$	$-0.0108$
	$+50\%$	$-0.027568923$	$-0.0217$
	$-50\%$	$0.753712365$	$0.6191$
	$-25\%$	$0.376856183$	$0.3030$
$A_s$	$0\%$	0	0
	$+25\%$	$-0.376849441$	$-0.2914$
	$+50\%$	$-0.753705623$	$-0.5725$
	$-50\%$	$1.012667411$	$1.2986$
	$-25\%$	$0.526452479$	$0.6191$
$A_b$	$0\%$	0	0
	$+25\%$	$-0.519683294$	$-0.5725$
	$+50\%$	$-1.021378354$	$-1.1075$

present the results of the sensitivity analysis of Problem 1.

From sensitivity analysis, provided in Table 6 and Table 7, we observe that the ordering cost for the buyer is very sensitive to the profit under the decentralized and centralized SCM. The second most sensitive parameter is the setup cost for the seller in both cases. This trend is very similar for unreliable and reliable seller cases. The SCM planner should consider the ordering cost for the buyer to be a critical factor while making the decisions.

Managerial Insights

The aim of the supply chain initially started with achieving more profit together, i.e., a centralized system. However, with time researchers have developed different coordination schemes to convince the seller and buyer to undertake cooperative decision-making to make the supply chain more profitable as a whole. In this study, the proposed model is also supported for the same strategy. Even though different shipping modes are adopted, the centralized supply chain always has given more profit than the decentralized one. For decades, the distribution-free approach had been adopted in the industry to calculate the expected amount of shortages during lead times. Still, the industry has trouble due to uncertainty in demand and longer lead times. Another aspect that makes the case worse is the unreliability of the seller. If there is an increase, how the industry managers or practitioners will tackle these situations can be solved or modeled by the suggested solution methodology in the proposed model. The lead time should be decreased to control the expected amount of shortages, even if extra cost is required, i.e., the faster shipping mode comes into practice with some additional cost to obtain more profit. The significant impact of shorter lead time is on service level and increase in service level usually increases the profitability of the supply chain. Generally, the seller is considered sufficiently reliable, but this is not the same in practical situations. Thus, considering the reliability of the seller will help managers to plan accordingly to obtain more profit. Therefore, the industry managers and practitioners can adopt these policies together to obtain the global maximum profit for their system.

7. Conclusions

Herein, we established transportation lead-time shortening as a coordination mechanism between the seller and buyer by considering a reliable seller and unreliable seller. The variable setup cost, order quantity, and service level were the significant factors to optimize the profitability of the whole supply chain. For the first time, we considered reliable and unreliable sellers for the coordination supply-chain model. To include a real-life-based scenario to the model, we considered lead-time demand as stochastic with an unknown distribution and used a distribution-free approach to solve it. The application of the proposed model led to notable setup cost reduction, service-level improvement, and an increase in profitability of the whole system. In the presented model, the demand is stochastic fuzzy and lead time was controllable by the seller. The lead-time demand distribution is unknown with limited information, i.e., only with known mean and variance. Investing more to the initial setup cost, the seller can reduce his setup cost per setup, and this improves profit significantly for the seller and the whole system. At the seller’s end, transportation lead time is reduced by spending more on the shipping mode and hence the seller can convince the buyer to take part in coordination and optimize decisions centrally. From the model, the smaller lead time and information about the seller’s reliability are beneficial for the buyer because of lower inventory costs and improved service level. Thus, the lead-time reduction is performed as a coordination scheme to convince the buyer and seller to take part in coordinated decision-making. In this study, we discussed three different scenarios: (1) centralized decision-making; (2) decentralized decision-making with the buyer as leader and sellers as the follower; and (3) a coordinating decision-making. The solution suggests that the shift from decentralized to the centralized system must guarantee the increased profitability for each supply-chain member. In the proposed study, each of the three cases (decentralized, centralized, and coordinated) were studied separately for unreliable and reliable sellers. We consider the variance of demand as $\sigma =0$ when the seller is reliable, and there is the value for $\sigma$ when the seller is not reliable or is unreliable. In each case, the profitability for SC is more when the seller is reliable and vice versa.

To make the mathematical model realistic, we include the reliability of the seller in the model. With the proposed incentive scheme, we consider the CRLT function for the seller to reduce the lead time with two different transportation modes, slow and fast. Slow shipping mode takes a longer time to deliver the order, but it is cheaper. However, fast shipping mode has a shorter delivery time with additional cost. Lead-time reduction within the same shipping mode is possible only to a certain limit. The seller can use a faster shipping mode where the lead-time reduction is required beyond the specified limit. The application of this coordination model leads to a higher supply-chain profitability as compared to the non-cooperative or decentralized decision-making.

There are several limitations to the proposed model. The model is applied to single-seller single-buyer-based supply-chain management with single-stage manufacturing. Also, this model does not consider the environmental impact of shipping modes in terms of carbon emissions. Another limitation of this model is the linear cost function for different shipping modes. Therefore, this model is extendable to a few new directions by considering multiple reliable and unreliable sellers and a single buyer [62]. This paper can also be extended by considering non-linear and complicated function instead of a linear step fixed-charge function. Another extension is to consider the carbon emission cost for both slow and fast shipping modes and observe the economic and environmental effect of it [63]. Another possible extension would be product-channeling in SCM with an online to offline (O2O) strategy [64].