Characterization of n-Vertex Graphs of Metric Dimension n − 3 by Metric Matrix

Abstract

Let $G=\left(V\right(G),E(G\left)\right)$ be a connected graph. An ordered set $W\subset V\left(G\right)$ is a resolving set for G if every vertex of G is uniquely determined by its vector of distances to the vertices in W. The metric dimension of G is the minimum cardinality of a resolving set. In this paper, we characterize the graphs of metric dimension $n-3$ by constructing a special distance matrix, called metric matrix. The metric matrix makes it so a class of graph and its twin graph are bijective and the class of graph is obtained from its twin graph, so it provides a basis for the extension of graphs with respect to metric dimension. Further, the metric matrix gives a new idea of the characterization of extremal graphs based on metric dimension.

1. Introduction

Let $G=\left(V\right(G),V(E\left)\right)$ be a simple connected graph in this paper. The distance between two vertices $u,v\in V\left(G\right)$, denoted by $d(u,v)$, is the length of a shortest path between u and v in G. The diameter of G is denoted by $d\left(G\right)$ and $d\left(G\right)=max\left\{d\right(u,v\left)\right|u,v\in V\left(G\right)\}$. Let $W=\{w_1,w_2,\cdots ,w_m\}\subseteq V\left(G\right)$ be an ordered set of G, the representation of $v\in V\left(G\right)$ with respect to W is the vector $r\left(v\right|W)=(d(v,w_1),d(v,w_2),\cdots ,d(v,w_m))$. We say that W is a resolving set of G if $r\left(v\right|W)\ne r(u\left|W\right)$ for every pair of distinct vertices $u,v\in V\left(G\right)$. A resolving set of minimum cardinality is called a metric basis of G. The metric dimension of a graph G, denoted by dim$\left(G\right)$, is the cardinality of a metric basis. For $S,W_0\subseteq V\left(G\right)$, we say that the set $W_0$ resolves S if $r\left(v\right|W_0)\ne r\left(u\right|W_0)$ for every pair of distinct vertices $u,v\in S$. Moreover, for distinct vertices $u,v,w\in V\left(G\right)$, if $d(w,u)\ne d(w,v)$, then we say that w resolves u and v.

The concepts of resolving set of a graph was first introduced by Slater [1] in 1975 and independently by Harary and Melter [2] in 1976. The metric dimension of a graph has been widely studied and a large number of related concepts have been extended (see [3,4,5,6,7,8,9,10,11]). As a parameter of a graph, it has been applied to lots of practical problems, such as robot navigation [12], connected joins in graphs and combinatorial optimization [13], and pharmaceutical chemistry [14].

There have been lots of results about the metric dimension of graphs. Some researchers focus on characterizations of metric dimension of graph families. For instance, the metric dimension of trees, cycles and wheels was considered in [14,15], respectively. Moreover, the metric dimension of some constructions of graphs was given. For example, the metric dimension of cartesian products of graphs and corona product of graphs was obtained in [16,17], respectively, the effect of vertex or edge deletion on the metric dimension of graphs was considered in [18] and the metric dimensions of symmetric graphs obtained by rooted product were given in [19].

In addition, some graphs with a fixed value of metric dimension have been characterized. Let G be a graph on n-vertex. In [14], the following conclusions were given: $\left(1\right)$ G has metric dimension 1 if and only if $G=P_n$, where $P_n$ denotes a path on n vertices; $\left(2\right)$ G has metric dimension $n-1$ if and only if $G=K_n$, where $K_n$ denotes a complete graph on n vertices; and $\left(3\right)$ all graphs G of metric dimension $n-2$ were characterized (see Lemma 8). In [20,21], all the graphs of metric dimension $n-3$ and $n-d$ are characterized, respectively, where d is the diameter of G. Some other results on metric dimension of a graph are considered in [22,23,24,25].

It is interesting to extend a low-order graph to a high-order graph based on the given rulers. In this paper, we give a novel and effective method on the extension of graphs with respect to metric dimension and characterize the graphs with metric dimension $n-3$ via the method. Hernando et al. [21] gave an idea of using the twin graph (Definition 1) to characterize the graphs with dimension $n-r$, that is, to determine all the twin graphs of these graphs and extend them to corresponding graphs. We define the metric matrix of a graph (Definition 2) to determine and extend the twin graphs, which is different from that used by Jannesari and Omoomi [20] and Hernando et al. [21]. Since the metric matrix makes that a class of graph and its twin graph are bijective, the method makes the proof concise and readable. In addition, it has certain applicability to some other problems of metric dimension. For instance, it can be used to consider the graphs with dimension $n-4$ and even $n-r$ for $r\ge 5$. More importantly, it can be used as an effective basis for the extension of graphs with respect to metric dimension.

The remainder of this paper is organized as follows. In Section 2, we give some preliminaries, including definitions, symbols and results used in this paper. In Section 3, we characterize all extremal graphs of dim$\left(G\right)=n-3$ and diameter 2 by constructing a special distance matrix and discussing the structure of graphs.

2. Preliminaries

Let $n\left(G\right)$ and $G\left[S\right]$ denote the order and the subgraph induced by a subset $S\subseteq V\left(G\right)$ of a graph G, respectively. We say that S is an independent set of G if every pair of vertices in S are nonadjacent in G, and S is a clique of G if every pair of vertices in S are adjacent in G. The neighborhood of $u\in V\left(G\right)$ is denoted by $N\left(u\right)$ and $N\left(u\right)=\left\{v\right|uv\in E\left(G\right)\}$. Let $N\left[u\right]=N\left(u\right)\cup \left\{u\right\}$. We use deg$\left(u\right)$, $\delta \left(G\right)$ to denote the degree of v and the minimum degree of G, respectively, where deg$\left(u\right)=\left|N\right(u\left)\right|$. A pair of vertices $u,v\in V\left(G\right)$ are twins in G if $N\left(u\right)=N\left(v\right)(uv\notin E(G\left)\right)$ or $N\left[u\right]=N\left[v\right](uv\in E(G\left)\right)$. We say that a subset $V_i$ of vertices is a twin set of G if its vertices are pairwise twins in G, and a maximal twin set is a twin class. Clearly, if $V_i$ is a twin set of a graph G, then it is an independent set or a clique of G. The circumference of a graph G, denoted by $c\left(G\right)$, is the length of a longest circle of G.

Definition 1.

The twin graph of a graph G, denoted by $G_{\mathrm{T}}$, is the subgraph induced by $\{v_1,v_2,\dots ,v_k\}$, that is, $G_{\mathrm{T}}=G\left[\{v_1,v_2,\dots ,v_k\}\right]$, where $v_i\in V_i$ for $1\le i\le k$ and $V_1,V_2,\dots ,V_k$ are the all distinct twin classes of G.

Definition 2.

For a graph G, let $V\left(G_{\mathrm{T}}\right)=\{v_1,v_2,\dots ,v_k\}$ and let $V_i$ be the twin class of G with $v_i\in V_i$ for $1\le i\le k$, the metric matrix of G is denoted by $D={\left[d_{ij}\right]}_{k\times k}$ and

$$d_{ij}=\left\{\begin{array}{cc}d(v_i,v_j),& i\ne j,\hfill \\ d(v_i,v_i^{\prime }),& i=jand|V_i|\ge 2,\hfill \\ 0,& i=jand|V_i|=1,\hfill \end{array}\right.$$

where $v_i^{\prime }\in V_i$ and $v_i^{\prime }\ne v_i$.

Let $d_i$ denote $d_{ii}$ in the following sections. Since $V_i$ is an independent set or a clique of G, we have $d_i=0or1or2$. The metric matrix determines different classes of graphs with the same twin graph.

The graph $G_1+G_2$ is obtained from $G_1$ and $G_2$ by adding the edges from every vertex of $G_1$ to every vertex of $G_2$, which is represented as in Figure 1 in this paper. The union $G_1\cup G_2$ of $G_1$ and $G_2$ is the graph whose vertex set and edge set are $V\left(G_1\right)\cup V\left(G_2\right)$ and $E\left(G_1\right)\cup E\left(G_2\right)$, respectively. The graph $G-v$ is obtained from G by deleting the vertex v. The graph $G-e$ is obtained from G by deleting the edge e. Let $\overline{K_s}$ be the complement of $K_s$ and let $K_{1,m}$ denote a star with $m+1$ vertices.

Unless explicitly noted during the rest of this paper, let $V_i$ be the twin classes of G with $v_i\in V_i$, and if $|V_i|\ge 2$, then assume that $v_i^{\prime }\in V_i$ and $v_i^{\prime }\ne v_i$.

Lemma 1 

([20]). For a graph G, we have $n\left(G_{\mathrm{T}}\right)-\dim \left(G_{\mathrm{T}}\right)\le n\left(G\right)-\dim \left(G\right)$.

Lemma 2.

For a graph G, if $v_i$ and $v_j$ are twins in $G_{\mathrm{T}}$, then at least one of $V_i$ and $V_j$ have cardinality at least 2. Moreover, if $|V_i|=s\ge 2$, then $G\left[V_i\right]=\overline{K_s}$ when $d(v_i,v_j)=1$ and $G\left[V_i\right]=K_s$ when $d(v_i,v_j)=2$.

Proof. 

Since $v_i$ and $v_j$ are twins in $G_{\mathrm{T}}$, we have $d(u,v_i)=d(u,v_j)$ for every $u\in V\left(G\right)\backslash (V_i\cup V_j)$. Moreover, by the definition of $G_{\mathrm{T}}$, we obtain that $v_i$ and $v_j$ are not twins in G, so there is $x\notin \{v_i,v_j\}$ and $x\in V_i$ or $x\in V_j$ such that $d(x,v_i)\ne d(x,v_j)$. Thus, at least one of $V_i$ and $V_j$ have cardinality at least 2. Assume that $x\in V_i$, that is, $|V_i|=s\ge 2$. If $d(v_i,v_j)=1$, then $d(x,v_j)=1$, so $d(x,v_i)=2$, that is, $G\left[V_i\right]=\overline{K_s}$. Otherwise, $d(v_i,v_j)=2$, then $d(x,v_i)=1$, that is, $G\left[V_i\right]=K_s$. □

Corollary 1.

For a graph G, if $S=\{v_{i_1},v_{i_2},\dots ,v_{i_t}\}$ is a twin set in $G_{\mathrm{T}}$, then we have that if $G\left[S\right]=K_t$, then all but one of the sets $V_{i_1}$, $V{i}_2$,…,$V_{i_t}$ have cardinality at least 2 and induce an empty graph, and if $G\left[S\right]=\overline{K_t}$, then all but one of the sets $V_{i_1}$, $V{i}_2$,…,$V_{i_t}$ have cardinality at least 2 and induce an complete graph.

Lemma 3 

([21]). Let W be a metric basis of G and let $S\subseteq V$ be a nonempty subset. If S is a twin set of G, then at most one of the vertices in S is not in W and the set $(W\backslash S)\cup \left\{s\right\}$ resolves the set $V\left(G\right)\backslash S$ for each $s\in S$.

Let $G_{\mathrm{T}}$ and D be the twin graph and the metric matrix of G, respectively. Let $S_1=\left\{v_i^{\prime }\right|v_i\in V\left(G_{\mathrm{T}}\right)\mathrm{and}{d}_i>0\}$, $S_2=\{v_i\in V\left(G_{\mathrm{T}}\right)|d_i=0\}$, and U be an arbitrary subset of $S_2$. The matrix $D_U$ is obtained from D by deleting the corresponding rows of all vertices in U and the corresponding columns of all vertices in $S_2\backslash U$. We can get that $r\left(v\right|S_1\cup U)=D_U\left(v\right)$ for each $v\in V\left(G_{\mathrm{T}}\right)\backslash U$, where $D_U\left(v\right)$ is the row vectors corresponding to v in $D_U$. Moreover, each subset of $S_2$ corresponds to a matrix $D_U$. Let $\mathcal{D}=\{D_U:U\subseteq S_2\}$ be the set constituting of all matrix $D_U$. We have the following result.

Lemma 4.

For a graph G, dim$\left(G\right)=n\left(G\right)-r$ if and only if for each $U\subseteq S_2$ the matrix $D_U$ has at most r different row vectors, and there exists a subset $U_0\subseteq S_2$ such that $D_{U_0}$ has exactly r different row vectors.

Proof. 

Suppose that W and $V_i$ are a metric basis and a twin class of G, respectively. By Lemma 3, at most one of the vertices in $V_i$ is not in W. Let $W_0$ be a set obtained from W by replacing $v_i$ with v for each vertex $v\notin W$, where $v\in V_i$. Then $W_0$ is a metric basis of G, and we get that $V\left(G\right)\backslash W_0\subseteq V\left(G_{\mathrm{T}}\right)$ and $S_1\subseteq W_0$. Moreover, we have that $(W_0\cap S_2)\cup S_1$ resolves $V\left(G\right)\backslash W_0$ by Lemma 3.

Necessity. Since dim$\left(G\right)=n\left(G\right)-r$, there are exactly r vertices in $V\left(G_{\mathrm{T}}\right)$ not in $W_0$. Thus the set $S_1\cup U$ resolves at most r vertices in $V\left(G_{\mathrm{T}}\right)\backslash U$ for each subset U, which implies that each $D_U\in \mathcal{D}$ has at most r different row vectors. Let $U_0=W_0\cap S_2$, then $S_1\cup U_0$ resolves exactly r vertices in $V\left(G_{\mathrm{T}}\right)\backslash U_0$. Thus, $D_{U_0}$ has exactly r different row vectors.

Sufficiency. Since each $D_U\in \mathcal{D}$ has at most r different row vectors, $S_1\cup U$ resolves at most r vertices in $V\left(G_{\mathrm{T}}\right)\backslash U$ for each subset $U\subseteq S_2$, then $S_1\cup (W_0\cap S_2)$ resolves at most r vertices in $V\left(G_{\mathrm{T}}\right)\backslash (W_0\cap S_2)$. Thus, dim$\left(G\right)\ge n-r$. In addition, since there exists $D_{U_0}\in \mathcal{D}$ with exactly r different row vectors, $S_1\cup (W_0\cap S_2)$ resolves at least r vertices in $V\left(G_{\mathrm{T}}\right)\backslash (W_0\cap S_2)$, so dim$\left(G\right)\le n-r$. Thus, dim$\left(G\right)=n-r$. □

Corollary 2.

For a graph G, we have $n\left(G\right)-\dim \left(G\right)\le n\left(G_T\right)$.

Let $D_{i_1{i}_2\cdots i_k}$ be the matrix consisting of the $i_1$, $i_2$,⋯,$i_k$ columns of the metric matrix D of G. Let $p_{i_1{i}_2\cdots i_k}$ be the number of different row vectors without zero element in $D_{i_1{i}_2\cdots i_k}$.

Corollary 3.

If $p_{i_1{i}_2\cdots i_k}=r$, then dim$\left(G\right)\le n\left(G\right)-r$.

Lemma 5.

Let G be a graph of dim$\left(G\right)=n\left(G\right)-r$. If the set T is a twin class of $G_{\mathrm{T}}$ with $\left|T\right|=t\ge 2$, then $r=t$ if $n\left(G_{\mathrm{T}}\right)=t$, and $r\ge t+1$ if $n\left(G_{\mathrm{T}}\right)>t$.

Proof. 

Suppose that $T=\{v_1,v_2,\cdots ,v_t\}$. Then $G\left[T\right]\cong K_t$ or $\overline{K_t}$. By Corollary 1, assume that $|V_i|\ge 2$ for $1\le i\le t-1$, then we have that $d(v_i,v_i^{\prime })=2$, $d(v_j,v_i^{\prime })=1$ when $G\left[T\right]\cong K_t$, and $d(v_i,v_i^{\prime })=1$, $d(v_j,v_i^{\prime })=2$ when $G\left[T\right]\cong \overline{K_t}$ for $1\le i<j\le t$. Let $W_0=\{v_1^{\prime },v_2^{\prime },\dots ,v_{t-1}^{\prime }\}$, then $W_0$ resolves the set $\{v_1,v_2,\cdots ,v_t\}$. Thus, we have $r\ge t$. Since $r=n\left(G\right)-\dim \left(G\right)\le n\left(G_{\mathrm{T}}\right)$ by Corollary 2, if $n\left(G_{\mathrm{T}}\right)=t$, then $r=t$. If $n\left(G_T\right)>t$, then there exists $v_{t+1}\in V\left(G_{\mathrm{T}}\right)\backslash T$. Since $v_{t+1}\notin T$, there is $x\in V\left(G_{\mathrm{T}}\right)$ such that $d(v_{t+1},x)\ne d(v_i,x)$ for all $i\in \{1,2,\cdots ,t\}$. If $x\in T$, then $W_0$ resolves the set $\{v_1,v_2,\cdots ,v_{t+1}\}$. Otherwise, $W_0\cup \left\{x\right\}$ resolves the set $\{v_1,v_2,\cdots ,v_{t+1}\}$. Therefore, $r\ge t+1$. □

Corollary 4.

For a graph G, if $G_{\mathrm{T}}=K_{1,m}$ or $G_{\mathrm{T}}=K_m$, then dim$\left(G\right)=n\left(G\right)-n\left(G_T\right)$.

Lemma 6 

([14]). Let G be a graph of order $n\left(G\right)>2$ and diameter d, then $\dim \left(G\right)\le n\left(G\right)-d$.

Lemma 7 

([14]). Let G be graph of order $n\left(G\right)>2$. Then dim$\left(G\right)=n\left(G\right)-1$ if and only if $G=K_n$.

Lemma 8 

([14]). Let G be graph of order $n\left(G\right)\ge 4$. Then dim$\left(G\right)=n\left(G\right)-2$ if and only if $G=K_{s,t}$$(s,t\ge 1)$, $G=K_s+\overline{K_t}(s\ge 1,t\ge 2)$, or $G=K_s+(K_1\cup K_t)(s,t\ge 1)$.

Lemma 9.

Let G be a graph with dim$\left(G\right)=n\left(G\right)-3$ and a metric basis W. Then there exists a set $W_0\subseteq W$ and $|W_0|\le 2$ such that it resolves $V\left(G\right)\backslash W$.

Proof. 

Suppose that $V\left(G\right)\backslash W=\{v_1,v_2,v_3\}$. Then there is a vertex $w_1\in W$ such that $d(w_1,v_1)\ne d(w_1,v_2)$. If $d(w_1,v_i)\ne d(w_1,v_3)$ for $i\in \{1,2\}$, then $w_1$ resolves $\{v_1,v_2,v_3\}$. Let $W_0=\left\{w_1\right\}$, then we are done. Otherwise, assume that $d(w_1,v_1)=d(w_1,v_3)$, then there is $w_2\in W$ such that $d(w_2,v_1)\ne d(w_2,v_3)$. Thus, $\{w_1,w_2\}$ resolves $\{v_1,v_2,v_3\}$. Let $W_0=\{w_1,w_2\}$, then we are done. □

3. Extremal Graphs G of dim$\left(\mathit{G}\right)=\mathit{n}\left(\mathit{G}\right)-\mathbf{3}$

By Lemma 6, if dim$\left(G\right)=n\left(G\right)-3$, then $d\left(G\right)\le 3$. Moreover, if $d\left(G\right)=1$, then dim$\left(G\right)=n\left(G\right)-1$. Thus, dim$\left(G\right)=n\left(G\right)-3$ only if $d\left(G\right)=2or3$. Since all the graphs of dim$\left(G\right)=n\left(G\right)-d\left(G\right)$ were characterized in [21], we only need to consider the graphs of $d\left(G\right)=2$.

In the following, unless noted otherwise, let D, W be the metric matrix and a resolving set of G, respectively. Let $e_{ij}=v_i{v}_j$ and $B_m=K_{m}or\overline{K_m}$.

Lemma 10.

Let G be a graph of $d\left(G\right)=2$ and $n\left(G_{\mathrm{T}}\right)=3$. Then dim$\left(G\right)=n\left(G\right)-3$ if and only if $G=(K_s\cup B_r)+K_t(s,r\ge 2,t\ge 1)$ or $G=(K_s\cup B_r)+\overline{K_t}(s,t\ge 2,r\ge 1)$ or $G=(\overline{K_s}+\overline{K_t})+B_r(s,t\ge 2,r\ge 1)$.

Proof. 

Suppose that $V\left(G_{\mathrm{T}}\right)=\{v_1,v_2,v_3\}$, there are two cases to be considered as follows.

Case 1. $G_{\mathrm{T}}\cong P_3=v_1{v}_2{v}_3$. Since $v_1$ and $v_3$ are twins in $G_{\mathrm{T}}$ and $e_{13}\notin E\left(G_{\mathrm{T}}\right)$, by Lemma 2, we may assume that $d_1=1$, then

$$D=\left[\begin{array}{ccc}1& 1& 2\\ 1& d_2& 1\\ 2& 1& d_3\end{array}\right].$$

Since there are at most three different row vectors in D, by Lemma 4, dim$\left(G\right)=n\left(G\right)-3$ if and only if there are exactly three different row vectors in some $D_U$, which implies that $\left(1\right)$ $d_2=0or1$, $d_3=1or2$, or $\left(2\right)$ $d_2=2$, $d_3=0or1or2$. Therefore, $G=(K_s\cup B_r)+K_t(s,r\ge 2,t\ge 1)$ or $(K_s\cup B_r)+\overline{K_t}(s,t\ge 2,r\ge 1)$.

Case 2. $G_T\cong C_3$. Since any two vertices in $\{v_1,v_2,v_3\}$ are twins in $G_{\mathrm{T}}$, by Corollary 1, we may assume that $d_1=d_2=2$, then

$$D=\left[\begin{array}{ccc}2& 1& 1\\ 1& 2& 1\\ 1& 1& d_3\end{array}\right].$$

Since there are at most three different row vectors in D and $p_{12}=3$, by Lemma 4, dim$\left(G\right)=n\left(G\right)-3$ if and only if $d_3=0or1or2$, which implies that $G=(\overline{K_s}+\overline{K_t})+B_r(s,t\ge 2,r\ge 1)$. □

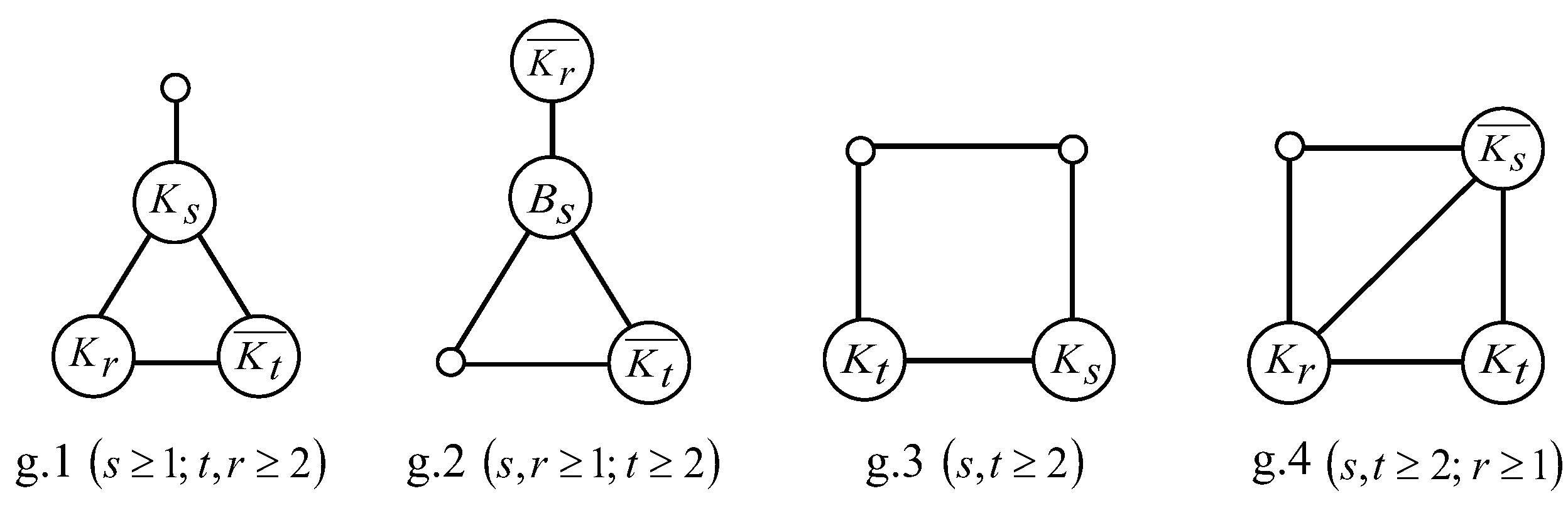
Lemma 11.

Let G be a graph of $d\left(G\right)=2$ and $n\left(G_{\mathrm{T}}\right)=4$. Then dim$\left(G\right)=n\left(G\right)-3$ if and only if G is one of the graphs in Figure 2, where a small circle denotes $K_1$ (similarly in the following figures).

Proof. 

Let $V\left(G_{\mathrm{T}}\right)=\{v_1,v_2,v_3,v_4\}$. There are the following cases to be considered depending on the circumference of $G_{\mathrm{T}}$.

Case 1. $G_{\mathrm{T}}$ is acyclic. In such a case, $G_{\mathrm{T}}\cong K_{1,3}$. There is no graph G with dim$\left(G\right)=n\left(G\right)-3$ by Corollary 4.

Case 2. $c\left(G_{\mathrm{T}}\right)=3$. Let $C_3=v_1{v}_2{v}_3{v}_1$, we may assume that $G_{\mathrm{T}}\cong C_3\cup e_{14}$. Since $v_2$ and $v_3$ are twins in $G_{\mathrm{T}}$ and $e_{23}\in E\left(G_{\mathrm{T}}\right)$, by Lemma 2, we may assume that $d_2=2$, then

$$D=\left[\begin{array}{cccc}{d}_1& 1& 1& 1\\ 1& 2& 1& 2\\ 1& 1& d_3& 2\\ 1& 2& 2& d_4\end{array}\right].$$

By Corollary 3, we obtain that $d_3\ne 2$ and $d_4\ne 1$; if not, $p_{23}=4$ or $p_{24}=4$, which contradicts dim$\left(G\right)=n\left(G\right)-3$. If $d_3=1$, then $d_1\ne 2$ and $d_4=0$; otherwise, $p_{123}=4$ or $p_{234}=4$. By Lemma 4, dim$\left(G\right)=n\left(G\right)-3$ when $d_3=1$, $d_1=0or1$, $d_4=0$; or $d_3=0$, $d_1=0or1or2$, $d_4=0or2$. Thus dim$\left(G\right)=n\left(G\right)-3$ if and only if $\left(1\right)$ $d_1=0or1$, $d_2=2$, $d_3=1$, $d_4=0$, or $\left(2\right)$ $d_1=0or1or2$, $d_2=2$, $d_3=0$, $d_4=0or2$, which implies that G is the graph g.1 or g.2 in Figure 2.

Case 3. $c\left(G_{\mathrm{T}}\right)=4$. Let $C_4=v_1{v}_2{v}_3{v}_4{v}_1$ is a longest circle of $G_{\mathrm{T}}$.

Case 3.1. $G_{\mathrm{T}}\cong C_4$. Since the pairs of vertices $v_1,v_3$ and $v_2,v_4$ are twins in $G_{\mathrm{T}}$, respectively, we may suppose that $d_1=d_2=1$ by Lemma 2, then

$$D=\left[\begin{array}{cccc}1& 1& 2& 1\\ 1& 1& 1& 2\\ 2& 1& d_3& 1\\ 1& 2& 1& d_4\end{array}\right].$$

By Corollary 3, we have that $d_3=d_4=0$; if not, $P_{123}=4$ or $P_{124}$ = 4. Since dim$\left(G\right)=n\left(G\right)-3$ when $d_3=d_4=0$ by Lemma 4, dim$\left(G\right)=n\left(G\right)-3$ if and only if $d_1=d_2=1$ and $d_3=d_4=0$, which implies that G is the graph g.3 in Figure 2.

Case 3.2. $G_{\mathrm{T}}\cong C_4\cup e_{13}$. Since the pairs of vertices $v_1,v_3$ and $v_2,v_4$ are twins in $G_{\mathrm{T}}$, respectively, we may assume that $d_1=2$, $d_2=1$ by Lemma 2, then

$$D=\left[\begin{array}{cccc}2& 1& 1& 1\\ 1& 1& 1& 2\\ 1& 1& d_3& 1\\ 1& 2& 1& d_4\end{array}\right].$$

By Corollary 3, $d_3\ne 2$ and $d_4=0$; if not, $P_{123}=4$ or $P_{124}=4$. Since dim$\left(G\right)=n\left(G\right)-3$ when $d_3=0or1$, $d_4=0$ by Lemma 4, dim$\left(G\right)=n\left(G\right)-3$ if and only of $d_1=2$, $d_2=1$, $d_3=0or1$ and $d_4=0$, which implies that G is the graph g.4 in Figure 2.

Case 3.3. $G_{\mathrm{T}}\cong K_4$. There is no graph G with dim$\left(G\right)=n\left(G\right)-3$ by Corollary 4. □

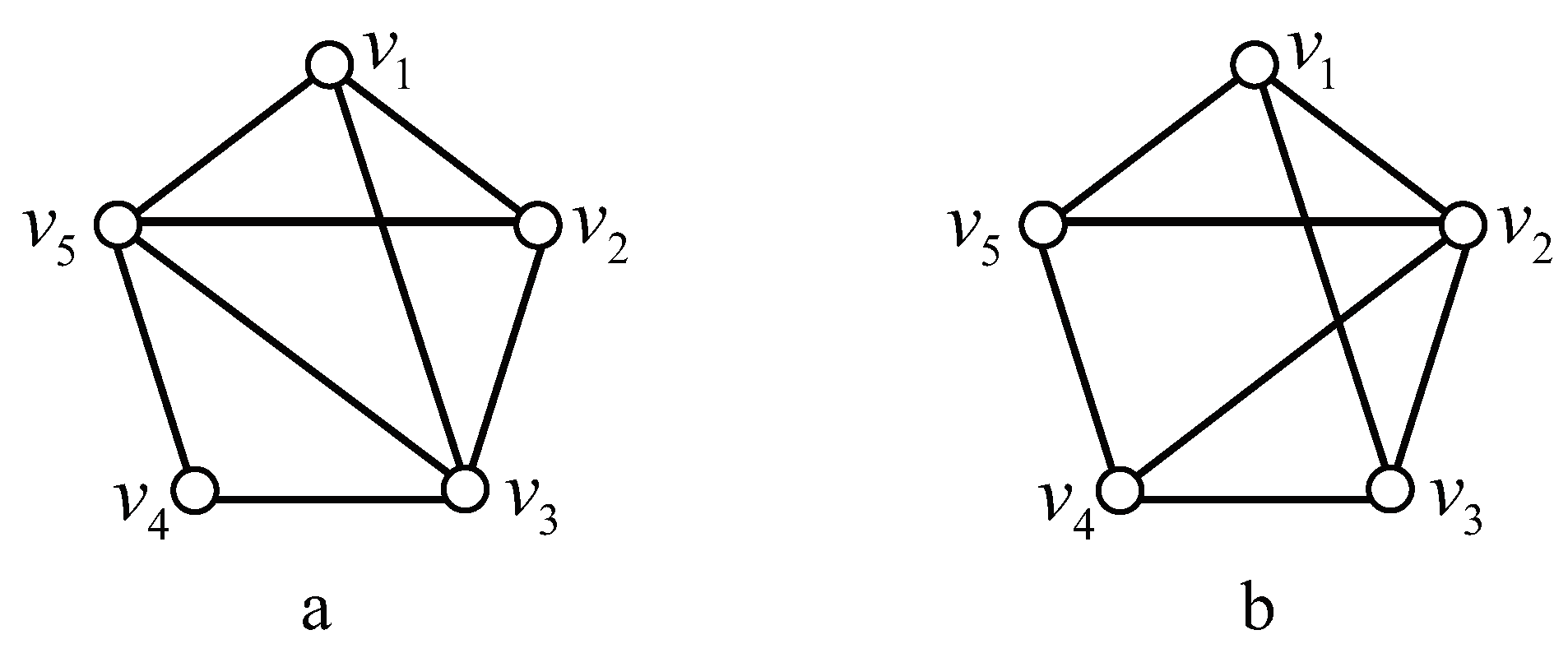
Lemma 12.

Let G be a graph of $d\left(G\right)=2$ and $n\left(G_{\mathrm{T}}\right)=5$. Then dim$\left(G\right)=n\left(G\right)-3$ if and only if G is $C_5$ or one of graphs in Figure 3.

Proof. 

Let $V\left(G_{\mathrm{T}}\right)=\{v_1,v_2,v_3,v_4,v_5\}$. There are the following cases to be considered depending on the circumference of $G_{\mathrm{T}}$.

Case 1. $G_{\mathrm{T}}$ is acyclic. In such a case, $G_{\mathrm{T}}\cong K_{1,4}$. There is no graph G with dim$\left(G\right)=n\left(G\right)-3$ by Corollary 4.

Case 2. $c\left(G_{\mathrm{T}}\right)=3$. Let $C_3=v_1{v}_2{v}_3{v}_1$ be a longest circle of $G_{\mathrm{T}}$, then $G_{\mathrm{T}}$ is isomorphic to the graph (a) or (b) in Figure 4. Since the pairs of vertices $v_2,v_3$ and $v_4,v_5$ are twins in $G_{\mathrm{T}}$, respectively, we may assume that $|V_2| \ge 2$ and $|V_4| \ge 2$, then, for graph (a), $\{v_2^{\prime },v_4^{\prime }\}$ resolves $V\left(G_{\mathrm{T}}\right)$, and for graph (b), $\{v_2,v_4^{\prime }\}$ resolves $\{v_1,v_3,v_4,v_5\}$, a contradiction.

Case 3. $c\left(G_{\mathrm{T}}\right)=4$. Let $C_4=v_1{v}_2{v}_3{v}_4{v}_1$ be a longest circle of $G_{\mathrm{T}}$. Then $v_5$ is nonadjacent to two adjacent vertices of $C_4$; otherwise, $c\left(G_{\mathrm{T}}\right)=5$.

Case 3.1. The vertex $v_5$ is exactly adjacent to one vertex of $C_4$. Then $G_{\mathrm{T}}$ is isomorphic to the graph (a) or (b) in Figure 5.

For Figure 5a, since $v_2$ and $v_4$ are twins in $G_{\mathrm{T}}$, we may assume that $d_2=1$, then

$$D=\left[\begin{array}{ccccc}{d}_1& 1& 1& 1& 1\\ 1& 1& 1& 2& 2\\ 1& 1& d_3& 1& 2\\ 1& 2& 1& d_4& 2\\ 1& 2& 2& 2& d_5\end{array}\right].$$

By Corollary 3, we have that $d_1\ne 2$, $d_3\ne 2$ and $d_4=d_5=0$. Otherwise, if $d_1=2$, then $p_{123}\ge 4$; if $d_3=2$, then $p_{23}=4$; and if $d_4\ne 0$ or $d_5\ne 0$, then $p_{245}\ge 4$, which is a contradiction. Since dim$\left(G\right)=n\left(G\right)-3$ when $d_1=0or1$, $d_3=0or1$ and $d_4=d_5=0$ by Lemma 4, dim$\left(G\right)=n\left(G\right)-3$ if and only if G is the graph g.1 in Figure 3.

For Figure 5b, since $\{v_2,v_3,v_4\}$ is a twin set of $G_{\mathrm{T}}$, by Lemma 5, dim$\left(G\right)<n\left(G\right)-3$. Thus, there is no G with dim$\left(G\right)=n\left(G\right)-3$.

Case 3.2. The vertex $v_5$ is exactly adjacent to two vertices of $C_4$. Then $c\left(G\right)=4$ if and only if $G_{\mathrm{T}}$ is isomorphic to the graph (a) or (b) in Figure 6. Since $\{v_1,v_3,v_5\}$ is a twin set of $G_{\mathrm{T}}$, dim$\left(G\right)<n\left(G\right)-3$ by Lemma 5.

Case 4. $c\left(G_{\mathrm{T}}\right)=5$. Let $C_5=v_1{v}_2{v}_3{v}_4{v}_5{v}_1$ be a longest circle in $G_{\mathrm{T}}$. Since $5\le \left|E\right(G_{\mathrm{T}}\left)\right|\le 10$, we consider the five subcases as follows.

Case 4.1. $\left|E\right(G_{\mathrm{T}}\left)\right|=5$. We obtain that $G_{\mathrm{T}}\cong C_5$, then

$$D=\left[\begin{array}{ccccc}{d}_1& 1& 2& 2& 1\\ 1& d_2& 1& 2& 2\\ 2& 1& d_3& 1& 2\\ 2& 2& 1& d_4& 1\\ 1& 2& 2& 1& d_5\end{array}\right].$$

By Corollary 3, $d_1=0$. Otherwise, if $d_1=1$, then $p_{12}\ge 4$; and if $d_1=2$, then $p_{13}\ge 4$. By the symmetry of $G_{\mathrm{T}}$, $d_i=0(2\le i\le 5)$. Since dim$\left(C_5\right)=2$, dim$\left(G\right)=n\left(G\right)-3$ if and only if $G\cong C_5$.

Case 4.2. $\left|E\right(G_{\mathrm{T}}\left)\right|=6$. We obtain that $c\left(G_{\mathrm{T}}\right)=5$ if and only if $G_{\mathrm{T}}$ is isomorphic to Figure 7, then

$$D=\left[\begin{array}{ccccc}{d}_1& 1& 2& 2& 1\\ 1& d_2& 1& 2& 1\\ 2& 1& d_3& 1& 2\\ 2& 2& 1& d_4& 1\\ 1& 1& 2& 1& d_5\end{array}\right].$$

By Corollary 3, we have that $d_i\ne 2(1\le i\le 5)$ and $d_3,d_4\ne 1$. Otherwise, if $d_1=2$ or $d_3=2$, then $p_{13}\ge 4$; if $d_2=2$, then $p_{12}\ge 4$; if $d_3=1$, then $p_{23}\ge 4$. By the symmetry of $G_{\mathrm{T}}$, we get that $d_4\ne 1or2$ and $d_5\ne 2$. Since dim$\left(G\right)=n\left(G\right)-3$ when $d_i=0or1(i=1,2,5)$ and $d_3=d_4=0$ by Lemma 4, dim$\left(G\right)=n\left(G\right)-3$ if and only if G is the graph g.2 in Figure 3.

Case 4.3. $\left|E\right(G_{\mathrm{T}}\left)\right|=7$. We obtain that $c\left(G_{\mathrm{T}}\right)=5$ if and only if $G_{\mathrm{T}}$ is isomorphic to the graph (a) or (b) in Figure 8.

For Figure 8a, since the pairs of vertices $v_1,v_2$ and $v_3,v_5$ are twins in $G_{\mathrm{T}}$, respectively, we may assume that $d_1=2$ and $d_3=1$, then $\{v_1^{\prime },v_2,v_3^{\prime }\}$ resolves $\{v_1,v_3,v_4,v_5\}$, which is a contradiction.

For Figure 8b, since

$$D=\left[\begin{array}{ccccc}{d}_1& 1& 1& 1& 1\\ 1& d_2& 1& 2& 2\\ 1& 1& d_3& 1& 2\\ 1& 2& 1& d_4& 1\\ 1& 2& 2& 1& d_5\end{array}\right],$$

by Corollary 3, $d_i\ne 2(2\le i\le 5)$. Otherwise, if $d_2=2$ or $d_3=2$, then $p_{25}\ge 4$ or $p_{23}\ge 4$. By the symmetry of $G_{\mathrm{T}}$, we get that $d_4,d_5\ne 2$.

If $d_1=0or1$, then $d_2=0$ or 1. Assume $d_2=1$, then $d_4=d_5=0$, if not, $p_{245}=4$. In this case, $d_3=0or1$ by Lemma 4. Now we assume that $d_2=0$. By the symmetry of $G_{\mathrm{T}}$, we may assume that $d_5=0$; if not, it is the same as $d_2=1$. By Lemma 4, we have that $d_3=d_4=0or1$.

If $d_1=2$, then $d_i=0$ for $2\le i\le 5$. Otherwise, if $d_2=1$, then $p_{124}=4$; if $d_3=1$, then $p_{123}=4$; if $d_4=1$, then $p_{134}=4$; and if $d_5=1$, then $p_{145}=4$.

Thus, we have that dim$\left(G\right)=n\left(G\right)-3$ when $\left(1\right)$ $d_2=1$, $d_i=0or1(i=1,3)$, $d_4=d_5=0$, $\left(2\right)$ $d_i=0or1(i=1,3,4)$, $d_2=d_5=0$, or $\left(3\right)$ $d_1=2$, $d_i=0(2\le i\le 5)$, which implies that dim$\left(G\right)=n\left(G\right)-3$ if and only if G is one of the graphs g.3, g.4 and g.5 in Figure 3.

Case 4.4. $\left|E\right(G_{\mathrm{T}}\left)\right|=8$. We obtain that $c\left(G_{\mathrm{T}}\right)=5$ if and only if $G_{\mathrm{T}}$ is isomorphic to the graph (a) or (b) in Figure 9.

For Figure 9a, since the pairs of vertices $v_1,v_2$ and $v_3,v_5$ are twins in $G_{\mathrm{T}}$, respectively, we may assume that $d_1=d_3=1$, then $\{v_1^{\prime },v_3^{\prime },v_4\}$ resolves $\{v_1,v_2,v_3,v_5\}$, which contradicts dim$\left(G\right)=n\left(G\right)-3$.

For Figure 9b, the pairs of vertices $v_1,v_2$ and $v_3,v_5$ are twins in $G_{\mathrm{T}}$, respectively, we may assume that $d_1=d_3=2$, then

$$D=\left[\begin{array}{ccccc}1& 1& 1& 2& 1\\ 1& d_2& 1& 1& 1\\ 1& 1& 1& 1& 2\\ 2& 1& 1& d_4& 1\\ 1& 1& 2& 1& d_5\end{array}\right].$$

By Corollary 3, we obtain that $d_4=d_5=0$ and $d_2\ne 2$. Otherwise, if $d_4\ne 0$, then $p_{134}=4$, by the symmetry of $G_{\mathrm{T}}$, $d_5=0$; and if $d_2=2$, then $p_{125}=4$. By Lemma 4, we get that dim$\left(G\right)=n\left(G\right)-3$ when $d_1=d_3=1$, $d_2=0or1$, $d_4=d_5=0$, which implies that G is the graph g.6 in Figure 3.

Case 4.5. $\left|E\right(G_{\mathrm{T}}\left)\right|\ge 9$. We obtain that $G_{\mathrm{T}}$ is isomorphic to $K_5-e$ or $K_5$. By Lemma 5 and Corollary 4, there is no graph G with dim$\left(G\right)=n\left(G\right)-3$. □

Lemma 13.

Let G be a graph with $d\left(G\right)=2$ and dim$\left(G\right)=n\left(G\right)-3$. If $G_{\mathrm{T}}=G$, then $n\left(G\right)\le 5$.

Proof. 

Since $G_{\mathrm{T}}=G$, there are no twins in G. Let $V\left(G\right)=\{v_1,v_2,\cdots ,v_n\}$. We consider the both cases $n\left(G\right)>6$ and $n\left(G\right)=6$.

Case 1. $n\left(G\right)>6$. By Lemma 9, we may assume that $W_0=\{v_1,v_2\}$ resolves $\{v_3,v_4,v_5\}$. Since dim$\left(G\right)=n\left(G\right)-3$, $r\left(v_6\right|W_0),r\left(v_7\right|W_0)\in \{r\left(v_3\right|W_0),r\left(v_4\right|W_0),r\left(v_5\right|W_0)\}$.

Case 1.1. $r\left(v_6\right|W_0)\ne r\left(v_7\right|W_0)$. We may assume that $r\left(v_6\right|W_0)=r\left(v_3\right|W_0)$ and $r\left(v_7\right|W_0)=r\left(v_4\right|W_0)$. Since there are no twins in G, there exists $x\in V\left(G\right)$ such that $d(v_6,x)\ne d(v_3,x)$. Then $x=v_5$; if not, $\{v_1,v_2,x\}$ resolves $\{v_3,v_4,v_5,v_6\}$ or $\{v_3,v_5,v_6,v_7\}$. Similarly, $d(v_4,v_5)\ne d(v_7,v_5)$. Thus $\{v_1,v_2,v_5\}$ resolves $\{v_3,v_4,v_6,v_7\}$, which contradicts dim$\left(G\right)=n\left(G\right)-3$.

Case 1.2. $r\left(v_6\right|W_0)=r\left(v_7\right|W_0)$. We may assume that $r\left(v_6\right|W_0)=r\left(v_7\right|W_0)=r\left(v_3\right|W_0)$. Since there are no twins in G, there exists $x\in V\left(G\right)$ such that x resolves two vertices in $\{v_3,v_6,v_7\}$. Assume that $d(v_6,x)\ne d(v_3,x)$, then $x\in \{v_4,v_5\}$; if not, $\{v_1,v_2,x\}$ resolves $\{v_3,v_4,v_5,v_6\}$, which is a contradiction. Thus $\{v_4,v_5\}$ resolves both $\{v_3,v_6,v_7\}$ and $\{v_1,v_2\}$, it becomes case 1.1.

Case 2. $n\left(G\right)=6$. We first prove that $\delta \left(G\right)\ge 2$. Assume for a contradiction that deg$\left(v_1\right)=1$. We may assume that $e_{12}\in E\left(G\right)$. Since $d\left(G\right)=2$, $N\left(v_2\right)=\{v_1,v_3,v_4,v_5,v_6\}$. Since $v_1$ and $v_3$ are not twins, we may assume that $e_{34}\in E\left(G\right)$. Similarly, assume that $e_{35}\notin E\left(G\right)$, $e_{45}\in E\left(G\right)$, $e_{36}\notin E\left(G\right)$ and $e_{56}\in E\left(G\right)$. In such a case, $e_{46}\notin E\left(G\right)$, otherwise $v_5$ and $v_6$ are twins. Thus, $\{v_3,v_6\}$ is a resolving set of G, then dim$\left(G\right)=n\left(G\right)-4$, which is a contradiction.

Now we construct G. Let $P_3=v_1{v}_2{v}_3$ be a shortest path of length 2 of G. Since $v_1$ and $v_3$ are not twins, we may assume that $e_{14}\notin E\left(G\right)$ and $e_{34}\in E\left(G\right)$. There are two subcases to be considered as follows.

Case 2.1. $e_{24}\in E\left(G\right)$. Since $v_3$ and $v_4$ are not twins, we may assume that $e_{35}\notin E\left(G\right)$ and $e_{45}\in E\left(G\right)$. There are four subcases to be considered by the adjacency relationship between $v_5$ and $v_1$, $v_2$ as fallows.

Case 2.1.1. $e_{15}\in E\left(G\right)$, $e_{25}\notin E\left(G\right)$. We obtain that the metric matrix of $G-v_6$ is

$$D=\left[\begin{array}{ccccc}0& 1& 2& 2& 1\\ 1& 0& 1& 1& 2\\ 2& 1& 0& 1& 2\\ 2& 1& 1& 0& 1\\ 1& 2& 2& 1& 0\end{array}\right].$$

The distance from $v_6$ to $v_i$ and $v_j(1\le i<j\le 5)$ is denoted by $(v_i,v_j|d(v_i,v_6),d(v_j,v_6))$. For dim$\left(G\right)=n\left(G\right)-3=3$, by Corollary 3, any one of $(v_1,v_3|2,2)$, $(v_1,v_5|1,1)$, $(v_2,v_3|2,1)$, $(v_2,v_4|2,2)$, $(v_3,v_4|1,2)$ and $(v_3,v_5|2,2)$ does not hold. Hence there is at least one of $v_1$ and $v_3$ adjacent to $v_6$. If $e_{16}\in E\left(G\right)$, then $e_{56}\notin E\left(G\right)$, $e_{36}\in E\left(G\right)$ and $e_{26},e_{46}\in E\left(G\right)$, which implies that $v_2$ and $v_6$ are twins. If $e_{36}\in E\left(G\right)$, then $e_{16}\notin E\left(G\right)$, $e_{26},e_{46}\in E\left(G\right)$. If $e_{56}\in E\left(G\right)$ then $v_4$ and $v_6$ are twins; and if $e_{56}\notin E\left(G\right)$, then $v_3$ and $v_6$ are twins. Therefore, there is no graph G with dim$\left(G\right)=n\left(G\right)-3$.

Case 2.1.2. $e_{15}\notin E\left(G\right)$, $e_{25}\in E\left(G\right)$. Since $v_3$ and $v_5$ are not twins, $d(v_3,v_6)\ne d(v_5,v_6)$. We may assume that $e_{36}\notin E\left(G\right)$, $e_{56}\in E\left(G\right)$. Since $\delta \left(G\right)\ge 2$, deg$\left(v_1\right)\ge 2$, and we get that $e_{16}\in E\left(G\right)$. Then $\{v_1,v_3\}$ is a resolving set of G. Thus dim$\left(G\right)=4$, which is a contradiction.

Case 2.1.3. $e_{15},e_{25}\in E\left(G\right)$. The metric matrix of $G-v_6$ is

$$D=\left[\begin{array}{ccccc}0& 1& 2& 2& 1\\ 1& 0& 1& 1& 1\\ 2& 1& 0& 1& 2\\ 2& 1& 1& 0& 1\\ 1& 1& 2& 1& 0\end{array}\right].$$

By Corollary 3, we obtain that any one of $(v_1,v_3|2,2)$, $(v_1,v_5|1,2)$, $(v_3,v_4|1,2)$ and $(v_4,v_5|2,2)$ does not holds. Hence there is at least one of $v_1$ and $v_3$ adjacent to $v_6$. Assume that $e_{16}\in E\left(G\right)$, which implies that $e_{56}\in E\left(G\right)$. For $e_{36}$, if $e_{36}\in E\left(G\right)$, then $e_{46}\in E\left(G\right)$, which implies that $v_2$ and $v_6$ are twins, therefore $e_{36}\notin E\left(G\right)$. For $e_{26}$ and $e_{46}$, if $e_{26}\in E\left(G\right)$, $e_{46}\notin E\left(G\right)$, then $v_1$ and $v_6$ are twins; if $e_{26},e_{46}\in E\left(G\right)$, then $v_5$ and $v_6$ are twins; if $e_{26}\notin E\left(G\right)$, $e_{46}\in E\left(G\right)$, then $\{v_1,v_6\}$ is a resolving set of G, and if $e_{26},e_{46}\notin E\left(G\right)$, then $d(v_3,v_6)=3$. Thus, there is no graph G with dim$\left(G\right)=n\left(G\right)-3$.

Case 2.1.4. $e_{15},e_{25}\notin E\left(G\right)$. Since $d(v_1,v_5)\le 2$, $e_{16},e_{56}\in E\left(G\right)$. Then $\{v_1,v_5\}$ is a resolving set of G, which contradicts dim$\left(G\right)=3$.

Case 2.2. $e_{24}\notin E\left(G\right)$. Since $d(v_1,v_4)\le 2$, we may assume that $e_{15},e_{45}\in E\left(G\right)$. There are three subcases to be considered as follows.

Case 2.2.1. $e_{25}\in E\left(G\right)$, $e_{35}\notin E\left(G\right)$ or $e_{25}\notin E\left(G\right)$, $e_{35}\in E\left(G\right)$. Then the graph $G-v_6$ is isomorphic to that of case 2.1.1.

Case 2.2.2. $e_{25},e_{35}\in E\left(G\right)$. Then the graph $G-v_6$ is isomorphic to that of case 2.1.3.

Case 2.2.3. $e_{25},e_{35}\notin E\left(G\right)$. Since there are no twins in G and $\delta \left(G\right)\ge 2$, $v_6$ must be adjacent to two adjacent vertices. Assume that $e_{16},e_{26}\in E\left(G\right)$, then $\{v_1,v_2\}$ is a resolving set of G, which contradicts dim$\left(G\right)=3$.

Thus, there is no graph G with dim$\left(G\right)=n\left(G\right)-3$ and we are done. □

Lemma 14.

Let G be a graph with $d\left(G\right)=2$ and dim$\left(G\right)=n\left(G\right)-3$, then $n\left(G_{\mathrm{T}}\right)\le 5$.

Proof. 

Suppose instead that G is a graph with $d\left(G\right)=2$, dim$\left(G\right)=n\left(G\right)-3$ and $n\left(G_{\mathrm{T}}\right)\ge 6$. Now we prove that dim$\left(G_{\mathrm{T}}\right)=n\left(G_{\mathrm{T}}\right)-3$. Since dim$\left(G\right)=n\left(G\right)-3$, dim$\left(G_{\mathrm{T}}\right)\ge n\left(G_{\mathrm{T}}\right)-3$ by Lemma 1. If dim$\left(G_{\mathrm{T}}\right)=n\left(G_{\mathrm{T}}\right)-1$, then by Lemma 7, we have $G_{\mathrm{T}}=K_{n\left(G_{\mathrm{T}}\right)}$. By Corollary 4, we get that dim$\left(G\right)=n\left(G\right)-n\left(G_{\mathrm{T}}\right)$, which is a contradiction. If dim$\left(G_{\mathrm{T}}\right)=n\left(G_{\mathrm{T}}\right)-2$, then $G_{\mathrm{T}}=K_{s,t}(s,t\ge 1)$ or $K_s+\overline{K_t}(s\ge 1,t\ge 2)$ or $K_s+(K_1\cup K_t)(s,t\ge 1)$ by Lemma 8. Since $n\left(G_{\mathrm{T}}\right)\ge 6$, $s+t\ge 5$, which contradicts dim$\left(G\right)=n\left(G\right)-3$ by Lemma 5. Thus, dim$\left(G_{\mathrm{T}}\right)=n\left(G_{\mathrm{T}}\right)-3$.

For $n\left(G_{\mathrm{T}}\right)\ge 6$, by Lemma 13, there exist twins in $G_{\mathrm{T}}$. Assume that $v_1$, $v_2$ are twins in $G_{\mathrm{T}}$ and $|V_1|\ge 2$, then $v_1^{\prime }$ resolves $v_1$ and $v_2$ by Lemma 2. Moreover, by Lemma 5, the size of every twin set of $G_{\mathrm{T}}$ is no more than 2. Thus, for each $v\in V\left(G_{\mathrm{T}}\right)$ and $v\notin \{v_1,v_2\}$, $v_1$, $v_2$ and v are not twins. Let $W\left(G_{\mathrm{T}}\right)$ be a metric basis of $G_{\mathrm{T}}$ and $V\left(G_{\mathrm{T}}\right)\backslash W\left(G_{\mathrm{T}}\right)=\{u_1,u_2,u_3\}$. By Lemma 8, there exists $W_0=\{w_1,w_2\}\subset W\left(G_{\mathrm{T}}\right)$ such that $W_0$ resolves $\{u_1,u_2,u_3\}$. Since $v_1$ and $v_2$ are twins in $G_{\mathrm{T}}$, there is at most one of $v_1$ and $v_2$ in $\{u_1,u_2,u_3\}$. Similarly, there is at most one of $v_1$ and $v_2$ in $W_0$.

Then we prove that one of $v_1$ and $v_2$ is in $\{u_1,u_2,u_3\}$ and the other is in $W_0$. Assume that $v_1,v_2\notin \{u_1,u_2,u_3\}$, then $v_1,v_2\in W\left(G_{\mathrm{T}}\right)$. If $v_1,v_2\notin W_0$, then $r\left(v_1\right|W_0)=r\left(v_2\right|W_0)\in \{r\left(u_1\right|W_0),$$r\left(u_2\right|W_0),r\left(u_3\right|W_0)\}$. We may assume that $r\left(v_1\right|W_0)=r\left(v_2\right|W_0)=r\left(u_1\right|W_0)$, then $\{w_1,w_2,v_1^{\prime }\}$ resolves $\{u_2,u_3,v_1,v_2\}$, which is a contradiction. Otherwise, we may assume that $v_1=w_1$, then $\{v_1^{\prime },w_2\}$ resolves $\{u_1,u_2,u_3\}$ and $\{v_1,v_2\}$. Without loss of generality suppose that $r\left(v_i\right|\{v_1^{\prime },w_2\})=r\left(u_i\right|\{v_1^{\prime },w_2\})$ for $i\in \{1,2\}$. Since the pairs $u_1$, $v_1$ and $u_2$, $v_2$ are not twins in $G_{\mathrm{T}}$, then $\{v_1^{\prime },w_2,u_3\}$ resolves $\{u_1,u_2,v_1,v_2\}$, the argument is similar to that of the case 1.1 of Lemma 13, which is a contradiction. Thus, there is one of $v_1$ and $v_2$ in $\{u_1,u_2,u_3\}$. We may assume that $v_1\in \{u_1,u_2,u_3\}$, then $v_2\in W_0$; otherwise, $\{v_1^{\prime },w_1,w_2\}$ resolves $\{u_1,u_2,u_3,v_2\}$, which is a contradiction.

Thus, we have that at most two pairs of vertices are twins in $G_{\mathrm{T}}$ and dim$(G_{\mathrm{T}}-v_1)=n(G_{\mathrm{T}}-v_1)-2$. Moreover, for $x_1,x_2\notin \{v_1,v_2\}$, if $x_1$ and $x_2$ are twins in $G_{\mathrm{T}}-v_1$, it easy to see that they are twins in $G_{\mathrm{T}}$. Thus, there is at most one pair of vertices that are twins in $G_{\mathrm{T}}-v_1$. By Lemma 8, $G_{\mathrm{T}}-v_1=K_{s,t}(s,t\ge 1)$ or $K_s+\overline{K_t}(s\ge 1,t\ge 2)$ or $K_s+(K_1\cup K_t)(s,t\ge 1)$. Since $n\left(G_{\mathrm{T}}\right)\ge 6$, $n(G_{\mathrm{T}}-v_1)\ge 5$. Thus, $s+t\ge 4$, there are at most two pairs of vertices are twins in $G_{\mathrm{T}}-v_1$, which is a contradiction. Therefore, the assumption $n\left(G_{\mathrm{T}}\right)\ge 6$ does not hold and we are done. □

Theorem 1.

For a graph G, dim$\left(G\right)=n\left(G\right)-3$ and $d\left(G\right)=2$ if and only if G is $(K_s\cup B_r)+K_t(s,r\ge 2,t\ge 1)$, $(K_s\cup B_r)+\overline{K_t}(s,t\ge 2,r\ge 1)$, $G=(\overline{K_s}+\overline{K_t})+B_r(s,t\ge 2,r\ge 1)$, $C_5$ or one of the graphs in Figure 2 and Figure 3.

Proof. 

It holds by Lemmas 10, 11, 12 and 14. □

Remark 1.

This method can help us to address the extension problem of a given graph with respect to metric dimension. It is theoretically realized the characterization of extremal graphs with dim$\left(G\right)=n\left(G\right)-r$ for any $r>0$. In addition, we also find that the problem will become more and more difficult with the increase of r based on the proof of the case $r=3$.

4. Conclusions

In this paper, by constructing the metric matrix of G, we make a necessary and sufficient condition of dim$\left(G\right)=n\left(G\right)-r$ and characterize the graphs of dim$\left(G\right)$ = $n\left(G\right)-3$ via this condition. Moreover, we give a new idea for the extension of graphs based on metric dimension.