On Subtrees of Fan Graphs, Wheel Graphs, and “Partitions” of Wheel Graphs under Dynamic Evolution
Abstract
1. Introduction
- denotes the graph obtained from G by removing all elements of X;
- (resp. ) denotes the set of subtrees of G (resp. containing v);
- denotes the set of subtrees of G containing the edge ;
- denotes the weight of subtree ;
- is the sum of weights of subtrees in ;
- is the cardinality (namely the number) of the corresponding set of subtrees.
2. Subtree Generating Functions of and Wheel Graph
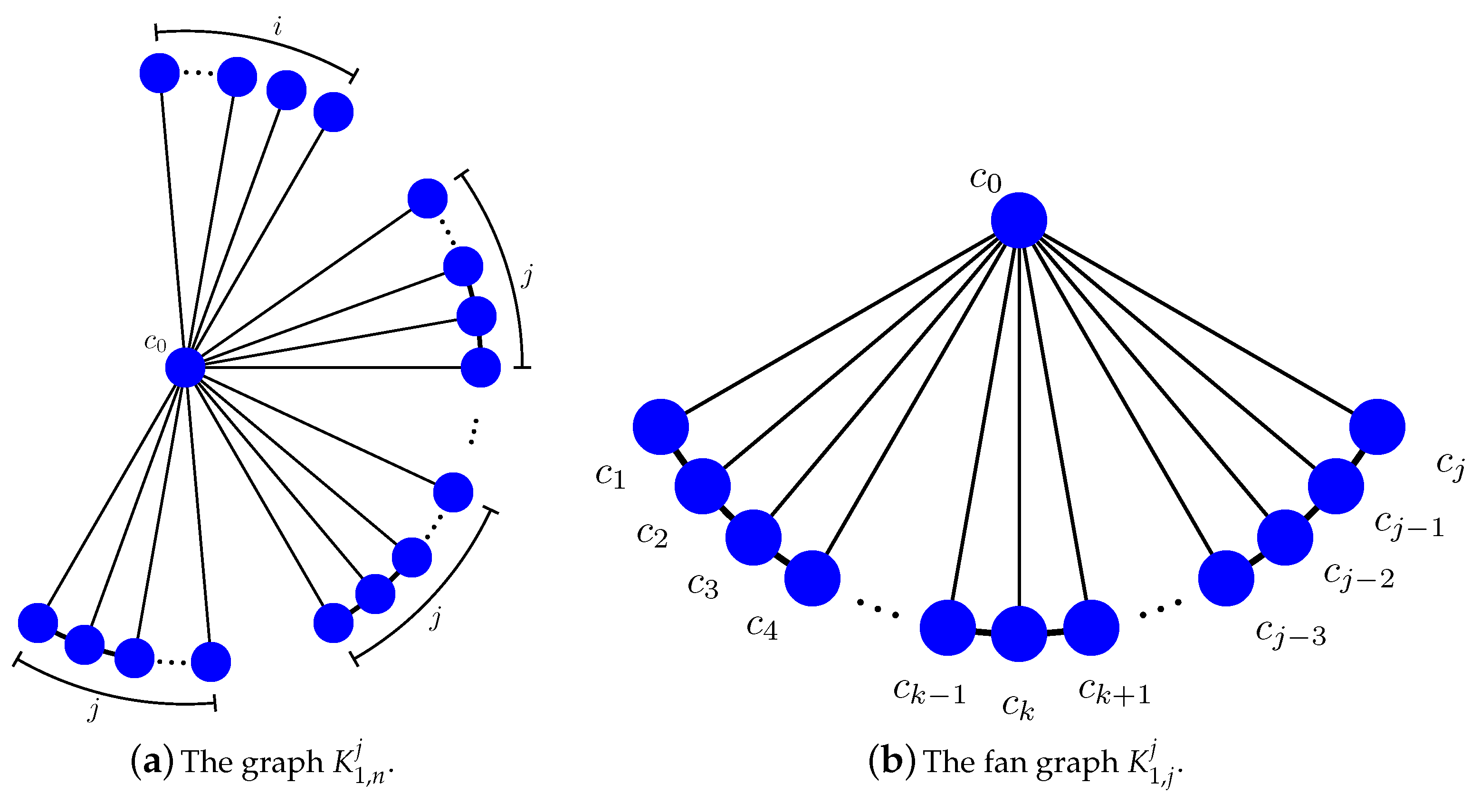
2.1. Subtree Generating Functions and Subtree Numbers of
- (i)
- not containing the center ,
- (ii)
- containing the center .
- is the collection of subtrees that contain neither nor ;
- is the collection of subtrees that contain , but not ;
- is the collection of subtrees that contain , but not ;
- is the collection of subtrees that contain both and .
2.2. Subtree Generating Function and Subtree Number of Wheel Graph
- is the set of subtrees of that contain neither nor ;
- is the set of subtrees of that contain , but not ;
- is the set of subtrees of that contain but not ;
- is the set of subtrees of that contain both and .
- is the set of subtrees in that contain neither nor ;
- is the set of subtrees in that contain , but not ;
- is the set of subtrees in that contain but not ;
- is the set of subtrees in that contain both and .
3. Behaviors of and in Terms of Subtrees
3.1. Subtree Numbers and
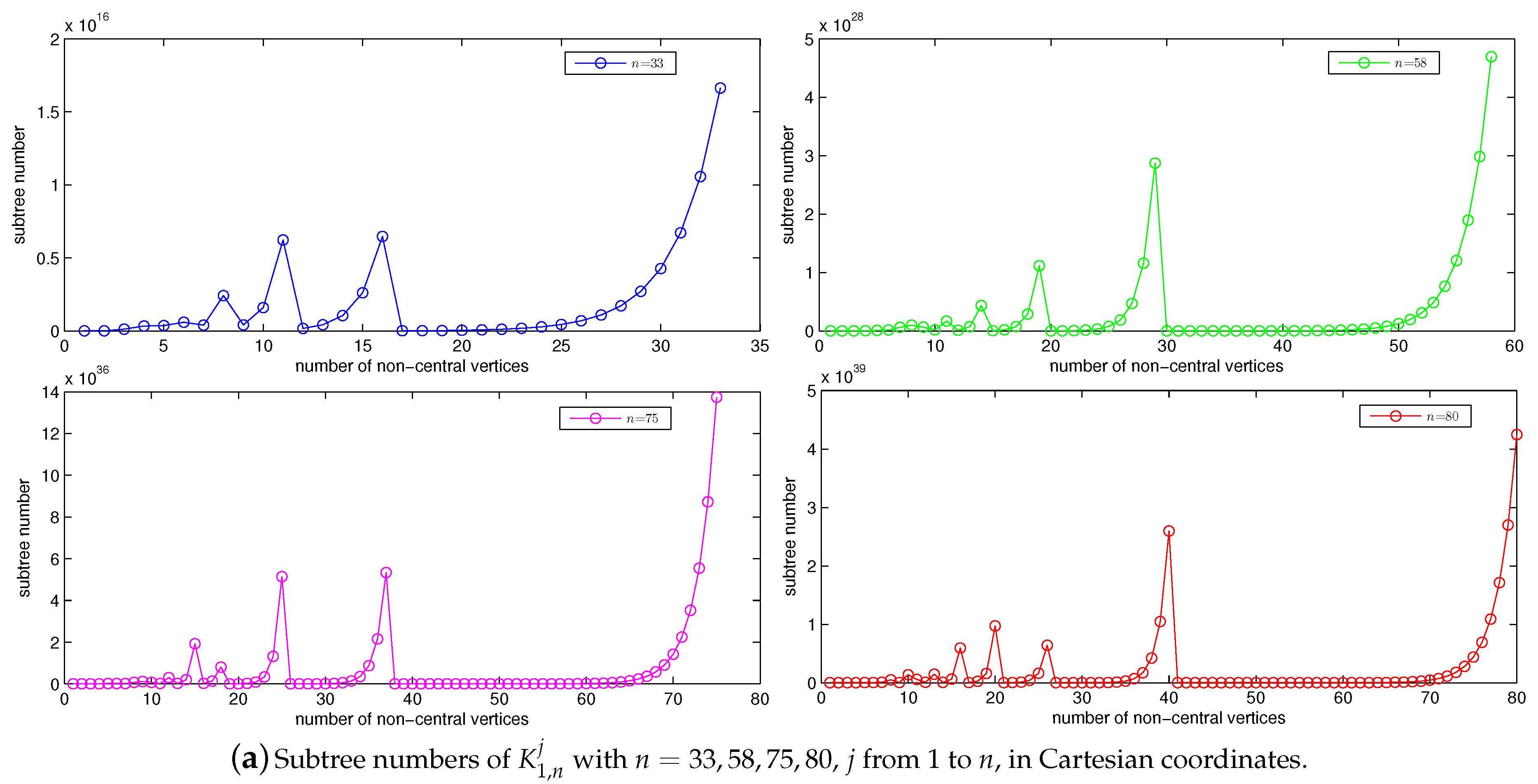
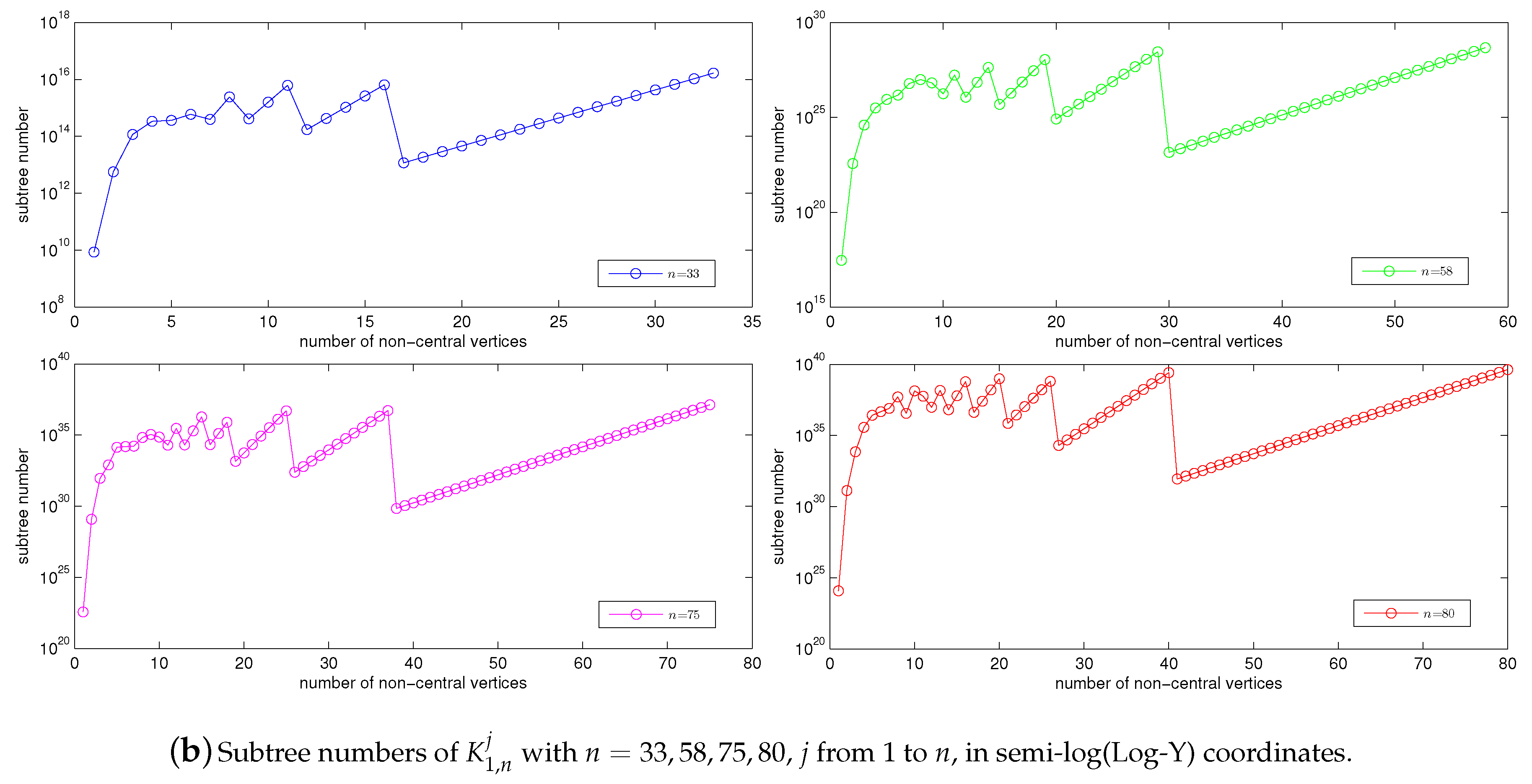
- the graph has subtrees, fewer than any other ; and
- the graph has subtrees (where and ), more than any other .
- has the second-largest subtree number; and
- has the third-largest subtree number for odd (or sufficiently large) n.
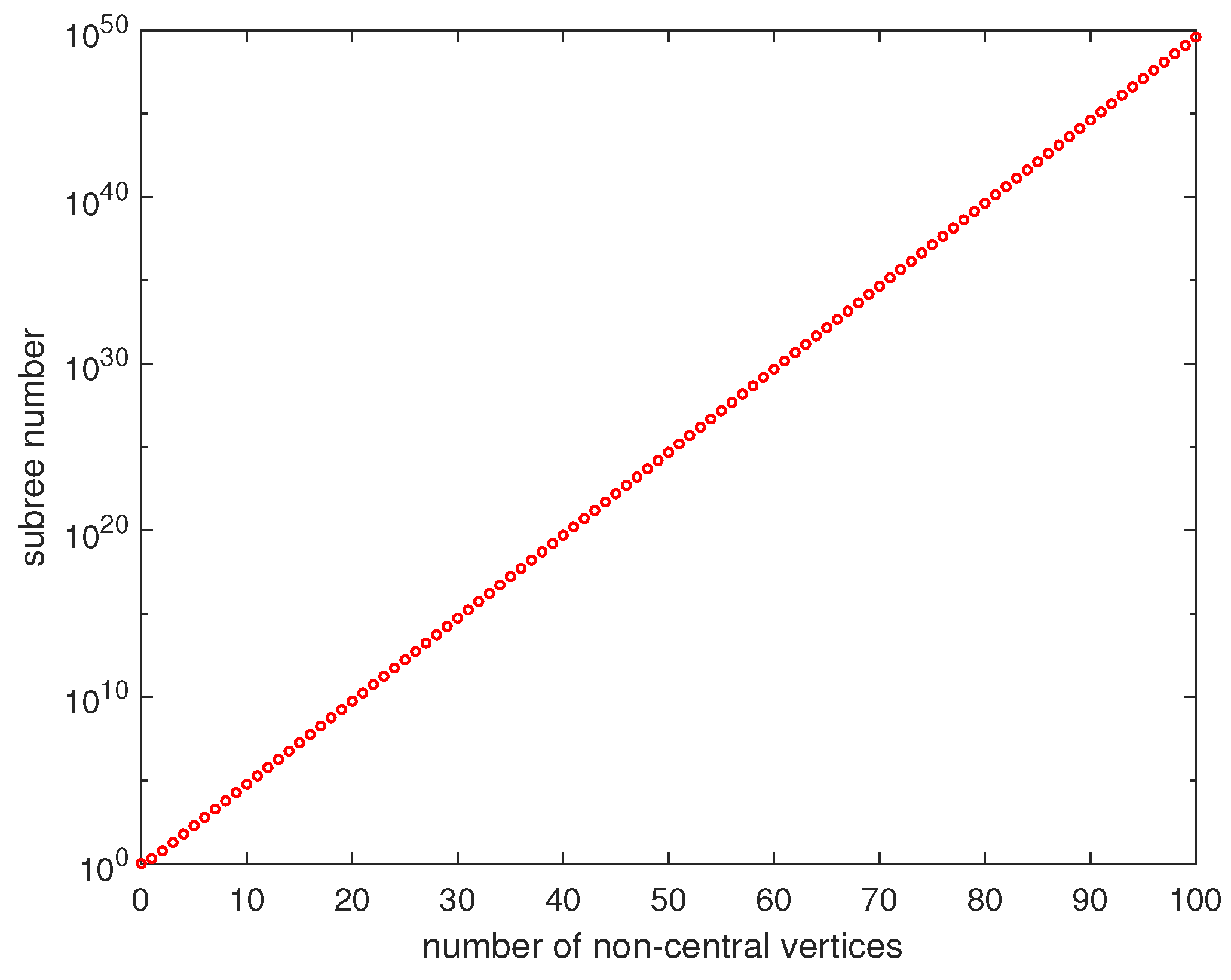
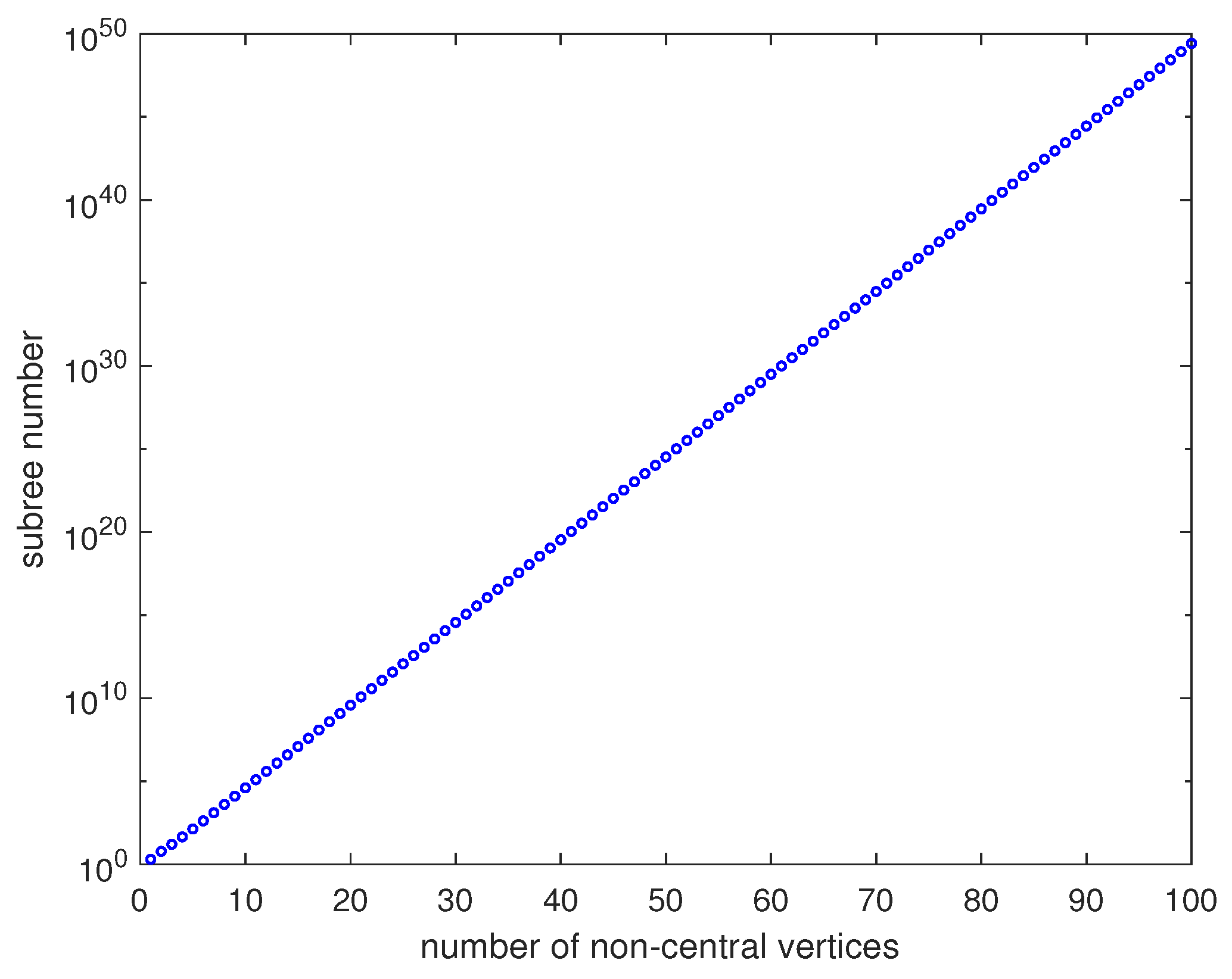
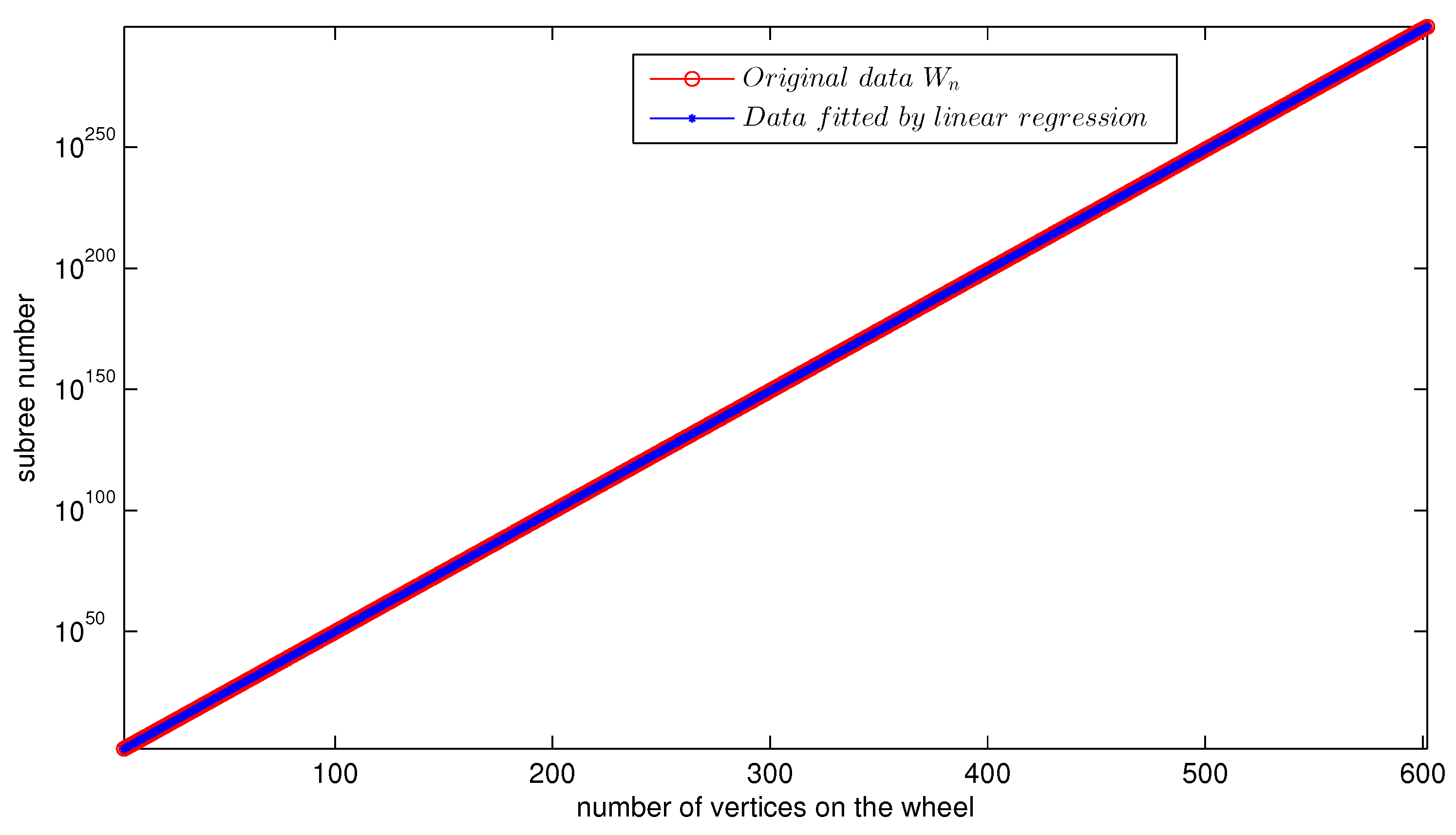
- the subtree number increment trend meets exponential growth when .
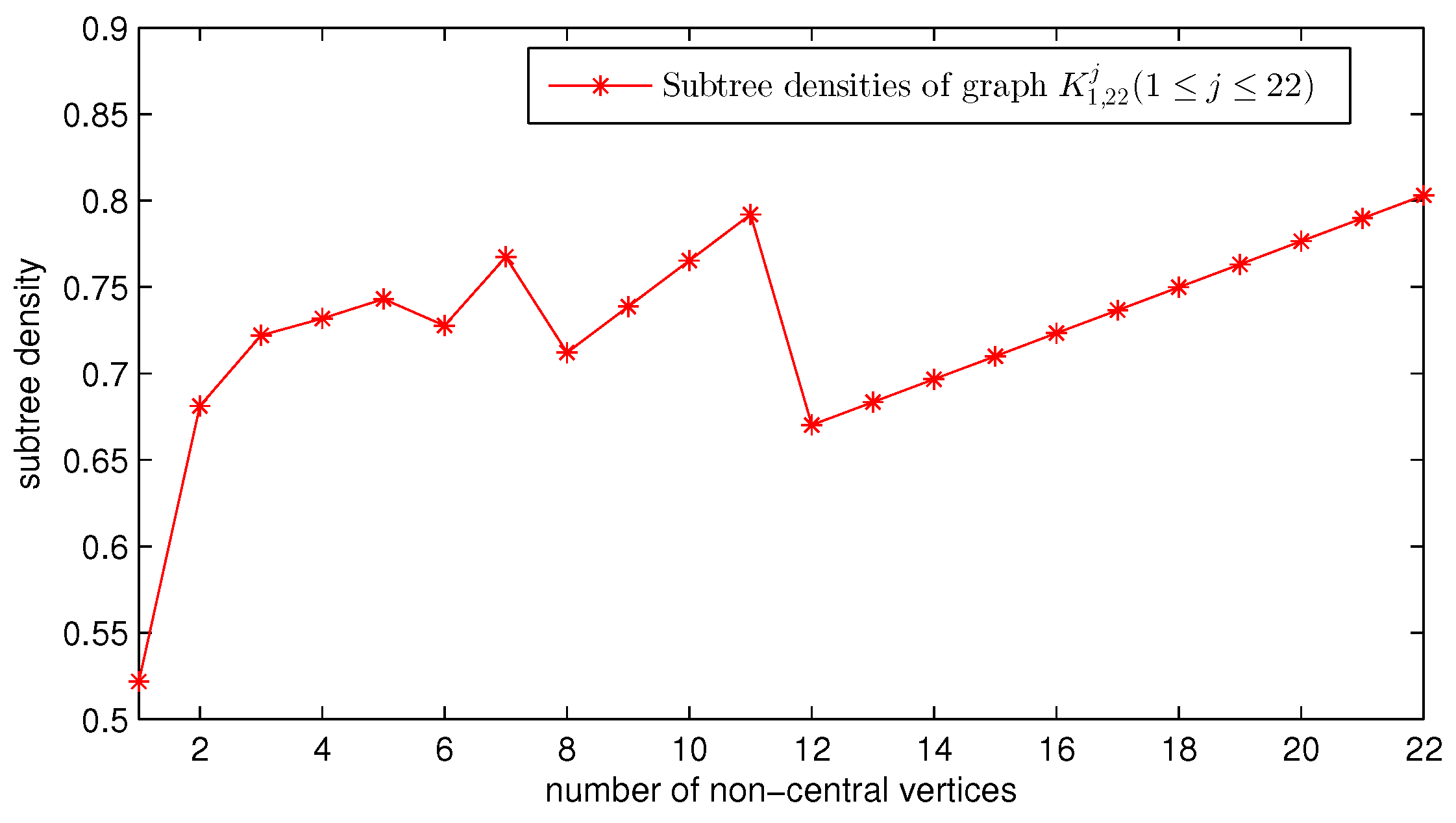
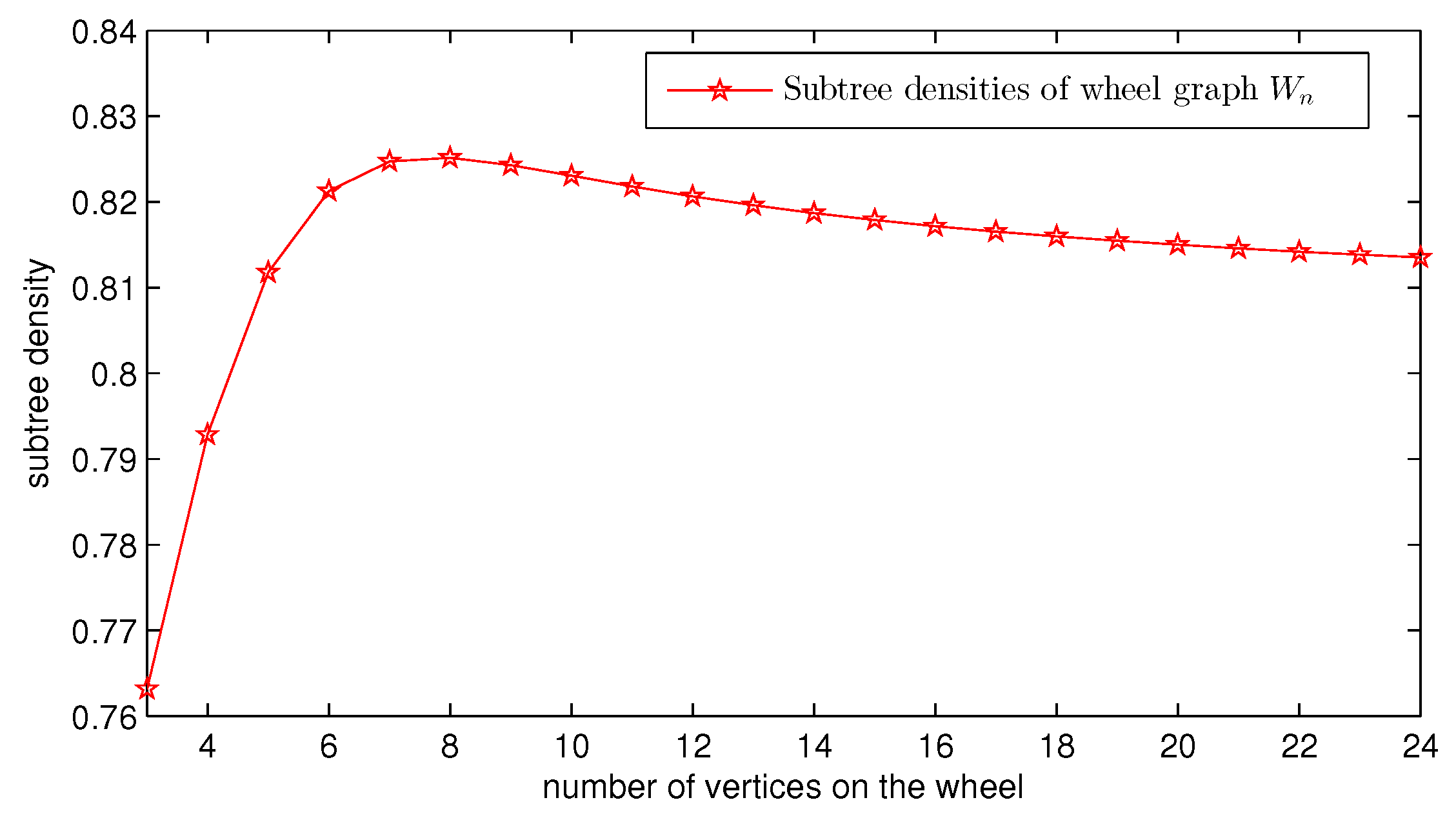
3.2. Subtree Densities of and
4. Concluding Remarks
Author Contributions
Funding
Conflicts of Interest
Appendix A. Matlab Code, Python Code, And Data
| Pythoncode1. The Python code for computing the subtree number of . | |
| 1 | n=int (input()) |
| 2 | b=[−1 for i in range (n+1)] |
| 3 | b[0]=1 |
| 4 | b[1]=2 |
| 5 | for j in range (1,n+1): |
| 6 | sum1=0 |
| 7 | for r in range (1,j+1): |
| 8 | sum1=sum1+r∗b[j−r] |
| 9 | b[j]=b[j−1]+sum1 |
| 10 | file_name="n="+str(n)+".txt" |
| 11 | file = open (file_name,’w’) |
| 12 | for j in range (1,n+1): |
| 13 | i = n%j |
| 14 | s=(j+1)∗(n−i)/2+i+2∗∗(i)∗b[j]∗∗((n−i)/j) |
| 15 | file.write (str(s)) |
| 16 | file.write (’\n’) |
| 17 | print (s) |
| MCF1a. MATLAB source code for Figure 1a. | |
| 1 | clear; |
| 2 | clc; |
| 3 | s1 = load(’n=33.txt’); |
| 4 | s2 = load(’n=58.txt’); |
| 5 | s3 = load(’n=75.txt’); |
| 6 | s4 = load(’n=80.txt’); |
| 7 | format long; |
| 8 | A =cell(1,10); |
| 9 | A{1,1}=’−bo’; |
| 10 | A{1,2}=’−go’; |
| 11 | A{1,3}=’−mo’; |
| 12 | A{1,4}=’−ro’; |
| 13 | subplot(2,2,1); |
| 14 | plot(s1,A{1,1}); |
| 15 | axis normal; |
| 16 | set(legend(’n=33’),’fontsize’,8); |
| 17 | xlabel(’number of non-central vertices’); |
| 18 | ylabel(’subtree number’); |
| 19 | subplot(2,2,2); |
| 20 | plot(s2,A{1,2}); |
| 21 | set(legend(’n=58’),’fontsize’,8); |
| 22 | xlabel(’number of non-central vertices’); |
| 23 | ylabel(’subtree number’); |
| 24 | subplot(2,2,3); |
| 25 | plot(s3,A{1,3}); |
| 26 | axis normal; |
| 27 | set(legend(’n=75’),’fontsize’,8); |
| 28 | xlabel(’number of non-central vertices’); |
| 29 | ylabel(’subtree number’); |
| 30 | subplot(2,2,4); |
| 31 | plot(s4,A{1,4}); |
| 32 | set(legend(’n=80’),’fontsize’,8); |
| 33 | xlabel(’number of non-central vertices’); |
| 34 | ylabel(’subtree number’); |
| MCF1b: The MATLAB source code for Figure 1b. | |
| 1 | clear; |
| 2 | clc; |
| 3 | s1 = load(’n=33.txt’); |
| 4 | s2 = load(’n=58.txt’); |
| 5 | s3 = load(’n=75.txt’); |
| 6 | s4 = load(’n=80.txt’); |
| 7 | format long; |
| 8 | A =cell(1,10); |
| 9 | A{1,1}=’−bo’; |
| 10 | A{1,2}=’−go’; |
| 11 | A{1,3}=’−mo’; |
| 12 | A{1,4}=’−ro’; |
| 13 | subplot(2,2,1); |
| 14 | semilogy(s1,A{1,1}); |
| 15 | axis normal; |
| 16 | set(legend(’n=33’,’location’,’southeast’),’fontsize’,8); |
| 17 | xlabel(’number of non-central vertices’); |
| 18 | ylabel(’subtree number’); |
| 19 | subplot(2,2,2); |
| 20 | semilogy(s2,A{1,2}); |
| 21 | set(legend(’n=58’,’location’,’southeast’),’fontsize’,8); |
| 22 | xlabel(’number of non-central vertices’); |
| 23 | ylabel(’subtree number’); |
| 24 | subplot(2,2,3); |
| 25 | semilogy(s3,A{1,3}); |
| 26 | axis normal; |
| 27 | set(legend(’n=75’,’location’,’southeast’),’fontsize’,8); |
| 28 | xlabel(’number of non-central vertices’); |
| 29 | ylabel(’subtree number’); |
| 30 | subplot(2,2,4); |
| 31 | semilogy(s4,A{1,4}); |
| 32 | set(legend(’n=80’,’location’,’southeast’),’fontsize’,8); |
| 33 | xlabel(’number of non-central vertices’); |
| 34 | ylabel(’subtree number’); |
References
- Das, K.C. Atom-bond connectivity index of graphs. Discret. Appl. Math. 2010, 158, 1181–1188. [Google Scholar] [CrossRef]
- Dobrynin, A.A.; Entringer, R.; Gutman, I. Wiener index of trees: Theory and applications. Acta Appl. Math. 2001, 66, 211–249. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of paraffin boiling points. J. Am. Chem. Soc. 1947, 1, 17–20. [Google Scholar] [CrossRef]
- Yan, W.; Yeh, Y. Enumeration of subtrees of trees. Theor. Comput. Sci. 2006, 369, 256–268. [Google Scholar] [CrossRef]
- Ingalalli, V.; Ienco, D.; Poncelet, P. Mining frequent subgraphs in multigraphs. Inf. Sci. 2018, 451, 50–66. [Google Scholar] [CrossRef]
- Tilk, C.; Irnich, S. Combined column-and-row-generation for the optimal communication spanning tree problem. Comput. Oper. Res. 2018, 93, 113–122. [Google Scholar] [CrossRef]
- Zetina, C.A.; Contreras, I.; Fernández, E.; Luna-Mota, C. Solving the optimum communication spanning tree problem. Eur. J. Oper. Res. 2019, 273, 108–117. [Google Scholar] [CrossRef]
- Chechik, S.; Emek, Y.; Patt-Shamir, B.; Peleg, D. Sparse reliable graph backbones. Inf. Comput. 2012, 210, 31–39. [Google Scholar] [CrossRef][Green Version]
- Xiao, Y.; Zhao, H.; Liu, Z.; Mao, Y. Trees with large numbers of subtrees. Int. J. Comput. Math. 2017, 94, 372–385. [Google Scholar] [CrossRef]
- Knudsen, B. Optimal multiple parsimony alignment with affine gap cost using a phylogenetic tree. Algorithms Bioinform. Lect. Notes Comput. Sci. 2003, 2812, 433–446. [Google Scholar]
- Wagner, S.G. Correlation of graph-theoretical indices. SIAM J. Discret. Math. 2007, 21, 33–46. [Google Scholar] [CrossRef]
- Székely, L.; Wang, H. On subtrees of trees. Adv. Appl. Math. 2005, 34, 138–155. [Google Scholar]
- Székely, L.; Wang, H. Binary trees with the largest number of subtrees. Discret. Appl. Math. 2007, 155, 374–385. [Google Scholar]
- Zhang, X.; Zhang, X.; Gray, D.; Wang, H. The number of subtrees of trees with given degree sequence. J. Graph Theory 2013, 73, 280–295. [Google Scholar] [CrossRef]
- Wang, H. The extremal values of the Wiener index of a tree with given degree sequence. Discret. Appl. Math. 2008, 156, 2647–2654. [Google Scholar] [CrossRef]
- Deng, H. Wiener indices of spiro and polyphenyl hexagonal chains. Math. Comput. Model. 2012, 55, 634–644. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.; Wang, H.; Fu, H. Subtrees of spiro and polyphenyl hexagonal chains. Appl. Math. Comput. 2015, 268, 547–560. [Google Scholar] [CrossRef]
- Czabarka, É.; Székely, L.A.; Wagner, S. On the number of nonisomorphic subtrees of a tree. J. Graph Theory 2018, 87, 89–95. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, X. The Minimal Number of Subtrees with a Given Degree Sequence. Graphs Comb. 2015, 31, 309–318. [Google Scholar] [CrossRef]
- Jamison, R.E. On the average number of nodes in a subtree of a tree. J. Comb. Theory Ser. B 1983, 35, 207–223. [Google Scholar] [CrossRef]
- Vince, A.; Wang, H. The average order of a subtree of a tree. J. Comb. Theory Ser. B 2010, 100, 161–170. [Google Scholar] [CrossRef]
- Wagner, S.; Wang, H. On the Local and Global Means of Subtree Orders. J. Graph Theory 2016, 81, 154–166. [Google Scholar] [CrossRef]
- Nakayama, T.; Fujiwara, Y. BCT Representation of Chemical Structures. J. Chem. Inf. Comput. Sci. 1980, 20, 23–28. [Google Scholar] [CrossRef]
- Nakayama, T.; Fujiwara, Y. Computer representation of generic chemical structures by an extended block-cutpoint tree. J. Chem. Inf. Comput. Sci. 1983, 23, 80–87. [Google Scholar] [CrossRef]
- Frederickson, G.N.; Hambrusch, S.E. Planar linear arrangements of outerplanar graphs. IEEE Trans. Circuits Syst. 1988, 35, 323–333. [Google Scholar] [CrossRef]
- Wada, K.; Luo, Y.; Kawaguchi, K. Optimal fault-tolerant routings for connected graphs. Inf. Process. Lett. 1992, 41, 169–174. [Google Scholar] [CrossRef]
- Heath, L.; Pemmaraju, S. Stack and queue layouts of directed acyclic graphs: Part II. SIAM J. Comput. 1999, 28, 1588–1626. [Google Scholar] [CrossRef]
- Misiolek, E.; Chen, D.Z. Two flow network simplification algorithms. Inf. Process. Lett. 2006, 97, 197–202. [Google Scholar] [CrossRef]
- Fox, D. Block cutpoint decomposition for markovian queueing systems. Appl. Stoch. Model. Data Anal. 1988, 4, 101–114. [Google Scholar] [CrossRef]
- Barefoot, C. Block-cutvertex trees and block-cutvertex partitions. Discret. Math. 2002, 256, 35–54. [Google Scholar] [CrossRef][Green Version]
- Mkrtchyan, V. On trees with a maximum proper partial 0-1 coloring containing a maximum matching. Discret. Math. 2006, 306, 456–459. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.; Wang, H.; Feng, S. On algorithms for enumerating BC-subtrees of unicyclic and edge-disjoint bicyclic graphs. Discret. Appl. Math. 2016, 203, 184–203. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.; Wang, H.; Makeig, S. Enumeration of BC-subtrees of trees. Theor. Comput. Sci. 2015, 580, 59–74. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, H.; Wang, H.; Deng, A.; Magnant, C. On Algorithms for Enumerating Subtrees of Hexagonal and Phenylene Chains. Comput. J. 2017, 60, 690–710. [Google Scholar] [CrossRef]
- Chin, A.J.; Gordon, G.; MacPhee, K.J.; Vincent, C. Subtrees of graphs. J. Graph Theory 2018, 89, 413–438. [Google Scholar] [CrossRef]
- Cahit, I. Spiral chains: A new proof of the four color theorem. arXiv 2004, arXiv:0408247. [Google Scholar]
- Yang, Z.; Liu, Y.; Li, X.Y. Beyond trilateration: On the localizability of wireless ad hoc networks. IEEE/ACM Trans. Netw. (ToN) 2010, 18, 1806–1814. [Google Scholar] [CrossRef]
- Allen, B.; Lippner, G.; Chen, Y.T.; Fotouhi, B.; Momeni, N.; Yau, S.T.; Nowak, M.A. Evolutionary dynamics on any population structure. Nature 2017, 544, 227. [Google Scholar] [CrossRef]
- Haslegrave, J. Extremal results on average subtree density of series-reduced trees. J. Comb. Theory Ser. B 2014, 107, 26–41. [Google Scholar] [CrossRef]
| n | n | n | |||
|---|---|---|---|---|---|
| 3 | 38 | 19 | 2,899,980,984 | 35 | 269,604,917,347,967,886 |
| 4 | 112 | 20 | 9,128,846,611 | 36 | 848,689,059,340,934,448 |
| 5 | 332 | 21 | 28,736,686,630 | 37 | 2,671,587,471,512,527,895 |
| 6 | 1007 | 22 | 90,460,187,232 | 38 | 8,409,887,625,375,274,755 |
| 7 | 3110 | 23 | 284,759,535,167 | 39 | 26,473,477,146,304,448,341 |
| 8 | 9704 | 24 | 896,394,265,075 | 40 | 83,335,833,180,604,495,475 |
| 9 | 30,431 | 25 | 2,821,758,641,457 | 41 | 262,332,788,908,879,910,034 |
| 10 | 95,643 | 26 | 8,882,611,305,147 | 42 | 825,797,133,240,010,600,373 |
| 11 | 300,885 | 27 | 27,961,563,560,618 | 43 | 2,599,525,999,414,007,165,103 |
| 12 | 946,923 | 28 | 88,020,178,967,761 | 44 | 8,183,045,386,844,876,767,480 |
| 13 | 2,980,538 | 29 | 277,078,636,493,555 | 45 | 25,759,400,682,377,496,173,050 |
| 14 | 9,382,101 | 30 | 872,215,572,630,716 | 46 | 81,087,992,568,389,361,552,840 |
| 15 | 29,533,519 | 31 | 2,745,646,560,009,062 | 47 | 255,256,813,613,269,834,457,576 |
| 16 | 92,968,088 | 32 | 8,643,018,158,636,696 | 48 | 803,522,677,430,288,749,342,627 |
| 17 | 292,653,642 | 33 | 27,207,348,527,149,292 | 49 | 2,529,408,261,449,734,855,548,318 |
| 18 | 921,243,536 | 34 | 85,645,986,192,695,055 | 50 | 7,962,321,827,121,343,008,620,568 |
| 1 | 50,331,670 | 4,194,326 | 0.521736621869847 |
| 2 | 5,683,820,588 | 362,797,089 | 0.681159363604678 |
| 3 | 29,685,950,982 | 1,787,743,521 | 0.721967947748206 |
| 4 | 52,358,400,102 | 3,110,400,052 | 0.731884047161090 |
| 5 | 87,226,395,622 | 5,103,959,426 | 0.743041170007376 |
| 6 | 56,400,430,972 | 3,370,318,067 | 0.727584934777173 |
| 7 | 231,968,014,120 | 13,141,451,319 | 0.767462100378713 |
| 8 | 36,440,865,014 | 2,224,820,302 | 0.712140856484914 |
| 9 | 93,645,742,414 | 5,511,577,694 | 0.738727501280144 |
| 10 | 240,339,417,442 | 13,653,922,612 | 0.765314128820302 |
| 11 | 616,080,713,876 | 33,825,095188 | 0.791900742502907 |
| 12 | 9,137,267,062 | 592,843,864 | 0.670113169892776 |
| 13 | 14,666,890,448 | 933,106,276 | 0.683406494463958 |
| 14 | 23,533,982,520 | 1,468,662,129 | 0.696699813456106 |
| 15 | 37,748,062,639 | 2,311,599,999 | 0.709993128330647 |
| 16 | 60,525,953,078 | 3,638,341,646 | 0.723286440182849 |
| 17 | 97,015,668,926 | 5,726,566,014 | 0.736579749833999 |
| 18 | 155,453,553,144 | 9,013,325,743 | 0.749873057893726 |
| 19 | 249,013,516,065 | 14,186,519,625 | 0.763166364810336 |
| 20 | 398,761,664,190 | 22,328,865,632 | 0.776459670910826 |
| 21 | 638,376,020,719 | 35,144,507,194 | 0.789752976431952 |
| 22 | 1,021,684,176,864 | 55,315,680,041 | 0.803046281543951 |
| 3 | 116 | 0.7631578947368421 | 14 | 115,215,423 | 0.8186895664414613 |
| 4 | 444 | 0.7928571428571428 | 15 | 386,480,089 | 0.8178844370865525 |
| 5 | 1617 | 0.8117469879518072 | 16 | 1,291,505,336 | 0.8171718247840813 |
| 6 | 5789 | 0.8212512413108243 | 17 | 4,301,328,493 | 0.8165375712479791 |
| 7 | 20,519 | 0.8247186495176849 | 18 | 14,282,430,812 | 0.8159697793983819 |
| 8 | 72,064 | 0.8251351103783091 | 19 | 47,296,291,958 | 0.815458656779937 |
| 9 | 250,841 | 0.8242943051493543 | 20 | 156,239,476,051 | 0.8149961728004785 |
| 10 | 865,923 | 0.8230636087039588 | 21 | 514,980,557,554 | 0.8145757185906111 |
| 11 | 2,967,219 | 0.8218031806171793 | 22 | 1,693,994,724,188 | 0.8141918205521789 |
| 12 | 10,102,071 | 0.8206394655271703 | 23 | 5,561,968,202,536 | 0.813839912225434 |
| 13 | 34,200,012 | 0.8196030381092273 | 24 | 18,230,780,418,139 | 0.8135161559345164 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Wang, A.; Wang, H.; Zhao, W.-T.; Sun, D.-Q. On Subtrees of Fan Graphs, Wheel Graphs, and “Partitions” of Wheel Graphs under Dynamic Evolution. Mathematics 2019, 7, 472. https://doi.org/10.3390/math7050472
Yang Y, Wang A, Wang H, Zhao W-T, Sun D-Q. On Subtrees of Fan Graphs, Wheel Graphs, and “Partitions” of Wheel Graphs under Dynamic Evolution. Mathematics. 2019; 7(5):472. https://doi.org/10.3390/math7050472
Chicago/Turabian StyleYang, Yu, An Wang, Hua Wang, Wei-Ting Zhao, and Dao-Qiang Sun. 2019. "On Subtrees of Fan Graphs, Wheel Graphs, and “Partitions” of Wheel Graphs under Dynamic Evolution" Mathematics 7, no. 5: 472. https://doi.org/10.3390/math7050472
APA StyleYang, Y., Wang, A., Wang, H., Zhao, W.-T., & Sun, D.-Q. (2019). On Subtrees of Fan Graphs, Wheel Graphs, and “Partitions” of Wheel Graphs under Dynamic Evolution. Mathematics, 7(5), 472. https://doi.org/10.3390/math7050472





