1. Introduction
Multiscale features widely exist in many engineering problems. For instance, in porous media flow, the media properties typically vary over many scales and contain high contrast. Multiscale finite element methods (MsFEM) [
1,
2,
3] and generalized multiscale finite element methods (GMsFEM) [
4,
5] are designed for solving multiscale problems using local model reduction techniques. In these methods, the computational domain is partitioned into a coarse grid
, which does not necessarily resolve all multiscale features. We further perform a refinement of
to obtain a fine grid
, which essentially resolves all multiscale features. The idea of local model reduction in these methods is based on idenfications of local multiscale basis functions supported in coarse regions on the fine grid, and replacement of the macroscopic equations by a coarse-scale system using a limited number of local multiscale basis functions. As in many model reduction techniques, the computations of multiscale basis functions, which constitute a small dimensional subspace, can be performed in an offline stage. For a fixed medium, these multiscale basis functions are reusable for any force terms and boundary conditions. Therefore, these methods provide substantial computational savings in the online stage, in which a coarse-scale system is constructed and solved on the reduced-order space.
However, difficulties arise in situations with uncertainties in the media properties in some local regions, which are common for oil reservoirs or aquifers. One straightforward approach for quantifying the uncertainties is to sample realizations of media properties. In such cases, it is challenging to find an offline principal component subspace which is able to universally solve the multiscale problems with different media properties. The computation of multiscale basis functions has to be performed in an online procedure for each medium. Even though the multiscale basis functions are reusable for different force terms and boundary conditions, the computational effort can grow very huge for a large number of realizations of media properties. To this end, building a functional relationship between the media properties and the multiscale model in an offline stage can avoid repeating expensive computations and thus vastly reduce the computational complexity. Due to the diversity of complexity of the media properties, the functional relationship is highly nonlinear. Modelling such a nonlinear functional relationship typically involves high-order approximations. Therefore, it is natural to use machine learning techniques to devise such complex models. In [
6,
7], the authors make use of a Bayesian approach for learning multiscale models and incorporating essential observation data in the presence of uncertainties.
Deep neural networks is one class of machine learning algorithm that is based on an artificial neural network, which is composed of a relatively large number of layers of nonlinear processing units, called neurons, for feature extraction. The neurons are connected to other neurons in the successive layers. The information propagates from the input, through the intermediate hidden layers, and to the output layer. In the propagation process, the output in each layer is used as input in the consecutive layer. Each layer transforms its input data into a little more abstract feature representation. In between layers, a nonlinear activation function is used as the nonlinear transformation on the input, which increases the expressive power of neural networks. Recently, deep neural network (DNN) has been successfully used to interpret complicated data sets and applied to tasks with pattern recognition, such as image recognition, speech recognition and natural language processing [
8,
9,
10]. Extensive researches have also been conducted on investigating the expression power of deep neural networks [
11,
12,
13,
14,
15].
Results show that neural networks can represent and approximate a large class of functions. Recently, deep learning has been applied to model reductions and partial differential equations. In [
16], the authors studied deep convolution networks for surrogate model construction. on dynamic flow problems in heterogeneous media. In [
17], the authors studied the relationship between residual networks (ResNet) and characteristic equations of linear transport, and proposed an interpretation of deep neural networks by continuous flow models. In [
18], the authors combined the idea of the Ritz method and deep learning techniques to solve elliptic problems and eigenvalue problems. In [
19], a neural network has been designed to learn the physical quantities of interest as a function of random input coefficients. The concept of using deep learning to generate a reduced-order model for a dynamic flow has been applied to proper orthogonal decomposition (POD) global model reduction [
20] and nonlocal multi-continuum upscaling (NLMC) [
21].
In this work, we propose a deep-learning-based method for fast computation of the GMsFEM discretization. Our approach makes use of deep neural networks as a fast proxy to compute GMsFEM discretizations for flow problems in channelized porous media with uncertainties. More specifically, neural networks are used to express the functional relationship between the media properties and the multiscale model. Such networks are built up in an offline stage. Sufficient sample pairs are required to ensure the expressive power of the networks. With different realizations of media properties, one can use the built network and avoid computations of local problems and spectral problems.
The paper is organized as follows. We start with the underlying partial differential equation that describes the flow within a heterogeneous media and the main ingredients of GMsFEM in
Section 2. Next, in
Section 3, we present the idea of using deep learning as a proxy for prediction of GMsFEM discretizations. The networks will be precisely defined and the sampling will be explained in detail. In
Section 4, we present numerical experiments to show the effectiveness of our presented networks on several examples with different configurations. Finally, a conclusive discussion is provided in
Section 5.
2. Preliminaries
In this paper, we are considering the flow problem in highly heterogeneous media
where
is the computational domain,
is the permeability coefficient in
, and
f is a source function in
. We assume the coefficient
is highly heterogeneous with high contrast. The classical finite element method for solving (
1) numerically is given by: find
such that
where
is a standard conforming finite element space over a partition
of
with mesh size
h.
However, with the highly heterogeneous property of coefficient
, the mesh size
h has to be taken extremely small to capture the underlying fine-scale features of
. This ends up with a large computational cost. GMsFEM [
4,
5] serves as a model reduction technique to reduce the number of degrees of freedom and attain both efficiency and accuracy to a considerable extent. GMsFEM has been successfully extended to other formulations and applied to other problems. Here we provide a brief introduction of the main ingredients of GMsFEM. For a more detailed discussion of GMsFEM and related concepts, the reader is referred to [
22,
23,
24,
25,
26].
In GMsFEM, we define a coarse mesh
over the domain
and refine to obtain a fine mesh
with mesh size
, which is fine enough to restore the multiscale properties of the problem. Multiscale basis functions are defined on coarse grid blocks using linear combinations of finite element basis functions on
, and designed to resolve the local multiscale behaviors of the exact solution. The multiscale finite element space
, which is a principal component subspace of the conforming finite space
with
, is constructed by the linear span of multiscale basis functions. The multiscale solution
is then defined by
We consider the identification of dominant modes for solving (
1) by multiscale basis functions, including spectral basis functions and simplified basis functions, in GMsFEM. Here, we present the details of the construction of multiscale basis functions in GMsFEM. Let
be the set of nodes of the coarse mesh
. For each coarse grid node
, the coarse neighborhood
is defined by
that is, the union of the coarse elements
containing the coarse grid node
. An example of the coarse and fine mesh, coarse blocks and a coarse neighborhood is shown in
Figure 1. For each coarse neighbourhood
, we construct multiscale basis functions
supported on
.
For the construction of spectral basis functions, we first construct a snapshot space
spanned by local snapshot basis functions
for each local coarse neighborhood
. The snapshot basis function
is the solution of a local problem
The fine grid function
is a function defined for all
, where
denote the fine degrees of freedom on the boundary of local coarse region
. Specifically,
The linear span of these harmonic extensions forms the local snapshot space
. One can also use randomized boundary conditions to reduce the computational cost associated with snapshot calculations [
25]. Next, a spectral problem is designed based on our analysis and used to reduce the dimension of local multiscale space. More precisely, we seek for eigenvalues
and corresponding eigenfunctions
satisfying
where the bilinear forms in the spectral problem are defined as
where
, and
denotes the multiscale partition of the unity function. We arrange the eigenvalues
of the spectral problem (
7) in ascending order, and select the first
eigenfunctions
corresponding to the small eigenvalues as the multiscale basis functions.
An alternative way to construct the multiscale basis function is by using the idea of simplified basis functions. This approach assumes the number of channels and position of the channelized permeability field are known. Therefore we can obtain multiscale basis functions
using these information and without solving the spectral problem [
27].
Once the multiscale basis functions are constructed, the span of the multiscale basis functions will form the offline space
We will then seek a multlscale solution
satisfying
which is a Galerkin projection of the (
1) onto
, and can be written as a system of linear equations
where
and
are the coarse-scale stiffness matrix and load vector. If we collect all the multiscale basis functions and arrange the fine-scale coordinate representation in columns, we obtain the downscaling operator
R. Then the fine-scale representation of the multiscale solution is given by
3. Deep Learning for GMsFEM
In applications, there are uncertainties within some local regions of the permeability field
in the flow problem. Thousands of forward simulations are needed to quantify the uncertainties of the flow solution. GMsFEM provides us with a fast solver to compute the solutions accurately and efficiently. Considering that there is a large amount of simulation data, we are interested in developing a method utilizing the existing offline data and reducing direct computational effort later. In this work, we aim at using DNN to model the relationship between heterogeneous permeability coefficient
and the key ingredients of GMsFEM solver, i.e., coarse scale stiffness matrices and multiscale basis functions. When the relation is built up, we can feed the network any realization of the permeability field and obtain the corresponding GMsFEM ingredients, and further restore fine-grid GMsFEM solution of (
1). The general idea of utilizing deep learning in the GMsFEM framework is illustrated in
Figure 2.
Suppose that there are uncertainties for the heterogeneous coefficient in a local coarse block
, which we call the target block, and the permeability outside the target block remains the same. For example, for a channelized permeability field, the position, location and the permeability values of the channels in the target block can vary. The target block
is inside three coarse neighborhoods, denoted by
. The union of the 3 neighborhoods, i.e.,
are constituted of by the target block
and 12 other coarse blocks, denoted by
A target block and its surrounding neighborhoods are depicted in
Figure 3.
For a fixed permeability field
, one can compute the multiscale basis functions
defined by (
7), for
, and the local coarse-scale stiffness matrices
, defined by
for
. We are interested in constructing the maps
and
, where
maps the permeability coefficient
to a local multiscale basis function
, where
i denotes the index of the coarse block, and
m denotes the index of the basis in coarse block
maps the permeability coefficient
to the coarse grid parameters
(
)
In this work, our goal is to make use of deep learning to build fast approximations of these quantities associated with the uncertainties in the permeability field
, which can provide fast and accurate solutions to the heterogeneous flow problem (
1).
For each realization
, one can compute the images of
under the local multiscale basis maps
and the local coarse-scale matrix maps
. These forward calculations serve as training samples for building a deep neural network for approximation of the corresponding maps, i.e.,
In our networks, the permeability field
is the input, while the multiscale basis functions
and the coarse-scale matrix
are the outputs. Once the neural networks are built, we can use the networks to compute the multiscale basis functions and coarse-scale parameters in the associated region for any permeability field
. Using these local information from the neural networks together with the global information which can be pre-computed, we can form the downscale operator
R with the multiscale basis functions, form and solve the linear system (
11), and obtain the multiscale solution by (
12).
3.1. Network Architecture
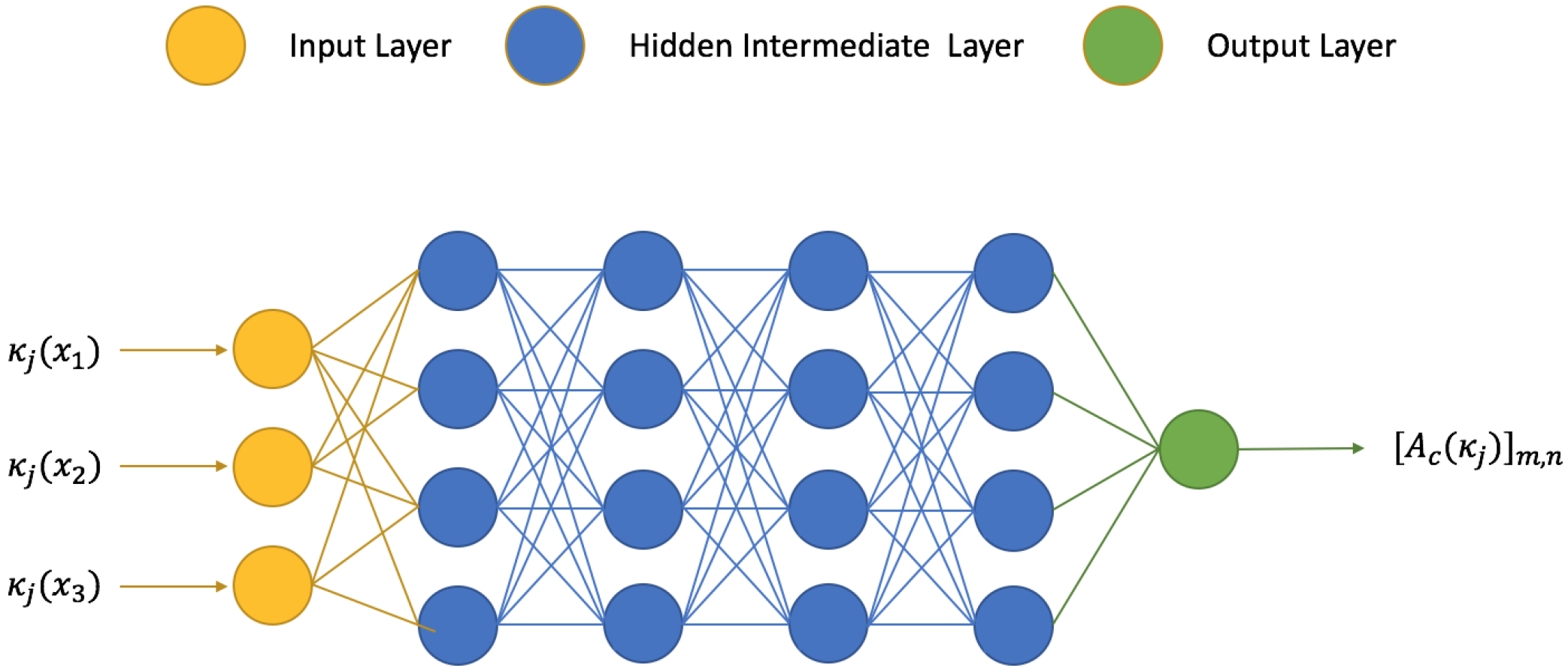
In general, an
L-layer neural network
can be written in the form
where
,
W’s are the weight matrices and
b’s are the bias vectors,
is the activation function,
x is the input. Such a network is used to approximate the output
y. Our goal is then to find
by solving an optimization problem
where
is called loss function, which measures the mismatch between the image of the input
x under the the neural network
and the desired output
y in a set of training samples
. In this paper, we use the mean-squared error metric to be our loss function
where
N is the number of the training samples. An illustration of a deep neural network is shown in
Figure 4.
Suppose we have a set of different realizations of the permeability
in the target block. In our network, the input
is a vector containing the permeability image pixels in the target block. The output
is an entry of the local stiffness matrix
, or the coordinate representation of a multiscale basis function
. We will make use of these sample pairs
to train a deep neural network
and
by minimizing the loss function with respect to the network parameter
, such that the trained neural networks can approximate the functions
and
, respectively. Once the neural is constructed, for some given new permeability coefficient
, we use our trained networks to compute a fast prediction of the outputs, i.e., local multiscale basis functions
by
and local coarse-scale stiffness matrix
by
3.2. Network-Based Multiscale Solver
Once the neural networks are built, we can assemble the predicted multiscale basis functions to obtain a prediction
for the downscaling operator, and assemble the predicted local coarse-scale stiffness matrix
in the global matrix
. Following (
11) and (
12), we solve the predicted coarse-scale coefficient vector
from the following linear system
and obtain the predicted multiscale solution
by
4. Numerical Results
In this section, we present some numerical results for predicting the GMsFEM ingredients and solutions using our proposed method. We considered permeability fields with high-contrast channels inside the domain , which consist of uncertainties in a target cell . More precisely, we considered a number of random realizations of permeability fields . Each permeability field contained two high-conductivity channels, and the fields differ in the target cell by:
in experiment 1, the channel configurations were all distinct, and the permeability coefficients inside the channels were fixed in each sample (see
Figure 5 for illustrations), and
in experiment 2, the channel configurations were randomly chosen among five configurations, and the permeability coefficients inside the channels followed a random distribution (see
Figure 6 for illustrations).
In these numerical experiments, we assumed there were uncertainties in only the target block . The permeability field in was fixed across all the samples.
We followed the procedures in
Section 3 and generated sample pairs using GMsFEM. Local spectral problems were solved to obtain the multiscale basis functions
. In the neural network, the permeability field
was considered to be the input, while the local multiscale basis functions
and local coarse-scale matrices
were regarded as the output. These sample pairs were divided into the training set and the learning set in a random manner. A large number
N of realizations, namely
, were used to generate sample pairs in the training set, while the remaining
M realizations, namely,
are used in testing the predictive power of the trained network. We remark that, for each basis function and each local matrix, we solved an optimization problem in minimizing the loss function defined by the sample pairs in the training set, and build a separate deep neural network. We summarize the network architectures for training local coarse scale stiffness matrix and multiscale basis functions as below:
For the multiscale basis function , we built a network using
- –
Input: vectorized permeability pixels values ,
- –
Output: coefficient vector of multiscale basis on coarse neighborhood ,
- –
Loss function: mean squared error ,
- –
Activation function: leaky ReLu function,
- –
DNN structure: 10–20 hidden layers, each layer have 250–350 neurons,
- –
Training optimizer: Adamax.
For the local coarse scale stiffness matrix , we build a network using
- –
Input: vectorized permeability pixels values ,
- –
Output: vectorized coarse scale stiffness matrix on the coarse block ,
- –
Loss function: mean squared error ,
- –
Activation function: ReLu function (rectifier),
- –
DNN structure: 10–16 hidden layers, each layer have 100–500 neurons,
- –
Training optimizer: Proximal Adagrad.
For simplicity, the activation functions ReLU function [
28] and Leaky ReLU function were used as they have the simplest derivatives among all nonlinear functions. The ReLU function proved to be useful in training deep neural network architectures. The Leaky ReLU function can resolve the vanishing gradient problem which can accelerate the training in some occasions. The optimizers Adamax and Proximal Adagrad are stochastic gradient descent (SGD)-based methods commonly used in neural network training [
29]. In both experiments, we trained our network using Python API Tensorflow and Keras [
30].
Once a neural network was built on training, it can be used to predict the output given a new input. The accuracy of the predictions is essential in making the network useful. In our experiments, we used
M sample pairs, which were not used in training the network, to examine the predictive power of our network. On these sample pairs, referred to as the testing set, we compared the prediction and the exact output and computed the mismatch in some suitable metric. Here, we summarize the metric used in our numerical experiment. For the multiscale basis functions, we compute the relative error in
and
norm, i.e.,
For the local stiffness matrices, we computed the relative error in entrywise
, entrywise
and Frobenius norm, i.e.,
A more important measure of the usefulness of the trained neural network is the predicted multiscale solution
given by (
23) and (
24). We compared the predicted solution to
defined by (
11) and (
12), and computed the relative error in
and energy norm, i.e.,
4.1. Experiment 1
In this experiment, we considered curved channelized permeability fields. Each permeability field contained a straight channel and a curved channel. The straight channel was fixed and the curved channel struck the boundary of the target cell
at the same points. The curvature of the sine-shaped channel inside
varied among all realizations. We generated 2000 realizations of permeability fields, where the permeability coefficients were fixed. Samples of permeability fields are depicted in
Figure 5. Among the 2000 realizations, 1980 sample pairs were randomly chosen and used as training samples, and the remaining 20 sample pairs were used as testing samples.
For each realization, we computed the local multiscale basis functions and local coarse-scale stiffness matrix. In building the local snapshot space, we solved for harmonic extension of all the fine-grid boundary conditions. Local multiscale basis functions were then constructed by solving the spectral problem and multiplied the spectral basis functions with the multiscale partition of unity functions. With the offline space constructed, we computed the coarse-scale stiffness matrix. We used the training samples to build deep neural networks for approximating these GMsFEM quantities, and examined the performance of the approximations on the testing set.
Table 1,
Table 2 and
Table 3 record the error of the prediction by the neural networks in each testing sample and the mean error measured in the defined metric. It can be seen that the predictions were of high accuracy. This is vital in ensuring the predicted GMsFEM solver is useful.
Table 4 records the error of the multiscale solution in each testing sample and the mean error using our proposed method. It can be observed that using the predicted GMsFEM solver, we obtained a good approximation of the multiscale solution compared with the exact GMsFEM solver.
4.2. Experiment 2
In this experiment, we considered sine-shaped channelized permeability fields. Each permeability field contained a straight channel and a sine-shaped channel. There were altogether five channel configurations, where the straight channel was fixed and the sine-shaped channel struck the boundary of the target cell
at the same points. The curvature of the sine-shaped channel inside
varied among these configurations. For each channel configuration, we generated 500 realizations of permeability fields, where the permeability coefficients followed random distributions. Samples of permeability fields are depicted in
Figure 6. Among the 2500 realizations, 2475 sample pairs were randomly chosen and used as training samples, and the remaining 25 sample pairs were used as testing samples.
Next, for each realization, we computed the local multiscale basis functions and local coarse-scale stiffness matrix. In building the local snapshot space, we solved for harmonic extension of randomized fine-grid boundary conditions, so as to reduce the number of local problems to be solved. Local multiscale basis functions were then constructed by solving the spectral problem and multiplied the spectral basis functions with the multiscale partition of unity functions. With the offline space constructed, we computed the coarse-scale stiffness matrix. We used the training samples to build deep neural networks for approximating these GMsFEM quantities, and examined the performance of the approximations on the testing set.
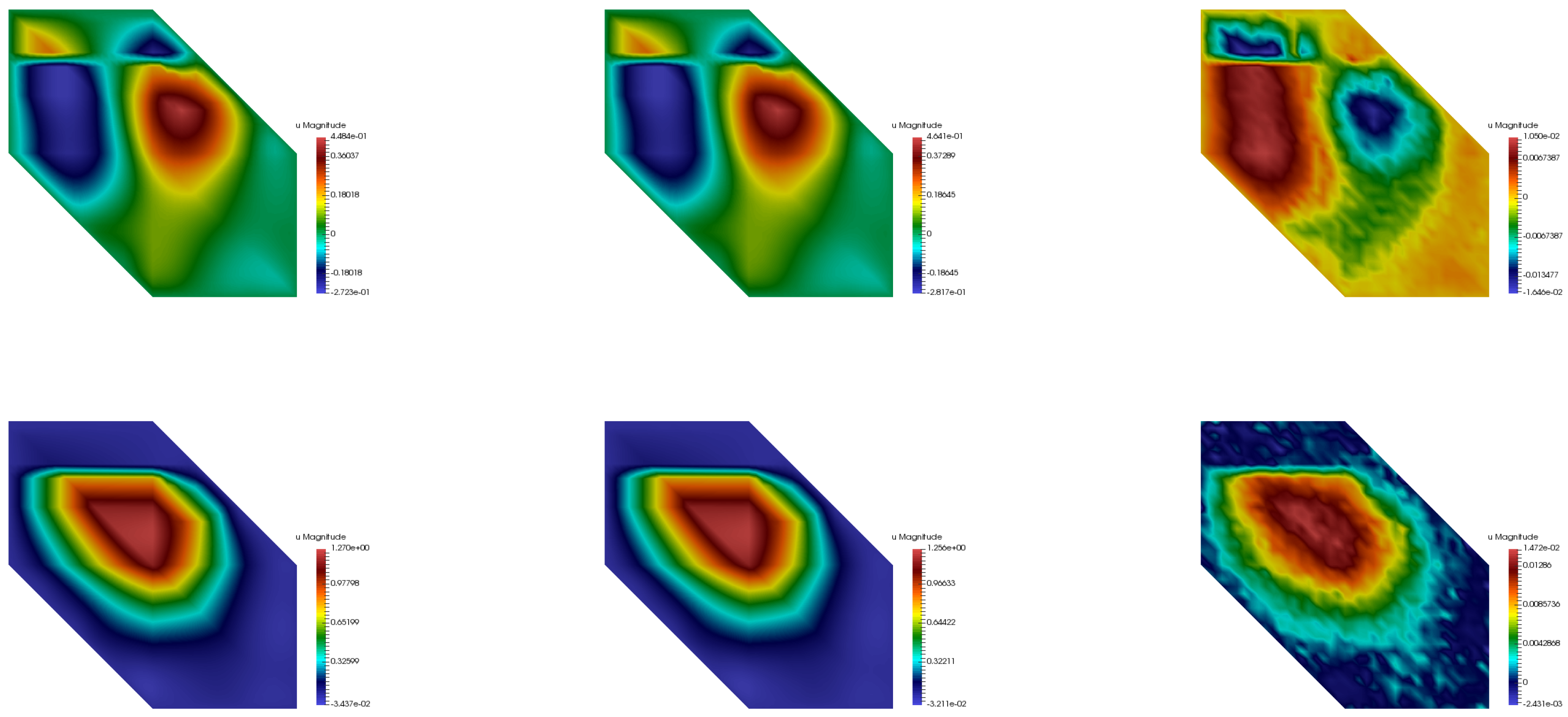
Figure 7,
Figure 8 and
Figure 9 show the comparison of the multiscale basis functions in two respective coarse neighborhoods. It can be observed that the predicted multiscale basis functions were in good agreement with the exact ones. In particular, the neural network successfully interpreted the high conductivity regions as the support localization feature of the multiscale basis functions.
Table 5 and
Table 6 record the mean error of the prediction by the neural networks, measured in the defined metric. Again, it can be seen that the prediction are of high accuracy.
Table 7 records the mean error between the multiscale solution using the neural-network-based multiscale solver and using exact GMsFEM. we obtain a good approximation of the multiscale solution compared with the exact GMsFEM solver.