1. Introduction
The Theory of Connections (ToC), as introduced in [
1], consists of a general analytical framework to obtain
constrained expressions,
, in one-dimension. A constrained expression is a function expressed in terms of another function,
, that is freely chosen and, no matter what the
is, the resulting expression always satisfies a set of
n constraints. ToC generalizes the one-dimensional interpolation problem subject to
n constraints using the general form,
where
are
n user-selected linearly independent functions,
are derived by imposing the
n constraints, and
is a
freely chosen function subject to be
defined and nonsingular where the constraints are specified. Besides this requirement,
can be any function, including, discontinuous functions, delta functions, and even functions that are undefined in some domains. Once the
coefficients have been derived, then Equation (
1) satisfies all the
n constraints,
no matter what the function is.
Constrained expressions in the form given in Equation (
1) are provided for a wide class of constraints, including constraints on points and derivatives, linear combinations of constraints, as well as infinite and integral constraints [
2]. In addition, weighted constraints [
3] and point constraints on continuous and discontinuous periodic functions with assigned period can also be obtained [
1]. How to extend ToC to inequality and nonlinear constraints is currently a work in progress.
The Theory of Connections framework can be considered the generalization of interpolation; rather than providing a class of functions (e.g., monomials) satisfying a set of
n constraints, it derives
all possible functions satisfying the
n constraints by spanning all possible
functions. This has been proved in Ref. [
1]. A simple example of a constrained expression is,
This equation always satisfies and , as long as and are defined and nonsingular. In other words, the constraints are embedded into the constrained expression.
Constrained expressions can be used to transform constrained optimization problems into unconstrained optimization problems. Using this approach, fast least-squares solutions of linear [
4] and nonlinear [
5] ODE have been obtained at machine error accuracy and with low (actually, very low) condition number. Direct comparisons of ToC versus MATLAB’s ode45 [
6] and Chebfun [
7] have been performed on a small test of ODE with excellent results [
4,
5]. In particular, the ToC approach to solve ODE consists of a unified framework to solve IVP, BVP, and multi-value problems. The extension of differential equations subject to component constraints [
8] has opened the possibility for ToC to solve
in real-time a class of direct optimal control problems [
9], where the constraints connect state and costate.
This study first extends the Theory of Connections to two-dimensions by providing, for rectangular domains, all surfaces that are subject to: (1) Dirichlet constraints; (2) Neumann constraints; and (3) any combination of Dirichlet and Neumann constraints. This theory is then generalized to the Multivariate Theory of Connections which provide in n-dimensional space all possible manifolds that satisfy boundary constraints on the value and boundary constraints on any-order derivative.
This article is structured as follows. First, it shows that the one-dimensional ToC can be used in two dimensions when the constraints (functions or derivatives) are provided along one axis only. This is a particular case, where the original univariate theory [
1] can be applied with basically no modifications. Then, a two dimensional ToC version is developed for Dirichlet type boundary constraints. This theory is then extended to include Neumann and mixed type boundary constraints. Finally, the theory is extended to
n-dimensions and to incorporate arbitrary-order derivative boundary constraints followed by a mathematical proof validating it.
3. Connecting Functions in Two Directions
In this section, the Theory of Connections is extended to the two-dimensional case. Note that dealing with constraints in two (or more) directions (functions or derivatives) requires particular attention. In fact, two orthogonal constraint functions cannot be completely distinct as they intersect at one point where they need to match in value. In addition, if the formalism derived for the 1-D case is applied to 2-D case, some complications arise. These complications are highlighted in the following simple clarifying example.
Consider the two boundary constraint functions, and . Searching the constrained expression as originally done for the one-dimensional case implies the expression,
The constraints imply the two constraints,
To obtain the values of and , the determinant of the matrix to invert is . This determinant is y by selecting and , or it is x by selecting and . Therefore, to avoid singularities, this approach requires paying particular attention to the domain definition and/or on the user-selected functions, . To avoid dealing with these issues, a new (equivalent) formalism to derive constrained expressions is devised for the higher dimensional case.
The Theory of Connections extension to the higher dimensional case (with constraints on all axes) can be obtained by re-writing the constrained expression into an equivalent form, highlighting a general and interesting property. Let us show this by an example. Equation (
2) can be re-written as,
These two components, and , of a constrained expression have a specific general meaning. The term, , represents an (any) interpolating function satisfying the constraints while the term represents all interpolating functions that are vanishing at the constraints. Therefore, the generation of all functions satisfying multiple orthogonal constraints in n-dimensional space can always be expressed by the general form, , where is any function satisfying the constraints and must represent all functions vanishing at the constraints. Equation is actually an alternative general form to write a constrained expression, that is, an alternative way to generalize interpolation: rather than derive a class of functions (e.g., monomials) satisfying a set of constraints, it represents all possible functions satisfying the set of constraints.
To prove that this additive formalism can describe all possible functions satisfying the constraints is immediate. Let be all functions satisfying the constraints and be the sum of a specific function satisfying the constraints, , and a function, , representing all functions that are null at the constraints. Then, will be equal to iff , representing all functions that are null at the constraints.
As shown in Equation (
5), once the
function is obtained, then the
function can be immediately derived. In fact,
can be obtained by subtracting the
function, where all the constraints are specified in terms of the
free function, from the free function
. For this reason, let us write the general expression of a constrained expression as,
where
indicates the function satisfying the constraints where the constraints are specified in term of
.
The previous discussion serves to prove that the problem of extending Theory of Connections to higher dimensional spaces consists of the problem of finding the function,
, only. In two dimensions, the function
is provided in literature by the Coons surface [
11],
. This surface satisfies the Dirichlet boundary constraints,
where the surface is contained in the
domain. This surface is used in computer graphics and in computational mechanics applications to smoothly join other surfaces together, particularly in finite element method and boundary element method, to mesh problem domains into elements. The expression of the Coons surface is,
where the four subtracting terms are there for continuity. Note the constraint functions at boundary corners must have the same value,
,
,
, and
. This equation can be written in matrix form as,
or, equivalently,
where
Since the
boundaries match the boundaries of the
constraint function, then the identity,
, holds for
any function. Therefore, the
function can be set as,
representing all functions that are always zero at the boundary constraints, as
is a free function.
4. Theory of Connections Surface Subject to Dirichlet Constraints
Equations (
8) and (
9) can be merged to provide
all surfaces with the boundary constraints defined in Equation (
7) in the following compact form,
where, again,
indicates an expression satisfying the boundary function constraints defined by
and
an expression that is zero at the boundaries. In matrix form, Equation (
10) becomes,
where
is a freely chosen function. In particular, if
, then the ToC surface becomes the Coons surface.
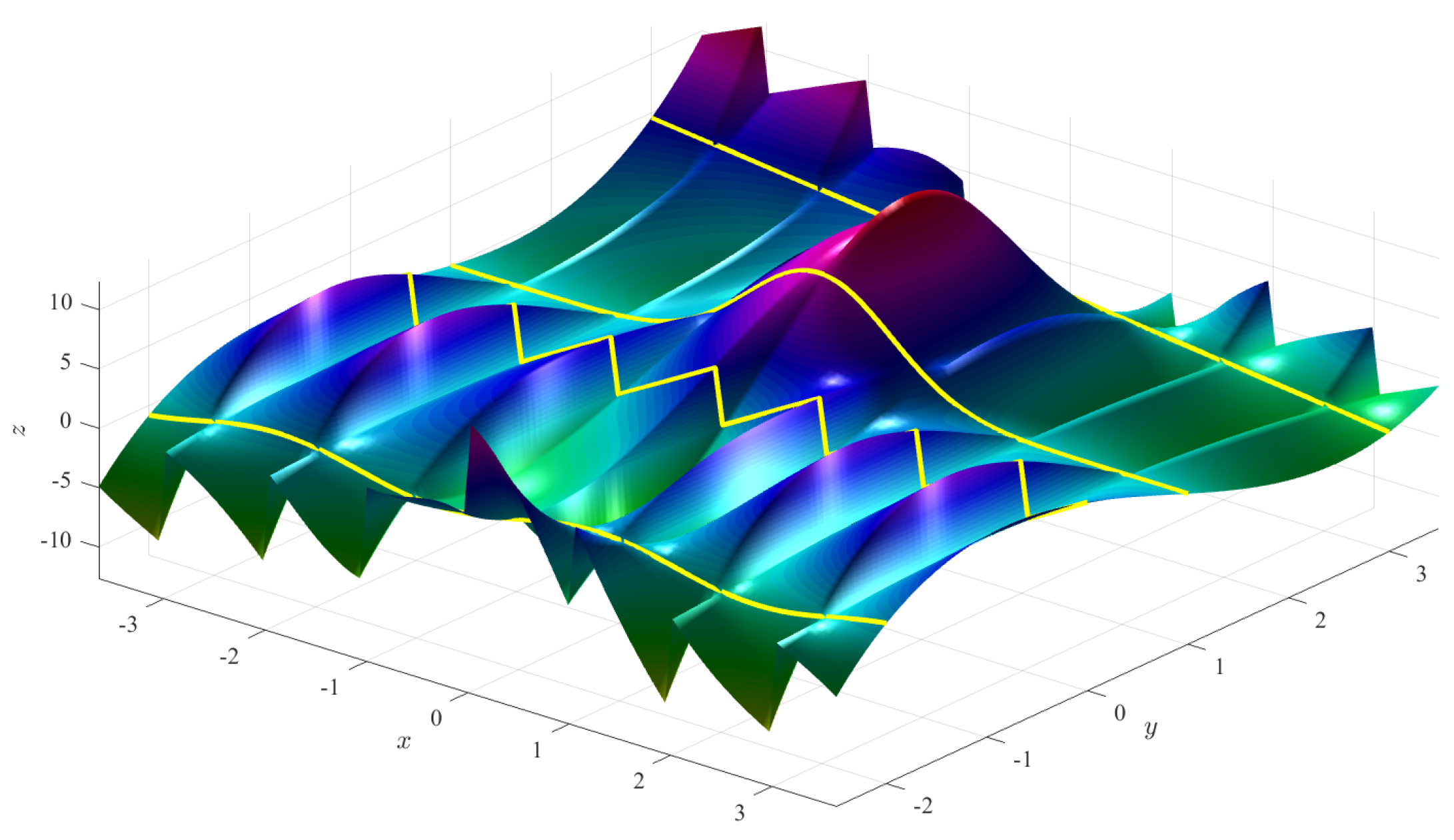
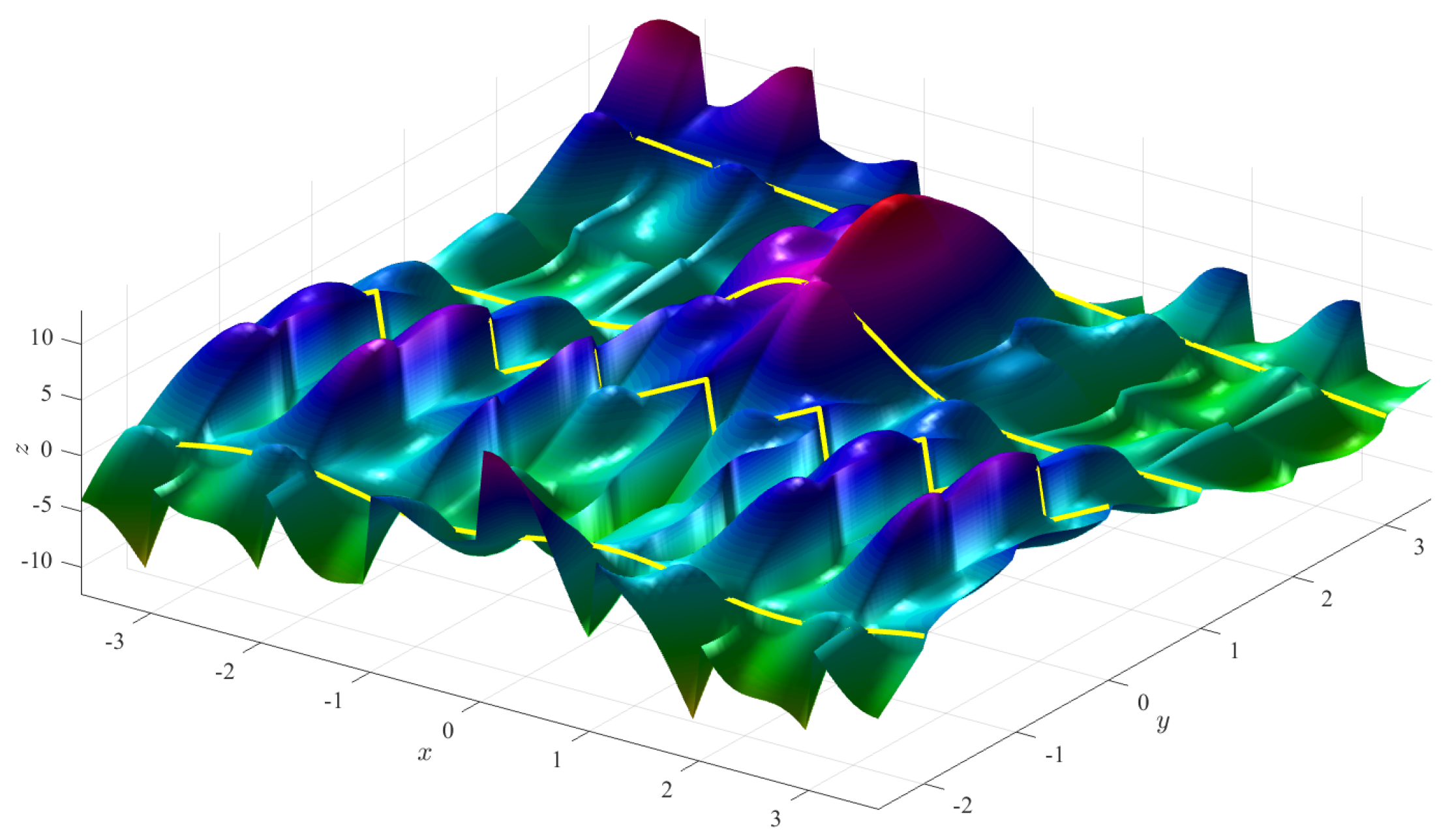
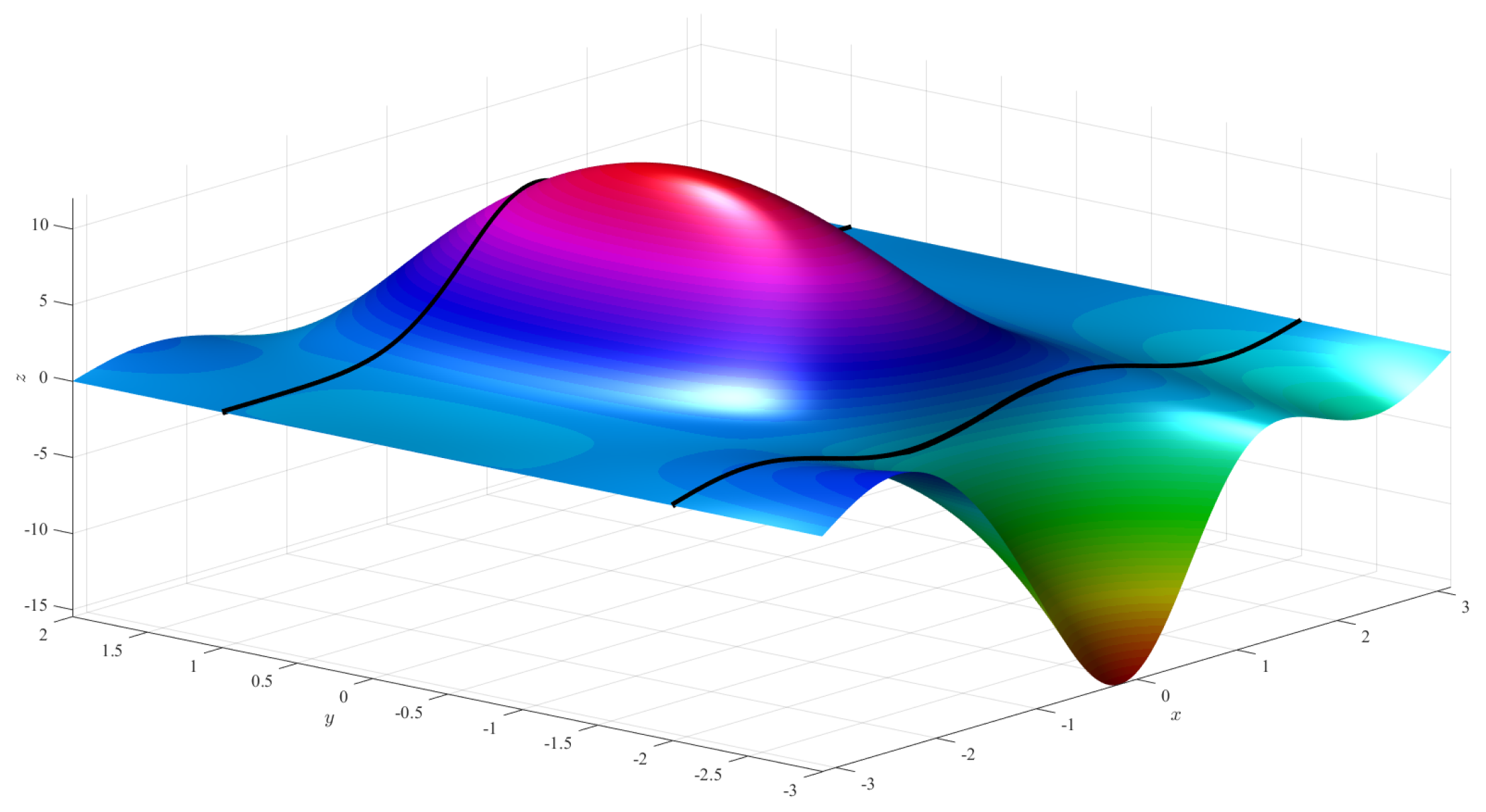
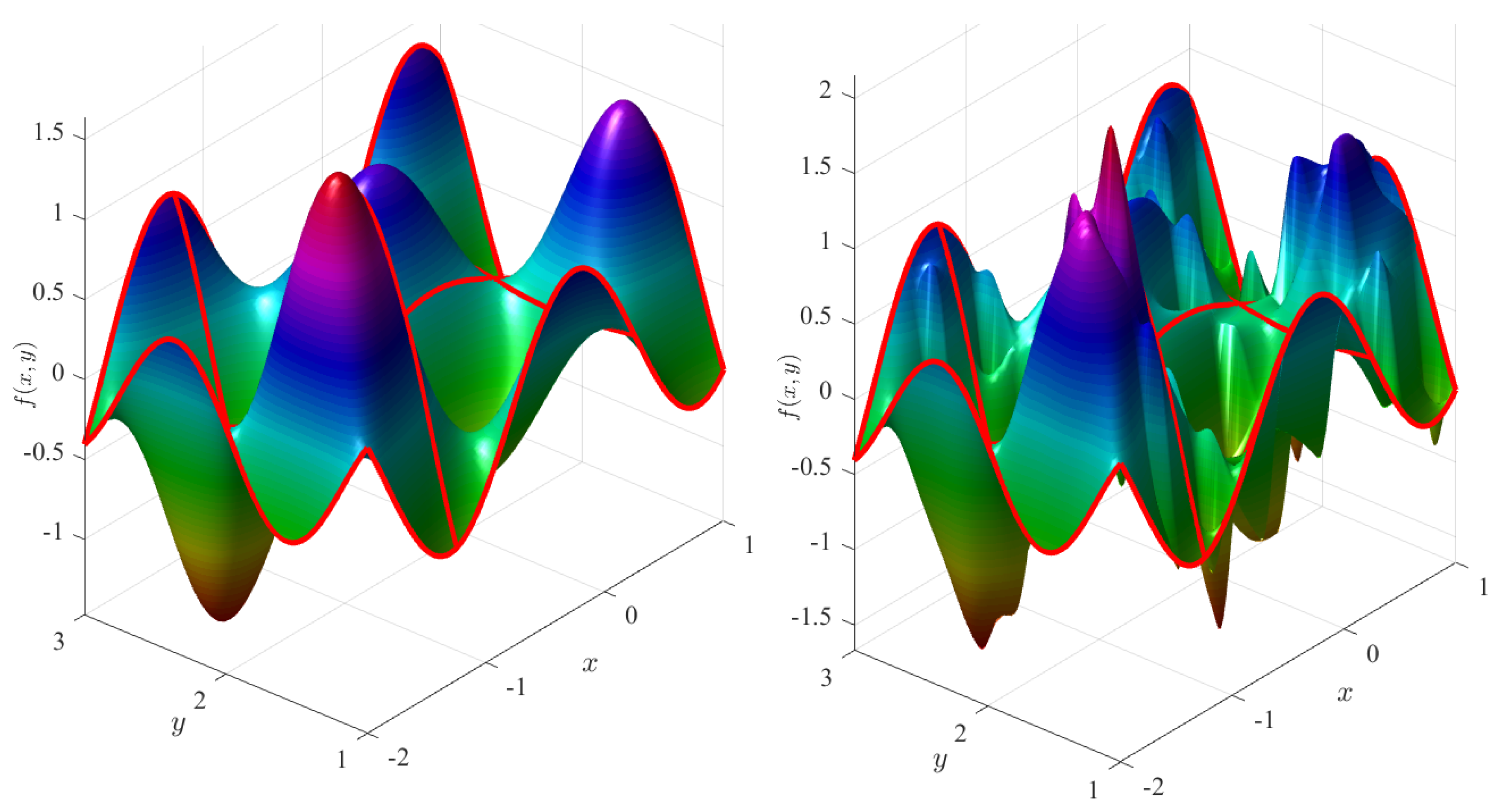
Figure 5 (left) shows the Coons surface subject to the constraints,
and
Figure 5 (right) shows a ToC surface that is obtained using the free function,
For generic boundaries defined in the rectangle
, the ToC surface becomes,
Equation (
12) can also be set in matrix form,
where
and
Note that all the ToC surfaces provided are linear in , and, therefore, they can be used to solve, by linear/nonlinear least-squares, two-dimensional optimization problems subject to boundary function constraints, such as linear/nonlinear partial differential equations.
6. Constraints on Function and Derivatives
The “Boolean sum formulation” was provided by Farin [
12] (also called “Hermite–Coons formulation”) of the Coons surface that includes boundary derivatives,
where
and
The formulation provided in Equation (
14) can be put in the matrix compact form,
where
and the
matrix,
, has the expression,
To verify the boundary derivative constraints, the following partial derivatives of Equation (
15) are used,
where
The ToC in 2D with function and derivative boundary constraints is simply,
where the
matrix and the
vectors are provided by Equations (
17) and (
16), respectively.
Dirichlet/Neumann mixed constraints can be derived, as shown in the examples provided in
Section 6.1 through
Section 6.4. The matrix compact form is simply obtained from the matrix defined in Equation (
17) by removing the rows and the columns associated with the boundary constraints not provided, while the vectors
and
are derived by specifying the constraints. Note that in general the vectors
and
are
not unique. The reason the vectors
and
are not unique comes from the fact that the
term in Equation (
6) is not unique.
In the next subsections, four Dirichlet/Neumann mixed constraint examples providing the simplest expressions for
and
are derived. The
Appendix A contains the expressions for the
and
vectors associated with all the combinations of Dirichlet and Neumann constraints.
6.1. Constraints: and
In this case, the Coons-type surface satisfying the boundary constraints can be expressed as,
where
and
are unknown functions. Expanding, we obtain
. The two constraints are satisfied if,
Therefore, the
and
functions must satisfy
and
. The simplest expressions satisfying these equations can be obtained by selecting
and
. In this case, the associated ToC surface is given by,
Note that any functions satisfying and can be adopted to obtain the ToC surface satisfying the constraints and . This is because there are infinite Coons-type surfaces satisfying the constraints. Consequently, the vectors and are not unique.
6.2. Constraints: and
For these boundary constraints, the Coons-type surface is expressed by,
The constraints are satisfied if,
Therefore, the
and
functions must satisfy
and
. One solution is
and
. Therefore, the associated ToC surface is given by,
6.3. Neumann Constraints: , , , and
In this case, the Coons-type surface satisfying the boundary constraints can be expressed as,
The constraints are satisfied if,
These equations imply
,
,
, and
. Therefore, the simplest solution is
and
. Then, the associated ToC surface satisfying the Neumann constraints is given by,
where
6.4. Constraints: , , and
In this case, the Coons-type surface satisfying the boundary constraints is in the form,
The constraints are satisfied if
,
,
,
, and
. Therefore, the associated ToC surface is,
6.5. Generic Mixed Constraints
Consider the case of mixed constraints,
In this case, the surface satisfying the boundary constraints is built using the matrix,
and all surfaces subject to the constraints defined in Equation (
19) can be obtained by,
where
are vectors made of the (not unique) function vectors
and
whose expressions can be found by satisfying the constraints (as done in the previous four subsections) along with a methodology similar to that given in
Section 5.
7. Extension to -Dimensional Spaces and Arbitrary-Order Derivative Constraints
This section provides the
Multivariate Theory of Connections, as the generalization to
n-dimensional rectangular domains with arbitrary-order boundary derivatives of what is presented above for two-dimensional space. Using tensor notation, this generalization is represented in the following compact form,
where
n is the number of orthogonal coordinates defined by the vector
,
is the
th element of a vector function of the variable
,
is an
n-dimensional tensor that is a function of the boundary constraints defined in
, and
is the free-function.
In Equation (
20), the term
represents any function satisfying the boundary constraints defined by
and the term
represents all possible functions that are zero on the boundary constraints. The subsections that follow explain how to construct the
tensor and the
vectors for assigned boundary constraints, and provides a proof that the tensor formulation of the ToC defined by Equation (
20) satisfies all boundary constraints defined by
, independently of the choice of the free function,
.
Consider a generic boundary constraint on the hyperplane, where . This constraint specifies the d-derivative of the constraint function evaluated at and it is indicated by . Consider a set of constraints defined in various hyperplanes. This set of constraints is indicated by , where and are vectors of elements indicating the order of derivatives and the values of where the boundary constraints are defined, respectively. A specific boundary constraint, e.g. the mth boundary constraint, can then be written as .
Additionally, let us define an operator, called the boundary constraint operator, whose purpose is to take the
dth derivative with respect to coordinate
and then evaluate that function at
. Equation (
21) shows the idea.
In general, for a function of
n variables, the boundary constraint operator identifies an
-dimensional manifold. As the boundary constraint operator is used throughout this proof, it is important to note its properties when acting on sums and products of functions. Equation (
22) shows how the boundary constraint operator acts on sums, and Equation (
23) shows how the boundary constraint operator acts on products.
This section shows how to build the
tensor and the vectors
given the boundary constraints defined by the boundary constraint operators. Moreover, this section contains a proof that, in Equation (
20), the boundary constraints defined by
satisfy the function
and, by extension, the function
projects the free-function
onto the sub-space of functions that are zero on the boundary constraints. Then, it follows that the expression for the ToC surface given in Equation (
20) represents
all possible functions that meet the boundary defined by the boundary constraint operators.
7.1. The Tensor
There is a step-by-step method for constructing the tensor.
To better clarify how to use Equation (
24), consider the example of the following constraints in three-dimensional space.
From Step 1:
From Step 3, a single example is provided,
which, thanks to Clairaut’s theorem, can also be written as,
Three additional examples are given to help further illustrate the procedure,
7.2. The v Vectors
Each vector,
, is associated with the
constraints that are specified by
. The
vector is built as follows,
where
are
linearly independent functions. The simplest set of linearly independent functions are monomials, that is,
. The
coefficients,
, can be computed by matrix inversion,
To supplement the above explanation, let us look at the example of Dirichlet boundary conditions on
from the example in
Section 7.1. There are two boundary conditions,
and
, and thus two linearly independent functions are needed,
Let us consider,
and
. Then, following Equation (
25),
and substituting the values of
, we obtain
.
7.3. Proof
This section demonstrates that the term
from Equation (
20) generates a surface satisfying the boundary constraints defined by the function
. First, it is shown that
satisfies boundary constraints on the value, and then that
satisfies boundary constraints on arbitrary-order derivatives.
Equation (
23) for
allows us to write,
The boundary constraint operator applied to
yields,
Since the only nonzero terms are associated with , we have,
Applying the boundary constraint operator to the
-dimensional
tensor where index
has no effect, because all of the functions already have coordinate
substituted for the value
(see Equation (
24)). Moreover, applying the boundary constraint operator to the
tensor where index
causes all terms in the sum within the parenthesis in Equation (
28) to cancel each other, except when all of the non-
indices are equal to one. This leads to Equation (
29).
Since
when
and
by definition, then,
which proves Equation (
20) works for boundary constraints on the value.
Now, we show that Equation (
20) holds for arbitrary-order derivative type boundary constraints. Equation (
23) for
allows us to write,
From Equation (
23), we note that boundary constraint operators that take a derivative follow the usual product rule when applied to a product. Moreover, we note that all of the
vectors except
do not depend on
, thus applying the boundary constraint operator to them results in a vector of zeros. Applying the boundary constraint operator to
yields,
and applying the boundary constraint operator to
yields,
Substituting these simplifications into
, after applying the boundary constraint operator, results in Equation (
31).
Similar to the proof for value-based boundary constraints, based on Equation (
24), all terms in the sum within the parenthesis in Equation (
31) cancel each other, except when all of the non-
indices are equal to one. Thus, Equation (
31) can be simplified to Equation (
32).
Again, all of the vectors
were designed such that their first component is 1, and the value of the element of
for all indices equal to 1 is 0. Therefore, Equation (
32) simplifies to,
which proves Equation (
20) works for arbitrary-order derivative boundary constraints.
In conclusion, the term
from Equation (
20) generates a manifold satisfying the boundary constraints given in terms of arbitrary-order derivative in
n-dimensional space. The term
from Equation (
20) projects any free function
onto the space of functions that are vanishing at the specified boundary constraints. As a result, Equation (
20) can be used to produce the family of
all possible functions satisfying assigned boundary constraints (functions or derivatives) in rectangular domains in
n-dimensional space.
8. Conclusions
This paper extends to
n-dimensional spaces the Univariate Theory of Connections (ToC), introduced in Ref. [
1]. First, it provides a mathematical tool to express
all possible surfaces subject to constraint functions and arbitrary-order derivatives in a boundary rectangular domain, and then it extends the results to the multivariate case by providing the Multivariate Theory of Connections, which allows one to obtain
n-dimensional manifolds subject to any-order derivative boundary constraints.
In particular, if the constraints are provided along one axis only, then this paper shows that the univariate ToC, as defined in Ref. [
1], can be adopted to describe
all possible surfaces satisfying the constraints. If the boundary constraints are defined in a rectangular domain, then the constrained expression is found in the form
, where
can be
any function satisfying the constraints and
describes
all functions that are vanishing at the constraints. This is obtained by introducing a free function,
, into the function
in such a way that
is zero at the constraints no matter what the
is. This way, by spanning all possible
surfaces (even discontinuous, null, or piece-wise defined) the resulting
generates
all surfaces that are zero at the constraints and, consequently,
, describes all surfaces satisfying the constraints defined in the rectangular boundary domain. The function
has been selected as a Coons surface [
11] and, in particular, a Coons surface is obtained if
is selected. All possible combinations of Dirichlet
and Neumann constraints are also provided in
Appendix A.
The last section provides the Multivariate Theory of Connections extension, which is a mathematical tool to transform n-dimensional constraint optimization problems subject to constraints on the boundary value and any-order derivative into unconstrained optimization problems. The number of applications of the Multivariate Theory of Connections are many, especially in the area of partial and stochastic differential equations: the main subjects of our current research.