Skew-Reflected-Gompertz Information Quantifiers with Application to Sea Surface Temperature Records
Abstract
:1. Introduction
2. The Skew-Reflected-Gompertz Distribution
- E-step. From (6)–(8), we haveand
- M-step. Update , by solving the following equation
3. Entropic Quantifiers
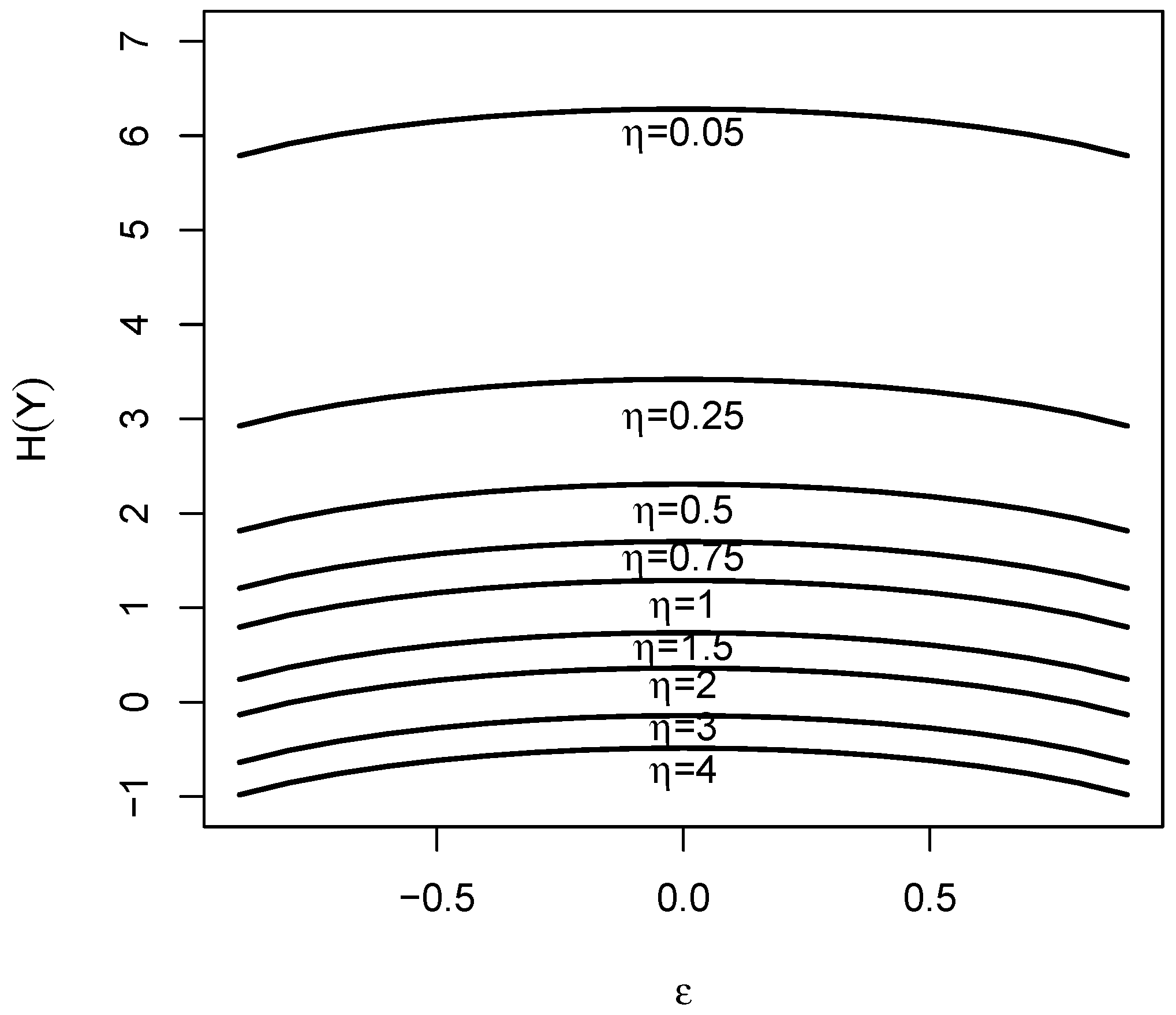
3.1. Shannon Entropy
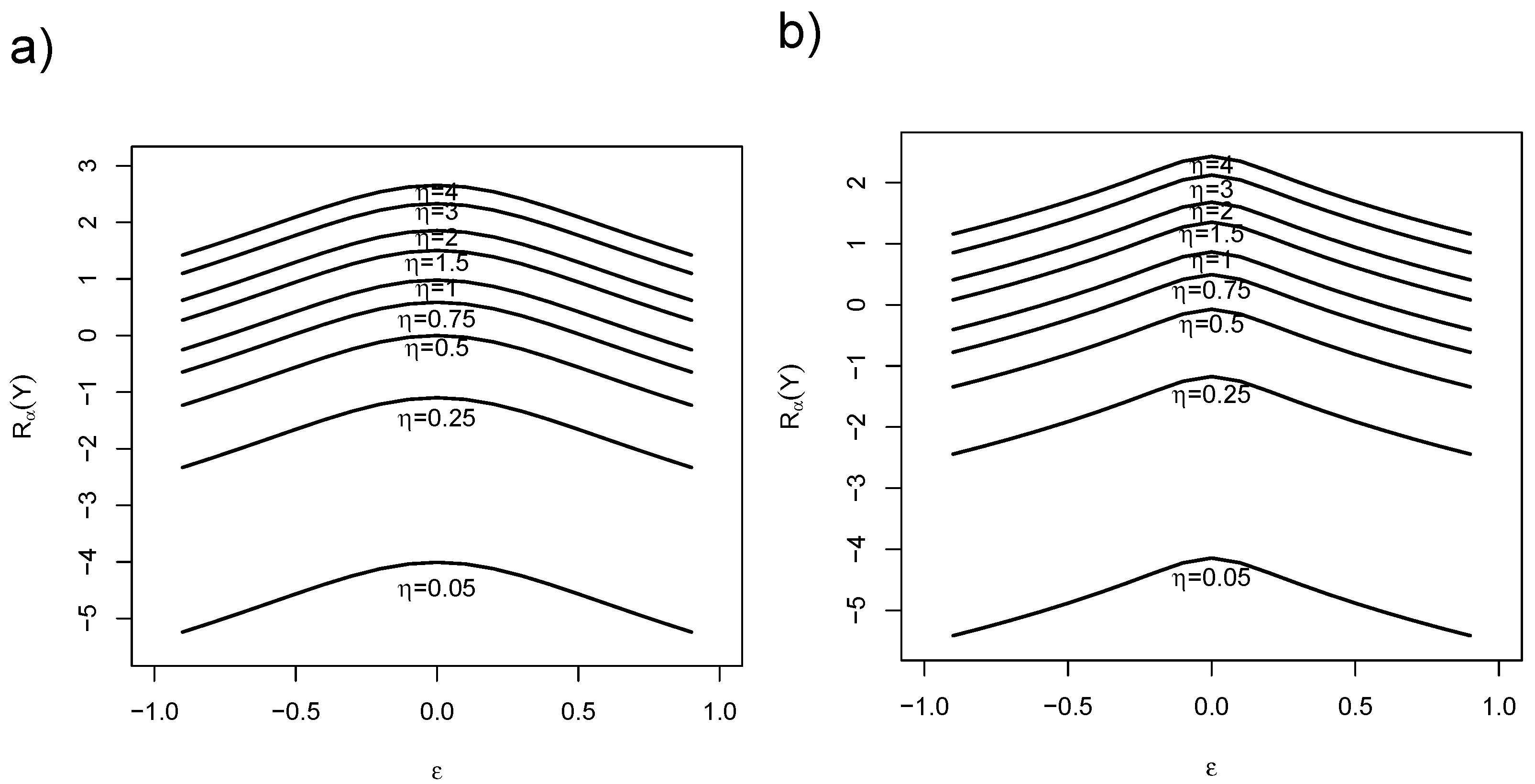
3.2. Rényi Entropy
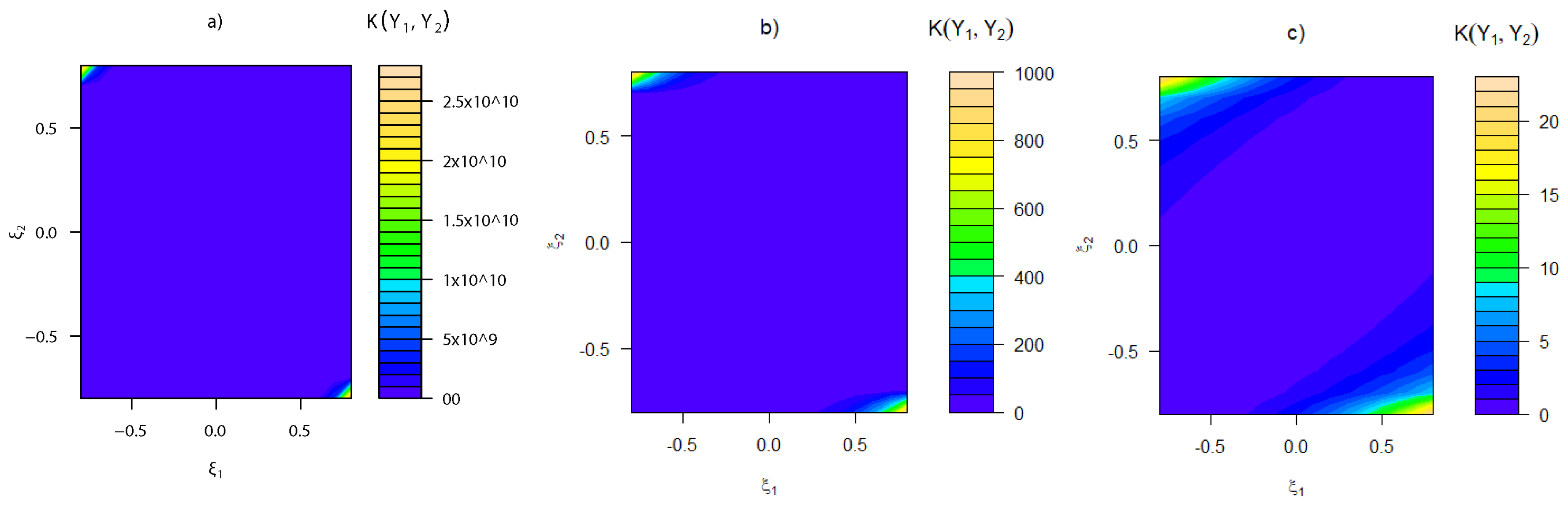
3.3. Kullback–Leibler Divergence
3.4. Asymptotic Test
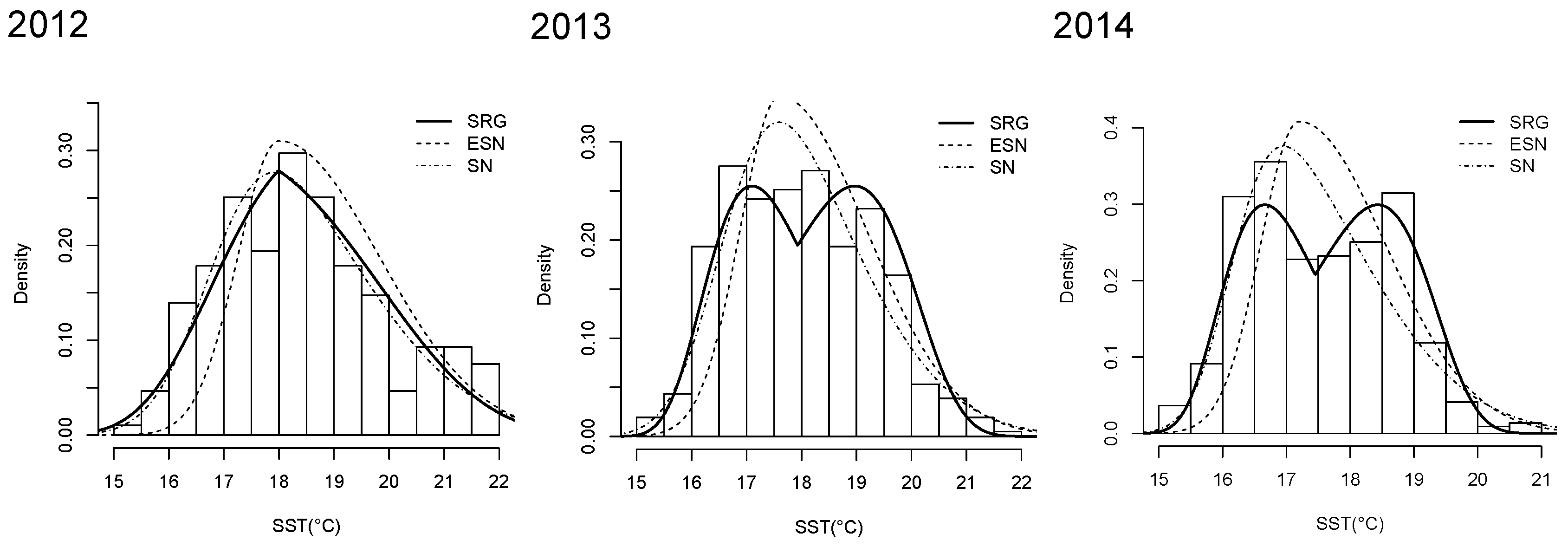
4. Application
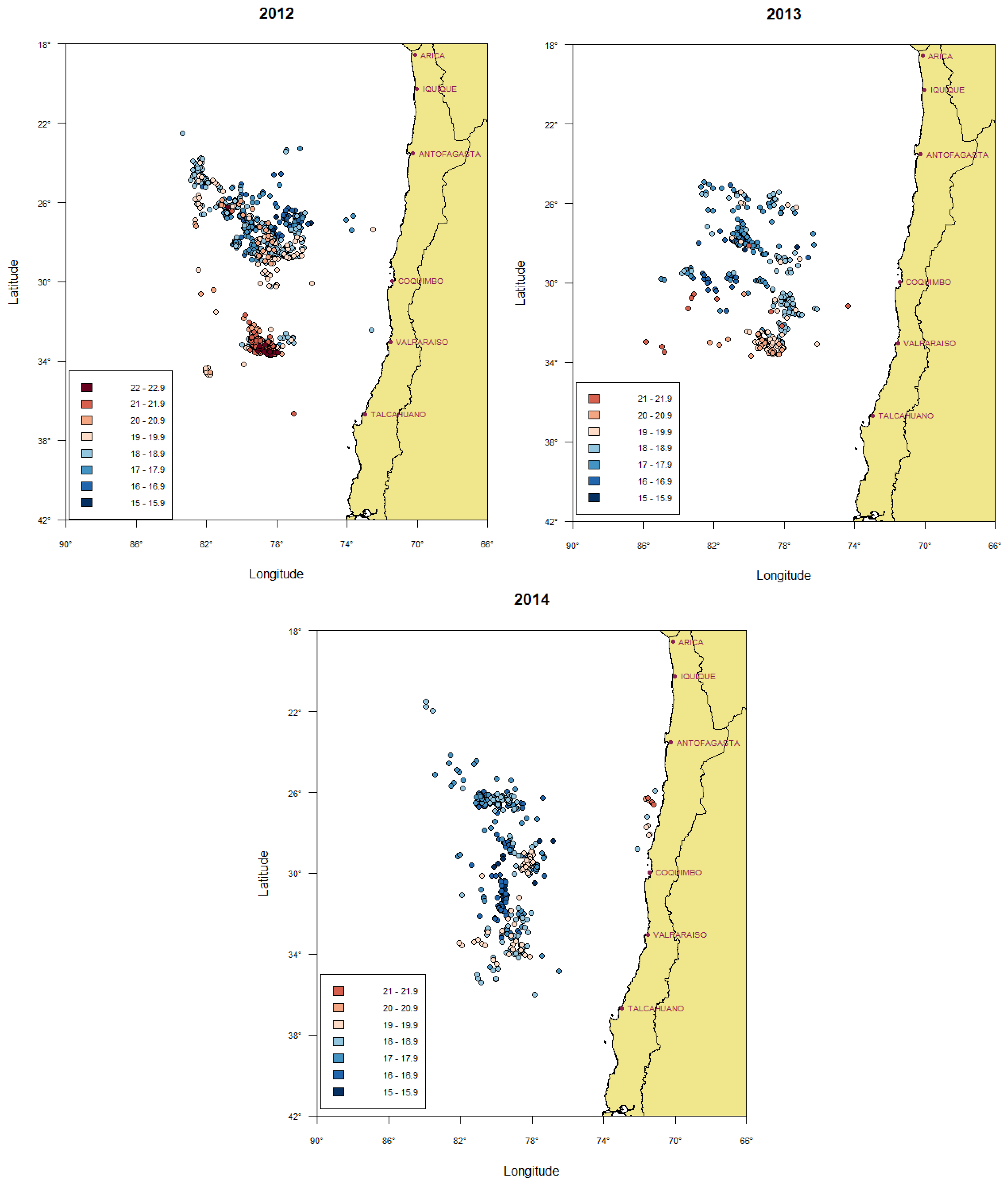
4.1. Sea Surface Temperature Data
4.1.1. SRG Parameter Estimates
4.1.2. Information Quantifiers and Asymptotic Test
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| A–D | Anderson–Darling |
| AIC | Akaike’s information criterion |
| BIC | Bayesian information criterion |
| C–V | Cramer–von Mises |
| CDF | Cumulative distribution function |
| EM | Expectation maximization |
| ESN | Epsilon-skew-normal |
| FIM | Fisher information matrix |
| GZ | Gompertz |
| K–S | Kolmogorov–Smirnov |
| KL | Kullback–Leibler |
| MGF | Moment-generating function |
| MLE | Maximum Likelihood Estimator |
| Probability density function | |
| RE | Rényi entropy |
| SD | Standard deviation |
| SE | Shannon entropy |
| SN | Skew-normal |
| SRG | Skew-Reflected-Gompertz |
| SST | Sea surface temperature |
Appendix A. The Epsilon-Skew-Normal Distribution
Appendix B. The Skew-Normal Distribution
References
- Hoseinzadeh, A.; Maleki, M.; Khodadadi, Z.; Contreras-Reyes, J.E. The Skew-Reflected-Gompertz distribution for analyzing symmetric and asymmetric data. J. Comput. Appl. Math. 2019, 349, 132–141. [Google Scholar] [CrossRef]
- Gompertz, B. On the nature of the function expressive of the law of human mortality, and on a new mode of determining the value of life contingencies. Philos. Trans. R. Soc. Lond. 1825, 115, 513–583. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Contreras-Reyes, J.E.; Stehlík, M. Generalized skew-normal negentropy and its application to fish condition factor time series. Entropy 2017, 19, 528. [Google Scholar] [CrossRef]
- Mudholkar, G.S.; Hutson, A.D. The epsilon-skew-normal distribution for analyzing near-normal data. J. Stat. Plan. Inference 2000, 83, 291–309. [Google Scholar] [CrossRef]
- Maleki, M.; Mahmoudi, M.R. Two-Piece Location-Scale Distributions based on Scale Mixtures of Normal family. Commun. Stat. Theor. Meth. 2017, 46, 12356–12369. [Google Scholar] [CrossRef]
- Moravveji, B.; Khodadai, Z.; Maleki, M. A Bayesian Analysis of Two-Piece distributions based on the Scale Mixtures of Normal Family. Iran. J. Sci. Technol. Trans. A 2019, 43, 991–1001. [Google Scholar] [CrossRef]
- Contreras-Reyes, J.E. Rényi entropy and complexity measure for skew-gaussian distributions and related families. Physica A 2015, 433, 84–91. [Google Scholar] [CrossRef] [Green Version]
- Contreras-Reyes, J.E. Analyzing fish condition factor index through skew-gaussian information theory quantifiers. Fluct. Noise Lett. 2016, 15, 1650013. [Google Scholar] [CrossRef]
- Wang, Y.Q.; Derksen, R.W. The confirmation of the α–β model and the maximum entropy formulation in a thermal wake. Environmetrics 1998, 9, 269–282. [Google Scholar] [CrossRef]
- De Queiroz, M.M.; Silva, R.W.; Loschi, R.H. Shannon entropy and Kullback–Leibler divergence in multivariate log fundamental skew-normal and related distributions. Can. J. Stat. 2016, 44, 219–237. [Google Scholar] [CrossRef]
- Di Lorenzo, E.; Combes, V.; Keister, J.E.; Strub, P.T.; Thomas, A.C.; Franks, P.J.; Ohman, M.D.; Furtado, J.C.; Bracco, A.; Bograd, S.J.; et al. Synthesis of Pacific Ocean climate and ecosystem dynamics. Oceanography 2013, 26, 68–81. [Google Scholar] [CrossRef]
- Salicrú, M.; Menéndez, M.L.; Pardo, L.; Morales, D. On the applications of divergence type measures in testing statistical hypothesis. J. Multivar. Anal. 1994, 51, 372–391. [Google Scholar] [CrossRef]
- Maleki, M.; Contreras-Reyes, J.E.; Mahmoudi, M.R. Robust Mixture Modeling Based on Two-Piece Scale Mixtures of Normal Family. Axioms 2019, 8, 38. [Google Scholar] [CrossRef]
- Arellano-Valle, R.B.; Gómez, H.W.; Quintana, F.A. Statistical inference for a general class of asymmetric distributions. J. Stat. Plan. Inference 2005, 128, 427–443. [Google Scholar] [CrossRef]
- Jafari, A.A.; Tahmasebi, S.; Alizadeh, M. The beta-Gompertz distribution. Rev. Colomb. Estad. 2014, 37, 141–158. [Google Scholar] [CrossRef]
- Shannon, C.E. A mathematical theory of communication. Bell Syst. Tech. J. 1948, 27, 379–423. [Google Scholar] [CrossRef]
- Cover, T.M.; Thomas, J.A. Elements of Information Theory; Wiley & Son, Inc.: New York, NY, USA, 2006. [Google Scholar]
- Rényi, A. Probability Theory; Dover Publications: New York, NY, USA, 2012. [Google Scholar]
- Abu-Zinadah, H.H.; Aloufi, A.S. Some characterizations of the exponentiated Gompertz distribution. Int. Math. Forum 2014, 9, 1427–1439. [Google Scholar] [CrossRef] [Green Version]
- Kullback, S.; Leibler, R.A. On information and sufficiency. Ann. Math. Stat. 1951, 22, 79–86. [Google Scholar] [CrossRef]
- Bauckhage, C. Characterizations and Kullback–Leibler Divergence of Gompertz Distributions. arXiv 2014, arXiv:1402.3193. [Google Scholar]
- R Core Team. A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2018; ISBN 3-900051-07-0. [Google Scholar]
- Barría, P.; González, A.; Cortés, D.D.; Mora, S.; Miranda, H.; Cerna, F.; Cid, L.; Ortega, J.C. Seguimiento Pesquerías Recursos Altamente Migratorios, 2016. Convenio de Desempeño 2016; Informe Final, Subsecretaría de Economía y EMT; Instituto de Fomento Pesquero: Valparaíso, Chile, 2017. [Google Scholar]
- Alheit, J.; Bernal, P. Effects of physical and biological changes on the biomass yield of the Humboldt Current ecosystem. In Large Marine Ecosystems—Stress, Mitigation and Sustainability; American Association for the Advancement of Science: Washington, DC, USA, 1993; pp. 53–68. [Google Scholar]
- Oerder, V.; Bento, J.P.; Morales, C.E.; Hormazabal, S.; Pizarro, O. Coastal Upwelling Front Detection off Central Chile (36.5–37°S) and Spatio-Temporal Variability of Frontal Characteristics. Remote Sens. 2018, 10, 690. [Google Scholar] [CrossRef]
- Lenart, A.; Missov, T.I. Goodness-of-fit tests for the Gompertz distribution. Commun. Stat. Theor. Meth. 2016, 45, 2920–2937. [Google Scholar] [CrossRef]
- Bondon, P. Estimation of autoregressive models with epsilon-skew-normal innovations. J. Multivar. Anal. 2009, 100, 1761–1776. [Google Scholar] [CrossRef] [Green Version]
- Azzalini, A. A Class of Distributions which includes the Normal Ones. Scand. J. Stat. 1985, 12, 171–178. [Google Scholar]
- Henze, N. A probabilistic representation of the ‘skew-normal’ distribution. Scand. J. Stat. 1986, 13, 271–275. [Google Scholar]
| Year | Model | Param. | Estim. | (S.D) | AIC | BIC | K–S | A–D | C–V | |
|---|---|---|---|---|---|---|---|---|---|---|
| 2012 () | SRG | 17.992 | 0.103 | −1401.896 | 2811.793 | 2830.399 | 0.044 (0.095) | 2.014 (0.090) | 0.214 (0.242) | |
| 2.590 | 0.067 | |||||||||
| 1.444 | 0.027 | |||||||||
| −0.207 | 0.075 | |||||||||
| ESN | 18.000 | 0.031 | −1507.534 | 3021.069 | 3035.023 | 0.118 (<0.01) | 26.417 (<0.01) | 2.059 (<0.01) | ||
| 1.657 | 0.015 | |||||||||
| −0.418 | 0.069 | |||||||||
| SN | 16.777 | 0.114 | −1404.581 | 2815.161 | 2829.116 | 0.041 (0.143) | 1.752 (0.126) | 0.198 (0.271) | ||
| 5.199 | 0.043 | |||||||||
| 2.527 | 0.311 | |||||||||
| 2013 () | SRG | 17.935 | 0.061 | −687.420 | 1382.839 | 1398.942 | 0.082 (0.010) | 2.632 (0.042) | 0.491 (0.041) | |
| 1.112 | 0.026 | |||||||||
| 0.432 | 0.021 | |||||||||
| −0.108 | 0.029 | |||||||||
| ESN | 17.600 | 0.046 | −716.375 | 1438.750 | 1450.827 | 0.089 (<0.01) | 7.721 (<0.01) | 0.970 (0.002) | ||
| 1.328 | 0.026 | |||||||||
| −0.376 | 0.092 | |||||||||
| SN | 16.598 | 0.200 | −691.531 | 1389.063 | 1401.140 | 0.066 (0.054) | 2.002 (0.092) | 0.328 (0.113) | ||
| 3.812 | 0.054 | |||||||||
| 2.421 | 0.617 | |||||||||
| 2014 () | SRG | 17.454 | 0.048 | −653.082 | 1314.164 | 1330.502 | 0.092 (<0.01) | 2.848 (0.033) | 0.533 (0.032) | |
| 0.896 | 0.020 | |||||||||
| 0.375 | 0.020 | |||||||||
| −0.106 | 0.025 | |||||||||
| ESN | 17.200 | 0.053 | −703.748 | 1413.496 | 1425.750 | 0.109 (<0.01) | 11.996 (<0.01) | 1.529 (<0.01) | ||
| 0.956 | 0.035 | |||||||||
| −0.384 | 0.090 | |||||||||
| SN | 16.146 | 0.098 | −666.984 | 1339.968 | 1352.222 | 0.096 (<0.01) | 4.055 (<0.01) | 0.711 (0.011) | ||
| 3.245 | 0.045 | |||||||||
| 3.434 | 0.618 |
| Year | Quantifier | 2012 | 2013 | 2014 |
|---|---|---|---|---|
| 0.765 | 0.781 | 2.754 | ||
| 0.384 | −0.362 | −0.365 | ||
| 0.252 | −0.417 | −0.418 | ||
| 0.163 | −0.457 | −0.457 | ||
| 2012 | - | 0.266 | 0.911 | |
| Statistic | - | 143.740 | 520.41 | |
| p-value | - | <0.01 | <0.01 | |
| 2013 | 0.080 | - | 0.071 | |
| Statistic | 43.192 | - | 30.233 | |
| p-value | <0.01 | - | <0.01 | |
| 2014 | 0.143 | 0.043 | - | |
| Statistic | 80.327 | 18.282 | - | |
| p-value | <0.01 | <0.01 | - |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Contreras-Reyes, J.E.; Maleki, M.; Devia Cortés, D. Skew-Reflected-Gompertz Information Quantifiers with Application to Sea Surface Temperature Records. Mathematics 2019, 7, 403. https://doi.org/10.3390/math7050403
Contreras-Reyes JE, Maleki M, Devia Cortés D. Skew-Reflected-Gompertz Information Quantifiers with Application to Sea Surface Temperature Records. Mathematics. 2019; 7(5):403. https://doi.org/10.3390/math7050403
Chicago/Turabian StyleContreras-Reyes, Javier E., Mohsen Maleki, and Daniel Devia Cortés. 2019. "Skew-Reflected-Gompertz Information Quantifiers with Application to Sea Surface Temperature Records" Mathematics 7, no. 5: 403. https://doi.org/10.3390/math7050403
APA StyleContreras-Reyes, J. E., Maleki, M., & Devia Cortés, D. (2019). Skew-Reflected-Gompertz Information Quantifiers with Application to Sea Surface Temperature Records. Mathematics, 7(5), 403. https://doi.org/10.3390/math7050403







