Predicting Maximal Gaps in Sets of Primes
Abstract
1. Introduction
1.1. Notation
| q, r | coprime integers, |
| the n-th prime; | |
| increasing sequence of primes p such that (i) (mod q) and | |
| (ii) p is the least prime in a prime k-tuple with a given pattern . | |
| Note: depends on q, r, k, and on the pattern of the k-tuple. | |
| When , is the sequence of all primes (mod q). | |
| the k-tuple pattern of offsets: (see Section 1.2) | |
| the greatest common divisor of m and n | |
| Euler’s totient function (OEIS A000010) | |
| Golubev’s generalization (5) of Euler’s totient (see Section 2.1.1) | |
| the Gumbel distribution cdf: | |
| the exponential distribution cdf: | |
| the scale parameter of exponential/Gumbel distributions, as applicable | |
| the location parameter (mode) of the Gumbel distribution | |
| the Euler–Mascheroni constant: | |
| the Hardy–Littlewood constants (see Appendix B) | |
| the natural logarithm of x | |
| the logarithmic integral of x: | |
| the integral (see Appendix C) | |
| Gap measure functions: | |
| the maximal gap between primes | |
| the maximal gap between primes (case ) | |
| the maximal gap between primes not exceeding x | |
| the n-th record (maximal) gap between primes | |
| a, , | the expected average gaps between primes in (see Section 2.2) |
| T, , | trend functions predicting the growth of maximal gaps (see Section 2.3) |
| Gap counting functions: | |
| the number of maximal gaps with endpoints | |
| the number of maximal gaps with endpoints (case ) | |
| the number of gaps of a given even size between successive | |
| primes (mod q), with ; if or . | |
| Prime counting functions: | |
| the total number of primes | |
| the total number of primes not exceeding x | |
| the total number of primes (case ) |
1.2. Definitions: Prime k-Tuples, Gaps, Sequence
- Twin primes are pairs of consecutive primes that have the form (p, ). This is the densest admissible pattern of two; .
- Prime quadruplets are clusters of four consecutive primes of the form (p, , , ). This is the densest admissible pattern of four; .
- Prime sextuplets are clusters of six consecutive primes (p, , , , , ). This is the densest admissible pattern of six; .
- (i)
- In Section 2 we derive formulas predicting the most probable sizes of maximal gaps . It is not known how close these most probable sizes might be to the maximal order of . Thus, in the special case , , , probable values of seem to be about [13]; but it is not implausible that the maximal order of is closer to [6]. For further discussion of extremely large gaps, see Section 3.5.
- (ii)
- How hard is it to compute gaps in sequence ? Given , and r coprime to q, our PARI/GP code (Appendix A) takes several hours to compute all maximal gaps in sequence up to 14-digit primes. In some numerical experiments, we carried out the computation all the way to . In most cases, however, we stopped the computation at or at or even earlier, to quickly gather statistics for all r coprime to q. A similar strategy was also used for sequences with (source code for is not included). See Section 3 for a detailed discussion of our numerical results.
1.3. Generalization to Other Subsets of Primes
1.4. When Are Equations (1), (2) Inapplicable?
2. Heuristics and Conjectures
2.1. Equidistribution of k-Tuples
2.1.1. Counting the -Allowed Residue Classes
2.1.2. The k-Tuple Infinitude Conjecture
2.1.3. The k-Tuple Equidistribution Conjecture
2.2. Average Gap Sizes
2.3. Maximal Gap Sizes
2.3.1. Case of k-Tuples:
2.3.2. Case of Primes:
2.4. How Many Maximal Gaps Are There?
3. Numerical Results
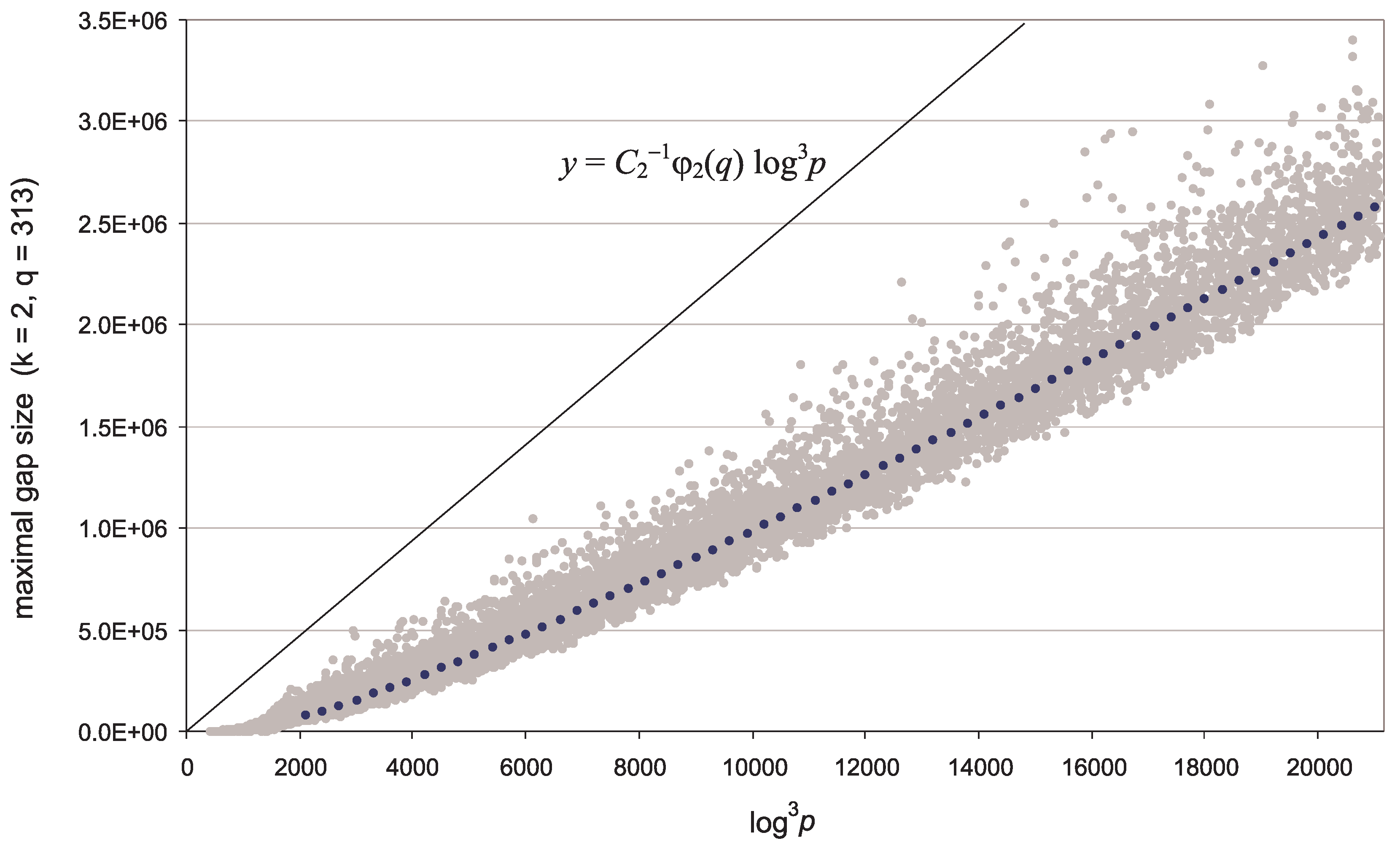
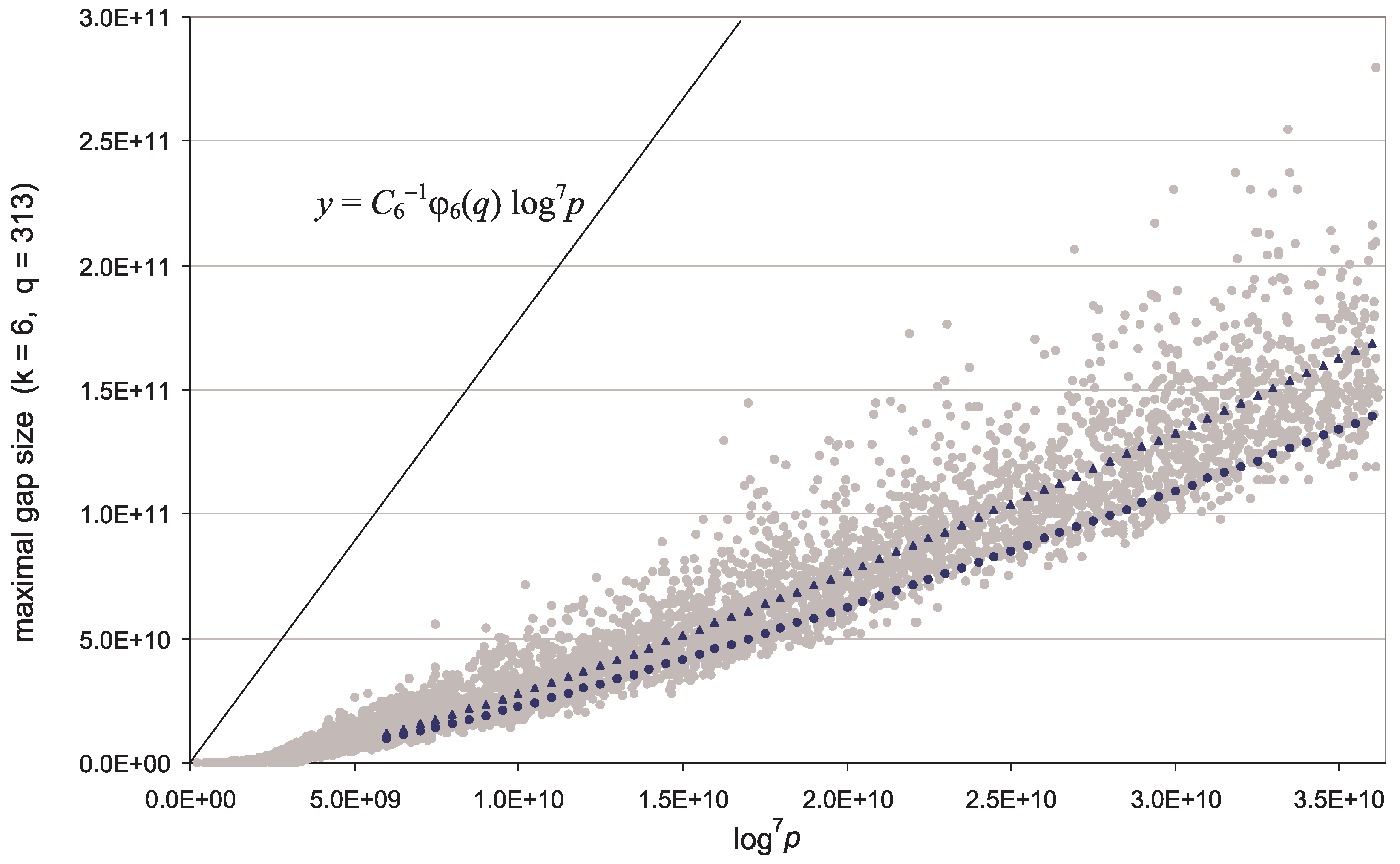
3.1. The Growth Trend of Maximal Gaps
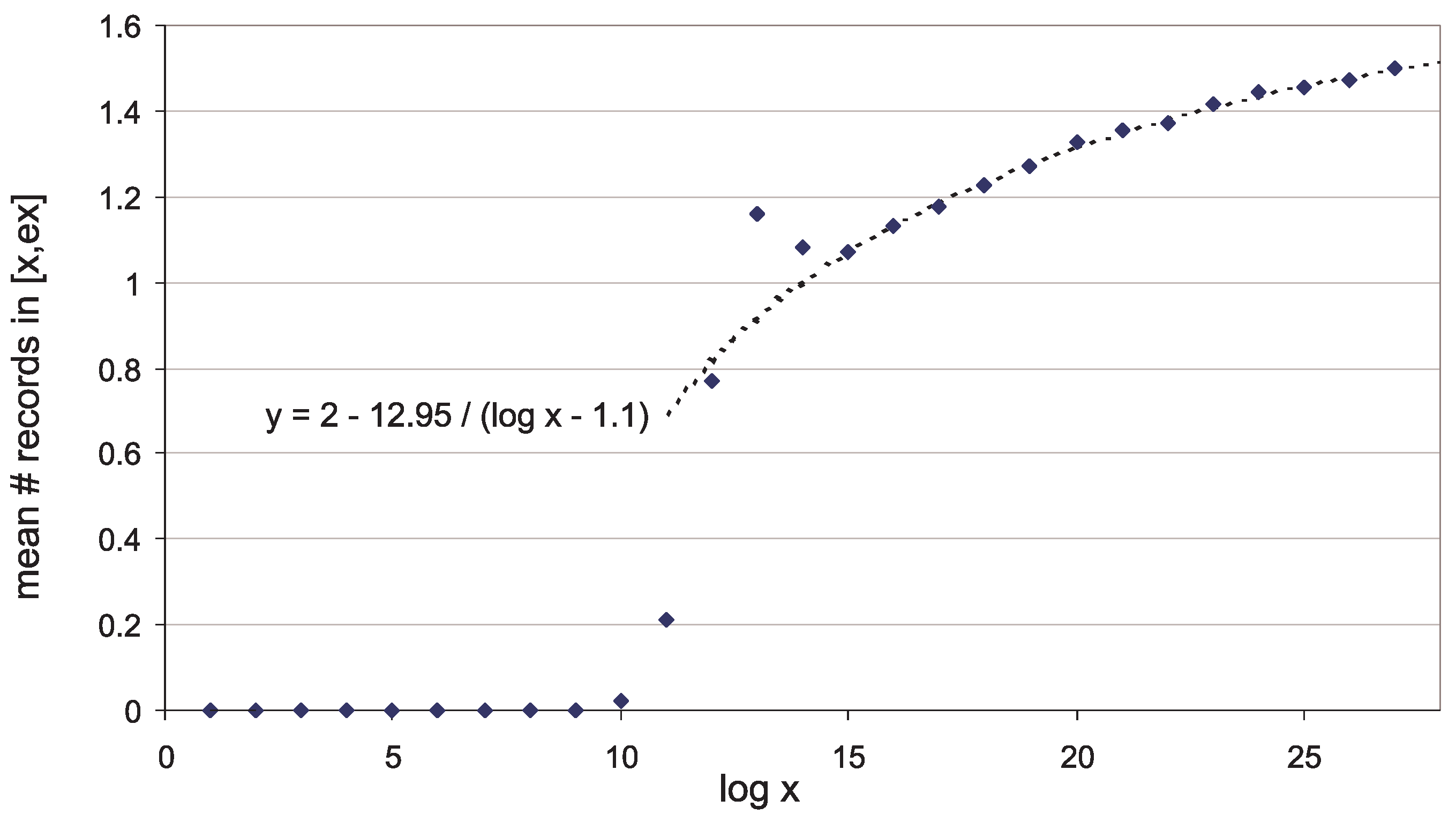
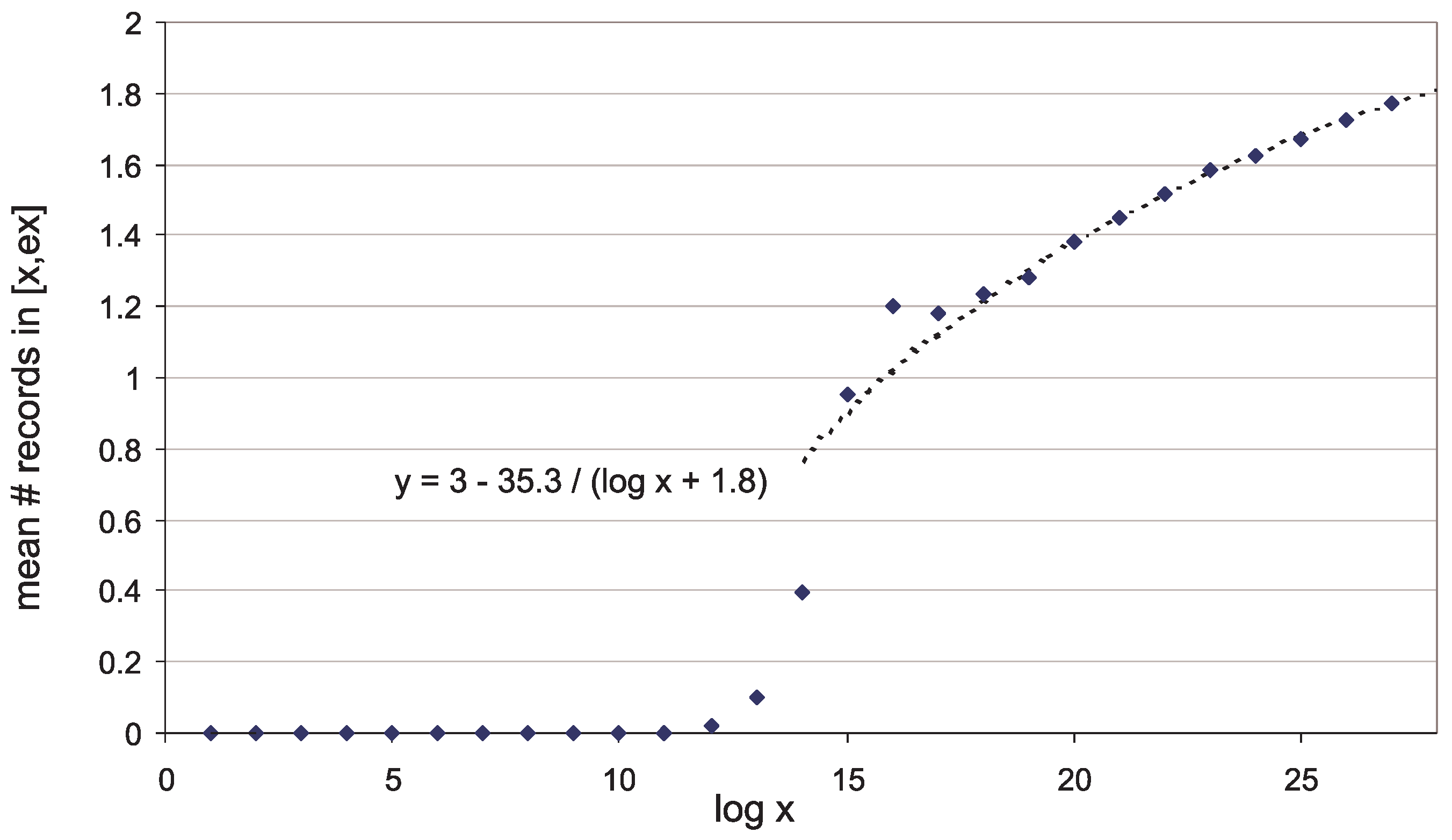
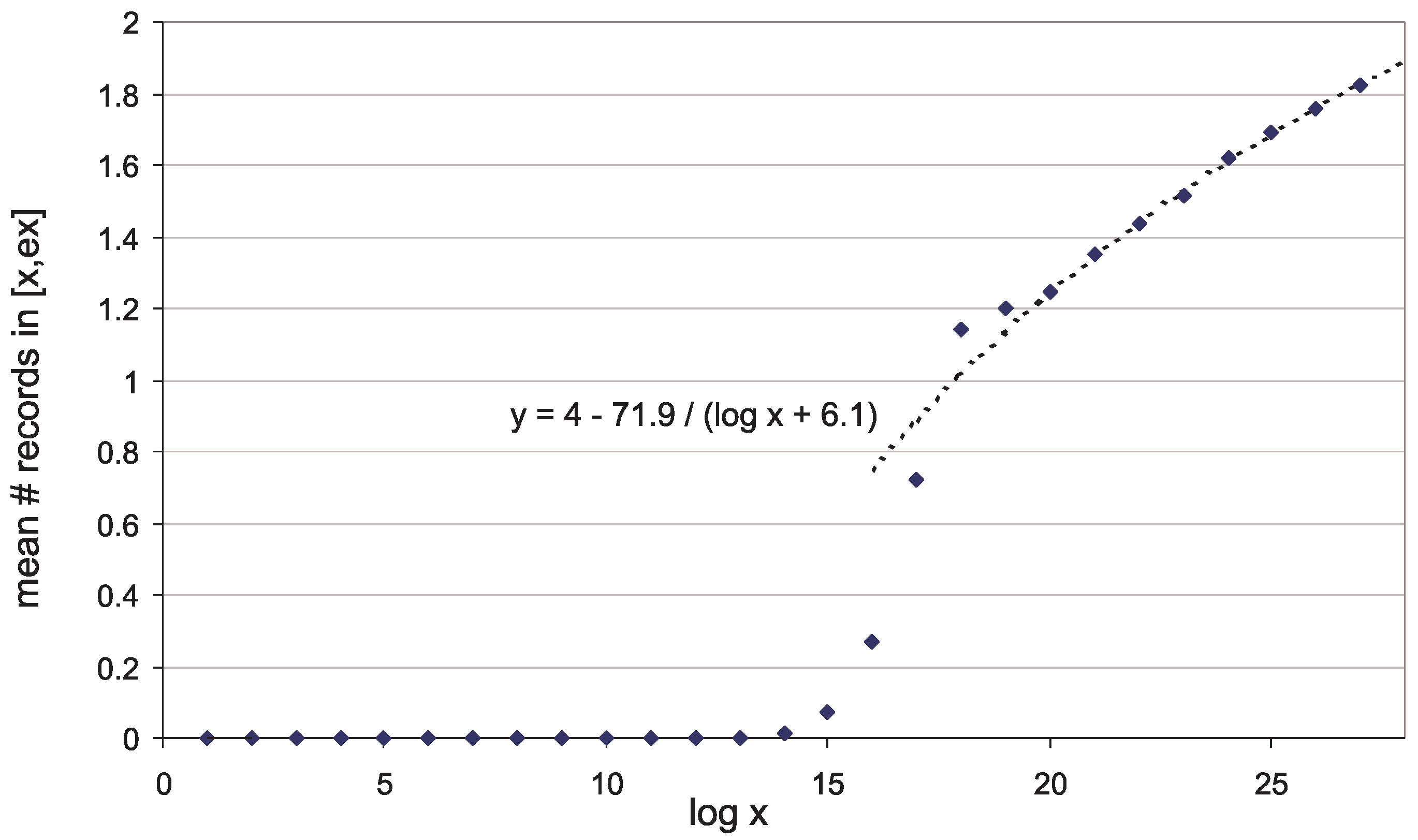
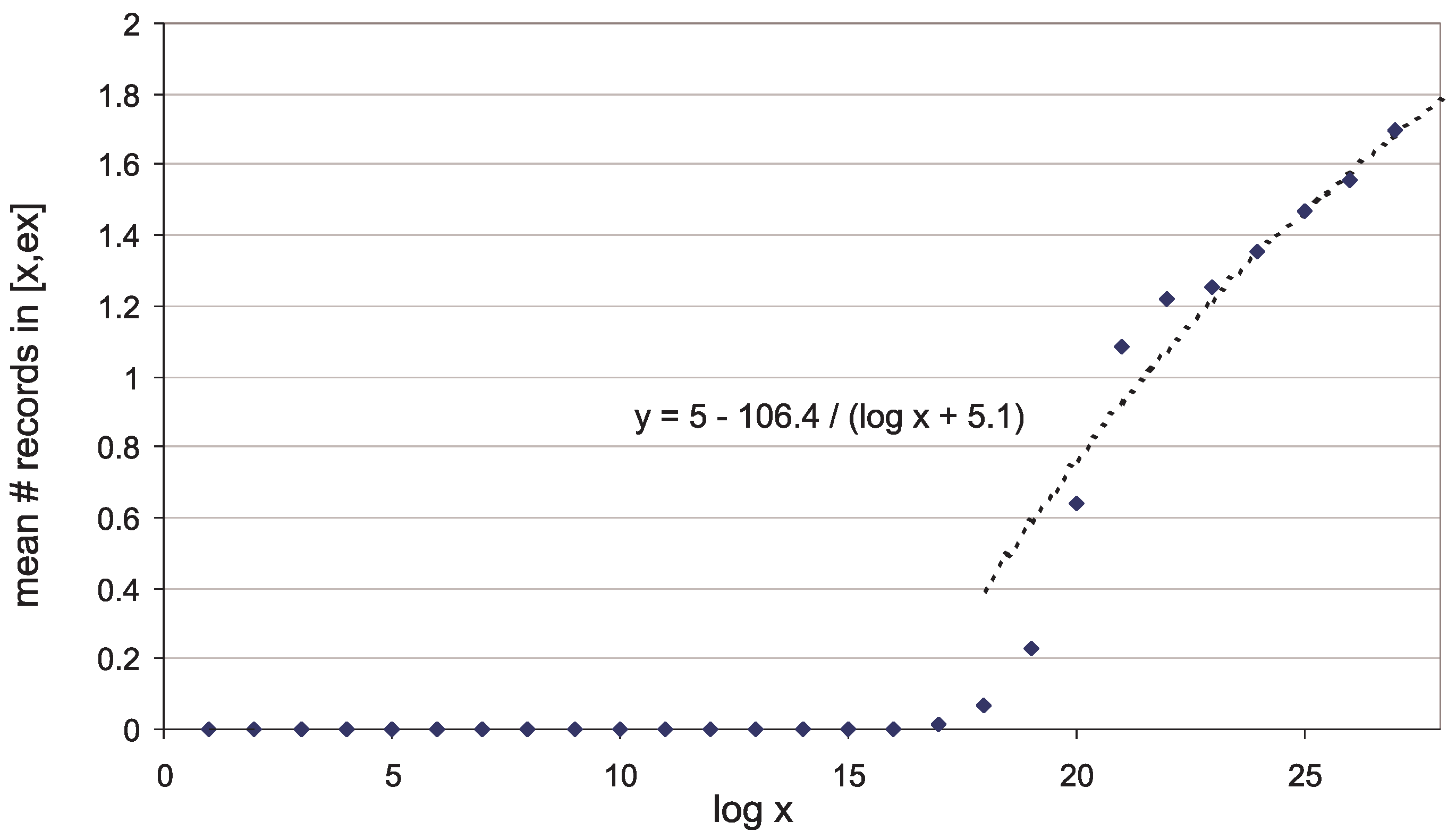
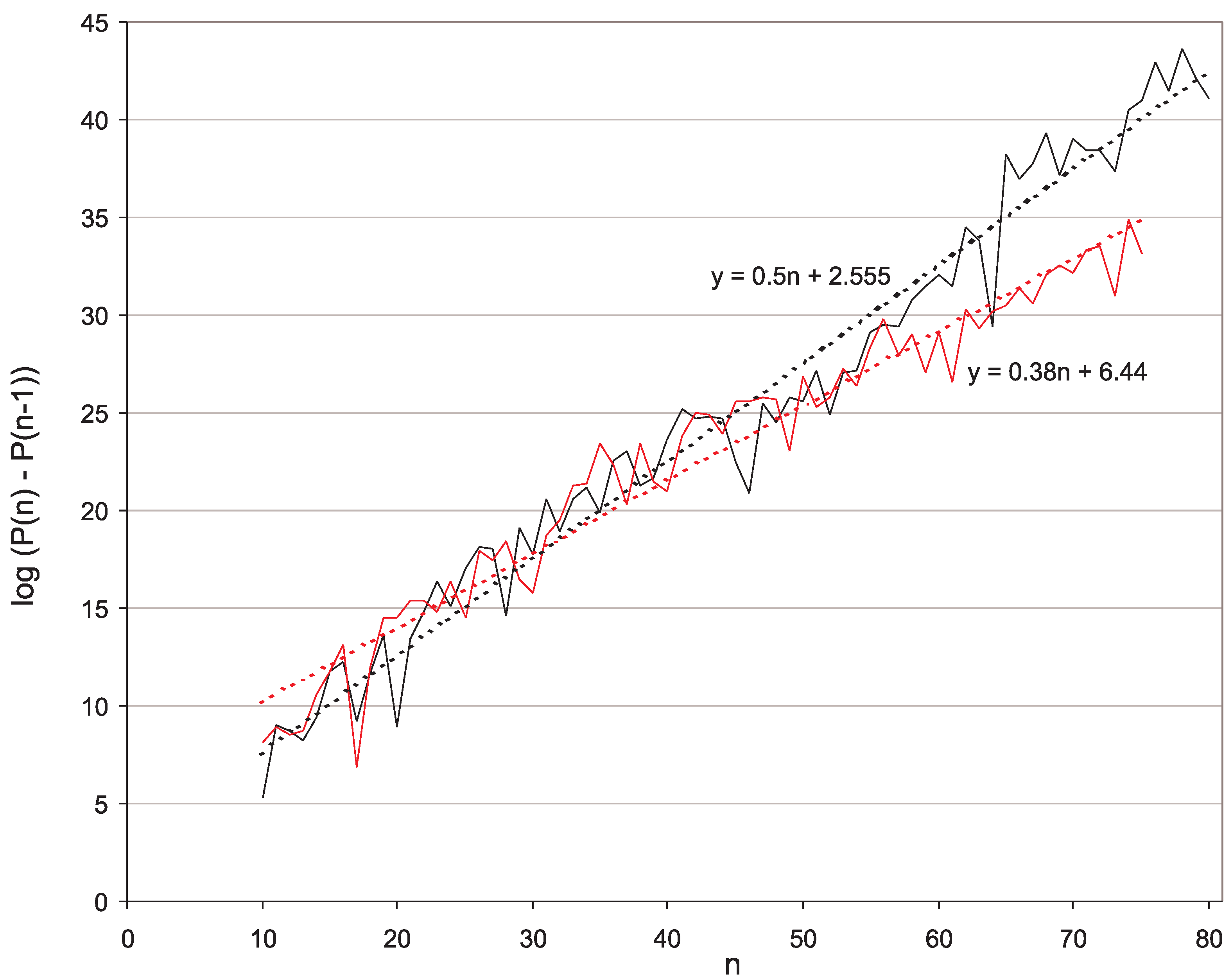
- For (the case of maximal gaps between primes ) the EVT-based trend curve goes too high (Figure 1, blue curve). Meanwhile, the trend (33) (Figure 1, red curve)satisfactorily predicts gap sizes , with the empirical correction termwhere the parameter valuesare close to optimal for and . Here the qualifier optimal is to be understood in conjunction with the rescaling transformation (47) introduced below in Section 3.2. A trend is optimal if after transformation (47) the most probable rescaled values w turn out to be near zero, and the mode of best-fit Gumbel distribution for w-values is also close to zero, ; see Figure 4. In view of (45) it is possible that, for all q, the optimal term b in (33) has the form , where very slowly decreases to zero as . (Note that in Section 2.3.2 we correctly estimated b to be but did not predict the appearance of Euler’s function in the term b.)
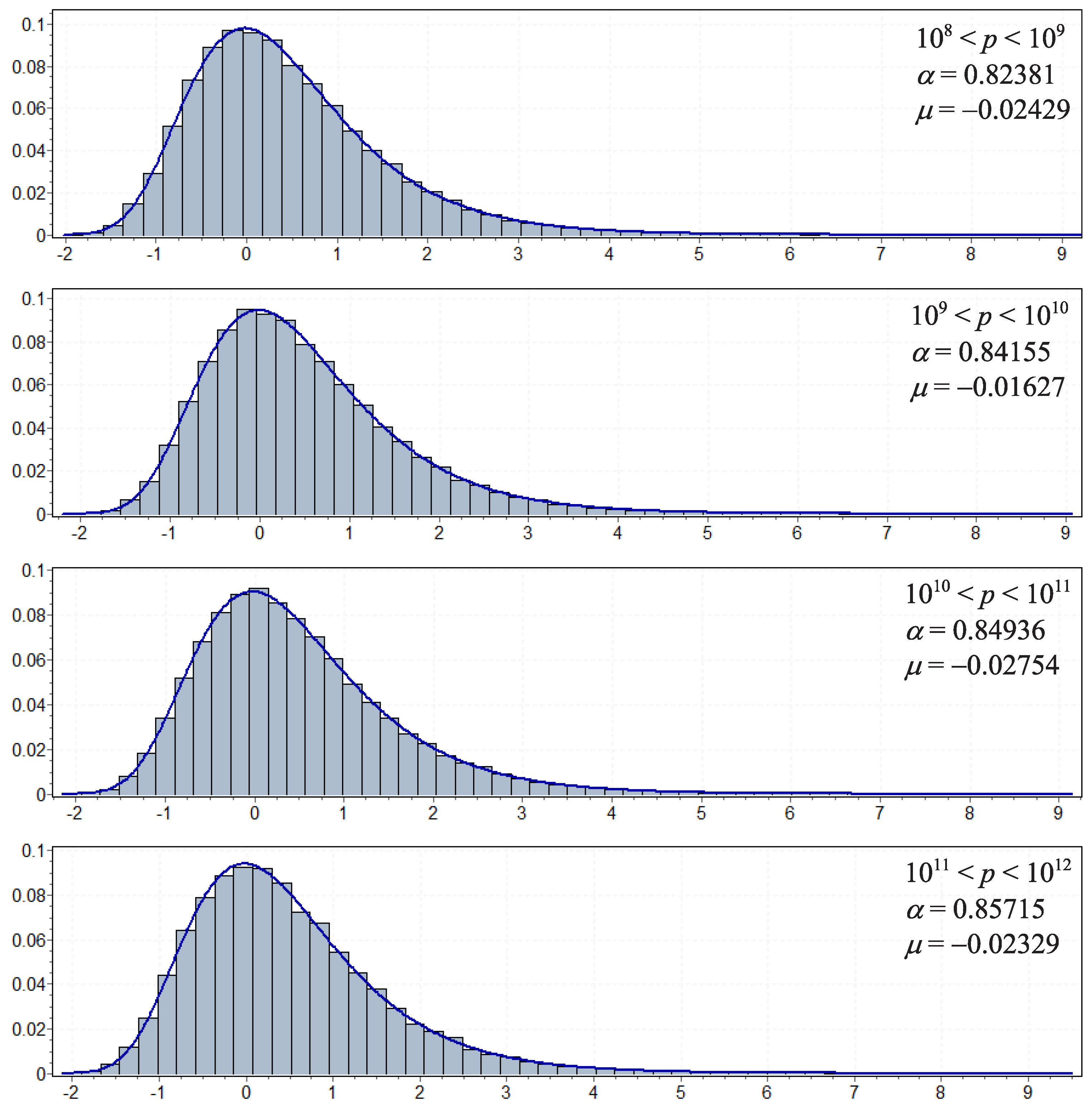
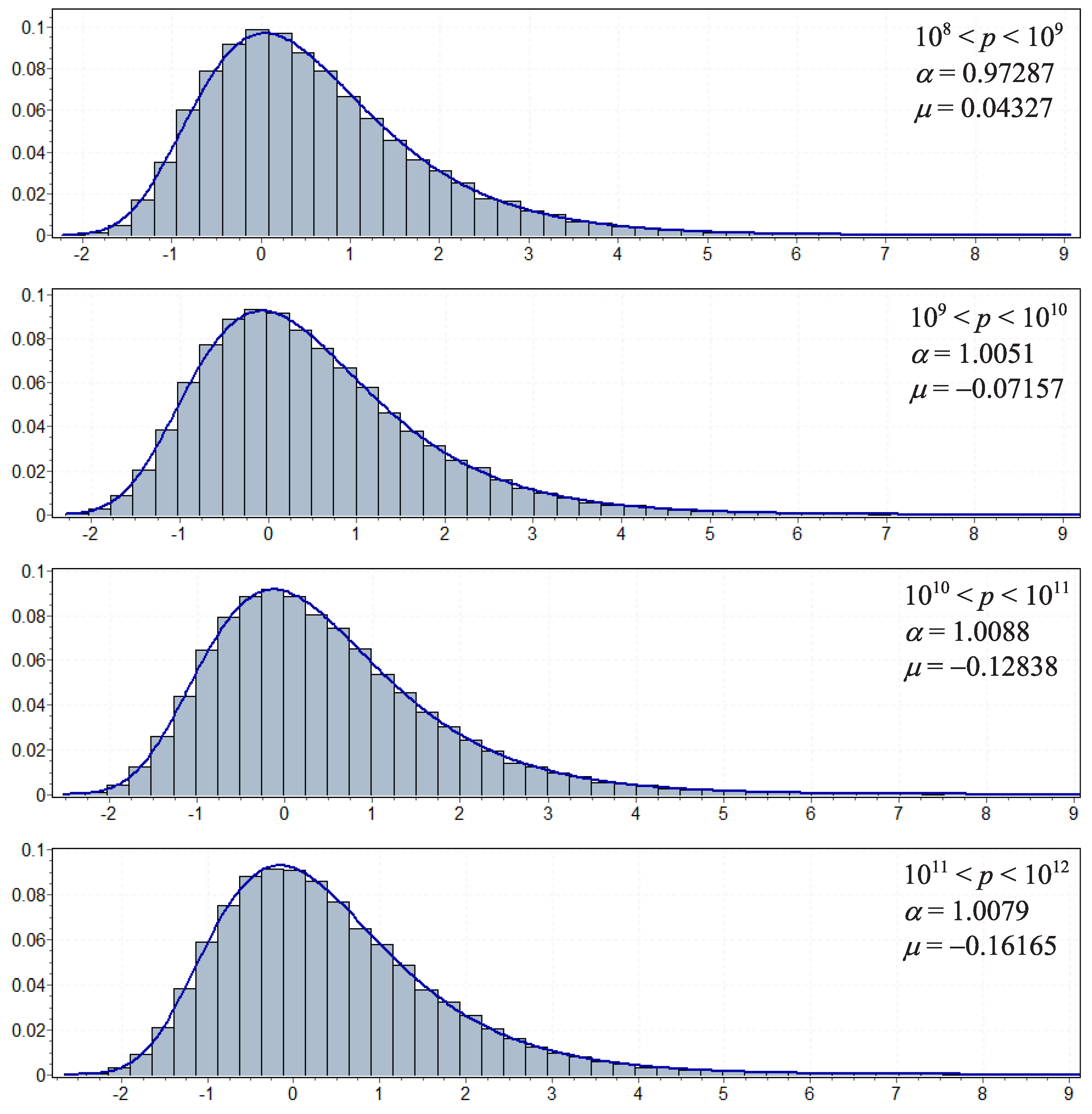
3.2. The Distribution of Maximal Gaps
3.3. Counting the Maximal Gaps
3.4. How Long Do We Wait for the Next Maximal Gap?
3.5. Exceptionally Large Gaps:
4. Summary
- The Gumbel distribution, after proper rescaling, is a possible limit law for as well as . The existence of such a limiting distribution is an open question.
- We conjecture that the total number of maximal gaps observed up to x is below for some .
- More generally, we conjecture: the number of maximal gaps between primes in up to x satisfies the inequality for some , where k is the number of integers in the pattern defining the sequence .
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| cdf | cumulative distribution function |
| probability density function | |
| EVT | extreme value theory |
| GEV | Generalized Extreme Value distribution |
| GRH | Generalized Riemann Hypothesis |
Appendix A. Details of Computational Experiments
Appendix A.1. PARI/GP Program maxgap.gp
Appendix A.2. PARI/GP: Auxiliary Functions for maxgap.gp
Appendix A.3. Notes on Distribution Fitting
- From the File menu, choose Open.
- Select the data file.
- Specify Field Delimiter = space.
- Click Update, then OK.
Appendix B. The Hardy–Littlewood Constants
Appendix C. Integrals Lik (x)
References
- Sloane, N.J.A. (Ed.) The On-Line Encyclopedia of Integer Sequences. 2019. Available online: https://oeis.org/ (accessed on 2 May 2019).
- Berndt, B.C. Ramanujan’s Notebooks, IV; Springer: New York, NY, USA, 1994. [Google Scholar]
- Nicely, T.R. First Occurrence Prime Gaps, Preprint. 2018. Available online: http://www.trnicely.net/gaps/gaplist.html (accessed on 2 May 2019).
- Cramér, H. On the order of magnitude of the difference between consecutive prime numbers. Acta Arith. 1936, 2, 23–46. [Google Scholar] [CrossRef]
- Shanks, D. On maximal gaps between successive primes. Math. Comp. 1964, 18, 646–651. [Google Scholar] [CrossRef]
- Granville, A. Harald Cramér and the distribution of prime numbers. Scand. Actuar. J. 1995, 1, 12–28. [Google Scholar] [CrossRef]
- Baker, R.C.; Harman, G.; Pintz, J. The difference between consecutive primes, II. Proc. Lond. Math. Soc. 2001, 83, 532–562. [Google Scholar] [CrossRef]
- Ford, K.; Green, B.; Konyagin, S.; Maynard, J.; Tao, T. Long gaps between primes. J. Am. Math. Soc. 2018, 31, 65–105. [Google Scholar] [CrossRef]
- Funkhouser, S.; Ledoan, A.H.; Goldston, D.A. Distribution of large gaps between primes. arXiv 2018, arXiv:1802.07609. [Google Scholar]
- Nicely, T.R.; Nyman, B. New prime gaps between 1015 and 5 × 1016. J. Integer Seq. 2003, 6, 03.3.1. [Google Scholar]
- Oliveira e Silva, T.; Herzog, S.; Pardi, S. Empirical verification of the even Goldbach conjecture and computation of prime gaps up to 4 × 1018. Math. Comp. 2014, 83, 2033–2060. [Google Scholar] [CrossRef]
- Wolf, M. Some Conjectures on the Gaps between Consecutive Primes, Preprint. 1998. Available online: http://www.researchgate.net/publication/2252793 (accessed on 2 May 2019).
- Wolf, M. Some heuristics on the gaps between consecutive primes. arXiv 2011, arXiv:1102.0481. [Google Scholar]
- Wolf, M. Nearest neighbor spacing distribution of prime numbers and quantum chaos. Phys. Rev. E 2014, 89, 022922. [Google Scholar] [CrossRef] [PubMed]
- Cadwell, J.H. Large intervals between consecutive primes. Math. Comp. 1971, 25, 909–913. [Google Scholar] [CrossRef]
- Kourbatov, A. Maximal gaps between prime k-tuples: A statistical approach. J. Integer Seq. 2013, 16, 13.5.2. [Google Scholar]
- Kourbatov, A. Tables of record gaps between prime constellations. arXiv 2013, arXiv:1309.4053. [Google Scholar]
- Ford, K. Large Gaps in Sets of Primes and Other Sequences. Presented at the School on Probability in Number Theory. Centre De Recherches Mathématiques, University of Montreal. 2018. Available online: http://www.crm.umontreal.ca/2018/Nombres18/horaireecole/pdf/montreal_talk1.pdf (accessed on 2 May 2019).
- Oliveira e Silva, T. Gaps between Twin Primes, Preprint. 2015. Available online: http://sweet.ua.pt/tos/twin_gaps.html (accessed on 2 May 2019).
- Broughan, K.A.; Barnett, A.R. On the subsequence of primes having prime subscripts. J. Integer Seq. 2009, 12, 09.2.3. [Google Scholar]
- Bayless, J.; Klyve, D.; Oliveira e Silva, T. New bounds and computations on prime-indexed primes. Integers 2013, 13, A43. [Google Scholar]
- Batchko, R.G. A prime fractal and global quasi-self-similar structure in the distribution of prime-indexed primes. arXiv 2014, arXiv:1405.2900v2. [Google Scholar]
- Guariglia, E. Primality, fractality and image analysis. Entropy 2019, 21, 304. [Google Scholar] [CrossRef]
- Wolf, M. Some conjectures on primes of the form m2 + 1. J. Comb. Number Theory 2013, 5, 103–131. [Google Scholar]
- Baker, R.C.; Zhao, L. Gaps between primes in Beatty sequences. Acta Arith. 2016, 172, 207–242. [Google Scholar] [CrossRef]
- Mills, W.H. A prime-representing function. Bull. Am. Math. Soc. 1947, 53, 604. [Google Scholar] [CrossRef]
- Salas, C. Base-3 repunit primes and the Cantor set. Gen. Math. 2011, 19, 103–107. [Google Scholar]
- Fine, B.; Rosenberger, G. Number Theory. An Introduction via the Density of Primes; Birkhäuser: Cham, Switzerland, 2016. [Google Scholar]
- Friedlander, J.B.; Goldston, D.A. Variance of distribution of primes in residue classes. Q. J. Math. Oxf. 1996, 47, 313–336. [Google Scholar] [CrossRef][Green Version]
- Hardy, G.H.; Littlewood, J.E. Some Problems of ‘Partitio Numerorum.’ III. On the Expression of a Number as a Sum of Primes. Acta Math. 1923, 44, 1–70. [Google Scholar] [CrossRef]
- Bateman, P.T.; Horn, R.A. A heuristic asymptotic formula concerning the distribution of prime numbers. Math. Comp. 1962, 16, 363–367. [Google Scholar] [CrossRef]
- Golubev, V.A. Generalization of the functions φ(n) and π(x). Časopis Pro Pěstování Matematiky 1953, 78, 47–48. [Google Scholar]
- Golubev, V.A. Sur certaines fonctions multiplicatives et le problème des jumeaux. Mathesis 1958, 67, 11–20. [Google Scholar]
- Golubev, V.A. Exact formulas for the number of twin primes and other generalizations of the function π(x). Časopis Pro Pěstování Matematiky 1962, 87, 296–305. [Google Scholar]
- Sándor, J.; Crstici, B. Handbook of Number Theory II; Kluwer: Dordrecht, The Netherlands, 2004. [Google Scholar]
- Alder, H.L. A generalization of the Euler phi-function. Am. Math. Mon. 1958, 65, 690–692. [Google Scholar]
- Dirichlet, P.G.L. Beweis des Satzes, dass jede unbegrenzte arithmetische Progression, deren erstes Glied und Differenz ganze Zahlen ohne gemeinschaftlichen Factor sind, unendlich viele Primzahlen enthält. Abhandlungen der Königlichen Preußischen Akademie der Wissenschaften zu Berlin 1837, 48, 45–71. [Google Scholar]
- Gumbel, E.J. Statistics of Extremes; Columbia University Press: New York, NY, USA, 1958. [Google Scholar]
- Ares, S.; Castro, M. Hidden structure in the randomness of the prime number sequence? Physica A 2006, 360, 285–296. [Google Scholar] [CrossRef]
- Goldston, D.A.; Ledoan, A.H. On the differences between consecutive prime numbers, I. In Proceedings of the Integers Conference 2011: Combinatorial Number Theory, Carrollton, GA, USA, 26–29 October 2011; pp. 37–44. [Google Scholar]
- Kourbatov, A. On the nth record gap between primes in an arithmetic progression. Int. Math. Forum 2018, 13, 65–78. [Google Scholar] [CrossRef][Green Version]
- Krug, J. Records in a changing world. J. Stat. Mech. Theory Exp. 2007, 2007, P07001. [Google Scholar] [CrossRef]
- Kourbatov, A. On the distribution of maximal gaps between primes in residue classes. arXiv 2016, arXiv:1610.03340. [Google Scholar]
- Brent, R.P. Twin primes (seem to be) more random than primes. Presented at the Second Number Theory Down Under Conference, Newcastle, Australia, 24–25 October 2014; Available online: http://maths-people.anu.edu.au/~brent/pd/twin_primes_and_primes.pdf (accessed on 2 May 2019).
- Pintz, J. Cramér vs Cramér: On Cramér’s probabilistic model for primes. Functiones Approximatio 2007, 37, 361–376. [Google Scholar] [CrossRef]
- Kourbatov, A. The distribution of maximal prime gaps in Cramér’s probabilistic model of primes. Int. J. Stat. Probab. 2014, 3, 18–29. [Google Scholar] [CrossRef][Green Version]
- Li, J.; Pratt, K.; Shakan, G. A lower bound for the least prime in an arithmetic progression. Q. J. Math. 2017, 68, 729–758. [Google Scholar] [CrossRef]
- Wolf, M. First Occurrence of a Given Gap Between Consecutive Primes, Preprint. 1997. Available online: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.52.5981&rep=rep1&type=pdf (accessed on 2 May 2019).
- Sun, Z.-W. Conjectures involving arithmetical sequences. In Number Theory: Arithmetic in Shangri-La, Proceedings of the 6th China-Japan Seminar, Shanghai, China, 15–17 August 2011; Kanemitsu, S., Li, H., Liu, J., Eds.; World Sci.: Singapore, 2013; pp. 244–258. [Google Scholar]
- Kourbatov, A. Upper bounds for prime gaps related to Firoozbakht’s conjecture. J. Integer Seq. 2015, 18, 15.11.2. [Google Scholar]
- MathWave Technologies. EasyFit—Distribution Fitting Software. 2013. Available online: http://www.mathwave.com/easyfit-distribution-fitting.html (accessed on 2 May 2019).
- Riesel, H. Prime Numbers and Computer Methods for Factorization; Birkhäuser: Boston, MA, USA, 1994. [Google Scholar]
- Forbes, A.D. Prime k-Tuplets, Preprint. 2018. Available online: http://anthony.d.forbes.googlepages.com/ktuplets.htm (accessed on 2 May 2019).
- Finch, S.R. Mathematical Constants; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Prudnikov, A.; Brychkov, Y.; Marichev, O. Integrals and Series. Vol. 1: Elementary Functions; Gordon and Breach: New York, NY, USA, 1986. [Google Scholar]

| Gap | Start of Gap | End of Gap (p) | ) | ||
|---|---|---|---|---|---|
| (i) 208650 | 3415781 | 3624431 | 1605 | 341 | 1.0786589153 |
| 316790 | 726611 | 1043401 | 2005 | 801 | 1.0309808771 |
| 229350 | 1409633 | 1638983 | 2085 | 173 | 1.0145547849 |
| 532602 | 355339 | 887941 | 4227 | 271 | 1.0081862161 |
| 984170 | 5357381 | 6341551 | 4279 | 73 | 1.0339720553 |
| 1263426 | 10176791 | 11440217 | 4897 | 825 | 1.0056800570 |
| 2306938 | 82541821 | 84848759 | 6907 | 3171 | 1.0022590147 |
| 3415794 | 376981823 | 380397617 | 8497 | 3921 | 1.0703375544 |
| 2266530 | 198565889 | 200832419 | 8785 | 7319 | 1.0335372951 |
| 7326222 | 222677837 | 230004059 | 20017 | 8729 | 1.0166221904 |
| 6336090 | 10862323 | 17198413 | 23467 | 20569 | 1.0064940453 |
| 7230930 | 130172279 | 137403209 | 24595 | 15539 | 1.0468373915 |
| 5910084 | 51763573 | 57673657 | 28971 | 21367 | 1.0199911211 |
| (ii) 411480 | 470669167 | 471080647 | 3048 | 55 | 1.0235488825 |
| 208650 | 3415781 | 3624431 | 3210 | 341 | 1.0786589153 |
| 316790 | 726611 | 1043401 | 4010 | 801 | 1.0309808771 |
| 229350 | 1409633 | 1638983 | 4170 | 173 | 1.0145547849 |
| 657504 | 896016139 | 896673643 | 4566 | 2563 | 1.0179389550 |
| 1530912 | 728869417 | 730400329 | 6896 | 3593 | 1.0684247390 |
| 532602 | 355339 | 887941 | 8454 | 271 | 1.0081862161 |
| 984170 | 5357381 | 6341551 | 8558 | 73 | 1.0339720553 |
| 1263426 | 10176791 | 11440217 | 9794 | 825 | 1.0056800570 |
| 2119706 | 665152001 | 667271707 | 10046 | 6341 | 1.0223668231 |
| 1885228 | 163504573 | 165389801 | 10532 | 5805 | 1.0000704209 |
| 1594416 | 145465687 | 147060103 | 13512 | 9007 | 1.0026889378 |
| 2306938 | 82541821 | 84848759 | 13814 | 3171 | 1.0022590147 |
| 3108778 | 524646211 | 527754989 | 15622 | 12585 | 1.0098218219 |
| 1896608 | 164663 | 2061271 | 16934 | 12257 | 1.0598397341 |
| 3415794 | 376981823 | 380397617 | 16994 | 3921 | 1.0703375544 |
| 2266530 | 198565889 | 200832419 | 17570 | 7319 | 1.0335372951 |
| 2937868 | 71725099 | 74662967 | 17698 | 12803 | 1.0103309882 |
| 2823288 | 37906669 | 40729957 | 18098 | 9457 | 1.0162761199 |
| 2453760 | 11626561 | 14080321 | 18176 | 12097 | 1.0107626289 |
| 3906628 | 190071823 | 193978451 | 18692 | 11567 | 1.1480589845 |
| 2157480 | 13074917 | 15232397 | 27660 | 19397 | 1.0716522452 |
| 5450496 | 366870073 | 372320569 | 28388 | 11949 | 1.0140771094 |
| 3422630 | 735473 | 4158103 | 29762 | 21185 | 1.0368176014 |
| (iii) 657504 | 896016139 | 896673643 | 2283 | 280 | 1.0179389550 |
| 2119706 | 665152001 | 667271707 | 5023 | 1318 | 1.0223668231 |
| 3108778 | 524646211 | 527754989 | 7811 | 4774 | 1.0098218219 |
| 1896608 | 164663 | 2061271 | 8467 | 3790 | 1.0598397341 |
| 2937868 | 71725099 | 74662967 | 8849 | 3954 | 1.0103309882 |
| 2823288 | 37906669 | 40729957 | 9049 | 408 | 1.0162761199 |
| 3422630 | 735473 | 4158103 | 14881 | 6304 | 1.0368176014 |
| 3758772 | 144803717 | 148562489 | 15927 | 11360 | 1.0000152764 |
| 3002682 | 8462609 | 11465291 | 16869 | 11240 | 1.0107025944 |
| 8083028 | 344107541 | 352190569 | 19619 | 9900 | 1.1134625422 |
| 4575906 | 20250677 | 24826583 | 22653 | 21548 | 1.0463153374 |
| 5609136 | 34016537 | 39625673 | 26967 | 11150 | 1.0412524005 |
| 7044864 | 302145839 | 309190703 | 27519 | 14738 | 1.0048671503 |
| 6580070 | 9659921 | 16239991 | 28609 | 18688 | 1.0046426332 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kourbatov, A.; Wolf, M. Predicting Maximal Gaps in Sets of Primes. Mathematics 2019, 7, 400. https://doi.org/10.3390/math7050400
Kourbatov A, Wolf M. Predicting Maximal Gaps in Sets of Primes. Mathematics. 2019; 7(5):400. https://doi.org/10.3390/math7050400
Chicago/Turabian StyleKourbatov, Alexei, and Marek Wolf. 2019. "Predicting Maximal Gaps in Sets of Primes" Mathematics 7, no. 5: 400. https://doi.org/10.3390/math7050400
APA StyleKourbatov, A., & Wolf, M. (2019). Predicting Maximal Gaps in Sets of Primes. Mathematics, 7(5), 400. https://doi.org/10.3390/math7050400




