Generalized Viscosity Implicit Iterative Process for Asymptotically Non-Expansive Mappings in Banach Spaces

Abstract

In this paper, we propose a generalized viscosity implicit iterative method for asymptotically non-expansive mappings in Banach spaces. The strong convergence theorem of this algorithm is proved, which solves the variational inequality problem. Moreover, we provide some applications to zero-point problems and equilibrium problems. Further, a numerical example is given to illustrate our convergence analysis. The results generalize and improve corresponding results in the literature.

1. Introduction

Variational inequality theory and fixed point theory are two important fields in non-linear analysis and optimization. Much attention has been given to developing implementable viscosity iterative methods for solving variational inequality problems, due to their applications in many real world problems, such as signal processing, saddle point problems, equilibrium problems, and game theory, in the frameworks of Hilbert spaces or Banach spaces; see [1,2,3,4,5,6,7,8,9] and the references therein.

The implicit midpoint rule is one of the most important numerical methods for solving certain differential algebraic equations. Convergence analysis for viscosity iterative algorithms using the implicit midpoint rule have been introduced by many authors; see [10,11,12,13,14,15,16] and the references therein. More precisely, in 2015, Xu et al. [17] introduced the viscosity implicit midpoint rule for non-expansive mappings in Hilbert spaces, wherein they showed that the sequence $\left\{x_n\right\}$ generated by

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T(\frac{x_{n+1}+x_n}{2}),n\ge 0,$$

converges strongly to a fixed point of T, which was also the solution of the following variational inequality (VI):

$$⟨(I-f)q,x-q⟩\ge 0,x\in F(T),$$

where $F(T)$ is the set of fixed points of T. In 2017, Luo et al. [14] extended the work of Xu et al. [17] to uniformly smooth Banach spaces, which contains Hilbert spaces as a special case. They proved a strong convergence theorem for the iterative scheme. In 2015, Ke et al. [18] studied the following generalized viscosity implicit rule for nonexpansive mappings in Hilbert spaces:

$$x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_{n}T(s_n{x}_n+(1-s_n)x_{n+1}),n\ge 0,$$

which converges strongly to a fixed point of T under certain assumptions, and is also solved by the variational inequality (VI). In 2017, He et al. [19] considered the generalized viscosity implicit rule of asymptotically non-expansive mappings in Hilbert spaces. They proved that the iterative algorithm, defined by

$$x_{n+1}={\alpha }_{n}f(x_n)+(1-{\alpha }_n)T^n({\beta }_n{x}_n+(1-{\beta }_n)x_{n+1}),n\ge 0,$$

converges strongly to a fixed point of T, which was also the solution of the variational inequality (VI).

Motivated and inspired by the above works, we present a generalized viscosity implicit iterative method for an asymptotically non-expansive mapping in a Banach space. Then, we prove a strong convergence theorem of this algorithm, which solves the variational inequality problem. Applications to zero-point problems and equilibrium problems are presented. Finally, a numerical example is given, to illustrate our convergence analysis. Therefore, the results in this paper generalize and improve the corresponding results found in [13,14,15,17,18,19].

2. Preliminaries

Throughout this paper, let K be a subset of a real Banach space E and let $E^{*}$ be the dual space of E. Let $T:K\to K$ be a mapping, and denote by $F(T)$ the set of fixed points of T. Recall that the duality mapping $J:E\to 2^{E^{*}}$ is defined by

$$J(x)=\{x^{*}\in E^{*}:⟨x,x^{*}⟩=\parallel x{\parallel }^2=\parallel x^{*}{\parallel }^2\},\forall x\in E.$$

A mapping T is said to be contractive on K if there exists a constant $\rho \in (0,1)$ such that $\parallel Tx-Ty\parallel \le \rho \parallel x-y\parallel$ for all $x,y\in K$. Further, T is said to be nonexpansive if $\parallel Tx-Ty\parallel \le \parallel x-y\parallel$ for all $x,y\in K$, and T is said to be asymptotically nonexpansive if there exists a sequence $\left\{k_n\right\}\subset [1,\infty )$: ${lim}_{n\to \infty }{k}_n=1$ such that $\parallel T^{n}x-T^{n}y\parallel \le k_n\parallel x-y\parallel$ for all $x,y\in K$, and $\left\{k_n\right\}$ is called an asymptotic coefficient sequence of T.

We need some Lemmas for the proof of our main results.

Lemma 1

([20]). Let $\left\{{\alpha }_n\right\}$ be a sequence of non-negative real numbers satisfying the condition

$${\alpha }_{n+1}\le (1-{\gamma }_n){\alpha }_n+{\gamma }_n{\sigma }_n,\forall n\ge 0,$$

where $\left\{{\gamma }_n\right\}\subset (0,1)$ and $\left\{{\sigma }_n\right\}$ satisfy

(i) 

${lim}_{n\to \infty }{\gamma }_n=0$ and ${\sum }_{n=0}^{\infty }{\gamma }_n=\infty ;$ and

(ii) 

either ${lim\; sup}_{n\to \infty }{\sigma }_n\le 0$ or ${\sum }_{n=0}^{\infty }\left|{\gamma }_n{\sigma }_n\right|<\infty .$

Then, $\left\{{\alpha }_n\right\}$ converges to zero.

Lemma 2

([15]). Let $\left\{x_n\right\}$ and $\left\{y_n\right\}$ be bounded sequences in a Banach space E and $\left\{{\beta }_n\right\}$ be a sequence in $[0,1]$ with $0<{lim\; inf}_{n\to \infty }{\beta }_n\le {lim\; sup}_{n\to \infty }{\beta }_n<1$. Suppose that $x_{n+1}=(1-{\beta }_n)x_n+{\beta }_n{z}_n$ for all $n\ge 0$ and ${lim\; sup}_{n\to \infty }(\parallel z_{n+1}-z_n\parallel -\parallel x_{n+1}-x_n\parallel )\le 0$. Then, ${lim}_{n\to \infty }\parallel z_n-x_n\parallel =0$.

Lemma 3

([21]). Let K be a non-empty closed convex subset of a Banach space E, and let $T:K\to K$ be an asymptotically non-expansive mapping with a fixed point. Suppose that E admits a weakly sequentially continuous duality mapping. Then, the mapping $I-T$ is demiclosed at zero (i.e., where I is the identity mapping, if $x_n\rightharpoonup x$ and $\parallel x_n-T{x}_n\parallel \to 0$, then $x=Tx$).

Lemma 4

([22]). Let E be a uniformly smooth Banach space, K be a nonempty closed convex subset of E, and $T:K\to K$ be a nonexpansive mapping with $F(T)\ne \mathsf{\varnothing }$. Let $f:K\to K$ be a contractive mapping. Then, the sequence $x_t$ defined by $x_t=tf(x_t)+(1-t)T{x}_t,t\in (0,1)$ converges strongly to a point in $F(T)$. If we define a mapping $Q:{\mathsf{\Pi }}_c\to F(T)$ by $Q(f)={lim}_{t\to 0}{x}_t,f\in {\mathsf{\Pi }}_c$, then $Q(f)$ solves the variational inequality

$$⟨(I-f)Q(f),j(Q(f)-p)⟩\le 0,\forall p\in F(T).$$

Lemma 5

([23]). Let E be strictly convex, and $T_1$ and $T_2$ be an attracting non-expansive and a non-expansive mapping, respectively, which have a common fixed point. Then, $F(T_1{T}_2)=F(T_2{T}_1)=F(T_1)\bigcap F(T_1)$.

3. Main Results

Theorem 1.

Let K be a non-empty closed convex subset of a uniformly smooth Banach space E, which has a weakly continuous duality mapping. Let $T:K\to K$ be an asymptotically nonexpansive mapping with its asymptotic coefficient sequence $\left\{k_n\right\}\subset [1,\infty )$: ${lim}_{n\to \infty }{k}_n=1$. Assume that $F(T)\ne \mathsf{\varnothing }$ and $f:K\to K$ is a contraction with coefficient $\rho \in (0,1)$. For a given $x_0\in K$, let $\left\{x_n\right\}$ be a sequence generated in the following manner:

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_n{T}^n(t_n{x}_n+(1-t_n)x_{n+1}),\end{array}$$

(1)

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\},\left\{t_n\right\}\subset (0,1)$ satisfy the following conditions:

$$\begin{array}{l}(i){\alpha }_n+{\beta }_n+{\gamma }_n=1,{\displaystyle \underset{n\to \infty }{lim}}{\beta }_n=0,{\Sigma }_{n=0}^{\infty }{\beta }_n=\infty ,k_n-1=ϵ{\beta }_n,0<ϵ<1-\rho ;\\ (ii)0<{\displaystyle \underset{n\to \infty }{lim\; inf}}{\alpha }_n\le {\displaystyle \underset{n\to \infty }{lim\; sup}}{\alpha }_n<1,{\displaystyle \underset{n\to \infty }{lim}}|{\alpha }_{n+1}-{\alpha }_n|=0,{\displaystyle \underset{n\to \infty }{lim}}|{\beta }_{n+1}-{\beta }_n|=0;\\ (iii)0<t_n\le t_{n+1}<1,{\gamma }_n(1-t_n)k_n<1;\mathit{and}\\ (iv)T\mathit{satisfies}\mathit{the}\mathit{uniformly}\mathit{asymptotic}\mathit{regular}\mathit{condition}(i.e.,li{m}_{n\to \infty }{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel =0).\end{array}$$

Then, $\left\{x_n\right\}$ converges strongly to a fixed point $x^{*}$ of the asymptotically nonexpansive mapping T, which solves the variational inequality:

$$⟨(I-f)p,j(p-y)⟩\le 0,\forall y\in F(T).$$

Proof. 

We divide the proof into five steps.

Step 1: We show that $\left\{x_n\right\}$ is bounded. Indeed, if we let $p\in F(T)$, then we have

$$\begin{array}{cc}\hfill \parallel x_{n+1}-p\parallel & =\parallel {\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_n{T}^n(t_n{x}_n+(1-t_n)x_{n+1})-p\parallel \hfill \\ & =\parallel {\alpha }_n(x_n-p)+{\beta }_n(f(x_n)-f(p))+{\beta }_n(f(p)-p)+{\gamma }_n(T^n(t_n{x}_n+(1-t_n)x_{n+1})-p)\parallel \hfill \\ & \le {\alpha }_n\parallel x_n-p\parallel +{\beta }_n\parallel f(x_n)-f(p)\parallel +{\beta }_n\parallel f(p)-p\parallel +{\gamma }_n\parallel T^n(t_n{x}_n+(1-t_n)x_{n+1})-p\parallel \hfill \\ & \le {\alpha }_n\parallel x_n-p\parallel +{\beta }_n\rho \parallel x_n-p\parallel +{\beta }_n\parallel f(p)-p\parallel +{\gamma }_n{k}_n\parallel (t_n{x}_n+(1-t_n)x_{n+1})-p\parallel \hfill \\ & \le {\alpha }_n\parallel x_n-p\parallel +{\beta }_n\rho \parallel x_n-p\parallel +{\beta }_n\parallel f(p)-p\parallel +{\gamma }_n{k}_n{t}_n\parallel x_n-p\parallel +{\gamma }_n{k}_n(1-t_n)\parallel x_{n+1}-p\parallel \hfill \\ & =({\alpha }_n+\rho {\beta }_n+{\gamma }_n{k}_n{t}_n)\parallel x_n-p\parallel +{\beta }_n\parallel f(p)-p\parallel +{\gamma }_n{k}_n(1-t_n)\parallel x_{n+1}-p\parallel .\hfill \end{array}$$

It follows that

$$\begin{array}{c}\hfill [1-{\gamma }_n{k}_n(1-t_n)]\parallel x_{n+1}-p\parallel \le ({\alpha }_n+\rho {\beta }_n+{\gamma }_n{k}_n{t}_n)\parallel x_n-p\parallel +{\beta }_n\parallel f(p)-p\parallel .\end{array}$$

(2)

As $k_n-1=ϵ{\beta }_n$, we can get

$$\begin{array}{cc}\hfill \parallel x_{n+1}-p\parallel & \le \frac{{\alpha }_n+\rho {\beta }_n+{\gamma }_n{k}_n{t}_n}{1-{\gamma }_n{k}_n(1-t_n)}\parallel x_n-p\parallel +\frac{{\beta }_n}{1-{\gamma }_n{k}_n(1-t_n)}\parallel f(p)-p\parallel \hfill \\ & =[1-\frac{1-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n}{1-{\gamma }_n{k}_n(1-t_n)}]\parallel x_n-p\parallel +\frac{{\beta }_n}{1-{\gamma }_n{k}_n(1-t_n)}\parallel f(p)-p\parallel \hfill \\ & =[1-\frac{{\beta }_n(1-\rho )-{\gamma }_n(k_n-1)}{1-{\gamma }_n{k}_n(1-t_n)}]\parallel x_n-p\parallel +\frac{{\beta }_n}{1-{\gamma }_n{k}_n(1-t_n)}\parallel f(p)-p\parallel \hfill \\ & \le [1-\frac{{\beta }_n[1-\rho -ϵ]}{1-{\gamma }_n{k}_n(1-t_n)}]\parallel x_n-p\parallel +\frac{{\beta }_n[1-\rho -ϵ]}{1-{\gamma }_n{k}_n(1-t_n)}\frac{\parallel f(p)-p\parallel }{1-\rho -ϵ}.\hfill \end{array}$$

We deduce that

$$\parallel x_{n+1}-p\parallel \le max\{\parallel x_n-p\parallel ,\frac{1}{1-\rho -ϵ}\parallel f(p)-p\parallel \},\forall n\ge 0.$$

By induction, we get

$$\parallel x_n-p\parallel \le max\{\parallel x_0-p\parallel ,\frac{1}{1-\rho -ϵ}\parallel f(p)-p\parallel \},\forall n\ge 0.$$

Then, we obtain that $x_n$ is bounded, and so are $f(x_n)$, $T^n(t_n{x}_n+(1-t_n)x_{n+1})$.

Step 2: Show that $\parallel x_{n+1}-x_n\parallel \to 0,n\to \infty$. Setting $z_n=\frac{x_{n+1}-{\alpha }_n{x}_n}{1-{\alpha }_n},\mathrm{for}\mathrm{all}n\ge 0$, we have

$$\begin{array}{cc}\hfill z_{n+1}-z_n& =\frac{x_{n+2}-{\alpha }_{n+1}{x}_{n+1}}{1-{\alpha }_{n+1}}-\frac{x_{n+1}-{\alpha }_n{x}_n}{1-{\alpha }_n}\hfill \\ & =\frac{{\beta }_{n+1}f(x_{n+1})+{\gamma }_{n+1}{T}^{n+1}(t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2})}{1-{\alpha }_{n+1}}\hfill \\ & -\frac{{\beta }_{n}f(x_n)+{\gamma }_n{T}^n(t_n{x}_n+(1-t_n)x_{n+1})}{1-{\alpha }_n}\hfill \\ & =\frac{{\beta }_{n+1}f(x_{n+1})+(1-{\alpha }_{n+1}-{\beta }_{n+1})T^{n+1}(t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2})}{1-{\alpha }_{n+1}}\hfill \\ & -\frac{{\beta }_{n}f(x_n)+(1-{\alpha }_n-{\beta }_n)T^n(t_n{x}_n+(1-t_n)x_{n+1})}{1-{\alpha }_n}\hfill \\ & =\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}[f(x_{n+1})-f(x_n)]+(\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n})f(x_n)\hfill \\ & -(\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n})T^n(t_n{x}_n+(1-t_n)x_{n+1})\hfill \\ & -\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}[T^{n+1}(t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2})-T^n(t_n{x}_n+(1-t_n)x_{n+1})]\hfill \\ & +[T^{n+1}(t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2})-T^n(t_n{x}_n+(1-t_n)x_{n+1})]\hfill \\ & =\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}[f(x_{n+1})-f(x_n)]+(\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n})[f(x_n)-T^n(t_n{x}_n+(1-t_n)x_{n+1})]\hfill \\ & -\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}[T^{n+1}(t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2})-T^n(t_n{x}_n+(1-t_n)x_{n+1})]\hfill \\ & +[T^{n+1}(t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2})-T^n(t_n{x}_n+(1-t_n)x_{n+1})]\hfill \\ \hfill =& \frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}[f(x_{n+1})-f(x_n)]+(\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n})[f(x_n)-T^n(t_n{x}_n+(1-t_n)x_{n+1})]\hfill \\ \hfill +& (1-\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}})[T^{n+1}(t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2})-T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})]\hfill \\ \hfill +& (1-\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}})[T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})-T^n(t_n{x}_n+(1-t_n)x_{n+1})],\hfill \end{array}$$

which implies that

$$\begin{array}{cc}\hfill \parallel z_{n+1}-z_n\parallel & \le \frac{\rho {\beta }_{n+1}}{1-{\alpha }_{n+1}}\parallel x_{n+1}-x_n\parallel +|\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n}|C+\frac{{\gamma }_{n+1}}{1-{\alpha }_{n+1}}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel \hfill \\ & +(1-\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}})k_{n+1}\parallel t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2}-(t_n{x}_n+(1-t_n)x_{n+1})\parallel \hfill \\ & \le \frac{\rho {\beta }_{n+1}}{1-{\alpha }_{n+1}}\parallel x_{n+1}-x_n\parallel +|\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n}|C+\frac{{\gamma }_{n+1}}{1-{\alpha }_{n+1}}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel \hfill \\ & +(1-\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}})k_{n+1}\parallel t_n(x_{n+1}-x_n)+(1-t_{n+1})(x_{n+2}-x_{n+1})\parallel \hfill \\ & \le \frac{\rho {\beta }_{n+1}}{1-{\alpha }_{n+1}}\parallel x_{n+1}-x_n\parallel +|\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n}|C+\frac{{\gamma }_{n+1}}{1-{\alpha }_{n+1}}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel \hfill \\ & +(1-\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}})k_{n+1}[t_n\parallel x_{n+1}-x_n\parallel +(1-t_{n+1})\parallel x_{n+2}-x_{n+1}\parallel ],\hfill \end{array}$$

(3)

where $C>0$ is a constant that satisfies:

$$\begin{array}{cc}\hfill C& \ge \{su{p}_{n\ge 0}\parallel x_n-T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})\parallel ,su{p}_{n\ge 0}\parallel f(x_n)-T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})\parallel ,\hfill \\ & su{p}_{n\ge 0}\parallel f(x_n)-T^n(t_n{x}_n+(1-t_n)x_{n+1}\parallel \}.\hfill \end{array}$$

By (1), we can get

$$\begin{array}{cc}\hfill \parallel x_{n+2}-x_{n+1}\parallel & =\parallel {\alpha }_{n+1}{x}_{n+1}+{\beta }_{n+1}f(x_{n+1})+{\gamma }_{n+1}{T}^{n+1}(t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2})\hfill \\ & -{\alpha }_n{x}_n-{\beta }_{n}f(x_n)-{\gamma }_n{T}^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel \hfill \\ & =\parallel {\alpha }_{n+1}(x_{n+1}-x_n)+({\alpha }_{n+1}-{\alpha }_n)x_n+{\beta }_{n+1}(f(x_{n+1})-f(x_n))+({\beta }_{n+1}-{\beta }_n)f(x_n)\hfill \\ & +{\gamma }_{n+1}[T^{n+1}(t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2})-T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})]\hfill \\ & +({\gamma }_{n+1}-{\gamma }_n)T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})\hfill \\ & +{\gamma }_n[T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})-T^n(t_n{x}_n+(1-t_n)x_{n+1})]\parallel \hfill \\ & =\parallel {\alpha }_{n+1}(x_{n+1}-x_n)+({\alpha }_{n+1}-{\alpha }_n)x_n+{\beta }_{n+1}(f(x_{n+1})-f(x_n))+({\beta }_{n+1}-{\beta }_n)f(x_n)\hfill \\ & +{\gamma }_{n+1}[T^{n+1}(t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2})-T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})]\hfill \\ & -[({\alpha }_{n+1}-{\alpha }_n)+({\beta }_{n+1}-{\beta }_n)]T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})\hfill \\ & +{\gamma }_n[T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})-T^n(t_n{x}_n+(1-t_n)x_{n+1})]\parallel \hfill \\ & =\parallel {\alpha }_{n+1}(x_{n+1}-x_n)+({\alpha }_{n+1}-{\alpha }_n)[x_n-T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})]\hfill \\ & +({\beta }_{n+1}-{\beta }_n)[f(x_n)-T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})]+{\beta }_{n+1}(f(x_{n+1})-f(x_n))\hfill \\ & +{\gamma }_{n+1}[T^{n+1}(t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2})-T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})]\hfill \\ & +{\gamma }_n[T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})-T^n(t_n{x}_n+(1-t_n)x_{n+1})]\parallel \hfill \\ & \le {\alpha }_{n+1}\parallel x_{n+1}-x_n\parallel +|{\alpha }_{n+1}-{\alpha }_n|\parallel x_n-T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})\parallel \hfill \\ & +|{\beta }_{n+1}-{\beta }_n|\parallel f(x_n)-T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})\parallel +\rho {\beta }_{n+1}\parallel x_{n+1}-x_n\parallel \hfill \\ & +{\gamma }_n\parallel T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel \hfill \\ & +{\gamma }_{n+1}{k}_{n+1}\parallel t_{n+1}{x}_{n+1}+(1-t_{n+1})x_{n+2}-t_n{x}_n-(1-t_n)x_{n+1}\parallel \hfill \\ & \le {\alpha }_{n+1}\parallel x_{n+1}-x_n\parallel +|{\alpha }_{n+1}-{\alpha }_n|C+|{\beta }_{n+1}-{\beta }_n|C+\rho {\beta }_{n+1}\parallel x_{n+1}-x_n\parallel \hfill \\ & +{\gamma }_{n+1}{k}_{n+1}\parallel (1-t_{n+1})(x_{n+2}-x_{n+1})+t_n(x_{n+1}-x_n)\parallel \hfill \\ & +{\gamma }_n\parallel T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel \hfill \\ & \le ({\alpha }_{n+1}+\rho {\beta }_{n+1}+{\gamma }_{n+1}{k}_{n+1}{t}_n)\parallel x_{n+1}-x_n\parallel +{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})\parallel x_{n+2}-x_{n+1}\parallel \hfill \\ & +(|{\alpha }_{n+1}-{\alpha }_n|+|{\beta }_{n+1}-{\beta }_n|)C\hfill \\ & +{\gamma }_n\parallel T^{n+1}(t_n{x}_n+(1-t_n)x_{n+1})-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel \hfill \\ \hfill \le & ({\alpha }_{n+1}+\rho {\beta }_{n+1}+{\gamma }_{n+1}{k}_{n+1}{t}_n)\parallel x_{n+1}-x_n\parallel +{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})\parallel x_{n+2}-x_{n+1}\parallel \hfill \\ \hfill +& (|{\alpha }_{n+1}-{\alpha }_n|+|{\beta }_{n+1}-{\beta }_n|)C+{\gamma }_n{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel .\hfill \end{array}$$

This implies that

$$\begin{array}{cc}\hfill [1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})]\parallel x_{n+2}-x_{n+1}\parallel & \le ({\alpha }_{n+1}+\rho {\beta }_{n+1}+{\gamma }_{n+1}{k}_{n+1}{t}_n)\parallel x_{n+1}-x_n\parallel \hfill \\ & +(|{\alpha }_{n+1}-{\alpha }_n|+|{\beta }_{n+1}-{\beta }_n|)C+{\gamma }_n{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel .\hfill \end{array}$$

Then,

$$\begin{array}{c}\parallel x_{n+2}-x_{n+1}\parallel \hfill \\ \le \frac{{\alpha }_{n+1}+\rho {\beta }_{n+1}+{\gamma }_{n+1}{k}_{n+1}{t}_n}{1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})}\parallel x_{n+1}-x_n\parallel +\frac{C}{1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})}(|{\alpha }_{n+1}-{\alpha }_n|+|{\beta }_{n+1}-{\beta }_n|)\hfill \\ +\frac{{\gamma }_n}{1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel \hfill \\ =[1-\frac{{\beta }_{n+1}(1-\rho )+{\gamma }_{n+1}{k}_{n+1}(t_{n+1}-t_n)-{\gamma }_{n+1}(k_{n+1}-1)}{1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})}]\parallel x_{n+1}-x_n\parallel \hfill \\ +\frac{C}{1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})}(|{\alpha }_{n+1}-{\alpha }_n|+|{\beta }_{n+1}-{\beta }_n|)+\frac{{\gamma }_n}{1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel \hfill \\ \le [1-\frac{{\beta }_{n+1}[1-\rho -ϵ]+{\gamma }_{n+1}{k}_{n+1}(t_{n+1}-t_n)}{1-{\gamma }_n{k}_{n+1}(1-t_{n+1})}]\parallel x_{n+1}-x_n\parallel \hfill \\ +\frac{C}{1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})}(|{\alpha }_{n+1}-{\alpha }_n|+|{\beta }_{n+1}-{\beta }_n|)+\frac{{\gamma }_n}{1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel .\hfill \end{array}$$

(4)

Substituting (4) into (3), we have

$$\begin{array}{cc}\hfill \parallel z_{n+1}-z_n\parallel & \le [\frac{\rho {\beta }_{n+1}}{1-{\alpha }_{n+1}}+(1-\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}})k_{n+1}{t}_n+(1-\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}})k_{n+1}(1-t_{n+1})]\parallel x_{n+1}-x_n\parallel \hfill \\ & +\frac{{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})C}{(1-{\alpha }_{n+1})[1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})]}(|{\alpha }_{n+1}-{\alpha }_n|+|{\beta }_{n+1}-{\beta }_n|)\hfill \\ & +\frac{{\gamma }_{n+1}}{1-{\alpha }_{n+1}}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel \hfill \\ & +\frac{{\gamma }_n{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})}{(1-{\alpha }_{n+1})[1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})]}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel +|\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n}|C\hfill \\ & \le \frac{\rho {\beta }_{n+1}+{\gamma }_{n+1}{k}_{n+1}{t}_n+{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})}{1-{\alpha }_{n+1}}\parallel x_{n+1}-x_n\parallel +|\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n}|C\hfill \\ & +\frac{1}{(1-{\alpha }_{n+1})[1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})]}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel \hfill \\ & +\frac{{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})C}{(1-{\alpha }_{n+1})[1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})]}(|{\alpha }_{n+1}-{\alpha }_n|+|{\beta }_{n+1}-{\beta }_n|)\hfill \\ & \le \frac{\rho {\beta }_{n+1}+{\gamma }_{n+1}{k}_{n+1}}{1-{\alpha }_{n+1}}\parallel x_{n+1}-x_n\parallel +|\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n}|C\hfill \\ & +\frac{1}{(1-{\alpha }_{n+1})[1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})]}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel \hfill \\ & +\frac{{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})C}{(1-{\alpha }_{n+1})[1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})]}(|{\alpha }_{n+1}-{\alpha }_n|+|{\beta }_{n+1}-{\beta }_n|)\hfill \\ & =[1-\frac{(1-\rho ){\beta }_{n+1}-{\gamma }_{n+1}(k_{n+1}-1)}{1-{\alpha }_{n+1}}]\parallel x_{n+1}-x_n\parallel +|\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n}|C\hfill \\ & +\frac{1}{(1-{\alpha }_{n+1})[1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})]}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel \hfill \\ & +\frac{{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})C}{(1-{\alpha }_{n+1})[1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})]}(|{\alpha }_{n+1}-{\alpha }_n|+|{\beta }_{n+1}-{\beta }_n|)\hfill \\ & \le [1-\frac{[1-\rho -ϵ]{\beta }_{n+1}}{1-{\alpha }_{n+1}}]\parallel x_{n+1}-x_n\parallel +|\frac{{\beta }_{n+1}}{1-{\alpha }_{n+1}}-\frac{{\beta }_n}{1-{\alpha }_n}|C\hfill \\ & +\frac{1}{(1-{\alpha }_{n+1})[1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})]}{\displaystyle \underset{x\in K}{sup}}\parallel T^{n+1}x-T^{n}x\parallel \hfill \\ & +\frac{{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})C}{(1-{\alpha }_{n+1})[1-{\gamma }_{n+1}{k}_{n+1}(1-t_{n+1})]}(|{\alpha }_{n+1}-{\alpha }_n|+|{\beta }_{n+1}-{\beta }_n|).\hfill \end{array}$$

By conditions (i), (ii), and (iv), we have

$${\displaystyle \underset{n\to \infty }{lim\; sup}}(\parallel z_{n+1}-z_n\parallel -\parallel x_{n+1}-x_n\parallel )\le 0.$$

Applying Lemma 2, we can get

$${\displaystyle \underset{n\to \infty }{lim}}\parallel z_n-x_n\parallel =0.$$

Note that

$$z_n-x_n=\frac{x_{n+1}-x_n}{1-{\alpha }_n},$$

and so we have

$${\displaystyle \underset{n\to \infty }{lim}}\parallel x_{n+1}-x_n\parallel =0.$$

Step 3: We show that ${lim}_{n\to \infty }\parallel x_n-T{x}_n\parallel =0$.

$$\begin{array}{c}\parallel x_{n+1}-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel \hfill \\ =\parallel {\alpha }_n{x}_n+{\beta }_{n}f(x_n)-{\alpha }_n{T}^n(t_n{x}_n+(1-t_n)x_{n+1})-{\beta }_n{T}^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel \hfill \\ =\parallel {\alpha }_n[x_n-T^n(t_n{x}_n+(1-t_n)x_{n+1})]+{\beta }_n[f(x_n)-T^n(t_n{x}_n+(1-t_n)x_{n+1})]\parallel \hfill \\ \le {\alpha }_n\parallel x_n-x_{n+1}\parallel +{\alpha }_n\parallel x_{n+1}-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel +{\beta }_n\parallel f(x_n)-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel .\hfill \end{array}$$

Moreover, we know that

$$(1-{\alpha }_n)\parallel x_{n+1}-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel \le {\alpha }_n\parallel x_n-x_{n+1}\parallel +{\beta }_n\parallel f(x_n)-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel .$$

That is,

$$\parallel x_{n+1}-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel \le \frac{{\alpha }_n}{1-{\alpha }_n}\parallel x_n-x_{n+1}\parallel +\frac{{\beta }_n}{1-{\alpha }_n}\parallel f(x_n)-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel .$$

From conditions (i) and (ii), and Step 2, we obtain

$$\begin{array}{c}\hfill \parallel x_{n+1}-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel \to 0,(n\to \infty ).\end{array}$$

(5)

Then,

$$\begin{array}{cc}\hfill \parallel x_n-T^n{x}_n\parallel & =\parallel x_n-x_{n+1}+x_{n+1}-T^n(t_n{x}_n+(1-t_n)x_{n+1})+T^n(t_n{x}_n+(1-t_n)x_{n+1})-T^n{x}_n\parallel \hfill \\ & \le \parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel +\parallel T^n(t_n{x}_n+(1-t_n)x_{n+1})-T^n{x}_n\parallel \hfill \\ & \le \parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel +k_n\parallel t_n{x}_n+(1-t_n)x_{n+1}-x_n\parallel \hfill \\ & =\parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel +k_n(1-t_n)\parallel x_{n+1}-x_n\parallel \hfill \\ & =(1+k_n(1-t_n))\parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^n(t_n{x}_n+(1-t_n)x_{n+1})\parallel .\hfill \end{array}$$

By (5) and Step 2, we have

$$\begin{array}{c}\hfill \parallel x_n-T^n{x}_n\parallel \to 0,n\to \infty .\end{array}$$

(6)

We know that T is an asymptotically non-expansive mapping, and so we have

$$\begin{array}{cc}\hfill \parallel x_n-T{x}_n\parallel & =\parallel x_n-x_{n+1}+x_{n+1}-T^{n+1}{x}_{n+1}+T^{n+1}{x}_{n+1}-T^{n+1}{x}_n+T^{n+1}{x}_n-T{x}_n\parallel \hfill \\ & \le \parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^{n+1}{x}_{n+1}\parallel +\parallel T^{n+1}{x}_{n+1}-T^{n+1}{x}_n\parallel +\parallel T^{n+1}{x}_n-T{x}_n\parallel \hfill \\ & \le \parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^{n+1}{x}_{n+1}\parallel +k_{n+1}\parallel x_{n+1}-x_n\parallel +k_1\parallel T^n{x}_n-x_n\parallel \hfill \\ & \le (1+k_{n+1})\parallel x_n-x_{n+1}\parallel +\parallel x_{n+1}-T^{n+1}{x}_{n+1}\parallel +k_1\parallel T^n{x}_n-x_n\parallel .\hfill \end{array}$$

By Step 2 and (6), we can get

$$\parallel x_n-T{x}_n\parallel \to 0,n\to \infty .$$

Step 4: We prove that ${lim\; sup}_{n\to \infty }⟨(I-f)p,j(p-x_n)⟩\le 0$.

As K is a uniformly smooth Banach space and $x_n$ is bounded, then there exists a subsequence of $x_n$ which converges weakly to y. Further,

$${\displaystyle \underset{k\to \infty }{lim}}⟨(I-f)p,j(p-x_{n_k})⟩={\displaystyle \underset{n\to \infty }{lim\; sup}}⟨(I-f)p,j(p-x_n)⟩.$$

It follows from Step 3 and Lemma 3, we can get $y\in F(T)$. Then, $p\in F(T)$ satisfies

$$⟨(I-f)p,j(p-y)⟩\le 0,\forall y\in F(T),$$

by the weakly sequential continuous duality mapping and Lemma 4, we have

$${\displaystyle \underset{n\to \infty }{lim\; sup}}⟨(I-f)p,j(p-x_n)⟩={\displaystyle \underset{k\to \infty }{lim}}⟨(I-f)p,j(p-x_{n_k})⟩=⟨(I-f)p,j(p-y)⟩\le 0.$$

Step 5: Finally, we prove that $x_n$ converges strongly to $p\in F(T)$.

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-p\parallel }^2& =⟨{\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_n{T}^n(t_n{x}_n+(1-t_n)x_{n+1})-p,j(x_{n+1}-p)⟩\hfill \\ & ={\alpha }_n⟨x_n-p,j(x_{n+1}-p)⟩+{\beta }_n⟨f(x_n)-p,j(x_{n+1}-p)⟩\hfill \\ & +{\gamma }_n⟨T^n(t_n{x}_n+(1-t_n)x_{n+1})-p,j(x_{n+1}-p)⟩\hfill \\ & \le {\alpha }_n⟨x_n-p,j(x_{n+1}-p)⟩+{\beta }_n⟨f(x_n)-f(p),j(x_{n+1}-p)⟩\hfill \\ & +{\beta }_n⟨f(p)-p,j(x_{n+1}-p)⟩+{\gamma }_n⟨T^n(t_n{x}_n+(1-t_n)x_{n+1})-p,j(x_{n+1}-p)⟩\hfill \\ & \le {\alpha }_n\parallel x_n-p\parallel \parallel x_{n+1}-p\parallel +{\beta }_n\rho \parallel x_n-p\parallel \parallel x_{n+1}-p\parallel \hfill \\ & +{\beta }_n⟨f(p)-p,j(x_{n+1}-p)⟩+{\gamma }_n{k}_n\parallel t_n{x}_n+(1-t_n)x_{n+1}-p\parallel \parallel x_{n+1}-p\parallel \hfill \\ & \le {\alpha }_n\parallel x_n-p\parallel \parallel x_{n+1}-p\parallel +{\beta }_n\rho \parallel x_n-p\parallel \parallel x_{n+1}-p\parallel +{\beta }_n⟨f(p)-p,j(x_{n+1}-p)⟩\hfill \\ & +{\gamma }_n{k}_n{t}_n\parallel x_n-p\parallel \parallel x_{n+1}-p\parallel +{\gamma }_n{k}_n(1-t_n){\parallel x_{n+1}-p\parallel }^2\hfill \\ & =[{\alpha }_n+{\beta }_n\rho +{\gamma }_n{k}_n{t}_n]\parallel x_n-p\parallel \parallel x_{n+1}-p\parallel +{\gamma }_n{k}_n(1-t_n){\parallel x_{n+1}-p\parallel }^2\hfill \\ & +{\beta }_n⟨f(p)-p,j(x_{n+1}-p)⟩\hfill \\ & \le \frac{{\alpha }_n+{\beta }_n\rho +{\gamma }_n{k}_n{t}_n}{2}\parallel x_n{-p\parallel }^2+\frac{{\alpha }_n+{\beta }_n\rho +{\gamma }_n{k}_n{t}_n}{2}{\parallel x_{n+1}-p\parallel }^2\hfill \\ & +{\gamma }_n{k}_n(1-t_n){\parallel x_{n+1}-p\parallel }^2+{\beta }_n⟨f(p)-p,j(x_{n+1}-p)⟩\hfill \\ & =\frac{{\alpha }_n+{\beta }_n\rho +{\gamma }_n{k}_n{t}_n}{2}\parallel x_n{-p\parallel }^2+\frac{{\alpha }_n+{\beta }_n\rho +{\gamma }_n{k}_n(2-t_n)}{2}{\parallel x_{n+1}-p\parallel }^2\hfill \\ & +{\beta }_n⟨f(p)-p,j(x_{n+1}-p)⟩,\hfill \end{array}$$

which implies taht

$$[1-\frac{{\alpha }_n+{\beta }_n\rho +{\gamma }_n{k}_n(2-t_n)}{2}]\parallel x_{n+1}{-p\parallel }^2\le \frac{{\alpha }_n+{\beta }_n\rho +{\gamma }_n{k}_n{t}_n}{2}{\parallel x_n-p\parallel }^2+{\beta }_n⟨f(p)-p,j(x_{n+1}-p)⟩.$$

That is,

$$\begin{array}{cc}\hfill \parallel x_{n+1}{-p\parallel }^2& \le \frac{{\alpha }_n+{\beta }_n\rho +{\gamma }_n{k}_n{t}_n}{2-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n(2-t_n)}{\parallel x_{n+1}-p\parallel }^2\hfill \\ & +\frac{2{\beta }_n}{2-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n(2-t_n)}⟨f(p)-p,j(x_{n+1}-p)⟩\hfill \\ & =[1-\frac{2(1-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n)}{2-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n(2-t_n)}]{\parallel x_{n+1}-p\parallel }^2\hfill \\ & +\frac{2{\beta }_n}{2-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n(2-t_n)}⟨f(p)-p,j(x_{n+1}-p)⟩\hfill \\ & \le [1-\frac{2((1-\rho ){\beta }_n-{\gamma }_n(k_n-1)}{2-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n(2-t_n)}]{\parallel x_{n+1}-p\parallel }^2\hfill \\ & +\frac{2{\beta }_n}{2-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n(2-t_n)}⟨f(p)-p,j(x_{n+1}-p)⟩\hfill \\ & \le [1-\frac{2((1-\rho -ϵ){\beta }_n}{2-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n(2-t_n)}]{\parallel x_{n+1}-p\parallel }^2\hfill \\ & +\frac{2{\beta }_n}{2-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n(2-t_n)}⟨f(p)-p,j(x_{n+1}-p)⟩;\hfill \end{array}$$

(7)

we note that

$$\begin{array}{c}2-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n(2-t_n)\hfill \\ =1-{\alpha }_n-\rho {\beta }_n-{\gamma }_n{k}_n+[1-{\gamma }_n{k}_n(1-t_n)]\hfill \\ ={\beta }_n(1-\rho )-{\gamma }_n(k_n-1)+[1-{\gamma }_n{k}_n(1-t_n)]\hfill \\ ={\beta }_n(1-\rho -ϵ{\gamma }_n)+[1-{\gamma }_n{k}_n(1-t_n)]\hfill \\ >{\beta }_n(1-\rho )(1-{\gamma }_n)+[1-{\gamma }_n{k}_n(1-t_n)]>0.\hfill \end{array}$$

By Step 4, we have $⟨(I-f)p,j(p-y)⟩\le 0,\forall y\in F(T)$. Thus, by condition (i) and applying Lemma 1 to (7), we conclude that ${lim}_{n\to \infty }\parallel x_n-p\parallel =0$. This completes the proof. □

Theorem 2.

Let K be a nonempty closed convex subset of a uniformly smooth Banach space E, which has a weakly continuous duality mapping. Let $T:K\to K$ be a non-expansive mapping. Assume that $F(T)\ne \mathsf{\varnothing }$ and $f:K\to K$ is a contraction. For a given $x_0\in K$, let $\left\{x_n\right\}$ be a sequence generated in the following manner:

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_{n}T(t_n{x}_n+(1-t_n)x_{n+1}),\end{array}$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\},\left\{t_n\right\}\subset (0,1)$, satisfy the following conditions:

$$\begin{array}{c}(i){\alpha }_n+{\beta }_n+{\gamma }_n=1,{\displaystyle \underset{n\to \infty }{lim}}{\beta }_n=0,{\Sigma }_{n=0}^{\infty }{\beta }_n=\infty ;\hfill \\ (ii)0<{\displaystyle \underset{n\to \infty }{lim\; inf}}{\alpha }_n\le {\displaystyle \underset{n\to \infty }{lim\; sup}}{\alpha }_n<1,{\displaystyle \underset{n\to \infty }{lim}}|{\alpha }_{n+1}-{\alpha }_n|=0,{\displaystyle \underset{n\to \infty }{lim}}|{\beta }_{n+1}-{\beta }_n|=0;\mathit{and}\hfill \\ (iii)0<t_n\le t_{n+1}<1.\hfill \end{array}$$

Then, $\left\{x_n\right\}$ converges strongly to a fixed point $x^{*}$ of the nonexpansive mapping T, which solves the variational inequality:

$$⟨(I-f)p,j(p-y)⟩\le 0,\forall y\in F(T).$$

Remark 1.

The aim of this paper is to study the general viscosity implicit midpoint rule for asymptotically non-expansive mappings in Banach spaces. In Theorem 1, if $t_n=\frac{1}{2}$ in a Hilbert space, this is the main result of Yan et al. [24]. We know that every non-expansive mapping is an asymptotically non-expansive mapping. In Theorem 1, if $k_n\equiv 1$, then T is a non-expansive mapping. Thus, we extend and generalize the Hilbert space results to Banach spaces, the non-expansive mapping to asymptotically non-expansive mapping, and the implicit midpoint rule to the generalized viscosity implicit midpoint rule, which includes some corresponding recent results (see, for example, [13,14,17,18,19]) as special cases.

4. Applications

4.1. Application to Zero-Point Problems

Consider the zero-point problem: Find $x\in E$, such that

$$0\in Ax,$$

where $A\subset E\times E$ is an accretive operator: An operator is accretive if, for $\forall x,y\in E$, there exists $j(x-y)\in J(x-y)$ such that $⟨Ax-Ay,j(x-y)⟩\ge 0$. Further, $J_r:R(I+rA)\to D(A)$ is called the resolvent of A, which we define by $J_r={(I+rA)}^{-1}$. It is well-known that $J_r$ is a non-expansive mapping and that $A^{-1}(0)=F(J_r)$, where $A^{-1}(0)=\{x\in E:0\in Ax\}$ is the set of zeros of A and $F(J_r)$ is the fixed point set of $J_r$. Thus, we can apply the our results by taking $T=J_r$.

Corollary 1.

Let K be a nonempty closed convex subset of a uniformly smooth Banach space E, which has a weakly continuous duality mapping. Let A be a m-accretive operator in E, such that $A^{-1}(0)\ne \mathsf{\varnothing }$ and $f:K\to K$ is a contraction. For a given $x_0\in K$, let $\left\{x_n\right\}$ be a sequence generated in the following manner:

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_n{J}_r(t_n{x}_n+(1-t_n)x_{n+1}),\end{array}$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\},\left\{t_n\right\}\subset (0,1)$, satisfy the following conditions:

$$\begin{array}{c}(i){\alpha }_n+{\beta }_n+{\gamma }_n=1,{\displaystyle \underset{n\to \infty }{lim}}{\beta }_n=0,{\Sigma }_{n=0}^{\infty }{\beta }_n=\infty ;\hfill \\ (ii)0<{\displaystyle \underset{n\to \infty }{lim\; inf}}{\alpha }_n\le {\displaystyle \underset{n\to \infty }{lim\; sup}}{\alpha }_n<1,{\displaystyle \underset{n\to \infty }{lim}}|{\alpha }_{n+1}-{\alpha }_n|=0,{\displaystyle \underset{n\to \infty }{lim}}|{\beta }_{n+1}-{\beta }_n|=0;\mathit{and}\hfill \\ (iii)0<t_n\le t_{n+1}<1.\hfill \end{array}$$

Then, $\left\{x_n\right\}$ converges strongly to $x^{*}\in A^{-1}(0)$, which solves the variational inequality:

$$⟨(I-f)p,j(p-y)⟩\le 0,\forall y\in A^{-1}(0).$$

4.2. Application to Equilibrium Problems

Let B be a non-empty, closed, and convex subset of a Hilbert space H. Consider the equilibrium problem: Find $x\in B$, such that

$$G(x,y)\ge 0,forally\in B,$$

where $G:B\times B\to R$ is a bi-function satisfying the following conditions:

(H1)

$G(x,x)=0$ for all $x\in B$;

(H2)

$G(x,y)+G(y,x)\le 0$, for all $x,y\in B$;

(H3)

for each $x,y,z,\in B$,${lim}_{t\to \infty }G(tz+(1-t)x,y)\le G(x,y)$; and

(H4)

for all $x\in B$, $G(x,y)$ is convex and weakly lower semi-continuous.

Assume that G satisfies $H(1)$–$H(4)$. For $r>0$ and $x\in H$, we define $T_r:H\to B$ by $T_r=\{u\in B:G(u,y)+\frac{1}{r}⟨y-u,u-x⟩\ge 0,\forall y\in B\}$, and the set of solutions of the equilibrium problem is denoted by $EP$. It is well-known that the single-valued mapping $T_r$ is firmly non-expansive and that $EP(G)=F(T_r)$, where $EP(G)$ is a closed and convex set. Thus, we can apply our results by Lemma 5.

Corollary 2.

Let B be a non-empty, closed, and convex subset of a real Hilbert space H and $G:B\times B\to R$ be a bi-function satisfying the conditions $(H1)$–$(H4)$. Let $T:B\to B$ be a non-expansive mapping such that $\mathsf{\Omega }=F(T)\bigcap EP(G)\ne \mathsf{\varnothing }$ and $f:B\to B$ is a contraction. For a given $x_0\in B$, let $\left\{x_n\right\}$ be a sequence generated in the following manner:

$$\begin{array}{c}\hfill x_{n+1}={\alpha }_n{x}_n+{\beta }_{n}f(x_n)+{\gamma }_{n}T{T}_r(t_n{x}_n+(1-t_n)x_{n+1}),\end{array}$$

where $\left\{{\alpha }_n\right\},\left\{{\beta }_n\right\},\left\{{\gamma }_n\right\},\left\{t_n\right\}\subset (0,1)$, satisfy the following conditions:

$$\begin{array}{c}(i){\alpha }_n+{\beta }_n+{\gamma }_n=1,{\displaystyle \underset{n\to \infty }{lim}}{\beta }_n=0,{\Sigma }_{n=0}^{\infty }{\beta }_n=\infty ;\hfill \\ (ii)0<{\displaystyle \underset{n\to \infty }{lim\; inf}}{\alpha }_n\le {\displaystyle \underset{n\to \infty }{lim\; sup}}{\alpha }_n<1,{\displaystyle \underset{n\to \infty }{lim}}|{\alpha }_{n+1}-{\alpha }_n|=0,{\displaystyle \underset{n\to \infty }{lim}}|{\beta }_{n+1}-{\beta }_n|=0;\mathit{and}\hfill \\ (iii)0<t_n\le t_{n+1}<1.\hfill \end{array}$$

Then, $\left\{x_n\right\}$ converges strongly to $x^{*}\in \mathsf{\Omega }$, which solves the variational inequality:

$$⟨(I-f)p,p-y⟩\le 0,\forall y\in \mathsf{\Omega }.$$

5. Numerical Examples

Example 1.

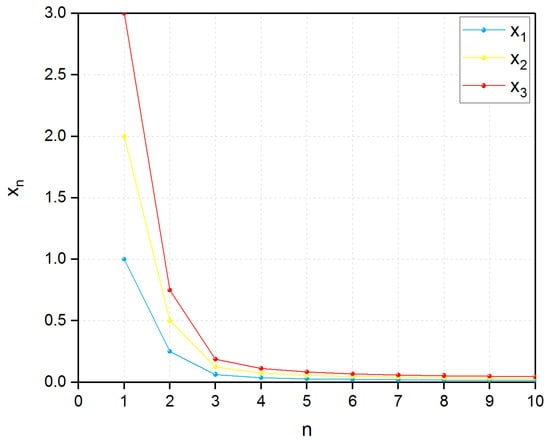
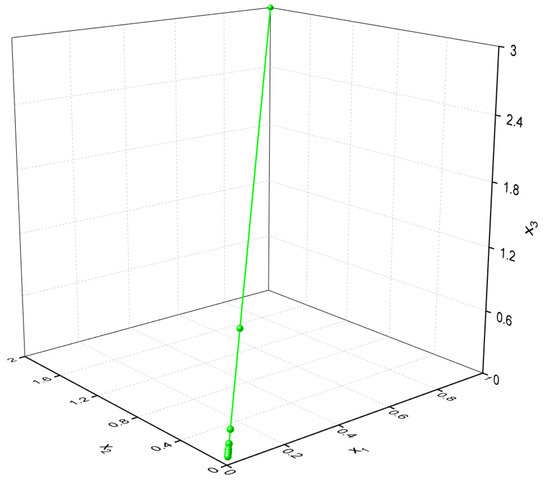
Let the inner product $⟨.,.⟩:R^3\times R^3\to R$ be $⟨x,y⟩=x_1{y}_1+x_2{y}_2+x_3{y}_3$. We set $T^{n}x=(1+\frac{1}{3n})x$ and $f(x)=\frac{1}{4}x$, where $x=(x_1,x_2,x_3)\in R^3$. We take ${\alpha }_n=\frac{1}{3}+\frac{1}{n}$, ${\beta }_n=\frac{1}{n}$, ${\gamma }_n=2(\frac{1}{3}-\frac{1}{n})$, and $t_n=1-\frac{1}{3n}$, for all $n\in N$. It is easy to see that $k_n=1+\frac{1}{3n}$, $ϵ=\frac{1}{3}$, and $\rho =\frac{1}{4}$ satisfy the conditions (i)–(iv) in Theorem 1. Then, we get

$$x_{n+1}=\frac{108n^3-81n^2-8n+24}{108n^3-24n^2+64n+24}{x}_n.$$

Starting with $x_1=(1,2,3)$ and using the algorithm in Theorem 1, we get the following numerical results, as shown in Figure 1 and Figure 2.

Figure 1. Two dimensions.

Figure 2. Three dimensions.