B-Spline Solutions of General Euler-Lagrange Equations
Abstract
1. Introduction
2. Preliminary
3. B-Spline Solutions of the Second-Order PDEs
| terms | ⋯ | v | 1 | ||
| ⋯ | |||||
| ⋯ | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| u | ⋯ | u | |||
| 1 | ⋯ | v | 1 |
| Algorithm 1 Algorithm to get the B-spline solution of Euler-Lagrange Equation (2) |
|
4. B-Spline Solutions of the 4th Order PDEs
| terms | ⋯ | v | 1 | ||
| ⋯ | |||||
| ⋯ | |||||
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| u | ⋯ | u | |||
| 1 | ⋯ | v | 1 |
| Algorithm 2 Algorithm to get the B-spline solution of the Euler-Lagrange Equation (4) |
|
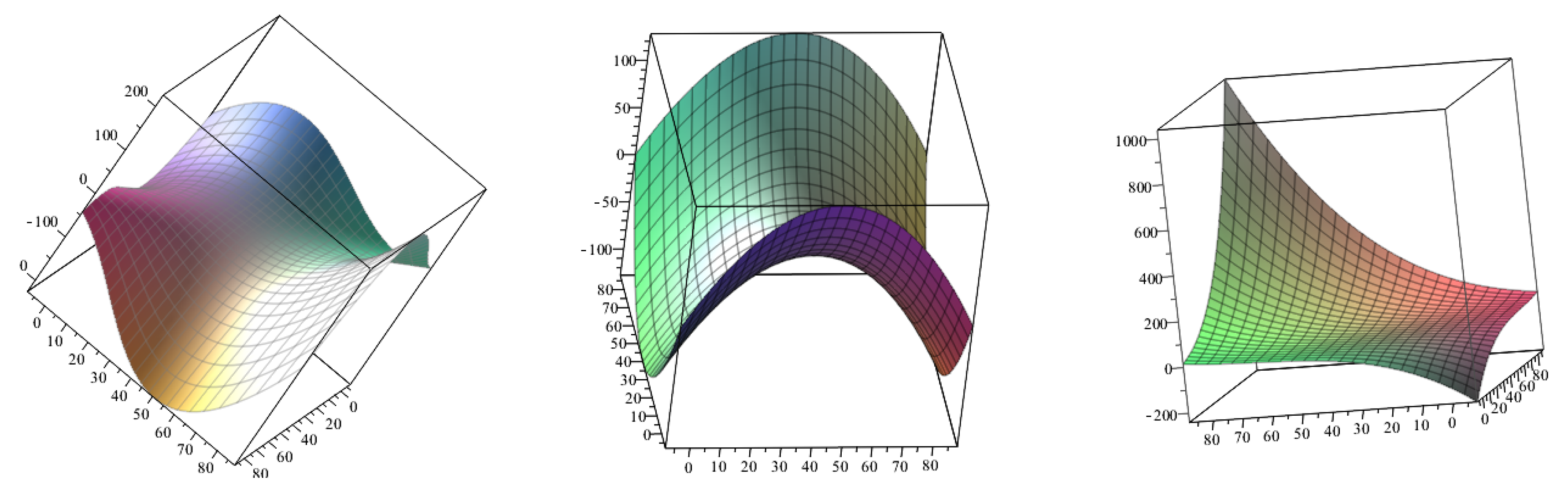
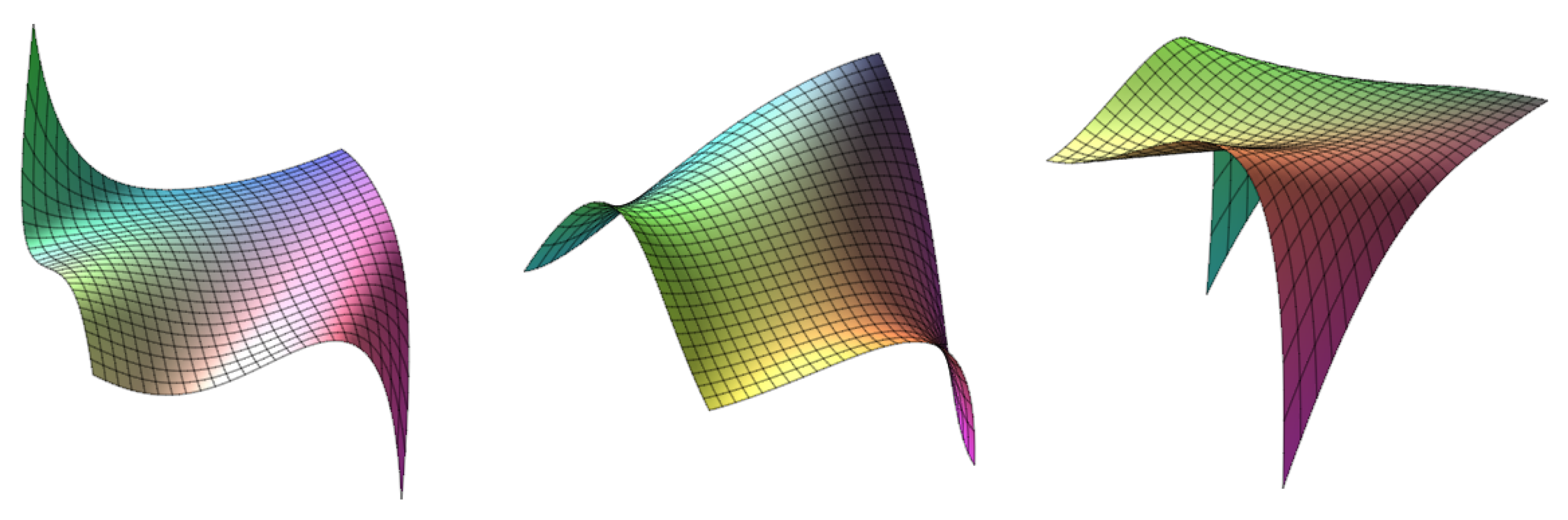
5. Applications in Geometrical Modeling
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Bloor, M.I.G.; Wilson, M.J. Blend Design As a Boundary-Value Problem. In Theory and Practice of Geometric Modeling; Springer: Berlin/Heidelberg, Germany, 1989; pp. 221–234. [Google Scholar]
- Bloor, M.I.G.; Wilson, M.J. Generating blend surfaces using partial differential equations. Comput.-Aided Des. 1989, 21, 165–171. [Google Scholar] [CrossRef]
- Ugail, H.; Willis, P.; Palmer, I. A survey of partial differential equations in geometric design. Vis. Comput. Int. J. Comput. Graph. 2008, 24, 213–225. [Google Scholar]
- Ugail, H. Partial Differential Equations for Geometric Design; Springer Publishing Company, Incorporated: Berlin/Heidelberg, Germany, 2011; Available online: https://www.springer.com/gb/book/9780857297839 (accessed on 22 March 2019).
- Bloor, M.I.G.; Wilson, M.J. Representing PDE surfaces in terms of B-splines. Comput.-Aided Des. 1990, 22, 324–331. [Google Scholar] [CrossRef]
- Xu, G.; Pan, Q.; Bajaj, C.L. Discrete Surface Modelling Using Partial Differential Equations. Comput. Aided Geom. Des. 2006, 23, 125. [Google Scholar] [CrossRef] [PubMed]
- Feng, P.; Warren, J. Discrete bi-Laplacians and biharmonic b-splines. ACM Trans. Graph. (TOG) 2012, 31, 115. [Google Scholar] [CrossRef]
- Rao, J.S. Euler-Lagrange Equations; Springer International Publishing: Cham, Switzerland, 2017. [Google Scholar]
- Arnal, A.; Monterde, J. Explicit Bézier control net of a PDE surface. Comput. Math. Appl. 2017, 73, 483–493. [Google Scholar] [CrossRef]
- Farin, G.; Hansford, D. Discrete Coons Patches. Comput. Aided Geom. Des. 1999, 16, 691–700. [Google Scholar] [CrossRef]
- Monterde, J.; Ugail, H. On harmonic and biharmonic Bézier surfaces. Comput. Aided Geom. Des. 2004, 21, 697–715. [Google Scholar] [CrossRef]
- Monterde, J.; Ugail, H. A general 4th-order PDE method to generate Bézier surfaces from the boundary. Comput. Aided Geom. Des. 2006, 23, 208–225. [Google Scholar] [CrossRef]
- Zhang, J.J.; You, L.H. Fast Surface Modelling Using a 6th Order PDE. In Computer Graphics Forum; Blackwell Publishing, Inc.: Oxford, UK; Boston, FL, USA, 2004; pp. 311–320. [Google Scholar]
- Arnal, A.; Lluch, A.; Monterde, J. PDE triangular Bézier surfaces: Harmonic, biharmonic and isotropic surfaces. J. Comput. Appl. Math. 2011, 235, 1098–1113. [Google Scholar] [CrossRef]
- Wang, Z.Z.; Wang, G.J. Generating Bézier Surfaces Based on 8th-order PDE. Commun. Inf. Sci. Manag. Eng. 2012, 2, 10–17. [Google Scholar]
- Beltran, J.V.; Monterde, J. Bézier Solutions of the Wave Equation. In Proceedings of the International Conference on Computational Science and ITS Applications—ICCSA 2004, Assisi, Italy, 14–17 May 2004; pp. 631–640. [Google Scholar]
- Bloor, M.I.G.; Wilson, M.J. Generating n-Sided Patches with Partial Differential Equations; Springer: Tokyo, Japan, 1989. [Google Scholar]
- Bloor, M.I.G.; Wilson, M.J. Using partial differential equations to generate free-form surfaces. Comput.-Aided Des. 1990, 22, 202–212. [Google Scholar] [CrossRef]
- Monterde, J.; Ugail, H. A Comparative Study Between Biharmonic Bézier Surfaces and Biharmonic Extremal Surfaces. Int. J. Comput. Appl. 2015, 31, 90–96. [Google Scholar]
- Agrawal, O.P. Generalized Variational Problems and Euler-Lagrange equations. Comput. Math. Appl. 2010, 59, 1852–1864. [Google Scholar] [CrossRef]
- Olver, P.J. Applications of Lie Groups to Differential Equations; Springer: Berlin/Heidelberg, Germany, 1999; pp. 312–315. [Google Scholar]
- Patrikalakis, N.M.; Maekawa, T. Shape Interrogation for Computer Aided Design and Manufacturing; Springer: Berlin/Heidelberg, Germany, 2002; pp. 341–352. [Google Scholar]
- Boor, C.D.; Höllig, K.; Riemenschneider, S. Box Splines; Springer: New York, NY, USA, 1993. [Google Scholar]
- Tiller, W. The NURBS Book; Springer: Berlin/Heidelberg, Germany, 1995; pp. 133–158. [Google Scholar]
- Schneider, R.; Kobbelt, L. Geometric fairing of irregular meshes for free-form surface design. Comput. Aided Geom. Des. 2001, 18, 359–379. [Google Scholar] [CrossRef]
- Bloor, M.I.G.; Wilson, M.J. An analytic pseudo-spectral method to generate 3- and 5-sided patches. Geom. Model. Comput. Seattle 2005, 22, 203–219. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sun, L.; Zhu, C. B-Spline Solutions of General Euler-Lagrange Equations. Mathematics 2019, 7, 365. https://doi.org/10.3390/math7040365
Sun L, Zhu C. B-Spline Solutions of General Euler-Lagrange Equations. Mathematics. 2019; 7(4):365. https://doi.org/10.3390/math7040365
Chicago/Turabian StyleSun, Lanyin, and Chungang Zhu. 2019. "B-Spline Solutions of General Euler-Lagrange Equations" Mathematics 7, no. 4: 365. https://doi.org/10.3390/math7040365
APA StyleSun, L., & Zhu, C. (2019). B-Spline Solutions of General Euler-Lagrange Equations. Mathematics, 7(4), 365. https://doi.org/10.3390/math7040365



