Graphs Based on Hoop Algebras

Abstract

In this paper, we investigate the graph structures on hoop algebras. First, by using the quasi-filters and r-prime (one-prime) filters, we construct an implicative graph and show that it is connected and under which conditions it is a star or tree. By using zero divisor elements, we construct a productive graph and prove that it is connected and both complete and a tree under some conditions.

1. Introduction

Non-classical logic has become a formal and useful tool for computer science to deal with uncertain information and fuzzy information. The algebraic counterparts of some non-classical logics satisfy residuation and those logics can be considered in a frame of residuated lattices [1]. For example, Hájek’s BL (basic logixc [2]), Lukasiewicz’s MV (many-valued logic [3]) and MTL (monoidal t-norm-based logic [4]) are determined by the class of BL-algebras, MV-algebras and MTL-algebras, respectively. All of these algebras have lattices with residuation as a common support set. Thus, it is very important to investigate properties of algebras with residuation.

Hoops are naturally ordered commutative residuated integral monoids, as introduced by Bosbach [5,6], and then studied by Büchi and Owens, in a paper never published. In the last years, hoop theory has been enriched with deep structure theorems [7,8,9,10]. Many of these results have a strong impact with fuzzy logic.

Graph theory has existed for many years not only as an area of mathematical study, but also as an intuitive and illustrative tool. Graph theory has found many applications in engineering and science, such as chemical, electrical, civil and mechanical engineering; architecture; management and control; communication; operational research; sparse matrix technology; combinatorial optimization; and computer science. Therefore, many books have been published on applied graph theory, e.g. the book by Bondy and Murty [11]; especially in the field of universal algebras and graph theory, graph algebra is a way of giving a directed graph of algebraic structure. This was introduced by McNulty [12], and has seen many uses in the field of universal algebra since then. Algebraic graph theory comprises both the study of algebraic objects arising in connection with graphs. The rapidly expanding area of algebraic graph theory uses two different branches of algebra to explore various aspects of graph theory: linear algebra (for spectral theory) and group theory (for studying graph symmetry). These areas have links with other areas of mathematics, such as logic and harmonic analysis, and are increasingly being used in such areas as computer networks where symmetry is an important feature, for example, automorphism groups of graphs along with the use of algebraic tools to establish interesting properties of combinatorial objects. One of the oldest themes in the area is the investigation of the relation between properties of a graph and the spectrum of its adjacency matrix. In addition, algebraic graph theory can be viewed as an extension to graph theory in which algebraic methods are applied to problems about graphs. Many authors studied graph theory in connection with semigroups and rings. In [13], Beck introduced the zero-divisor graph $\Gamma \left(R\right)$ associated with the zero-divisor set of a commutative ring, whose vertex set is the set of zero divisors. Two distinct zero divisors $x,y$ are adjacent in $\Gamma \left(R\right)$ if and only if $xy=0$. The zero-divisor graph establishes a connection between graph theory and commutative ring theory, which hopefully will turn out to be mutually beneficial for those two branches of mathematics. Axtell and Stickles [14], remarked that, in general, the set of zero-divisors lacks algebraic structure, suggesting that turning to the zero-divisor graph may both reveal both ring-theoretical properties and impose a graph-theoretical structure. Beck’s hopes have certainly been met: his now classical paper motivated an explosion of research in this and similar associated graphs in the past decade. His definition has since been modified to emphasize the fundamental structure of the zero-divisor set: Anderson’s definition given in [15], which excludes the vertex 0 from the graph, is now considered standard. In [16], Jun and Lee introduced the notion of associated graph of BCK/BCI-algebras by zero divisors in BCK/BCI-algebras and verified some properties of this graph. In addition, Torkzadeh and Ahmadpanah [17] defined the notion of zero divisors of a non-empty subset A of a residuated lattice L and associated a graph to a residuated lattice L. They proved that this graph is always a connected graph and its diameter is at most two.

In this paper, the graphs of hoop algebras are studied. For this, the notion of zero divisors of a non-empty subset of a hoop algebra is introduced by two methods and some related properties are investigated. Several examples of hoop graphs are proved. These graphs are connected and also some necessary conditions for the hoop graph to be a star graph are found. Finally, hoop graphs that are provided by two methods together are compered.

2. Preliminaries

At first, we recall the definition of a hoop algebra and some properties.

By a hoop, we mean an algebraic structure $(A,\odot ,\to ,1)$ where, for all $x,y,z\in A$:

(HP1)

$(A,\odot ,1)$ is a commutative monoid.

(HP2)

$x\to x=1$.

(HP3)

$(x\odot y)\to z=x\to (y\to z)$.

(HP4)

$x\odot (x\to y)=y\odot (y\to x)$.

On hoop A we define $x\le y$ if and only if $x\to y=1$. It is easy to see that ≤ is a partial order relation on A. A hoop A is bounded if there is an element $0\in A$ such that $0\le x$, for all $x\in A$.

Let A be a bounded hoop. We define a negation “−” on A by $\overline{x}=x\to 0$, for all $x\in A$. For $\varnothing \ne X\subseteq A$, we define $\overline{X}=\{\overline{x}\mid x\in X\}$. If $\overline{\left(\overline{x}\right)}=x$, for all $x\in A$, then the bounded hoop A is said to have the double negation property (DNP).

The following proposition provides some properties of hoops.

Proposition 1

([5,6]). Let $(A,\odot ,\to ,1)$ be a bounded hoop. Then, the following condition hold, for all $x,y,z,a\in A$:

(i)

$(A,\le )$ is a meet-semilattice with $x\wedge y=x\odot (x\to y)$.

(ii)

$x\odot y\le z$ if and only if $x\le y\to z$.

(iii)

$x\odot y\le x,y$ and $x\le y\to x$.

(iv)

$x\to x=1$ and $1\to x=x$.

(v)

$x\le y\to (x\odot y)$.

(vi)

$x\to y\le (y\to z)\to (x\to z)$.

(vii)

$x\le \overline{\overline{x}}$ and $x\odot \overline{x}=0$.

(viii)

$x\le y$ implies $x\odot a\le y\odot a$ and $z\to x\le z\to y$ and $y\to z\le x\to z$.

Let A be a hoop and for any $x,y\in A$; define

$$x\bigsqcup y=\left(\right(x\to y)\to y)\wedge \left(\right(y\to x)\to x).$$

Then, a hoop A is called a ⊔-hoop, if ⊔ is the join operation on A. It is easy to see that, for any $x,y,z\in A$,

$$x\odot (y\bigsqcup z)=(x\odot y)\bigsqcup (x\odot z).$$

A non-empty subset I of ⊔-hoop A is called an ideal of A if it satisfies the following conditions:

(I1)

If $x,y\in I$, then $x\bigsqcup y\in I$.

(I2)

If $x\in A$, $y\in I$ and $x\le y$, then $x\in I$.

A non-empty subset F of A is a filter of A if,

(F1)

$x,y\in F$ implies $x\odot y\in F$.

(F2)

$x\in F$ and $x\le y$ imply $y\in F$, for any $x,y\in A$.

The set of all filters of A is denoted by $\mathcal{F}\left(A\right)$. F is a proper filter if F is a filter of A and $F\ne A$. A proper filter of A is called a maximal filter, if it is not properly contained in any other proper filters of A.

Let G be a graph with the vertex set V and edge set E. The edge that connects two distinct vertices x and y is denoted by $x-y$. Note that $x-y$ and $y-x$ are the same. A graph $H=(V_1,E_1)$ is called a subgraph of $G=(V,E)$, if $V_1\subseteq V$ and $E_1\subseteq E$. A graph $G=(V,E)$ is called connected, if any two distinct vertices x and y of G linked by a path in G, otherwise the graph is called disconnected. For distinct vertices x and y of G, let $d(x,y)$ be the length of the shortest path from x to y. If there is no $x-y$ path, then $d(x,y)=\infty$. The diameter of G is

$$diam\left(G\right)=sup\left\{d\right(x,y)\mid x\mathrm{and}y\mathrm{are}\mathrm{distinct}\mathrm{vertices}\mathrm{of}V(G\left)\right\}.$$

A tree is a connected graph with no cycles. A graph G is called complete graph if $x-y\in E\left(G\right)$, for any distinct elements $x,y\in V\left(G\right)$. A graph G is called a star graph in the case there is a vertex x in G such that every other vertex in G is an end, connected to x and no other vertex by an edge [18].

Notation. From now on, $(A,\odot ,\to ,1)$ or simply A is a hoop algebra, unless otherwise stated.

3. Implicative Graph of a Hoop Algebra

In this section, we study associated implicative graph of a hoop algebra. We first introduce the notions of r-prime quasi-filter and zero divisors and investigate related properties. Then, we introduce the concept of associated implicative graph $\mathsf{\Omega }\left(A\right)$ of a hoop A and provide several examples.

Notation. For any non-empty subset X of A, we use the notation $r\left(X\right)$ and $l\left(X\right)$ to denote the sets,

$$r\left(X\right)=\{a\in A\mid x\to a=1,\forall x\in X\}\mathrm{and}l\left(X\right)=\{a\in A\mid a\to x=1,\forall x\in X\}.$$

Definition 1.

Let F be a non-empty subset of A. Then,

(i) 

F is called a quasi-filter of A if for all $x\in A$, $y\in F$ and $y\le x$, then $x\in F$.

(ii) 

A quasi-filter F of A is called a r-prime (l-prime) filter if it satisfies the following conditions:

$\left(rlF1\right)$ F is proper, that is $F\ne A$; and

$\left(rF2\right)\left(\right(lF2\left)\right)$ for any $x,y\in A$, if $r\left(\right\{x,y\left\}\right)\subseteq F,\left(l\right(\{x,y\})\subseteq F)$, then $x\in F$ or $y\in F$.

Example 1.

Let $A=\{0,a,b,c,d,1\}$. Define the operations ⊙ and → on A as follows

$$\begin{array}{cc}\begin{array}{ccccccc}\hfill \to & 0& a& b& c& d& 1\\ 0\hfill & 1& 1& 1& 1& 1& 1\\ a\hfill & d& 1& d& 1& d& 1\\ b\hfill & c& c& 1& 1& 1& 1\\ c\hfill & b& c& d& 1& d& 1\\ d\hfill & a& a& b& c& 1& 1\\ 1\hfill & 0& a& b& c& d& 1\end{array}\hfill & \begin{array}{ccccccc}\odot \hfill & 0& a& b& c& d& 1\\ 0\hfill & 0& 0& 0& 0& 0& 0\\ a\hfill & 0& a& 0& a& 0& a\\ b\hfill & 0& 0& 0& 0& b& b\\ c\hfill & 0& a& 0& a& b& c\\ d\hfill & 0& 0& b& b& d& d\\ 1\hfill & 0& a& b& c& d& 1\end{array}\hfill \end{array}$$

We can easily see that A with these operations is a bounded hoop. Let $X=\{a,b,c\}$ and $Y=\{c,d\}$. Then, by routine calculation, we can see that $r\left(X\right)=\{1,c\}$ and $l\left(Y\right)=\{b,0\}$. Now, $F=\{1,a,c\}$ and $G=\{1,c,d\}$ are quasi-filters of A but G is not a filter of A, because $c\odot d=b\notin G$. Moreover, F is an r-prime filter of A.

Proposition 2.

Let X and Y be two non-empty subsets of A. Then, the following statements hold:

(i)

$X\subseteq l\left(r\right(X\left)\right)$ and $X\subseteq r\left(l\right(X\left)\right)$.

(ii)

If $X\subseteq Y$, then $l\left(Y\right)\subseteq l\left(X\right)$ and $r\left(Y\right)\subseteq r\left(X\right)$.

(iii)

$l\left(X\right)=l\left(r\right(l\left(X\right)\left)\right)$ and $r\left(X\right)=r\left(l\right(r\left(X\right)\left)\right)$.

Proof. 

$\left(i\right)$ Let $l\left(X\right)=Y$. Then, for any $y\in Y$ and for any $x\in X$, we get that $y\to x=1$. Thus, we have for any $x\in X$ and for any $y\in Y$, $y\to x=1$. Hence, $x\in r\left(Y\right)$. Therefore, $x\in r\left(l\right(X\left)\right)$. Similarly, we can prove that $X\subseteq l\left(r\right(X\left)\right)$.

$\left(ii\right)$ Let $a\in r\left(Y\right)$. Then, for any $y\in Y$, $y\to a=1$. Since $X\subseteq Y$, for any $x\in X$, $x\to a=1$, too. Hence, $a\in r\left(X\right)$. Similarly, $l\left(Y\right)\subseteq l\left(X\right)$.

$\left(iii\right)$ By (i), $X\subseteq l\left(r\right(X\left)\right)$, then by (ii), $r\left(l\right(r\left(X\right)\left)\right)\subseteq r\left(X\right)$. Let $Y=r\left(X\right)$. Then, by (i), $Y\subseteq r\left(l\right(Y\left)\right)$, and thus $r\left(X\right)\subseteq r\left(l\right(r\left(X\right)\left)\right)$. Hence, $r\left(X\right)=r\left(l\right(r\left(X\right)\left)\right)$. Similarly, $l\left(X\right)=l\left(r\right(l\left(X\right)\left)\right)$. □

Theorem 1.

A proper quasi-filter F of A is r-prime if and only if $r\left(\{x_1,x_2,\dots ,x_n\}\right)\subseteq F$ implies, there exists $1\le i\le n$ such that $x_i\in F$.

Proof. 

We proceed by induction on n. If $n=2$, then $r\left(\{x_1,x_2\}\right)\subseteq F$. Since F is an r-prime quasi-filter of A, by Definition 1$\left(r{F}_2\right)$, the result is clear. Now, suppose the statement holds for $n-1$. Let $x_1,x_2,\dots ,x_n\in A$ such that $r\left(\{x_1,x_2,\dots ,x_{n-1},x_n\}\right)\subseteq F$. If $y\in r\left(\{x_1,x_2,\dots ,x_{n-1}\}\right)$, then by routine calculation, we can see that

$$r\left(\{y,x_n\}\right)\subseteq r\left(\{x_1,x_2,\dots ,x_{n-1},x_n\}\right)\subseteq F.$$

Now, assume that $x_n\notin F$. Since F is r-prime, we get $y\in F$, which shows that $r\left(\{x_1,x_2,\dots ,x_{n-1}\}\right)\subseteq F$. Using the induction hypothesis, we conclude that $x_i\in F$, for some $i\in \{1,\dots ,n-1\}$. The converse is clear. □

Remark 1.

(i)

For any $x,y\in A$, $1\in r\left(\right\{x,y\left\}\right)$. Thus, $r\left(\right\{x,y\left\}\right)\ne \varnothing$.

(ii)

$r\left(\right\{x,y\left\}\right)=r\left(\right\{x\left\}\right)\cap r\left(\right\{y\left\}\right)$, for any $x,y\in A$. Thus, we have,

$$t\in r\left(\right\{x,y\left\}\right)⟺x\to t=1andy\to t=1⟺t\in r\left(\right\{x\left\}\right)andt\in r\left(\right\{y\left\}\right)⟺t\in r\left(\right\{x\left\}\right)\cap r\left(\right\{y\left\}\right).$$

Definition 2.

For any $x\in A$, we use the notion ${\mathcal{Z}}_x$ to denote the set of all elements $y\in A$ such that $r\left(\right\{x,y\left\}\right)=\left\{1\right\}$. It means that ${\mathcal{Z}}_x=\{y\in A\mid r\left(\{x,y\}\right)=\left\{1\right\}\}$.

Example 2.

According to Example 1,

$${\mathcal{Z}}_0={\mathcal{Z}}_b=\left\{1\right\}{\mathcal{Z}}_1=A{\mathcal{Z}}_a={\mathcal{Z}}_c=\{1,d\}and{\mathcal{Z}}_d=\{a,c,1\}.$$

Proposition 3.

For any $x\in A$, $r\left(\right\{x,1\left\}\right)=\left\{1\right\}$.

Proof. 

Let $x\in A$. Since

$$r\left(\right\{x,1\left\}\right)=\{y\in A\mid x\to y=1\mathrm{and}1\to y=1\}=\{y\in A\mid x\to y=1\mathrm{and}y=1\}=\left\{1\right\},$$

we have $r\left(\right\{x,1\left\}\right)=\left\{1\right\}$. □

Proposition 4.

For any elements a and b of A, if $a\to b=1$, then $r\left(\right\{b\left\}\right)\subseteq r\left(\right\{a\left\}\right)$ and ${\mathcal{Z}}_a\subseteq {\mathcal{Z}}_b$.

Proof. 

Let $x\in r\left(\right\{b\left\}\right)$. Then, $b\to x=1$. By assumption, $a\to b=1$, then by Proposition 1(vi), $a\to b\le (b\to x)\to (a\to x)$. Then, $1\le a\to x$, and thus $a\to x=1$. Thus, $x\in r\left(\right\{a\left\}\right)$. Hence, $r\left(\right\{b\left\}\right)\subseteq r\left(\right\{a\left\}\right)$. Now, suppose $x\in {\mathcal{Z}}_a$. Then, by Remark 1(ii),

$$1\in r\left(\right\{b,x\left\}\right)=r\left(\right\{b\left\}\right)\cap r\left(\right\{x\left\}\right)\subseteq r\left(\right\{a\left\}\right)\cap r\left(\right\{x\left\}\right)=r\left(\right\{a,x\left\}\right)=\left\{1\right\}.$$

Thus, $r\left(\right\{b,x\left\}\right)=\left\{1\right\}$, and so $x\in {\mathcal{Z}}_b$. Therefore, ${\mathcal{Z}}_a\subseteq {\mathcal{Z}}_b$. □

By the following example, we show that the converse of relation in Proposition 4 may not be true in general.

Example 3.

In Example 1, $b\to d=1$. By routine calculation, we have $r\left(\right\{b\left\}\right)=\{b,c,d,1\}$, $r\left(\right\{d\left\}\right)=\{d,1\}$, ${\mathcal{Z}}_b=\left\{1\right\}$ and ${\mathcal{Z}}_d=\{a,c,1\}$. We can easily see that $r\left(\right\{b\left\}\right)⊈r\left(\right\{d\left\}\right)$ and ${\mathcal{Z}}_d⊈{\mathcal{Z}}_b$.

Theorem 2.

For any element x of A, ${\mathcal{Z}}_x$ is a quasi-filter of A containing the element 1. Moreover, if ${\mathcal{Z}}_x$ is maximal in $\{{\mathcal{Z}}_a\mid a\in Aand{\mathcal{Z}}_a\ne \varnothing \}$, then ${\mathcal{Z}}_x$ is an r-prime.

Proof. 

At first, we prove that ${\mathcal{Z}}_x$ is a quasi-filter of A. For this, suppose $b\in A$ and $a\in {\mathcal{Z}}_x$ are two arbitrary elements such that $a\le b$. Then, it is enough to prove that $b\in {\mathcal{Z}}_x$. Since $a\le b$, we have $a\to b=1$. By Proposition 4, $r\left(\right\{b\left\}\right)\subseteq r\left(\right\{a\left\}\right)$. In addition, since $a\in {\mathcal{Z}}_x$, we have $r\left(\right\{x,a\left\}\right)=\left\{1\right\}$. Moreover, we know that $1\in r\left(\right\{x,b\left\}\right)$, then by Remark 1,

$$1\in r\left(\right\{x,b\left\}\right)=r\left(\right\{x\left\}\right)\cap r\left(\right\{b\left\}\right)\subseteq r\left(\right\{x\left\}\right)\cap r\left(\right\{a\left\}\right)=r\left(\right\{x,a\left\}\right)=\left\{1\right\}.$$

Thus, $r\left(\right\{x,b\left\}\right)=\left\{1\right\}$. Hence, $b\in {\mathcal{Z}}_x$. Thus, ${\mathcal{Z}}_x$ is a quasi-filter of A. Now, suppose ${\mathcal{Z}}_x$ is maximal in $\{{\mathcal{Z}}_a\mid a\in Aand{\mathcal{Z}}_a\ne \varnothing \}$. By Proposition 3, for any $x\in A$, $r\left(\right\{x,1\left\}\right)=\left\{1\right\}$. Then, $1\in {\mathcal{Z}}_x$, and so ${\mathcal{Z}}_x\ne \varnothing$. Now, we prove that ${\mathcal{Z}}_x$ is an r-prime. For this, let $a,b\in A$ and $r\left(\{a,b\}\right)\subseteq {\mathcal{Z}}_x$ such that $a\notin {\mathcal{Z}}_x$. It is enough to prove that $b\in {\mathcal{Z}}_x$. Since ${\mathcal{Z}}_x$ is maximal, ${\mathcal{Z}}_x$ is proper. Moreover, since $r\left(\{a,b\}\right)\subseteq {\mathcal{Z}}_x$ such that $a\notin {\mathcal{Z}}_x$, $r\left(\right\{a,b,x\left\}\right)=\left\{1\right\}$. Suppose $r\left(\right\{a,b,x\left\}\right)\ne \left\{1\right\}$. Then,

$$1\in r\left(\{a,b,x\}\right)=r\left(\left\{a\right\}\right)\cap r\left(\left\{b\right\}\right)\cap r\left(\left\{x\right\}\right)=r\left(\{a,b\}\right)\cap r\left(\left\{x\right\}\right)\subseteq {\mathcal{Z}}_x\cap r\left(\left\{x\right\}\right).$$

Let ${\mathcal{Z}}_x\cap r\left(\left\{x\right\}\right)\ne \left\{1\right\}$. Then, there exists $t\ne 1$ such that $t\in {\mathcal{Z}}_x\cap r\left(\left\{x\right\}\right)$. Since $t\in {\mathcal{Z}}_x$, we have $r\left(\right\{t,x\left\}\right)=\left\{1\right\}$. In addition, $t\in r\left(\right\{x\left\}\right)$, then $x\to t=1$. Moreover, since $x\to t=1$ and $t\to t=1$, we have $t\in r\left(\right\{t,x\left\}\right)$, which is a contradiction. Then, ${\mathcal{Z}}_x\cap r\left(\left\{x\right\}\right)=\left\{1\right\}$, and thus $r\left(\right\{a,b,x\left\}\right)=\left\{1\right\}$. In addition, from $a\notin {\mathcal{Z}}_x$, $r\left(\right\{a,x\left\}\right)\ne \left\{1\right\}$. Then, there exists $1\ne y\in r\left(\right\{a,x\left\}\right)$, and so $x\to y=1$. Thus, by Proposition 4, ${\mathcal{Z}}_x\subseteq {\mathcal{Z}}_y$. If ${\mathcal{Z}}_y=A$, then, for any $a\in A$, $a\in {\mathcal{Z}}_y$, and so $r\left(\right\{a,y\left\}\right)=\left\{1\right\}$. Since $y\in r\left(\right\{a,x\left\}\right)$, we get $a\to y=1$. In addition, $y\to y=1$, then $y\in r\left(\right\{a,y\left\}\right)=\left\{1\right\}$, which is a contradiction. Then, ${\mathcal{Z}}_y$ is proper. Since ${\mathcal{Z}}_x$ is maximal, ${\mathcal{Z}}_x={\mathcal{Z}}_y$. In addition, from $y\in r\left(\right\{a,x\left\}\right)$, we have,

$$\varnothing \ne r\left(\right\{b,y\left\}\right)=r\left(\right\{b\left\}\right)\cap r\left(\right\{y\left\}\right)\subseteq r\left(\right\{b\left\}\right)\cap r\left(\right\{x\left\}\right)\cap r\left(\right\{a\left\}\right)=r\left(\right\{a,b,x\left\}\right)=\left\{1\right\}.$$

Then, $r\left(\right\{y,b\left\}\right)=\left\{1\right\}$, thus $b\in {\mathcal{Z}}_y$. Since ${\mathcal{Z}}_x={\mathcal{Z}}_y$, we get $b\in {\mathcal{Z}}_x$. Thus, ${\mathcal{Z}}_x$ is an r-prime of A. □

Definition 3.

By the implicative graph of a hoop A, denoted $\mathsf{\Omega }\left(A\right)$, we mean the graph which vertices are just the elements of A, and for distinct $x,y\in \mathsf{\Omega }\left(A\right)$, there is an edge connecting x and y if and only if $r\left(\right\{x,y\left\}\right)=\left\{1\right\}$.

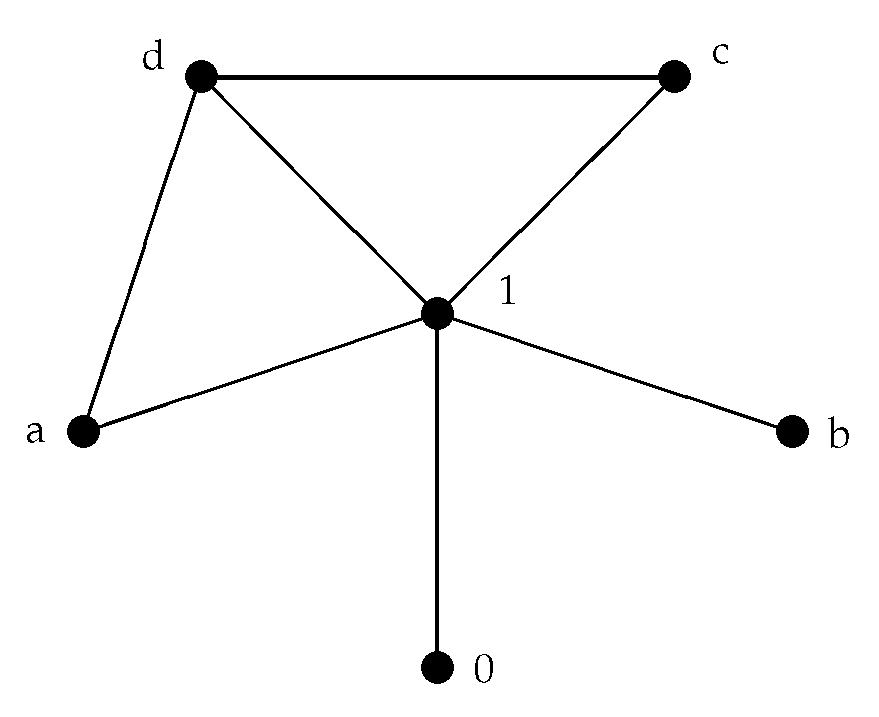
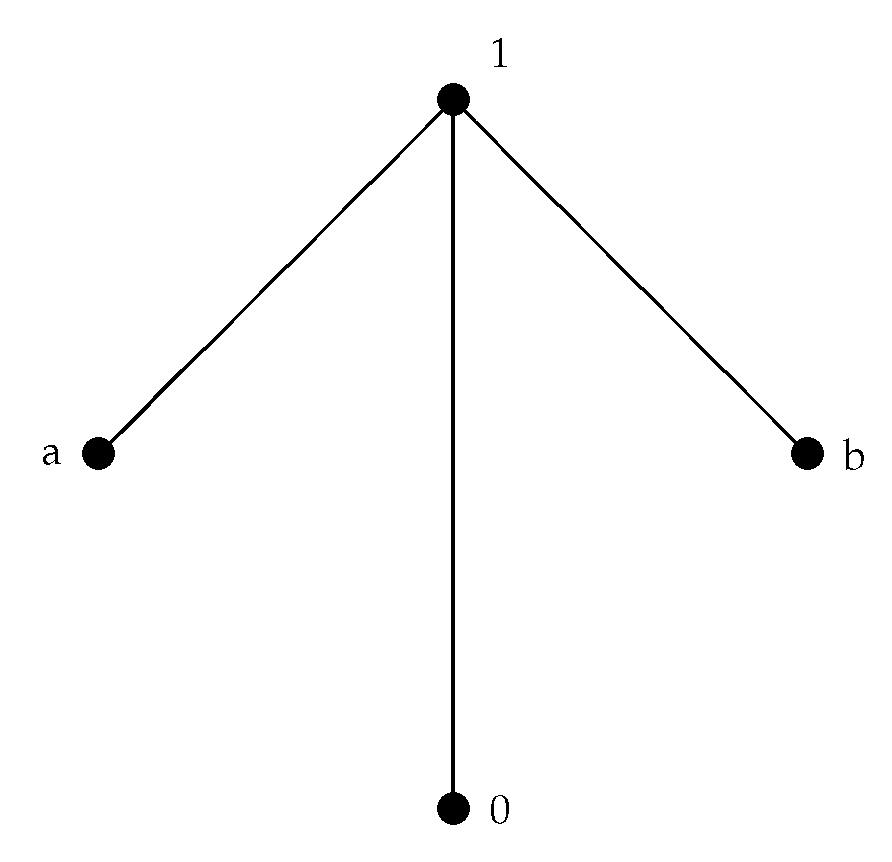
Example 4.

According to Example 1, we have, $r\left(\right\{x,1\left\}\right)=r\left(\right\{a,d\left\}\right)=r\left(\right\{c,d\left\}\right)=\left\{1\right\},$ $r\left(\right\{a,b\left\}\right)=r\left(\right\{a,c\left\}\right)=r\left(\right\{b,c\left\}\right)=r\left(\right\{c,0\left\}\right)=\{c,1\},$ $r\left(\right\{a,0\left\}\right)=\{a,c,1\},r\left(\right\{b,0\left\}\right)=\{b,c,d,1\},$ and $r\left(\right\{b,d\left\}\right)=r\left(\right\{d,0\left\}\right)=\{d,1\}$, as Figure 1.

Theorem 3.

For any $x,y\in \mathsf{\Omega }\left(A\right)$, if ${\mathcal{Z}}_x$ and ${\mathcal{Z}}_y$ are distinct r-prime quasi-filters of A, then there is an edge connecting x and y.

Proof. 

Let $x,y\in A$. It is sufficient to prove that $r\left(\right\{x,y\left\}\right)=\left\{1\right\}$. Suppose $r\left(\right\{x,y\left\}\right)\ne \left\{1\right\}$. Then, $x\notin {\mathcal{Z}}_y$ and $y\notin {\mathcal{Z}}_x$. If $x\in {\mathcal{Z}}_y$, then $r\left(\right\{x,y\left\}\right)=\left\{1\right\}$, which is a contradiction. Let $a\in {\mathcal{Z}}_x$. Then, $r\left(\right\{x,a\left\}\right)=\left\{1\right\}$. Since ${\mathcal{Z}}_y$ is a quasi-filter, $1\in {\mathcal{Z}}_y$, thus, $r\left(\{x,a\}\right)\subseteq {\mathcal{Z}}_y$. By assumption, ${\mathcal{Z}}_y$ is an r-prime, then $x\in {\mathcal{Z}}_y$ or $a\in {\mathcal{Z}}_y$. Since $x\notin {\mathcal{Z}}_y$, we get that $a\in {\mathcal{Z}}_y$. Hence, ${\mathcal{Z}}_x\subseteq {\mathcal{Z}}_y$. Similarly, we can see that ${\mathcal{Z}}_y\subseteq {\mathcal{Z}}_x$. Thus, ${\mathcal{Z}}_x={\mathcal{Z}}_y$, which is a contradiction. By assumption, ${\mathcal{Z}}_x$ and ${\mathcal{Z}}_y$ are distinct. Therefore, $r\left(\right\{x,y\left\}\right)=\left\{1\right\}$ and there is an edge connecting x and y. □

Theorem 4.

The graph $\mathsf{\Omega }\left(A\right)$ is connected with diameter at most two.

Proof. 

By Proposition 3, for any $x\in A$, $r\left(\right\{x,1\left\}\right)=\left\{1\right\}$. Then, 1 is connected to all points of A. Hence, both vertices are connected by a path, and so $\mathsf{\Omega }\left(A\right)$ is connected. Now, let $x,y$ be two vertices in $\mathsf{\Omega }\left(A\right)$. If $r\left(\right\{x,y\left\}\right)=\left\{1\right\}$, then $d(x,y)=1$. If $r\left(\right\{x,y\left\}\right)\ne \left\{1\right\}$, then the path $(x-1-y)$ exists, thus, $d(x,y)=2$. Since

$$diam\left(\mathsf{\Omega }\right(A\left)\right)=sup\left\{d\right(x,y)\mid x,y\in V(\mathsf{\Omega }\left(A\right)\left)\right\},$$

we have $diam\left(\mathsf{\Omega }\right(A\left)\right)\le 2$. □

Theorem 5.

If A is a totally ordered hoop, then $\mathsf{\Omega }\left(A\right)$ is a star.

Proof. 

Suppose A is a totally ordered hoop and $\mid A\mid =n$. We proceed by induction on n. If $n=3$, then $0\le a\le 1$. Since $r\left(\right\{0,1\left\}\right)=r\left(\right\{a,1\left\}\right)=\left\{1\right\}$, it is enough to investigate on $r\left(\right\{0,a\left\}\right)$. It is easily to see that $r\left(\right\{0,a\left\}\right)=\{a,1\}$. Then, 1 is just connected to all points of A, and so $\mathsf{\Omega }\left(A\right)$ is a star. Let $\mid A\mid =n$. Without loss of generality, suppose $A=\{0,a_1,\dots ,a_{n-2},1\}$ such that $0\le a_1\le \dots \le a_{n-2}\le 1$. Using the induction hypothesis, we conclude that $\mathsf{\Omega }\left(B\right)$ is a star such that $B\subseteq A$ and $\mid B\mid =n-1$. Suppose $C=\{0,a_1,\dots ,a_{n-3},1\}\subseteq A$. By assumption, for any $x\in C-\left\{1\right\}$, $x\le a_{n-2}$, then it is easy to see that

$$r\left(\{x,a_{n-2}\}\right)=\{a_{n-2},1\}\ne \left\{1\right\}.$$

Thus, there is no edge $x-a_{n-2}$. Hence, $\mathsf{\Omega }\left(A\right)$ is a star. □

Corollary 1.

If A is a totally ordered hoop, then $\mathsf{\Omega }\left(A\right)$ is a tree.

4. Productive Graph of a Hoop Algebra

In this section, we study associated productive graph of a hoop algebra. We first introduce the notion of zero divisors by product operation and investigate related properties. By means of the set of all zero divisors of elements of a hoop A, the associated productive graph $\Gamma \left(A\right)$ is defined and several examples are provided.

Note. From now one, in this section, A will be a bounded hoop algebra.

Definition 4.

Let X be a non-empty subset of A. The set of all zero divisors of X is denoted by $Z_X$ and is defined as follows:

$$Z_X=\{a\in A\mid a\odot x=0,\forall x\in X\}.$$

Proposition 5.

Let X and Y be non-empty subsets of A. Then, the following statements hold:

(i)

$0\in Z_X$.

(ii)

If $X\subseteq Y$, then $Z_Y\subseteq Z_X$.

(iii)

If $\overline{Z_X}-\left\{1\right\}\ne \varnothing$, then $Z_{\overline{Z_X}-\left\{1\right\}}\subseteq Z_X$.

(iv)

If $1\in X$, then $Z_X=\left\{0\right\}$.

(v)

$Z_F=\left\{0\right\}$, for all $F\in \mathcal{F}\left(A\right)$.

(vi)

$1\in Z_X$ if and only if $X=\left\{0\right\}$ if and only if $Z_X=A$.

(vii)

If $0\in X$, then $Z_X=Z_{X-\left\{0\right\}}$.

(viii)

$Z_X\cup Z_Y\subseteq Z_{X\wedge Y}$, where $X\wedge Y=\{x\wedge y\mid x\in Xandy\in Y\}$.

Proof. 

$\left(i\right)$ Since A is a bounded hoop, then $0\in A$. Thus, for any $x\in X$, $x\odot 0=0$. Hence, $0\in Z_X$.

$\left(ii\right)$ Let $a\in Z_Y$. Then, for any $y\in Y$, $a\odot y=0$. Since $X\subseteq Y$, for any $x\in X$, $a\odot x=0$. Hence, $a\in Z_X$. Therefore, $Z_Y\subseteq Z_X$.

$\left(iii\right)$ Assume that $p\in Z_{\overline{Z_X}-\left\{1\right\}}$, then $p\odot x=0$, for all $x\in \overline{Z_X}-\left\{1\right\}$. Put $x=\overline{t}$, for $t\in Z_X-\left\{0\right\}$. Hence, $p\odot \overline{t}=0$, for all $t\in Z_X-\left\{0\right\}$, and we get that $\overline{t}\le \overline{p}$, for all $t\in Z_X-\left\{0\right\}$. Since $t\in Z_X-\left\{0\right\}$, then $t\odot a=0$, for all $a\in X$, i.e, $a\le \overline{t}$, for all $a\in X$. Thus, we can obtain $a\le \overline{p}$, that is $p\odot a=0$, for all $a\in X$. Therefore, $p\in Z_X$.

$\left(iv\right)$ Let $1\in X$ and $x\in Z_X$. Then, $x=x\odot 1=0$, and so $Z_X=\left\{0\right\}$.

$\left(v\right)$ The proof follows by (iv).

$\left(vi\right)$ Let $1\in Z_X$. Then, $1\odot x=0$, for all $x\in X$ and so $X=\left\{0\right\}$. Conversely, let $X=\left\{0\right\}$. Then, $Z_X=A$. We get that $1\in Z_X$. It is easy to prove that $Z_X=A$ if and only if $1\in Z_X$.

$\left(vii\right)$ The proof is straightforward.

$\left(viii\right)$ Let $a\in Z_X\cup Z_Y$. Then, by Definition 4, $a\odot x=0$ or $a\odot y=0$, for all $x\in X$ or $y\in Y$. Suppose $a\odot x=0$, for all $x\in X$. Since $x\wedge y\le x$, by Proposition 1(viii), $a\odot (x\wedge y)\le a\odot x$. From $a\odot x=0$, we have $a\odot (x\wedge y)=0$. Hence, $a\in Z_{X\wedge Y}$. □

By the following example, we show that the inverse inclusions of Proposition 5(iii) and (viii) may not be true, in general.

Example 5.

According to Example 1:

$\left(i\right)$ Let $X=\left\{b\right\}$. Then, by routine calculations, we can see that $Z_X=\{0,a,b,c\}$, Thus, $\overline{Z_X}=\{1,d,c,b\}$, and so $\overline{Z_X}-\left\{1\right\}=\{d,c,b\}$. Hence, $Z_{\overline{Z_X}-\left\{1\right\}}=\left\{0\right\}$. Thus, it is clear that $Z_{\overline{Z_X}-\left\{1\right\}}\ne Z_X$.

$\left(ii\right)$ Let $X=\left\{c\right\}$ and $Y=\left\{d\right\}$. Then, $Z_X=\{0,b\}$ and $Z_Y=\{0,a\}$, respectively. Thus, $Z_X\cup Z_Y=\{0,a,b\}$. We can easily see that $X\wedge Y=\left\{b\right\}$ and $Z_{X\wedge Y}=\{0,a,b,c\}$. Hence, $Z_{X\wedge Y}⊈Z_X\cup Z_Y$.

Proposition 6.

Let X be a non-empty subset of ⊔-hoop A. Then, $Z_X$ is an ideal of A.

Proof. 

By Proposition 5(i), $0\in Z_X$, then $Z_X$ is non-empty. Let $x\le y$, for any $y\in Z_X$ and $x\in A$. Then, $y\odot a=0$, for all $a\in X$. By Proposition 1(viii), $x\odot a\le y\odot a=0$, then $x\odot a=0$, for all $a\in X$. Thus, $x\in Z_X$. Now, let $x,y\in Z_X$. Then, $x\odot a=y\odot a=0$, for all $a\in X$. Hence, for all $a\in X$,

$$a\odot (x\bigsqcup y)=(a\odot x)\bigsqcup (a\odot y)=0,$$

that is $x\bigsqcup y\in Z_X$. Therefore, $Z_X$ is an ideal of A. □

For $x\in A$, the set $D_x=\{y\in A\mid Z_{\{x,y\}}=\left\{0\right\}\}$ is called the set of all zero divisors of x.

By Proposition 5, we have $D_1=A$ and $1\in D_x$, for all $x\in A$.

Proposition 7.

$D_x$ is a filter of A, for any $x\in A$.

Proof. 

Let $x\in A$. Then, by Proposition 5(iv), $Z_{\{1,x\}}=\left\{0\right\}$, thus, $1\in D_x$, i.e., $D_x\ne \varnothing$. Now, we show that $D_x$ is a filter of A. Let $y,z\in D_x$. Then, $Z_{\{x,y\}}=Z_{\{x,z\}}=\left\{0\right\}$. Suppose $h\in Z_{\{x,y\odot z\}}$. Then, $h\odot x=h\odot (y\odot z)=0$. Since A is a monoid, $0=h\odot (y\odot z)=(h\odot y)\odot z$, then $h\odot y\in Z_{\{x,z\}}=\left\{0\right\}$. Hence, $h\odot y=0$. Since $h\odot x=0$, we have $h\in Z_{\{x,y\}}=\left\{0\right\}$. Thus, $h=0$, and so $Z_{\{x,y\odot z\}}=\left\{0\right\}$. Now, suppose $y\in D_x$ and $z\in A$ such that $y\le z$. Let $h\in Z_{\{x,z\}}$. Then, $h\odot x=h\odot z=0$. Since $y\le z$, by Proposition 1(viii), $h\odot y\le h\odot z=0$, then $h\odot y=0$. Thus, $h\in Z_{\{x,y\}}=\left\{0\right\}$. Hence, $h=0$. Then, $Z_{\{x,z\}}=\left\{0\right\}$, and so $z\in D_x$. Therefore, $D_x\in \mathcal{F}\left(A\right)$. □

The set of dense elements of a hoop A is denoted by $D_s\left(A\right)=\{x\in A\mid \overline{x}=0\}$.

Theorem 6.

$D_0=D_s\left(A\right)$.

Proof. 

Let $a\in D_0$. Then,

$$Z_{\{a,0\}}=\left\{0\right\}=\{t\mid t\odot a=0\}=\{t\mid t\le \overline{a}\}.$$

Since $\overline{a}\odot 0=0$ and by Proposition 1(vii), $\overline{a}\odot a=0$, we have $\overline{a}\in Z_{\{a,0\}}=\left\{0\right\}$. Then, $\overline{a}=0$, and so $a\in D_s\left(A\right)$. Conversely, let $a\in D_s\left(A\right)$. Then, $\overline{a}=0$. Since $\overline{a}\odot 0=0$ and by Proposition 1(vii), $\overline{a}\odot a=0$, $\overline{a}\in Z_{\{a,0\}}$. Now, suppose $t\in Z_{\{a,0\}}$. Then, $t\odot a=0$, and so $t\le \overline{a}$. Since $\overline{a}=0$, we have $t=0$. Thus, $Z_{\{a,0\}}=\left\{0\right\}$. Hence, $a\in D_0$. □

Definition 5.

$\Gamma \left(A\right)$ is called an associated productive graph if vertices are just the elements of A, and for distinct $x,y\in A$, there is an edge connecting x and y if and only if $Z_{\{x,y\}}=\left\{0\right\}$. The edge that connects two vertices x and y is denoted by $x-y$.

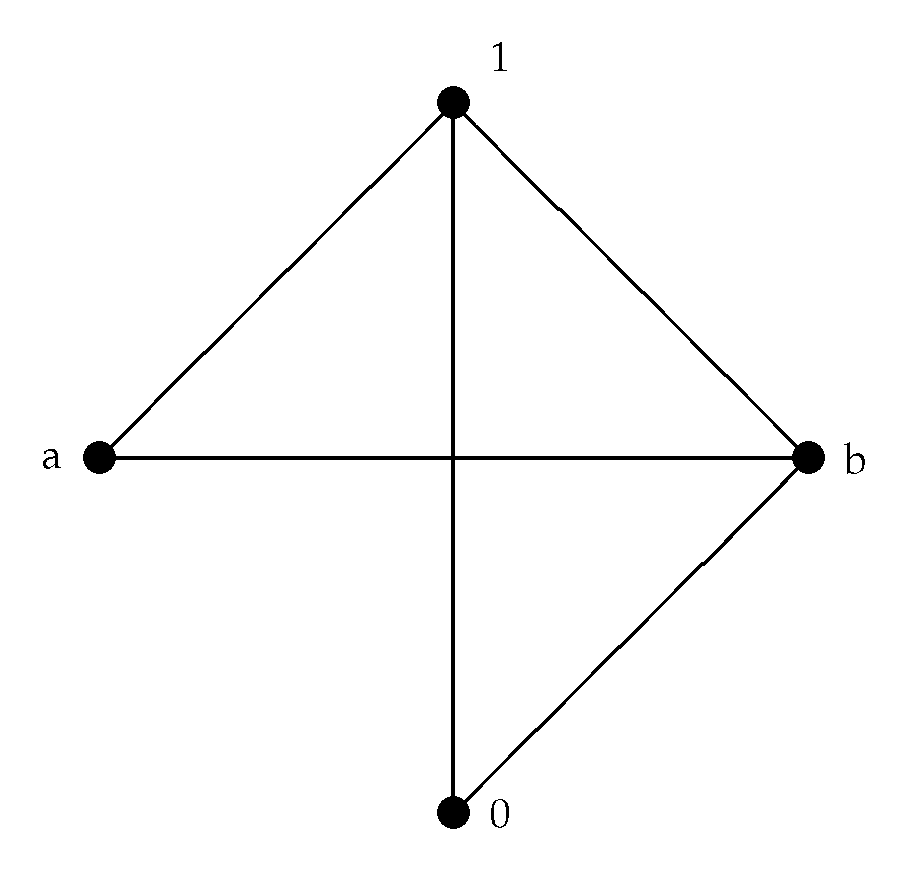
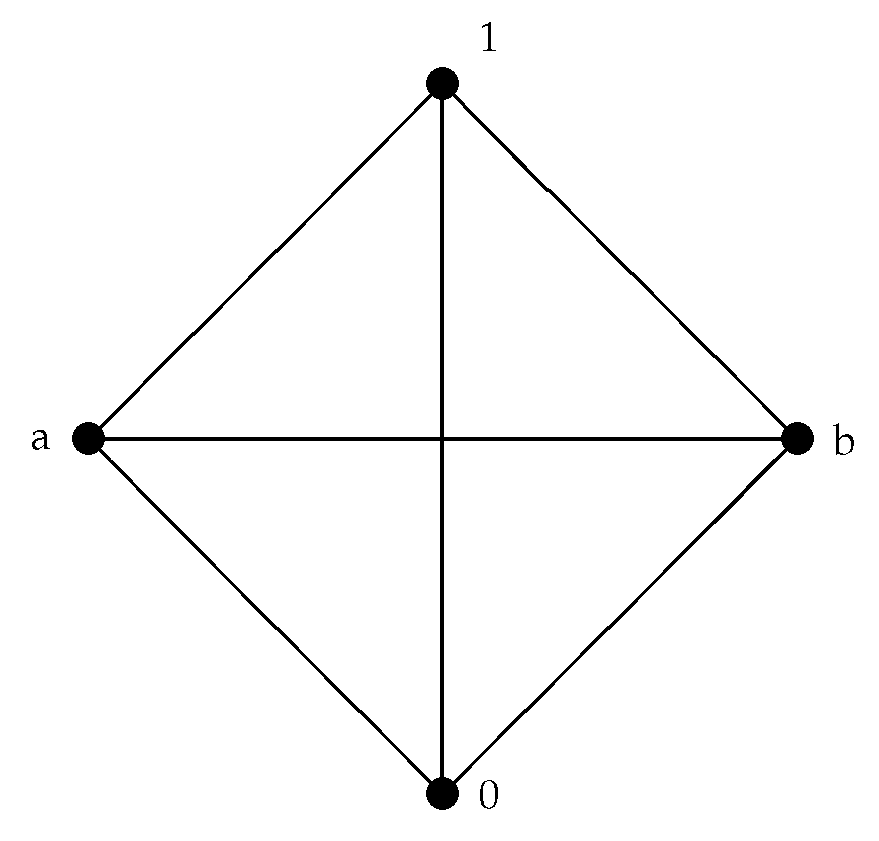
Example 6.

$\left(i\right)$ Let $A=\{0,a,b,1\}$. Define the operations ⊙ and → on A as follows

$$\begin{array}{cc}\begin{array}{ccccc}\hfill \to & 0& a& b& 1\\ 0\hfill & 1& 1& 1& 1\\ a\hfill & a& 1& 1& 1\\ b\hfill & 0& a& 1& 1\\ 1\hfill & 0& a& b& 1\end{array}\hfill & \begin{array}{ccccc}\odot \hfill & 0& a& b& 1\\ 0\hfill & 0& 0& 0& 0\\ a\hfill & 0& 0& a& a\\ b\hfill & 0& a& b& b\\ 1\hfill & 0& a& b& 1\end{array}\hfill \end{array}$$

By routine calculations, we see that A with these operations is a bounded hoop. Then, for any $1\ne x\in A$, we have:

$$Z_{\{x,1\}}=Z_{\{a,b\}}=Z_{\{b,0\}}=\left\{0\right\}and{Z}_{\{a,0\}}=\{a,0\}.$$

as Figure 2.

$\left(ii\right)$ Let $A=0,a,b,c,1$. Define the operations ⊙ and → on A as follows

$$\begin{array}{cc}\begin{array}{cccccc}\hfill \to & 0& a& b& c& 1\\ 0\hfill & 1& 1& 1& 1& 1\\ a\hfill & b& 1& 0& 0& 1\\ b\hfill & c& 0& 1& 0& 1\\ c\hfill & c& 0& 0& 1& 1\\ 1\hfill & 0& a& b& c& 1\end{array}\hfill & \begin{array}{cccccc}\odot \hfill & 0& a& b& c& 1\\ 0\hfill & 0& 0& 0& 0& 0\\ a\hfill & 0& a& 0& 0& a\\ b\hfill & 0& 0& b& 0& b\\ c\hfill & 0& 0& 0& c& c\\ 1\hfill & 0& a& b& c& 1\end{array}\hfill \end{array}$$

Then, A with these operations is a bounded hoop. Then, for any $1\ne x\in A$, we have: $Z_{\{x,1\}}=\left\{0\right\},$ $Z_{\{0,a\}}=\{0,b,c\},Z_{\{0,b\}}=\{0,a,c\},Z_{\{0,c\}}=\{0,a,b\},$ $Z_{\{a,b\}}=\{0,c\},Z_{\{a,c\}}=\{0,b\},Z_{\{b,c\}}=\{0,a\}$, as Figure 3.

Theorem 7.

$\Gamma \left(A\right)$ is a connected graph with diameter at most two.

Proof. 

By Proposition 5(iv), $Z_{\{1,x\}}=\left\{0\right\}$, for any $x\in A$. Then, 1 is connected to all points of A. Hence, both vertices are connected by a path, and so $\Gamma \left(A\right)$ is connected. Now, let $x,y$ be two vertices in $\Gamma \left(A\right)$. If $Z_{\{x,y\}}=\left\{0\right\}$, then $d(x,y)=1$. If $Z_{\{x,y\}}\ne \left\{0\right\}$, then the path $(x-1-y)$ exists, thus $d(x,y)=2$. Since

$$diam(\Gamma (A\left)\right)=sup\left\{d\right(x,y)\mid x,y\in V(\Gamma \left(A\right)\left)\right\},$$

we have $diam(\Gamma (A\left)\right)\le 2$. □

Theorem 8.

$D_s\left(A\right)=A-\left\{0\right\}$ if and only if $\Gamma \left(A\right)$ is complete.

Proof. 

$(\Rightarrow )$ Let $x,y\in A-\left\{0\right\}$ such that $x\ne y$. Then, $x,y\in D_s\left(A\right)$, and so $\overline{x}=\overline{y}=0$. By definition of $Z_{\{x,y\}}$,

$$Z_{\{x,y\}}=\{t\mid t\odot x=0\mathrm{and}t\odot y=0\}=\{t\mid t\le \overline{x}\mathrm{and}t\le \overline{y}\}.$$

Since $\overline{x}=\overline{y}=0$, we have $t=0$. Then, $Z_{\{x,y\}}=\left\{0\right\}$. Hence, $x-y$ exists. By Theorem 6, $D_0=D_s\left(A\right)$, then $D_0=A-\left\{0\right\}$. Thus, for any $0\ne x\in A$, $x\in D_0$. Hence, $Z_{\{x,0\}}=\left\{0\right\}$. Therefore, $\Gamma \left(A\right)$ is complete.

$(\Leftarrow )$ Since $\Gamma \left(A\right)$ is complete, for any $x,y\in V(\Gamma (A\left)\right)$, $x-y$ exists. Let $y=0$ and $x\ne 0$. Then, $x-0$ exists, and so $Z_{\{x,0\}}=\left\{0\right\}$. By Proposition 1(vii), $\overline{x}\odot x=\overline{x}\odot 0=0$. Then, $\overline{x}\in Z_{\{x,0\}}=\left\{0\right\}$. Thus, $x\in D_0$. Hence, $D_0=A-\left\{0\right\}$. By Theorem 6, $D_0=D_s\left(A\right)$. Therefore, $D_s\left(A\right)=A-\left\{0\right\}$. □

Corollary 2.

If $D_s\left(A\right)=A-\left\{0\right\}$ and $\mid A\mid >2$, then $\Gamma \left(A\right)$ is not a tree.

Example 7.

Let $A=\{0,a,b,1\}$. Define the operations ⊙ and → on A as follows,

$$\begin{array}{cc}\begin{array}{ccccc}\hfill \to & 0& a& b& 1\\ 0\hfill & 1& 1& 1& 1\\ a\hfill & 0& 1& 1& 1\\ b\hfill & 0& b& 1& 1\\ 1\hfill & 0& a& b& 1\end{array}\hfill & \begin{array}{ccccc}\odot \hfill & 0& a& b& 1\\ 0\hfill & 0& 0& 0& 0\\ a\hfill & 0& a& a& a\\ b\hfill & 0& a& a& b\\ 1\hfill & 0& a& b& 1\end{array}\hfill \end{array}$$

By routine calculations, we see that A with these operations is a bounded hoop and $D_s\left(A\right)=A-\left\{0\right\}$. Then, $\Gamma \left(A\right)$ is complete. Because $Z_{\{x,1\}}=Z_{\{0,a\}}=Z_{\{0,b\}}=Z_{\{a,b\}}=\left\{0\right\},$ as Figure 4.

Theorem 9.

If $\Gamma \left(A\right)$ is a tree, then $\mid D_s\left(A\right)\mid =1$.

Proof. 

By Proposition 5(iv), $Z_{\{1,x\}}=\left\{0\right\}$, for any $x\in A$. Then, $\Gamma \left(A\right)$ is connected. Since $\overline{1}=0$, $1\in D_s\left(A\right)\ne \varnothing$. Suppose $\mid D_s\left(A\right)\mid \ne 1$. Then, there exists $t\in D_s\left(A\right)$ such that $\overline{t}=0$. Then,

$$Z_{\{t,0\}}=\{y\mid y\odot t=0\}=\{y\mid y\le \overline{t}\}.$$

Since $\overline{t}=0$, $Z_{\{t,0\}}=\left\{0\right\}$. Then, the path $(0-t-1-0)$ is a circle, which is a contradiction. Because $\Gamma \left(A\right)$ is tree. Therefore, $\mid D_s\left(A\right)\mid =1$. □

The converse of the above theorem may not be true, in general.

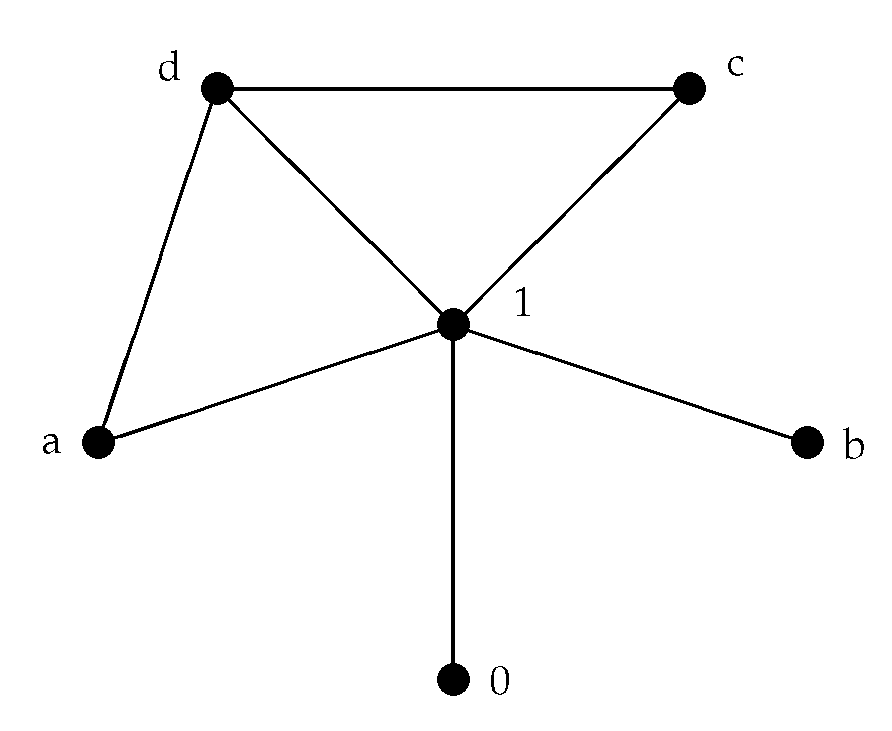
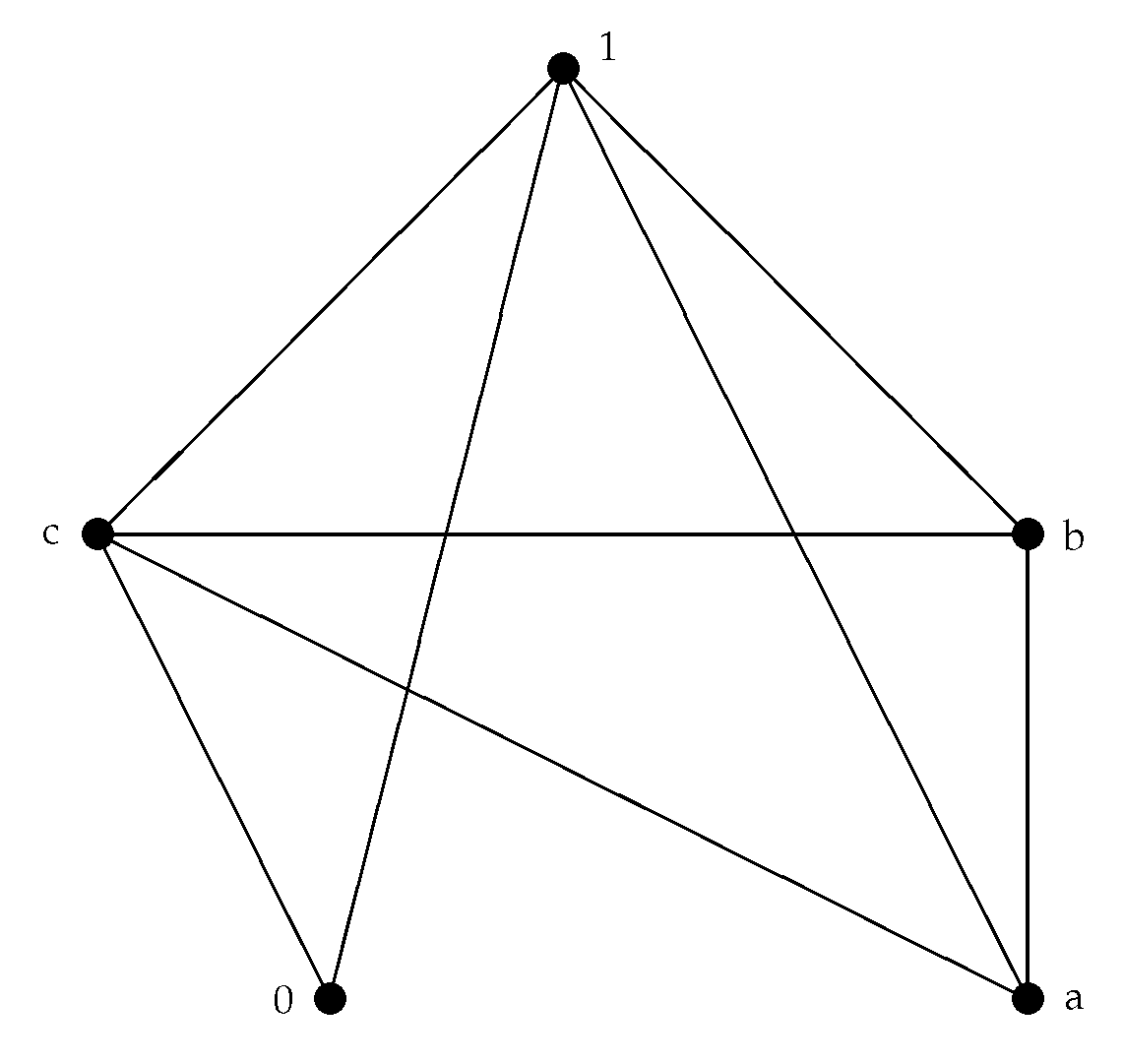
Example 8.

According to Example 1, $\mid D_s\left(A\right)\mid =1$ and by routine calculation (see Figure 5), we have:

$$Z_{\{x,1\}}=Z_{\{c,d\}}=Z_{\{a,d\}}=\left\{0\right\}{Z}_{\{0,c\}}=Z_{\{a,b\}}=Z_{\{a,c\}}=Z_{\{b,c\}}=\{0,b\},$$

$$Z_{\{b,d\}}=Z_{\{0,d\}}=\{0,a\},Z_{\{0,a\}}=\{0,b,d\},Z_{\{0,b\}}=\{0,a,b,c\}.$$

Theorem 10.

$\Gamma \left(A\right)$ is a star graph if it satisfies the following conditions:

(i)

$\mid D_s\left(A\right)\mid =1$.

(ii)

There is $a\in A-\left\{0\right\}$ such that $a\le x$, for any $x\in A-\left\{0\right\}$.

Proof. 

By Proposition 5(iv), $Z_{\{1,x\}}=\left\{0\right\}$, for any $x\in A$. Then, $\Gamma \left(A\right)$ is connected and by Theorem 7, diameter at most two. Let $x,y\in A-\left\{1\right\}$ such that $x\ne y$. If $\overline{x}\ne 0$ and $\overline{y}=0$ or vice versa, since $\overline{1}=0$, we have $\mid D_s\left(A\right)\mid >1$, which is a contradiction. In addition, if $\overline{x}=\overline{y}=0$, then $x,y\in D_s\left(A\right)$, and so $\mid D_s\left(A\right)\mid >1$, which is a contradiction. Thus, $\overline{x},\overline{y}\ne 0$. Thus, $\overline{x},\overline{y}\in A-\left\{0\right\}$. Then, by (ii), there is $a\in A-\left\{0\right\}$ such that $a\le \overline{x},\overline{y}$. Thus, $a\odot x=0$ and $a\odot y=0$. Hence, $a\in Z_{\{x,y\}}$, and so $Z_{\{x,y\}}\ne \left\{0\right\}$. Then, there is not the edge $x-y$. Therefore, $\Gamma \left(A\right)$ is a star graph. □

Corollary 3.

Under Conditions (i) and (ii) of Theorem 10, $\Gamma \left(A\right)$ is a tree.

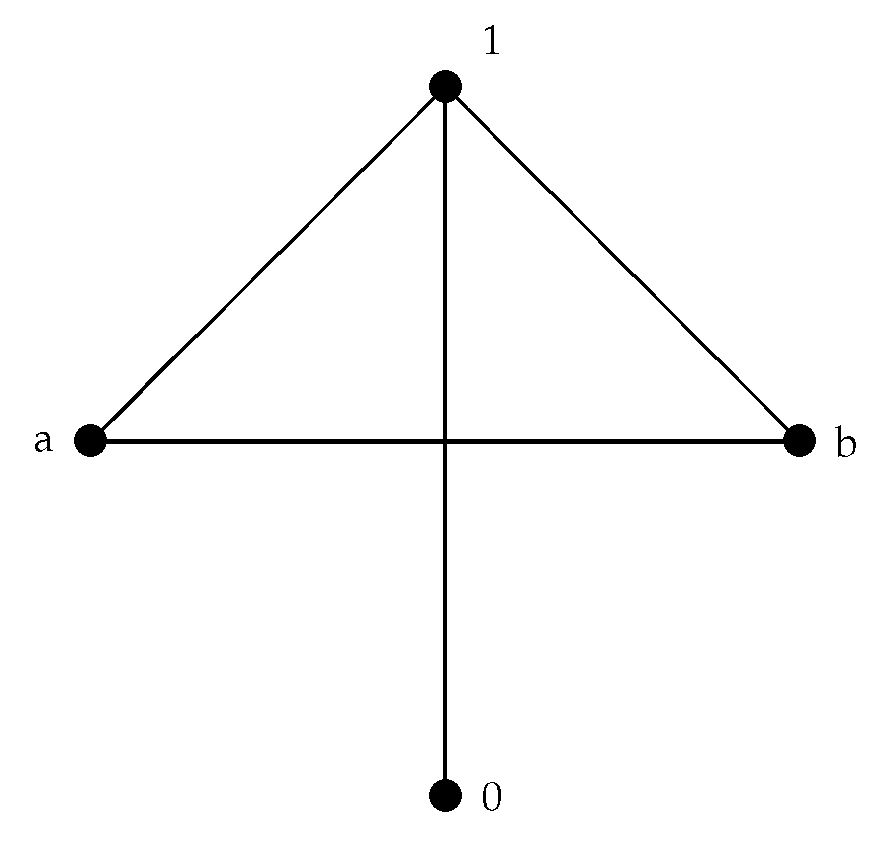
Example 9.

Let $A=\{0,a,b,1\}$. Define the operations ⊙ and → on A as follows

$$\begin{array}{cc}\begin{array}{ccccc}\hfill \to & 0& a& b& 1\\ 0\hfill & 1& 1& 1& 1\\ a\hfill & b& 1& 1& 1\\ b\hfill & a& b& 1& 1\\ 1\hfill & 0& a& b& 1\end{array}\hfill & \begin{array}{ccccc}\odot \hfill & 0& a& b& 1\\ 0\hfill & 0& 0& 0& 0\\ a\hfill & 0& 0& 0& a\\ b\hfill & 0& 0& a& b\\ 1\hfill & 0& a& b& 1\end{array}\hfill \end{array}$$

We can easily see that A with these operations is a bounded hoop. By routine calculation, we can see that two conditions of the above theorem hold because A is a chain and there is an element $a\in A-\left\{0\right\}$ such that $a\le x$, for any $x\in A-\left\{0\right\}$. In addition, it is clear that $\mid D_s\left(A\right)\mid =1$. Thus, the graph is a star. We have: $Z_{\{x,1\}}=\left\{0\right\},Z_{\{0,a\}}=\{0,a,b\},Z_{\{0,b\}}=Z_{\{a,b\}}=\{0,a\}$, as Figure 6.

By the following example, we show that both conditions listed in Theorem 10 are necessary.

Example 10.

$\left(i\right)$ Let $A=\{0,a,b,c,1\}$. Define the operations ⊙ and → on A as follows

$$\begin{array}{cc}\begin{array}{cccccc}\hfill \to & 0& a& b& c& 1\\ 0\hfill & 1& 1& 1& 1& 1\\ a\hfill & b& 1& b& 1& 1\\ b\hfill & a& a& 1& 1& 1\\ c\hfill & 0& a& b& 1& 1\\ 1\hfill & 0& a& b& c& 1\end{array}\hfill & \begin{array}{cccccc}\odot \hfill & 0& a& b& c& 1\\ 0\hfill & 0& 0& 0& 0& 0\\ a\hfill & 0& a& 0& a& a\\ b\hfill & 0& 0& b& b& b\\ c\hfill & 0& a& b& c& c\\ 1\hfill & 0& a& b& c& 1\end{array}\hfill \end{array}$$

It can easily be seen that A with these operations is a bounded hoop. In this hoop neither condition holds. Because A is not a chain, there is not an element $a\in A-\left\{0\right\}$ such that $a\le x$, for any $x\in A-\left\{0\right\}$. In addition, it is clear that $D_s\left(A\right)=\{c,1\}$, and so $\mid D_s\left(A\right)\mid =2\ne 1$. We can easily see that the graph is not a star. As Figure 7, we have:

$$Z_{\{x,1\}}=Z_{\{a,c\}}=Z_{\{a,b\}}=Z_{\{0,c\}}=Z_{\{b,c\}}=\left\{0\right\},$$

$$Z_{\{0,a\}}=\{0,b\},Z_{\{0,b\}}=\{0,a\}.$$

$\left(ii\right)$ Let $A=\{0,a,b,1\}$. Define the operations ⊙ and → on A as follows

$$\begin{array}{cc}\begin{array}{ccccc}\hfill \to & 0& a& b& 1\\ 0\hfill & 1& 1& 1& 1\\ a\hfill & b& 1& b& 1\\ b\hfill & a& a& 1& 1\\ 1\hfill & 0& a& b& 1\end{array}\hfill & \begin{array}{ccccc}\odot \hfill & 0& a& b& 1\\ 0\hfill & 0& 0& 0& 0\\ a\hfill & 0& a& 0& a\\ b\hfill & 0& 0& b& b\\ 1\hfill & 0& a& b& 1\end{array}\hfill \end{array}$$

By routine calculations, we can see that A with these operations is a bounded hoop. By routine calculation, we can see that $\mid D_s\left(A\right)\mid =1$ but the second condition does not hold because A is not a chain. Thus, the graph is not a star. We have:

$$Z_{\{x,1\}}=Z_{\{a,b\}}=\left\{0\right\},Z_{\{0,a\}}=\{0,b\},Z_{\{0,b\}}=\{0,a\}.$$

$\left(iii\right)$ According to Example 7, $\mid D_s\left(A\right)\mid =3\ne 1$ and we see that the graph is complete. Thus, as Figure 8, it is not a star.

5. Conclusions and Future Works

In this paper, graphs of hoop algebras are studied. For this, the notion of zero divisors of a non-empty subset of a hoop algebra is introduced by two methods and some related properties are investigated. Several examples of hoop graphs are proved. These graphs are connected, and also some necessary conditions for the hoop graph to be a star graph are found. Finally, hoop graphs that are provided by two methods together are compared. Then we conclude that these graphs are connected and also some necessary conditions for the hoop graphs to be star graphs. By comparing the graph of two methods, we conclude that both graphs are connected and one is connected to all points of bounded hoop A. Finally, $\Gamma \left(A\right)$ and $\mathsf{\Omega }\left(A\right)$ are graphs with diameter at most two. However, the graph of any hoop in both methods is not the same, in general.

In our future work, we will investigate the relation between graphs $\Gamma (A/F)$ and $\Gamma \left(A\right)/\Pi$, where Π is a partition of A. In addition, we will try to find some kinds of filters in a hoop by two graphs $\mathsf{\Omega }\left(A\right)$ and $\Gamma \left(A\right)$.