Goodness of Fit Tests for the Log-Logistic Distribution Based on Cumulative Entropy under Progressive Type II Censoring

Abstract

In this paper, we propose two new methods to perform goodness-of-fit tests on the log-logistic distribution under progressive Type II censoring based on the cumulative residual Kullback-Leibler information and cumulative Kullback-Leibler information. Maximum likelihood estimation and the EM algorithm are used for statistical inference of the unknown parameter. The Monte Carlo simulation is conducted to study the power analysis on the alternative distributions of the hazard function monotonically increasing and decreasing. Finally, we present illustrative examples to show the applicability of the proposed methods.

1. Introduction

The log-logistic distribution is a kind of classical life distribution in reliability. Scholars have extensively studied this distribution. In  [1,2], they mainly studied the nature of the distribution, and a method for obtaining the exact confidence interval of the shape parameter of the log-logistic distribution based on the maximum likelihood estimation was proposed. In  [3,4], scholars found that log-logistic distribution was often used for life analysis, especially the reliability characteristics of the research model; while [5,6,7] studied the applications of this distribution in the fields of the economy, networks, and the environment.

The log-logistic distribution has two main advantages. One is that the hazard function is not strictly monotonous and has some flexibility in representing product failure rate. Second, its cumulative distribution function has a closed form, which is more advantageous for life analysis of censored data.

A random variable X is said to have the log-logistic distribution if its cumulative distribution function (cdf) is expressed as:

$$\begin{array}{cc}\hfill F_X(x)=1-{(1+x^{\beta })}^{-1}& x\ge 0,\beta >0.\end{array}$$

(1)

The probability density function (pdf) is as follows:

$$\begin{array}{cc}\hfill f_X(x)=\frac{\beta x^{\beta -1}}{{(1+x^{\beta })}^2}& x\ge 0,\beta >0.\end{array}$$

(2)

In many life analyses, sometimes, in order to save money and resources, the data will be truncated, and the data obtained are not complete. Such data are classified as censored data. Type I censoring, Type II censoring, and progressive censoring are the most common censoring methods.

Progressive Type I censoring is a time-fixed censorship in which individuals are deleted at a predetermined ratio at the same time interval at a fixed observation time. Progressive Type II censoring is a fixed amount of censorship, that is censoring at a certain percentage each time a failed individual occurs. Progressive censoring refers to the method of continually censoring in observation, which is different from only censoring at the end of the experiment. This article mainly discusses the progressive Type II censorship.

The steps to perform progressive Type II censoring are as follows: n individuals are tested, and after the first individual fails, randomly take $R_1$ individuals from the surviving $n-1$ individuals. Continue to observe until the next failed individual appears, then randomly select $R_2$ individuals from the surviving $n-2-R_1$ individuals to no longer observe, and repeat the process until the $m\mathrm{th}$ individual failure is observed, and all last $R_m$ remaining individuals are withdrawn from the observation, which results in a $(R_1,R_2,\cdots ,R_m)$ censoring scheme.

There are many studies on the statistical inference problem of censored data: In [8], different progressive censoring methods for samples in life testing were systematically studied. The confidence interval of the unknown parameter under Type II censoring was provided by [9]. They derived precise confidence intervals for different vital features, such as quantile, position, reliability, and scale. The method was also applied to the single-parameter and two-parameter exponential models to verify the feasibility and practicability. An algorithm was proposed in [10] for simulating the data generation of progressive Type II censoring, which will be used in the Monte Carlo simulations later.

In this article, we will present the log-logistic distribution fitting experiment based on cumulative entropy under progressive Type II censoring. The other parts of the article are arranged as follows: In Section 2, we will introduce Kullback-Leibler (KL) information and its related properties. In Section 3, maximum likelihood estimation and the EM algorithm are used for statistical inference of the unknown parameter. We construct two test statistics due to CRKL and CKL in Section 4. The Monte Carlo simulation is presented to study power on the alternative distributions in Section 5. Finally, we will provide an illustrative example in Section 6 and prove the applicability of the statistics.

2. Entropy and Kullback-Leibler Information

As the quantification of information, the average amount of information after redundancy is excluded is called information entropy. In 1948, Shannon proposed the concept of information entropy for the first time in order to clarify the relationship between probability and information redundancy. The Shannon entropy is for the discrete random variable X. Now that we want to extend this concept to the case of continuous random variables, we will get a very important concept, namely differential entropy. The definition is as follows:

$$\begin{array}{c}\hfill H(X)={\int }_0^{\infty }f(x)[-lnf(x)]dx,\end{array}$$

(3)

where $ln(·)$ represents the natural logarithm, $f(x)$ represents the probability density function of the random variable X.

In the last few years, information theory measures have been used in many fields to verify the consistency of the distribution in statistical inference. For example, Vasicek [11] first proposed a distribution fitting test for a normal distribution using maximum entropy. Vasicek’s contribution has greatly contributed to the development of entropy-based distribution fitting test topics. Afterwards, many scholars have studied this topic; refer to [12,13,14].

A distribution fitting test using Kullback-Leibler (KL) divergence was proposed in [15,16] , and its definition is as follows:

$$\begin{array}{c}\hfill \mathrm{KL}(F:G)={\int }_0^{\infty }f(x)ln\frac{f(x)}{g(x)}dx,\end{array}$$

(4)

where $f(x)$ and $g(x)$ represent the density functions related to $F(x)$ and $G(x)$ distributions.

Lemma 1.

It is known from the inequality $lnx\le x-1$ that $KL(F:G)$ is non-negative.

Lemma 2.

$F(x)$ and $G(x)$ are equally distributed if and only if $KL(F:G)=0$.

Proof. 

Under the premise that KL information is non-negative, Formula (4) shows that the smaller the distance between the two distributions, the smaller the corresponding KL divergence. When $\mathrm{KL}(F:G)=0$,

$$\begin{array}{cc}\hfill \mathrm{KL}(F:G)& ={\int }_0^{\infty }f(x)ln\frac{f(x)}{g(x)}dx\hfill \\ & ={\int }_0^{\infty }-f(x)ln\frac{g(x)}{f(x)}dx\hfill \\ & \ge {\int }_0^{\infty }f(x)(1-\frac{g(x)}{f(x)})dx=0,\hfill \end{array}$$

the equal sign holds, i.e., $ln\frac{g(x)}{f(x)}=\frac{g(x)}{f(x)}-1$. Referring to the inequality $lnx\le x-1$, we get $f(x)=g(x)$. Because $f(x)$ and $g(x)$ represent the density functions related to $F(x)$ and $G(x)$ distributions, $F(x)$ and $G(x)$ are equally distributed. □

According to Lemmas 1 and 2, when $G(x)$ is known as the log-logistic distribution, the empirical distribution function $F_n(x)$ can be obtained from the collected data. Then, the value of $\mathrm{KL}(F_n:G)$ can be calculated for the distribution fitting test. If the value of KL information is approximately zero to a certain extent, we can think that $F(x)$ and $G(x)$ are equally distributed.

The limitation of differential entropy is that it only applies to random variables that have continuous density functions. Authors of [17] presented the concept of cumulative residual entropy (CRE), in order to extend the scope of application to random variables without specific density functions. The scheme performs a distribution fitting test according to the survival function $\overline{F}(x)=1-F(x)$ in the reliability analysis. The cumulative residual entropy is applied to random variables that are non-negative, and the definition is:

$$\begin{array}{c}\hfill \mathrm{CRE}(X)={\int }_0^{\infty }\overline{F}(x)[-ln\overline{F}(x)]dx.\end{array}$$

(5)

Baratpour [14] proposed a new CRE-based method for comparing the distance between two distributions, named cumulative residual Kullback-Leibler (CRKL) divergence. They also constructed fitting tests under exponential distribution. It is also possible to verify that CRKL is non-negative with a method similar to that of KL information.

$$\begin{array}{c}\hfill \mathrm{CRKL}(F:G)={\int }_0^{\infty }\overline{F}(x)[-ln\frac{\overline{F}(x)}{\overline{G}(x)}]dx-[E(X)-E(Y)],\end{array}$$

(6)

where $\overline{F}(x)$ and $\overline{G}(x)$ are the survival functions of the random variables X and Y. $E(X)$ and $E(Y)$ are the expectations of X and Y.

Authors of [18] proposed cumulative entropy (CE), which is a new method based on classical differential information entropy. This cumulative entropy is the expected average of the inactivity time of the random lifetime X. This metric is particularly well-suited to address issues related to aging characteristics based on past and inactive time in reliability analysis. They defined CE as:

$$\begin{array}{c}\hfill \mathrm{CE}(X)={\int }_0^{\infty }F(x)[-lnF(x)]dx.\end{array}$$

(7)

Another cumulative KL information (CKL) related to the cumulative distribution function was proposed in [19] and was expressed as follows:

$$\begin{array}{c}\hfill \mathrm{CKL}(F:G)={\int }_0^{\infty }F(x)[-ln\frac{F(x)}{G(x)}]dx-[E(Y)-E(X)].\end{array}$$

(8)

According to $lnx\le x-1,x>0$, we can prove that $\mathrm{CKL}(F:G)\ge 0$. Only when the equation holds, $F(x)$=$G(x)$.

3. Parameter Estimations

3.1. Maximum Likelihood Estimation

We are going to discuss the maximum likelihood estimation of the log-logistic distribution under the progressive Type II censored data in this section. Suppose $X_{(1)},X_{(2)},\cdots ,X_{(m)}$ are the fail times obtained by m observations for a given censoring scheme $R_1,R_2,\cdots ,R_m$. In the following derivation, $X_{(i)}$ will be recorded as $x_i$. Then, we have:

$$\begin{array}{cc}\hfill L(\beta )& =c\prod _{i=1}^m{[1-F(x_i)]}^{R_i}f(x_i)\hfill \\ & =c\prod _{i=1}^m\beta \frac{x_i^{\beta -1}}{{(1+x_i^{\beta })}^{2+R_i}},\hfill \\ \hfill c& =n·(n-R_1-1)·(n-R_1-R_2-2)\cdots (n-R_1\cdots -R_{m-1}-m+1),\hfill \end{array}$$

(9)

where $\beta$ is the shape parameter, c is a fixed coefficient, and the corresponding log-likelihood function is as follows:

$$\begin{array}{c}\hfill {\displaystyle lnL(\beta )=lnc+ln{\beta }^m+\sum _{i=1}^m[(\beta -1)ln{x}_i-(2+R_i)ln(1+x_i^{\beta })].}\end{array}$$

(10)

The likelihood equation for the parameter $\beta$ is:

$$\begin{array}{c}\hfill {\displaystyle \frac{d}{d\beta }lnL(\beta )=\frac{m}{\beta }+\sum _{i=1}^{m}ln\frac{x_i[1-(1+R_i)x_i^{\beta }]}{1+x_i^{\beta }}=0.}\end{array}$$

(11)

From the above Formula (11), theoretically, we can get the maximum likelihood form $\widehat{\beta }$ of the parameter $\beta$, but the likelihood equation is complicated and nonlinear, so the explicit solution of $\beta$ cannot be calculated. The approximate solution obtained by the simulation method cannot prove the uniqueness of the solution.

Based on the deficiencies of the maximum likelihood in solving traditional problems, in the actual problem processing, the EM algorithm, dichotomy, or the Newton-Raphson method can be selected according to the convenience level to solve the estimated value. Considering that the existing research of the dichotomy and Newton-Raphson method has been perfected, this paper only elaborates on the EM algorithm to further complete the maximum likelihood estimation.

3.2. Expectation Maximization Algorithm

Dempster [20] first proposed an expected maximization algorithm named the EM algorithm. Originally derived from [21], it was gradually matured and modified, such as the GEM algorithm [22] and the Monte Carlo EM algorithm.

The EM algorithm is an iterative algorithm for solving the maximum likelihood estimations in incomplete data problems. It transforms the optimization problem of a complex likelihood function into a simple function optimization problem.

In general, the order statistic of the observed data is represented by $X=(x_1,x_2,\cdots ,x_m)$. $Z_i=(z_{i1},z_{i2},\cdots ,z_{i{R}_i})$ indicates missing data, that is when $x_i$ is observed, $R_i$ variables are randomly deleted from the remaining $n-i-{\sum }_{j=1}^{i-1}{R}_j$ individuals. The individual component lifetimes of $Z_i$ are greater than $x_i$ and are out of order.

X and Z are combined to form complete data $W=(X,Z)=(w_1,w_2,\cdots ,w_n)$. The key to the EM algorithm is that it is easy to obtain the combined density function of the data after completion. When the effective datum X is known, the conditional density of the missing variable Z can be quickly obtained. $\beta$ is the unknown parameter to be estimated. $p(x,z|\beta )$ is the distribution density of the complete data, and $p(z|\beta ,x)$ indicates the conditional distribution of the missing variable Z after given observation data.

The EM algorithm divides the problem into the following steps:

Step 1

Add the missing variable Z. Combined with the distribution function (1), it is easy to obtain:

$$\begin{array}{cc}\hfill p(z|\beta ,x)& =\prod _{j=1}^m\prod _{k=1}^{R_j}\frac{f(z_{jk}|\beta )}{1-F(x_j,\beta )}=\prod _{j=1}^m\prod _{k=1}^{R_j}\frac{\beta z_{jk}^{\beta -1}(1+x_j^{\beta })}{{(1+z_{jk}^{\beta })}^2}.\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill p(x,z|\beta )& =p(z|\beta ,x)p(x|\beta )=c\prod _{j=1}^m[f(x_j|\beta )\prod _{k=1}^{R_j}f(z_{jk}|\beta )]\hfill \\ & =c\prod _{j=1}^m[\frac{\beta x_j^{\beta -1}}{{(1+x_j^{\beta })}^2}\prod _{k=1}^{R_j}\frac{\beta z_{jk}^{\beta -1}}{{(1+z_{jk}^{\beta })}^2}].\hfill \\ \hfill c& =n·(n-R_1-1)·(n-R_1-R_2-2)\cdots (n-R_1\cdots -R_{m-1}-m+1).\hfill \end{array}$$

(13)

The log-likelihood function of full data $l(\beta |w)=l(\beta |x,z)$ is as follows:

$$\begin{array}{cc}\hfill l(\beta |x,z)& {\displaystyle =\sum _{j=1}^m[lnf(x_j|\beta )+\sum _{k=1}^{R_j}lnf(z_{jk}|\beta )]=\sum _{j=1}^m[ln\frac{\beta x_j^{\beta -1}}{{(1+x_j^{\beta })}^2}+\sum _{k=1}^{R_j}ln\frac{\beta z_{jk}^{\beta -1}}{{(1+z_{jk}^{\beta })}^2}].}\hfill \end{array}$$

(14)

Step 2

E step (expectation step): Derive the maximum likelihood function of the complete data. Find their conditional expectations $Q(\beta |{\beta }^{(i)},w)$.

$$\begin{array}{cc}\hfill Q(\beta |{\beta }^{(i)},w)& \stackrel{△}{=}E[l(\beta |w)|X=x,\beta ={\beta }^{(i)}]\hfill \\ & =\sum _{z}l(\beta |x,z)p(z|{\beta }^{(i)},x)\hfill \\ & {\displaystyle =\sum _{j=1}^m[(\beta -1)ln{x}_j+ln\beta -2ln(1+x_j^{\beta })}\hfill \\ & {\displaystyle +\sum _{k=1}^{R_j}((\beta -1)E(ln{z}_{jk})+ln\beta -2E(ln(1+z_{jk}^{\beta })))].}\hfill \end{array}$$

(15)

Step 3

M step (maximization step): Maximize the expected value and get the next iteration value ${\beta }^{(i+1)}$.

$$\begin{array}{cc}\hfill \frac{\partial Q}{\partial \beta }& {\displaystyle =\sum _{j=1}^m[\frac{1}{\beta }+ln{x}_j-2\frac{x_j^{\beta }ln{x}_j}{1+x_j^{\beta }}+\sum _{k=1}^{R_j}(\frac{1}{\beta }+E(ln{z}_{jk}))]=0,}\hfill \\ \hfill \beta & =\frac{{\displaystyle \sum _{j=1}^m(1+R_j)}}{{\displaystyle \sum _{j=1}^m[2\frac{x_j^{\beta }ln{x}_j}{1+x_j^{\beta }}-ln{x}_j-\sum _{k=1}^{R_j}E(ln{z}_{jk})]}}.\hfill \end{array}$$

(16)

Let:

$$A_j=\frac{x_j^{\beta }ln{x}_j}{1+x_j^{\beta }},E(ln{z}_{jk})=\beta ln(1+x_j^{\beta }){\int }_{x_j}^{\infty }\frac{z_{jk}^{\beta -1}ln{z}_{jk}}{{(1+z_{jk}^{\beta })}^2}d{z}_{jk}\stackrel{△}{=}B,$$

$$\begin{array}{c}\hfill {\beta }^{(i+1)}=\frac{{\displaystyle \sum _{j=1}^m(R_j+1)}}{{\displaystyle \sum _{j=1}^m[2A_j-ln{x}_j-\sum _{k=1}^{R_j}B]}}.\end{array}$$

(17)

Step 4

Use ${\beta }^{(i+1)}$ instead of ${\beta }^{(i)}$ in step E, repeating the E and M steps. When $|{\beta }^{(i+1)}-{\beta }^{(i)}|$ or $|Q({\beta }^{(i+1)}|{\beta }^{(i)},w)-Q({\beta }^{(i)}|{\beta }^{(i)},w)|$ is sufficiently small, stop the iteration.

4. Distribution Fitting Test Statistics

EDF test statistics are usually used to measure the distance between two empirical distribution functions $F_n(x)$ and $F_{\widehat{\beta }}(x)$. If the original hypothesis $H_0$ is established, the estimated value $\widehat{\beta }$ of $\beta$ can be obtained. In this paper, we will propose two EDF test statistics related to CRKL and CKL. We will use these two statistics to test whether the unknown distribution satisfies the log-logistic distribution of the null hypothesis and propose multiple alternative distributions at the same time.

Given a set of censored schemes $R=(R_1,R_2,...,R_m)$, let $x_{1:m:n}<x_{2:m:n}<\cdots <x_{m:m:n}$ be a sample of the distribution $F_{\beta }(x)$ under progressive Type II censoring. The distribution function of the log-logistic is $F_{\beta }(x)=1-{(1+x^{\beta })}^{-1}$, where $\beta$ is an unknown shape parameter.

Based on CRKL, CKL, and the obtained censored sample, we consider the following hypothesis.

$$H_0:F(x)=F_{\beta }(x)v.s.H_1:F(x)\ne F_{\beta }(x).$$

When the statistic is found to be large enough, we reject the null hypothesis.

The empirical distribution function of the complete data can be derived using order statistics. In the same way, we can estimate the empirical distribution function $F_{m:n}(x)$ of the censored data, which is presented as:

$$F_{m:n}(x)=\left\{\begin{array}{c}0x<x_{1:m:n}\hfill \\ {\alpha }_{i:m:n}{x}_{i:m:n}\le x<x_{i+1:m:n},i=1,\cdots ,m-1\hfill \\ {\alpha }_{m:m:n}x\ge x_{m:m:n}.\hfill \end{array}\right.$$

(18)

Balakrishnan [10] found that ${\alpha }_{i:m:n}$ was the $i\mathrm{th}$ expected value of statistical data obeying uniformly-distributed data under progressive Type II censoring, i.e., ${\alpha }_{i:m:n}=E(U_{i:m:n})$.

Since $U_i$ are not independent of each other, we let $0<V_1,V_2,\cdots ,V_m<1$ and:

$$\left\{\begin{array}{c}{\displaystyle V_1=\frac{1-U_m}{1-U_{m-1}}}\\ {\displaystyle V_2=\frac{1-U_{m-1}}{1-U_{m-2}}}\\ \cdots \\ {\displaystyle V_{m-1}=\frac{1-U_2}{1-U_1}}\\ V_m=1-U_1.\end{array}\right.$$

(19)

The joint density function of $V_1,V_2,\cdots ,V_m$ is obtained by the Jacobian transform method.

$$\begin{array}{c}\hfill f(V_1,V_2,\cdots ,V_m)=c\prod _{i=1}^m{V}_i^{i-1+{\sum }_{j=m-i+1}^m{R}_j}.\end{array}$$

(20)

According to the factorization theorem, $V_i$ are independent of each other and obey $Beta(i+{\sum }_{j=m-i+1}^m{R}_j,1)$$(i=1,\cdots ,m)$, respectively. Then, we have:

$$\begin{array}{c}\hfill {\alpha }_{i:m:n}=1-\prod _{j=m-i+1}^m\frac{j+R_{m-j+1}+\cdots +R_m}{j+1+R_{m-j+1}+\cdots +R_m}.\end{array}$$

(21)

When the sample obeys the log-logistic distribution function (1), the censored CRKL is able to be reduced as:

$$\begin{array}{cc}\hfill \mathrm{CRKL}(F_{m:n}:F_{\beta })=& {\int }_0^{x_{m:m:n}}(1-F_{m:n}(x))ln\frac{1-F_{m:n}(x)}{{(x^{\beta }+1)}^{-1}}dx\hfill \\ & -{\int }_0^{x_{m:m:n}}(1-F_{m:n}(x))dx+{\int }_0^{x_{m:m:n}}{(1+x^{\beta })}^{-1}dx\hfill \\ \hfill =& {\displaystyle \sum _{i=1}^{m-1}(1-{\alpha }_{i:m:n})ln(1-{\alpha }_{i:m:n})(x_{i+1:m:n}-x_{i:m:n})}\hfill \\ & {\displaystyle +\sum _{i=1}^{m-1}(1-{\alpha }_{i:m:n}){\int }_{x_{i:m:n}}^{x_{i+1:m:n}}ln(1+x^{\beta })dx}\hfill \\ & {\displaystyle -\sum _{i=1}^{m-1}(1-{\alpha }_{i:m:n})(x_{i+1:m:n}-x_{i:m:n})}\hfill \\ & +[x_{m:m:n}-\frac{1}{\beta }{x}_{m:m:n}ln(1+x_{m:m:n}^{\beta })+\frac{1}{\beta }{\int }_0^{x_{m:m:n}}ln(1+x^{\beta })dx].\hfill \end{array}$$

(22)

The unknown parameter $\beta$ should be replaced by its expectation maximization estimate ${\widehat{\beta }}_{\mathrm{EM}}$. In order to make the statistics free of units, divide (23) by ${\sum }_{i=0}^{m-1}(1-{\alpha }_{i:m:n})(x_{i+1:m:n}-x_{i:m:n})$. Get the following statistic $\widehat{\mathrm{CRKL}}$.

$$\begin{array}{c}\hfill \widehat{\mathrm{CRKL}}=A+B+C-1,\end{array}$$

(23)

where:

$$\begin{array}{cc}\hfill A& =\frac{{\displaystyle \sum _{i=1}^{m-1}(1-{\alpha }_{i:m:n})(x_{i+1:m:n}-x_{i:m:n})ln(1-{\alpha }_{i:m:n})}}{{\displaystyle \sum _{i=1}^{m-1}(1-{\alpha }_{i:m:n})(x_{i+1:m:n}-x_{i:m:n})}},\hfill \\ \hfill B& =\frac{{\displaystyle \sum _{i=1}^{m-1}(1-{\alpha }_{i:m:n}){\int }_{x_{i:m:n}}^{x_{i+1:m:n}}ln(1+x^{\beta })dx}}{{\displaystyle \sum _{i=1}^{m-1}(1-{\alpha }_{i:m:n})(x_{i+1:m:n}-x_{i:m:n})}},\hfill \\ \hfill C& =\frac{x_{m:m:n}-\frac{1}{\beta }{x}_{m:m:n}ln(1+x_{m:m:n}^{\beta })+\frac{1}{\beta }{\int }_0^{x_{m:m:n}}ln(1+x^{\beta })dx}{{\displaystyle \sum _{i=1}^{m-1}(1-{\alpha }_{i:m:n})(x_{i+1:m:n}-x_{i:m:n})}}.\hfill \end{array}$$

Similarly, the statistic based on CKL is as follows:

$$\begin{array}{c}\hfill \widehat{\mathrm{CKL}}=D-E-F+1,\end{array}$$

(24)

where:

$$\begin{array}{cc}\hfill D& =\frac{{\displaystyle \sum _{i=1}^{m-1}{\alpha }_{i:m:n}(x_{i+1:m:n}-x_{i:m:n})ln{\alpha }_{i:m:n}}}{{\displaystyle \sum _{i=1}^{m-1}(1-{\alpha }_{i:m:n})(x_{i+1:m:n}-x_{i:m:n})}},\hfill \\ \hfill E& =\frac{{\displaystyle \sum _{i=1}^{m-1}{\alpha }_{i:m:n}{\int }_{x_{i:m:n}}^{x_{i+1:m:n}}ln[1-{(1+x^{\beta })}^{-1}]dx}}{{\displaystyle \sum _{i=1}^{m-1}(1-{\alpha }_{i:m:n})(x_{i+1:m:n}-x_{i:m:n})}},\hfill \\ \hfill F& =\frac{x_{m:m:n}-\frac{1}{\beta }{x}_{m:m:n}ln(1+x_{m:m:n}^{\beta })+\frac{1}{\beta }{\int }_0^{x_{m:m:n}}ln(1+x^{\beta })dx}{{\displaystyle \sum _{i=1}^{m-1}(1-{\alpha }_{i:m:n})(x_{i+1:m:n}-x_{i:m:n})}}.\hfill \end{array}$$

Obviously, neither $\widehat{\mathrm{CRKL}}$ nor $\widehat{\mathrm{CKL}}$ depend on the scale; therefore, they are suitable for goodness-of-fit tests.

5. Monte Carlo Simulations

Monte Carlo simulation is a method of solving many computational problems using random numbers. Based on a probabilistic model, statistical simulations or samplings are performed using an electronic computer to obtain an approximate solution to the problem, according to the process depicted by the model. Currently, there is related research in many fields, such as: the environment [23], computer science and technology [24], physics [25], finance [26], etc.

For the $\widehat{\mathrm{CRKL}}$ and $\widehat{\mathrm{CKL}}$ tests, when the significance level $\alpha$ is determined and the statistic is larger than the critical value, we reject the null hypothesis. Since the quantile cannot be determined from the distribution of $\widehat{\mathrm{CRKL}}$ (23) and $\widehat{\mathrm{CKL}}$ (24), we use the Monte Carlo simulation method to obtain the critical values ${\widehat{\mathrm{CRKL}}}_{0.95}$, ${\widehat{\mathrm{CRKL}}}_{0.90}$, ${\widehat{\mathrm{CKL}}}_{0.95}$, and ${\widehat{\mathrm{CKL}}}_{0.90}$.

Lemma 3.

Suppose X obeys the log-logistic distribution, and let $Y=ln(1+x^{\beta })$, then Y obeys the standard exponential distribution.

Proof. 

Suppose the distribution functions of the random variables X and Y are $F_X(x)$ and $F_Y(y)$, respectively.

$$F_X(x)=1-{(1+x^{\beta })}^{-1}x\ge 0,\beta >0.$$

When $y>0$:

$$F_Y(y)=P(Y\le y)=P(ln(1+x^{\beta })\le y)=P(X\le {(e^y-1)}^{\frac{1}{\beta }})=F_X({(e^y-1)}^{\frac{1}{\beta }})=1-e^{-y}.$$

□

Let $X_1<X_2<\cdots <X_m$ be a sample for a given progressive Type II censored scheme from the log-logistic distribution of which the unknown parameter is $\beta$. Let $Y_i=ln(1+x_i^{\beta })$. From Lemma 3, we can see that $Y_1<Y_2<\cdots <Y_m$ is the order statistic of the data from the standard exponential distribution under progressive Type II censoring. Refer to [10] for the following transformation:

$$\left\{\begin{array}{c}{S}_1=n{Y}_1\hfill \\ S_2=(n-R_1-1)·(Y_2-Y_1)\hfill \\ \cdots \hfill \\ S_m=(n-R_1-\cdots -R_m-m+1)·(Y_m-Y_{m-1}).\hfill \end{array}\right.$$

According to the above transformation, Thomas [27] proved that $S_1,S_2,\cdots ,S_m$ were independent of each other and conformed to the standard exponential distribution. Ten thousand random samples $(S_1,S_2,\cdots ,S_m)$ can be generated by R software and part of the code is shown in the Appendix A. The samples under progressive Type II censoring were obtained by corresponding transformation.

Under the experimental assumption of size n, censored number m, significance level $\alpha$, censored scheme $(R_1,\cdots ,R_m)$, and distribution (1) with $\beta =2$, we randomly generated 10,000 sets of progressive Type II censoring samples. From the law of large numbers, we know that if a test is repeated multiple times under a constant condition, the probability can be replaced by the frequency of the random event.

Because the study of the exponential distribution [14] indicated that the hazard function had a great influence on the study of the power of statistics, we present alternatives in

Table 1. Alternative hypotheses for power study.

	Statistics	Hazard Function	Distributions
1	$\widehat{\mathrm{CRKL}}$	monotone decreasing	Pareto(5); Weibull: W(0.2,1); Generalized exponential distribution: Gexp(0.5,1)
2	$\widehat{\mathrm{CRKL}}$	monotone increasing	Bathtub-shaped: B(2,15)
3	$\widehat{\mathrm{CKL}}$	monotone decreasing	Pareto(12); Weibull: W(0.2,1); Generalized exponential distribution: Gexp(0.5,1)
4	$\widehat{\mathrm{CKL}}$	monotone increasing	Rayleigh: R(0.2); Bathtub-shaped: B(2,200)

classified by the type of hazard function:

The power study indicates the probability of rejecting the null hypothesis under the condition that the alternative hypothesis is established. It is a test of whether or not the test statistics we have proposed are feasible.

According to the classification method of the hazard function, the power study of this paper involved seven alternative hypotheses. To calculate the value of the test statistics, the parameters of the alternative distributions were estimated using the EM algorithm.

(a)

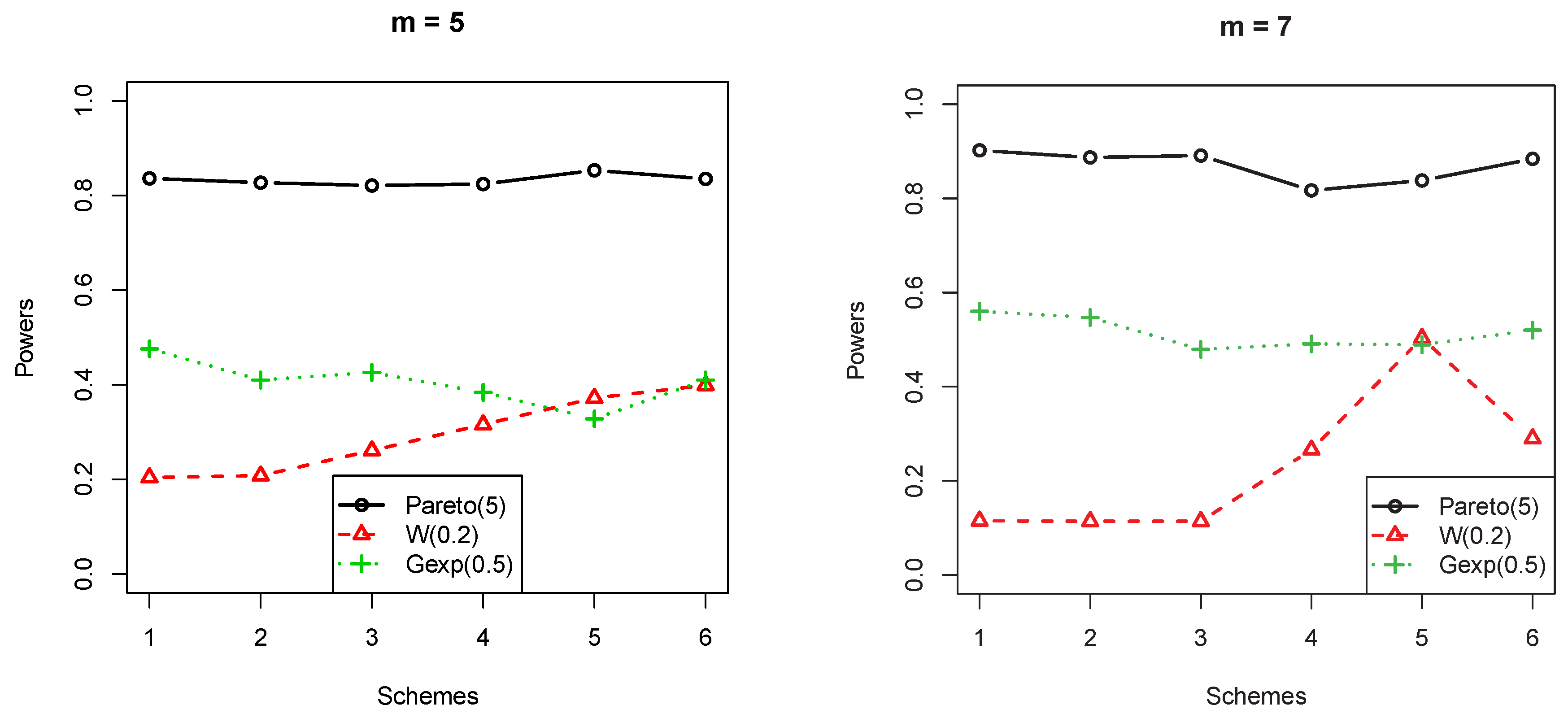
$H_0:X\sim$ log-logistic(2)    vs.    $H_1:X\sim$ Pareto(5):

$$\begin{array}{cc}\hfill f(x;\beta )& =\beta {(1+x)}^{-(\beta +1)},x\ge 0,\beta >0,\hfill \\ \hfill F(x;\beta )& =1-{(1+x)}^{-\beta },\hfill \\ \hfill h(x;\beta )& =\frac{\beta }{1+x},\hfill \\ \hfill L(\beta )& =c{\beta }^m\prod _{i=1}^m{(1+x_i)}^{-(\beta +1+\beta R_i)},\hfill \\ \hfill c& =n·(n-R_1-1)·(n-R_1-R_2-2)\cdots (n-R_1\cdots -R_{m-1}-m+1).\hfill \end{array}$$

The shape parameter is $\beta$, and the failure rate had a downward trend as x increased.

(b)

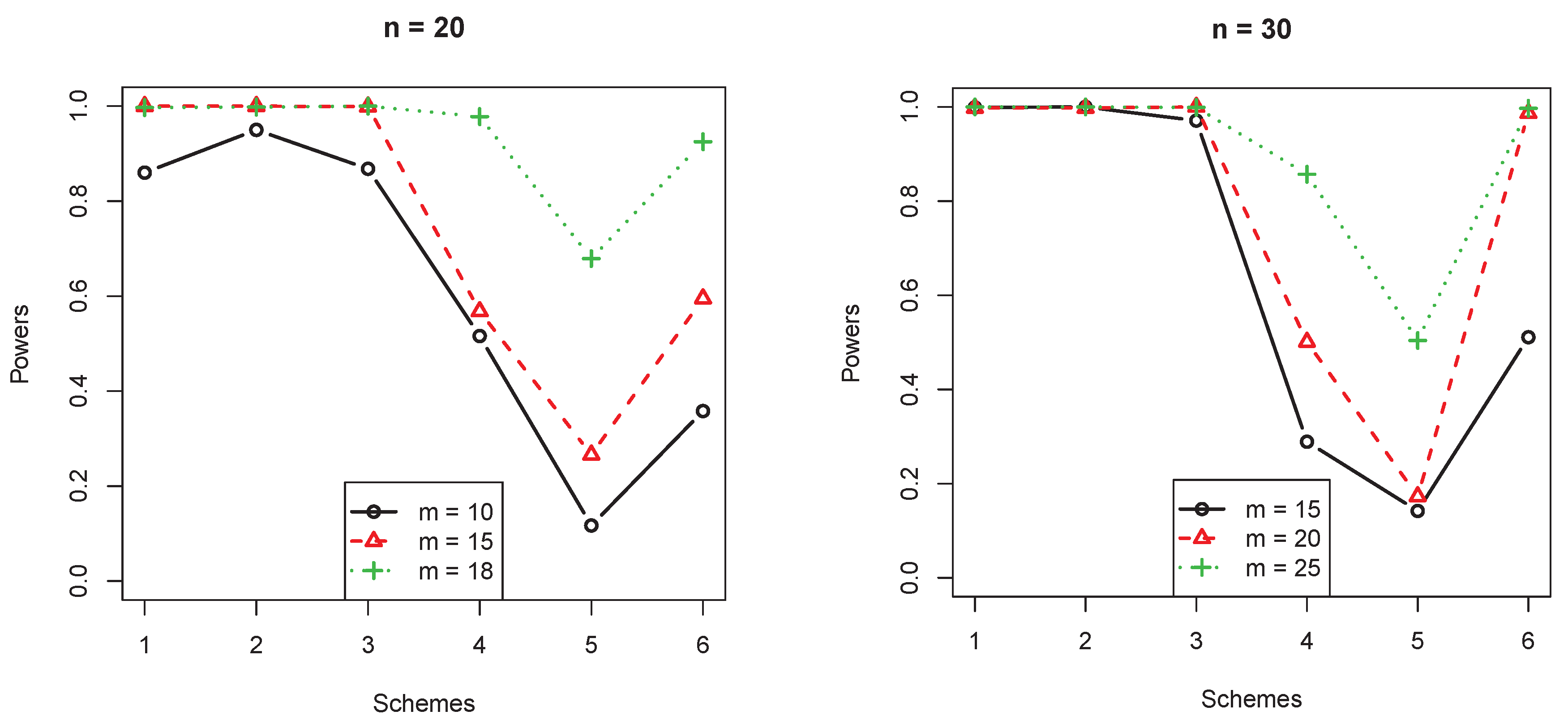
$H_0:X\sim$ log-logistic(2)    vs.    $H_1:X\sim$ Rayleigh(0.2):

$$\begin{array}{cc}\hfill f(x;\beta )& =\frac{x{e}^{-x^2/2{\beta }^2}}{{\beta }^2},x\ge 0,\beta >0,\hfill \\ \hfill F(x;\beta )& =1-e^{-x^2/2{\beta }^2},\hfill \\ \hfill h(x;\beta )& =\frac{x}{{\beta }^2},\hfill \\ \hfill L(\beta )& =c{\beta }^{-2m}\prod _{i=1}^m{x}_i{e}^{-x_i^2(R_i+1)/2{\beta }^2}.\hfill \end{array}$$

The shape parameter is $\beta$, and the failure rate was on the rise as x increased.

(c)

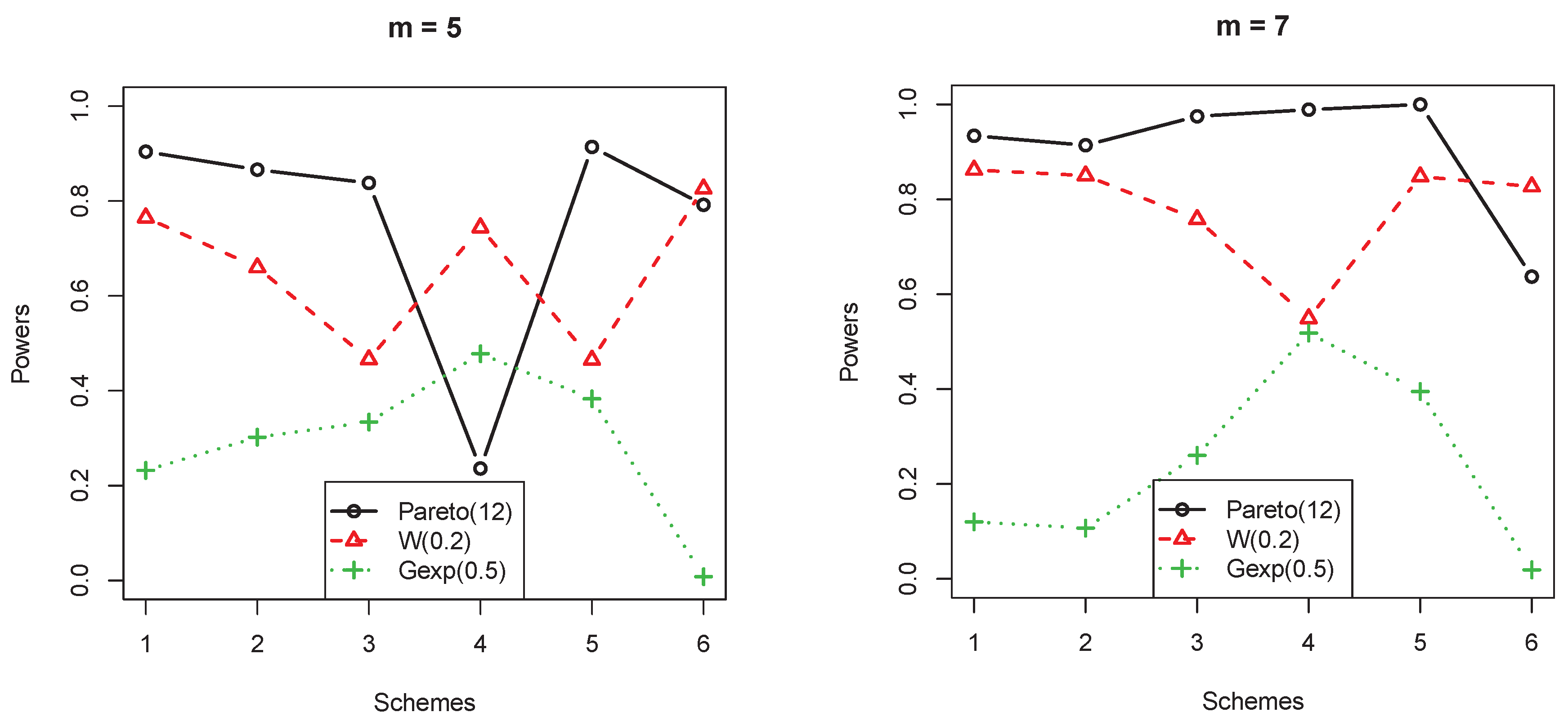
$H_0:X\sim$ log-logistic(2)    vs.    $H_1:X\sim$ Weibull(0.2,1):

$$\begin{array}{cc}\hfill f(x;k,\lambda )& =\frac{k}{\lambda }{(\frac{x}{\lambda })}^{k-1}{e}^{-{(x/\lambda )}^k},x\ge 0,k>0,\lambda >0,\hfill \\ \hfill F(x;k,\lambda )& =1-e^{-{(x/\lambda )}^k},\hfill \\ \hfill h(x;k,\lambda )& =\frac{k}{\lambda }{(\frac{x}{\lambda })}^{k-1},\hfill \\ \hfill L(k,\lambda )& =c{(\frac{k}{\lambda })}^m\prod _{i=1}^m{(\frac{x_i}{\lambda })}^{k-1}{e}^{-{(x_i/\lambda )}^k(R_i+1)},\hfill \end{array}$$

where $k>0$ and $\lambda >0$ are the shape parameter and scale parameter corresponding to the distribution, respectively. $k<1$ indicates that the failure rate tended to decrease as the experiment time elapsed. $k=1$ means that the change in failure rate was independent of time. $k>1$ indicates that the failure rate was increasing as the experiment time went on.

(d)

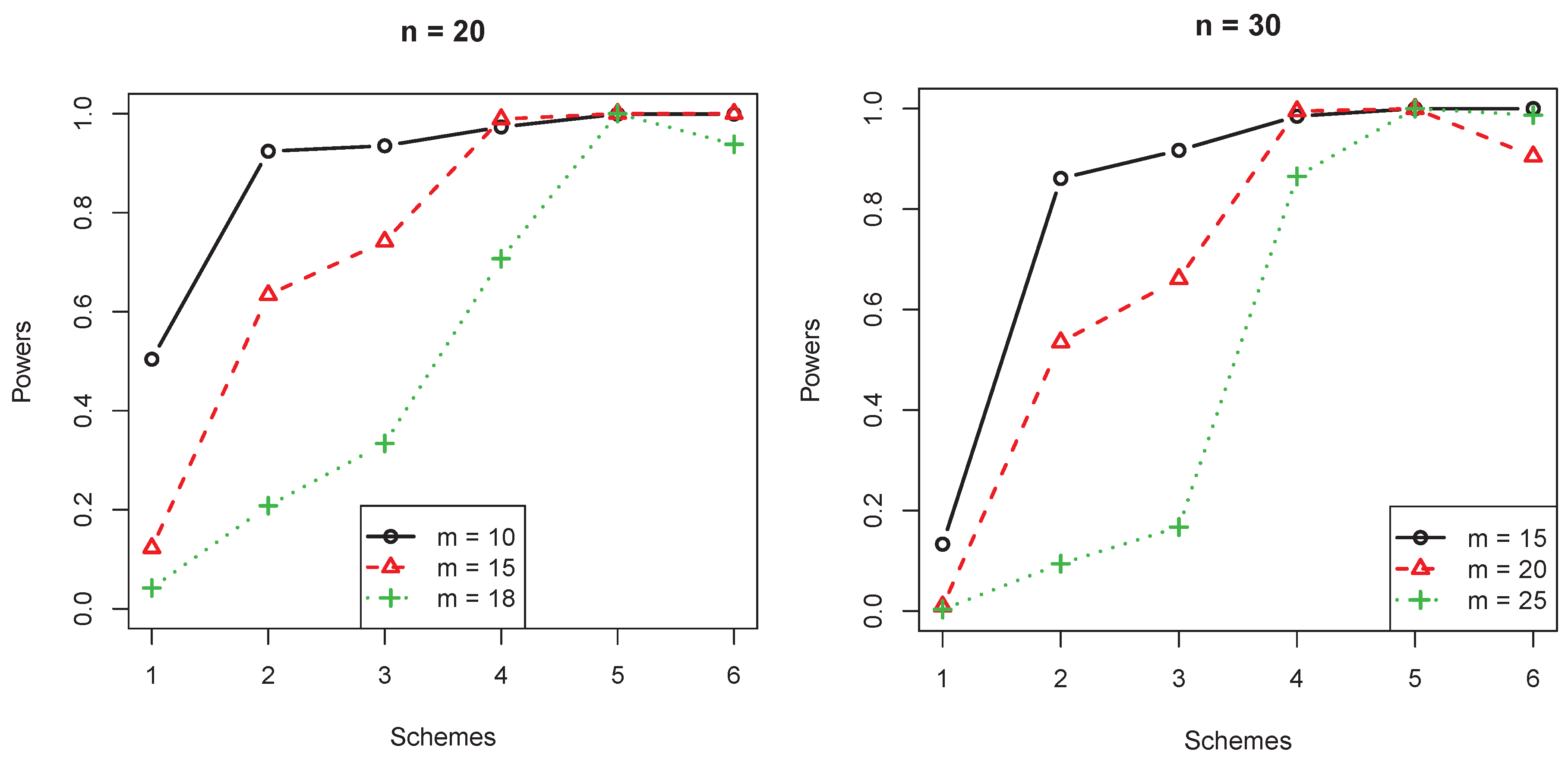
$H_0:X\sim$ log-logistic(2)    vs.    $H_1:X\sim$ Bathtub-shaped(2,15):

$$\begin{array}{cc}\hfill f(x;\beta ,\lambda )& =\lambda \beta x^{\beta -1}{e}^{\lambda (1-e^{x^{\beta }})+x^{\beta }},x\ge 0,\beta >0,\lambda >0,\hfill \\ \hfill F(x;\beta ,\lambda )& =1-e^{\lambda (1-e^{x^{\beta }})},\hfill \\ \hfill h(x;\beta ,\lambda )& =\lambda \beta x^{\beta -1}{e}^{x^{\beta }},\hfill \\ \hfill L(\beta ,\lambda )& =c{\lambda }^m{\beta }^m\prod _{i=1}^m{x}_i^{\beta -1}{e}^{x_i^{\beta }+\lambda (1-e^{x_i^{\beta }})(R_i+1)}.\hfill \end{array}$$

The unknown shape parameter and scale parameter of the distribution are $\beta$ and $\lambda$. In fact, $\lambda$ did not have an influence on $h(x)$. This distribution had an increased hazard function when $\beta >1$. Otherwise, $h(x)$ was bathtub shaped.

(e)

$H_0:X\sim$ log-logistic(2)    vs.    $H_1:X\sim$ Gexp(0.5,1):

$$\begin{array}{cc}\hfill f(x;\beta ,\lambda )& =\beta \lambda {(1-e^{-\lambda x})}^{\beta -1}{e}^{-\lambda x},x\ge 0,\beta >0,\lambda >0,\hfill \\ \hfill F(x;\beta ,\lambda )& ={(1-e^{-\lambda x})}^{\beta },\hfill \\ \hfill h(x;\beta ,\lambda )& =\frac{\beta \lambda e^{-\lambda x}{(1-e^{-\lambda x})}^{\beta -1}}{1-{(1-e^{-\lambda x})}^{\beta }},\hfill \\ \hfill L(\beta ,\lambda )& =c{\beta }^m{\lambda }^m\prod _{i=1}^m{(1-e^{-\lambda x_i})}^{\beta -1}{e}^{-\lambda x_i}{(1-{(1-e^{-\lambda x_i})}^{\beta })}^{R_i},\hfill \end{array}$$

where $\beta$ is the shape parameter and $\lambda$ is the scale parameter. The hazard function of this distribution tended to increase when $\beta >1$. $h(x)$ is constant over time if $\beta =1$. When $\beta <1$, $h(x)$ decreased.

To analyze the power of these alternative distributions, we selected 12–18 sets of censored schemes for n = 10, 20, and 30, and 10,000 Monte Carlo simulations were performed under each censorship plan.

Table 2. Powers of $\widehat{\mathrm{CRKL}}$ for the monotone decreasing hazard at the $5\%$ and $10\%$ significance levels for the different censorship schemes in the case of sample sizes n = 10, 20, and 30.

		Schemes	$5\%$			$10\%$
n	m	$({\mathit{R}}_1,\cdots ,{\mathit{R}}_{\mathit{m}})$	Pareto(5)	W(0.2)	Gexp(0.5)	Pareto(5)	W(0.2)	Gexp(0.5)
10	5	5,0,0,0,0	0.733	0.187	0.348	0.836	0.204	0.476
	5	0,5,0,0,0	0.716	0.200	0.282	0.827	0.208	0.410
	5	0,0,5,0,0	0.674	0.238	0.322	0.821	0.261	0.426
	5	0,0,0,5,0	0.722	0.283	0.285	0.824	0.316	0.384
	5	0,0,0,0,5	0.777	0.345	0.245	0.853	0.372	0.328
	5	1,1,1,1,1	0.711	0.378	0.336	0.835	0.399	0.410
	7	3,0,0,0,0,0,0	0.825	0.108	0.470	0.902	0.115	0.560
	7	0,3,0,0,0,0,0	0.766	0.107	0.421	0.887	0.114	0.547
	7	0,0,3,0,0,0,0	0.722	0.104	0.361	0.891	0.114	0.479
	7	0,0,0,0,0,3,0	0.672	0.247	0.353	0.817	0.266	0.491
	7	0,0,0,0,0,0,3	0.701	0.475	0.386	0.838	0.503	0.489
	7	1,0,0,1,0,0,1	0.770	0.265	0.379	0.884	0.290	0.520
20	10	10,0,0,0,0,0,0,0,0,0	0.918	0.068	0.585	0.969	0.074	0.704
	10	0,10,0,0,0,0,0,0,0,0	0.820	0.054	0.534	0.940	0.057	0.661
	10	0,0,0,0,0,10,0,0,0,0	0.866	0.106	0.419	0.937	0.114	0.580
	10	0,0,0,0,0,0,0,10,0,0	0.710	0.251	0.428	0.861	0.265	0.531
	10	0,0,0,0,0,0,0,0,0,10	0.823	0.627	0.454	0.901	0.645	0.526
	10	1,1,1,1,1,1,1,1,1,1	0.793	0.349	0.515	0.911	0.372	0.638
	15	5,0,0,...,0,0	0.980	0.026	0.714	0.992	0.029	0.880
	15	0,5,0,...,0,0	0.959	0.018	0.681	0.987	0.023	0.813
	15	0,...,0,5,0,...,0	0.963	0.038	0.663	0.983	0.045	0.735
	15	0,0,...,0,5,0	0.858	0.163	0.539	0.927	0.178	0.679
	15	0,0,0,...,0,5	0.860	0.453	0.647	0.931	0.475	0.761
	15	1,1,..,1,...,1,1	0.931	0.121	0.630	0.977	0.130	0.758
	18	2,0,0,...,0,0	0.995	0.004	0.785	0.998	0.004	0.906
	18	0,2,0,...,0,0	0.987	0.012	0.782	0.996	0.012	0.866
	18	0,...,0,2,0,...,0	0.987	0.017	0.738	0.994	0.018	0.861
	18	0,0,...,0,2,0	0.985	0.035	0.704	0.996	0.038	0.806
	18	0,0,0,...,0,2	0.967	0.082	0.694	0.994	0.092	0.803
	18	1,0,0,...,0,1	0.993	0.039	0.752	0.999	0.040	0.873
30	15	15,0,0,...,0,0	0.975	0.024	0.720	0.991	0.026	0.886
	15	0,15,0,...,0,0	0.930	0.020	0.651	0.978	0.024	0.795
	15	0,...,0,15,0,...,0	0.898	0.060	0.528	0.956	0.067	0.646
	15	0,0,...,0,15,0	0.761	0.379	0.454	0.850	0.398	0.567
	15	0,0,0,...,0,15	0.892	0.713	0.559	0.945	0.723	0.631
	15	1,1,...,1,...,1	0.876	0.287	0.653	0.945	0.300	0.401
	20	10,0,0,...,0,0	0.995	0.006	0.850	0.998	0.006	0.935
	20	0,10,0,...,0,0	0.982	0.006	0.792	0.998	0.008	0.913
	20	0,...,0,10,0,...0	0.978	0.013	0.734	0.992	0.016	0.848
	20	0,0,...,0,10,0	0.843	0.282	0.566	0.913	0.297	0.694
	20	0,0,0,...,0,10	0.898	0.712	0.666	0.947	0.740	0.779
	20	1,0,1,0,...,0,1,0	0.971	0.035	0.660	0.990	0.045	0.790
	25	5,0,0,...,0,0	0.995	0.001	0.909	0.997	0.002	0.967
	25	0,5,0,...,0,0	0.996	0.000	0.902	0.998	0.000	0.966
	25	0,...,0,5,0,...,0	0.989	0.002	0.827	0.998	0.003	0.935
	25	0,0,...,0,5,0	0.955	0.054	0.718	0.986	0.066	0.813
	25	0,0,0,...,0,5	0.977	0.163	0.780	0.999	0.182	0.910
	25	1,1,..,1,...,1,1	0.997	0.024	0.852	0.999	0.027	0.937

,

Table 3. Powers of $\widehat{\mathrm{CKL}}$ for the monotone decreasing hazard at the $5\%$ and $10\%$ significance levels for the different censorship schemes in the case of sample sizes n = 10, 20, and 30.

		Schemes	$5\%$			$10\%$
n	m	$({\mathit{R}}_1,\cdots ,{\mathit{R}}_{\mathit{m}})$	Pareto(12)	W(0.2)	Gexp(0.5)	Pareto(12)	W(0.2)	Gexp(0.5)
10	5	0,5,0,0,0	0.786	0.602	0.161	0.904	0.765	0.232
	5	0,0,5,0,0	0.678	0.424	0.195	0.866	0.660	0.302
	5	0,0,0,5,0	0.527	0.309	0.247	0.838	0.466	0.334
	5	0,0,0,0,5	0.084	0.703	0.366	0.236	0.744	0.478
	5	1,1,1,1,1	0.449	0.369	0.272	0.914	0.465	0.383
	7	3,0,0,0,0,0,0	0.590	0.708	0.051	0.792	0.826	0.080
	7	0,3,0,0,0,0,0	0.835	0.761	0.093	0.934	0.862	0.120
	7	0,0,3,0,0,0,0	0.828	0.712	0.077	0.914	0.850	0.107
	7	0,0,0,0,0,3,0	0.902	0.573	0.193	0.975	0.758	0.260
	7	0,0,0,0,0,0,3	0.851	0.429	0.385	0.989	0.549	0.518
	7	1,0,0,1,0,0,1	0.983	0.684	0.276	1.000	0.848	0.395
20	10	10,0,0,0,0,0,0,0,0,0	0.376	0.711	0.007	0.637	0.827	0.019
	10	0,10,0,0,0,0,0,0,0,0	0.855	0.870	0.053	0.920	0.914	0.073
	10	0,0,0,0,0,10,0,0,0,0	0.814	0.728	0.065	0.929	0.828	0.099
	10	0,0,0,0,0,0,0,10,0,0	0.928	0.679	0.185	0.969	0.793	0.228
	10	0,0,0,0,0,0,0,0,0,10	0.835	0.790	0.532	0.976	0.827	0.660
	10	1,1,1,1,1,1,1,1,1,1	0.998	0.707	0.370	1.000	0.859	0.506
	15	5,0,0,...,0,0	0.045	0.659	0.002	0.193	0.803	0.002
	15	0,5,0,...,0,0	0.494	0.883	0.004	0.717	0.927	0.005
	15	0,...,0,5,0,...,0	0.461	0.803	0.003	0.783	0.873	0.004
	15	0,0,...,0,5,0	0.974	0.746	0.081	0.992	0.849	0.135
	15	0,0,0,...,0,5	1.000	0.877	0.565	0.998	0.961	0.697
	15	1,1,..,1,...,1,1	1.000	0.965	0.131	1.000	0.989	0.216
	18	2,0,0,...,0,0	0.005	0.694	0.002	0.064	0.858	0.003
	18	0,2,0,...,0,0	0.155	0.850	0.003	0.337	0.916	0.005
	18	0,...,0,2,0,...,0	0.122	0.793	0.002	0.384	0.880	0.002
	18	0,0,...,0,2,0	0.547	0.793	0.001	0.848	0.896	0.004
	18	0,0,0,...,0,2	0.999	0.974	0.095	1.000	0.993	0.158
	18	1,0,0,...,0,1	0.913	0.937	0.005	0.980	0.966	0.011
30	15	15,0,0,...,0,0	0.054	0.670	0.002	0.191	0.829	0.002
	15	0,15,0,...,0,0	0.798	0.903	0.012	0.876	0.956	0.015
	15	0,...,0,15,0,...,0	0.730	0.763	0.024	0.856	0.854	0.033
	15	0,0,...,0,15,0	0.937	0.610	0.297	0.980	0.754	0.359
	15	0,0,0,...,0,15	0.945	0.885	0.631	1.000	0.905	0.762
	15	1,1,...,1,...,1	1.000	0.902	0.401	1.000	0.979	0.508
	20	10,0,0,...,0,0	0.004	0.631	0.002	0.026	0.852	0.001
	20	0,10,0,...,0,0	0.527	0.897	0.002	0.712	0.963	0.003
	20	0,...,0,10,0,...0	0.448	0.815	0.003	0.666	0.914	0.004
	20	0,0,...,0,10,0	0.993	0.712	0.174	0.999	0.885	0.269
	20	0,0,0,...,0,10	1.000	0.632	0.669	1.000	0.802	0.779
	20	1,0,1,0,...,0,1,0	0.830	0.806	0.007	0.955	0.904	0.013
	25	5,0,0,...,0,0	0.002	0.692	0.001	0.003	0.829	0.001
	25	0,5,0,...,0,0	0.095	0.928	0.001	0.273	0.974	0.002
	25	0,...,0,5,0,...,0	0.054	0.853	0.000	0.221	0.931	0.001
	25	0,0,...,0,5,0	0.894	0.781	0.003	0.988	0.911	0.011
	25	0,0,0,...,0,5	1.000	1.000	0.600	1.000	1.000	0.722
	25	1,1,..,1,...,1,1	0.990	0.980	0.002	1.000	0.991	0.007

and

Table 4. Powers for the monotone increasing hazard at the $5\%$ and $10\%$ significance levels for the different censorship schemes in the case of sample sizes n = 10, 20, and 30.

			$5\%$			$10\%$
		Schemes	$\widehat{\mathbf{CRKL}}$	$\widehat{\mathbf{CKL}}$		$\widehat{\mathbf{CRKL}}$	$\widehat{\mathbf{CKL}}$
n	m	$({\mathit{R}}_1,\cdots ,{\mathit{R}}_{\mathit{m}})$	B(15)	R(0.2)	B(200)	B(15)	R(0.2)	B(200)
10	5	5,0,0,0,0	0.572	0.848	0.665	0.910	0.929	0.906
	5	0,5,0,0,0	0.631	0.916	0.863	0.934	0.963	0.990
	5	0,0,5,0,0	0.557	0.841	0.300	0.841	0.954	0.793
	5	0,0,0,5,0	0.443	0.786	0.027	0.739	0.936	0.401
	5	0,0,0,0,5	0.509	0.757	0.020	0.770	0.918	0.001
	5	1,1,1,1,1	0.420	0.854	0.041	0.688	0.968	0.405
	7	3,0,0,0,0,0,0	0.569	0.658	0.474	0.970	0.806	0.801
	7	0,3,0,0,0,0,0	0.824	0.874	0.908	0.991	0.927	0.981
	7	0,0,3,0,0,0,0	0.859	0.911	0.924	0.992	0.964	0.987
	7	0,0,0,0,0,3,0	0.389	0.952	0.699	0.709	0.979	0.958
	7	0,0,0,0,0,0,3	0.325	0.993	0.255	0.539	1.000	0.789
	7	1,0,0,1,0,0,1	0.404	0.992	0.966	0.729	1.000	0.998
20	10	10,0,0,0,0,0,0,0,0,0	0.860	0.358	0.127	1.000	0.504	0.488
	10	0,10,0,0,0,0,0,0,0,0	0.950	0.858	0.988	1.000	0.924	1.000
	10	0,0,0,0,0,10,0,0,0,0	0.868	0.884	0.962	0.997	0.935	1.000
	10	0,0,0,0,0,0,0,10,0,0	0.516	0.925	0.939	0.788	0.973	0.998
	10	0,0,0,0,0,0,0,0,0,10	0.117	0.990	0.002	0.370	0.999	0.019
	10	1,1,1,1,1,1,1,1,1,1	0.358	0.995	0.999	0.645	0.999	0.999
	15	5,0,0,...,0,0	1.000	0.042	0.008	0.999	0.123	0.067
	15	0,5,0,...,0,0	1.000	0.463	0.536	1.000	0.634	0.846
	15	0,...,0,5,0,...,0	0.999	0.531	0.448	1.000	0.742	0.879
	15	0,0,...,0,5,0	0.568	0.960	0.906	0.885	0.989	0.996
	15	0,0,0,...,0,5	0.266	1.000	0.999	0.526	1.000	1.000
	15	1,1,..,1,...,1,1	0.595	0.998	0.999	0.909	1.000	1.000
	18	2,0,0,...,0,0	0.997	0.010	0.001	0.999	0.042	0.002
	18	0,2,0,...,0,0	0.998	0.101	0.013	1.000	0.208	0.132
	18	0,...,0,2,0,...,0	1.000	0.137	0.014	0.996	0.334	0.160
	18	0,0,...,0,2,0	0.978	0.422	0.141	1.000	0.707	0.596
	18	0,0,0,...,0,2	0.679	1.000	0.996	0.955	1.000	1.000
	18	1,0,0,...,0,1	0.925	0.803	0.548	1.000	0.938	0.872
30	15	15,0,0,...,0,0	0.999	0.040	0.001	0.998	0.133	0.017
	15	0,15,0,...,0,0	1.000	0.750	0.922	1.000	0.861	0.990
	15	0,...,0,15,0,...,0	0.971	0.824	0.864	0.996	0.917	0.996
	15	0,0,...,0,15,0	0.289	0.943	0.746	0.568	0.985	0.990
	15	0,0,0,...,0,15	0.142	1.000	0.017	0.254	1.000	0.122
	15	1,1,...,1,...,1	0.511	1.000	1.000	0.804	1.000	1.000
	20	10,0,0,...,0,0	0.998	0.002	0.002	0.998	0.009	0.005
	20	0,10,0,...,0,0	0.997	0.370	0.527	0.995	0.535	0.794
	20	0,...,0,10,0,...0	1.000	0.487	0.566	1.000	0.661	0.898
	20	0,0,...,0,10,0	0.501	0.977	0.987	0.734	0.995	1.000
	20	0,0,0,...,0,10	0.173	1.000	0.997	0.368	1.000	0.999
	20	1,0,1,0,...,0,1,0	0.987	0.764	0.738	1.000	0.905	0.996
	25	5,0,0,...,0,0	1.000	0.002	0.001	1.000	0.003	0.002
	25	0,5,0,...,0,0	1.000	0.044	0.023	1.000	0.094	0.110
	25	0,...,0,5,0,...,0	0.999	0.088	0.014	1.000	0.167	0.108
	25	0,0,...,0,5,0	0.857	0.658	0.309	0.999	0.865	0.886
	25	0,0,0,...,0,5	0.504	1.000	1.000	0.836	1.000	1.000
	25	1,1,..,1,...,1,1	0.997	0.925	0.940	1.000	0.987	0.998

and Figure 1, Figure 2, Figure 3 and Figure 4 show the simulation results.

The average values of power in Table 2, Table 3 and Table 4 were 0.575, 0.561, and 0.706, respectively. The ratio of power over 0.65 in each table reached $52.43\%$, $54.17\%$, and $66.32\%$.

The trend of the test statistic on the censored program can be obtained by the analysis of Figure 1, Figure 2, Figure 3 and Figure 4:

• From Figure 1, different censorship schemes had little effect on power for the $\widehat{\mathrm{CRKL}}$ test when the hazard function monotonically decreased.
• From Figure 2, for the $\widehat{\mathrm{CKL}}$ test, there was no obvious trend in power study for the monotone decreasing hazard function under different censored schemes.
• From Figure 3, when the censorship only happened at the end, the power for the monotone increasing hazard function for the $\widehat{\mathrm{CRKL}}$ test was lower.
• From Figure 4, when the censorship only happened at the beginning and the hazard function monotonically increased, the power for the $\widehat{\mathrm{CKL}}$ test was lower.

Therefore, we obtained the following conclusions: Before performing the goodness-of-fit test, we selected the test statistic by analyzing the hazard function of the relevant distributions. When the hazard function was monotonically decreasing, the statistic $\widehat{\mathrm{CKL}}$ was selected. When the hazard function increased monotonically, if the censoring occurred only at the beginning of the experiment, we used $\widehat{\mathrm{CRKL}}$; if the censoring only occurred at the end of the experiment, we used $\widehat{\mathrm{CKL}}$; in other cases, both test statistics were acceptable.

6. Illustrative Example

6.1. Application Prospect

The modern quality concept holds that product quality is a combination of characteristics that meet the requirements of use, that is, applicability. Improving quality in the process of product realization is an important way to improve product quality. Therefore, in the product reliability analysis, it is important to determine the product probability distribution to further analyze the shape characteristics of the function such as the failure rate.

For example, quality fluctuations common in product formation have unacceptable parts and installation errors. In order to establish a reliability model under two quality fluctuations, it is first necessary to determine the product probability distribution. When relevant research shows that the product may be the log-logistic distribution, the algorithm proposed in this paper can be used to test the goodness of fit.

Because the failure rate function is not strictly monotonic under the log-logistic distribution, there is flexibility in establishing a reliability model. Our proposed algorithm has practical value in effectively controlling quality fluctuations and improving product reliability. Below, we will introduce actual data for simulation studies.

6.2. Real Data Application

We have proven that the proposed goodness-of-fit tests are discriminative by analyzing the power of hypothesis testing. In this part, we will introduce a set of real data to continue to illustrate the applicability of the algorithm. The work in [9] proposed a progressive censored sample of the logarithmic lifetime of the insulating fluid tested by 34 KV to the breakdown data. These data of size $m=5$ generated from $n=13$ are listed in

Table 5. A progressive censored sample of the logarithmic lifetime of the insulating fluid.

i	1	2	3	4	5
$x_{i:5:13}$	0.2700	1.0224	1.5789	1.8718	1.9947
$R_i$	0	3	0	0	5

. We will use the two test statistics to test the collected censored data and analyze whether the sample obeys the log-logistic distribution.

Firstly, calculate the value of the test statistics according to Equations (23) and (24). The value of the unknown parameter $\beta$ was replaced by $\widehat{\beta }$ obtained under the parameter estimation method in the third section. The results of the calculations were $\widehat{\mathrm{CRKL}}=1.221995$ and $\widehat{\mathrm{CKL}}=0.025522$. Referring to the algorithm for calculating the p-values by R in the Monte Carlo simulation in Section 5, we obtained p-values corresponding to the two goodness-of-fit tests of 0.898 and 0.605, respectively. From the results, there is sufficient evidence to show that the sample observed under progressive Type II censoring obeyed the log-logistic distribution. Through the simulation of this set of data, we can get the conclusion that the test statistic is applicable.

7. Conclusions

In this paper, the fitting test of the log-logistic distribution was discussed under progressive Type II censoring. We established $\widehat{\mathrm{CRKL}}$ and $\widehat{\mathrm{CKL}}$ test statistics based on the cumulative residual entropy and cumulative entropy. Among them, we used the maximum likelihood estimation and EM algorithm for parameter estimation, and the Monte Carlo simulation was presented to analyze the multiple alternative hypotheses. Trend analysis of the power study under different censorship schemes demonstrated the feasibility of the test statistics.

We have come to the conclusion that the test statistic was chosen based on the monotonicity of the risk function of the relevant distribution. When the hazard function monotonically decreased, we selected the statistic $\widehat{\mathrm{CKL}}$. When the hazard function increased monotonically, it was necessary to select the statistic according to the time when the censorship occurred. The power analysis showed that the proposed goodness-of-fit test had the feasibility of discriminating whether the null hypothesis was true. At the same time, the actual data case showed the combination of algorithm and practical application. The idea of the fitting test in this paper can also be applied to more distributions in subsequent studies, such as: Weibull, Rayleigh, Pareto, etc.