An Enhanced Partial Search to Particle Swarm Optimization for Unconstrained Optimization
Abstract
:1. Introduction
2. Particle Swarm Optimization
2.1. Traditional PSO Operation
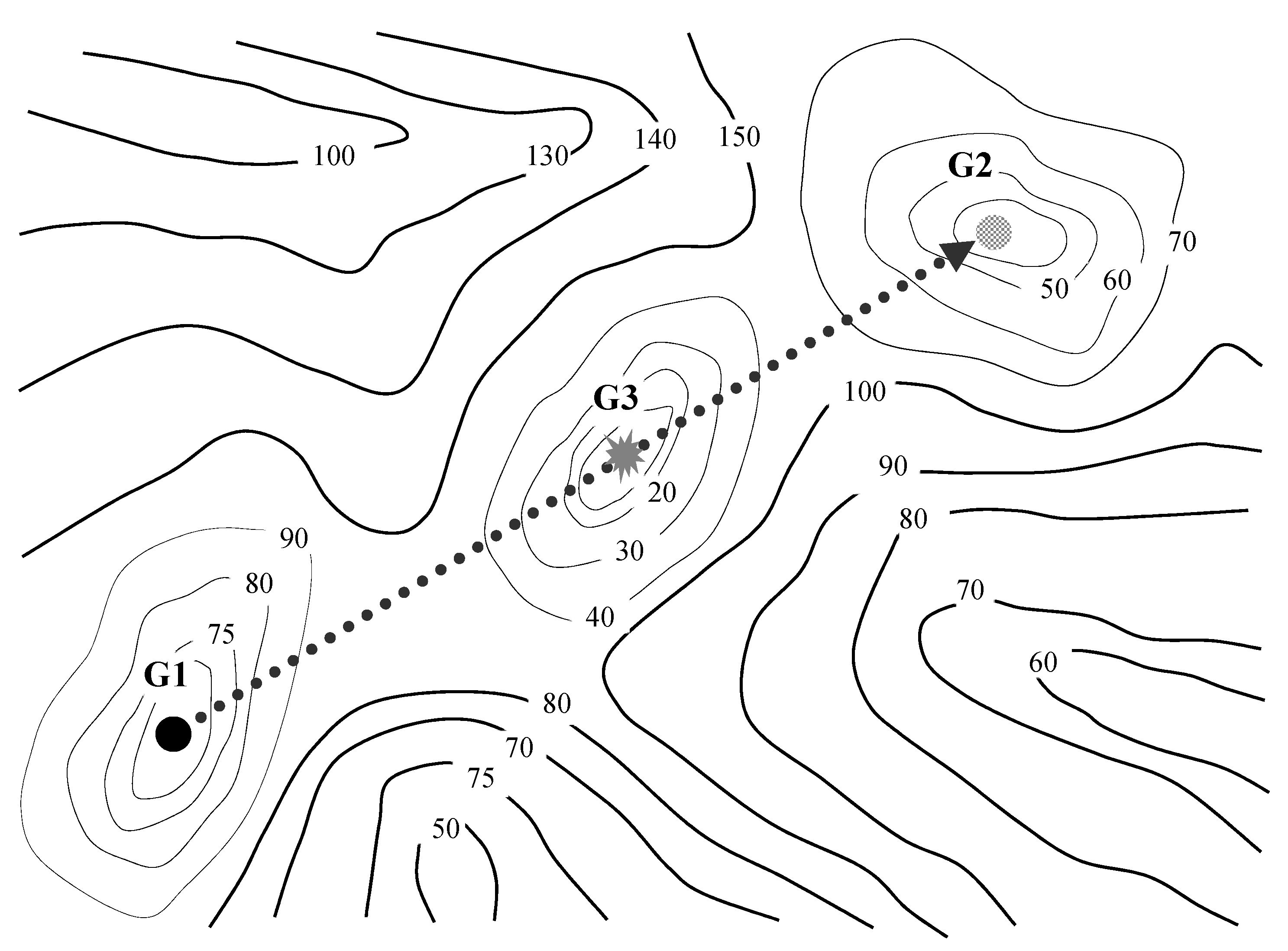
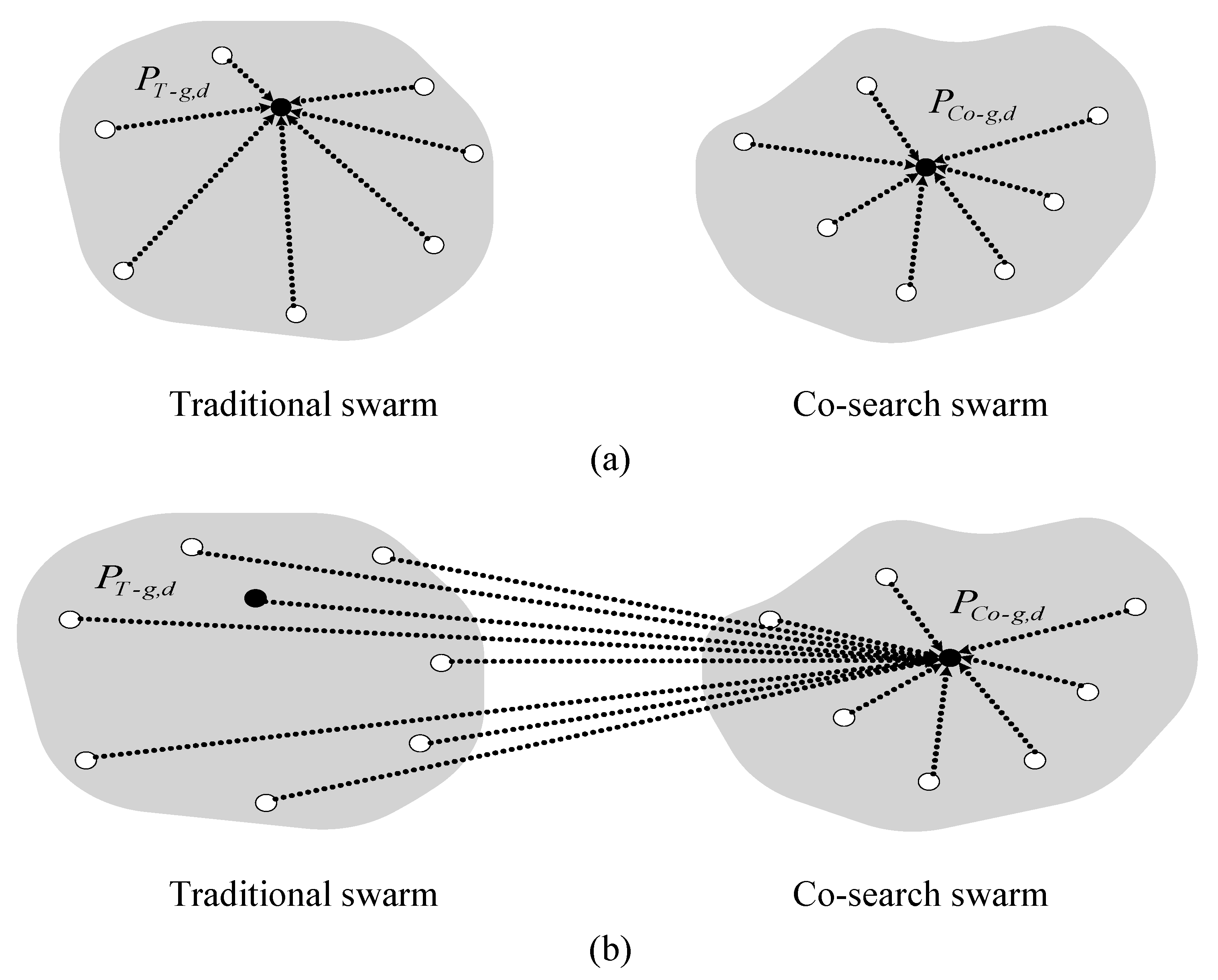
2.2. Cooperative Multiple Swarms
3. Enhanced Partial Search Particle Swarm Optimization (EPS-PSO) Algorithm
| The Enhanced Partial Search Particle Swarm Optimization (EPS-PSO) Algorithm 1 |
| Define |
| : Each swarm’s population size |
| : Swarm ID number |
| : Re-initialization period |
| k: function evaluation index |
| For each particle in each swarm |
| Circumscribe the search space for the traditional and co-search swarms within the box constraints |
| Initialize position , particle’s personal best and velocity for both swarms |
| Perform the function evaluation for each particle and update k, |
| Endfor |
| Repeat: |
| For each swarm : |
| For each particle : |
| If |
| then |
| If |
| then |
| Endfor |
| Perform particle velocity and position updates via Equations (1–2) |
| Endfor |
| Perform the function evaluation for both swarms and update k |
| If the criterion of the re-initialization period for the co-search swarm is met |
| For each particle in the co-search swarm |
| Circumscribe the search space within the box constraints |
| Re-initialize position , particle’s personal best and velocity for the co-search swarm |
| Perform the function evaluation for each particle and update k |
| Endfor |
| If then |
| Until the maximum number k of function evaluations is satisfied |
4. Experiment Setup
- CPSO-: A maximally “split” swarm where the search space vector is split into 30 parts.
- CPSO-: The search space vector for CPSO- is split into only six parts (of five components each).
- CPSO-: A hybrid swarm, consisting of a maximally split swarm, coupled with a plain swarm.
- CPSO-: A hybrid swarm, consisting of a CPSO- swarm, coupled with a plain swarm.
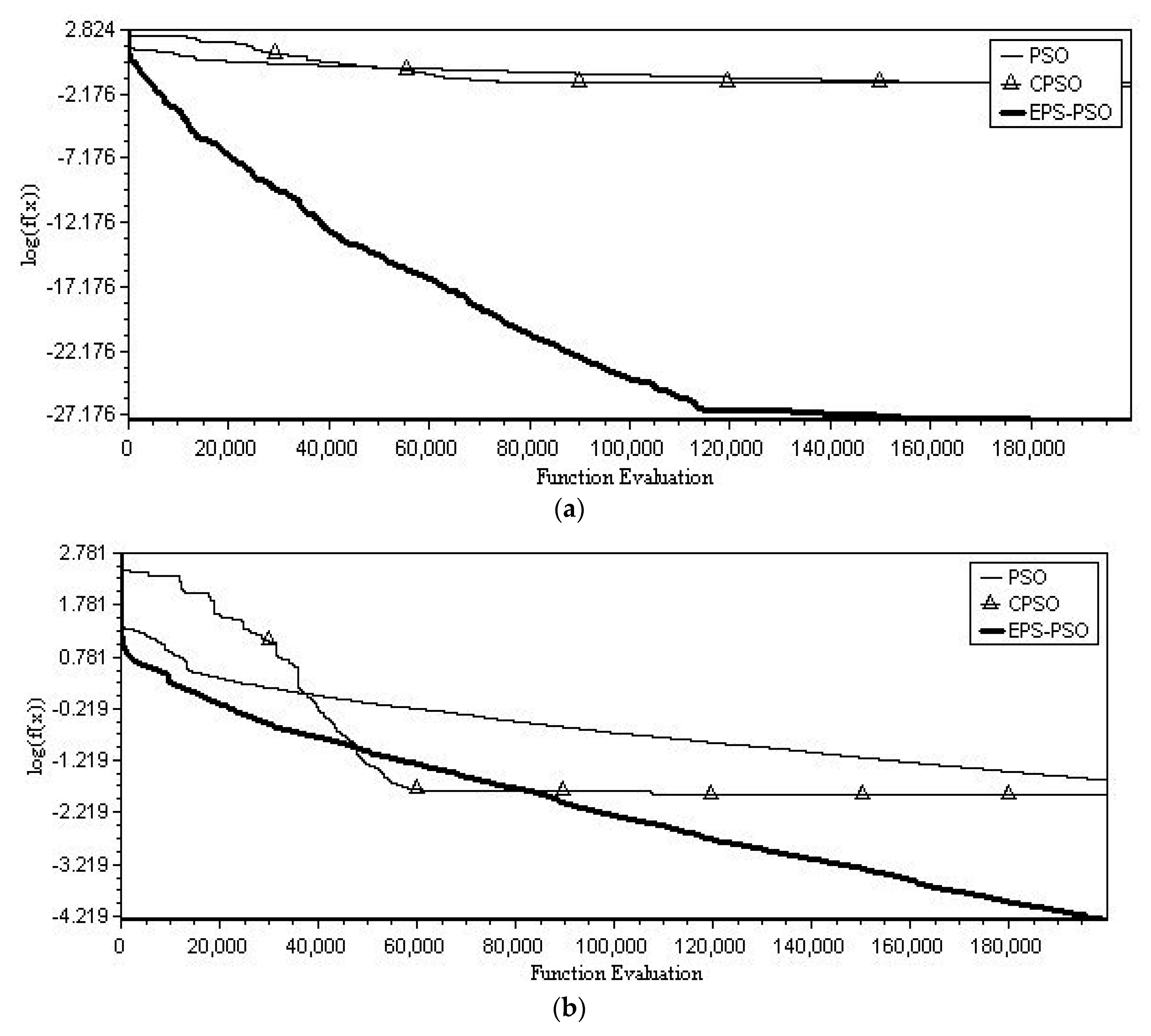
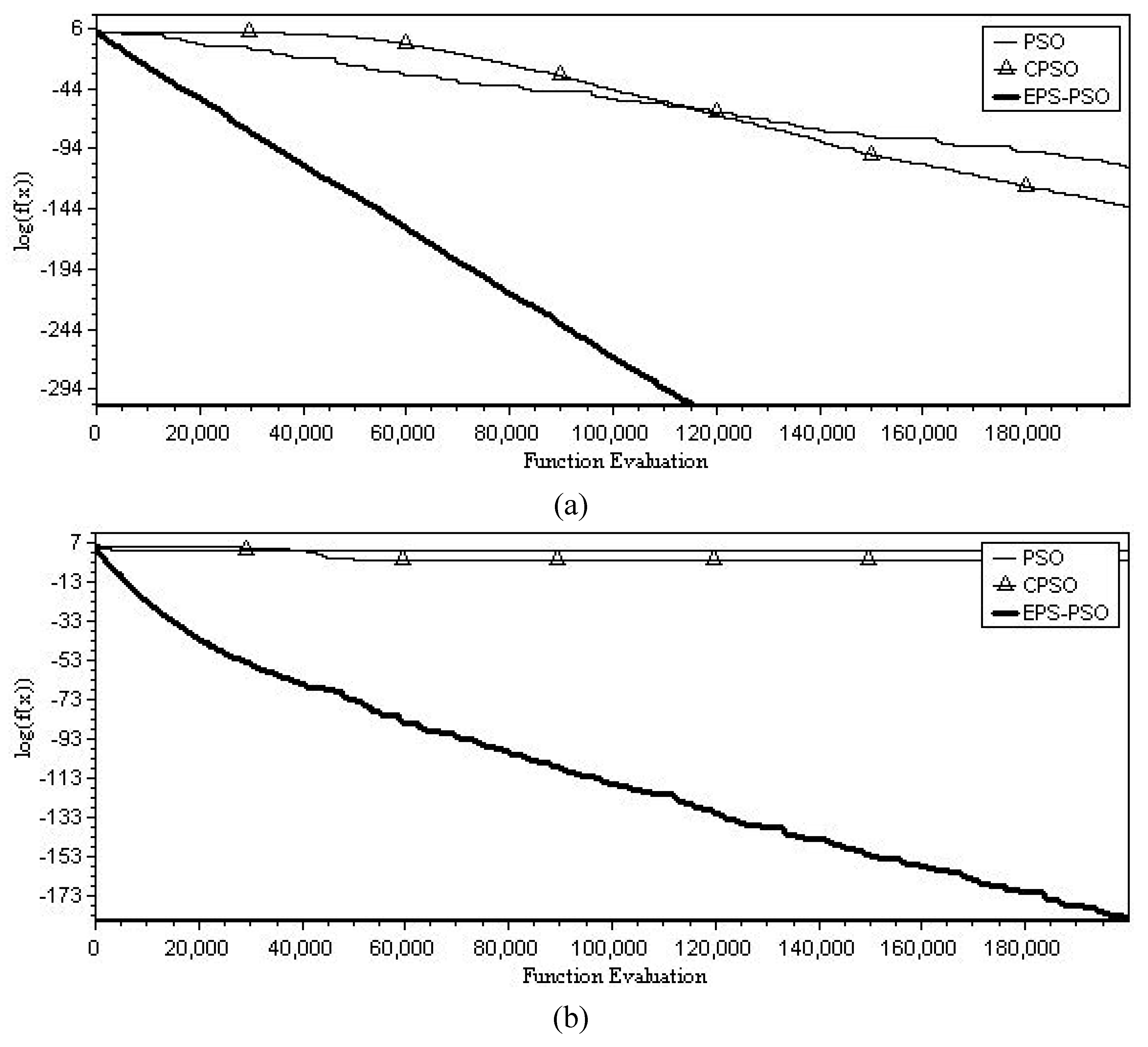
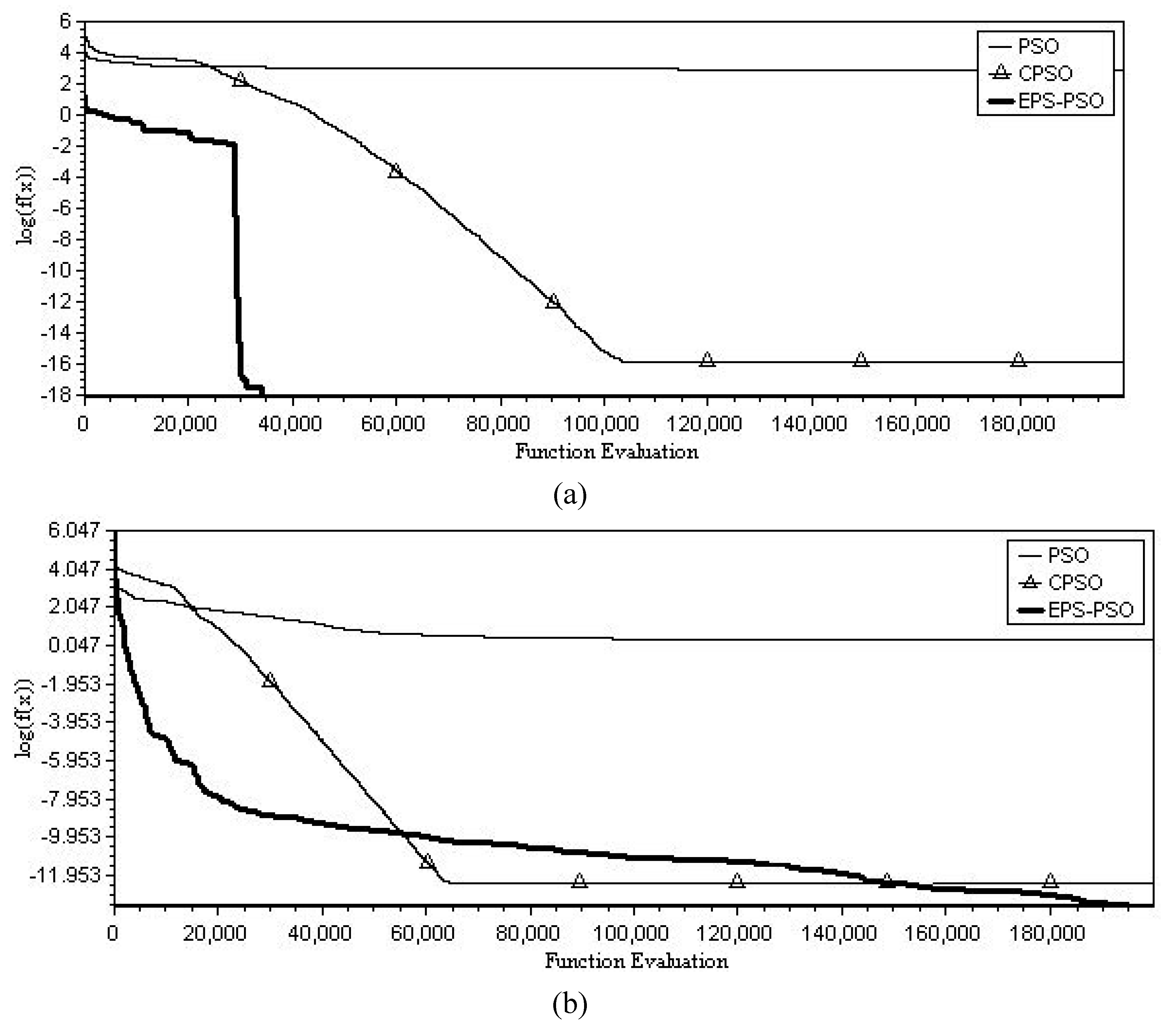
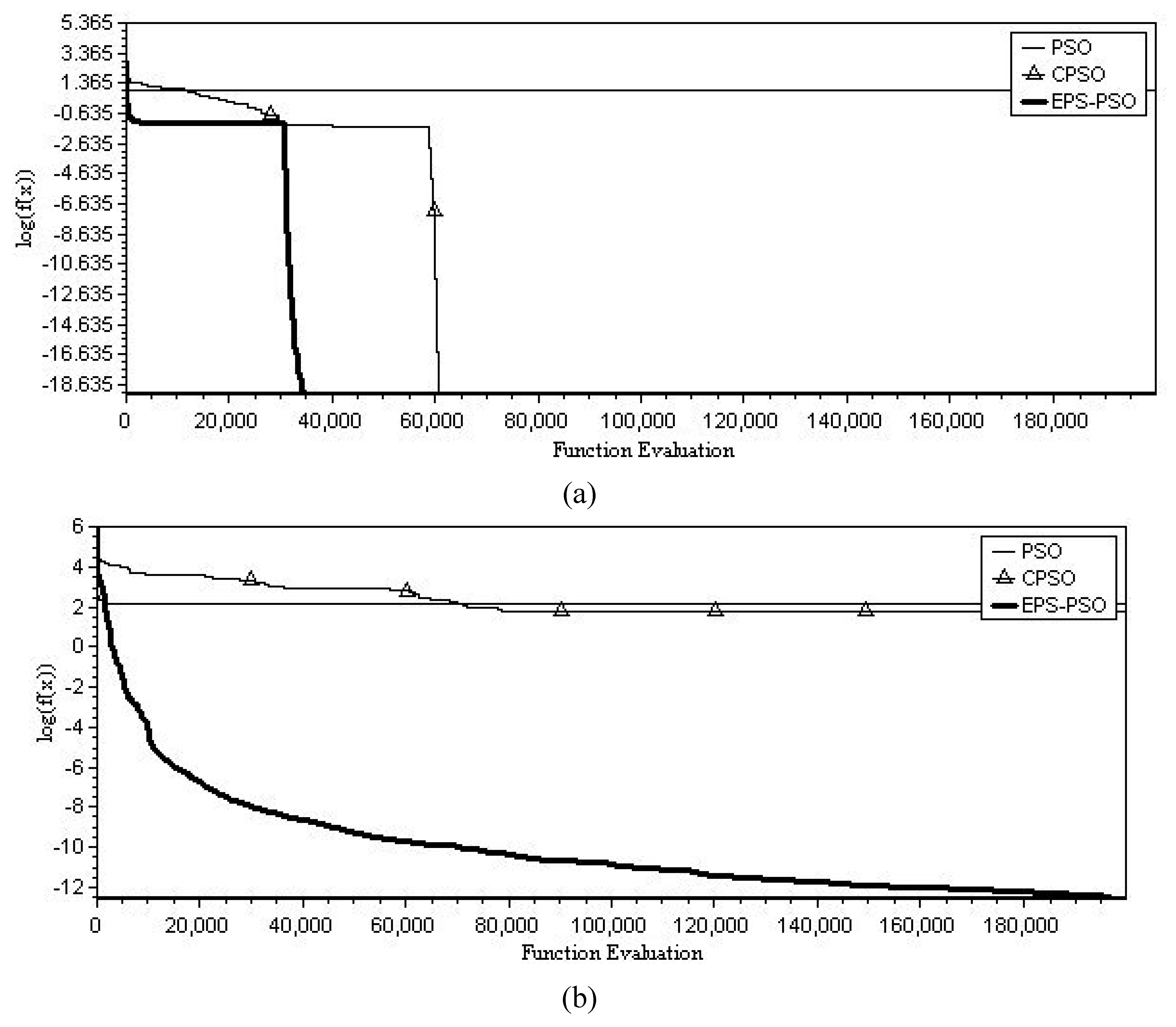
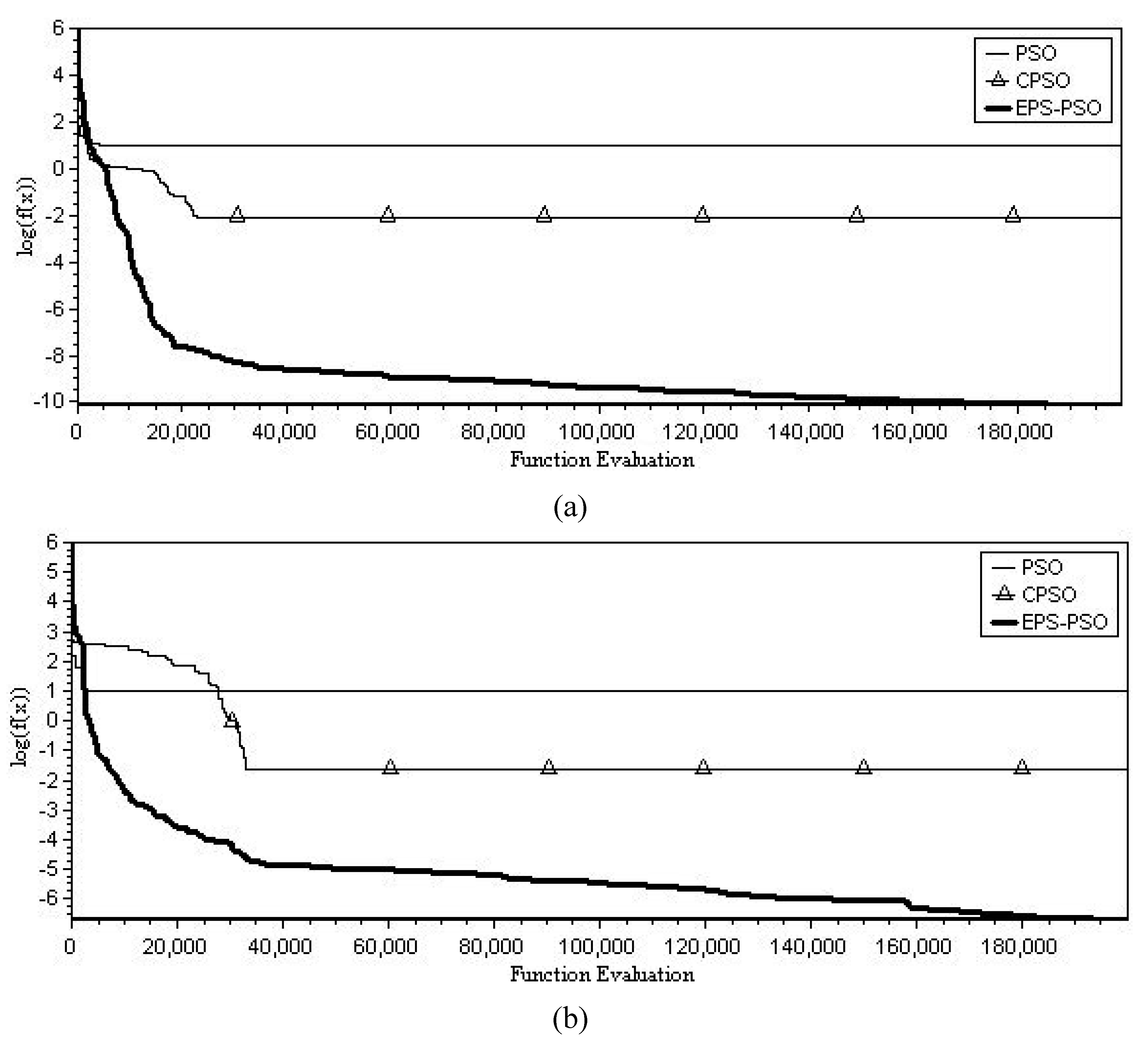
5. Computational Result and Discussion
6. Conclusions and Directions of Future Research
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Publishing Inc.: Reading, MA, USA, 1989. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Dorigo, M.; Caro, G.D. Ant colony optimization: A new meta-heuristic. In Proceedings of the Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; Volume 2, pp. 1470–1477. [Google Scholar]
- Shi, Y.; Eberhart, R.C. A modified particle swarm optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Wang, X.-H.; Jun-Jun, L. Hybrid particle swarm optimization with simulated annealing. In Proceedings of the Third International Conference on Machine Learning and Cybernetics, Shanghai, China, 26–29 August 2004; Volume 4, pp. 2402–2405. [Google Scholar]
- Cui, Z.H.; Zeng, J.C.; Cai, X.J. A new stochastic particle swarm optimizer. In Proceedings of the 2004 Congress on Evolutionary Computation, Piscataway, NJ, USA, 19–23 June 2004; pp. 316–319. [Google Scholar]
- Zahara, E.; Fan, S.K.-S.; Tsai, D.M. Optimal multi-thresholding using a hybrid optimization approach. Patten Recognit. Lett. 2004, 26, 1082–1095. [Google Scholar] [CrossRef]
- Fan, S.-K.S.; Liang, Y.C.; Zahara, E. A Hybrid Simplex Search and Particle Swarm Optimization for the Global Optimization of Multimodal Functions. Eng. Optim. 2004, 36, 401–418. [Google Scholar] [CrossRef]
- Fan, S.-K.S.; Zahara, E. A hybrid simplex search and particle swarm optimization for unconstrained optimization. Eur. J. Oper. Res. 2007, 181, 527–548. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A Cooperative Approach to Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 225–239. [Google Scholar] [CrossRef]
- Angeline, P.J. Using selection to improve particle swarm optimization. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AL, USA, 4–9 May 1998; pp. 84–89. [Google Scholar]
- Lovbjerg, M.; Rasmussen, T.K.; Krink, T. Hybrid particle swarm optimizer with breeding and subpopulations. In Proceedings of the Third Genetic and Evolutionary Computation Congress, San Diego, CA, USA, 7–11 July 2001; pp. 469–476. [Google Scholar]
- Lovbjerg, M.; Krink, T. Extending particle swarm optimizers with self-organized criticality. In Proceedings of the Fourth Congress on Evolutionary Conference, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1588–1593. [Google Scholar]
- Rada-Vilela, J.; Johnston, M.; Zhang, M. Population statistics for particle swarm optimization: Resampling methods in noisy optimization problems. Swarm Evol. Comput. 2014, 17, 37–59. [Google Scholar] [CrossRef]
- Taghiyeh, S.; Xu, J. A new particle swarm optimization algorithm for noisy optimization problems. Swarm Intell. 2016, 10, 161–192. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Dobbins, R.C.; Simpson, P. Computational Intelligence PC Tools; Academic Press Professional: Boston, MA, USA, 1996. [Google Scholar]
- Potter, M.A.; de Jong, K.A. A Cooperative Coevolutionary Approach to Function Optimization the Third Parallel Problem Solving from Nature; Springer: Berlin, Germany, 1994; pp. 249–257. [Google Scholar]
- Van den Bergh, F.; Engelbrecht, A.P. Effects of swarm size on cooperative particle swarm optimizers. In Proceedings of the Genetic and Evolutionary Computation Conference, San Francisco, CA, USA, 7–11 July 2001; pp. 892–899. [Google Scholar]
- Shang, Y.W.; Qiu, Y.H. A note on the extended Rosenbrock function. Evol. Comput. 2006, 14, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Črepinšek, M.; Liu, S.H.; Mernik, M. Replication and comparison of computational experiments in applied evolutionary computing: Common pitfalls and guidelines to avoid them. Appl. Soft Comput. 2014, 19, 161–170. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Piscataway, NJ, USA, 6–9 July 1999; pp. 1945–1950. [Google Scholar]
- Salomon, R. Reevaluating genetic algorithm performance under coordinate rotation of benchmark functions. BioSystems 1996, 39, 263–278. [Google Scholar]
| Problems | Search dom. | Objective Functions | Global min. | ||
|---|---|---|---|---|---|
| Rosenbrock | 30 | ||||
| Quadratic | 30 | ||||
| Ackley | 30 | ||||
| Rastrigin | 30 | ||||
| Griewank | 30 |
| Algorithm | s | t | Mean(Unrotated) | Mean(Rotated) |
|---|---|---|---|---|
| PSO | 10 | ― | 2.10e–01 ± 2.61e–01 | 2.12e–01 ± 7.12e–01 |
| 15 | ― | 1.53e–02 ± 3.31e–02 | 1.04e–01 ± 6.82e–01 | |
| 20 | ― | 4.52e–03 ± 6.18e–03 | 2.16e–01 ± 2.41e–01 | |
| CPSO-S | 10 | ― | 6.06e–01 ± 4.61e–01 | 2.21e+00 ± 6.78e–01 |
| 15 | ― | 3. 63e–01 ± 1.04e–02 | 1.42e+00 ± 2.23e–01 | |
| 20 | ― | 8.16e–01 ± 2.47e–02 | 4.71e+00 ± 7.50e–01 | |
| CPSO-H | 10 | ― | 6.11e–01 ± 2.13e–02 | 7.16e–01 ± 6.88e–01 |
| 15 | ― | 1.14e–02 ± 2.04e–02 | 2.92e–01 ± 1.13e–01 | |
| 20 | ― | 1.15e–01 ± 1.48e–01 | 2.59e+00 ± 2.06e–01 | |
| CPSO- | 10 | ― | 8.33e+00 ± 4.81e–01 | 6.38e+00 ± 9.48e–01 |
| 15 | ― | 1.07e+00 ± 7.26e–01 | 1.42e+00 ± 9.71e–01 | |
| 20 | ― | 6.29e–01 ± 5.03e–01 | 8.51e+00 ± 3.38e–01 | |
| CPSO- | 10 | ― | 2.94e–01 ± 2.11e–01 | 2.17e–01 ± 8.32e–01 |
| 15 | ― | 7.59e–01 ± 5.72e–01 | 7.24e–01 ± 7.13e–01 | |
| 20 | ― | 8.31e–01 ± 6.11e–01 | 1.13e–01 ± 6.05e–01 | |
| EPS-PSO | 20 | 100 | 2.92e–03 ± 1.02e–03 | 7.72e–03 ± 1.02e–02 |
| 20 | 500 | 2.58e–19 ± 5.28e–19 | 5.43e–05 ± 3.30e–05 | |
| 20 | 1000 | 2.90e–22 ± 1.71e–22 | 9.60e–03 ± 7.24e–03 | |
| 20 | 5000 | 2.54e–28 ± 1.93e–29 | 1.64e–03 ± 1.76e–04 | |
| 20 | 10000 | 1.89e–20 ± 5.01e–20 | 1.25e–04 ± 3.00e–04 |
| Algorithm | s | t | Mean(Unrotated) | Mean(Rotated) |
|---|---|---|---|---|
| PSO | 10 | ― | 2.11e+00 ± 6.11e+00 | 6.11e+02 ± 3.07+e02 |
| 15 | ― | 3.73e–71 ± 2.72e–71 | 7.15e+02 ± 1.73+e02 | |
| 20 | ― | 3.32e–95 ± 1.59e–96 | 3.82e+02 ± 6.12+e01 | |
| CPSO-S | 10 | ― | 1.72e–126 ± 7.18e–126 | 4.53e+02 ± 4.21+e02 |
| 15 | ― | 2.72e–90 ± 2.47e–89 | 6.81e+03 ± 2.96+e03 | |
| 20 | ― | 1.17e–67 ± 8.87e–66 | 2.12e+03 ± 5.81+e03 | |
| CPSO-H | 10 | ― | 1.26e–93 ± 1.93e–92 | 1.41e+01 ± 5.59+e01 |
| 15 | ― | 2.81e–80 ± 1.02e–79 | 3.75e+02 ± 3.11+e02 | |
| 20 | ― | 8.31e–61 ± 3.18e–62 | 2.62e+02 ± 2.31+e02 | |
| CPSO- | 10 | ― | 1.61e–07 ± 7.93e–07 | 2.05e+03 ± 3.18+e03 |
| 15 | ― | 2.12e–05 ± 4.06e–05 | 1.62e+03 ± 4.83+e03 | |
| 20 | ― | 8.22e–05 ± 4.75e–05 | 2.11e+03 ± 2.12+e03 | |
| CPSO- | 10 | ― | 4.13e–63 ± 2.11e–63 | 1.63e+03 ± 8.61+e03 |
| 15 | ― | 7.12e–46 ± 1.69e–45 | 1.42e+02 ± 1.17+e02 | |
| 20 | ― | 6.72e–27 ± 1.12e–28 | 8.64e+03 ± 4.92+e03 | |
| EPS-PSO | 20 | 100 | 0.00e+00 ± 0.00e+00 | 1.18e–120 ± 1.90e–121 |
| 20 | 500 | 0.00e+00 ± 0.00e+00 | 2.11e–140 ± 4.18e–140 | |
| 20 | 1000 | 0.00e+00 ± 0.00e+00 | 8.35e–183 ± 6.29e–184 | |
| 20 | 5000 | 0.00e+00 ± 0.00e+00 | 6.97e–157 ± 8.06e–157 | |
| 20 | 10000 | 0.00e+00 ± 0.00e+00 | 1.09e–112 ± 3.18e–112 |
| Algorithm | s | t | Mean(Unrotated) | Mean(Rotated) |
|---|---|---|---|---|
| PSO | 10 | ― | 6.13e+00 ± 8.01e+00 | 7.32e+00 ± 2.52e+00 |
| 15 | ― | 4.62e+00 ± 6.11e+00 | 9.65e+00 ± 1.88e+00 | |
| 20 | ― | 2.86e+00 ± 4.72e+00 | 8.12e–07 ± 1.70e–07 | |
| CPSO-S | 10 | ― | 4.12e–14 ± 7.25e–14 | 1.22e+01 ± 1.72e+00 |
| 15 | ― | 6.18e–14 ± 6.79e–14 | 2.11e+01 ± 8.92e+00 | |
| 20 | ― | 3.72e–14 ± 8.24e–14 | 8.16e–01 ± 4.37e–01 | |
| CPSO-H | 10 | ― | 1.63e–14 ± 2.92e–15 | 5.23e+01 ± 8.70e+00 |
| 15 | ― | 7.22e–14 ± 5.12e–15 | 4.13e+00 ± 2.18e+00 | |
| 20 | ― | 1.71e–14 ± 4.66e–15 | 3.16e+01 ± 1.92e+00 | |
| CPSO- | 10 | ― | 8.12e–07 ± 1.70e–07 | 3.08e+01 ± 1.06e+00 |
| 15 | ― | 4.61e–05 ± 4.11e–05 | 9.21e+01 ± 7.43e+00 | |
| 20 | ― | 7.13e–05 ± 4.16e–05 | 5.25e+00 ± 5.26e+00 | |
| CPSO- | 10 | ― | 3.84e–11 ± 6.82e–11 | 8.12e+00 ± 4.04e+00 |
| 15 | ― | 1.15e–12 ± 2.63e–12 | 6.02e–04 ± 6.51e–04 | |
| 20 | ― | 1.72e–12 ± 1.42e–12 | 2.11e–11 ± 1.23e–11 | |
| EPS-PSO | 20 | 100 | 0.00e+00 ± 0.00e+00 | 2.44e+00 ± 1.84e+00 |
| 20 | 500 | 6.51e–19 ± 6.51e–19 | 2.26e–13 ± 1.64e–12 | |
| 20 | 1000 | 3.72e–03 ± 2.95e–03 | 1.93e–07 ± 1.53e–08 | |
| 20 | 5000 | 3.31e–02 ± 3.06e–02 | 1.17e+00 ± 1.94e+00 | |
| 20 | 10000 | 2.05e+00 ± 2.50e+00 | 1.85e+00 ± 1.66e+00 |
| Algorithm | s | t | Mean(Unrotated) | Mean(Rotated) |
|---|---|---|---|---|
| PSO | 10 | ― | 6.37e+01 ± 5.03e+00 | 6.28e+02 ± 5.38e+01 |
| 15 | ― | 7.48e+01 ± 3.06e+00 | 5.28e+02 ± 1.29e+01 | |
| 20 | ― | 2.88e+01 ± 1.41e+00 | 5.49e+02 ± 7.16e+01 | |
| CPSO-S | 10 | ― | 0.00e+00 ± 0.00e+00 | 4.21e+01 ± 8.46e+01 |
| 15 | ― | 0.00e+00 ± 0.00e+00 | 7.73e+01 ± 4.43e+01 | |
| 20 | ― | 0.00e+00 ± 0.00e+00 | 7.16e+01 ± 2.73e+01 | |
| CPSO-H | 10 | ― | 0.00e+00 ± 0.00e+00 | 7.08e+01 ± 6.83e+01 |
| 15 | ― | 0.00e+00 ± 0.00e+00 | 8.35e+01 ± 6.86e+01 | |
| 20 | ― | 0.00e+00 ± 0.00e+00 | 8.06e+01 ± 9.92e+01 | |
| CPSO- | 10 | ― | 3.29e–02 ± 7.73e–02 | 5.11e+01 ± 5.28e+01 |
| 15 | ― | 6.80e–02 ± 6.62e–02 | 4.16e+01 ± 4.34e+01 | |
| 20 | ― | 6.59e–01 ± 8.03e–01 | 5.14e+01 ± 6.15e+01 | |
| CPSO- | 10 | ― | 9.45e–01 ± 2.12e–01 | 9.32e+01 ± 3.72e+01 |
| 15 | ― | 4.37e–01 ± 2.15e–01 | 4.12e+01 ± 5.84e+01 | |
| 20 | ― | 6.08e–01 ± 5.34e–01 | 5.20e+01 ± 7.46e+01 | |
| EPS-PSO | 20 | 100 | 5.81e–13 ± 6.67e–13 | 1.29e–04 ± 1.21e–05 |
| 20 | 500 | 0.00e+00 ± 0.00e+00 | 3.30e–11 ± 8.32e–12 | |
| 20 | 1000 | 0.00e+00 ± 0.00e+00 | 6.17e–02 ± 1.34e–02 | |
| 20 | 5000 | 4.08e–03 ± 1.40e–02 | 1.05e–02 ± 8.28e–01 | |
| 20 | 10000 | 8.89e–02 ± 9.31e–02 | 7.57e–01 ± 5.41e–01 |
| Algorithm | s | t | Mean(Unrotated) | Mean(Rotated) |
|---|---|---|---|---|
| PSO | 10 | ― | 1.05e+01 ± 4.36e+02 | 5.18e+01 ± 2.18e+01 |
| 15 | ― | 7.42e+01 ± 8.78e+02 | 1.48e+01 ± 2.43e+01 | |
| 20 | ― | 6.12e+01 ± 6.40e+02 | 2.76e+01 ± 2.15e+01 | |
| CPSO-S | 10 | ― | 2.16e–02 ± 2.77e–02 | 5.25e–01 ± 9.60e–01 |
| 15 | ― | 5.12e–02 ± 6.05e–02 | 6.78e–01 ± 6.45e–01 | |
| 20 | ― | 9.43e–03 ± 7.13e–03 | 6.21e–01 ± 5.86e–01 | |
| CPSO-H | 10 | ― | 2.88e–02 ± 3.04e–02 | 5.10e–01 ± 3.44e–01 |
| 15 | ― | 2.18e–02 ± 4.28e–02 | 3.15e–01 ± 9.01e–01 | |
| 20 | ― | 2.74e–02 ± 1.86e–02 | 4.81e–01 ± 2.78e–01 | |
| CPSO- | 10 | ― | 4.19e–02 ± 6.72e–02 | 5.12e–01 ± 2.48e–01 |
| 15 | ― | 4.48e–02 ± 5.49e–02 | 7.14e–01 ± 1.46e–01 | |
| 20 | ― | 4.18e–02 ± 7.29e–02 | 1.06e–01 ± 2.11e–01 | |
| CPSO- | 10 | ― | 6.98e–02 ± 5.40e–02 | 1.40e–01 ± 1.62e–01 |
| 15 | ― | 7.16e–02 ± 1.13e–02 | 1.80e–01 ± 4.05e–01 | |
| 20 | ― | 5.42e–02 ± 5.14e–02 | 4.21e–01 ± 1.94e–01 | |
| EPS-PSO | 20 | 100 | 2.20e–05 ± 3.32e–05 | 3.62e–04 ± 7.40e–05 |
| 20 | 500 | 2.09e–08 ± 6.68e–08 | 7.28e–06 ± 1.01e–07 | |
| 20 | 1000 | 4.01e–09 ± 3.95e–09 | 5.51e–06 ± 1.95e–06 | |
| 20 | 5000 | 2.04e–09 ± 2.11e–09 | 8.11e–05 ± 9.04e–05 | |
| 20 | 10000 | 7.44e–03 ± 3.08e–03 | 5.02e–05 ± 7.09e–05 |
| Functions | PSO | CPSO-S | CPSO-H | CPSO-S6 | CPSO-H6 | |
|---|---|---|---|---|---|---|
| Rosenbrock | EPS-PSO Unrotated | ○ | ○ | ○ | ○ | ○ |
| EPS-PSO Rotated | ○ | ○ | ○ | ○ | ○ | |
| Quadratic | EPS-PSO Unrotated | ○ | ○ | ○ | ○ | ○ |
| EPS-PSO Rotated | ○ | ○ | ○ | ○ | ○ | |
| Ackley | EPS-PSO Unrotated | ○ | × | × | × | × |
| EPS-PSO Rotated | × | ○ | ○ | ○ | × | |
| Rastrigin | EPS-PSO Unrotated | ○ | × | × | ○ | ○ |
| EPS-PSO Rotated | ○ | ○ | ○ | ○ | ○ | |
| Griewank | EPS-PSO Unrotated | ○ | ○ | ○ | ○ | ○ |
| EPS-PSO Rotated | ○ | ○ | ○ | ○ | ○ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fan, S.-K.S.; Jen, C.-H. An Enhanced Partial Search to Particle Swarm Optimization for Unconstrained Optimization. Mathematics 2019, 7, 357. https://doi.org/10.3390/math7040357
Fan S-KS, Jen C-H. An Enhanced Partial Search to Particle Swarm Optimization for Unconstrained Optimization. Mathematics. 2019; 7(4):357. https://doi.org/10.3390/math7040357
Chicago/Turabian StyleFan, Shu-Kai S., and Chih-Hung Jen. 2019. "An Enhanced Partial Search to Particle Swarm Optimization for Unconstrained Optimization" Mathematics 7, no. 4: 357. https://doi.org/10.3390/math7040357
APA StyleFan, S.-K. S., & Jen, C.-H. (2019). An Enhanced Partial Search to Particle Swarm Optimization for Unconstrained Optimization. Mathematics, 7(4), 357. https://doi.org/10.3390/math7040357






