Abstract
Particle swarm optimization (PSO) is a population-based optimization technique that has been applied extensively to a wide range of engineering problems. This paper proposes a variation of the original PSO algorithm for unconstrained optimization, dubbed the enhanced partial search particle swarm optimizer (EPS-PSO), using the idea of cooperative multiple swarms in an attempt to improve the convergence and efficiency of the original PSO algorithm. The cooperative searching strategy is particularly devised to prevent the particles from being trapped into the local optimal solutions and tries to locate the global optimal solution efficiently. The effectiveness of the proposed algorithm is verified through the simulation study where the EPS-PSO algorithm is compared to a variety of exiting “cooperative” PSO algorithms in terms of noted benchmark functions.
1. Introduction
The development of evolutionary computation is motivated by natural evolution. In a population of individuals employed to encode potential solutions of the problem, the evolution is emulated pertaining to the rule of “survival of the fittest”, and a better solution is then expected for generation to generation, such as genetic algorithm [1]. With contrast to evolutionary computation, Eberhart and Kennedy [2] developed a new population-based optimization technique, termed particle swarm optimization (PSO). PSO is a stochastic optimization algorithm that operates on a population of a set of initial solutions to explore the search space in a continuous domain. Akin to ant colony optimization [3], the idea of PSO is inspired by the interesting concept of a social behavior, communications and interactions in bird flocking and fish schooling. It has been widely recognized in the literature that PSO has demonstrated consistently good performance in solving various real-valued optimization problems. Even so, the ordinary PSO still suffers a serious problem that it, sometimes, fails to efficiently explore the local neighborhood of the found solution and accurately anchor the optimum. Many previous studies showed that PSO has an innate global search ability, but local search ability can vary mostly from case to case. Shi and Eberhart [4] introduced a time decreasing inertia factor to balance between global and local search ability of the swarm. The hybridization of PSO has been a popular topic in recent days. For instance, the SAPSO [5] is an optimization algorithm combining the PSO with the SA algorithm (Simulated Annealing), where the PSO is used for the global search and SA for the local search. Cui, Zeng and Cai [6] presented the SPSO where the PSO was combined with the Tabu technique to enhance the local search capability of PSO. Zahara, Fan and Tsai [7] presented the PSO hybridized with the Nelder–Mead simplex search method (NM–PSO) to solve the objective of Gaussian curve fitting and the Otsu’s method in the field of image thresholding. The algorithmic development of NM-PSO was fully addressed in Fan, Liang and Zahara [8] and Fan and Zahara [9].
The previously reviewed algorithms have been shown quite effective to improve PSO’s local search ability by hybridization. Nonetheless, the PSO is still vulnerable to a risk of falling into a local optimum as the dimensionality of the search space dramatically increases. On this account, various modifications of PSO were developed, trying to make search diversified as to locate the global optimum of high-dimensional problems. Among, one of the most noted cooperative PSO algorithms is the CPSO addressed by van den Bergh and Engelbrecht [10]. The search is conducted by using multiple swarms to optimize different components of the solution vector cooperatively. In addition, the evolutionary operators such as selection, crossover and mutation have been used in the PSO to keep the best particle mobilized, and also to improve the ability to escape from local minima [11,12]. In order to maintain the diversity and to jump from local optima, relocating the particles can be a promising strategy when most of the particles are too close to each other [13]. In their modified PSO, the search space is partitioned into several lower dimensional subspace and multiple swarms are applied to perform a cooperative search. On the other hand, Rada-Vilela et al. [14] proposed the hybrid PSO algorithms that incorporate noise mitigation mechanisms. The performance of the algorithms was analyzed by means of a set of population statistics that measure different characteristics of the swarms throughout the search process. Taghiyeh and Xu [15] proposed the algorithm that works with a set of statistically global best positions including one or more positions with objective function values of statistical equivalence. That PSO algorithm is also integrated with adaptive resampling procedures in order to enhance the capability of coping with noisy objective functions. In this paper, we develop an enhanced PSO termed enhanced partial search particle swarm optimization (EPS-PSO) by using a multi-swarm strategy in attempt to improve the ordinary PSO search that may easily get trapped in a local optimum.
2. Particle Swarm Optimization
From a practical point of view, the PSO is easy to implement and has been shown to perform well on abundant industrial optimization problems. In this section, the original PSO is first introduced, and various up-to-date researches are also reviewed that focus on parameter analysis and modifications of PSO.
2.1. Traditional PSO Operation
In the ordinary PSO, particles are evolved by cooperation among the individuals themselves; hence it can be classified as a population-based technique, where the entire population is called swarm. Each particle represents a possible solution to the optimization problem, and these particles adjust its flying trajectory according to its own flying experience and other particles’ flying experience. In other words, each particle is treated as a point in a multi-dimensional space. In iteration, each particle moves in the direction of its own personal best solution visited so far, as well as in the direction of the global best solution discovered so far in the swarm. Pertaining to this kind of social interaction, if a particle discovers a promising new solution that is better than current one, then all the other particles will move toward it, by this way, exploring the region more thoroughly in the search domain. In the PSO, if s denotes the swarm (population) size, then each individual has the following attributes. The and respectively represent the current position and velocity of the i-th particle in the dimension. The previous best position of each particle is recorded and represented as , and as the global best position of all the particles in the swarm. By the previous definitions, the velocity and position update of each particle is performed according to:
where and denote the acceleration coefficients reflecting the weighting of stochastic acceleration terms that pull each particle toward and positions respectively, as well as and are two random numbers sampled from the range (0, 1). When updating the velocity of a particle using (1), different dimensions have different random numbers and . Some research works set the two values equal; by this way, this version of PSO has a limited search space due to the unique random numbers being used for all dimensions. The value of each component in every vector can be clamped to the range [, ] to reduce the likelihood of particles leaving the search domain. The value of is usually chosen to be with (Eberhart, Dobbins and Simpson [16]). Note that this does not restrict the values of to fall within the range [, ], but only limits “the maximum movement distance” of a particle during each iteration.
A variety of papers have worked on improving the original PSO’s performance in different ways, and one of the most well-known modification was the one proposed by Shi and Eberhart [4] that introduced a special parameter called the inertia weight into the original PSO as follows:
The choice of the inertia weight can be judiciously made along with a proper selection of the maximum movement distance to optimize the contribution of global and local exploration capabilities. Moreover, Shi and Eberhart [4] observed that a reasonable choice for should decrease with a large value of . As a general remark, they theorized that a better performance would be obtained if the inertia weight were chosen a time varying, linearly decreasing quantity, rather than being a constant value and supported their statement with a single case study. It was inferred that the PSO search should start with a high inertia weight for coarse global exploration and the inertia weight should linearly decrease to facilitate finer local explorations in later iterations. This should help the search route to approach the optimum of the optimization problem quickly.
2.2. Cooperative Multiple Swarms
Most population-based algorithms attempt to optimize a problem through a single population. In a single population, each individual as agents interact by communicating information to each other while solving a problem. The information exchanged among agents may be misleading if the entire population has been attracted toward the local optima, and should sometimes alter the behavior of the agent receiving it. Therefore, the evolutionary procedure can be as a cooperative learner. With this cooperative conception, applying multiple swarms to execute different search assignment and exchanging the information between swarms appears to be promising. In order to evolve more and more complex landscapes, the cooperative multi-swarm idea has been implemented in the context of genetic algorithms (Cooperative Coevolutionary Genetic Algorithms, CCGAs) by Potter and De Jong [17]. Instead of optimizing the entire solution space simultaneously, the variables were treated individually and optimized by their assigned subpopulations. In doing so, each subpopulation is to optimize an individual variable of the solution vector, then reducing to the multi-tasking of one-dimensional optimization problems. To maintain the feasibility, all the subpopulations need to cooperate each other by information exchange to generate a valid solution vector. The use of multiple interacting subpopulations has also been applied to the PSO, creating a family of CPSOs [10]. In the CPSO, the solution vector was first split into n parts, each part being optimized by a swarm with its m particles. It indicates that each swarm only needs to exert its search capability on n dimensions of the original problem, and individual current best solutions found by every swarm are shared to evolve a unique global best position.
3. Enhanced Partial Search Particle Swarm Optimization (EPS-PSO) Algorithm
In the standard PSO, there always exists a phenomenon that it might lead to a stagnant state if the global best position cannot be improved in several consecutive iterations. In van den Bergh [18], a premature convergence of the standard PSO algorithm has been addressed. To avoid this pitfall, a supplementary search direction may be well supplied as to help the swarm jump out of the local optimum. In Figure 1, an example illustrates a scenario of how the standard PSO should be improved for escaping from the local optimum. The figure displays a contour map of a two-dimensional problem having multiple local optima. The points G1 and G2 are local optima and the point G3 is the global optimum. If the current global best solution/position is very close to G1, then the swarm may be entirely contracted toward G1 and has difficulty to escape from the local region. If the point G2 that exhibits a better solution than the point G1 appears during the optimization steps, then information exchange between these two local regions must rejuvenate the swarm being stagnated. As such, a new search direction (or path) will be developed from G1 to G2. This type of local partial search, if regularly changed in time, will definitely increase the chance of anchoring the global optimum, like G3 in Figure 1.
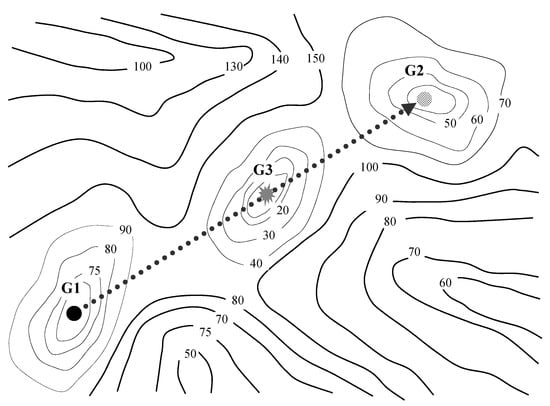
Figure 1.
Diagram illustrating how the EPS-PSO algorithm assists the standard PSO in escaping from local optima.
To achieve the foregoing cooperative strategy for unconstrained optimization, an additional population is required to take up the local search assignment. The additional population can be regarded as an enhanced local explorer in addition to the ordinary PSO search, hence the new algorithm to be proposed is termed the Enhanced Partial Search-Particle Swarm Optimization (EPS-PSO) algorithm. To start the EPS-PSO algorithm, first, the entire population is divided into two equal-sized sub-swarms, named the traditional swarm and the co-search swarm, respectively. Every t generations (or iterations), where t is called the re-initialization period, the EPS-PSO algorithm will re-initialize the co-search swarm. There is one exception if the current global best position of the co-search swarm outperforms that of the traditional swarm, then the re-initialization of the co-search swarm will be called off. In other words, the primary difference between the traditional swarm and the co-search swarm is the search topology assigned. The traditional swarm is mainly aimed at global exploration in the entire search space. By contrast, the co-search swarm is re-initialized periodically for local exploration. In the context of unconstrained optimization, the search space is restrained within the box constraints. Note also that the enhanced partial search is done within the given solution domain and the cooperation/communication occurs only as the co-search swarm exploits better outcomes than the traditional swarm. In a minimization case, let and be the global best positions of the co-search swarm and the traditional swarm, respectively. If the fitness improves by the co-search swarm, , then replaces to be the global best position of the traditional swarm (see the illustration in Figure 2b). Otherwise, both swarms proceed on their own without any communication (see the illustration in Figure 2a). The co-search swam provides a new search path to assists the particles of the traditional swarm to jump out of the local optimum, implying that the favorable search information is periodically supplied if appropriate.
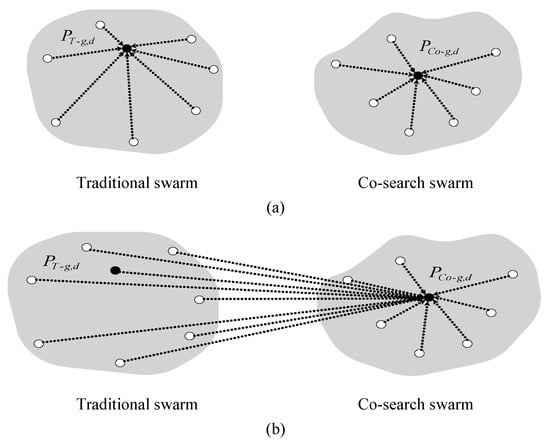
Figure 2.
Diagram illustrating the two swarms’ convergence situations: (a) If , (b) If .
For the clarity of presentation, the procedure of the EPS-PSO Algorithm 1 can be formalized as below:
| The Enhanced Partial Search Particle Swarm Optimization (EPS-PSO) Algorithm 1 |
| Define |
| : Each swarm’s population size |
| : Swarm ID number |
| : Re-initialization period |
| k: function evaluation index |
| For each particle in each swarm |
| Circumscribe the search space for the traditional and co-search swarms within the box constraints |
| Initialize position , particle’s personal best and velocity for both swarms |
| Perform the function evaluation for each particle and update k, |
| Endfor |
| Repeat: |
| For each swarm : |
| For each particle : |
| If |
| then |
| If |
| then |
| Endfor |
| Perform particle velocity and position updates via Equations (1–2) |
| Endfor |
| Perform the function evaluation for both swarms and update k |
| If the criterion of the re-initialization period for the co-search swarm is met |
| For each particle in the co-search swarm |
| Circumscribe the search space within the box constraints |
| Re-initialize position , particle’s personal best and velocity for the co-search swarm |
| Perform the function evaluation for each particle and update k |
| Endfor |
| If then |
| Until the maximum number k of function evaluations is satisfied |
4. Experiment Setup
To evaluate the performance of the EPS-PSO algorithm, a suite of benchmark functions with different difficulties are chosen. All the functions presented here have the objective value 0 in their global minima. The definitions of each test problem are tabulated in Table 1. Among the five benchmark functions, Rosenbrock and Quadric are unimodal functions while the others are multimodal (i.e., Ackley, Rastrigin and Griewank functions). However, Shang and Qiu [19] had verified that the n-dimensional () Rosenbrock function is not unimodal and has two minima, one with the optimal objective of zero and the other with the optimal objective of around 3.7~3.9. The performance of the EPS-PSO algorithm will be assessed by these five 30-dimensional bench mark functions , and then the comparison is made against the other two algorithms: the traditional PSO [2] and 4 different versions of CPSO [10]. The CPSO algorithms are briefly mentioned as follows:

Table 1.
The definition of the benchmark functions.
- CPSO-: A maximally “split” swarm where the search space vector is split into 30 parts.
- CPSO-: The search space vector for CPSO- is split into only six parts (of five components each).
- CPSO-: A hybrid swarm, consisting of a maximally split swarm, coupled with a plain swarm.
- CPSO-: A hybrid swarm, consisting of a CPSO- swarm, coupled with a plain swarm.
All the experiments were conducted using three different swarm sizes of 10, 15 and 20 except the EPS-PSO algorithm that used the population size of 20 (i.e., the sub-swarm size of 10 is used for the traditional swarm and the co-search swarm each). Every algorithm was halted after function evaluations. Regarding the replication and comparison of computational experiments in applied evolutionary computing, interested readers can refer to the work by Črepinšek et al. [20]. Note again that all the benchmark functions have the same problem dimension of 30. For all the PSO-based algorithms compared in the experimental study, the two random numbers, and in (1), were randomly generated from the range . The value of is clamped to the allowable range of , and . In all the implementations, the inertia weight parameter decreases with the number of iteration, akin to the scheme described in Shi and Eberhart [21] except the traditional PSO. That is, decreases linearly over iteration from 1 down to 0, and the traditional PSO using [4]. Moreover, to pose a more challenging optimization task, all the algorithms were further tested using the transformed benchmark functions using Salomon’s coordinate rotation [22]. Prior to each individual optimization, a new rotation was independently executed, and therefore no bias was introduced because of a specific rotation. In the co-search swarm, the size of limited search space is set to half the allowable range of each dimension.
Note that all the tested cooperative PSO variants and the proposed EPS-PSO use the same initialization procedure, i.e., the random generation within the box constraints. In the proposed EPS-PSO algorithm, two sub-swarms, traditional and co-search ones, are initialized by random generation. Since then, the co-search swarm is to be re-initialized every re-initialization period only if the co-search swarm is not able to locate a better global best solution than the traditional swarm. If the co-search swarm exploits better outcomes than the traditional swarm, then the re-initialization will not be executed. The proposed EPS-PSO algorithm will be compared to the other 5 PSO variants in terms of the unrotated and rotated versions of the five benchmark functions.
5. Computational Result and Discussion
In this section, the experimental results of five benchmark functions obtained by running 6 different versions of PSO (i.e., including the traditional PSO, 4 different versions of CPSO, and EPS-PSO) are presented. To conduct fair comparisons among algorithms, all experiments were run 50 times, and the computational results are exhibited in Table 2, Table 3, Table 4, Table 5 and Table 6. In the tables, the second column lists the entire population size for the PSOs. The third column lists how many iterations the co-search swarm would be re-initialized in a limited search space for the EPS-PSO algorithm. Five levels of the re-initialization period are examined, t = 100, 500, 1000, 5000, 10,000. As t = 10,000 is used, indicating two traditional swarms of 10 particles each without communication throughout the search process. The use of stands for 10 re-initializations and communications. The fourth and fifth columns list the mean function error with 95% confidence interval after function evaluations for the unrotated and rotated versions of the benchmark functions. Note that a “new” rotation is performed prior to every individual optimization, so each rotated function has a different functional form but the same global minimum. Thus, the minimum objective value is still zero.

Table 2.
Computational results of Rosenbrock obtained by using 6 PSO-based algorithms after function evaluations, averaged over 50 independent runs.

Table 3.
Computational results of Quadric obtained by using 6 PSO-based algorithms after function evaluations, averaged over 50 independent runs.

Table 4.
Computational results of Ackley obtained by using 6 PSO-based algorithms after function evaluations, averaged over 50 independent runs.

Table 5.
Computational results of Rastrigin obtained by using 6 PSO-based algorithms after function evaluations, averaged over 50 independent runs.

Table 6.
Computational results of Griewank obtained by using 6 PSO-based algorithms after function evaluations, averaged over 50 independent runs.
In evolutionary computation, the Rosenbrock function is frequently chosen to evaluate the performance of optimization algorithms due to its highly nonlinear and non-convex properties. The global minimum hides within an elongated valley, as known as “Banana” function. To reach the valley is trivial but to locate accurately the global minimum is of primary importance. In Shang and Qiu [19], the function has been shown to own multiple local minima as the problem size exceeds 4. Table 2 shows that the Rosenbrock function in its unrotated form can be easily solved by the EPS-PSO algorithm as the re-initialization period is . The other 5 algorithms cannot compete with the EPS-PSO algorithm. However, when the search space is rotated, the quality of solutions generated by the EPS-PSO algorithm has deteriorated quickly but the other 5 algorithms seem invariant to the coordinate rotation. Even so, the EPS-PSO algorithm still takes the lead. Figure 3 shows the best convergence result of the algorithms among 50 independent runs in terms of the logarithm of function error over iteration. For the un-rotated case, the EPS-PSO algorithm has achieved the global optimum after function evaluations. For the rotated case, the EPS-PSO algorithm dominates the other algorithms after function evaluations. Note that the CPSO result shown in Figure 3 corresponds to the best convergence result among 4 versions of the CPSO algorithms over 50 independent runs. For further details about the family of CPSOs, interested readers can refer to van den Bergh and Engelbrecht [10].
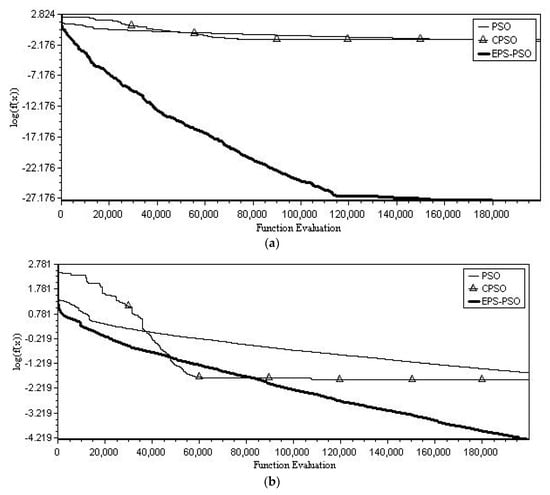
Figure 3.
The best convergence results versus function evaluation among 50 independent runs for Rosenbrock (): (a) unrotated case, (b) rotated case.
The computational results of the Quadric function solved by the 6 algorithms are tabulated in Table 3. All the algorithms perform well for the unrotated case; the EPS-PSO algorithm converges perfectly to the optimal point without any function error. Although the Quadric function is convex and unimodal, the coordinate rotation really makes it difficult to solve. The EPS-PSO algorithm is only slightly influenced by the coordinate rotation and still yields competitive performance. The other 5 algorithms cannot provide satisfactory performance. The best convergence results among 50 independent runs are displayed in Figure 4. For the unrotated case, the EPS-PSO algorithm converges the way faster than the other algorithms. In spite of the coordinate rotation as exhibited in Figure 4b, the EPS-PSO algorithm is still able to continuously improve the function error as iterations elapsed. Surprisingly, the traditional PSO and CPSO algorithms fail to solve the rotated Quadric function and the improvement in the function error becomes stagnated after function evaluations.
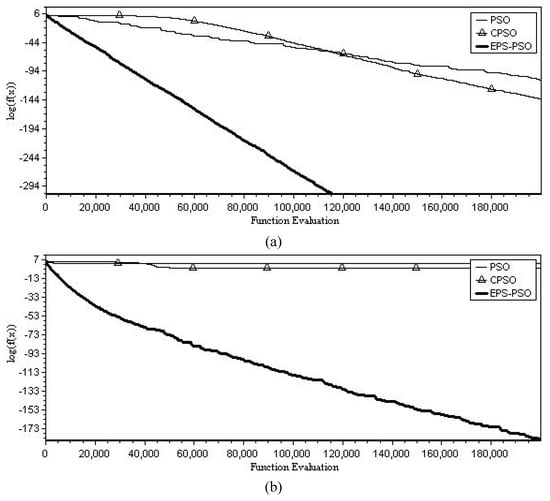
Figure 4.
The best convergence results versus function evaluation among 50 independent runs for Quadric (): (a) unrotated case, (b) rotated case.
The Ackley’s Function is a multimodal function with many local minima positioned on a regular grid. The computational results are shown in Table 4. For the un-rotated case, the traditional PSO algorithm cannot solve the problem successfully; the 4 CPSO algorithms perform quite well except the algorithm. The performance of the EPS-PSO algorithm deteriorates quickly as the re-initialization period increases. The global optimum is attained as . The explanation of how the EPS-PSO algorithm works using is that re-initializing the co-search swarm more often definitely helps the search jump out of the local optima. For the rotated case, all the 6 algorithms are seriously affected by the coordinate rotation except for the algorithm with and the EPS-PSO algorithm with . As before, the performance of the EPS-PSO algorithm becomes worse as increases. The best convergence results are plotted in Figure 5. For the un-rotated case, the EPS-PSO algorithm converges to the global optimum after function evaluations. For the rotated case, the traditional PSO algorithm is trapped in a local solution, as can be seen from Figure 5b; the CPSO and EPS-PSO algorithms perform equally well.
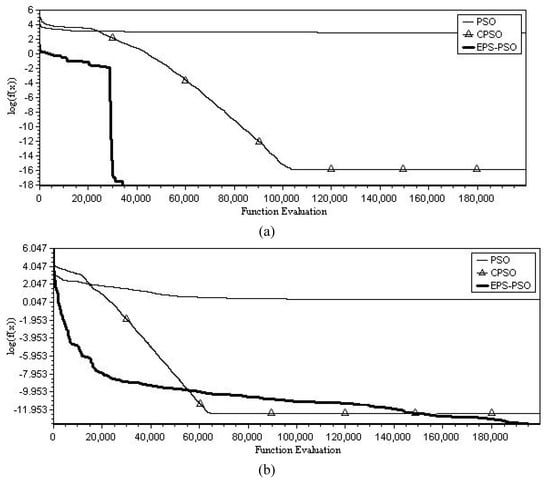
Figure 5.
The best convergence results versus function evaluation among 50 independent runs for Ackley (): (a) unrotated case, (b) rotated case.
The Rastrigin function is a typical nonlinear multimodal function, which contains only one global optimum with a large number of local minima, making the problem more difficult to solve. The computational results are listed in Table 5. For the un-rotated case, only the algorithm, the algorithm and the EPS-PSO algorithm with can locate the global optimum. Once the search space is rotated, only the EPS-PSO algorithm with can produce satisfactory performance. The best convergence plots are shown in Figure 6.
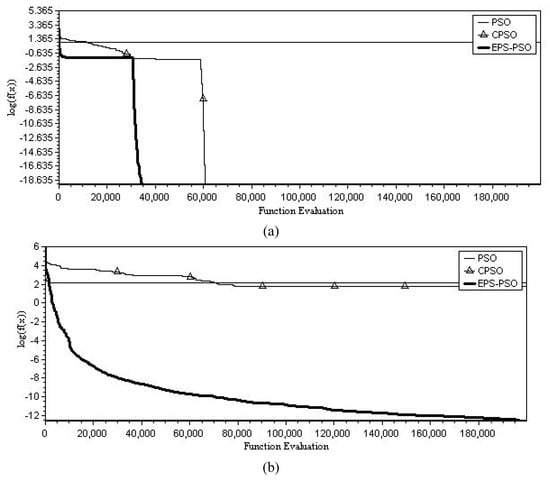
Figure 6.
The best convergence results versus function evaluation among 50 independent runs for Rastrigin (): (a) unrotated case, (b) rotated case.
Table 6 shows that the EPS-PSO algorithm performs better than the other PSO algorithms in all experiments on the un-rotated Griewank function. For the rotated case, the EPS-PSO algorithm still performs best among the studied algorithms. The best convergence performance is plotted in Figure 7. It can clearly be seen from the figure that the traditional PSO and CPSO algorithms have almost no improvement in the function error after function evaluations due to the multimodal structure. The EPS-PSO algorithm converges really fast from the outset, but the convergence slows down after function evaluations.
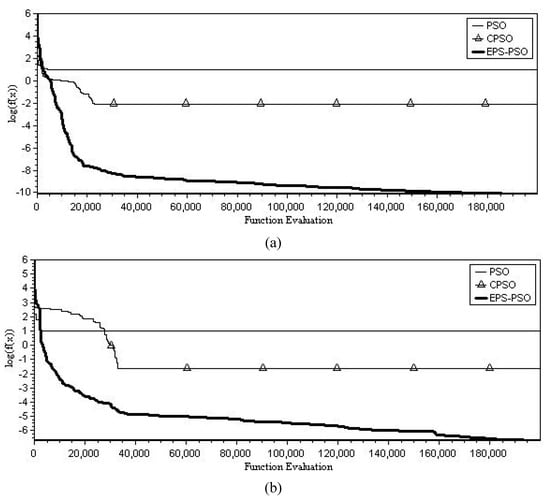
Figure 7.
The best convergence results versus function evaluation among 50 independent runs for Griewank (): (a) unrotated case, (b) rotated case.
In Table 7, the performances between the proposed EPS-PSO and different PSO algorithms are compared for verifying the effectiveness of EPS-PSO. In the table, the t-test was used to test whether the proposed EPS-PSO algorithm can outperform significantly the other algorithms in the minimization case. In terms of the two-sample t-test, the null and alternative hypotheses on the difference of the objective functions achieved are constructed to be and , respectively. The p-value of the test statistic less than 0.05 indicates that the proposed EPS-PSO algorithm generates a significantly smaller objective function than the compared PSO variant, which is marked “○”. Conversely, the p-value greater than 0.05 indicates that the EPS-PSO algorithm does not return a significantly smaller objective function than the compared PSO variant, which is marked as “×”. Overall, the EPS-PSO algorithm exhibits a significantly better performance than the other five algorithms except the functions Ackley and Rastrigin in the unrotated case. For the rotated case, the EPS-PSO algorithm outperforms overwhelmingly the other 5 PSO variants.

Table 7.
The performance comparisons between the proposed EPS-PSO algorithm and five different PSO variants over five benchmark functions.
As evidenced by the foregoing computational results, the enhanced partial search (EPS) mechanism has proved a valuable investment that helps to prevent the particles from being trapped in the local optima more likely than purely using the traditional PSO search. The re-initialization period is designed to control the frequency of how the co-search swarm is reinitialized. The five levels of are tested for the five unrotated and rotated benchmark functions, and the EPS-PSO algorithm using the level of 500 iterations produces the most reliable performance. To summarize, the better results obtained by the proposed EPS-PSO algorithm are attributed largely to (i) the topology of two sub-swarms between which the communication is carried out periodically and (ii) the re-initialization of the co-search swarm that is augmented to diversify local exploitation.
6. Conclusions and Directions of Future Research
This paper presents a cooperative multi-swarm structure in order to enhance the searching ability of the traditional PSO algorithm. The new search mechanism is called the enhanced partial search (EPS), making the new algorithm dubbed EPS-PSO. The EPS is a rerandomization strategy that works on an auxiliary swarm, termed the co-search swarm. The intension is to mobilize the particles and then make the swarm have more chances to explore different search areas. Moreover, the EPS mechanism has been implemented to allow the co-search swarm to share information with the traditional swarm during the evaluation process. Five benchmark functions in the unrotated and rotated versions are used as the test bed to compare the EPS-PSO algorithm to the traditional PSO and 4 different cooperative PSO algorithms. Five levels of the re-initialization period are examined, . The EPS-PSO algorithm performs best when the re-initialization period is set to 500 iterations. The comparison results show that the proposed algorithm improves upon the traditional PSO algorithm and outperforms the other 4 cooperative PSO algorithms. In other words, the EPS is shown to be a simple but effective way that helps to prevent the swarm from becoming stuck in the local optima.
Built upon the current research, there are still several PSO-related research topics that deserve further scrutiny. The first potential investigation is to extend the propose EPS-PSO algorithm to constrained optimization. In this case, a mechanism to handle the constraint violation should be invented and comprehensively tested. A further study can be done by comparing the proposed EPS-PSO algorithm to some PSO variants equipped with the swarm collapse detection mechanism. Furthermore, the co-search swarm strategy may also be useful for PSO dealing with noisy function evaluations.
Author Contributions
This is a joint work of the two authors; nevertheless, each author was especially in charge of his expert and capability: S.K.S.F. for conceptualization, methodology, investigation and formal analysis, S.K.S.F. and C.H.J. for validation, original draft preparation and writing.
Funding
This research was partially funded by Ministry of Science and Technology, grant numbers MOST 105-2221-E-027-052-MY3 and MOST 105-2221-E-027-071-MY3.
Acknowledgments
The authors are deeply grateful to J.M. Chang’s great efforts for conducting an earlier experimental study.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Goldberg, D.E. Genetic Algorithms in Search, Optimization and Machine Learning; Addison-Wesley Publishing Inc.: Reading, MA, USA, 1989. [Google Scholar]
- Kennedy, J.; Eberhart, R.C. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948. [Google Scholar]
- Dorigo, M.; Caro, G.D. Ant colony optimization: A new meta-heuristic. In Proceedings of the Congress on Evolutionary Computation, Washington, DC, USA, 6–9 July 1999; Volume 2, pp. 1470–1477. [Google Scholar]
- Shi, Y.; Eberhart, R.C. A modified particle swarm optimizer. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Wang, X.-H.; Jun-Jun, L. Hybrid particle swarm optimization with simulated annealing. In Proceedings of the Third International Conference on Machine Learning and Cybernetics, Shanghai, China, 26–29 August 2004; Volume 4, pp. 2402–2405. [Google Scholar]
- Cui, Z.H.; Zeng, J.C.; Cai, X.J. A new stochastic particle swarm optimizer. In Proceedings of the 2004 Congress on Evolutionary Computation, Piscataway, NJ, USA, 19–23 June 2004; pp. 316–319. [Google Scholar]
- Zahara, E.; Fan, S.K.-S.; Tsai, D.M. Optimal multi-thresholding using a hybrid optimization approach. Patten Recognit. Lett. 2004, 26, 1082–1095. [Google Scholar] [CrossRef]
- Fan, S.-K.S.; Liang, Y.C.; Zahara, E. A Hybrid Simplex Search and Particle Swarm Optimization for the Global Optimization of Multimodal Functions. Eng. Optim. 2004, 36, 401–418. [Google Scholar] [CrossRef]
- Fan, S.-K.S.; Zahara, E. A hybrid simplex search and particle swarm optimization for unconstrained optimization. Eur. J. Oper. Res. 2007, 181, 527–548. [Google Scholar] [CrossRef]
- Van den Bergh, F.; Engelbrecht, A.P. A Cooperative Approach to Particle Swarm Optimization. IEEE Trans. Evol. Comput. 2004, 8, 225–239. [Google Scholar] [CrossRef]
- Angeline, P.J. Using selection to improve particle swarm optimization. In Proceedings of the IEEE International Conference on Evolutionary Computation, Anchorage, AL, USA, 4–9 May 1998; pp. 84–89. [Google Scholar]
- Lovbjerg, M.; Rasmussen, T.K.; Krink, T. Hybrid particle swarm optimizer with breeding and subpopulations. In Proceedings of the Third Genetic and Evolutionary Computation Congress, San Diego, CA, USA, 7–11 July 2001; pp. 469–476. [Google Scholar]
- Lovbjerg, M.; Krink, T. Extending particle swarm optimizers with self-organized criticality. In Proceedings of the Fourth Congress on Evolutionary Conference, Honolulu, HI, USA, 12–17 May 2002; Volume 2, pp. 1588–1593. [Google Scholar]
- Rada-Vilela, J.; Johnston, M.; Zhang, M. Population statistics for particle swarm optimization: Resampling methods in noisy optimization problems. Swarm Evol. Comput. 2014, 17, 37–59. [Google Scholar] [CrossRef]
- Taghiyeh, S.; Xu, J. A new particle swarm optimization algorithm for noisy optimization problems. Swarm Intell. 2016, 10, 161–192. [Google Scholar] [CrossRef]
- Eberhart, R.C.; Dobbins, R.C.; Simpson, P. Computational Intelligence PC Tools; Academic Press Professional: Boston, MA, USA, 1996. [Google Scholar]
- Potter, M.A.; de Jong, K.A. A Cooperative Coevolutionary Approach to Function Optimization the Third Parallel Problem Solving from Nature; Springer: Berlin, Germany, 1994; pp. 249–257. [Google Scholar]
- Van den Bergh, F.; Engelbrecht, A.P. Effects of swarm size on cooperative particle swarm optimizers. In Proceedings of the Genetic and Evolutionary Computation Conference, San Francisco, CA, USA, 7–11 July 2001; pp. 892–899. [Google Scholar]
- Shang, Y.W.; Qiu, Y.H. A note on the extended Rosenbrock function. Evol. Comput. 2006, 14, 119–126. [Google Scholar] [CrossRef] [PubMed]
- Črepinšek, M.; Liu, S.H.; Mernik, M. Replication and comparison of computational experiments in applied evolutionary computing: Common pitfalls and guidelines to avoid them. Appl. Soft Comput. 2014, 19, 161–170. [Google Scholar] [CrossRef]
- Shi, Y.; Eberhart, R.C. Empirical study of particle swarm optimization. In Proceedings of the IEEE Congress on Evolutionary Computation, Piscataway, NJ, USA, 6–9 July 1999; pp. 1945–1950. [Google Scholar]
- Salomon, R. Reevaluating genetic algorithm performance under coordinate rotation of benchmark functions. BioSystems 1996, 39, 263–278. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).