Distance Degree Index of Some Derived Graphs
Abstract
:1. Introduction
1.1. Some Derived Graphs
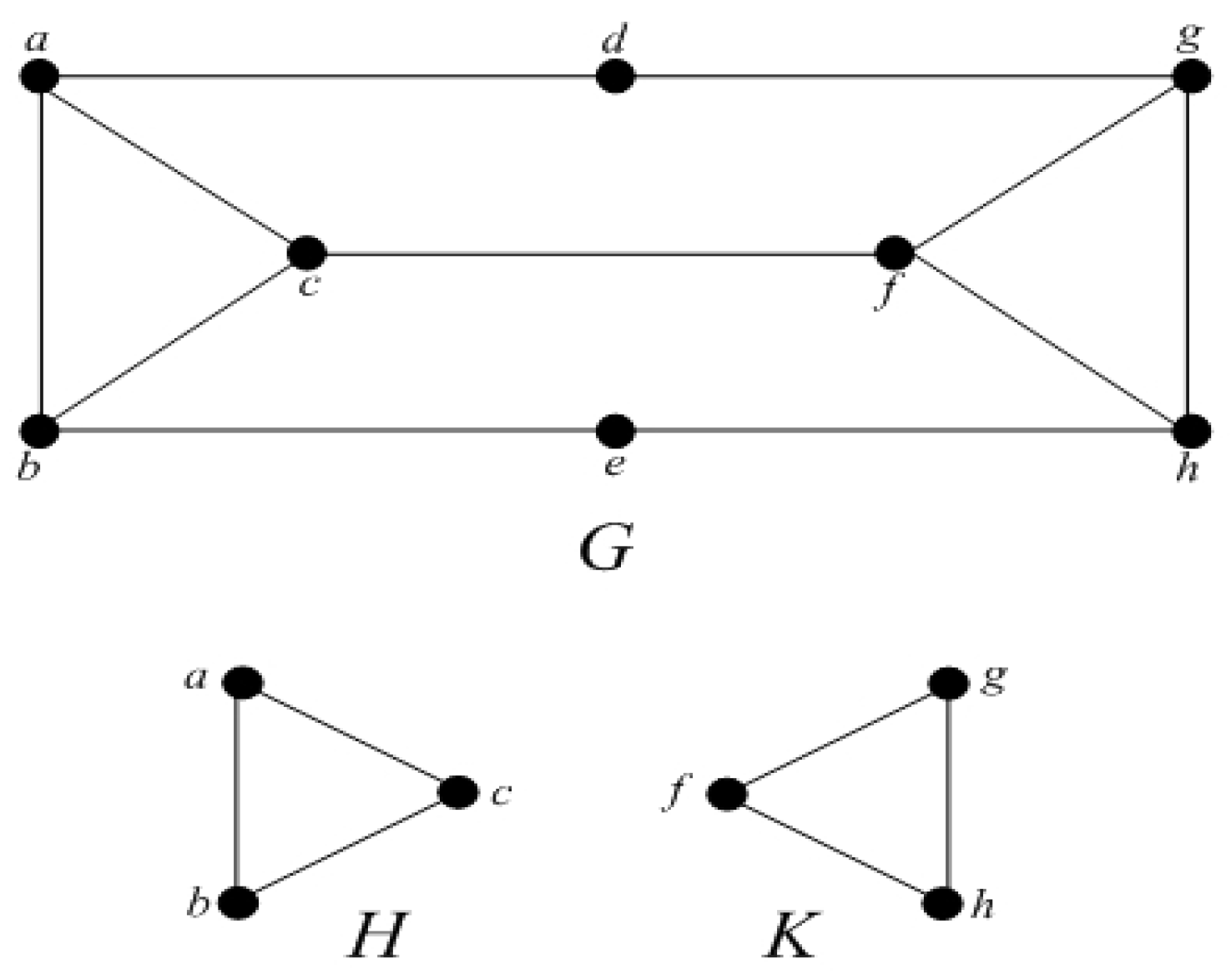
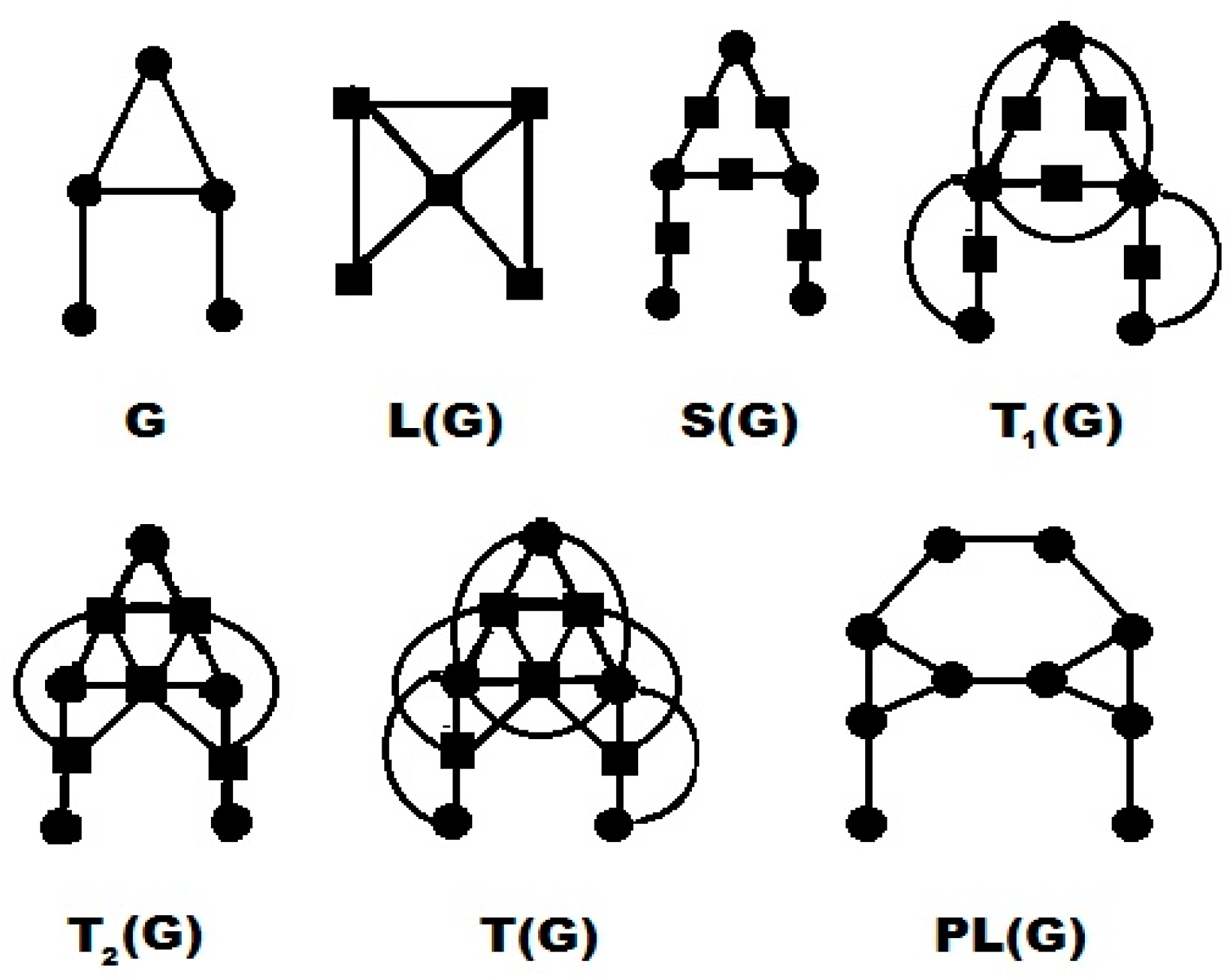
- Line Graph: Line graph of a graph is denoted by such that and there is an edge between two vertices of if and only if corresponding edges are incident in . Clearly, and by hand shaking-lemma one can easily see that .
- Subdivision Graph: Subdivision graph of a graph is obtained by inserting a vertex of degree in each edge. Therefore, and .
- Vertex-Semitotal Graph: Vertex-Semitotal graph of a graph is denoted as and is obtained by adding a new vertex to each edge of and then joining a new vertex to the end vertices of the corresponding edge. Thus, and
- Edge-Semitotal Graph: The edge-semitotal graph of a graph is denoted as and is obtained by inserting a new vertex ateach edge of , joining those new vertices by edges whose corresponding edges are incident in . We have and
- Total Graph: The union of edge-semitotal graph and vertex-semitotal graph is called total graph of a graph . It is denoted by . Also,
- Paraline Graph: The paraline graph is the line graph of subdivision graph denoted by . Also and
1.2. Index of Some Derived Graphs
- -edge, an edge between two -type vertices,
- -edge, an edge between two -type vertices,
- -edge, an edge between an -type vertex and a -type vertex.
- In the first term, for any vertex there are a total of pairs of vertices in of degrees and having a distance of 1 between them in the corresponding .
- Before discussing the second term, it is important to see that there is exactly one shortest path in between any two different vertices, because has no cycle of even length. Consequently, there is exactly one shortest path between their corresponding complete graphs in .
- Case-1:
- There is exactly one pair of terminal vertices in and , having distance between them.
- Case-2:
- There are pairs of non-terminal vertices in and , having distance between them.
- Case-3:
- There are pairs of vertices having a non-terminal vertex in and a terminal vertex in , and having distance between them. Similarly, there are pairs of vertices having a terminal vertex in and a non-terminal vertex in , and having distance between them. So we have a total of such pairs.
2. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Tadic, B.; Ziukovic, J. The graph theory frame work for odeling nano scale systems. Nanoscale Syst. MMTA 2013, 2, 30–48. [Google Scholar]
- Balaban, A.T. Applications of graph theory in chemistry. J. Chem. Inf. Comput. Sci 1985, 25, 334–343. [Google Scholar] [CrossRef]
- Abdullahi, S. Anapplication of graph theory to the electrical circuit using matrix method. J. Math. 2014, 164–166. [Google Scholar] [CrossRef]
- Shirinivas, S.G.; Vetrivel, S.; Elango, N.M. Applications of graph theory in computer science an overview. J. Eng. Technol. 2010, 2, 4610–4621. [Google Scholar]
- Gold, V.; Loening, K.L.; McNaught, A.D.; Shemi, P. Compendium of Chemical Terminology; Blackwell Science Oxford: Oxford, UK, 1997; Volume 1669. [Google Scholar]
- Bonchev, D.; Rouvray, D.H. Chemical Graph Theory Introductions and Fundamentals; CRC Press: Boca Raton, FL, USA, 1991; Volume 1. [Google Scholar]
- Dobrynin, A.A.; Kochetova, A.A. Degree distance of a graph: A degree analogue of the Wiener index. J. Chem. Inf. Comput. Sci. 1994, 34, 1082–1086. [Google Scholar] [CrossRef]
- Gutman, I.; Trinajstić, N. Graph theory and molecular orbitals III. Total Electron Energy Altern. Hydrocarb. Chem. Phys. Lett. 1972, 17, 535–538. [Google Scholar]
- Balaban, A.T. From Chemical Topology to Three-Dimensional Geometry; Plenum Press: New York, NY, USA, 1997. [Google Scholar]
- Devillers, J.; Balaban, A.T. (Eds.) Topological Indices and Related Descriptors in QSAR and QSPR; Gordon and Breach: Amsterdam, The Netherlands, 1999. [Google Scholar]
- Todeschini, R.; Consonni, V. Handbook of Molecular Descriptors; Wiley–VCH: Weinheim, Germany, 2000. [Google Scholar]
- Furtula, B.; Gutman, I. A forgotten topological index. J. Math. Chem. 2015, 53, 1184–1190. [Google Scholar] [CrossRef]
- De, N.; Nayeem, S.M.A.; Pal, A. The F-coindex of some graph operations. Springer Plus 2016, 5, 221. [Google Scholar] [CrossRef] [PubMed]
- Došlic, T. Vertex-weighted Wiener polynomials for composite graphs. Ars Math. Contemp. 2008, 1, 66–80. [Google Scholar] [CrossRef]
- Wiener, H. Structural determination of Paraffin boiling points. J. Am. Chem. Soc. 1947, 69, 17–20. [Google Scholar] [CrossRef]
- Ashrafi, A.R.; Yousafi, S. An exact expression for the Wiener index of a polyhex nanotorus. MATCH Commun. Math. Comput. Chem. 2006, 56, 169–178. [Google Scholar]
- Ashrafi, A.R.; Yousafi, S. A new algorithm for computing distance matrix and Wiener index of zig-zag polyhex nano-tubes, nano-scale. Res. Lett. 2007, 2, 202–206. [Google Scholar]
- Chepoi, V.; Kalvzar, S. The Wiener index and the Szeged index of benzoid systems in linear time. J. Chem. Inf. Comput. Sci. 1997, 37, 752–755. [Google Scholar] [CrossRef]
- Cai, X.; Zhou, B. Reverse Wiener index of connected graphs, MATCH Commun. Math. Comput. Chem. 2008, 60, 95–105. [Google Scholar]
- Dobrynin, A.A.; Entringer, R.; Gutman, I. Wiener index of trees, Theory and applications. Acta App. Math. 2011, 66, 211–249. [Google Scholar] [CrossRef]
- Dobrynin, A.A.; Gutman, I.; Klavzar, S.; Zigerl, P. Wiener index of hexagonal systems. Accta. Appl. Math. 2001, 72, 247–294. [Google Scholar] [CrossRef]
- Sandberg, T.O.; Weinberger, C.; Smått, J.H. Molecular dynamics on wood-derived lignans analyzed by intermolecular network theory. Molecules 2018, 23, 1990. [Google Scholar] [CrossRef] [PubMed]
- Iranmanesh, A.; Gutman, I.; Khormali, O.; Mahmiani, A. The edge versions of Wiener index. Match Commun. Math. Comput. Chem. 2009, 61, 663–672. [Google Scholar]
- Ali, P.; Mukwembi, S.; Munyria, S. Degree distance and vertex connectivity. Disc. Appl. Math. 2013, 161, 2802–2811. [Google Scholar] [CrossRef]
- Du, Z.; Zhou, B. Degree distance of a graph. Filomat 2010, 24, 95–120. [Google Scholar] [CrossRef]
- Ilic, A.; Stevanovic, D.; Feng, L.; Yu, G.; Danklemann, P. Degree distance of unicyclic graphs. Discr. Appl. Math. 2011, 159, 779–788. [Google Scholar] [CrossRef]
- Tomescu, I. Unicyclic and bicyclic graphs having minmum degree distance. Discr. Appl. Math. 2008, 156, 125–130. [Google Scholar] [CrossRef]
- Tomescu, I. Properties of connected graphs having minimum degree distance. Discr. Appl. Math. 2008, 309, 2745–2748. [Google Scholar] [CrossRef]
- Tomsecu, I. Ordering connected graphs having small degree distance. Discr. Appl. Math. 2010, 158, 1714–1717. [Google Scholar] [CrossRef]
- Bondy, J.A.; Murty, U.S.R. Graph Theory; Springer: Berlin, Germany, 2008. [Google Scholar]
- Gutman, I.; Furtula, B.; Kovijanic, Z.; Vukicevic; Popivoda, G. On Zagreb indices and coindices. Match Commun. Math. Comput. Chem. 2015, 74, 5–16. [Google Scholar]
- Basavanagoud, B.; Gutman, I.; Gali, C.S. On second Zagreb index and coindex of some derived graphs. Kragujev. J. Sci. 2015, 37, 113–121. [Google Scholar]
- Basavanagoud, B.; Patil, S. Multiplicative Zagreb indices and coindices of some derived graphs. Opusc. Math. 2016, 36, 287–299. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Liu, J.-B.; Bilal, A.; Ahmad, U.; Siddiqui, H.M.A.; Ali, B.; Farahani, M.R. Distance Degree Index of Some Derived Graphs. Mathematics 2019, 7, 283. https://doi.org/10.3390/math7030283
Xu J, Liu J-B, Bilal A, Ahmad U, Siddiqui HMA, Ali B, Farahani MR. Distance Degree Index of Some Derived Graphs. Mathematics. 2019; 7(3):283. https://doi.org/10.3390/math7030283
Chicago/Turabian StyleXu, Jianzhong, Jia-Bao Liu, Ahsan Bilal, Uzma Ahmad, Hafiz Muhammad Afzal Siddiqui, Bahadur Ali, and Muhammad Reza Farahani. 2019. "Distance Degree Index of Some Derived Graphs" Mathematics 7, no. 3: 283. https://doi.org/10.3390/math7030283
APA StyleXu, J., Liu, J.-B., Bilal, A., Ahmad, U., Siddiqui, H. M. A., Ali, B., & Farahani, M. R. (2019). Distance Degree Index of Some Derived Graphs. Mathematics, 7(3), 283. https://doi.org/10.3390/math7030283





