Line Integral Solution of Hamiltonian PDEs
Abstract
:1. Introduction
- (a)
- the search for methods suited for specific relevant classes of problems;
- (b)
- their efficient implementation on a computer;
- (c)
- the extension of existing methods to cope with wider classes of problems.
- in Section 2 we recall the main facts about HBVMs, also sketching their efficient blended implementation;
- in Section 3 we describe the space discretization of the semilinear wave equation, and the efficient solution of the resulting Hamiltonian ODE problem via HBVMs. For this equation we shall provide full details, whereas the whole procedure will be only sketched for the subsequent equations;
- in Section 4 we see that the same approach can be used for the nonlinear Schrödinger equation;
- in Section 5 we consider, instead, the Korteweg–de Vries equation;
- Section 6 contains some numerical tests, aimed at showing the effectiveness of the proposed approach;
- at last, a few conclusions are made in Section 7.
2. Hamiltonian Boundary Value Methods (HBVMs)
- an exact conservation of energy, when H is a polynomial;
- a practical conservation of energy, otherwise. In fact, in such a case, it is enough that the energy error falls within the round-off error level.
2.1. Runge-Kutta form of HBVM
2.2. Special Second-Order Problems
2.3. Blended Iteration
2.4. Blended Iteration for Semilinear Problems
2.5. HBVMs as Spectral Methods in Time
- on the other hand, SHBVMs will allow the use of relatively large time-steps.
3. The Semilinear Wave Equation
3.1. Discretization
3.2. The Nonlinear Iteration
3.3. Extension to Higher Space Dimensions
4. The Nonlinear Schrödinger Equation
The Nonlinear Iteration
5. The Korteweg-de Vries (KdV) Equation
The Nonlinear Iteration
6. Numerical Tests
- the symplectic s-stage Gauss methods, ;
- the energy-conserving HBVM methods, , and k suitably chosen;
- the SHBVM method.
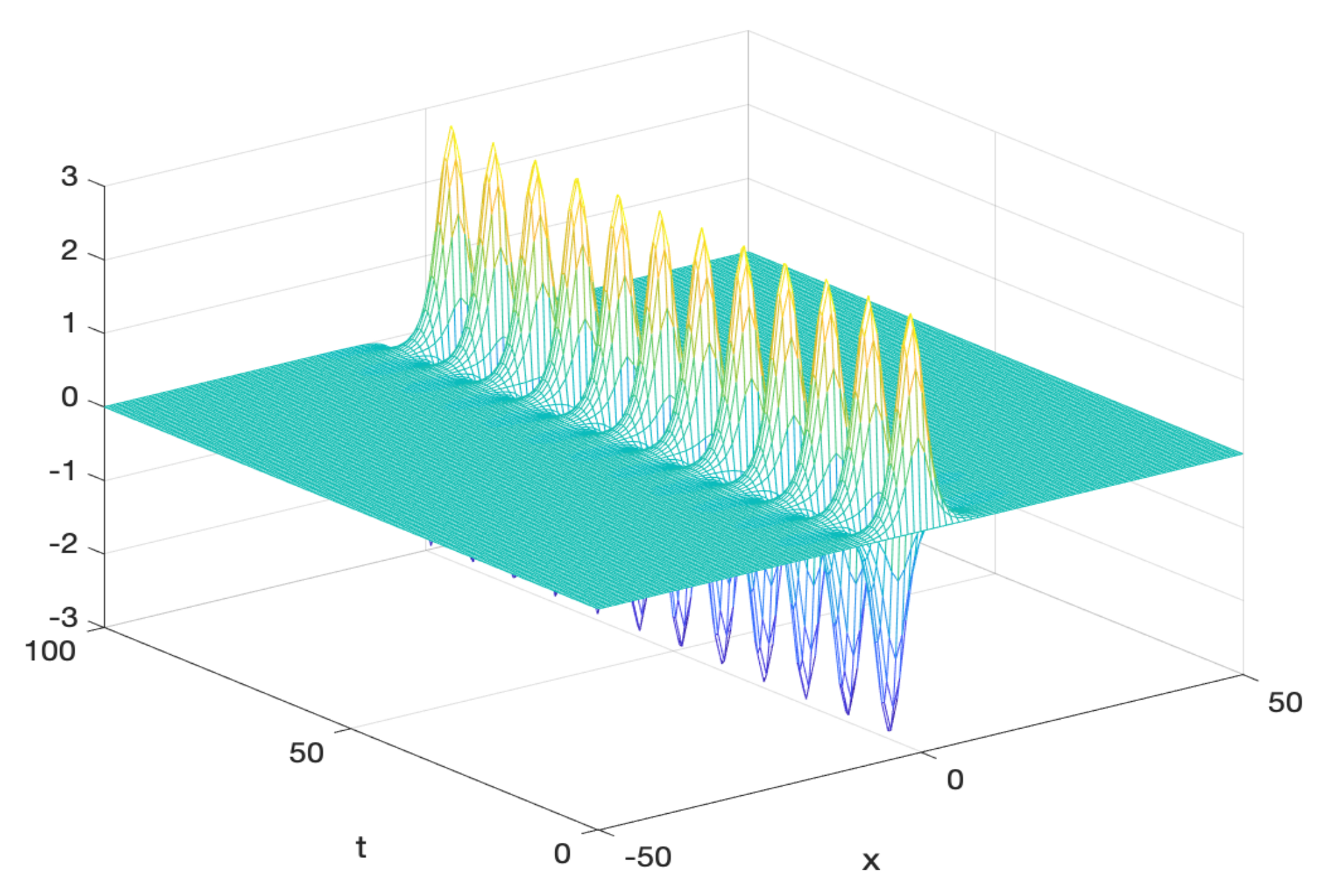
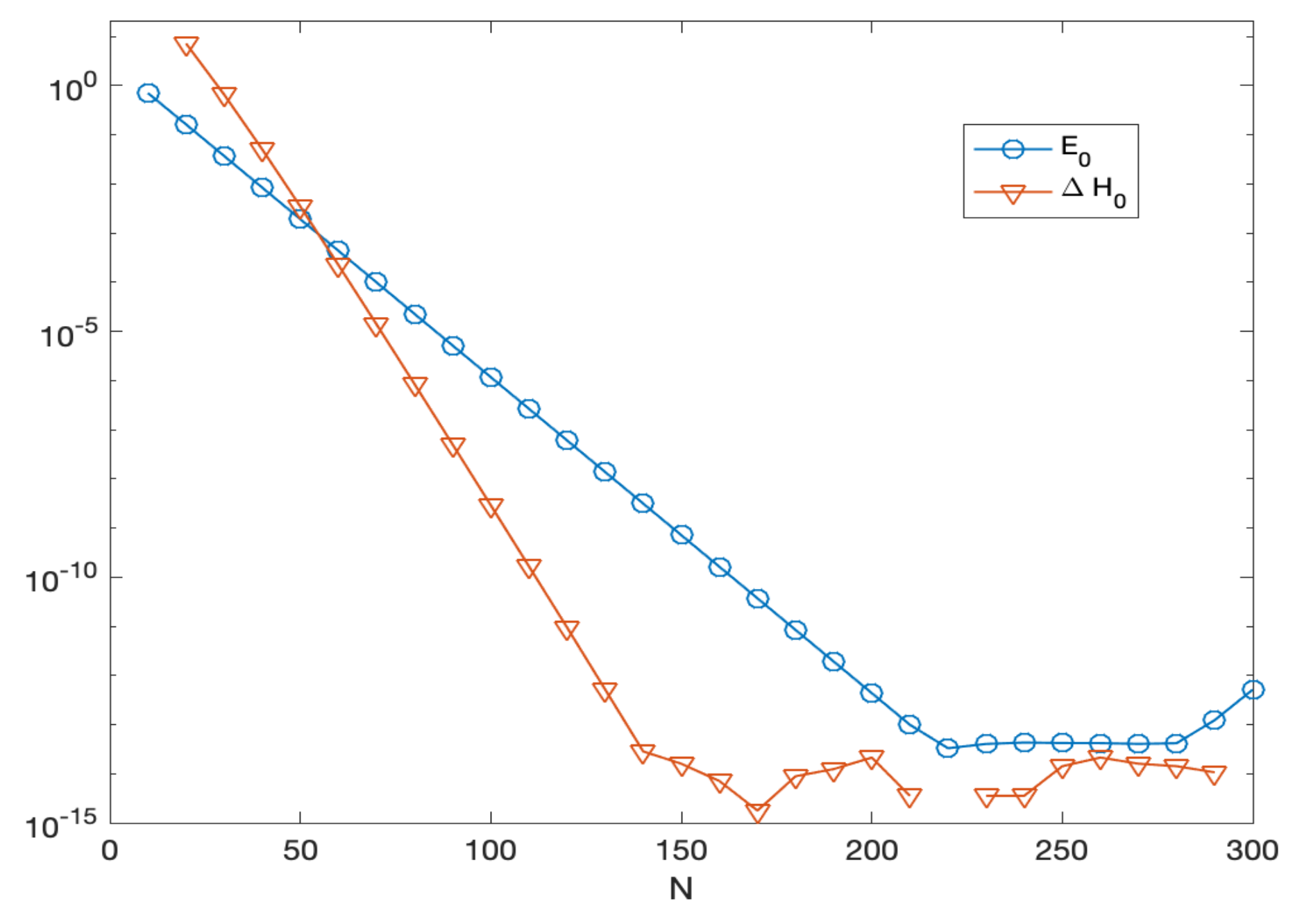
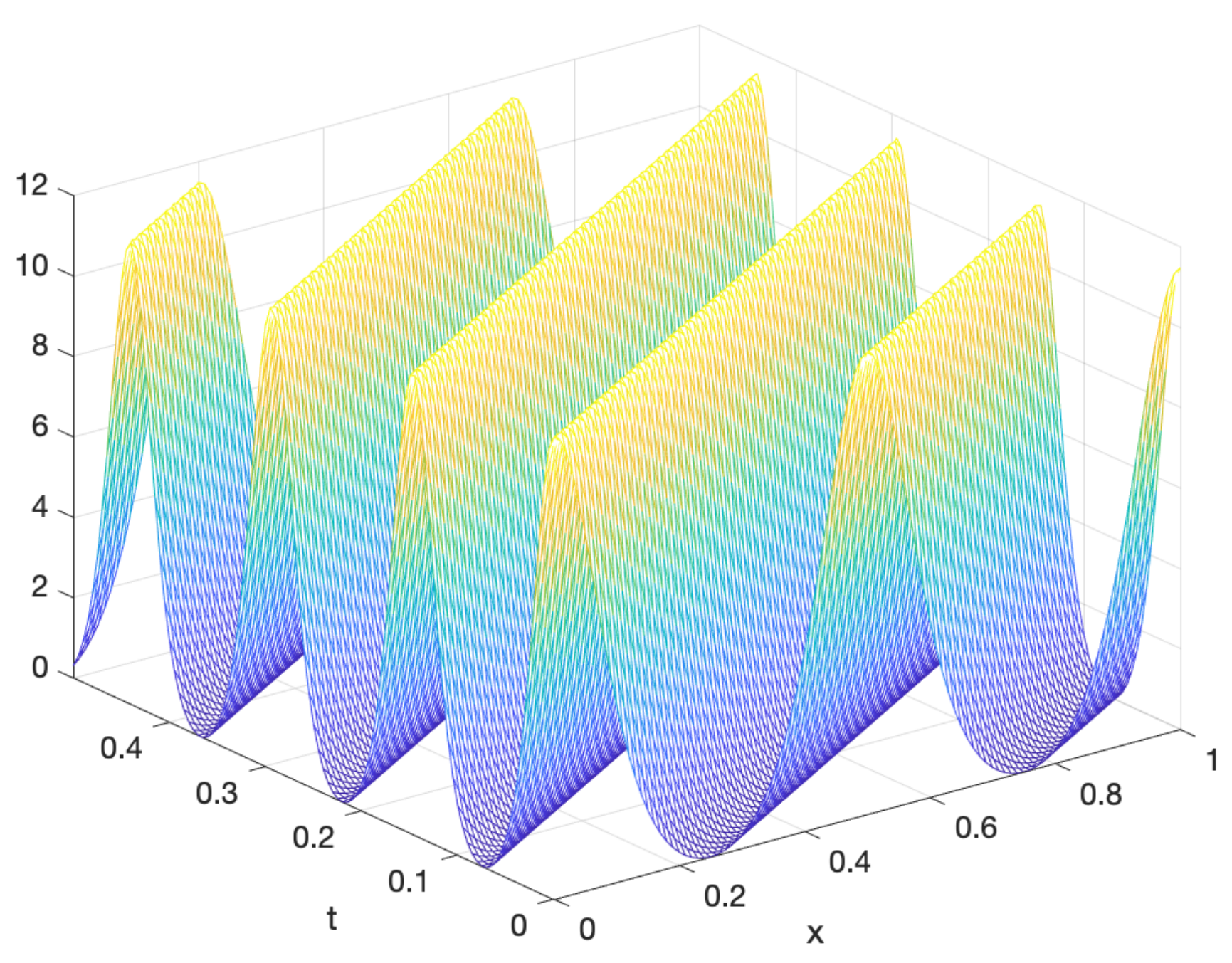
6.1. The Semilinear Wave Equation
- the higher-order methods perform better than the lower-order ones;
- the energy-conserving methods are slightly more efficient than the symplectic ones, when the largest time-steps are used;
- the spectral method turns out to be the most effective one, and uses much larger time-steps.
6.2. The Nonlinear Schrödinger Equation
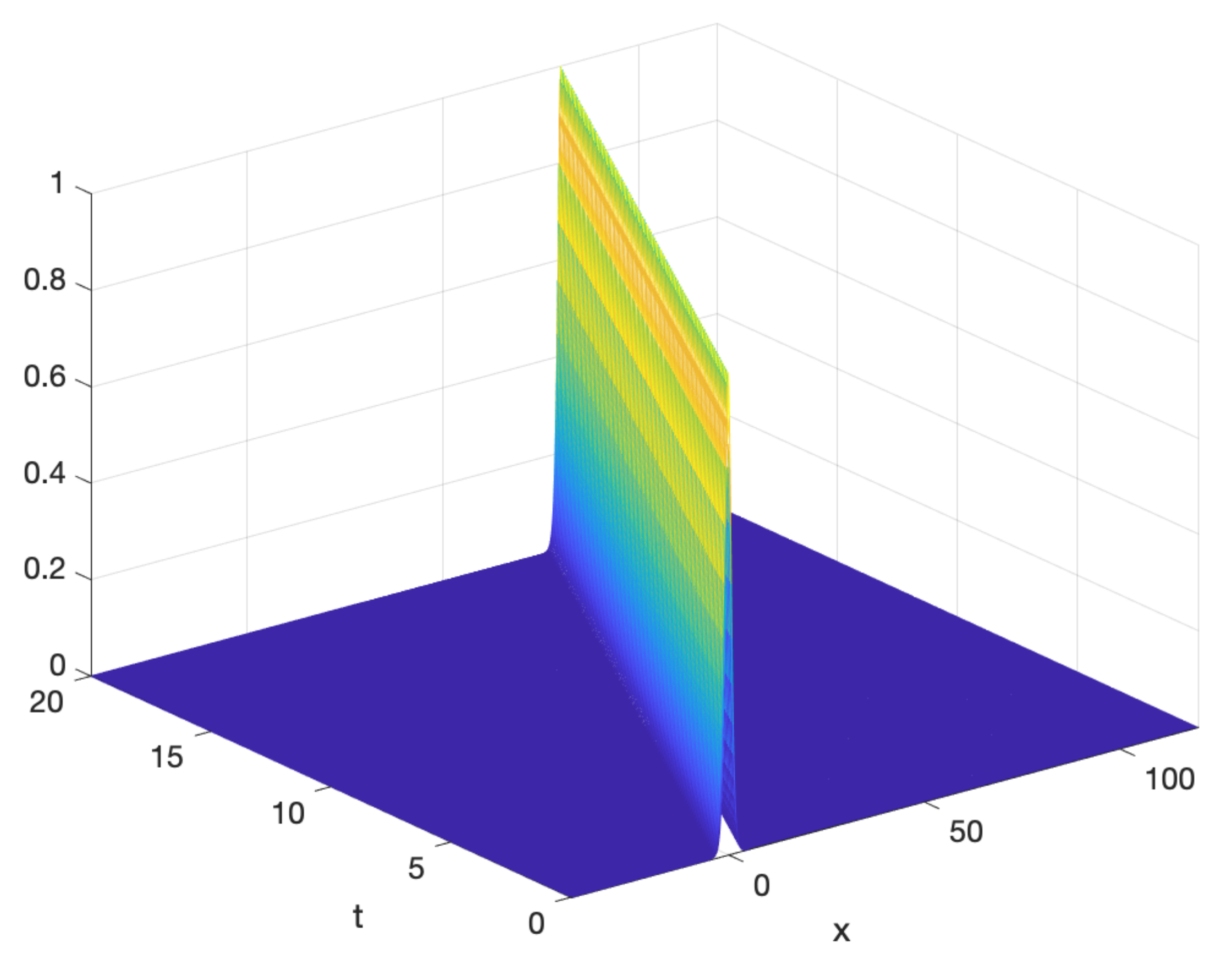
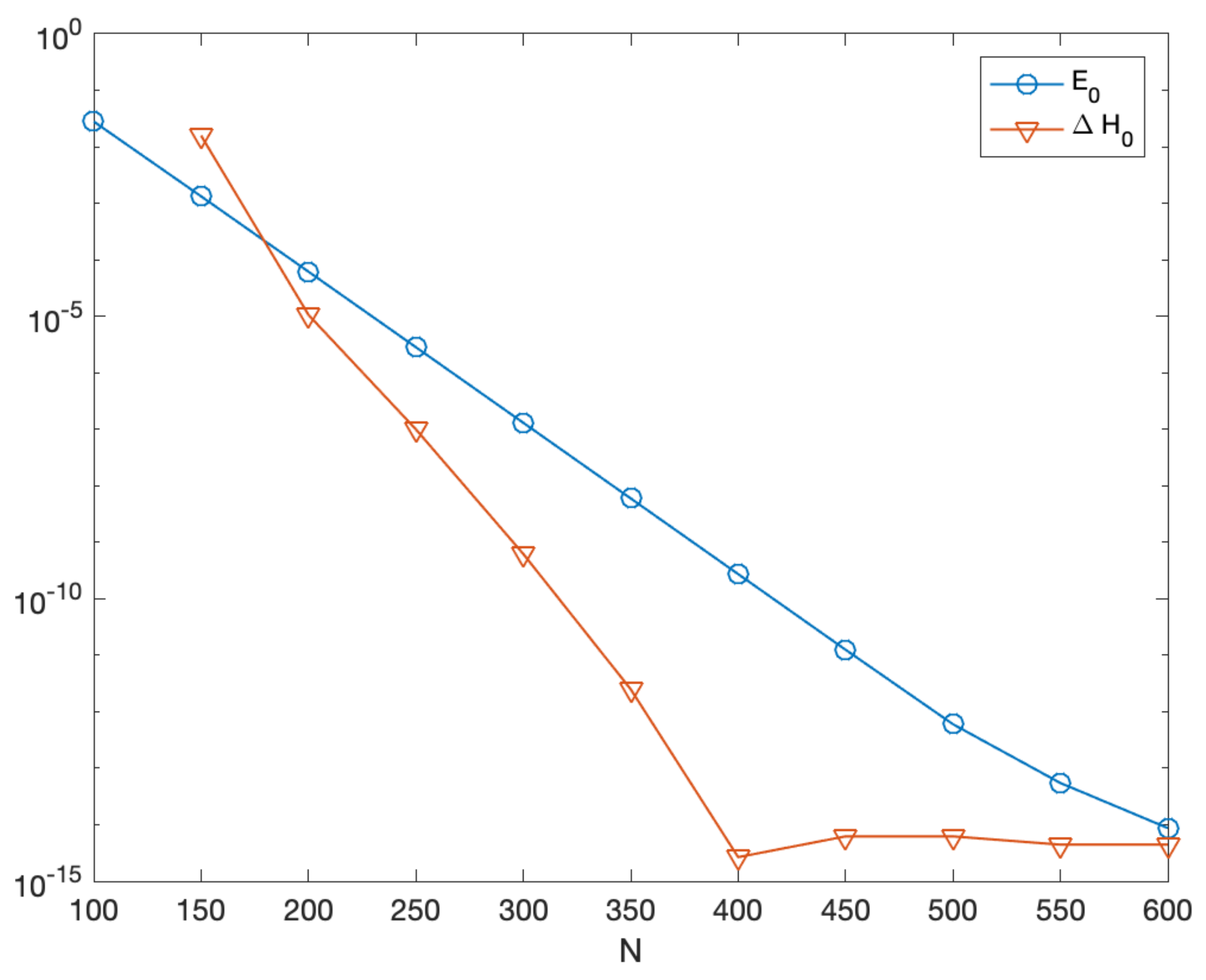
6.3. The Korteweg-de Vries Equation
6.4. A Few Remarks
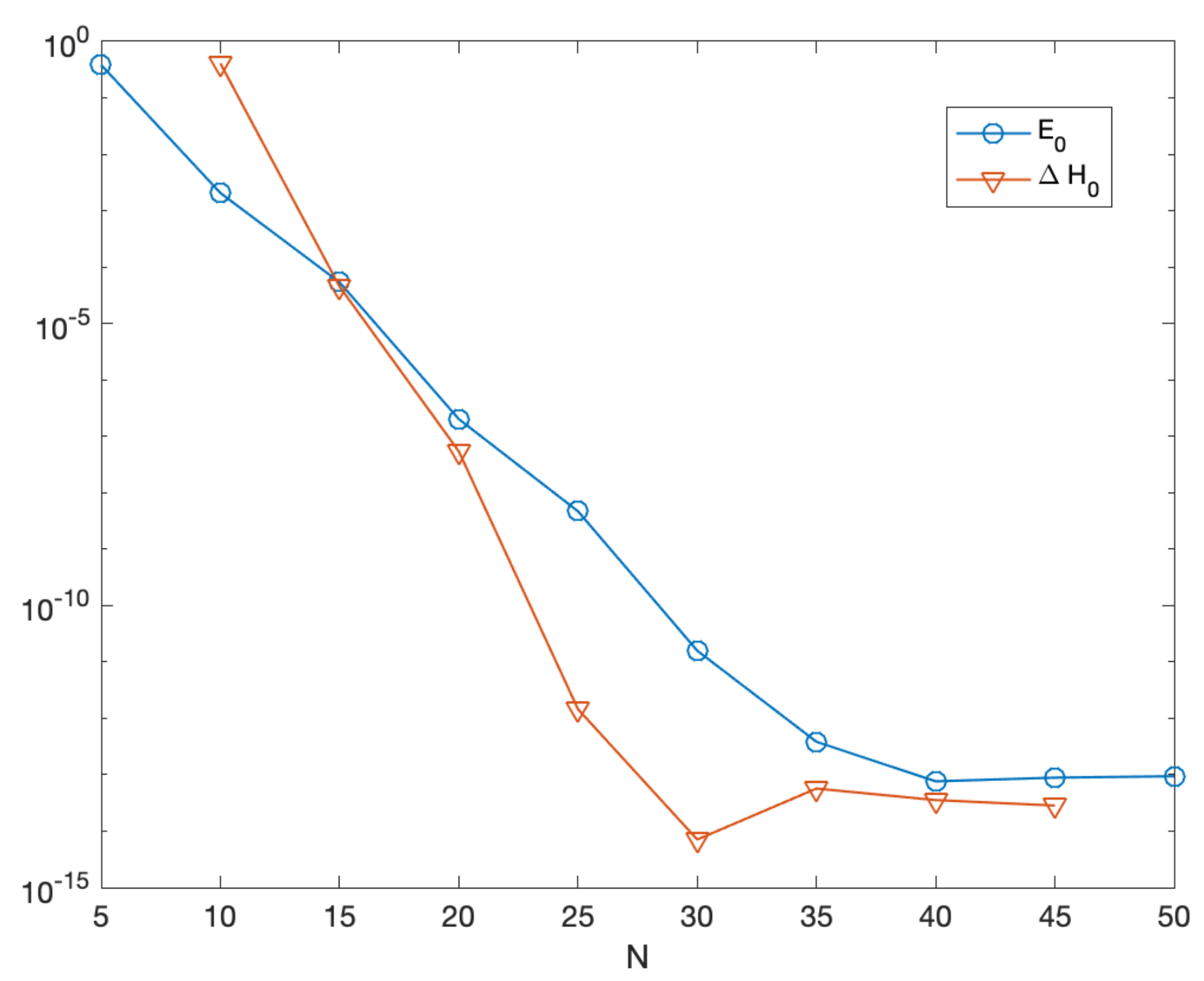
- Energy-conservation.
- Order of the methods.
- From the numerical results, one clearly sees that the second-order methods are outperformed by higher-order HBVMs and/or Gauss methods. In particular, for problems (94) and (96), the second-order HBVM(2,1) method is exactly energy-conserving, and can be regarded as a high-performance implementation of the AVF method in [73]. Despite this, its performance is not comparable with that of the higher-order methods.
- Spectral methods in time.
7. Conclusions
Funding
Conflicts of Interest
References
- Blanes, S.; Casas, F. A Concise Introduction to Geometric Numerical Integration; Chapman et Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Brugnano, L.; Iavernaro, F. Line Integral Methods for Conservative Problems; Chapman et Hall/CRC: Boca Raton, FL, USA, 2016. [Google Scholar]
- Hairer, E.; Lubich, C.; Wanner, G. Geometric Numerical Integration, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Leimkuhler, B.; Reich, S. Simulating Hamiltonian Dynamics; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Sanz-Serna, J.M.; Calvo, M.P. Numerical Hamiltonian Problems; Chapman & Hall: London, UK, 1994. [Google Scholar]
- Celledoni, E.; Grimm, V.; McLachlan, R.I.; McLaren, D.I.; O’Neal, D.; Owren, B.; Quispel, G.R.W. Preserving energy resp. dissipation in numerical PDEs using the “Average Vector Field” method. J. Comput. Phys. 2012, 231, 6770–6789. [Google Scholar] [CrossRef]
- Gong, Y.; Cai, J.; Wang, Y. Some new structure-preserving algorithms for general multi-symplectic formulations of Hamiltonian PDEs. J. Comput. Phys. 2014, 279, 80–102. [Google Scholar] [CrossRef]
- Gong, Y.; Wang, Y. An Energy-Preserving Wavelet Collocation Method for General Multi-Symplectic Formulations of Hamiltonian PDEs. Commun. Comput. Phys. 2016, 20, 1313–1339. [Google Scholar] [CrossRef]
- Jiang, C.; Sun, J.; Li, H.; Wang, Y. A fourth-order AVF method for the numerical integration of sine-Gordon equation. Appl. Math. Comput. 2017, 313, 144–158. [Google Scholar] [CrossRef]
- Karasözen, B.; Şimşek, G. Energy preserving integration of bi-Hamiltonian partial differential equations. Appl. Math. Lett. 2013, 26, 1125–1133. [Google Scholar] [CrossRef]
- McLachlan, R.I.; Quispel, G.R.W. Discrete gradient methods have an energy conservation law. Discrete Contin. Dyn. Syst. 2014, 34, 1099–1104. [Google Scholar] [CrossRef]
- Dahlby, M.; Owren, B. A general framework for deriving integral preserving numerical methods for PDEs. SIAM J. Sci. Comput. 2011, 33, 2318–2340. [Google Scholar] [CrossRef]
- Durán, A.; López-Marcos, M.A. Conservative numerical methods for solitary wave interactions. J. Phys. A Math. Gen. 2003, 36, 7761–7770. [Google Scholar] [CrossRef]
- Durán, A.; Sanz-Serna, J.M. The numerical integration of relative equilibrium solutions. Geometric theory. Nonlinearity 1998, 11, 1547–1567. [Google Scholar] [CrossRef]
- Frasca-Caccia, G.; Hydon, P.E. Simple bespoke preservation of two conservation laws. IMA J. Numer. Anal. 2018, 1–36. [Google Scholar] [CrossRef]
- De Frutos, J.; Sanz-Serna, J.M. Accuracy and conservation properties in numerical integration: The case of the Korteweg-de Vries equation. Numer. Math. 1997, 75, 421–445. [Google Scholar] [CrossRef]
- Furihata, D. Finite Difference Schemes for ∂u/∂t = (∂/∂x)αδG/δu that inherit energy conservation or dissipation property. J. Comput. Phys. 1999, 156, 181–205. [Google Scholar] [CrossRef]
- Furihata, D.; Matsuo, T. Discrete Variational Derivative Method: A Structure-Preserving Numerical Method for Partial Differential Equations; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Matsuo, T.; Furihata, D. Dissipative or conservative finite-difference schemes for complex-valued nonlinear partial differential equations. J. Comput. Phys. 2001, 171, 425–447. [Google Scholar] [CrossRef]
- Guo, L.; Xu, Y. Energy Conserving Local Discontinuous Galerkin Methods for the Nonlinear Schrödinger Equation with Wave Operator. J. Sci. Comput. 2015, 65, 622–647. [Google Scholar] [CrossRef]
- Iavernaro, F.; Pace, B. s-stage trapezoidal methods for the conservation of Hamiltonian functions of polynomial type. AIP Conf. Proc. 2007, 936, 603–606. [Google Scholar]
- Iavernaro, F.; Pace, B. Conservative block-Boundary Value Methods for the solution of polynomial Hamiltonian systems. AIP Conf. Proc. 2008, 1048, 888–891. [Google Scholar]
- Iavernaro, F.; Trigiante, D. On some conservation properties of the trapezoidal method applied to Hamiltonian systems. In ICNAAM, International Conference on Numerical Analysis and Applied Mathematics 2005; Wiley-Vch Verlag GmbH & Co.: Weinheim, Germany, 2005; pp. 254–257. [Google Scholar]
- Iavernaro, F.; Trigiante, D. Discrete Conservative Vector Fields Induced by the Trapezoidal Method. JNAIAM J. Numer. Anal. Ind. Appl. Math. 2006, 1, 113–130. [Google Scholar]
- Iavernaro, F.; Trigiante, D. High-order Symmetric Schemes for the Energy Conservation of Polynomial Hamiltonian Problems. JNAIAM J. Numer. Anal. Ind. Appl. Math. 2009, 4, 87–101. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Susca, T. Numerical comparisons between Gauss-Legendre methods and Hamiltonian BVMs defined over Gauss points. Monografías Real Academia Ciencias Zaragoza 2010, 33, 95–112. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Hamiltonian BVMs (HBVMs): A family of “drift-free” methods for integrating polynomial Hamiltonian systems. AIP Conf. Proc. 2009, 1168, 715–718. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Hamiltonian Boundary Value Methods (Energy Preserving Discrete Line Integral Methods). JNAIAM. J. Numer. Anal. Ind. Appl. Math. 2010, 5, 17–37. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. The lack of continuity and the role of Infinite and infinitesimal in numerical methods for ODEs: The case of symplecticity. Appl. Math. Comput. 2012, 218, 8053–8063. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. A simple framework for the derivation and analysis of effective one-step methods for ODEs. Appl. Math. Comput. 2012, 218, 8475–8485. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Analisys of Hamiltonian Boundary Value Methods (HBVMs): A class of energy-preserving Runge-Kutta methods for the numerical solution of polynomial Hamiltonian systems. Commun. Nonlinear Sci. Numer. Simul. 2015, 20, 650–667. [Google Scholar] [CrossRef]
- Brugnano, L.; Calvo, M.; Montijano, J.I.; Ràndez, L. Energy preserving methods for Poisson systems. J. Comput. Appl. Math. 2012, 236, 3890–3904. [Google Scholar] [CrossRef]
- Brugnano, L.; Gurioli, G.; Iavernaro, F. Analysis of Energy and QUadratic Invariant Preserving (EQUIP) methods. J. Comput. Appl. Math. 2018, 335, 51–73. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F. Line Integral Methods which preserve all invariants of conservative problems. J. Comput. Appl. Math. 2012, 236, 3905–3919. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Energy and Quadratic Invariants Preserving Integrators of Gaussian Type. AIP Conf. Proc. 2010, 1281, 227–230. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. A two-step, fourth-order method with energy preserving properties. Comput. Phys. Commun. 2012, 183, 1860–1868. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. Energy and QUadratic Invariants Preserving integrators based upon Gauss collocation formulae. SIAM J. Numer. Anal. 2012, 50, 2897–2916. [Google Scholar] [CrossRef]
- Brugnano, L.; Sun, Y. Multiple invariants conserving Runge-Kutta type methods for Hamiltonian problems. Numer. Algorithms 2014, 65, 611–632. [Google Scholar] [CrossRef]
- Amodio, P.; Brugnano, L.; Iavernaro, F. Energy-conserving methods for Hamiltonian Boundary Value Problems and applications in astrodynamics. Adv. Comput. Math. 2015, 41, 881–905. [Google Scholar] [CrossRef]
- Brugnano, L.; Gurioli, G.; Iavernaro, F.; Weinmüller, E.B. Line integral solution of Hamiltonian systems with holonomic constraints. Appl. Numer. Math. 2018, 127, 56–77. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F.; Montijano, J.I.; Rández, L. Spectrally accurate space-time solution of Hamiltonian PDEs. Numer. Algorithms 2018, 1–20. [Google Scholar] [CrossRef]
- Brugnano, L.; Montijano, J.I.; Rández, L. On the effectiveness of spectral methods for the numerical solution of multi-frequency highly-oscillatory Hamiltonian problems. Numer. Algorithms 2018, 1–32. [Google Scholar] [CrossRef]
- Amodio, P.; Brugnano, L.; Iavernaro, F. Analysis of Spectral Hamiltonian Boundary Value Methods (SHBVMs) for the numerical solution of ODE problems. arXiv 2018, arXiv:1811.06800. [Google Scholar]
- Barletti, L.; Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F. Energy-conserving methods for the nonlinear Schrödinger equation. Appl. Math. Comput. 2018, 318, 3–18. [Google Scholar] [CrossRef]
- Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F. Energy conservation issues in the numerical solution of the semilinear wave equation. Appl. Math. Comput. 2015, 270, 842–870. [Google Scholar] [CrossRef]
- Brugnano, L.; Gurioli, G.; Sun, Y. Energy-conserving Hamiltonian Boundary Value Methods for the numerical solution of the Korteweg-de Vries equation. J. Comput. Appl. Math. 2019, 351, 117–135. [Google Scholar] [CrossRef]
- Brugnano, L.; Gurioli, G.; Zhang, C. Spectrally Accurate Energy-preserving Methods for the Numerical Solution of the “Good” Boussinesq Equation. Numer. Meth. Part. Differ. Equ. 2019, 1–20. [Google Scholar] [CrossRef]
- Brugnano, L.; Zhang, C.; Li, D. A class of energy-conserving Hamiltonian boundary value methods for nonlinear Schrödinger equation with wave operator. Commun. Nonlinear Sci. Numer. Simul. 2018, 60, 33–49. [Google Scholar] [CrossRef]
- Brugnano, L.; Iavernaro, F. Line Integral Solution of Differential Problems. Axioms 2018, 7, 36. [Google Scholar] [CrossRef]
- Dahlquist, G.; Björk, Å. Numerical Methods in Scientific Computing; SIAM: Philadelphia, PA, USA, 2008; Volume 1. [Google Scholar]
- Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F. Efficient implementation of Gauss collocation and Hamiltonian Boundary Value Methods. Numer. Algorithms 2014, 65, 633–650. [Google Scholar] [CrossRef]
- Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F. Hamiltonian Boundary Value Methods (HBVMs) and their efficient implementation. Math. Eng. Sci. Aerosp. 2014, 5, 343–411. [Google Scholar]
- Brugnano, L.; Iavernaro, F.; Trigiante, D. A note on the efficient implementation of Hamiltonian BVMs. J. Comput. Appl. Math. 2011, 236, 375–383. [Google Scholar] [CrossRef]
- Brugnano, L. Blended Block BVMs (B3VMs): A Family of Economical Implicit Methods for ODEs. J. Comput. Appl. Math. 2000, 116, 41–62. [Google Scholar] [CrossRef]
- Brugnano, L.; Magherini, C. Blended Implementation of Block Implicit Methods for ODEs. Appl. Numer. Math. 2002, 42, 29–45. [Google Scholar] [CrossRef]
- Brugnano, L.; Magherini, C. Blended Implicit Methods for solving ODE and DAE problems, and their extension for second order problems. J. Comput. Appl. Math. 2007, 205, 777–790. [Google Scholar] [CrossRef]
- Brugnano, L.; Magherini, C. Recent advances in linear analysis of convergence for splittings for solving ODE problems. Appl. Numer. Math. 2009, 59, 542–557. [Google Scholar] [CrossRef]
- Brugnano, L.; Magherini, C. Blended General Linear Methods based on Boundary Value Methods in the Generalized BDF family. JNAIAM J. Numer. Anal. Ind. Appl. Math. 2009, 4, 23–40. [Google Scholar]
- Brugnano, L.; Magherini, C. The BiM code for the numerical solution of ODEs. J. Comput. Appl. Math. 2004, 164–165, 145–158. [Google Scholar] [CrossRef]
- Brugnano, L.; Magherini, C.; Mugnai, F. Blended Implicit Methods for the Numerical Solution of DAE Problems. J. Comput. Appl. Math. 2006, 189, 34–50. [Google Scholar] [CrossRef]
- The Codes BiM and BiMD Home Page. Available online: http://web.math.unifi.it/users/brugnano/BiM/index.html (accessed on 4 January 2019).
- Test Set for IVP Solvers. Available online: https://archimede.dm.uniba.it/~testset/testsetivpsolvers/ (accessed on 4 January 2019).
- Line Integral Methods for Conservative Problems. Available online: http://web.math.unifi.it/users/brugnano/LIMbook/ (accessed on 4 January 2019).
- Wang, B.; Meng, F.; Fang, Y. Efficient implementation of RKN-type Fourier collocation methods for second-order differential equations. Appl. Numer. Math. 2017, 119, 164–178. [Google Scholar] [CrossRef]
- Simoncini, V. Computational methods for linear matrix equations. SIAM Rev. 2016, 58, 377–441. [Google Scholar] [CrossRef]
- Betsch, P.; Steinmann, P. Inherently Energy Conserving Time Finite Elements for Classical Mechanics. J. Comput. Phys. 2000, 160, 88–116. [Google Scholar] [CrossRef]
- Betsch, P.; Steinmann, P. Conservation properties of a time FE method. I. Time-stepping schemes for N-body problems. Int. J. Numer. Methods Eng. 2000, 49, 599–638. [Google Scholar] [CrossRef]
- Bottasso, C.L. A new look at finite elements in time: a variational interpretation of Runge-Kutta methods. Appl. Numer. Math. 1997, 25, 355–368. [Google Scholar] [CrossRef]
- Tang, Q.; Chen, C.M. Continuous finite element methods for Hamiltonian systems. Appl. Math. Mech. 2007, 28, 1071–1080. [Google Scholar] [CrossRef]
- Boyd, J.P. Chebyshev and Fourier Spectral Methods, 2nd ed.; Dover Publications Inc.: Mineola, NY, USA, 2001. [Google Scholar]
- Kappeler, T.; Pöschel, J. On the well-posedness of the periodic KdV equation in high regularity classes. In Hamiltonian Systems and Applications; Craig, W., Ed.; Springer: Berlin, Germany, 2008; pp. 431–441. [Google Scholar]
- Olver, P.J. Hamiltonian and non-Hamiltonian models for water waves. In Trends and Applications of Pure Mathematics to Mechanics; Springer: Berlin/Heidelberg, Germany, 1984; Volume 195, pp. 273–290. [Google Scholar]
- Quispel, G.R.W.; McLaren, D.I. A new class of energy-preserving numerical integration methods. J. Phys. A Math. Theor. 2008, 41, 045206. [Google Scholar] [CrossRef]
| Gauss 1 | |||||
| n | time | rate | rate | ||
| 2000 | 2.1 | — | — | ||
| 3000 | 2.8 | 2.0 | 2.0 | ||
| 4000 | 3.8 | 2.0 | 2.0 | ||
| 5000 | 4.8 | 2.0 | 2.0 | ||
| 6000 | 6.1 | 2.0 | 2.0 | ||
| Gauss 2 | |||||
| n | time | rate | rate | ||
| 1000 | 2.4 | — | — | ||
| 1500 | 3.3 | 4.0 | 4.0 | ||
| 2000 | 3.9 | 4.0 | 4.0 | ||
| 2500 | 5.3 | 4.0 | 4.0 | ||
| 3000 | 6.6 | 4.0 | 4.0 | ||
| HBVM (4,1) | |||||
| n | time | rate | |||
| 1000 | 2.4 | — | |||
| 1500 | 3.3 | 2.0 | |||
| 2000 | 4.2 | 2.0 | |||
| 2500 | 5.7 | 2.0 | |||
| 3000 | 7.0 | 2.0 | |||
| HBVM (4,2) | |||||
| n | time | rate | |||
| 1000 | 2.8 | — | |||
| 1500 | 4.0 | 4.0 | |||
| 2000 | 4.6 | 4.0 | |||
| 2500 | 6.0 | 4.0 | |||
| 3000 | 7.0 | 4.0 | |||
| SHBVM | |||||
| n | time | k | s | ||
| 50 | 2.7 | 22 | 20 | ||
| 75 | 1.6 | 20 | 18 | ||
| 100 | 1.3 | 15 | 12 | ||
| Gauss 1 | ||||||||
| n | time | rate | rate | |||||
| 400 | 19.1 | — | — | |||||
| 600 | 26.3 | 1.9 | 4.1 | |||||
| 800 | 33.2 | 2.0 | 4.1 | |||||
| 1000 | 40.7 | 2.0 | 4.0 | |||||
| Gauss 2 | ||||||||
| n | time | rate | rate | |||||
| 400 | 41.3 | — | — | |||||
| 600 | 60.4 | 4.0 | 7.9 | |||||
| 800 | 72.1 | 4.0 | 7.9 | |||||
| 1000 | 84.7 | 4.0 | 8.0 | |||||
| HBVM (2,1) | ||||||||
| n | time | rate | rate | rate | ||||
| 400 | 36.3 | — | — | — | ||||
| 600 | 50.7 | 1.9 | 4.1 | 4.1 | ||||
| 800 | 60.1 | 2.0 | 4.1 | 4.1 | ||||
| 1000 | 74.5 | 2.0 | 4.0 | 4.0 | ||||
| HBVM (4,2) | ||||||||
| n | time | rate | rate | rate | ||||
| 400 | 43.2 | — | — | — | ||||
| 600 | 61.4 | 4.0 | 7.9 | 7.9 | ||||
| 800 | 77.0 | 4.0 | 8.0 | 7.9 | ||||
| 1000 | 92.3 | 4.0 | 8.0 | 8.0 | ||||
| SHBVM | ||||||||
| n | time | k | s | |||||
| 50 | 55.0 | 20 | 18 | |||||
| 75 | 53.6 | 16 | 14 | |||||
| 100 | 61.6 | 14 | 12 | |||||
| Gauss 1 | |||||
| n | time | rate | rate | ||
| 10,000 | 5.1 | — | — | ||
| 20,000 | 8.6 | 2.0 | 4.0 | ||
| 30,000 | 13.8 | 2.0 | 4.0 | ||
| 40,000 | 17.6 | 2.0 | 4.0 | ||
| 50,000 | 20.7 | 2.0 | 4.0 | ||
| Gauss 2 | |||||
| n | time | rate | rate | ||
| 10,000 | 9.4 | — | — | ||
| 20,000 | 18.1 | 4.0 | 5.2 | ||
| 30,000 | 25.3 | 4.0 | *** | ||
| 40,000 | 31.3 | 4.0 | *** | ||
| 50,000 | 39.5 | 4.0 | *** | ||
| HBVM (2,1) | |||||
| n | time | rate | |||
| 10,000 | 9.4 | — | |||
| 20,000 | 16.6 | 2.0 | |||
| 30,000 | 21.8 | 2.0 | |||
| 40,000 | 29.0 | 2.0 | |||
| 50,000 | 33.6 | 2.0 | |||
| HBVM (3,2) | |||||
| n | time | rate | |||
| 10,000 | 12.8 | — | |||
| 20,000 | 24.4 | 4.0 | |||
| 30,000 | 34.6 | 4.0 | |||
| 40,000 | 43.0 | 4.0 | |||
| 50,000 | 54.5 | 4.0 | |||
| SHBVM | |||||
| n | time | k | s | ||
| 400 | 7.2 | 20 | 18 | ||
| 600 | 7.4 | 16 | 14 | ||
| 800 | 8.6 | 14 | 12 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brugnano, L.; Frasca-Caccia, G.; Iavernaro, F. Line Integral Solution of Hamiltonian PDEs. Mathematics 2019, 7, 275. https://doi.org/10.3390/math7030275
Brugnano L, Frasca-Caccia G, Iavernaro F. Line Integral Solution of Hamiltonian PDEs. Mathematics. 2019; 7(3):275. https://doi.org/10.3390/math7030275
Chicago/Turabian StyleBrugnano, Luigi, Gianluca Frasca-Caccia, and Felice Iavernaro. 2019. "Line Integral Solution of Hamiltonian PDEs" Mathematics 7, no. 3: 275. https://doi.org/10.3390/math7030275
APA StyleBrugnano, L., Frasca-Caccia, G., & Iavernaro, F. (2019). Line Integral Solution of Hamiltonian PDEs. Mathematics, 7(3), 275. https://doi.org/10.3390/math7030275






