An Efficient Numerical Technique for the Nonlinear Fractional Kolmogorov–Petrovskii–Piskunov Equation
Abstract
:1. Introduction
2. Preliminaries
3. Proposed Algorithm for the Fractional Kolmogorov–Petrovskii–Piskunov (KPP) Equation
4. Convergence Analysis of the Technique
5. Solution for the fractional KPP equation
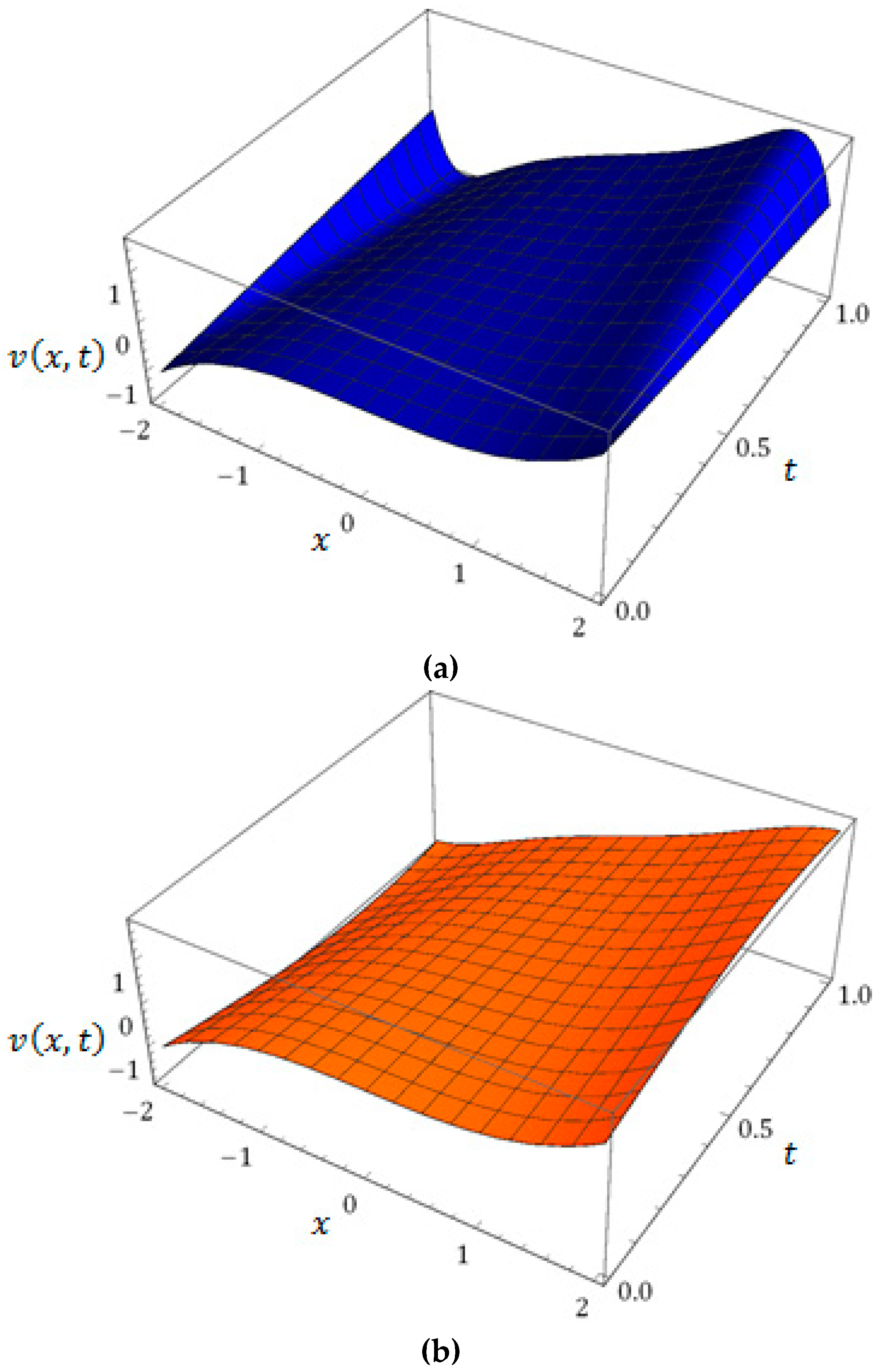
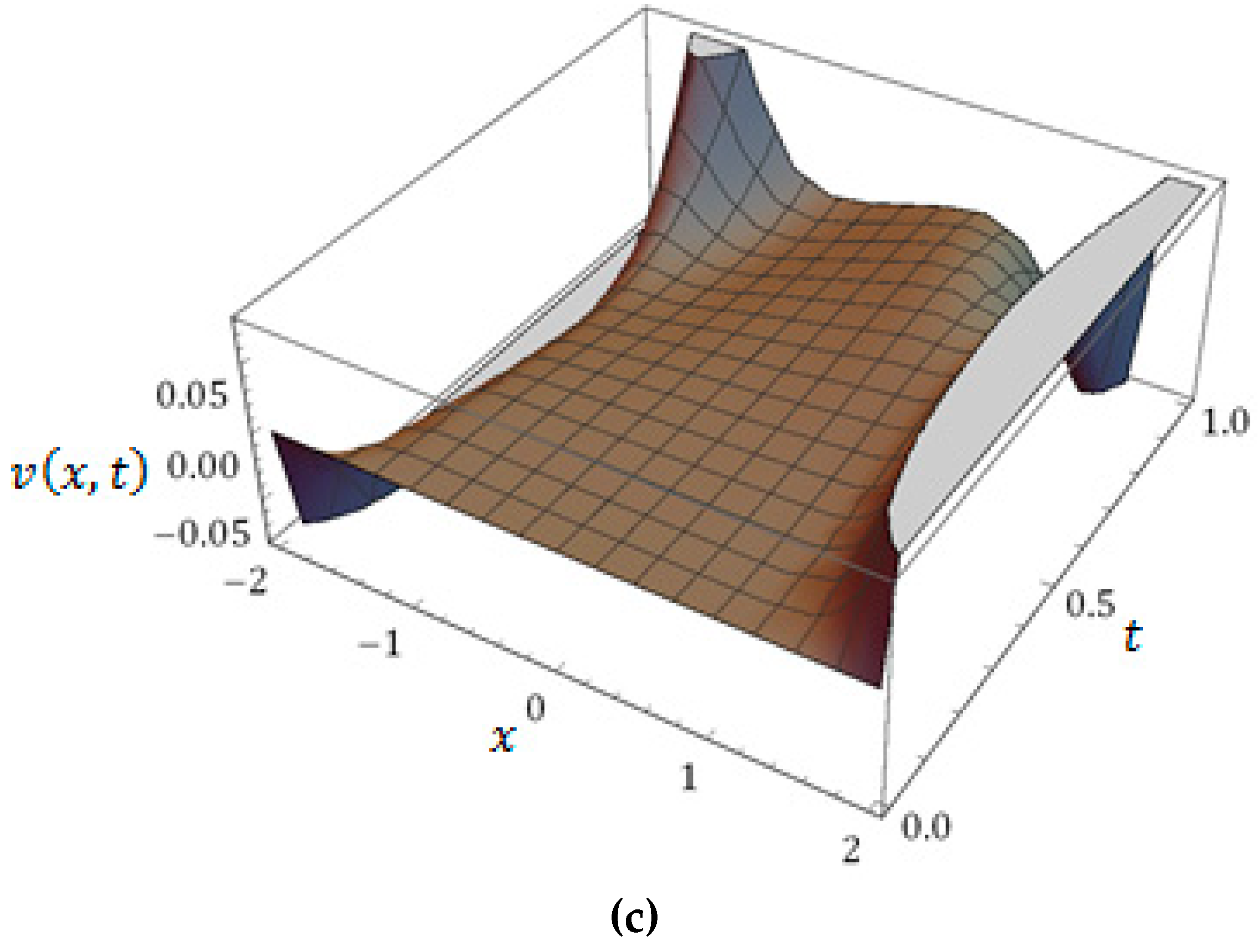
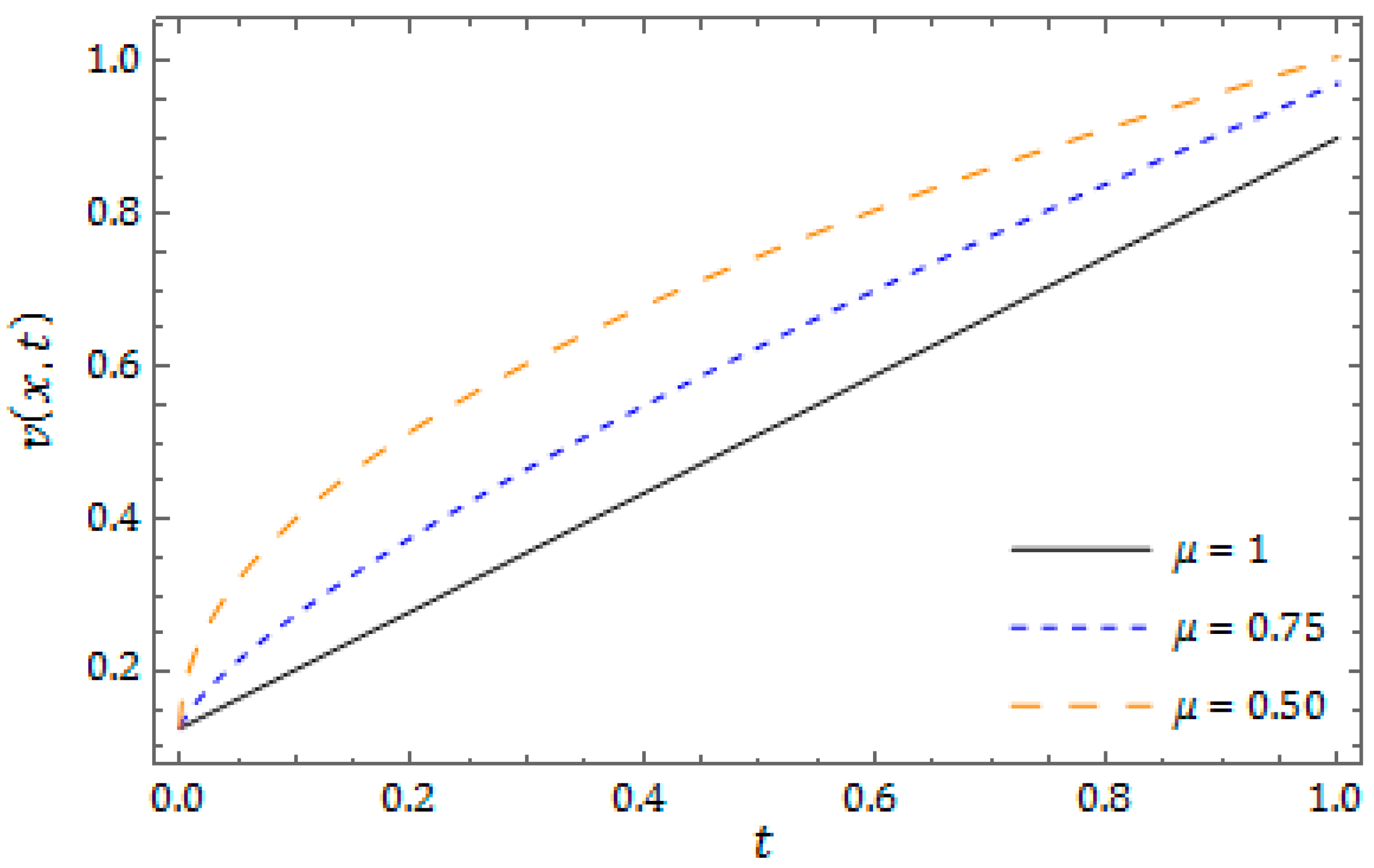
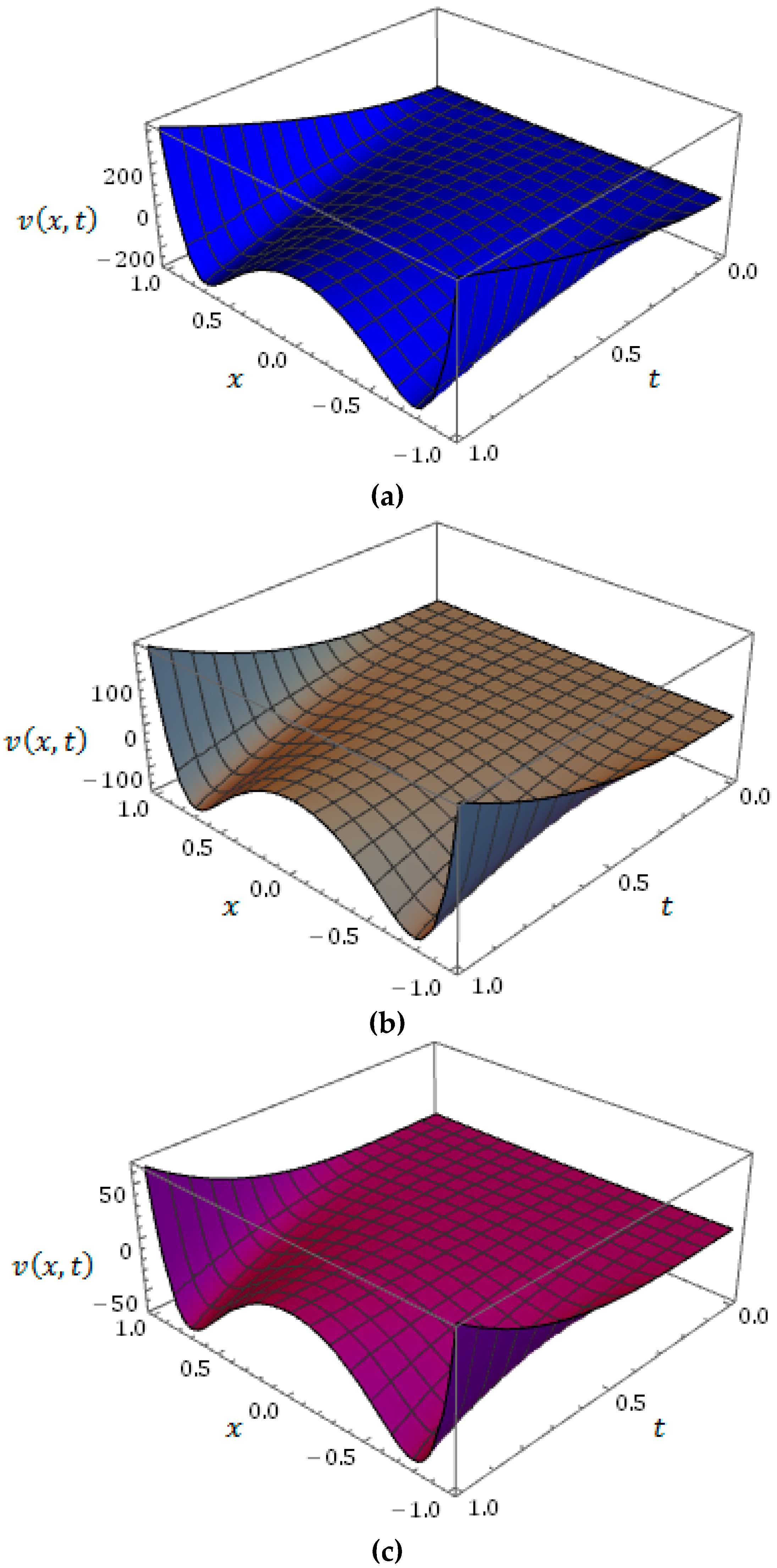
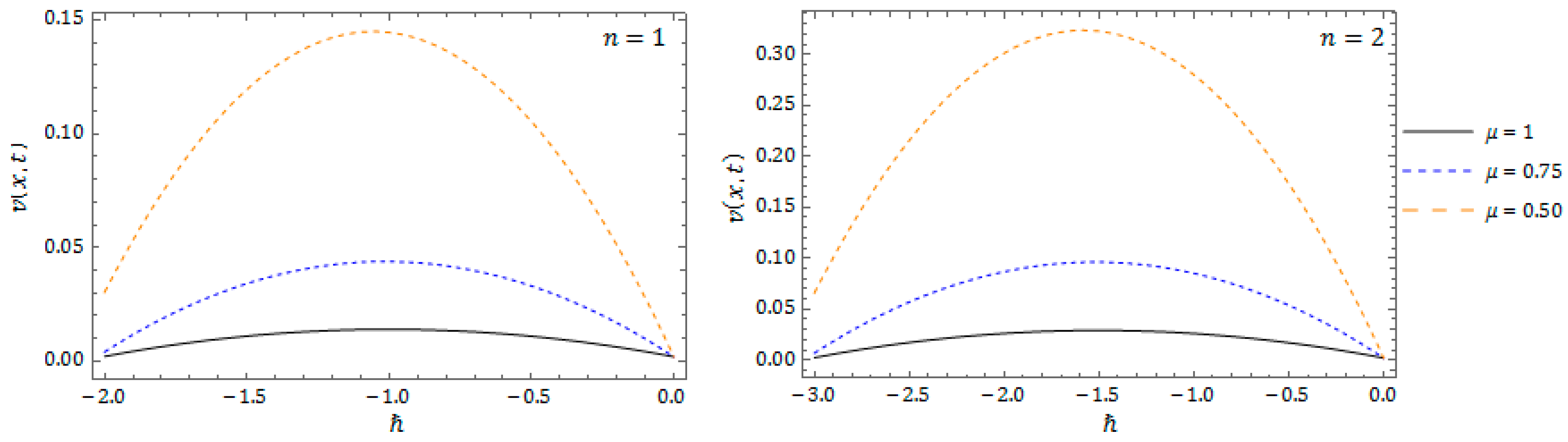
6. Numerical Results and Discussion
7. Conclusions
Author Contributions
Conflicts of Interest
References
- Liouville, J. Memoire sur quelques questions de geometrie et de mecanique, et sur un nouveau genre de calcul pour resoudre ces questions. J. Ecole Polytech. 1832, 13, 71–162. [Google Scholar]
- Riemann, G.F.B. Versuch Einer Allgemeinen Auffassung der Integration und Differentiation; Gesammelte Mathematische Werke: Leipzig, Germany, 1896. [Google Scholar]
- Caputo, M. Elasticita e Dissipazione; Zanichelli: Bologna, Italy, 1969. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to Fractional Calculus and Fractional Differential Equations; A Wiley: New York, NY, USA, 1993. [Google Scholar]
- Podlubny, I. Fractional Differential Equations; Academic Press: New York, NY, USA, 1999. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Applications of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Baleanu, D.; Wu, G.-C.; Zeng, S.-D. Chaos analysis and asymptotic stability of generalized Caputo fractional differential equations. Chaos Solitons Fractals 2017, 102, 99–105. [Google Scholar] [CrossRef]
- Baleanu, D.; Guvenc, Z.B.; Machado, J.A.T. New Trends in Nanotechnology and Fractional Calculus Applications; Springer: New York, NY, USA, 2010. [Google Scholar]
- Sweilam, N.H.; Hasan, M.M.A.; Baleanu, D. New studies for general fractional financial models of awareness and trial advertising decisions. Chaos Solitons Fractals 2017, 104, 772–784. [Google Scholar] [CrossRef]
- Esen, A.; Sulaiman, T.A.; Bulut, H.; Baskonus, H.M. Optical solitons and other solutions to the conformable space–time fractional Fokas–Lenells equation. Optik 2018, 167, 150–156. [Google Scholar] [CrossRef]
- Hilfer, R. Applications of Fractional Calculus in Physics; World Scientific: Singapore, 2000. [Google Scholar]
- Ogata, K. Modern Control Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 2010. [Google Scholar]
- Arkhincheev, V.E. Anomalous diffusion in inhomogeneous media: Some exact results. Model. Meas. Control A 1993, 26, 11–29. [Google Scholar]
- Krishna, B.T. Studies on fractional order differentiators and integrators: A survey. Signal Process. 2011, 91, 386–426. [Google Scholar] [CrossRef]
- Djordjevic, V.D.; Atanackovic, T.M. Similarity solutions to nonlinear heat conduction and Burgers/Korteweg-deVries fractional equations. J. Comput. Appl. Math. 2008, 222, 701–714. [Google Scholar] [CrossRef]
- Cole, K.S. Electric Conductance of Biological Systems; Cold Spring Harbor: New York, NY, USA, 1993. [Google Scholar]
- Glockle, W.G.; Nonnenmacher, T.F. A fractional calculus approach to self-similar protein dynamics. Biophys. J. 1995, 68, 46–53. [Google Scholar] [CrossRef]
- Laskin, N. Fractional market dynamics. Phys. A 2000, 287, 482–492. [Google Scholar] [CrossRef]
- Kolmogorov, A.N.; Petrovskii, I.; Piskunov, N. A study of the diffusion equation with increase in the amount of substance and its application to a biology problem. Byul. Moskovskogo Gos. Univ. 1937, 1, 1–25. [Google Scholar]
- Fuentes, M.A.; Kuperman, M.N.; Kenkre, V.M. Nonlocal interaction effects on pattern formation in population dynamics. Phys. Rev. Lett. 2003, 91, 158104. [Google Scholar] [CrossRef] [PubMed]
- Murray, J.D. Mathematical Biology. I: An Introduction, 3rd ed.; Springer: New York, NY, USA, 2001. [Google Scholar]
- Unal, A.O. On the Kolmogorov-Petrovskii-Piskunov equation. Commun. Fac. Sci. Univ. Ank. Series A1 2013, 62, 1–10. [Google Scholar]
- Gepreel, K.A. The homotopy perturbation method applied to the nonlinear fractional Kolmogorov–Petrovskii–Piskunov equations. Appl. Math. Lett. 2011, 24, 1428–1434. [Google Scholar] [CrossRef]
- Song, L.-N.; Wang, W.-G. Approximate solutions of nonlinear fractional Kolmogorov-Petrovskii-Piskunov equations using an enhanced algorithm of the generalized two-dimensional differential transform method. Commun. Theor. Phys. 2012, 58, 182–188. [Google Scholar] [CrossRef]
- Liao, S.J. Homotopy analysis method and its applications in mathematics. J. Basic Sci. Eng. 1997, 5, 111–125. [Google Scholar]
- Liao, S.J. Homotopy analysis method: A new analytic method for nonlinear problems. Appl. Math. Mech. 1998, 19, 957–962. [Google Scholar]
- Singh, J.; Kumar, D.; Swroop, R. Numerical solution of time- and space-fractional coupled Burgers’ equations via homotopy algorithm. Alex. Eng. J. 2016, 55, 1753–1763. [Google Scholar] [CrossRef]
- Srivastava, H.M.; Kumar, D.; Singh, J. An efficient analytical technique for fractional model of vibration equation. Appl. Math. Model. 2017, 45, 192–204. [Google Scholar] [CrossRef]
- Singh, J.; Kumar, D.; Baleanu, D.; Rathore, S. An efficient numerical algorithm for the fractional Drinfeld–Sokolov–Wilson equation. Appl. Math. Comput. 2018, 335, 12–24. [Google Scholar] [CrossRef]
- Bulut, H.; Kumar, D.; Singh, J.; Swroop, R.; Baskonus, H.M. Analytic study for a fractional model of HIV infection of CD4+T lymphocyte cells. Math. Nat. Sci. 2018, 2, 33–43. [Google Scholar] [CrossRef]
- Kumar, D.; Agarwal, R.P.; Singh, J. A modified numerical scheme and convergence analysis for fractional model of Lienard’s equation. J. Comput. Appl. Math. 2018, 399, 405–413. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. New numerical surfaces to the mathematical model of cancer chemotherapy effect in Caputo fractional derivatives. Chaos 2019, 29, 013119. [Google Scholar] [CrossRef] [PubMed]
- Veeresha, P.; Prakasha, D.G.; Magesh, N.; Nandeppanavar, M.M.; Christopher, A.J. Numerical simulation for fractional Jaulent-Miodek equation associated with energy-dependent Schrodinger potential using two novel techniques. arXiv, 2019; arXiv:1810.06311. [Google Scholar]
- Prakash, A.; Veeresha, P.; Prakasha, D.G.; Goyal, M. A homotopy technique for fractional order multi-dimensional telegraph equation via Laplace transform. Eur. Phys. J. Plus 2019, 134, 1–18. [Google Scholar] [CrossRef]
- Veeresha, P.; Prakasha, D.G.; Baskonus, H.M. Novel simulations to the time-fractional Fisher’s equation. Math. Sci. 2019, 1–10. [Google Scholar] [CrossRef]
- Wang, D.S.; Li, H.B. Single and multi-solitary wave solutions to a class of nonlinear evolution equations. J. Math. Anal. Appl. 2008, 343, 273–298. [Google Scholar] [CrossRef]
- Feng, J.S.; Li, W.J.; Wan, Q.L. Using (G’/G)-expansion method to seek the traveling wave solution of Kolmogorov-Petrovskii-Piskunov equation. Appl. Math. Comput. 2011, 217, 5860–5865. [Google Scholar]
- Hariharan, G. The homotopy analysis method applied to the Kolmogorov-Petrovskii-Piskunov (KPP) and fractional KPP equations. J. Math. Chem. 2013, 51, 992–1000. [Google Scholar] [CrossRef]
- Nikitin, A.G.; Barannyk, T.A. Solitary waves and other solutions for nonlinear heat equations. Cent. Eur. J. Math. 2005, 2, 840–858. [Google Scholar] [CrossRef]
- Ma, W.X.; Fuchssteiner, B. Explicit and exact solutions to a Kolmogorov-Petrovskii-Piskunov equation. Int. J. Non-Linear Mech. 1996, 31, 329–338. [Google Scholar] [CrossRef]
- Qin, C.-Y.; Tian, S.-F.; Wang, X.-B.; Zou, L.; Zhang, T.-T. Lie symmetry analysis, conservation laws and analytic solutions of the time fractional Kolmogorov–Petrovskii–Piskunov equation. Chin. J. Phys. 2018, 56, 1734–1742. [Google Scholar] [CrossRef]
- Zayed, E.M.; Alurrf, K.A.; Nowehy, A.G.A. Many Exact Solutions of the Nonlinear KPP Equation Using the Bäcklund Transformation of the Riccati Equation. Int. J. Opt. Photonic Eng. 2017, 2, 1–7. [Google Scholar]
- Prakasha, D.G.; Veeresha, P.; Rawashdeh, M.S. Numerical solution for (2+1)-dimensional time-fractional coupled Burger equations using fractional natural decomposition method. Math. Meth. Appl. Sci. 2019, 42, 1–19. [Google Scholar] [CrossRef]
- Odibat, Z.M.; Shawagfeh, N.T. Generalized Taylor’s formula. Appl. Math. Comput. 2007, 186, 286–293. [Google Scholar]
- Argyros, I.K. Convergence and Applications of Newton-Type Iterations; Springer Science & Business Media: Berlin, Germany, 2008. [Google Scholar]
- Magrenan, A.A. A new tool to study real dynamics: The convergence plane. Appl. Math. Comput. 2014, 248, 215–224. [Google Scholar] [CrossRef]




| x | t | |||
|---|---|---|---|---|
| 0.2 | 0.02 | 0.004048 | 0.001614 | |
| 0.04 | 0.006276 | 0.002612 | ||
| 0.06 | 0.007984 | 0.003405 | ||
| 0.08 | 0.009382 | 0.004070 | ||
| 0.1 | 0.010561 | 0.004641 | ||
| 0.4 | 0.02 | 0.008131 | 0.003243 | |
| 0.04 | 0.012647 | 0.005266 | ||
| 0.06 | 0.016140 | 0.006892 | ||
| 0.08 | 0.019029 | 0.008272 | ||
| 0.1 | 0.021493 | 0.009474 | ||
| 0.6 | 0.02 | 0.012305 | 0.004914 | |
| 0.04 | 0.019220 | 0.0080222 | ||
| 0.06 | 0.024642 | 0.010555 | ||
| 0.08 | 0.029180 | 0.012738 | ||
| 0.1 | 0.033108 | 0.014673 | ||
| 0.8 | 0.02 | 0.016605 | 0.006656 | |
| 0.04 | 0.026002 | 0.010896 | ||
| 0.06 | 0.033399 | 0.014373 | ||
| 0.08 | 0.039628 | 0.017386 | ||
| 0.1 | 0.045047 | 0.020072 | ||
| 1 | 0.02 | 0.020854 | 0.008402 | |
| 0.04 | 0.032340 | 0.013606 | ||
| 0.06 | 0.041138 | 0.017723 | ||
| 0.08 | 0.048301 | 0.021142 | ||
| 0.1 | 0.054307 | 0.024043 |
| x | t | μ = 0.7 | μ = 0.8 | μ = 0.9 | μ = 1 |
|---|---|---|---|---|---|
| 0.01 | 0.2 | 0.71354 | 0.59265 | 0.48863 | 0.40010 |
| 0.4 | 1.15909 | 1.03179 | 0.91172 | 0.80012 | |
| 0.6 | 1.53948 | 1.42709 | 1.31320 | 1.20010 | |
| 0.8 | 1.88289 | 1.79638 | 1.70125 | 1.60010 | |
| 1 | 2.20119 | 2.14744 | 2.07961 | 2.00011 | |
| 0.05 | 0.2 | 0.71591 | 0.59502 | 0.49101 | 0.40249 |
| 0.4 | 1.16139 | 1.03412 | 0.91407 | 0.80246 | |
| 0.6 | 1.54170 | 1.42936 | 1.31549 | 1.20242 | |
| 0.8 | 1.88502 | 1.79856 | 1.70347 | 1.60236 | |
| 1 | 2.20323 | 2.14953 | 2.08174 | 2.00227 | |
| 0.1 | 0.2 | 0.72283 | 0.60217 | 0.49829 | 0.40986 |
| 0.4 | 1.16738 | 1.04053 | 0.92080 | 0.80942 | |
| 0.6 | 1.54654 | 1.43477 | 1.32138 | 1.20870 | |
| 0.8 | 1.88855 | 1.80275 | 1.70827 | 1.60769 | |
| 1 | 2.20530 | 2.15230 | 2.08521 | 2.00640 |
| x | t | μ = 0.8 | μ = 0.9 | μ = 1 |
|---|---|---|---|---|
| 0.1 | 0.02 | 0.39544 | 0.31857 | 0.25627 |
| 0.04 | 0.73580 | 0.63051 | 0.53892 | |
| 0.06 | 1.07771 | 0.95890 | 0.84998 | |
| 0.08 | 1.42750 | 1.30632 | 1.18942 | |
| 0.1 | 1.78728 | 1.67345 | 1.55725 | |
| 0.2 | 0.02 | 1.03187 | 0.79132 | 0.61147 |
| 0.04 | 2.17367 | 1.76387 | 1.43330 | |
| 0.06 | 3.48467 | 2.94515 | 2.48151 | |
| 0.08 | 4.95178 | 4.32609 | 3.75607 | |
| 0.1 | 6.56361 | 5.89892 | 5.25702 | |
| 0.3 | 0.02 | 2.14834 | 1.57388 | 1.16766 |
| 0.04 | 4.99339 | 3.89101 | 3.03371 | |
| 0.06 | 8.49589 | 6.94886 | 5.65234 | |
| 0.08 | 12.5737 | 10.6995 | 9.02354 | |
| 0.1 | 17.1721 | 15.1092 | 13.1473 | |
| 0.4 | 0.02 | 3.92819 | 2.79270 | 2.01364 |
| 0.04 | 9.67310 | 7.36715 | 5.60298 | |
| 0.06 | 16.9775 | 13.6543 | 10.8974 | |
| 0.08 | 25.6269 | 21.5326 | 17.8969 | |
| 0.1 | 35.4848 | 30.9193 | 26.6014 | |
| 0.5 | 0.02 | 6.27845 | 4.41081 | 3.14532 |
| 0.04 | 15.8083 | 11.9311 | 8.98311 | |
| 0.06 | 28.0760 | 22.4336 | 17.7701 | |
| 0.08 | 42.6940 | 35.7006 | 29.5059 | |
| 0.1 | 59.4191 | 51.5854 | 44.1909 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Veeresha, P.; Prakasha, D.G.; Baleanu, D. An Efficient Numerical Technique for the Nonlinear Fractional Kolmogorov–Petrovskii–Piskunov Equation. Mathematics 2019, 7, 265. https://doi.org/10.3390/math7030265
Veeresha P, Prakasha DG, Baleanu D. An Efficient Numerical Technique for the Nonlinear Fractional Kolmogorov–Petrovskii–Piskunov Equation. Mathematics. 2019; 7(3):265. https://doi.org/10.3390/math7030265
Chicago/Turabian StyleVeeresha, Pundikala, Doddabhadrappla Gowda Prakasha, and Dumitru Baleanu. 2019. "An Efficient Numerical Technique for the Nonlinear Fractional Kolmogorov–Petrovskii–Piskunov Equation" Mathematics 7, no. 3: 265. https://doi.org/10.3390/math7030265
APA StyleVeeresha, P., Prakasha, D. G., & Baleanu, D. (2019). An Efficient Numerical Technique for the Nonlinear Fractional Kolmogorov–Petrovskii–Piskunov Equation. Mathematics, 7(3), 265. https://doi.org/10.3390/math7030265






