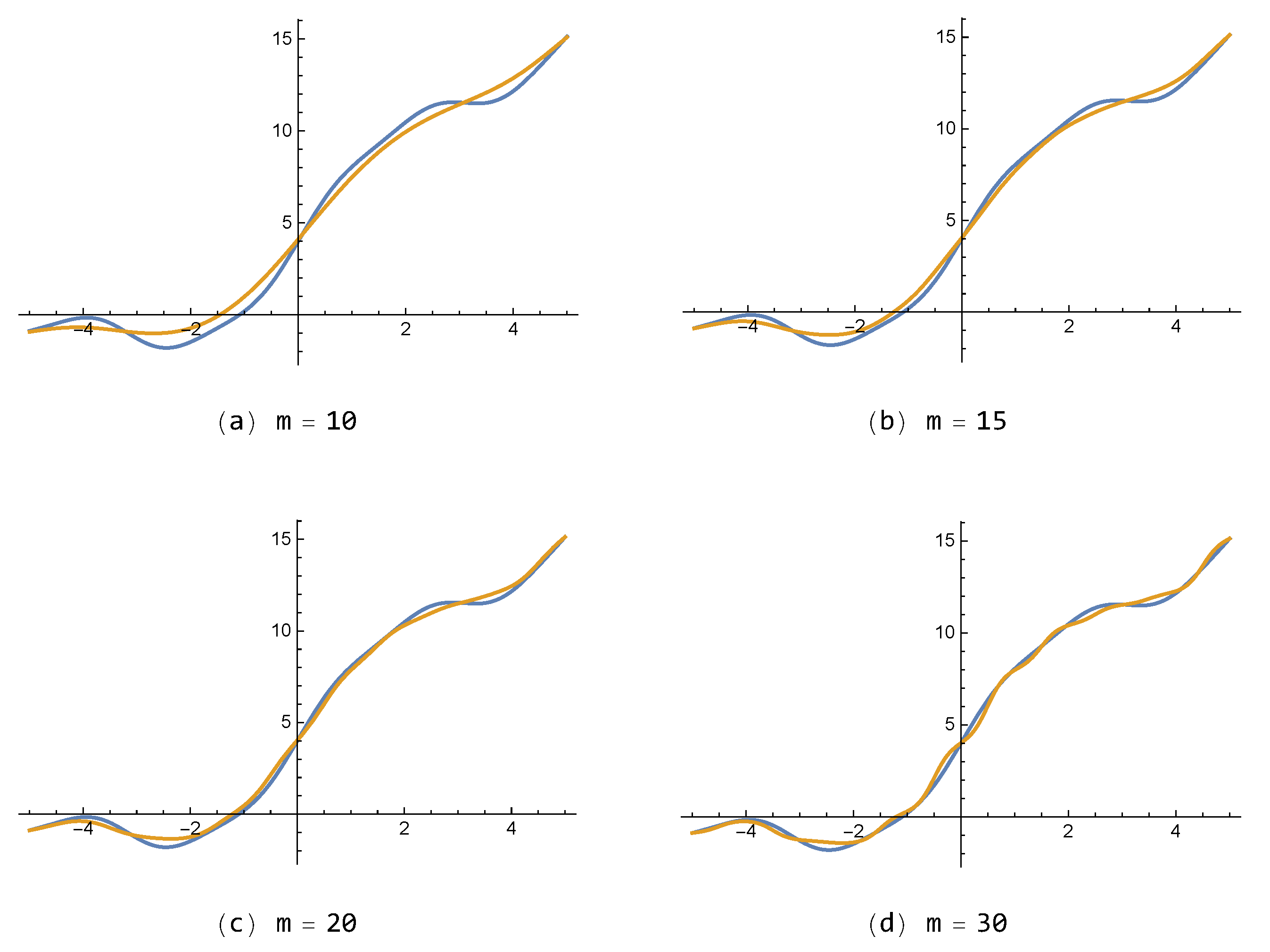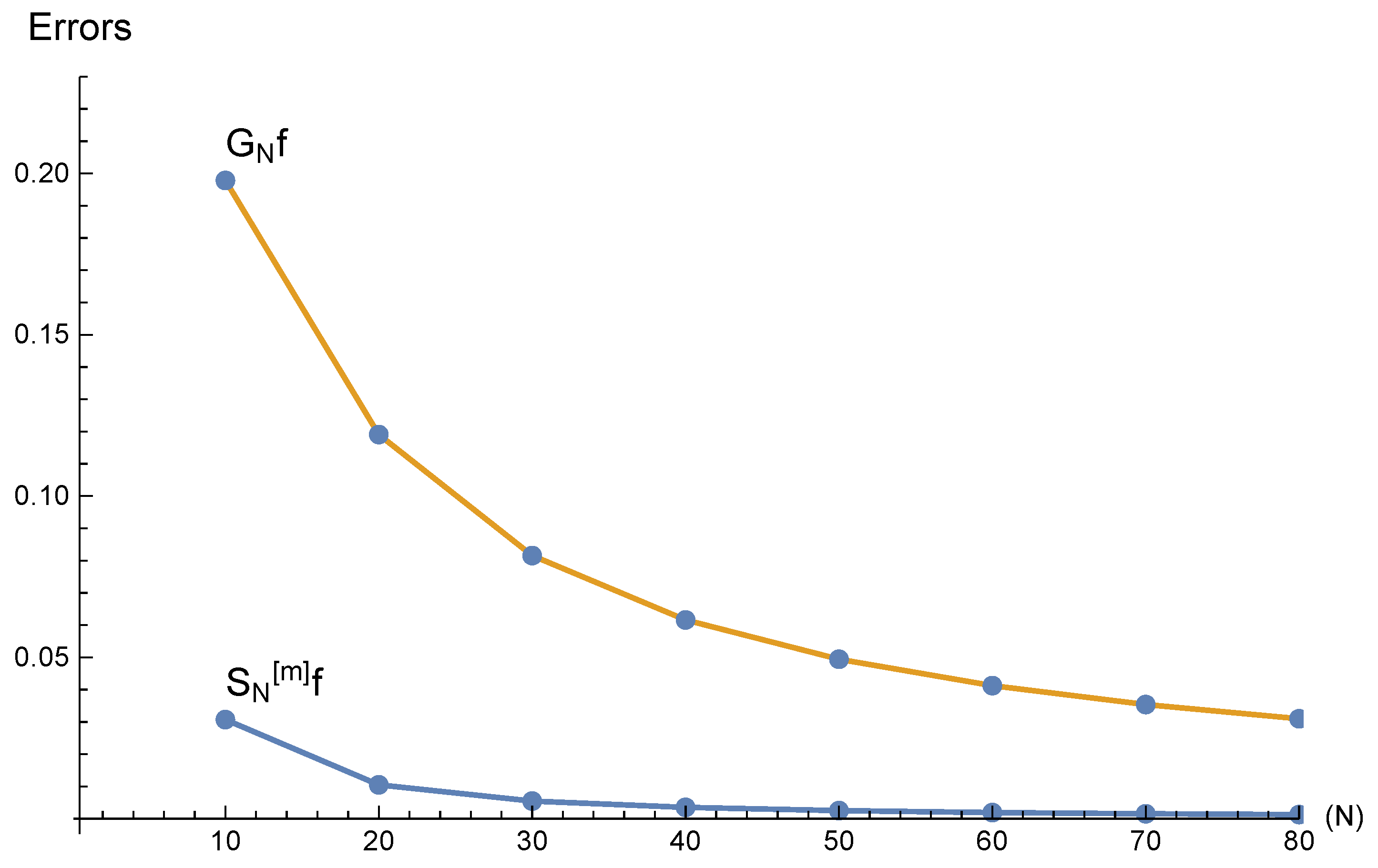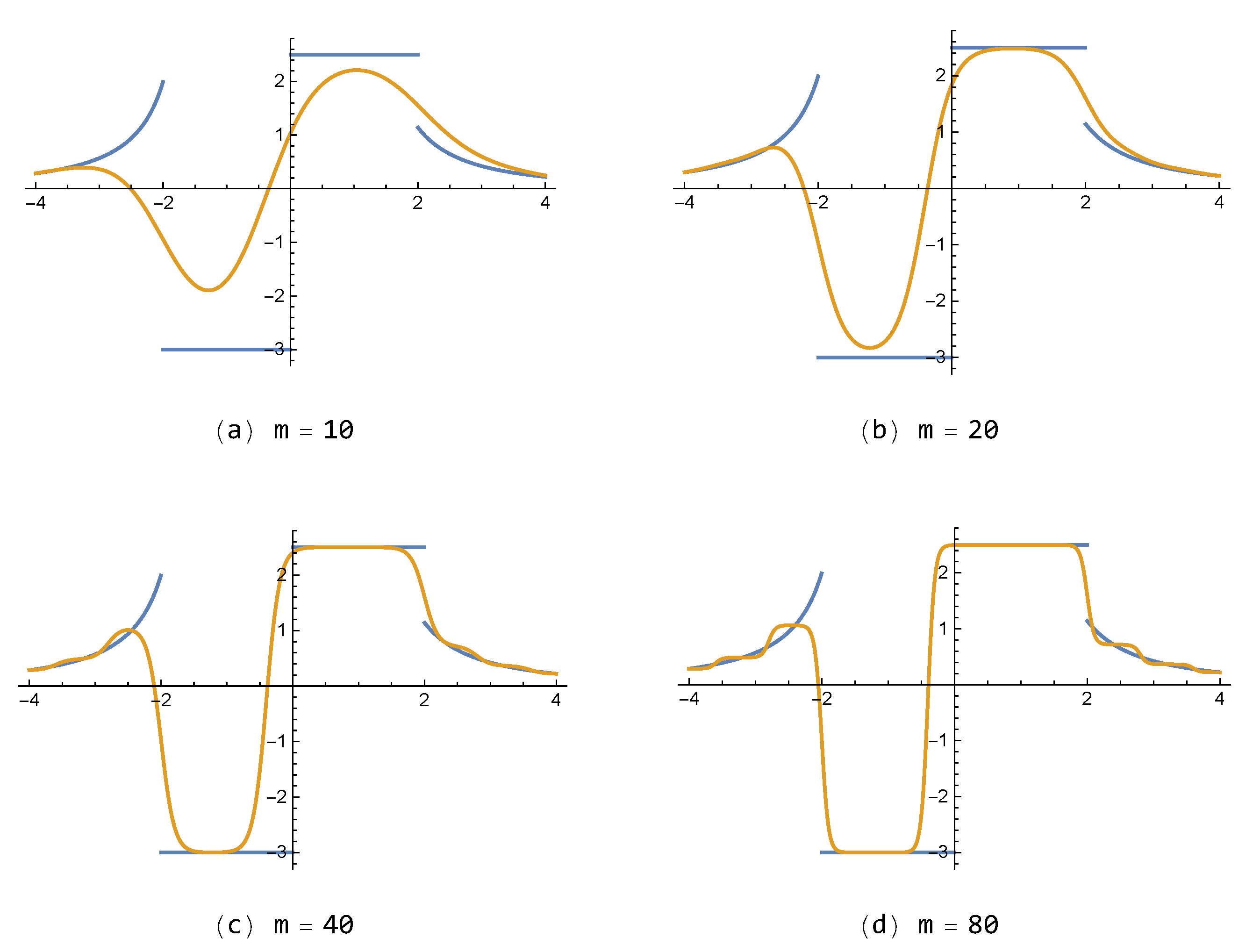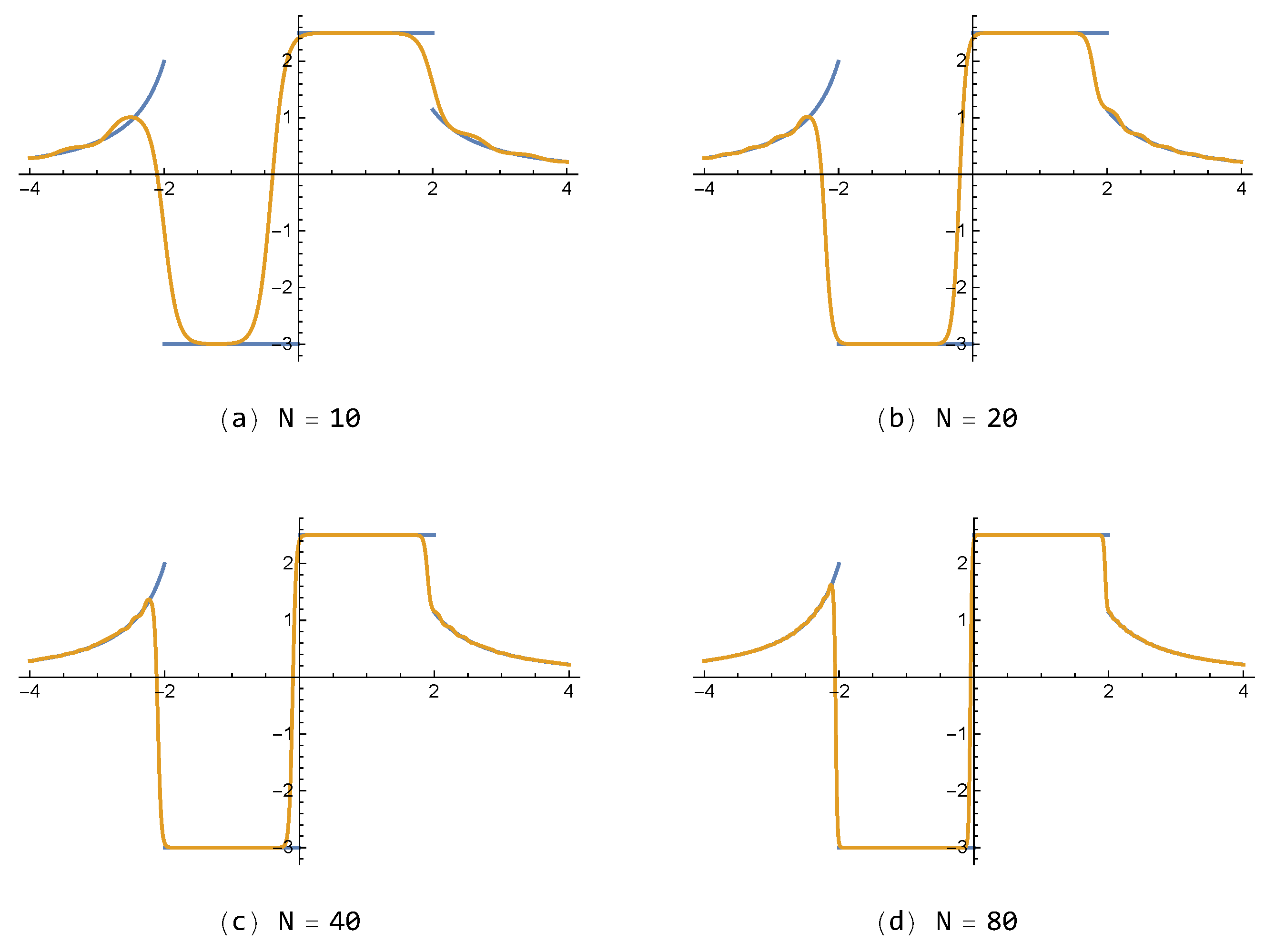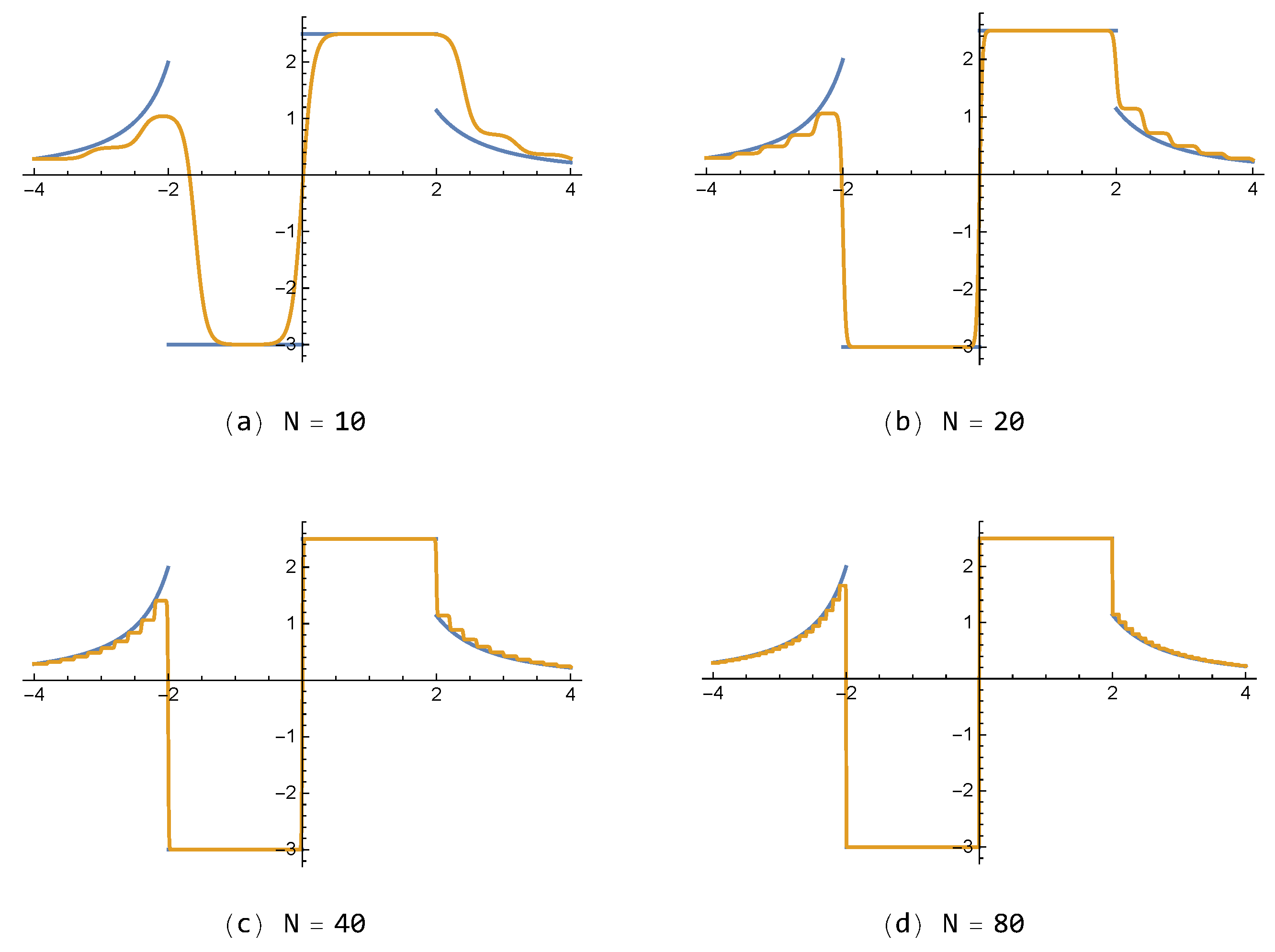A Neural Network Approximation Based on a Parametric Sigmoidal Function

Abstract

It is well known that feed-forward neural networks can be used for approximation to functions based on an appropriate activation function. In this paper, employing a new sigmoidal function with a parameter for an activation function, we consider a constructive feed-forward neural network approximation on a closed interval. The developed approximation method takes a simple form of a superposition of the parametric sigmoidal function. It is shown that the proposed method is very effective in approximation of discontinuous functions as well as continuous ones. For some examples, the availability of the presented method is demonstrated by comparing its numerical results with those of an existing neural network approximation method. Furthermore, the efficiency of the method in extended application to the multivariate function is also illustrated.

1. Introduction

Cybenko [1] and Funahashi [2] proved that any continuous function can be uniformly approximated on a compact set $I\subset {\mathbf{R}}^n$ by the feed-forward neural networks (FNN) in the form of

$$F_N\left(x\right)=\sum _{k=0}^N{\alpha }_k\sigma \left({\omega }_k·x+{\theta }_k\right),x\in I,$$

(1)

where $\sigma$ is called an activation function, ${\omega }_k\in {\mathbf{R}}^n$ are weights, ${\theta }_k\in \mathbf{R}$ are thresholds, and ${\alpha }_k\in \mathbf{R}$ are coefficients. It is called the universal approximation theorem. Moreover, Hornik et al. [3] showed that any measurable function can be approximated on a compact set by the form of the FNN. Some constructive approximation methods by the FNN were developed in the literature [4,5,6,7]. Other examples of the function approximation by the FNN can be found in the works of Cao et al. [8], Chui and Li [9], Ferrari and Stengel [10], and Suzuki [11]. Particularly, the activation function $\sigma$ is a basic architecture of the neural networks because it imports non-linear properties into the networks. This allows the artificial neural networks to learn from complicated non-linear mappings between inputs in general.

In this paper, aiming efficient approximation to the data obtained from continuous or discontinuous functions on a closed interval, we develop a feed-forward neural network approximation method based on a sigmoidal activation function. First, in the following section, we propose a parametric sigmoidal function ${\sigma }^{\left[m\right]}$ of the form (6) for an activation function. In Section 3 we construct an approximation formula $S_N^{\left[m\right]}f\left(x\right)$ in (19) based on the proposed sigmoidal function ${\sigma }^{\left[m\right]}$. It is shown that $S_N^{\left[m\right]}f\left(x\right)$ approximates every given data with error $O\left({\delta }^m\right)$, $0<\delta <1$, for the parameter m large enough. This implies the so-called quasi-interpolation property of the presented FNN approximation. Furthermore, in order to better the interpolation errors near the end-points of the given interval, a correction formula (27) is introduced in Section 4. The efficiency of the presented FNN approximation is demonstrated by the numerical results for the data sets extracted from continuous and discontinuous functions. The aforementioned efficiency means that the proposed method requires less neurons to reach similar or lower error levels than the compared FNN approximation method using the conventional logistic function.

In addition, an extended FNN approximation formula for two variable functions is proposed in Section 5 with some numerical examples showing the superiority of the presented FNN approximation method.

2. A Parametric Sigmoidal Function

The role of the activation function in the artificial neural networks is to introduce non-linearity of the input data into the output of the neural network. One of the useful activation functions commonly used in practice is the sigmoidal function $\sigma$ having the property below.

$$\sigma \left(t\right)\to \left\{\begin{array}{cc}0\hfill & \mathrm{as}t\to -\infty \hfill \\ 1\hfill & \mathrm{as}t\to \infty \hfill \end{array}\right.$$

(2)

For example, two traditional sigmoidal functions are

(i)

Heaviside function:

$${\sigma }_H\left(t\right)=\left\{\begin{array}{cc}0,\hfill & t<0\hfill \\ 1,\hfill & t>0\hfill \end{array}\right.$$

(3)

(ii)

Logistic function:

$${\sigma }_L\left(t\right)=\frac{1}{1+e^{-t}}=\frac{1}{2}\left\{1+tanh(t/2)\right\},-\infty <t<\infty$$

(4)

We recall the following approximation theorem shown in the literature [6].

Theorem 1.

(Costarelli and Spigler [6]) For a bounded sigmoidal function σ and a function $f\in C[a,b]$ let $G_{N}f$ be a neural network approximation to f of the form

$$G_{N}f\left(x\right)=f\left(x_0\right)\sigma \left(\omega (x-x_{-1})\right)+\sum _{k=1}^N\left\{f\left(x_k\right)-f\left(x_{k-1}\right)\right\}\sigma \left(\omega (x-x_k)\right)$$

(5)

for $x\in [a,b]$, $h=(b-a)/N$, and $x_k=a+kh$ $(k=-1,0,1,\cdots ,N)$. Then for every $ϵ>0$ there exists an integer $N>0$ and a real number $\omega >0$ such that

$${∥G_{N}f-f∥}_{\infty }<ϵ.$$

Sigmoidal functions have been used in various applications including the artificial neural networks (See the literature [12,13,14,15,16,17]). In this work we employ an algebraic type sigmoidal function, containing a parameter $m>0$, as follows.

$${\sigma }^{\left[m\right]}\left(t\right)=\left\{\begin{array}{cc}0,\hfill & t<-L\hfill \\ \frac{{(L+t)}^m}{{(L+t)}^m+{(L-t)}^m},\hfill & \left|t\right|\le L\hfill \\ 1,\hfill & t>L\hfill \end{array}\right.$$

(6)

for a fixed $L>0$. This function has the following properties.

(A1)

${\sigma }^{\left[m\right]}$ is strictly increasing over $[-L,L]$ and ${\sigma }^{\left[m\right]}\in C^{\infty }(-L,L)\cap C^{m-1}\left(\mathbf{R}\right)$ for an integer $m\ge 1$. In addition, referring to the literature [12], we can see that the Hausdorff distance d between the heaviside function ${\sigma }_H$ and the presented sigmoidal function ${\sigma }^{\left[m\right]}$ satisfies

$${\left(\frac{L+d}{L-d}\right)}^m=\frac{1}{d}-1,0<d<\min \left\{\frac{1}{2},L\right\}.$$

(7)

That is, $m=O\left(\frac{ln\left(1/d\right)}{ln(1+d)}\right)$ for d small enough.

(A2)

For m large enough ${\sigma }^{\left[m\right]}$ has the asymptotic behavior

$${\sigma }^{\left[m\right]}\left(t\right)=\left\{\begin{array}{cc}O\left(\theta {\left(t\right)}^m\right),\hfill & -L\le t<0\hfill \\ 1+O\left(\theta {\left(t\right)}^m\right),\hfill & 0<t\le L\hfill \end{array}\right.$$

(8)

where

$$\theta \left(t\right)={\left(\frac{L-t}{L+t}\right)}^{\mathrm{sgn}\left(t\right)},$$

(9)

satisfying $0\le \theta \left(t\right)<1$ for all $t\in [-L,L]\backslash \left\{0\right\}$. In addition, for any integer $m\ge 2$

$$\frac{d^j}{d{x}^j}{\sigma }^{\left[m\right]}(\pm L)=0,j=1,2,\cdots ,m-1.$$

(10)

(A3)

For every $m>0$

$${\sigma }^{\left[m\right]}(-t)+{\sigma }^{\left[m\right]}\left(t\right)=1,t\in \mathbf{R}$$

(11)

with ${\sigma }^{\left[m\right]}\left(0\right)=\frac{1}{2}$.

3. Constructing a Neural Network Approximation

Suppose for a real valued function $f\left(x\right)$, $a\le x\le b$, a set of data

$$\{f_k=f\left(x_k\right)|k=0,1,2,\cdots ,N\}$$

is given, where $N\ge 2$ is an integer and $x_k$ are nodes on the interval $[a,b]$. For simplicity, we assume equally spaced nodes as

$$x_k=a+k·h,h=(b-a)/N.$$

(12)

We can observe that, for sufficiently large m, the function ${\sigma }^{\left[m\right]}$ with $L=b-a$ in (6) satisfies

$${\sigma }^{\left[m\right]}\left(t\right)\approx \left\{\begin{array}{cc}0,\hfill & t<0\hfill \\ 1,\hfill & t>0\hfill \end{array}\right.$$

(13)

due to the property (A2).

Moreover, noting that ${\sigma }^{\left[m\right]}$ is an increasing function as mentioned in (A1), we can see that

$${\sigma }^{\left[m\right]}\left(t\right)<\frac{1}{N},\mathrm{for}\mathrm{all}t<{\left({\sigma }^{\left[m\right]}\right)}^{-1}\left(\frac{1}{N}\right)=-L·\frac{{(N-1)}^{1/m}-1}{{(N-1)}^{1/m}+1}$$

(14)

and from the property (A3)

$$1-{\sigma }^{\left[m\right]}\left(t\right)<\frac{1}{N},\mathrm{for}\mathrm{all}t>L·\frac{{(N-1)}^{1/m}-1}{{(N-1)}^{1/m}+1}.$$

(15)

To find a lower bound of the parameter m we set $L·\frac{{(N-1)}^{1/m}-1}{{(N-1)}^{1/m}+1}=h(=L/N)$. Then we have the lower bound $m=m^{*}$, satisfying this equation, as

$$m^{*}=\frac{logN-1}{log\frac{N+1}{N-1}}.$$

(16)

That is, for every $m>m^{*}$ it follows that

$${\sigma }^{\left[m\right]}\left(t\right)<\frac{1}{N},\mathrm{for}\mathrm{all}t<-h$$

(17)

and

$$1-{\sigma }^{\left[m\right]}\left(t\right)<\frac{1}{N},\mathrm{for}\mathrm{all}t>h.$$

(18)

The lower bound $m^{*}$ given in (16) will be used for a threshold of the parameter m in the numerical implementation of the proposed neural network approximation later.

Referring to the above features of ${\sigma }^{\left[m\right]}$ in (13), (17) and (18), we propose a superposition of ${\sigma }^{\left[m\right]}$ to approximate the given data $\{f_k=f\left(x_k\right)|k=0,1,2,\cdots ,N\}$ as follows.

$$S_N^{\left[m\right]}f\left(x\right)=f_0+\sum _{k=1}^N\left(f_k-f_{k-1}\right){\sigma }^{\left[m\right]}\left(x-{\overline{x}}_k\right),x_0\le x\le x_N,$$

(19)

where ${\overline{x}}_k=(x_{k-1}+x_k)/2=x_k-h/2$.

We can see that $S_N^{\left[m\right]}f\left(x\right)$ interpolates $f\left(x\right)$ at $N+1$ nodes, approximately, as implied in the following theorem. Thus we call $S_N^{\left[m\right]}f\left(x\right)$ a quasi-interpolation of $f\left(x\right)$.

Theorem 2.

The FNN $S_N^{\left[m\right]}f\left(x\right)$ with m large enough as defined in $\left(19\right)$ satisfies

$$S_N^{\left[m\right]}f\left(x_j\right)=f_j+C_j{f}^{″}\left({\xi }_j\right)h^2{\delta }^m,1\le j\le N-1$$

(20)

for some ${\xi }_j\in (x_{j-1},x_{j+1})$, $0<\delta <1$ and a constant $C_j$. Moreover,

$$S_N^{\left[m\right]}f\left(x_0\right)=f_0+C_0{f}^{\prime }\left({\xi }_0\right)h{\delta }^m,S_N^{\left[m\right]}f\left(x_N\right)=f_N+C_N{f}^{\prime }\left({\xi }_N\right)h{\delta }^m,$$

for some ${\xi }_0\in (x_0,x_1)$, ${\xi }_N\in (x_{N-1},x_N)$ and constants $C_0,C_N$.

Proof. 

Since ${\sigma }^{\left[m\right]}$ is an increasing function and it satisfies the asymptotic behaviour in (8), for each $1\le j\le N-1$ with m large enough, we have

$$\begin{array}{cc}\hfill S_N^{\left[m\right]}f\left(x_j\right)& \sim f_{j-1}+\left(f_j-f_{j-1}\right){\sigma }^{\left[m\right]}\left(\frac{h}{2}\right)+\left(f_{j+1}-f_j\right){\sigma }^{\left[m\right]}\left(-\frac{h}{2}\right)\hfill \\ & =f_j\left\{1-{\sigma }^{\left[m\right]}\left(-\frac{h}{2}\right)\right\}+f_{j-1}{\sigma }^{\left[m\right]}\left(-\frac{h}{2}\right)+\left(f_{j+1}-f_j\right){\sigma }^{\left[m\right]}\left(-\frac{h}{2}\right)\hfill \\ & =f_j+\left\{f_{j-1}-2f_j+f_{j+1}\right\}{\sigma }^{\left[m\right]}\left(-\frac{h}{2}\right).\hfill \end{array}$$

The second equation above results from the relation ${\sigma }^{\left[m\right]}\left(\frac{h}{2}\right)=\left\{1-{\sigma }^{\left[m\right]}\left(-\frac{h}{2}\right)\right\}$ based on the property (A3). Denoting by $\Delta$ and ${\Delta }^2$ the first and the second forward difference operators, respectively, and using the function $\theta \left(t\right)$ defined in (9), we have

$$S_N^{\left[m\right]}f\left(x_j\right)=f_j+{\Delta }^2{f}_{j-1}O\left(\theta {\left(-\frac{h}{2}\right)}^m\right).$$

Since ${\Delta }^2{f}_{j-1}=f^{″}\left({\xi }_j\right)h^2$ for some ${\xi }_j\in (x_{j-1},x_{j+1})$, setting $\delta =\theta \left(-\frac{h}{2}\right)$, we have the formula (20).

On the other hand, for $x=x_0$ and m large enough

$$S_N^{\left[m\right]}f\left(x_0\right)\sim f_0+\left(f_1-f_0\right){\sigma }^{\left[m\right]}\left(-\frac{h}{2}\right)=f_0+\Delta f_{0}O\left(\theta {\left(-\frac{h}{2}\right)}^m\right).$$

Since $\Delta f_0=f^{\prime }\left({\xi }_0\right)h$ for some ${\xi }_0\in (x_0,x_1)$, we have

$$S_N^{\left[m\right]}f\left(x_0\right)=f_0+C_0{f}^{\prime }\left({\xi }_0\right)h{\delta }^m$$

for a constant $C_0$. For $x=x_N$ and m large enough

$$\begin{array}{cc}\hfill S_N^{\left[m\right]}f\left(x_N\right)& \sim f_{N-1}+\left(f_N-f_{N-1}\right){\sigma }^{\left[m\right]}\left(\frac{h}{2}\right)\hfill \\ & =f_{N-1}+\left(f_N-f_{N-1}\right)\left\{1-{\sigma }^{\left[m\right]}\left(-\frac{h}{2}\right)\right\}\hfill \\ & =f_N-\left(f_N-f_{N-1}\right){\sigma }^{\left[m\right]}\left(-\frac{h}{2}\right)\hfill \\ & =f_N+\Delta f_{N-1}O\left(\theta {\left(-\frac{h}{2}\right)}^m\right).\hfill \end{array}$$

Since $\Delta f_{N-1}=f^{\prime }\left({\xi }_N\right)h$ for some ${\xi }_N\in (x_{N-1},x_N)$, we have

$$S_N^{\left[m\right]}f\left(x_N\right)=f_N+C_N{f}^{\prime }\left({\xi }_N\right)h{\delta }^m$$

for a constant $C_N$. Thus the proof is completed.  □

Theorem 2 implies that, for N fixed(i.e., h fixed), approximation errors of $S_N^{\left[m\right]}f\left(x\right)$ at every nodes can be accelerated by increasing the value of the parameter m.

The sum $S_N^{\left[m\right]}f\left(x\right)$ in (19) can be written by

$$\begin{array}{cc}\hfill S_N^{\left[m\right]}f\left(x\right)& =f_0\left\{1-{\sigma }^{\left[m\right]}\left(x-{\overline{x}}_1\right)\right\}+f_N{\sigma }^{\left[m\right]}\left(x-{\overline{x}}_N\right)\hfill \\ & +\sum _{k=1}^{N-1}{f}_k\left\{{\sigma }^{\left[m\right]}\left(x-{\overline{x}}_k\right)-{\sigma }^{\left[m\right]}\left(x-{\overline{x}}_{k+1}\right)\right\}.\hfill \end{array}$$

(21)

Using a function ${\psi }^{\left[m\right]}$ defined as

$${\psi }^{\left[m\right]}\left(t\right)={\sigma }^{\left[m\right]}\left(t+h/2\right)-{\sigma }^{\left[m\right]}\left(t-h/2\right),-L\le t\le L,$$

(22)

with $L=b-a$, satisfying $0\le {\psi }^{\left[m\right]}\left(t\right)\le 1$ for all t, we may rewrite $S_N^{\left[m\right]}f\left(x\right)$ by

$$S_N^{\left[m\right]}f\left(x\right)=f_0\left\{1-{\sigma }^{\left[m\right]}\left(x-{\overline{x}}_1\right)\right\}+f_N{\sigma }^{\left[m\right]}\left(x-{\overline{x}}_N\right)+\sum _{k=1}^{N-1}{f}_k{\psi }^{\left[m\right]}\left(x-x_k\right)$$

(23)

for $x_0\le x\le x_N$. In fact, it follows that

$${\psi }^{\left[m\right]}\left(x-x_k\right)={\sigma }^{\left[m\right]}\left(x-{\overline{x}}_k\right)-{\sigma }^{\left[m\right]}\left(x-{\overline{x}}_{k+1}\right),1\le k\le N-1.$$

(24)

The formula (23) is a form of the feed-forward neural networks based on the activation function ${\psi }^{\left[m\right]}$ with constant weights $w_k=1$ and thresholds $x_k$.

Under the assumption that m is large enough, the proposed quasi-interpolation $S_N^{\left[m\right]}f\left(x\right)$ in (23) has the following properties:

(B1)

Since $1-{\sigma }^{\left[m\right]}\left(x-{\overline{x}}_1\right)\approx {\psi }^{\left[m\right]}\left(x-x_0\right)$ and ${\sigma }^{\left[m\right]}\left(x-{\overline{x}}_N\right)\approx {\psi }^{\left[m\right]}\left(x-x_N\right)$ over the interval $[a,b]=\left[x_0,x_N\right]$, it follows that

$$S_N^{\left[m\right]}f\left(x\right)\approx \sum _{k=0}^N{f}_k{\psi }^{\left[m\right]}\left(x-x_k\right),x_0\le x\le x_N.$$

(25)

(B2)

For each $k=0,1,2,\cdots ,N$,

$${\psi }^{\left[m\right]}\left(x_j-x_k\right)\approx \left\{\begin{array}{cc}1,\hfill & j=k\hfill \\ 0,\hfill & j\ne k\hfill \end{array}\right.$$

and

$${\psi }^{\left[m\right]}\left({\overline{x}}_k-x_k\right)={\psi }^{\left[m\right]}\left({\overline{x}}_{k+1}-x_k\right)={\psi }^{\left[m\right]}\left(\pm \frac{h}{2}\right)\approx \frac{1}{2}.$$

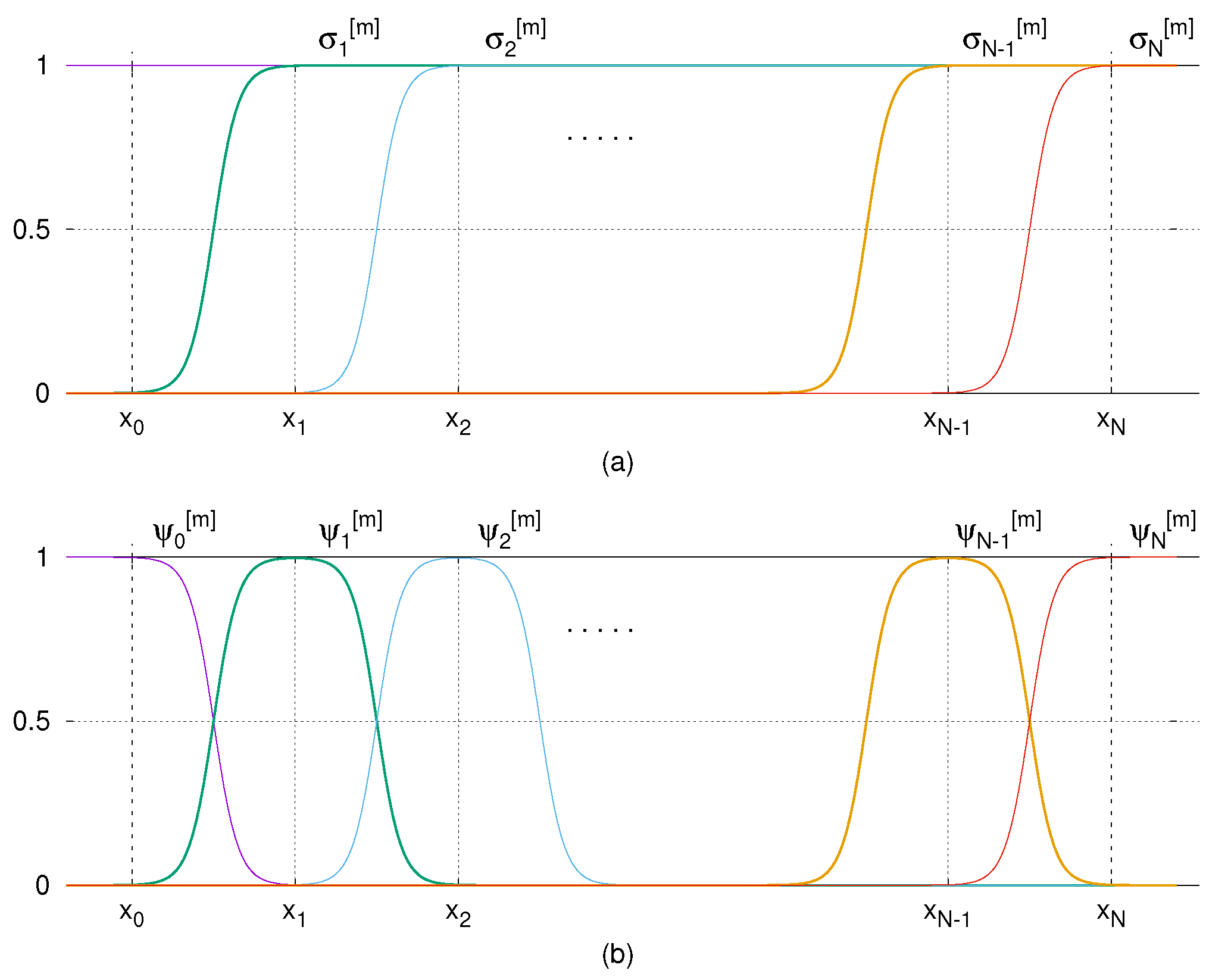
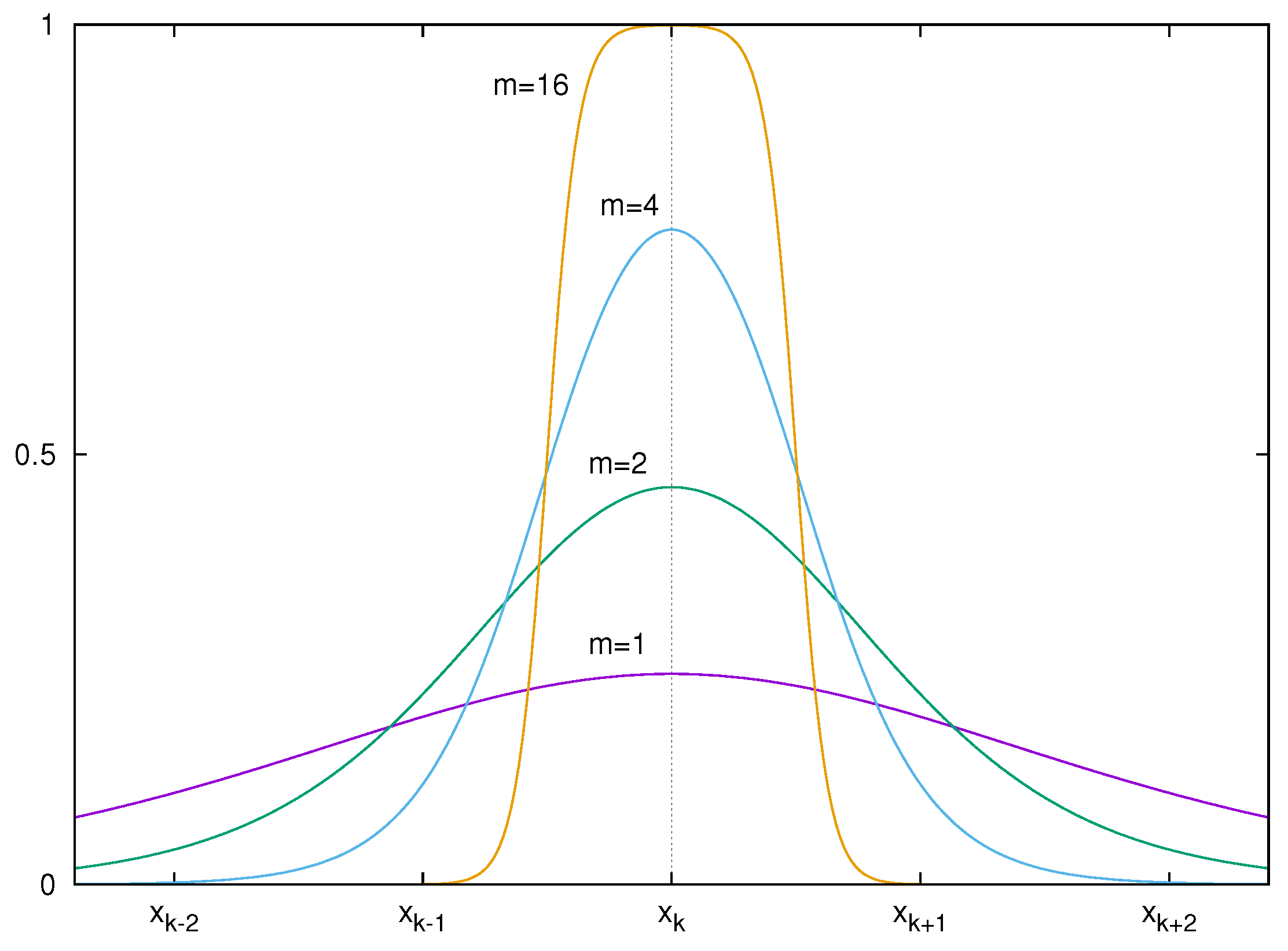
Graphs of the activation functions, ${\sigma }_k^{\left[m\right]}\left(x\right):={\sigma }^{\left[m\right]}\left(x-{\overline{x}}_k\right)$ and ${\psi }_k^{\left[m\right]}\left(x\right):={\psi }^{\left[m\right]}\left(x-x_k\right)$ shown in Figure 1 illustrate the intuition of the construction of the presented quasi-interpolation $S_N^{\left[m\right]}f\left(x\right)$. In addition, Figure 2 includes the graphs of ${\psi }_k^{\left[m\right]}\left(x\right)$ with respect to the values $m=1,2,4,16$, which shows that ${\psi }_k^{\left[m\right]}\left(x\right)$ becomes flatter near the node $x_k$ and far from the node as the parameter m goes higher.

Figure 1. Graphs of the sigmoidal functions ${\sigma }_k^{\left[m\right]}\left(x\right)$ in (a) and those of ${\psi }_k^{\left[m\right]}\left(x\right)$ in (b).

Figure 2. Graphs of ${\psi }_k^{\left[m\right]}\left(x\right)$ for each $m=1$, 2, 4, and 16.

It is well known that the interpolants for continuous functions are guaranteed to be good if and only if the Lebesgue constants are small [15]. Regarding the formula (25) as an interpolation with equispaced points ${\left\{x_k\right\}}_{k=0}^N$, its Lebesgue function satisfies

$${\lambda }_N\left(x\right):=\sum _{k=0}^N\left|{\psi }^{\left[m\right]}\left(x-x_k\right)\right|=\sum _{k=0}^N{\psi }^{\left[m\right]}\left(x-x_k\right)\approx 1$$

for all x, and thus the corresponding Lebesgue constant becomes ${\Lambda }_N={∥{\lambda }_N\left(x\right)∥}_{\infty }\approx 1$. Noting that for the polynomial interpolation, the Lebesgue constant grows exponentially such as ${\Lambda }_N\sim \frac{2^{N+1}}{eNlogN}$ as $N\to \infty$, we may expect that $S_N^{\left[m\right]}f\left(x\right)$ will be better than the polynomial interpolation in approximation to any continuous function, at least.

4. Correction Formula

In order to improve the interpolation errors near the end-points of the given interval, that is, to make the formula (20) in Theorem 2 hold for all $0\le j\le N$, we employ two values at the points $x_{-1}:=x_0-h=a-h$ and $x_{N+1}:=x_N+h=b+h$ defined as

$$f_{-1}=2f_0-f_1,f_{N+1}=2f_N-f_{N-1}.$$

(26)

Using these additional data, we define a correction formula of (23) as

$$S_N^{\left[m\right]}f\left(x\right)=f_{-1}\left\{1-{\sigma }^{\left[m\right]}\left(x-{\overline{x}}_0\right)\right\}+f_{N+1}\left(x\right){\sigma }^{\left[m\right]}\left(x-{\overline{x}}_{N+1}\right)+\sum _{k=0}^N{f}_k{\psi }^{\left[m\right]}\left(x-x_k\right).$$

(27)

To explore the availability of the proposed approximation method (27), we consider the following examples which were employed in the literature [6].

Example 1.

A smooth function on the interval $[-5,5]$.

$$f_1\left(x\right)=\left(2+{cos}^{2}x\right)sinx+2x+\frac{x^2}{8}+4,-5\le x\le 5,$$

Example 2.

A function with jump-discontinuities.

$$f_2\left(x\right)=\left\{\begin{array}{cc}\frac{4}{x^2-2},\hfill & x<-2\hfill \\ -3,\hfill & -2\le x<0\hfill \\ \frac{5}{2},\hfill & 0\le x<2\hfill \\ \frac{3x+2}{x^3-1},\hfill & x\ge 2,\hfill \end{array}\right.$$

We compare the results of the presented method with those of the existing neural network approximation method (5) using the activation function $\sigma ={\sigma }_L$ in (4). In the literature [6], it was proved that Theorem 1 holds if the weight $\omega$ is chosen such as

$$\omega >\frac{N}{L}log(N-1),L=b-a.$$

(28)

In practice, we have used $\omega =N^2/L$ in implementation of the existing FNN $G_{N}f\left(x\right)$ in (5) for the examples above. The high level software, Mathematica(V.10) has been used as a programming tool throughout the numerical performance for the examples.

For the smooth function $f_1$ in Example 1, approximations of the proposed FNN $S_N^{\left[m\right]}{f}_1\left(x\right)$, with small number of neurons ($N=10$) are shown in Figure 3 with respect to each parameter $m=10,15,20,30$. The higher the value of m is, the more clearly $S_N^{\left[m\right]}{f}_1\left(x\right)$ reveals the so-called quasi-interpolation property as shown in Theorem 2. Moreover, Figure 4 shows errors of $S_N^{\left[m\right]}{f}_1\left(x\right)$ with $m=2N>m^{*}$, for $m^{*}$ the lower bound of m as given in (16), compared with errors of $G_N{f}_1\left(x\right)$ for $N=10,20,30,\cdots ,80$. Therein the errors are defined as ${∥S_N^{\left[m\right]}{f}_1\left(x\right)-f_1∥}_{\infty }/{∥f_1∥}_{\infty }$ and ${∥G_N{f}_1\left(x\right)-f_1∥}_{\infty }/{∥f_1∥}_{\infty }$. The figure illustrates that the presented FNN is superior to the existing FNN $G_N{f}_1\left(x\right)$ for continuous test function $f_1$.

Figure 3. Approximations to $f_1\left(x\right)$ by the presented feed-forward neural networks (FNN) $S_N^{\left[m\right]}{f}_1\left(x\right)$ with $N=10$ for each $m=10,15,20,30$.

Figure 4. Errors of the presented FNN approximations $S_N^{\left[m\right]}{f}_1\left(x\right)$ with $m=2N$ and the existing FNN approximations $G_N{f}_1\left(x\right)$ for $N=10,20,30,\cdots ,80$.

For the discontinuous function $f_2$ in Example 2, approximations of the proposed FNN $S_N^{\left[m\right]}{f}_2\left(x\right)$, with small number of neurons ($N=10$), are shown in Figure 5 with respect to each $m=10,20,40,80$. In addition, approximations of $S_N^{\left[m\right]}{f}_2\left(x\right)$ for various values $N=10,20,40,80$, with $m=4N$, are also given in Figure 6. One can see that the results of the presented method $S_N^{\left[m\right]}{f}_2\left(x\right)$ are better than those of $G_N{f}_2\left(x\right)$ shown in Figure 7. On the other hand, it is noted that the FNN approximations are free from the so-called Gibbs phenomenon, generating wiggles (i.e., overshoots and undershoots) near the jump-discontinuity, which appears inevitably in partial sum approximations composed of the polynomial or trigonometric base functions in general.

Figure 5. Approximations to $f_2\left(x\right)$ by the presented FNN $S_N^{\left[m\right]}{f}_2\left(x\right)$ with $N=10$ for each $m=10,20,40,80$.

Figure 6. Approximations to $f_2\left(x\right)$ by the presented FNN $S_N^{\left[m\right]}{f}_2\left(x\right)$ for each $N=10,20,40,80$ with $m=4N$.

Figure 7. Approximations to $f_2\left(x\right)$ by the existing FNN $G_N{f}_2\left(x\right)$ for each $N=10,20,40,80$.

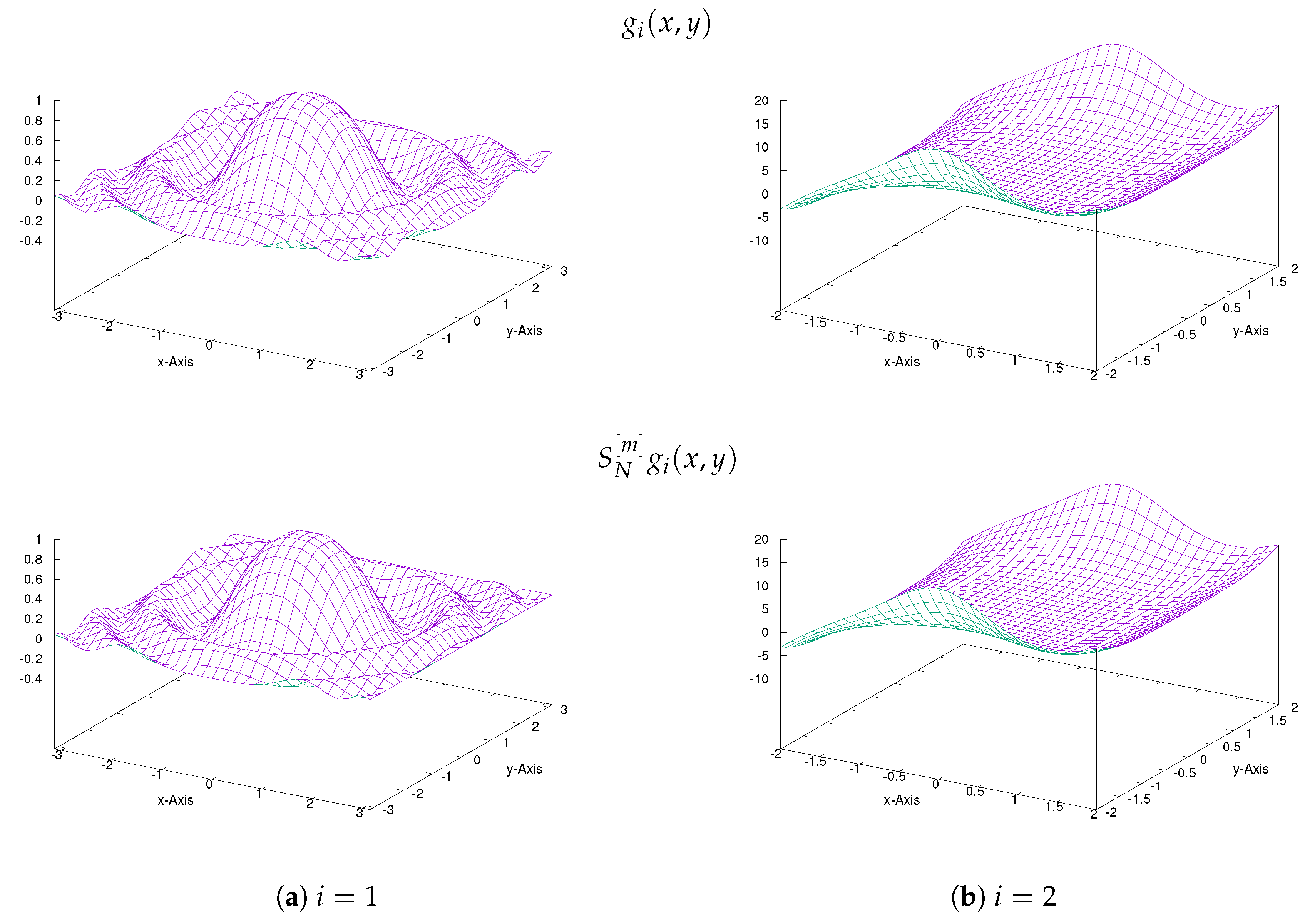
5. Multivariate Approximation

For simplicity we consider a function of two variables $g(x,y)$ on a region $[a,b]\times [c,d]\subset {\mathbf{R}}^2$, and assume that a set of data ${\left\{g_{ij}=g\left(x_i,y_j\right)\right\}}_{0\le i,j\le N}$ is given for the nodes

$$x_i=i·h_x,y_j=j·h_y,$$

where $h_x=(b-a)/N$, $h_y=(d-c)/N$. Set activation functions

$${\psi }_{i,j}^{\left[m\right]}(x,y)={\sigma }^{\left[m\right]}\left({\chi }_i\left(x\right)|x-{\overline{x}}_i|\right)·{\sigma }^{\left[m\right]}\left({\chi }_j\left(y\right)|y-{\overline{y}}_j|\right)$$

(29)

for $0\le i,j\le N$, where ${\overline{\xi }}_k=({\xi }_{k-1}+{\xi }_k)/2$,

$${\chi }_k\left(\xi \right)=\left\{\begin{array}{cc}1,\hfill & {\xi }_{k-1}<\xi \le {\xi }_k\hfill \\ -1,\hfill & \mathrm{otherwise}\hfill \end{array}\right.$$

(30)

and ${\sigma }^{\left[m\right]}$ is the parametric sigmoidal function in (6). Then, referring to the formula (25) under the assumption that m is large enough, we define an extended version of the FNN approximation to g as

$$\begin{array}{c}\hfill S_N^{\left[m\right]}g(x,y)=\sum _{i=0}^N\sum _{j=0}^N{g}_{ij}{\psi }_{i,j}^{\left[m\right]}(x,y).\end{array}$$

(31)

To testify the efficiency of the presented method (31), we choose functions of two variables below. In the numerical implementation for the examples the software, gnuplot(V.5) was used as it is rather fast for evaluating and graphing on two dimensional region.

Example 3.

$$g_1(x,y)=\frac{sin(x^2+y^2+1)}{x^2+y^2+1},-\pi \le x,y\le \pi .$$

(32)

Example 4.

$$g_2(x,y)=\frac{x^5+y^4}{x^2+1},-2\le x,y\le 2.$$

(33)

Figure 8 shows the approximations of the presented method $S_N^{\left[m\right]}{g}_i(x,y)$ to the test functions $g_i(x,y)$, $i=1,2$, for $N=30$ with $m=120$. We can see that $S_N^{\left[m\right]}{g}_i(x,y)$ approximates $g_i(x,y)$ properly over the whole region, while the existing method $G_N{g}_i(x,y)$ given in the literature [6] produces considerable errors as shown in Figure 9.

Figure 8. Test functions $g_i(x,y)$(: upper row), $i=1,2$, and their approximations by the presented FNN $S_N^{\left[m\right]}{g}_i(x,y)$(: lower row) for $N=30$ with $m=120$.

Figure 9. Test functions $g_i(x,y)$(: upper row), $i=1,2$, and their approximations by the existing FNN approximations $G_N{g}_i(x,y)$(: lower row) for $N=30$.

6. Conclusions

In this work we proposed an FNN approximation method based on a new parametric sigmoidal activation function ${\sigma }^{\left[m\right]}$. It has been shown that the presented method with the parameter m large enough has a feature of the quasi-interpolation at the given nodes. As a result, we can note that the presented method is better than the existing FNN approximation method as demonstrated by the numerical results for several examples of univariate continuous and discontinuous functions. Additionally, the availability of the method in extended application to the multivariate function was illustrated.