Abstract
Networks have an important role in our daily lives. The effectiveness of the network decreases with the breaking down of some vertices or links. Therefore, a less vulnerable communication network is required for greater stability. Vulnerability is the measure of resistance of the network after failure of communication links. In this article, a graph has been taken for modeling a network and integrity as a measure of vulnerability. The approach is to estimate the integrity or upper bound of integrity of at least one connected graph or network constructed from the given graphic integer sequence. Experiments have been done with random graphs, complex networks and also a comparison between two parameters, namely the vertex connectivity and graph integrity as a measure of the network vulnerability have been carried out by removing vertices randomly from various complex networks. A comparison with the existing method shows that the algorithm proposed in this article provides a much better integrity measurement.
1. Introduction
A communication network contains nodes or processors and communication links. Link cuts, software errors, node interruptions, hardware and transmission failures at various points can cause service interruption for a long time and as a consequence effectiveness may be lost. These events are termed as the vulnerability of communication networks [1,2]. Two parameters are important for analyzing the vulnerability of a communication network and they are (i) the number of non-functioning nodes, (ii) the remaining group size within which mutual communication can occur. It is very important and desirable for an adversarial relationship to make the above two quantities simultaneously small [3].
Many graph-theoretic parameters are there that can be used to measure the vulnerability of communication networks, which includes connectivity, tenacity, integrity, toughness, binding number and more [1]. This paper considers integrity as the measure of vulnerability as it is a useful measure of vulnerability with respect to other parameters [4]. The concept of integrity of a graph was introduced in [5]. The integrityof a simple connected graph G with V number of vertices is defined by I(G) = {|S| + m(G-S)}, where |S| and m(G-S) denote the subset of vertices V and the order of the largest component of G-S, respectively [3]. Integrity shows not only the difficulty to break down the network but also the damage that has been caused.
In Figure 1, a small comparison between connectivity [6,7] and integrity as the measure of vulnerability has been shown. It can be seen that integrity as the measure of vulnerability gives a good result. The connectivity of both graphs G1 and G2 is 1, so it clearly cannot differentiate the vulnerability of both graphs, but the integrity of G1 and G2 is 3 and 4, respectively. Therefore, with this measure it can be concluded that G2 is less vulnerable than G1.
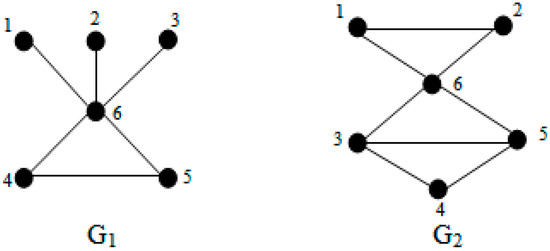
Figure 1.
Connectivity and integrity of graphG1 (graphic integer sequence 5, 2, 2, 1, 1, 1) and G2 (graphic integer sequence 4, 3, 3, 2, 2, 2) as the measure of the network vulnerability where the connectivity of both graphs is 1 but the integrity is 3 and 4, respectively.
An integer sequence is an ordered list ofintegers [8,9]. There are various integer sequences. This article considers integer sequences that are graphic. A graphic integer sequence [10,11] is a universal representation structure of a graph. It is an inherent characteristic of any graph. A sequence d1, d2, …, dn of non-negative integersis called graphic if there is at least one graph on vertices {1, 2, …, n},such that vertex k has degree dk [10,12]. If the labeling is added to a graphic integer sequence, at least one graph can be uniquely drawn. Therefore, this is a universal superset of all other graph representation [12].
As the determination of graph integrity is an NP-Complete problem [13], the measure of integrity cannot be done in polynomial time; especially for large networks. This is a novel approach which provides the estimate of integrity or upper bound ofintegrity of at least one connected graph constructed from the given graphic integer sequence in polynomial time and space. The algorithm proposed here uses the concept of [14,15], where the authors find the maximal clique number. Using this concept, the author of this article first finds the minimal vertex cover number and then the estimate of integrity of the given graph. The advantage is that the proposed algorithm finds the approximate integrity in seconds.
The organization of the article is as follows: Section 2 illustrates the preliminary ideas behind the proposed technique. Section 3 of this paper contains some known results related to graph integrity. Section 4 contains some related works with vulnerability measurement. In Section 5, the proposed algorithm has been described and in Section 6, the algorithm is illustrated with an example. Section 7 explains some results. Concluding remarks are given in Section 8.
2. Preliminaries
This section contains some terms and theorems that act as the basis of the proposed algorithm. For various graph-theoretic terminologies readers may refer to [6,7,16].
Definition 1.
A Vertex Cover in a graph G is a set of vertices that covers all edges of G [9]. The covering set with the minimum number of vertices of G is thecovering number of Gand is denoted by α(G) [6,7,16].
Definition 2.
A subset of vertices of G with no two adjacent vertices is called an independent set. The independent set with the maximum number of vertices is called a maximum independent set (MIS) of G and the number of vertices in MIS is the independence number of the graph Gand is denoted by β(G). “The order n of a graph G is defined by α(G) + β(G) = n” [6,7,16].
Definition 3.
A clique in a graphG is a complete subgraphofG. The order of the largest clique in a graph G is itsclique number of Gand is denoted by ω(G) [16,17].
Definition 4.
A sequence x = d1, d2, d3, …, dn of non-negative integers is said to be a graphic sequence if there exists a graph G whose vertices have degree di [1 ≤ i ≤ n] and G is called realization of x [14].
Definition 5.
If x = d1, d2, d3, …, dn is the graphic integer sequence of a graph G and x’= p1 ≥ p2 ≥ … ≥ pn is the graphic integer sequence of the complement of the graph G denoted by , then G contains the independence number k, then m = ∑(pi− k+1)[1 ≤ i ≤ k] and drop-m implies reducing the largest terms among pk+1, pk+2, …, pn by unity, where ‘m’ of operation drop-m is the number of edges between the vertices of the largest clique of and the remaining vertices of [14].
Theorem 1.
For a given graph G and an integer k, the problem of deciding whether the integrity of G is at most k is NP-Complete, even for planar graphs [13].
Theorem 2.
A vertex covering S of a graph G is minimum if and only if MIS = V(G)\S is a maximum independent set of G [18].
Theorem 3.
A subset of V(G) is a clique of G if and only if it is an independent set of . Furthermore, ω(G)= β() and ω() = β(G) [19].
Theorem 4.
Let x = d1, d2, d3, …, dn be the graphic integer sequence of a graph G and x’ = p1 ≥ p2 ≥ … ≥ pn be the graphic integer sequence of graph . The graph G contains the independence number k if and only if p1 ≥ p2 ≥ … ≥ pk ≥ k−1, k ≤ n and the sequence after drop-m, (pk+1, pk+2, …, pn) is graphic.
Proof.
Let x represent a graphic integer sequence of graph G and after drop-m from , a new sequence is generated that is not graphic. Drop-m implies deletion of complete subgraph from and reducing n-k term by unity. Therefore, after drop-m a new sequence x’ is produced. Since x is graphic, so x’ must be a graphic integer sequence, this contradicts the assumption. Hence, this proves the theorem. □
3. Known Results on Graph Integrity
Theorem 5.
([3]) For any graph G when I(G) is the integrity of G, then
- (a)
- I(G) ≤ α (G) + 1
- (b)
- I(G) ≥ δ (G) +1 [ where δ (G) =minimum vertex degree of G]
- (c)
- I(G) ≥ χ (G) [where χ (G) = chromatic number of G]
- (d)
- I(G) = κ (G) +1 if and only if κ (G) = α (G) [where κ (G) = connectivity of G].
Theorem 6.
([3]) The integrity of
- (a)
- The complete graph Kn is n [where n is the number of vertices]
- (b)
- The null graph is 1.
- (c)
- The Pn is −2.
- (d)
- The cycle Cn is −1.
- (e)
- The complete bipartite graph Kt,p is 1 + min {t, p}.
4. Related Works
There are many graph-theoretic parameters for measuring the vulnerability of thenetwork. This section contains some related works. First, in [20,21] authors used connectivity as the measure of vulnerability. Next, in [22] authors discussed the relationship between the safe number and integrity of a graph and in [23] authors studied the bounds and relationships among the scattering number, integrity, and tenacity which are better than other parameters for measuring the stability of networks. In addition, authors of [24,25,26,27] studied the integrity of fuzzy graphs, hub integrity, relationships among integrity and component order connectivity, domination integrity and edge, and hub integrity of the graph, respectively. Next, in [13,28] authors used tenacity as the vulnerability measure. The scattering number and rupture degree has been discussed in [29,30,31,32,33,34]. The authors of [4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37] proved that computing the vulnerability parameters such as integrity, scattering number etc. of a graph is NP-hard in general. Also in [38], authorsstudied the robustness and fragility of scale-free networks under topologically biased failure (degree-dependent percolation) based on the natural connectivity as the measure of vulnerability.
5. Proposed Algorithm
The problem is to find out the estimate of integrity or upper bound of the integrity of at least one connected graph G constructed from the given graphic integer sequence. The target is toestimateor compute the upper bound of α(G) which in turn gives the estimate of I(G) as I (G) ≤ α (G) + 1 (Theorem 5a). Therefore, in this algorithm at first ω(), i.e., the maximum clique number of the complement of the graph G is computed. If k be the maximum clique number of , then there must be at least k number of integers which are greater than or equal to k−1. Therefore, 1st k integers with a value greater than or equal to k−1 has been taken from the given graphic integer sequence, which represents a complete subgraphof k vertices. Deleting this subgraph from , a graph with total edges e’= e’−{k(k−1)/2+m} has been produced, where e’ is the total number of edges of and m = ∑(di’− k+1) [1 ≤ i ≤ k]. Then, after drop-m (from Definition 5) if the remaining sequence represents a graphic sequence, then k is the maximum clique number, otherwise the same process is continued. Therefore, from ω(), β(G) is computed according to Theorem 3. Lastly, α(G) is computed from β(G) according to the formula α(G) = n-β(G)(from Definition 2). The Algorithm 1 is depicted below:
| Algorithm 1. Calculate Graph Integrity |
| Input: Graphic integer sequence x = d1, d2, …, dn in non-increasing order, number of vertices (n). Output: Integrity (I(G)) of the graph G produced from x. Begin Step 1: x= d1 ≥ d2 ≥ d3 ≥ … ≥ dn; Step 2: If e=n(n − 1)/2, then I(G)=n, goto step 9; (where e = (d1+d2…+dn)/2). Step 3: If e=0, then I(G)=1, goto step 9. Step 4: Compute the complement of the given graphic integer sequence. x’ = (n − 1) −dn ≥ (n − 1) − dn−1 ≥ … ≥ (n − 1) − d1, k = (n − 1) − dn. Suppose, (n − 1) −dn= p1, (n − 1) − dn−1 = p2,…, (n − 1) − d1 = pn. Now, x’ = p1 ≥ p2 ≥ … ≥ pn and k = p1. Step 5: If (p1 ≥ p2 ≥ … ≥ pk≥ (k − 1)), then Continue. Else Goto step 7. End If Step 6: If (pk+1 ≥ pk+2 ≥ … ≥ pn) is graphic (using the Havel–Hakimi [7] algorithm) after drop-m (refer Section 2) Then Goto step 8. Else Continue. End If Step 7: If k ≠ 0, k=k − 1, goto step 5. Step 8: Compute minimal vertex cover (VC) = n-k and I(G)= |VC| +1. Step 9: End |
Claim 1.
The time complexity of the algorithm proposed in this article is O(n3) where n is the number of vertices and space complexity is O(n).
In step 6, the Havel–Hakimi algorithm [7] is used for checking if the sequence is graphic or not. For ‘n’ number of vertices the time complexity of Havel–Hakimi algorithm is O(n2). As the maximum number of iterations of the proposed algorithm is ‘n’, thus the overall time complexity of the proposed algorithm is O(n3). In addition, as this algorithm only considers a graphic integer sequence as the representation of graph, so its space complexity is O(n).
6. Illustration with Example
Example 1.
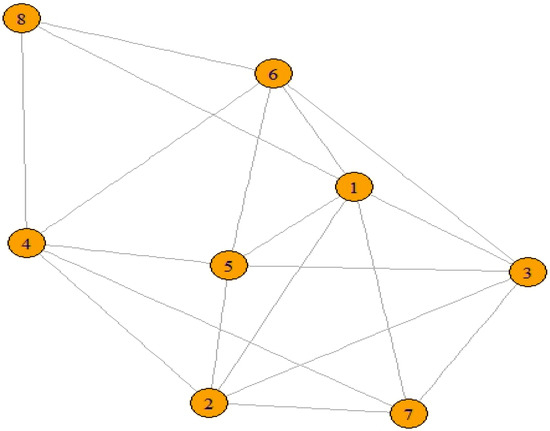
Let us consider the graphic integer sequence x= 6,5,5,5,5,5,4,3 and have to find integrity of graph G in Figure 2 produced from x.

Figure 2.
Graph with 8 vertices and graphic integer sequence 6, 5, 5, 5, 5, 5, 4, 3.
- First, compute x’ = 4,3,2,2,2,2,2,1.
- As d1′ = 4, so k = 4,
- As p3 = 2 <3, so condition of step 5 failed.
- Now, in next iteration k=k − 1=3 (according to step 7 of the algorithm),
- As p1 ≥ p2 ≥ p3 ≥ 2,
- m = ∑(pi− k+1) [1 ≤ i ≤ 3] = (2 + 1 + 0) = 3
- After drop-m from (p4, p5, p6, p7, p8) the new sequence x’’ = (2,1,1,1,1) which is graphic.
- So, the sequence contains VC = (8-3) = 5 and integrityI(G) = 6.
Example 2.
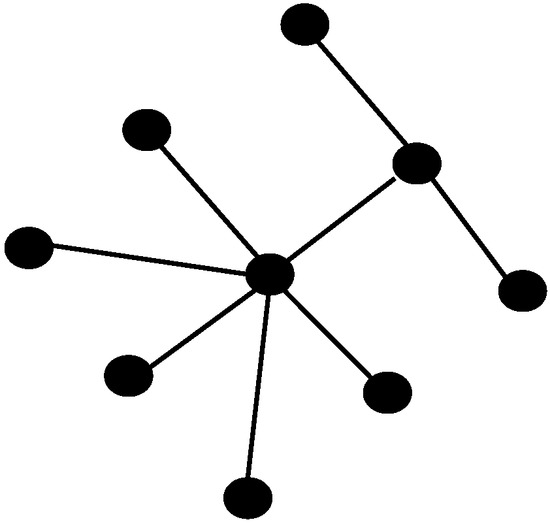
The Graph in Figure 3 has the actual integrity is 3 and with the proposed algorithm integrity is 3. Hence, in this case the algorithm gives exact integrity.

Figure 3.
Graph with 9 vertices and graphic integer sequence 6, 3, 1, 1, 1, 1, 1, 1, 1.
Example 3.
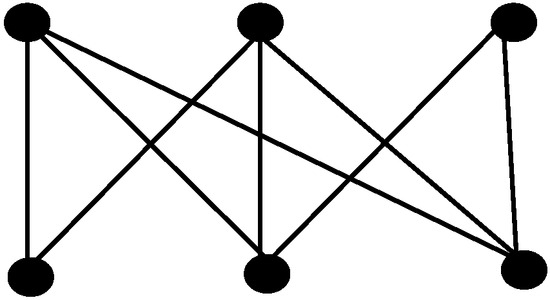
The Graph in Figure 4 has the actual integrity is 4 and with the proposed algorithm integrity is 5. Hence, in this case the algorithm gives estimate of integrity or upper bound of integrity.

Figure 4.
Graph with 6 vertices and graphic integer sequence 3,3, 3, 3, 3, 3.
7. Experimental Results
The algorithm proposed in the article has been coded in C, and compiled using a Cygwin 64 bit c++ compiler and an AMD APU 2.20 GHz processorwith 4 GBRAM. In Figure 5, Figure 6 and Figure 7, the integrity of the Random graph [39], scale-free graph [40] and small-world graph [41] respectively has been shown as measured by the proposed algorithm. Figure 8 shows the time complexity of the proposed algorithmand it can be seen that it follows moving average trend line with period 2. All graphs were generated with software R [42].
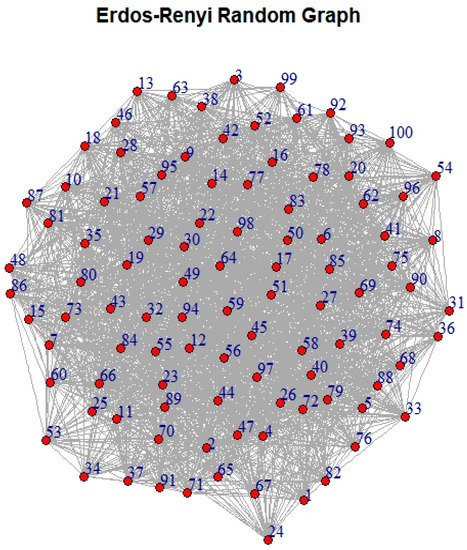
Figure 5.
Random graph (Erdos–Renyirandom graph model [39]) with integrity (measured by the proposed algorithm) = 49.
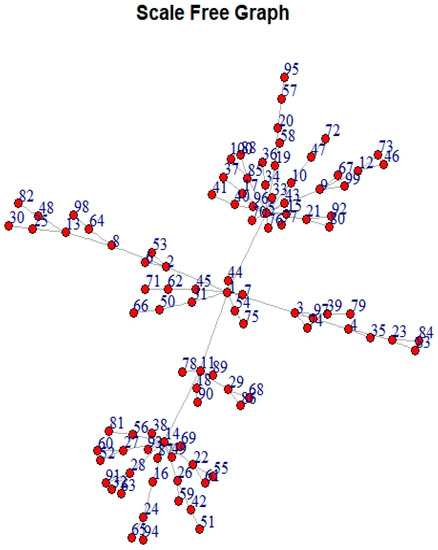
Figure 6.
Scale-free graph (Barabasi–Albert preferential attachment model [40]) with integrity (measured by the proposed algorithm) =35.

Figure 7.
Small-world graph (Watts–Strogatz small-world model [41]) with integrity (measured by the proposed algorithm) =44.
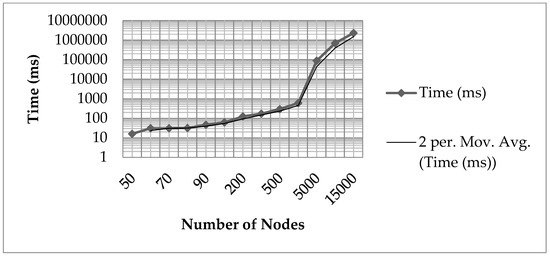
Figure 8.
Time complexity of the proposed algorithm (measured in milliseconds) with moving average trend line period 2.
Figure 9, Figure 10, Figure 11 and Figure 12 shows the effect of random vertex removal from the random graph, scale-free graph and small-world graph, respectively by removing 0, 20, 40, 60 vertices, respectively at random. It can be seen from the figures thatintegrity gives a better measurement of vulnerability than vertex connectivity.
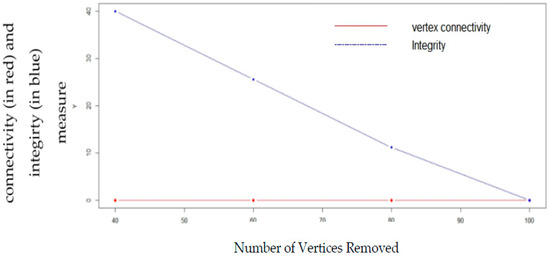
Figure 9.
Comparison of vertex connectivity and integrity with random node removal in Erdos–Renyirandom graph model with probability =0.05.
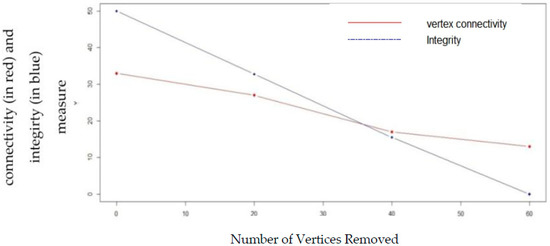
Figure 10.
Comparison of vertex connectivity and integrity with random node removal in Erdos–Renyirandom graph model with probability =0.5.
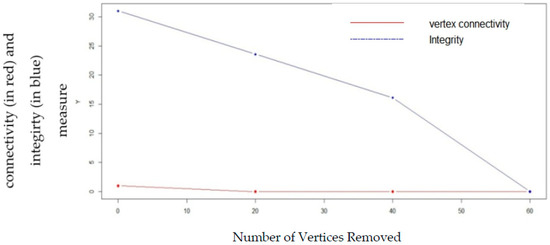
Figure 11.
Comparison of vertex connectivity and integrity with random node removal in Barabasi–Albert preferential attachment model.
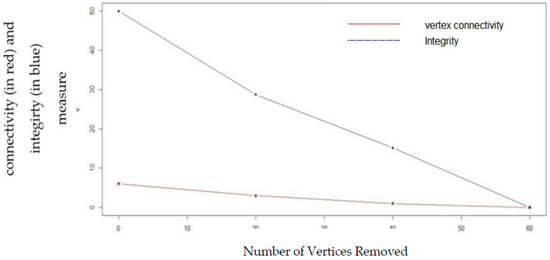
Figure 12.
Comparison of vertex connectivity and integrity with random node removal in Watts–Strogatz small-world model.
Table 1 compared the proposed method with the existing method in [43] termed as Method 1 in this paper. In Method 1, graph integrity has been measured using graph coloring. Random graph 100, 200 and 300 vertices and with probability 0.6, 0.5, 0.4, respectively, Valdis Krebs’ Initial Mapping of the 9/11 Hijackers’ Network [44] with 19 nodes and Road Network of Burdwan, W. Bengal, India [45] with 60 nodes and 70 edges has been used in this experiment. If the integrity of the graph in example 2 of Section 6 is measured with Method 1 then the output will be 4. Therefore, the integrity measure of the proposed method is more accurate than Method 1, at least for the data considered in Table 1 of this article. Though the time complexity of Method 1 is a little less, the proposed method surpasses Method 1 in terms of integrity measure. Additionally, in terms of space complexity, Method 1 required loadingtheentire graph in the memory at the time of execution but the proposed algorithm only requiredthe graphic integer sequence. Therefore, the proposed scheme required much less space compared to Method 1.

Table 1.
Comparison of integrity measure and time complexity of Method 1 and the proposed method.
8. Conclusions
Network vulnerability measures the robustness of the network. Among all other graph parameters, graph integrity is a well-known measure of vulnerability of the network because it considers two conditions after network failure like (i) the number of non-functioning nodes, (ii) the remaining size of the group within which communication can still occur. However, measuring graph integrity cannot be done in polynomial time especially for large complex networks as it is an NP-Hard problem. To cope with this, in this article authors proposed an algorithm that combines universal graph representation, i.e., a graphic integer sequence with the integrity to measure the network vulnerability in linear time. With respect to other methods, it gives a more accurate measurement of integrity. In terms of space, the proposed algorithm is much better also. Additionally, the integrity measure of large complex networks with the Erdos–Renyi random graph model, Watts–Strogatz small-world model and Barabasi–Albert preferential attachment model has been shown. A comparison between vertex connectivity and integrity shows that integrity gives a better measurement of vulnerability. This algorithm is very useful for engineers and researchers for network analysis. Different configuration of networks can be tested to find networks with higher integrity that produce networks with high security, reliability and robustness. Moreover, as in this article only the graphic integer sequence of a connected graph has been considered, further experiments need to carry out in future to see if the proposed algorithm works for more general graphs like edge-independent random graphs [46], and other real world networks. Last but not least, sincethe problem considered here is an open problem; a more detailed comparison study with the other methods of vulnerability measure can be done to design a more improved and efficient algorithm. Additionally, authors are interested in another open problem, i.e., to construct a graph or network with given integrity and order of vertices that can be applied to construct a less vulnerable network with the given constraints.
Author Contributions
All authors have equally contributed to this work. All authors read and approved the final manuscript.
Funding
This research received no external funding.
Acknowledgments
The authors would like to thank Department of Computer Science & Engineering, University of Calcutta, West Bengal, India, Vivekananda Mission Mahavidyalaya, Chaitanyapur (Haldia), PurbaMedinipur, West Bengal, India for supporting the work and the reviewers for their constructive and helpful comments, and specially the computer without which no work was possible.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ye, Q. On vulnerability of power and total graphs. WSEAS Trans. Math. 2012, 1028–1038. [Google Scholar]
- Shang, Y. Vulnerability of networks: Fractional percolation on random graphs. Phys. Rev. E 2014, 89, 012813. [Google Scholar] [CrossRef] [PubMed]
- Bagga, K.S.; Beineke, L.W.; Goddard, W.D.; Lipman, M.J.; Pippert, R.E. A survey of integrity. Discret. Appl. Math. 1992, 37, 13–28. [Google Scholar] [CrossRef]
- Moazzami, D. Vulnerability in graphs-A comparative survey. J. Comb. Math. Comb. Comput. 1999, 30, 23–32. [Google Scholar]
- Barefoot, C.A.; Entringer, R.; Swart, H. Vulnerability in graphs—A comparative survey. J. Comb. Math. Comb. Comput. 1987, 1, 13–22. [Google Scholar]
- Deo, N. Graph Theory with Applications to Engineering and Computer Science; Courier Dover Publications: New York, NY, USA, 2017. [Google Scholar]
- Hakimi, S.L. On realizability of a set of integers as degrees of the vertices of a linear graph. I. J. Soc. Ind. Appl. Math. 1962, 10, 496–506. [Google Scholar] [CrossRef]
- Sloane, N.J.A. A Handbook of Integer Sequences; Academic Press: New York, NY, USA, 2014. [Google Scholar]
- Sloane, N.J. The On-Line Encyclopedia of Integer Sequences. Available online: https://arxiv.org/pdf/math/0312448.pdf (accessed on 10 January 2019).
- Knuth, D.E. The Art of Computer Programming; Combinatorial Algorithms, Part 1; Addison-Wesley Professional: Boston, MA, USA, 2011; Volume 4A. [Google Scholar]
- Bondy, J.A.; Murty, U.S.R. Graph Theory with Applications; Macmillan: London, UK, 1976; Volume 290. [Google Scholar]
- Basuli, K. Graphic Integer Sequence and Its Applications. Ph.D. Thesis, University of Calcutta, Kolkata, India, 2017. [Google Scholar]
- Cozzens, M.B.; Moazzami, D.; Stueckle, S. The tenacity of the Harary graphs. J. Comb. Math. Comb. Comput. 1994, 16, 33–56. [Google Scholar]
- Basuli, K. Role of Degree Sequence in determination of Maximal Clique of a Graph. J. Glob. Res. Comput. Sci. 2010, 1, 5–7. [Google Scholar]
- Rao, A.R. Proceedings of the Symposium on Graph Theory held at the Indian Statistical Institute; Macmillan: London, UK, 1979. [Google Scholar]
- Chartrand, G.; Zhang, P. A First Course in Graph Theory; Courier Corporation: Washington, DC, USA, 2013. [Google Scholar]
- Shang, Y. Large dicliques in a directed inhomogeneous random graph. Int. J. Comput. Math. 2013, 90, 445–456. [Google Scholar] [CrossRef]
- Asratian, A.S.; Denley, T.M.; Häggkvist, R. Bipartite Graphs and Their Applications; Cambridge University Press: Cambridge, UK, 1998; Volume 131. [Google Scholar]
- Scheinerman, E. Mathematics: A Discrete Introduction; Nelson Education: Scarborough, ON, Canada, 2012. [Google Scholar]
- Doty, L.L. Extremal connectivity and vulnerability in graphs. Networks 1989, 19, 73–78. [Google Scholar] [CrossRef]
- Jun, W.U.; Barahona, M.; Yue-Jin, T.; Hong-Zhong, D. Natural connectivity of complex networks. Chin. Phys. Lett. 2010, 27, 078902. [Google Scholar] [CrossRef]
- Fujita, S.; Furuya, M. Safe Number and Integrity of Graphs. Discrete Appl. Math. 2018, 247, 398–406. [Google Scholar] [CrossRef]
- Li, Y.; Shi, Y.; Gu, X. Spectrum bounds for the scattering number, integrity, tenacity of regular graphs. Future Gener. Comput. Syst. 2018, 83, 450–453. [Google Scholar] [CrossRef]
- Saravanan, M.; Sujatha, R.; Sundareswaran, R.; Sahoo, S.; Pal, M. Concept of integrity and its value of fuzzy graphs. J. Intell. Fuzzy Syst. 2018, 34, 2429–2439. [Google Scholar] [CrossRef]
- Drange, P.G.; Dregi, M.; van’t Hof, P. On the computational complexity of vertex integrity and component order connectivity. Algorithmica 2016, 76, 1181–1202. [Google Scholar] [CrossRef]
- Mahde, S.S.; Mathad, V.; Sahal, A.M. Hub-integrity of graphs. Bull. Int. Math. Virtual Inst. 2015, 5, 57–64. [Google Scholar]
- Vaidya, S.K.; Kothari, N.J. Some new results on domination integrity of graphs. Open J. Discrete Math. 2012, 2, 96. [Google Scholar] [CrossRef]
- Moazzami, D. Towards a measure of vulnerability, tenacity of a Graph. J. Algorithms Comput. 2016, 48, 149–153. [Google Scholar]
- Aslan, E. A Measure of Graphs Vulnerability: Edge Scattering Number. Bull. Soc. Math. Banja Luka 2014, 4, 53–60. [Google Scholar]
- Bacak-Turan, G.; Şenoğlu, M.Ü.; Altundağ, F.N. Neighbor Rupture Degree of Some Middle Graphs. SüleymanDemirelÜniversitesi Fen BilimleriEnstitüsü Dergisi 2018, 22, 75–80. [Google Scholar] [CrossRef]
- Aytac, A. The common-neighbourhood of a graph. Boletim da SociedadeParanaense de Matemática 2017, 35, 23–32. [Google Scholar] [CrossRef]
- Bacak-Turan, G.; Demirtekin, E. Neighbor Rupture Degree of Gear Graphs. CBU J. Sci. 2017, 12, 319–323. [Google Scholar]
- Aslan, E. Weak-Rupture Degree of Graphs. Int. J. Found. Comput. Sci. 2016, 27, 725–738. [Google Scholar] [CrossRef]
- Aslan, E.; Bacak-Turan, G. Mean rupture degree of graphs. Univ. Politeh. Buchar. Sci. Bull.-Ser. A-Appl. Math. Phys. 2016, 78, 233–242. [Google Scholar]
- Clark, L.H.; Entringer, R.C.; Fellows, M.R. Computational complexity of integrity. J. Comb. Math. Comb. Comput. 1987, 2, 179–191. [Google Scholar]
- Li, F.; Li, X. Computing the rupture degrees of graphs. In Proceedings of the 7th International Symposium on Parallel Architectures, Algorithms and Networks, Hong Kong, China, 10–12 May 2004; pp. 368–373. [Google Scholar]
- Zhang, S.; Li, X.; Han, X. Computing the scattering number of graphs. Int. J. Comput. Math. 2002, 79, 179–187. [Google Scholar] [CrossRef]
- Shang, Y. Biased edge failure in scale-free networks based on natural connectivity. Indian J. Phys. 2012, 86, 485–488. [Google Scholar] [CrossRef]
- Erdds, P.; R&WI, A. On random graphs I. Publ. Math. Debrecen 1959, 6, 290–297. [Google Scholar]
- Albrt, R.; Barabási, A.L. Statistical mechanics of complex networks. Rev. Modern Phys. 2002, 74, 47. [Google Scholar] [CrossRef]
- Watts, D.J.; Strogatz, S.H. Collective dynamics of ‘small-world’networks. Nature 1998, 393, 440. [Google Scholar] [CrossRef]
- The R Manuals. Available online: https://cran.r-project.org/manuals.html (accessed on 10 January 2019).
- Burchett, I. Quantifying Network Reliability through Finding an Upper Bound for Graph Integrity Using Graph Coloring. Available online: https://digitalcommons.wku.edu/cgi/viewcontent.cgi?referer=https://www.google.com.au/&httpsredir=1&article=1229&context=stu_hon_theses (accessed on 10 January 2019).
- Krebs, V.E. Mapping networks of terrorist cells. Connections 2002, 24, 43–52. [Google Scholar]
- Kidwai, F.A.; Marwah, B.R.; Deb, K.; Karim, M.R. A genetic algorithm based bus scheduling model for transit network. In Proceedings of the Eastern Asia Society for Transportation Studies, Bangkok, Thailand, 21–24 September 2005; Volume 5, pp. 477–489. Available online: https://www.researchgate.net/profile/Mohamed_Karim/publication/228960835_A_Genetic_Algorithm_Based_Bus_Scheduling_Model_for_Transit_Network/links/54130f060cf2bb7347db1a0c.pdf (accessed on 15 January 2019).
- Shang, Y. Estrada and L-Estrada indices of edge-independent random graphs. Symmetry 2015, 7, 1455–1462. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).