The Prolongation Structure of the Modified Nonlinear Schrödinger Equation and Its Initial-Boundary Value Problem on the Half Line via the Riemann-Hilbert Approach

Abstract

In this paper, the Lax pair of the modified nonlinear Schrödinger equation (mNLS) is derived by means of the prolongation structure theory. Based on the obtained Lax pair, the mNLS equation on the half line is analyzed with the assistance of Fokas method. A Riemann-Hilbert problem is formulated in the complex plane with respect to the spectral parameter. According to the initial-boundary values, the spectral function can be defined. Furthermore, the jump matrices and the global relations can be obtained. Finally, the potential $q(x,t)$ can be represented by the solution of this Riemann-Hilbert problem.

1. Introduction

In mathematics and physics, nonlinear partial differential equations play an important role due to their abundant mathematical structure and properties. Many works on nonlinear evolution equations have been studied, such as the Hamiltonian structure [1,2], the infinite conservation laws [3,4], the Bäcklund transformation [5,6] and so on [7,8,9]. Besides, the exact solution of these equations, which can be expressed in various forms by different methods, is also a significant subject of soliton research [10,11,12,13,14,15,16,17,18,19,20,21,22]. In recent years, with the development of soliton theory, more and more researchers pay attention to the Riemann-Hilbert approach. The Riemann-Hilbert approach was introduced by Fokas to analyze the initial-boundary values problem for linear and nonlinear partial differential equations [23,24]. In the past 20 years, many researchers have discussed a lot of nonlinear integrable equations for the initial-boundary values problem [25,26,27,28,29,30,31,32,33,34,35,36,37,38,39,40,41,41]. They have all made a great contribution to the development of this method. The core idea of this method is to construct the associated Riemann-Hilbert problem by the Lax pair of the integrable equation, and then in addition to the initial-boundary values problem, the long-time asymptotic behavior of the solution can be analyzed [42,43,44,45,46]. However, as we all know, it is difficult to determine whether a nonlinear evolution equation possesses a Lax pair or not. As far as we are concerned, the prolongation structure method is an efficient way to obtain the Lax pair, which was firstly proposed in 1975 by Wahlquist and Estabrook [47]. In recent years, a large number of scholars have improved this method, for example, Hermann deduced the prolongation structure method connection in 1976 [48], Deconinck applied the prolongation structure method to semi-discrete systems firstly [49], Wang used this approach to get the integrability of many nonlinear wave equation [50] and so on [51,52]. In this way, we can get the Lax pair of the nonlinear evolution equation easily as long as it is integrable.

In this paper, we mainly talk about the modified nonlinear Schrödinger(mNLS) equation

$$i{q}_t+q_{xx}+{i\left(\right|q|}^2{q)}_x+2\rho {\left|q\right|}^{2}q=0,$$

(1)

which is very important in plasma physics. Recently, many properties of this equation have been studied, such as the Hamiltonian structure [53], the Darboux transformation [54], the numerical solutions [55,56] and so on [57,58]. Actually, it can become the derivative NLS equation by certain gauge transformation [59]. In this paper, we mainly discuss the mNLS equation on the half line. For simplicity, we let $\rho =1$. Supposing that the solution $q(x,t)$ of the mNLS equation exists, and the initial-boundary values are defined as follows,

Initial values:

$$q_0\left(x\right)=q(x,0),0<x<\infty ,$$

(2)

Boundary values:

$$g_0\left(t\right)=q(0,t),g_1\left(t\right)=q_x(0,t),0<t<T.$$

(3)

In order to formulate a Riemann-Hilbert problem, we need to reconstruct the Lax pair of Equation (1). Based on the initial-boundary values, the corresponding spectral functions can be defined. Eventually, the potential function $q(x,t)$ can be expressed in terms of the solution of this Riemann-Hilbert problem.

This paper is divided into four sections. The construction of the prolongation structure for the mNLS equation is in Section 2 and then in Section 3, we reconstruct the Lax pair to formulate the Riemann-Hilbert problem and some conditions and relations are derived. In the last section, we define the spectral functions according to the initial-boundary values and the Riemann-Hilbert problem is investigated.

2. The Prolongation Structures of the mNLS Equation

In order to obtain the Lax pair of the mNLS equation, we analyze the prolongation structure of this equation. This process mainly involves a fundamental theorem in Lie algebra [51].

Theorem 1.

Suppose X and Y are two elements of Lie algebra $g=sl(n+1,C)$ with $[X,Y]=aY$, $(a\ne 0)$ and $X\in range$ ad Y, it means that there exist $Z\in g$ such that $[Y,Z]=X$, so we obtain $Y=e_{\pm }$ and $X=\pm \frac{1}{2}ah$, where $e_{\pm }$ are the nilpotent and h is the neutral elements of g.

In the beginning, we introduce these variables

$$\overline{u}=p,u_x=v,\overline{u_x}=p_x=q.$$

(4)

Then Equation (1) is equivalent to this set of equations as follows

$$\left\{\begin{array}{c}{u}_x-v=0,\hfill \\ p_x-q=0,\hfill \\ i{u}_t+v_x+2iu{u}_x\overline{u}+i{u}^2{\overline{u}}_x+2u^2\overline{u}=0,\hfill \\ i{p}_t-q_x+2i\overline{u}{\overline{u}}_{x}u+i{\overline{u}}^2{u}_x-2{\overline{u}}^{2}u=0.\hfill \end{array}\right.$$

(5)

We define the set of two-forms $I=\{{\alpha }_1,{\alpha }_2,{\alpha }_3,{\alpha }_4\}$, where

$$\left\{\begin{array}{c}{\alpha }_1=du\wedge dt+vdt\wedge dx,\hfill \\ {\alpha }_2=dp\wedge dt+qdt\wedge dx,\hfill \\ {\alpha }_3=idu\wedge dx-dv\wedge dt+(2iuvp+i{u}^{2}q+2u^{2}p)dt\wedge dx,\hfill \\ {\alpha }_4=idp\wedge dx+dq\wedge dt+(i{p}^{2}v+2ipqu-2p^{2}u)dt\wedge dx.\hfill \end{array}\right.$$

(6)

It is easy to find that I is a closed ideal, actually, $dI\subset I$. After that, we define the differential one-forms

$${\omega }^i=d{y}^i-F^i(u,v,p,q;y^i)dx-G^i(u,v,p,q;y^i)dt.$$

(7)

At the same time, we suppose $F^i=F_j^i{y}^j,G^i=F_j^i{y}^j$. According to the general theory of exterior differential systems, if $\tilde{I}=I\bigcup {\omega }^i$ is a closed ideal, it must satisfy

$$d{\omega }^i=\sum _{i=1}^4(f_j^i{\alpha }^j)+n_j^i\wedge {\omega }^j.$$

(8)

Combining (5)–(8), we obtain

$$\left\{\begin{array}{c}{F}_v=F_q=0,\hfill \\ i{G}_v+F_u=0,\hfill \\ i{G}_q-F_p=0,\hfill \\ -G_{u}v-G_{p}q+(2iuvp+iq{u}^2+2u^{2}p)G_v\hfill \\ -(2ipqu+i{p}^{2}v-2p^{2}u)G_q+[F,G]=0.\hfill \end{array}\right.$$

(9)

where the bracket $[,]$ denotes the Lie bracket, namely $[F,G]=FG-GF$.

After a lengthy calculation, one solution of this set of equations can be derived

$$\begin{array}{c}F=x_0+u{x}_1+p{x}_2,\hfill \\ G=i{x}_{1}v-i{x}_{2}q-u^{2}p{x}_1-p^{2}u{x}_2+iu{x}_3-ip{x}_4-ipu{x}_5+x_6.\hfill \end{array}$$

(10)

with the integrability conditions

$$\begin{array}{c}2i{x}_1-x_3-i[x_1,x_5]=0,2i{x}_2+x_4+i[x_2,x_5]=0,\hfill \\ i[x_0,x_3]+[x_1,x_6]=0,-i[x_0,x_4]+[x_2,x_6]=0,\hfill \\ [x_0,x_5]+[x_1,x_4]-[x_2,x_3]=0,[x_1,x_3]=0,[x_2,x_4]=0,[x_0,x_6]=0.\hfill \end{array}$$

(11)

where all $\left\{x_i\right\}$, $i=\{1,2,\dots ,6.\}$ are pending matrices. Here $\{x_1,x_2,\dots ,x_6\}$ depend on an incomplete Lie algebra, called prolongation algebra.

The next step is to embed the prolongation algebra in $sl(n+1,C)$. According to (11) and Theorem 1, we deduce that $x_1$ and $x_2$ is nilpotent and $x_5$ is neutral element. So we have

$$x_1=\left(\begin{array}{cc}0& \xi \\ 0& 0\end{array}\right),x_2=\left(\begin{array}{cc}0& 0\\ -\xi & 0\end{array}\right),x_5=\left(\begin{array}{cc}-{\xi }^2& 0\\ 0& {\xi }^2\end{array}\right).$$

(12)

Bringing the above results into (11), we obtain

$$\begin{array}{c}{x}_0=\left(\begin{array}{cc}-i{\xi }^2+i& 0\\ 0& i{\xi }^2-i\end{array}\right),x_3=\left(\begin{array}{cc}0& -2i{\xi }^3+2i\xi \\ 0& 0\end{array}\right),\hfill \\ x_4=\left(\begin{array}{cc}0& 0\\ -2i{\xi }^3+2i\xi & 0\end{array}\right),x_6=\left(\begin{array}{cc}-2i{\xi }^4-2i+4i{\xi }^2& 0\\ 0& 2i{\xi }^4+2i+4i{\xi }^2\end{array}\right).\hfill \end{array}$$

(13)

where $\xi$ is spectral parameter. Hence, the expressions of F and G can be presented eventually

$$\begin{array}{c}F=\left(\begin{array}{cc}-i{\xi }^2+i& \xi q\\ -\xi \overline{q}& i{\xi }^2-i\end{array}\right),\hfill \\ G=\left(\begin{array}{cc}-2i{\xi }^4-2i+4i{\xi }^2+i{\xi }^2{\left|q\right|}^2& 2{\xi }^{3}q-2\xi q-\xi {\left|q\right|}^{2}q+i\xi q_x\\ -2{\xi }^3\overline{q}+2\xi \overline{q}+\xi {\left|q\right|}^2\overline{q}+i\xi {\overline{q}}_x& 2i{\xi }^4+2i-4i{\xi }^2-i{\xi }^2{\left|q\right|}^2\end{array}\right).\hfill \end{array}$$

(14)

So, the mNLS equation admits Lax pair

$${\psi }_x=F\psi ,{\psi }_t=G\psi ,$$

(15)

where $\psi ={(v_1,v_2)}^T$.

3. Spectral Analysis

From the previous paragraph, we know the Lax pair of the mNLS equation. By introducing

$$Q=\left(\begin{array}{cc}0& q\\ -\overline{q}& 0\end{array}\right),{\sigma }_3\left(\begin{array}{cc}1& 0\\ 0& -1\end{array}\right).$$

(16)

where the $\overline{q}$ denotes the conjugation of q, the Lax pair (15) can be rewritten in this form

$$\left\{\begin{array}{c}{\psi }_x+i{\xi }^2{\sigma }_3\psi -i{\sigma }_3\psi =\xi Q\psi ,\hfill \\ {\psi }_t+2i{\xi }^4{\sigma }_3+2i{\sigma }_3-4i{\xi }^2{\sigma }_3=-i{\xi }^2{Q}^2+2i{\xi }^{3}Q-2\xi Q+\xi Q^3+i\xi {\sigma }_3{Q}_x.\hfill \end{array}\right.$$

(17)

In our analysis, we assume that q decays to zero sufficiently fast as $x\to \pm \infty$. So, it is correct to extend the column vector $\psi$ to a $2\times 2$ matrix. For simplicity, we substitute ${\lambda }^2$ for ${\xi }^2-1$. Letting $\psi =\mathsf{\Psi }{e}^{-i({\xi }^{2}x+2{\xi }^{4}t){\sigma }_3}$, then the Lax pair (17) becomes

$$\begin{array}{c}{\mathsf{\Psi }}_x+i{\xi }^2[{\sigma }_3,\mathsf{\Psi }]=\xi Q\mathsf{\Psi },\hfill \\ {\mathsf{\Psi }}_t+2i{\xi }^4[{\sigma }_3,\mathsf{\Psi }]=(-i{\xi }^2{Q}^2{\sigma }_3+2{\xi }^{3}Q-2\xi Q+\xi Q^3+i\xi {\sigma }_3{Q}_x)\mathsf{\Psi }\hfill \end{array}$$

(18)

We can write (18) in full derivative form

$$d(e^{i({\xi }^{2}x+2{\xi }^{4}t){\widehat{\sigma }}_3}\mathsf{\Psi }(x,t;\xi ))=e^{i({\lambda }^{2}x+2{\lambda }^{4}t){\widehat{\sigma }}_3}U(x,t;\xi )\mathsf{\Psi }.$$

(19)

where

$$\begin{array}{cc}\hfill U& =U_{1}dx+U_{2}dt\hfill \\ & =\xi Qdx+(-i{\xi }^2{Q}^2{\sigma }_3+2{\xi }^{3}Q-2\xi Q+\xi Q^3+i\xi {\sigma }_3{Q}_x)dt.\hfill \end{array}$$

(20)

and ${\widehat{\sigma }}_3$ denotes the operator to matrix by ${\widehat{\sigma }}_{3}M=[{\sigma }_3,M]$, hence it is easy to prove $e^{{\widehat{\sigma }}_3}M=e^{{\sigma }_3}M{e}^{-{\sigma }_3}$, where M is a $2\times 2$ matrix.

3.1. The Reconstruction of Lax Pair

Expanding the solution of (19) in this way

$$\mathsf{\Psi }=D+\frac{{\mathsf{\Psi }}_1}{\xi }+\frac{{\mathsf{\Psi }}_2}{{\xi }^2}+\frac{{\mathsf{\Psi }}_3}{{\xi }^3}+\mathcal{O}(\frac{1}{{\xi }^4}),\xi \to \infty ,$$

(21)

where $D,{\mathsf{\Psi }}_1,{\mathsf{\Psi }}_2,{\mathsf{\Psi }}_3$ are independent of $\xi$. Bringing this equation into the first equation of (18), and comparing the same order of $\xi$’s frequency, we obtain the following equations

$$\begin{array}{c}O\left(1\right):D_x+i[{\sigma }_3,{\mathsf{\Psi }}_2]-i[{\sigma }_3,D]=Q{\mathsf{\Psi }}_1;\hfill \\ O\left(\xi \right):i[{\sigma }_3,{\mathsf{\Psi }}_1]=QD;\hfill \\ O\left({\xi }^2\right):i[{\sigma }_3,D]=0.\hfill \end{array}$$

(22)

Using the same method, taking (21) into another equation of (18), we have

$$\begin{array}{c}O\left(1\right):D_t-4i[{\sigma }_3,{\mathsf{\Psi }}_2]+2i[{\sigma }_3,D]=-i{Q}^2{\sigma }_3{\mathsf{\Psi }}_2+2Q{\mathsf{\Psi }}_3-2Q{\mathsf{\Psi }}_1+Q^3{\mathsf{\Psi }}_1+i{\sigma }_3{Q}_x{\mathsf{\Psi }}_1;\hfill \\ O\left(\xi \right):2i[{\sigma }_3,{\mathsf{\Psi }}_3]-4i[{\sigma }_3,{\mathsf{\Psi }}_1]=-i{Q}^2{\sigma }_3{\mathsf{\Psi }}_1+2Q{\mathsf{\Psi }}_2-2QD+Q^{3}D+i{\sigma }_3{Q}_{x}D;\hfill \\ O\left({\xi }^2\right):2i[{\sigma }_3,{\mathsf{\Psi }}_2]-4i[{\sigma }_3,D]=-i{Q}^2{\sigma }_{3}D+2Q{\mathsf{\Psi }}_1;\hfill \\ O\left({\xi }^3\right):2i[{\sigma }_3,{\mathsf{\Psi }}_1]=2QD;\hfill \\ O\left({\xi }^4\right):2i[{\sigma }_3,D]=0.\hfill \end{array}$$

(23)

For (22), We find that D is a diagonal matrix from $O\left({\xi }^2\right)$. Without loss of generality, we suppose

$$D=\left(\begin{array}{cc}{D}_0^{11}& 0\\ 0& D_0^{22}\end{array}\right).$$

(24)

From $O\left(\xi \right)$ we have

$${\mathsf{\Psi }}_1^o=\frac{i}{2}QD{\sigma }_3.$$

(25)

where ${\mathsf{\Psi }}_1^o$ denotes the off-diagonal part of ${\mathsf{\Psi }}_1$. So, we can get $D_x$ from $O\left(1\right)$ easily

$$D_x=\frac{i}{2}{Q}^2{\sigma }_{3}D.$$

(26)

For (23), after a lengthy calculation, we get

$$\begin{array}{cc}\hfill D_t& =\frac{3i}{4}{Q}^4{\sigma }_{3}D+\frac{1}{2}Q{Q}_{x}D-\frac{1}{2}{Q}_{x}QD\hfill \\ & =(\frac{3i}{4}{\left|q\right|}^4+\overline{q}{q}_x-q{\overline{q}}_x){\sigma }_{3}D.\hfill \end{array}$$

(27)

The mNLS equation admits the conservation law

$${2\left(\right|q|}^2{)}_t=(2i{q}_x\overline{q}-{3\left|q\right|}^4-2iq{\overline{q}}_x{)}_x.$$

(28)

From the above results, we find (26) and (27) admit the conservation law. Define

$$D(x,t)=e^{i{\int }_{(0,0)}^{(x,t)}\Delta (x,t){\sigma }_3}.$$

(29)

where $\Delta$ is the differential one-form, and it is given by

$$\Delta (x,t)={\Delta }_{1}dx+{\Delta }_{2}dt=-\frac{1}{2}q\overline{q}dx+[\frac{3}{4}{q}^2{\overline{q}}^2+\frac{i}{2}(q{\overline{q}}_x-q_x\overline{q})]dt.$$

(30)

It is not difficult to find that the integral is path independent. So, we introduce

$$\mathsf{\Psi }(x,t;\xi )=e^{i{\int }_{(0,0)}^{(x,t)}\Delta {\overline{\sigma }}_3}\mu (x,t;\xi )D(x,t),0<x<\infty ,0<t<T.$$

(31)

Then the form of the Lax pair (18) can be replaced with

$$d(e^{i({\lambda }^{2}x+2{\lambda }^{4}t){\widehat{\sigma }}_3}\mu (x,t;\xi ))=W(x,t;\xi ).$$

(32)

where

$$\begin{array}{c}W(x,t;\xi )=e^{i({\lambda }^{2}x+2{\lambda }^{4}t){\widehat{\sigma }}_3}V(x,t;\xi )\mu ,\hfill \\ V=V_{1}dx+V_{2}dt=e^{-i{\int }_{(0,0)}^{(x,t)}\Delta {\widehat{\sigma }}_3}(U-i\Delta {\sigma }_3).\hfill \end{array}$$

(33)

Considering the definitions of U and $\Delta$, we have

$$\begin{array}{c}{V}_1(x,t;\xi )=\left(\begin{array}{cc}\frac{i}{2}q\overline{q}& \xi q{e}^{-2i{\int }_{(0,0)}^{(x,t)}\Delta }\\ -\xi \overline{q}{e}^{2i{\int }_{(0,0)}^{(x,t)}\Delta }& -\frac{i}{2}q\overline{q}\end{array}\right),\hfill \\ V_2(x,t;\xi )=\left(\begin{array}{cc}{V}_2^{11}(x,t;\xi )& V_2^{12}(x,t;\xi )\\ V_2^{21}(x,t;\xi )& V_2^{22}(x,t;\xi )\end{array}\right).\hfill \end{array}$$

(34)

where

$$\begin{array}{cc}\hfill V_2^{11}(x,t;\xi )& =i{\xi }^{2}q\overline{q}-\frac{3i}{4}{q}^2{\overline{q}}^2+\frac{1}{2}(q{\overline{q}}_x-q_x\overline{q}),\hfill \\ \hfill V_2^{12}(x,t;\xi )& =(2{\xi }^3-2\xi q-{\xi q\left|q\right|}^2+i\xi q_x)e^{-2i{\int }_{(0,0)}^{(x,t)}\Delta },\hfill \\ \hfill V_2^{21}(x,t;\xi )& =(-2{\xi }^3\overline{q}+2\xi \overline{q}+\xi \overline{q}{\left|q\right|}^2+i\xi {\overline{q}}_x)e^{2i{\int }_{(0,0)}^{(x,t)}\Delta },\hfill \\ \hfill V_2^{22}(x,t;\xi )& =-i{\xi }^{2}q\overline{q}+\frac{3i}{4}{q}^2{\overline{q}}^2-\frac{1}{2}(q{\overline{q}}_x-q_x\overline{q}).\hfill \end{array}$$

Thus, (32) changes into

$$\left\{\begin{array}{c}{\mu }_x+i{\lambda }^2[{\sigma }_3,\mu ]=V_1\mu ,\hfill \\ {\mu }_t+2i{\lambda }^4[{\sigma }_3,\mu ]=V_2\mu .\hfill \end{array}\right.$$

(35)

3.2. The Riemann-Hilbert Problem And Some Relations

Supposing that $q(x,t)$ is smooth function in the domain $D=\{0<x<\infty ,0<t<T\}$. Then we define the eigenfunctions ${\mu }_j(x,t,;\xi )(j=1,2,3)$ of (34) as follows

$${\mu }_j(x,t;\xi )=I+{\int }_{(x_j,t_j)}^{(x,t)}{e}^{-i(\lambda x+2{\lambda }^{2}t){\widehat{\sigma }}_3}W(x^{\prime },t^{\prime };\xi ),0<x<\infty ,0<t<T.$$

(36)

The integral curve is from $(x_j,t_j)$ to $(x,t)$, where $(x_1,t_1)=(0,T),(x_2.t_2)=(0,0)$ and $(x_3,t_3)=(\infty ,t)$. Furthermore, the point $(x,t)$ is an arbitrary point in the domain D. We know that the integral of (36) is independent of the path of integration. Without loss of generality, we will consider the particular integral paths as follows, see Figure 1.

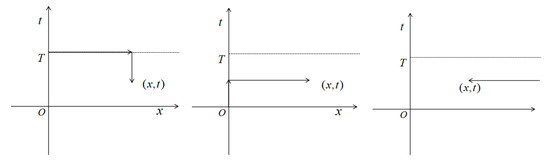
Figure 1. Integral paths.

By this method, we get

$$\left\{\begin{array}{c}{\mu }_1(x,t;\xi )=I+{\int }_0^x{e}^{i{\lambda }^2(x^{\prime }-x){\widehat{\sigma }}_3}\left(V_1{\mu }_1\right)(x^{\prime },t;\lambda )d{x}^{\prime }\hfill \\ -e^{-i{\lambda }^{2}x{\widehat{\sigma }}_3}{\int }_t^T{e}^{2i{\lambda }^4(t^{\prime }-t){\widehat{\sigma }}_3}\left(V_2{\mu }_1\right)(0,t^{\prime };\xi )d{t}^{\prime },\hfill \\ {\mu }_2(x,t;\xi )=I+{\int }_0^x{e}^{i{\lambda }^2(x^{\prime }-x){\widehat{\sigma }}_3}\left(V_1{\mu }_2\right)(x^{\prime },t;\xi )d{x}^{\prime }\hfill \\ -e^{-i{\lambda }^{2}x{\widehat{\sigma }}_3}{\int }_0^t{e}^{2i{\lambda }^4(t^{\prime }-t){\widehat{\sigma }}_3}\left(V_2{\mu }_2\right)(0,t^{\prime };\xi )d{t}^{\prime },\hfill \\ {\mu }_3(x,t,;\xi )=I-{\int }_{\infty }^x{e}^{i{\lambda }^2(x^{\prime }-x){\widehat{\sigma }}_3}\left(V_1{\mu }_3\right)(x^{\prime },t;\xi )d{x}^{\prime }.\hfill \end{array}\right.$$

(37)

Noting that the first column of ${\mu }_j$ includes $e^{-2i[{\lambda }^2(x^{\prime }-x)+2{\lambda }^4(t^{\prime }-t)]}$. So, in different integral paths, we have the following inequalities

$$\left\{\begin{array}{c}{\ell }_1:(x_1,t_1)\to (x,t):0<x^{\prime }<x,t<t^{\prime }<T,\hfill \\ {\ell }_2:(x_2,t_2)\to (x,t):0<x^{\prime }<x,0<t^{\prime }<t,\hfill \\ {\ell }_3:(x_3,t_3)\to (x,t):x<x^{\prime }<\infty .\hfill \end{array}\right.$$

(38)

Due to the exponential function decaying sufficiently, these inequalities imply that the first of the functions ${\mu }_j(x,t;\xi ),(j=1,2,3)$ are analytic if

$$\begin{array}{c}{\mu }_1^{\left(1\right)}(x,t;\xi ):\xi \in \{Im{\xi }^2\ge 0\}\cap \{Im{\xi }^4\le 0\},\hfill \\ {\mu }_2^{\left(1\right)}(x,t;\xi ):\xi \in \{Im{\xi }^2\ge 0\}\cap \{Im{\xi }^4\ge 0\},\hfill \\ {\mu }_3^{\left(1\right)}(x,t;\xi ):\xi \in \{Im{\xi }^2\le 0\}.\hfill \end{array}$$

(39)

At the same time, the second column of the functions ${\mu }_j(x,t;\xi ),(j=1,2,3)$ are analytic if

$$\begin{array}{c}{\mu }_1^{\left(2\right)}(x,t;\xi ):\xi \in \{Im{\xi }^2\le 0\}\cap \{Im{\xi }^4\ge 0\},\hfill \\ {\mu }_2^{\left(2\right)}(x,t;\xi ):\xi \in \{Im{\xi }^2\le 0\}\cap \{Im{\xi }^4\le 0\},\hfill \\ {\mu }_3^{\left(2\right)}(x,t;\xi ):\xi \in \{Im{\xi }^2\ge 0\}.\hfill \end{array}$$

(40)

Hence, we get

$$\begin{array}{c}{\mu }_1(x,t;\xi )=({\mu }_1^{D_2}(x,t;\xi ),{\mu }_1^{D_3}(x,t;\xi )),\hfill \\ {\mu }_2(x,t;\xi )=({\mu }_2^{D_1}(x,t;\xi ),{\mu }_2^{D_4}(x,t;\xi )),\hfill \\ {\mu }_3(x,t;\xi )=({\mu }_3^{D_3\cup D_4}(x,t;\xi ),{\mu }_3^{D_1\cup D_2}(x,t;\xi )).\hfill \end{array}$$

(41)

where ${\mu }_j^{D_i}$ stands for ${\mu }_j$ is analytic if $\xi \in D_i$, where $D_i={\omega }_i\cup (-{\omega }_i),-{\omega }_i=\{-\xi \in C|\xi \in {\omega }_i\},{\omega }_i=\{\xi \in C|\frac{i-1}{4}\pi <\xi <\frac{i}{4}\pi \}$, see Figure 2.

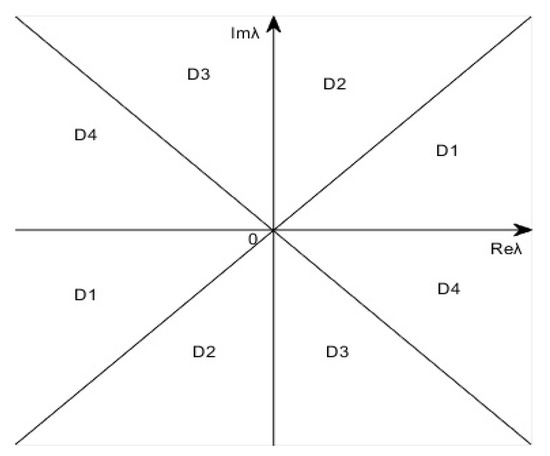
Figure 2. $D_j,j=1,2,3,4$.

The eigenfunctions ${\mu }_j(j=1,2,3)$ possess these properties.

• $\det {\mu }_1(x,t;\xi )=\det {\mu }_2(x,t;\xi )=\det {\mu }_3(x,t;\xi )=1$;
• ${\mu }_j^{11}(x,t;\xi )=\overline{{\mu }_j^{22}(x,t;\overline{\xi })},{\mu }_j^{12}(x,t;\xi )=\overline{{\mu }_j^{21}(x,t;\overline{\xi })}$;
• ${\mu }_j^{11}(x,t;-\xi )={\mu }_j^{11}(x,t;\xi ),{\mu }_j^{12}(x,t;-\xi )=-{\mu }_j^{12}(x,t;\xi ),$
  ${\mu }_j^{21}(x,t;-\xi )=-{\mu }_j^{21}(x,t;\xi ),{\mu }_j^{22}(x,t;-\xi )={\mu }_j^{22}(x,t;\xi ).$

where the eigenfunctions ${\mu }_j(x,t;\xi )=\left(\begin{array}{cc}{\mu }_j^{11}(x,t;\xi )& {\mu }_j^{12}(x,t;\xi )\\ {\mu }_j^{21}(x,t;\xi )& {\mu }_j^{22}(x,t;\xi )\end{array}\right)(j=1,2,3).$

For the purpose of formulating a Riemann-Hilbert problem, our main task is to find the jump matrices for every $D_i(i=1,2,3,4)$ to any other regions. Then we define the spectral functions $s\left(\xi \right)$ and $S\left(\xi \right)$

$$\left\{\begin{array}{c}{\mu }_3(x,t;\xi )={\mu }_2(x,t;\xi )e^{-i({\lambda }^{2}x+2{\lambda }^{4}t){\widehat{\sigma }}_3}s\left(\xi \right),\hfill \\ {\mu }_1(x,t;\xi )={\mu }_2(x,t;\xi )e^{-i({\lambda }^{2}x+2{\lambda }^{4}t){\widehat{\sigma }}_3}S\left(\xi \right).\hfill \end{array}\right.$$

(42)

According to the above definition, we have

$${\mu }_1(x,t;\xi )={\mu }_3(x,t;\xi )e^{-i({\lambda }^{2}x+2{\lambda }^{4}t){\widehat{\sigma }}_3}{\left(s\left(\xi \right)\right)}^{-1}S\left(\xi \right).$$

(43)

Combining (37) with (42), we acquire

$$s\left(\xi \right)={\mu }_3(0,0;\xi ),S\left(\xi \right)={(e^{2i{\lambda }^{4}T{\widehat{\sigma }}_3}{\mu }_2(0,T;\xi ))}^{-1}.$$

(44)

Owing to (37), it is clear to see that

$$\begin{array}{c}{\mu }_1(0,t;\xi )=I-{\int }_t^T{e}^{2i{\lambda }^4(t^{\prime }-t){\widehat{\sigma }}_3}\left(V_2{\mu }_1\right)(0,t^{\prime };\xi )d{t}^{\prime },\hfill \\ {\mu }_2(0,t;\xi )=I+{\int }_0^t{e}^{2i{\lambda }^4(t^{\prime }-t){\widehat{\sigma }}_3}\left(V_2{\mu }_2\right)(0,t^{\prime };\xi )d{t}^{\prime },\hfill \\ {\mu }_3(x,0;\xi )=I+{\int }_{\infty }^x{e}^{i{\lambda }^2(x^{\prime }-x){\widehat{\sigma }}_3}\left(V_1{\mu }_3\right)(x^{\prime },0;\xi )d{x}^{\prime },\hfill \\ {\mu }_2(x,0;\xi )=I+{\int }_0^x{e}^{i{\lambda }^2(x^{\prime }-x){\widehat{\sigma }}_3}\left(V_1{\mu }_2\right)(x^{\prime },0;\xi )d{x}^{\prime },\hfill \end{array}$$

(45)

Considering the initial values $q(x,0)=u_0\left(x\right)$, $q(0,t)=g_0\left(t\right)$, boundary values $q(0,t)=g_0\left(t\right)$ and $q_x(0,t)=g_1\left(t\right)$. For convenience, the initial-boundary values of $\overline{q}(x,t)$ can be written in this form, namely $\overline{q}(x,0)={\overline{u}}_0\left(x\right),\overline{q}(0,t)={\overline{g}}_0\left(t\right)$, and ${\overline{q}}_x(0,t)={\overline{g}}_1\left(t\right)$. Then $V_2(0,t;\xi )$ and $V_1(x,0;\xi )$ can be expressed with

$$\begin{array}{c}{V}_1(x,0;\xi )=\left(\begin{array}{cc}\frac{i}{2}{\left|u_0\right|}^2& \xi u_0{e}^{i{\int }_0^x{\left|u_0\right|}^{2}d{x}^{\prime }}\\ -\xi {\overline{u}}_0{e}^{-i{\int }_0^x{\left|u_0\right|}^{2}d{x}^{\prime }}& -\frac{i}{2}{\left|u_0\right|}^2\end{array}\right),\hfill \\ V_2(0,t;\xi )=\left(\begin{array}{cc}{V}_2^{11}(0,t;\xi )& V_2^{12}(0,t;\xi )\\ V_2^{21}(0,t;\xi )& V_2^{22}(0,t;\xi )\end{array}\right).\hfill \end{array}$$

(46)

where

$$\begin{array}{cc}\hfill V_2^{11}(0,t;\xi )& =i{\xi }^2|g_0{|}^2-\frac{3i}{4}{\left|g_0\right|}^4-\frac{1}{2}(g_0{\overline{g}}_1-g_1{\overline{g}}_0)=-V_2^{22}(x,t;\xi ),\hfill \\ \hfill V_2^{12}(0,t;\xi )& =(2{\xi }^3{g}_0-2\xi g_0-\xi g_0|g_0{|}^2+i\xi g_1)e^{-2i{\int }_0^t{\Delta }_2(0,t^{\prime })d{t}^{\prime }},\hfill \\ \hfill V_2^{21}(0,t;\xi )& =(-2{\xi }^3{\overline{g}}_0+2\xi {\overline{g}}_0+\xi {\overline{g}}_0|g_0{|}^2+i\xi {\overline{g}}_1)e^{2i{\int }_0^t{\Delta }_2(0,t^{\prime })d{t}^{\prime }}.\hfill \end{array}$$

with

$${\Delta }_2(0,t^{\prime })=\frac{3}{4}{\left|g_0\right|}^4+\frac{i}{2}(g_0\overline{g_1}-g_1{\overline{g}}_0).$$

Due to ${\mu }_j$ have symmetry, the $s\left(\xi \right)$ and $S\left(\xi \right)$ also have symmetry

$$s_{11}\left(\xi \right)=\overline{s_{22}\left(\overline{\xi }\right)},s_{21}\left(\xi \right)=\overline{s_{12}\left(\overline{\xi }\right)},$$

$$S_{11}\left(\xi \right)=\overline{S_{22}\left(\overline{\xi }\right)},S_{21}\left(\xi \right)=\overline{S_{12}\left(\overline{\xi }\right)}.$$

Without loss of generality, we assume

$$s\left(\xi \right)=\left(\begin{array}{cc}\overline{a\left(\overline{\xi }\right)}& b\left(\xi \right)\\ \overline{b\left(\overline{\xi }\right)}& a\left(\xi \right)\end{array}\right),S\left(\xi \right)=\left(\begin{array}{cc}\overline{A\left(\overline{\xi }\right)}& B\left(\xi \right)\\ \overline{B\left(\overline{\xi }\right)}& A\left(\xi \right)\end{array}\right).$$

(47)

According to (42) and (44), we have

$$\begin{array}{c}s\left(\xi \right)=I-{\int }_{\infty }^0{e}^{i{\lambda }^2(x^{\prime }-x){\widehat{\sigma }}_3}\left(V_1{\mu }_3\right)(x^{\prime },0;\xi )d{x}^{\prime },\hfill \\ S\left(\xi \right)={(I+{\int }_0^T{e}^{2i{\lambda }^4{t}^{\prime }{\widehat{\sigma }}_3}\left(V_2{\mu }_2\right)(0,t^{\prime };\xi )d{t}^{\prime })}^{-1}.\hfill \end{array}$$

(48)

The spectral functions $s\left(\xi \right),S\left(\xi \right)$ have the following properties

• $$\begin{gathered} \left(\begin{array}{c}b\left(\xi \right)\\ a\left(\xi \right)\end{array}\right)=\left(\begin{array}{c}{\mu }_3^{12}(0,0;\xi )\\ {\mu }_3^{22}(0,0;\xi )\end{array}\right)={\mu }_3^{\left(2\right)}(0,0;\xi ), \\ \left(\begin{array}{c}{e}^{-4i{\lambda }^{4}T}B\left(\xi \right)\\ \overline{A\left(\overline{\xi }\right)}\end{array}\right)=\left(\begin{array}{c}{\mu }_2^{12}(0,T;\xi )\\ {\mu }_2^{22}(0,T;\xi )\end{array}\right)={\mu }_2^{\left(2\right)}(0,T;\xi ). \end{gathered}$$
• $$\begin{gathered} a(-\xi )=a\left(\xi \right),b(-\xi )=-b\left(\xi \right), \\ A(-\xi )=A\left(\xi \right),B(-\xi )=-B\left(\xi \right). \end{gathered}$$
• $\det s\left(\xi \right)=\det S\left(\xi \right)=1.$
• $$\begin{gathered} a\left(\xi \right)=1+O(\frac{1}{\xi }),b\left(\xi \right)=O(\frac{1}{\xi }),\xi \to \infty ,Im{\xi }^2\ge 0, \\ A\left(\xi \right)=1+O(\frac{1}{\xi }),B\left(\xi \right)=O(\frac{1}{\xi }),\xi \to \infty ,Im{\xi }^4\ge 0. \end{gathered}$$

These spectral functions do not exist independently, but depend on each other and satisfy certain relationships, we call it global relation

$$B\left(\xi \right)a\left(\xi \right)-A\left(\xi \right)b\left(\xi \right)=e^{4i{\lambda }^{4}T}{c}^{+}\left(\xi \right),Im{\xi }^2\ge 0.$$

(49)

where

$$c^{+}\left(\xi \right)={\int }_0^{\infty }{e}^{2i{\lambda }^2{x}^{\prime }}\left(V_1{\mu }_3\right)(x^{\prime },T;\xi )d{x}^{\prime }.$$

For simplicity, we define $M(x,t;\xi )$

$$\begin{array}{c}{M}_{+}=(\frac{{\mu }_2^{D_1}}{a\left(\xi \right)},{\mu }_3^{D_1\cup D_2}),\xi \in D_1,\hfill \\ M_{-}=(\frac{{\mu }_1^{D_2}}{d\left(\xi \right)},{\mu }_3^{D_1\cup D_2}),\xi \in D_2,\hfill \\ M_{+}=({\mu }_3^{D_3\cup D_4},\frac{{\mu }_1^{D_3}}{\overline{d\left(\overline{\xi }\right)}}),\xi \in D_3,\hfill \\ M_{-}=({\mu }_3^{D_3\cup D_4},\frac{{\mu }_2^{D_4}}{\overline{a\left(\overline{\xi }\right)}}),\xi \in D_4.\hfill \end{array}$$

(50)

where

$$d\left(\xi \right)=a(\left(\xi \right)\overline{A\left(\overline{\xi }\right)}-b\left(\xi \right)\overline{B\left(\overline{\xi }\right)},\xi \in {\overline{D}}_2.$$

(51)

Synthesizing the above definitions, we can get

$$detM(x,t;\xi )=1,$$

(52)

and

$$M(x,t;\xi )=I+O(\frac{1}{\xi }),\xi \to \infty .$$

(53)

Theorem 2.

Given a smooth function $q(x,t)$. Define $M(x,t;\xi )$ as (50), and define ${\mu }_j(x,t;\xi )(j=1,2,3)$ like (37). Then the jump matrices can be derived through

$$M_{+}(x,t;\xi )=M_{-}(x,t;\xi )J(x,t;\xi ),{\xi }^4\in R,$$

(54)

where

$$J=\left\{\begin{array}{cc}{J}_1(x,t;\xi ),\hfill & arg{\xi }^2=0,\hfill \\ J_2(x,t;\xi ),\hfill & arg{\xi }^2=\frac{\pi }{2},\hfill \\ J_3(x,t;\xi )=J_2{J}_1^{-1}{J}_4,\hfill & arg{\xi }^2=\pi ,\hfill \\ J_4(x,t;\xi ),\hfill & arg{\xi }^2=\frac{3}{2}\pi .\hfill \end{array}\right.$$

(55)

and

$$\begin{array}{c}{J}_1=\left(\begin{array}{cc}\frac{1}{a\overline{a}}& \frac{b}{\overline{a}}{e}^{-2i\theta \left(\xi \right)}\\ \frac{\overline{b}}{a}{e}^{2i\theta \left(\xi \right)}& 1\end{array}\right),\hfill \\ J_2=\left(\begin{array}{cc}1& 0\\ -\Gamma \left(\xi \right)e^{2i\theta \left(\xi \right)}& 1\end{array}\right),\hfill \\ J_4=\left(\begin{array}{cc}1& \overline{\Gamma \left(\overline{\xi }\right)}{e}^{2i\theta \left(\xi \right)}\\ 0& 1\end{array}\right).\hfill \end{array}$$

(56)

with

$$\begin{array}{c}\theta \left(\xi \right)={\lambda }^{2}x+2{\lambda }^{4}t=({\xi }^2-1)x+2{({\xi }^2-1)}^{2}t,\hfill \\ \Gamma \left(\xi \right)=\frac{\overline{B\left(\overline{\xi }\right)}}{a\left(\xi \right)d\left(\xi \right)}.\hfill \end{array}$$

(57)

According to definition, we have to consider the residue conditions of $M(x,t;\xi )$. By analyzing, we can know that both $a\left(\xi \right)$ and $d\left(\xi \right)$ have an even zero. Hence, we suppose that

• $a\left(\xi \right)$ has $2n$ simple zeros ${\left\{{\epsilon }_j\right\}}_{j=1}^{2n}$, $2n=2n_1+2n_2$. Furthermore, ${\epsilon }_j(j=1,2,\dots ,2n_1)$ lie in $D_1$, ${\overline{\epsilon }}_j(j=1,2,\dots ,2n_2)$ lie in $D_2$.
• $d\left(\xi \right)$ has $2N$ simple zeros ${\left\{{\gamma }_j\right\}}_{j=1}^{2N}$, $2N=2N_1+2N_2$. In addition, ${\gamma }_j(j=1,2,\dots ,2N_1)$ lie in $D_3$, ${\overline{\gamma }}_j(j=1,2,\dots ,2N_2)$ lie in $D_4$.
• $a\left(\xi \right)$ and $d\left(\xi \right)$ do not have any of the same zeros.

Theorem 3.

For convenience, the mark ${\left[M(x,t;\xi )\right]}_1$ denotes the first column of $M(x,t;\xi )$. Similarly, ${\left[M(x,t;\xi )\right]}_2$ denotes the second column. At the same time, we let $\dot{a}\left(\xi \right)=\frac{da}{d\xi }$. Then, we get the residue condition as follows:

$$\begin{array}{ccc}\left(i\right)\hfill & Res\{{\left[M(x,t;\xi )\right]}_1,{\epsilon }_j\}\hfill & =\frac{1}{\dot{a}\left({\epsilon }_j\right)b\left({\epsilon }_j\right)}{e}^{2i\theta \left({\epsilon }_j\right)}{\left[M(x,t;{\epsilon }_j)\right]}_2,j=1,2,\dots ,2n_1,\hfill \\ \left(ii\right)\hfill & Res\{{\left[M(x,t;\xi )\right]}_2,{\overline{\epsilon }}_j\}\hfill & =\frac{1}{\overline{\dot{a}\left({\overline{\epsilon }}_j\right)b\left({\overline{\epsilon }}_j\right)}}{e}^{-2i\theta \left({\overline{\epsilon }}_j\right)}{\left[M(x,t;{\overline{\epsilon }}_j)\right]}_1,j=1,2,\dots ,2n_2,\hfill \\ \left(iii\right)\hfill & \hfill Res\{{\left[M(x,t;\xi )\right]}_1,{\gamma }_j\}& =\frac{\overline{B\left({\overline{\gamma }}_j\right)}}{a\left({\gamma }_j\right)\dot{d}\left({\gamma }_j\right)}{e}^{2i\theta \left({\gamma }_j\right)}{\left[M(x,t;{\gamma }_j)\right]}_2,j=1,2,\dots ,2N_1,\hfill \\ \left(iv\right)\hfill & \hfill Res\{{\left[M(x,t;\xi )\right]}_2,{\overline{\gamma }}_j\}& =\frac{B\left({\overline{\gamma }}_j\right)}{\overline{a\left({\overline{\gamma }}_j\right)\dot{d}\left({\overline{\gamma }}_j\right)}}{e}^{2i\theta \left({\overline{\gamma }}_j\right)}{\left[M(x,t;{\overline{\gamma }}_j)\right]}_1,j=1,2,\dots ,2N_2.\hfill \end{array}$$

(58)

Proof. 

Just prove $\left(i\right)$, and the other proof can be proved in the same way. Firstly, we take account of $M(x,t;\xi )=(\frac{{\mu }_2^{D_1}a\left(\xi \right)}{,}{\mu }_3^{D_1\cup D_2})$, the simple zeros ${\epsilon }_j(j=1,2,\dots ,2n_1)$ of $a\left(\xi \right)$ are the simple poles of $\frac{{\mu }_2^{D_1}}{a\left(\xi \right)}$. Then we get

$$Res\{\frac{{\mu }_2^{D_1}(x,t;\xi )}{a\left(\xi \right)},{\epsilon }_j\}=\underset{\xi \to {\epsilon }_j}{lim}(\xi -{\epsilon }_j)\frac{{\mu }_2^{D_1}(x,t;\xi )}{a\left(\xi \right)}=\underset{\xi \to {\epsilon }_j}{lim}\frac{{\mu }_2^{D_1}(x,t;{\epsilon }_j)}{\frac{a\left(\xi \right)-a\left({\epsilon }_j\right)}{\xi -{\epsilon }_j}}=\frac{{\mu }_2^{D_1}(x,t;{\epsilon }_j)}{\dot{a}\left({\epsilon }_j\right)},$$

Then taking $\xi ={\epsilon }_j$ into the equation

$${\mu }_3^{D_1\cup D_2}=e^{-2i\theta \left(\xi \right)}b\left(\xi \right){\mu }_2^{D_1}+a\left(\xi \right){\mu }_2^{D_4},$$

we obtain

$${\mu }_3^{D_1\cup D_2}(x,t;{\epsilon }_j)=e^{-2i\theta \left({\epsilon }_j\right)}b\left({\epsilon }_j\right){\mu }_2^{D_1}(x,t;{\epsilon }_j)+a\left({\epsilon }_j\right){\mu }_2^{D_4}(x,t;{\epsilon }_j),$$

Finally,

$$Res\{\frac{{\mu }_2^{D_1}}{a\left(\xi \right)},{\epsilon }_j\}=\frac{e^{2i\theta \left({\epsilon }_j\right)}}{\dot{a}\left({\epsilon }_j\right)b\left({\epsilon }_j\right)}{\mu }_3^{D_1\cup D_2}(x,t;{\epsilon }_j).$$

 □

Now, we discuss how to derive the potential $q(x,t)$ from the spectral functions ${\mu }_j(x,t;\xi )(j=1,2,3)$. Reviewing what we did before, when (21) is a solution of (19), we have ${\mathsf{\Psi }}_1^o=\frac{i}{2}QD{\sigma }_3$. Suppose

$$\mu =I+\frac{m^{\left(1\right)}}{\xi }+\frac{m^{\left(2\right)}}{{\xi }^2}+\frac{m^{\left(3\right)}}{{\xi }^3}+O\left({\xi }^4\right),\xi \to \infty ,$$

is a solution of (32).

As $\xi \to \infty$, letting $m(x,t)=m_{12}^{\left(1\right)}(x,t)$, namely

$$m(x,t)=\underset{\xi \to \infty }{lim}{\left(\xi {\mu }_j(x,t;\xi )\right)}_{12}.$$

By direct calculation, we have

$$q(x,t)=2im(x,t)e^{2i{\int }_{(0,0)}^{(x,t)}\Delta }m(x,t),$$

(59)

After that, it is clear to find that

$$q\overline{q}={4\left|m\right|}^2,q{\overline{q}}_x-q_x\overline{q}=4(m{\overline{m}}_x-m_x\overline{m})-32i{\left|m\right|}^4.$$

(60)

and

$$\Delta =-{2\left|m\right|}^{2}dx+[2i(m{\overline{m}}_x-m_x\overline{m})+{28\left|m\right|}^4]dt.$$

(61)

Eventually, we can get the final form of the potential $q(x,t)$.

4. The Spectral Map and the Regular Riemann-Hilbert Problem

4.1. The Spectral Map

Definition 1.

For initial values $q_0\left(x\right)=q(x,0)$, the map $\mathbb{S}$ can be defined by

$$\mathbb{S}:\left\{q_0\left(x\right)\right\}\to \{a\left(\xi \right),b\left(\xi \right)\}$$

with

$$\left(\begin{array}{c}b\left(\xi \right)\\ a\left(\xi \right)\end{array}\right)={\mu }_3^{\left(2\right)}(x,0;\xi ),Im{\xi }^2\ge 0,$$

where ${\mu }_3(x,0;\xi )$ is the unique solution of the Volterra linear integral equation

$${\mu }_3(x,0;\xi )=I+{\int }_{\infty }^x{e}^{i{\lambda }^2(x^{\prime }-x){\widehat{\sigma }}_3}{V}_1(x^{\prime },0;\xi ){\mu }_3(x^{\prime },0;\xi )d{x}^{\prime }$$

and $V_1(x,0;\xi )$ is given by Equation (46).

Proposition 1.

$a\left(\xi \right)$ and $b\left(\xi \right)$ possess these properties.

(i) 

$a\left(\xi \right)$ and $b\left(\xi \right)$ are analytic for $\{\xi \in C|Im{\xi }^2>0\}$ and continuous for $\{\xi \in C|Im{\xi }^2\ge 0\}$,

(ii) 

$a\left(\xi \right)\overline{a\left(\overline{\xi }\right)}-b\left(\xi \right)\overline{b\left(\overline{\xi }\right)}=1,{\xi }^2\in R$,

(iii) 

$a\left(\xi \right)=1+O(\frac{1}{\xi }),b\left(\xi \right)=O(\frac{1}{\xi }),\xi \to \infty ,Im{\xi }^2\ge 0$,

(iv) 

$a(-\xi )=a\left(\xi \right),b(-\xi )=-b\left(\xi \right),Im{\xi }^2\ge 0$,

(v) 

We define $\mathbb{Q}:\{a\left(\xi \right),b\left(\xi \right)\}\to \left\{q_0\left(x\right)\right\}$, as the inverse of map $\mathbb{S}$, with

$$q_0\left(x\right)=2im\left(x\right)e^{4i{\int }_0^x{\left|m\left(x^{\prime }\right)\right|}^{2}d{x}^{\prime }},m\left(x\right)=\underset{\xi \to \infty }{lim}{(\xi M^{\left(x\right)}(x,\xi ))}_{12}.$$

(62)

where $M^{\left(x\right)}(x,\xi )$ is the unique solution of the following Riemann-Hilbert problem.

• $M^{\left(x\right)}(x,\xi )=\left\{\begin{array}{cc}{M}_{-}^{\left(x\right)}(x,\xi ),\hfill & \hfill Im{\xi }^2\le 0\\ M_{+}^{\left(x\right)}(x,\xi ),\hfill & \hfill Im{\xi }^2\ge 0\end{array}\right.$ is a meromorphic function.
• $M_{+}^{\left(x\right)}(x,\xi )=M_{-}^{\left(x\right)}(x,\xi )J^{\left(x\right)}(x,\xi ),{\xi }^2\in R,$where

  $$J^{\left(x\right)}(x,\xi )=\left(\begin{array}{cc}\frac{1}{a\left(\xi \right)\overline{a\left(\overline{\xi }\right)}}& \frac{b\left(\xi \right)}{a\left(\xi \right)}{e}^{-2i{\lambda }^{2}x}\\ -\frac{\overline{b\left(\overline{\xi }\right)}}{a\left(\xi \right)}{e}^{2i{\lambda }^{2}x}& 1\end{array}\right),{\xi }^2\in R.$$

  (63)
• $M^{\left(x\right)}(x,\xi )=I+O\left(\frac{1}{\xi }\right),\xi \to \infty$.
• $a\left(\xi \right)$ has $2n$ simple zeros ${\left\{{\epsilon }_j\right\}}_{j=1}^{2n}$, $2n=2n_1+2n_2$, such that ${\epsilon }_j,(j=1,2,\dots ,2n_1)$ lie in $D_1$, and ${\overline{\epsilon }}_j,(j=1,2,\dots ,2n_2)$ lie in $D_2$.
• The first column of $M_{+}^{\left(x\right)}$ has simple poles at $\xi ={\epsilon }_j,j=1,2,\dots ,2n_1$. Furthermore, the second column of $M_{-}^{\left(x\right)}$ has simple poles at $\xi ={\overline{\epsilon }}_j,j=1,2,\dots ,2n_2$. The relevant residues are given by

  $$Res\{{[M^{\left(x\right)}(x,\xi )]}_1,{\epsilon }_j\}=\frac{e^{2i({\epsilon }_j^2-1)}x}{\dot{a}\left({\epsilon }_j\right)b\left({\epsilon }_j\right)}{[M^{\left(x\right)}(x,{\epsilon }_j)]}_2,j=1,2,\dots ,2n_1,$$

  (64)

  $$Res\{{[M^{\left(x\right)}(x,\xi )]}_2,{\overline{\epsilon }}_j\}=\frac{e^{-2i({\overline{\epsilon }}_j^2-1)}x}{\overline{\dot{a}\left({\overline{\epsilon }}_j\right)b\left({\overline{\epsilon }}_j\right)}}{[M^{\left(x\right)}(x,{\overline{\epsilon }}_j)]}_1,j=1,2,\dots ,2n_2.$$

  (65)

Definition 2.

For boundary values $g_0\left(t\right)=q(0,t),g_1\left(t\right)=q_x(0,t)$, the map $\tilde{\mathbb{S}}$ can be defined by

$$\tilde{\mathbb{S}}:\{g_0\left(t\right),g_1\left(t\right)\}\to \{A\left(\xi \right),B\left(\xi \right)\}$$

with

$$\left(\begin{array}{c}B\left(\xi \right)\\ A\left(\xi \right)\end{array}\right)={\mu }_1^{\left(2\right)}(0,t;\xi ),Im{\xi }^2\ge 0,$$

where ${\mu }_1(0,t;\xi )$ is the unique solution of the Volterra linear integral equation

$${\mu }_1(0,t;\xi )=I-{\int }_t^T{e}^{2i{\lambda }^4(t^{\prime }-t){\widehat{\sigma }}_3}{V}_2(0,t^{\prime };\xi ){\mu }_1(0,t^{\prime },\xi )d{t}^{\prime }$$

and $V_2(0,t;\xi )$ is given by (46).

Proposition 2.

$A\left(\xi \right)$ and $B\left(\xi \right)$ possess these properties.

(i) 

$A\left(\xi \right)$ and $B\left(\xi \right)$ are analytic for $\{\xi \in C|Im{\xi }^4>0\}$ and continuous $\{\xi \in C|Im{\xi }^4\ge 0\}$,

(ii) 

$A\left(\xi \right)\overline{A\left(\overline{\xi }\right)}-B\left(\xi \right)\overline{B\left(\overline{\xi }\right)}=1,{\xi }^4\in R$,

(iii) 

$A\left(\xi \right)=1+O\left(\frac{1}{\xi }\right),B\left(\xi \right)=O\left(\frac{1}{\xi }\right),\xi \to \infty ,Im{\xi }^4\ge 0$,

(iv) 

$A(-\xi )=A\left(\xi \right),B(-\xi )=-B\left(\xi \right),Im{\xi }^4\ge 0$,

(v) 

We define $\tilde{\mathbb{Q}}:\{A\left(\xi \right),B\left(\xi \right)\}\to \{g_0\left(t\right),g_1\left(t\right)\}$, as the inverse of map $\tilde{\mathbb{S}}$, with

$$\begin{array}{c}{g}_0\left(t\right)=2i{m}_{12}^{\left(1\right)}\left(t\right)e^{2i{\int }_0^t{\Delta }_2\left(t^{\prime }\right)d{t}^{\prime }},\hfill \\ g_1\left(t\right)=(4m_{12}^{\left(2\right)}+|g_0{\left(t\right)|}^2{m}_{12}^{\left(1\right)}\left(t\right))e^{2i{\int }_0^t{\Delta }_2\left(t^{\prime }\right)d{t}^{\prime }}+i{g}_0\left(t\right)(2m_{22}^{\left(2\right)}\left(t\right)+|g_0\left(t\right){|}^2),\hfill \end{array}$$

(66)

where

$${\Delta }_2\left(t\right)=4|m_{12}^{\left(1\right)}{|}^4+8(Re[m_{12}^{\left(1\right)}{\overline{m}}_{12}^{\left(3\right)}]-|m_{12}^{\left(1\right)}{|}^{2}Re[m_{22}^{\left(2\right)}]),$$

with the functions $m^{\left(i\right)}\left(t\right)(i=1,2,3.)$ are depend on

$$M^{\left(t\right)}(t,\xi )=I+\frac{m^{\left(1\right)}\left(t\right)}{\xi }+\frac{m^{\left(2\right)}\left(t\right)}{{\xi }^2}+\frac{m^{\left(3\right)}\left(t\right)}{{\xi }^3}+O(\frac{1}{{\xi }^4}),\xi \to \infty ,$$

where $M^t(t,\xi )$ is the unique solution of the following Riemann-Hilbert problem

• $M^{\left(t\right)}(t,\xi )=\left\{\begin{array}{cc}{M}_{-}^{\left(t\right)}(t,\xi ),\hfill & \hfill Im{\xi }^4\le 0\\ M_{+}^{\left(t\right)}(t,\xi ),\hfill & \hfill Im{\xi }^4\ge 0\end{array}\right.$ is a meromorphic function.
• $M_{+}^{\left(t\right)}(t,\xi )=M_{-}^{\left(t\right)}(t,\xi )J^{\left(t\right)}(t,\xi ),{\xi }^4\in R,$where

  $$J^{\left(t\right)}(t,\xi )=\left(\begin{array}{cc}\frac{1}{A\left(\xi \right)\overline{A\left(\overline{\xi }\right)}}& \frac{B\left(\xi \right)}{\overline{A\left(\overline{\xi }\right)}}{e}^{-4i{\lambda }^{4}t}\\ -\frac{\overline{B\left(\overline{\xi }\right)}}{A\left(\xi \right)}{e}^{4i{\lambda }^{4}t}& 1\end{array}\right),{\xi }^4\in R.$$

  (67)
• $M^{\left(t\right)}(t,\xi )=I+O\left(\frac{1}{\xi }\right),\xi \to \infty$.
• $A\left(\xi \right)$ has $2N$ simple zeros ${\left\{{\gamma }_j\right\}}_{j=1}^{2N}$, $2N=2N_1+2N_2$, such that ${\gamma }_j(j=1,2,\dots ,2N_1)$ lie in $D_3$, and ${\overline{\gamma }}_j(j=1,2,\dots ,2N_2)$ lie in $D_4$.
• The first column of $M_{+}^{\left(t\right)}$ has simple poles at $\xi ={\gamma }_j,j=1,2,\dots ,2N_1$. And the second column of $M_{-}^{\left(t\right)}$ has simple poles at $\xi ={\overline{\gamma }}_j,j=1,2,\dots ,2N_2$. The relevant residues are given by

  $$Res\{{[M^{\left(t\right)}(t,\xi )]}_1,{\gamma }_j\}=\frac{e^{4i{({\gamma }_j^2-1)}^{2}t}}{\dot{A}\left({\gamma }_j\right)B\left({\gamma }_j\right)}{[m^{\left(t\right)}(t,{\gamma }_j)]}_2,j=1,2,\dots ,2N_1,$$

  (68)

  $$Res\{{[M^{\left(t\right)}(t,\xi )]}_2,{\overline{\gamma }}_j\}=\frac{e^{-4i{({\overline{\gamma }}_j^2-1)}^{2}t}}{\overline{\dot{A}\left({\overline{\gamma }}_j\right)b\left({\overline{\gamma }}_j\right)}}{[M^{\left(t\right)}(t,{\overline{\gamma }}_j)]}_1,j=1,2,\dots ,2N_2.$$

  (69)

4.2. The Regular Riemann-Hilbert Problem

Theorem 4.

Given the smooth function $q_0\left(x\right)$, which is compatible with $g_0\left(t\right)$ and $g_1\left(t\right)$. The spectral functions $a\left(\xi \right)$,$b\left(\xi \right)$, $A\left(\xi \right)$, and $B\left(\xi \right)$ are defined according to the previous definitions. Furthermore, they satisfy the global relation (49). Clearly, it becomes $B\left(\xi \right)a\left(\xi \right)-A\left(\xi \right)b\left(\xi \right)=0$ when $\xi \to \infty$. Define the $M(x,t;\xi )$ as the solution of this following Riemann-Hilbert problem.

• $M(x,t;\xi )$ is a sectionally meromorphic function in $\{\xi \in C|{\xi }^4\in R\}$.
• The residue condition of $M(x,t;\xi )$ satisfies Theorem 3
• $M(x,t;\xi )$ satisfies the jump condition

  $$M_{+}(x,t;\xi )=M_{-}(x,t;\xi )J(x,t;\xi ),{\xi }^4\in R,$$

  where the jump matrices are defined by (55)–(57).
• $M(x,t;\xi )=I+O\left(\frac{1}{\xi }\right),\xi \to \infty .$

Then, $M(x,t;\xi )$ not only exists but is unique. In this way, the solution of the mNLS equation can be derived, which can be defined by

$$\begin{array}{c}q(x,t)=2im(x,t)e^{2i{\int }_{(0,0)}^{(x,t)}\Delta },\hfill \\ m(x,t)=\underset{\xi \to \infty }{lim}{\left(\xi {\mu }_j(x,t;\xi )\right)}_{12},\hfill \\ \Delta =-{2\left|m\right|}^{2}dx+[2i(m{\overline{m}}_x-m_{x}m)+{28\left|m\right|}^4]dt.\hfill \end{array}$$

(70)

Besides, $q(x,t)$ also satisfies the initial-boundary values condition

$$q(x,0)=q_0\left(x\right),q(0,t)=g_0\left(t\right),and{q}_x(0,t)=g_1\left(t\right).$$

Proof. 

Actually, if there are no zeros of $a\left(\xi \right)$ and $d\left(\xi \right)$, then the $2\times 2$ function $M(x,t;\xi )$ satisfies a non-singular Riemann-Hilbert problem. Due to the jump matrices $J(x,t;\xi )$ possessing symmetry, we can find that this problem has a unique solution. On the other hand, when $a\left(\xi \right)$ and $d\left(\xi \right)$ have a certain number of zeros, by specific mapping, the singular Riemann-Hilbert problem can become no zeros with a system of algebraic equations; the unique solvability can be proved by the following theorem. □

Theorem 5.

The Riemann-Hilbert problem in Theorem 4 with the vanishing boundary condition

$$M(x,t;\xi )\to 0,\xi \to \infty ,$$

has only the zero solution.

Proof. 

Firstly, we suppose that the matrix function $M(x,t;\xi )$ is a solution of the Riemann-Hilbert problem in Theorem 4. At the same time, $A^{†}$ means the complex conjugate transpose of A, where A is a $2\times 2$ matrix. We define

$$\begin{array}{c}{H}_{+}\left(\xi \right)=M_{+}\left(\xi \right)M_{-}^{†}(-\overline{\xi }),Im{\xi }^4\ge 0,\hfill \\ H_{-}\left(\xi \right)=M_{-}\left(\xi \right)M_{+}^{†}(-\overline{\xi }),Im{\xi }^4\le 0,\hfill \end{array}$$

(71)

where the x and t are dependent with each other. $H_{+}\left(\xi \right)$ and $H_{-}\left(\xi \right)$ are analytic in $\{\xi \in C|Im{\xi }^4>0\}$ and $\{\xi \in C|Im{\xi }^4<0\}$, respectively. Due to the symmetry, we can obtain from (54) and (55)

$$J_1^{†}(-\overline{\xi })=J_1\left(\xi \right),J_3^{†}(-\overline{\xi })=J_3\left(\xi \right),J_2^{†}(-\overline{\xi })=J_4\left(\xi \right).$$

(72)

Then

$$\begin{array}{c}{H}_{+}\left(\xi \right)=M_{-}\left(\xi \right)J\left(\xi \right)M_{-}^{†}(-\overline{\xi }),Im{\xi }^4\in R,\hfill \\ H_{-}\left(\xi \right)=M_{-}\left(\xi \right)J^{†}(-\overline{\xi })M_{-}^{†}(-\overline{\xi }),Im{\xi }^4\in R.\hfill \end{array}$$

(73)

From the above two equations, it is easy to find that $H_{+}\left(\xi \right)=H_{-}\left(\xi \right)$. This means that $H_{+}\left(\xi \right)$ and $H_{-}\left(\xi \right)$ define an entire function decaying at infinity, hence the $H_{+}\left(\xi \right)\equiv 0$ and $H_{-}\left(\xi \right)\equiv 0$. Finding $J_3(i\hslash )(\hslash \in R)$ is a $2\times 2$ unit Hermitian matrix for any $\hslash \in R$. It is not difficult to see that $J_3(i\hslash )(\hslash \in R)$ is a positive definite matrix. Now that $H_{-}(\hslash )=0$ for $\hslash \in iR$, we have

$$M_{+}(i\hslash )J_3(i\hslash )M_{+}^{†}(i\hslash )=0.$$

(74)

After simple calculation, we have $M_{+}(i\hslash )=0$ for $\hslash \in R$. Therefore, $M_{+}\left(\xi \right)=0$, $M_{-}\left(\xi \right)=0$. □

Remark 1.

$q(x,t)$ satisfies the mNLS equation.

In fact, if $M(x,t;\xi )$ is the solution of the Riemann-Hilbert problem defined by Theorem 4 and $q(x,t)$ is defined as the previous definition, with the help of the dressing method [45], we can find that $q(x,t)$ satisfies the Lax pair (18). Hence, $q(x,t)$ satisfies the mNLS equation.

Remark 2.

Using the same proof method in Reference [32] can we prove that $q(x,t)$ satisfies the initial values $q(x,0)=q_0\left(x\right)$ and boundary values $q(0,t)=g_0\left(t\right),q_x(0,t)=g_1\left(t\right)$, so in this paper, we leave this proof out.

5. Conclusions

In this paper, we mainly studied the initial-boundary values problem for the mNLS equation on the half line. Before we did this, with the help of prolongation structure theory, the Lax pair of this equation was derived. Then we reconstructed the Lax pair to obtain a Riemann-Hilbert problem, and therefore, the potential function has been represented by its solution. In future work, the long time asymptotic behavior for the solutions will be analyzed.