Equilibrium and Stability of Entropy Operator Model for Migratory Interaction of Regional Systems

Abstract

In this paper, we develop a dynamic model for migratory interaction of regional systems that is based on an entropy operator. Next, we study the properties of this operator and establish the existence of a unique singular point in the dynamic entropy model. Here, we use monotonicity property of entropy operator on corresponding vector interval. We study Lyapunov stability of a dynamic system with entropy operator. Stability conditions have been obtained in terms of eigenvalues of linearized system’s matrix. Finally, we give an illustrative example for migratory interaction of regional systems.

1. Introduction

The processes of migration and biological reproduction represent major factors determining the spatial distribution of populations. These factors are realized in considerably different time scales. In accordance with standard assumptions, the relaxation time of migratory processes is 2–3 years while the relaxation time of biological reproduction reaches 10–13 years, see [1,2,3]. An important characteristic of population is its size, more specifically, its distribution in some regionalized space. Migration considerably affects the spatiotemporal evolution of population distribution. For the time intervals comparable with the relaxation times of migratory processes, the influence of biological reproduction factors becomes rather small and therefore can be neglected.

Mathematical modeling and analysis of interregional migration was considered in numerous publications. First, it seems appropriate to mention the monographs [4,5], which were dedicated to a wide range of interregional migration problems, including mathematical modeling of migration flows. Note that the problem of migration touches upon many aspects of socioeconomic, psychological and political status of the space of migratory movements. So of crucial role is the structural analysis of inter- and intraregional migration flows [6] and motivations that generate them [7,8]. The results of structural and motivational analysis of migratory processes are used for computer simulation. There exist three directions of research in this field, each relying on some system of hypotheses. One of the directions involves the stochastic hypothesis about the origin of migratory motivations [9], which is simulated using agent technologies [10,11]. This direction is adjoined by investigations based on the thermodynamic model of migration flows [12,13]. The other two directions are connected with using balanced [4,5] and Markov [2] models. Of course, the short list above does not exhaust the whole variety of migration studies, merely outlining some topics of research.

This paper considers the interaction of two regional systems as follows. The first system has traditional migratory processes while the second is a source of immigration flows to the former. We suggest a mathematical model of such interaction in form of a dynamic system with an entropy operator. This model proceeds from the stochastic hypothesis about the origin of migration flows, which is realized by conditional maximization of the generalized information entropy. Next, we develop a qualitative analysis method for the dynamic system, including the existence of a unique equilibrium distribution of regional population sizes and its stability.

Finally, the method suggested in this paper is illustrated by modeling the migratory interactions between three EU countries (Germany, France, Italy—the system $\mathcal{GFI}$) and two countries as sources of immigration (Syria and Libya—the system $\mathcal{SL}$). We construct the set of equilibrium distributions for regional population size that is parameterized by the following characteristics: regional mobility, the prior probabilities of migratory movements, and the normalized specific regional cost of immigration (the system $\mathcal{GFI}$); the prior probabilities of immigratory movements (the system $\mathcal{SL}$).

2. Structure of Dynamic Entropy Model of Migration

Consider a spatial system partitioned into N regions that exchange population. At a time t, the state of this system is characterized by the population distribution among all regions, i.e., by the vector $\mathbf{K}(t)=\{K_1(t),\dots ,K_N(t)\}$. The population distribution varies with the course of time as the result of interregional migration within the system and also external immigration from M source regions outside the system.

We will employ the stochastic model of migration flows [14]. In accordance with this model, interregional flows are formed by a random independent distribution of potential migrants between system regions with some prior probabilities. A similar mechanism describes immigration flows from external regions to system regions. These mechanisms (the distribution of migration flows) are defined in probabilistic terms using appropriate entropy functions or functionals. Migratory interactions between system regions take place under constraints on the size of mobile population (the people inclined to migration). By standard assumption, the size of mobile population in a region is proportional to the regional population size, and the coefficient of proportionality has regional index. The potential amount of external immigration is often difficult or even impossible to calculate. However, sometimes there exists expert appraisals for immigration flows from external regions to system regions. Such appraisals often seem to be strongly overrated. Therefore, the constraints on external immigration have to be associated with regional absorption cost of immigrants. The entropy characteristics of migration flows as a function of flow distribution possess the so-called sharp maximum. This justifies the hypothesis about the existence of a realizable distribution of migration and immigration flows corresponding to the constrained maximum of the entropy [14].

Introduce the following notations for transforming the described phenomenology into a mathematical model (see [14]):

• $x_{in}(t),(i,n)=\overline{1,N},$ as the migration flows $(i\rightleftarrows j)$ within the system;
• $a_{in}(t),(i,n)=\overline{1,N},$ as the prior probabilities of individual migration between regions $(i,j)$ of the system;
• ${\alpha }_n,n=\overline{1,N},$ as the shares of mobile population in system regions;
• $y_{kn},k=\overline{1,M},n=\overline{1,N},$ as the immigration flows $(k\to j)$ from external regions to system regions;
• $b_{kn},k=\overline{1,M},n=\overline{1,N},$ as the prior probabilities of individual immigration from external region k to system region j;
• $c_{kn},k=\overline{1,M},n=\overline{1,N},$ as the normalized (Here, normalization means that the values of specific cost belong to the range [0, 1].) specific generalized cost of immigration to system regions;
• $c_{kn}^{(s)},k=\overline{1,M},n=\overline{1,N},s=\overline{1,r},$ as the normalized specific cost of immigration to system regions by the types of resources $(r)$;
• $T(K_1,\dots ,K_N)$ as the normalized (Here, the normalized supply functions are defined by

  $$T(K_1,\dots ,K_N)=\frac{1}{c}\tilde{T}(K_1,\dots ,K_N),c=max{c}_{kn},$$

  where $\tilde{T}(K_1,\dots ,K_N)$ denotes a given supply function.) supply function of generalized financial resources (cost) for immigration;
• $T^{(s)}(K_1,\dots ,K_N)$ as the normalized supply functions by $s=\overline{1,r}$ types of financial resources for immigration.

We will model the migration and immigration flows using the stochastic migration mechanisms characterized by

• the generalized Boltzmann information entropy

  $$H_M(X)=-\sum _{(i,n)=1;i\ne n}^N{x}_{in}ln\frac{x_{in}}{a_{in}}$$

  (1)

  for interregional migration within the system and
• by the generalized Boltzmann information entropy

  $$H_I(X)=-\sum _{k=1}^M\sum _{n=1}^N{y}_{kn}ln\frac{y_{kn}}{b_{kn}}$$

  (2)

  for the immigration from external regions to the system.

Migratory processes always have some constraints. For interregional migration, they are associated with the size of mobile population in regions, i.e.,

$$X\in \mathcal{D}(\mathbf{K})=\{X:\sum _{i=1}^N{x}_{ni}={\alpha }_n{K}_n(t),n=\overline{1,N}\}.$$

(3)

In the case of external immigration, such constraints are imposed on the system resources required for external immigration. In accordance with the classification above, we will consider the following models of immigration cost:

• the generalized cost of the form

  $$\begin{array}{c}Y\in {\mathcal{D}}_G(\mathbf{K})=\{Y:\sum _{k=1}^M\sum _{n=1}^N{c}_{kn}{y}_{kn}=T(\mathbf{K}(t))\},\hfill \\ c_{kn}\in [0,1];T(\mathbf{K}(t))=\frac{1}{c}\tilde{T}(\mathbf{K}(t)),c=\underset{kn}{max}{c}_{kn};\hfill \end{array}$$

  (4)
• the cost by the types of resources of the form

  $$\begin{array}{c}Y\in {\mathcal{D}}_D(\mathbf{K})=\{\sum _{k=1}^M\sum _{n=1}^N{c}_{kn}^{(s)}{y}_{kn}={\tilde{T}}^{(s)}(\mathbf{K}(t))\};\hfill \\ c_{kn}^{(s)}\in [0,1];{\tilde{T}}^{(s)}(\mathbf{K}(t))=\frac{1}{c^{(s)}}{T}^{(s)}(\mathbf{K}(t)),c^{(s)}=\underset{kn}{max}{c}_{kn}^{(s)},s=\overline{1,r}.\hfill \end{array}$$

  (5)

The functions $T(\mathbf{K}(t))$ and ${\mathbf{T}}^{(1)}(\mathbf{K}(t)),\dots ,{\mathbf{T}}^{(r)}(\mathbf{K}(t))$ depend on the population distribution in the system, and these relationships are linear [14]:

$$T(\mathbf{K}(t))=\sum _{n=1}^N{\gamma }_n{K}_n(t),T^{(s)}(\mathbf{K}(t))=\sum _{n=1}^N{\beta }_{sn}{K}_n(t),s=\overline{1,r}.$$

(6)

Therefore, the entropy models of population distribution have the following form:

• for the interregional migration flows within the system,

  $$x_{in}^{\ast }(t)=argmax\left(H_M(X),X\in \mathcal{D}(\mathbf{K})\right),(i,n)=\overline{1,N};$$

  (7)
• for the immigration flows from external regions to the system (with the generalized cost),

  $$y_{kn}^{\ast }(t)=argmax\left(H_I(Y),Y\in {\mathcal{D}}_G(\mathbf{K})\right),k=\overline{1,M},n=\overline{1,N};$$

  (8)
• for the immigration flows from external regions to the system (with the cost by the types of resources),

  $$y_{kn}^{\ast }(t)=argmax\left(H_I(Y),Y\in {\mathcal{D}}_D(\mathbf{K})\right),k=\overline{1,M},n=\overline{1,N}.$$

  (9)

These models represent the corresponding entropy operators that map the space $R_{+}^n$ of all vectors $\mathbf{K}(t)$ into the space $R_{+}^{N^2}$ of all matrices X, or into the space $R_{+}^{NM}$ of all matrices Y.

3. Analysis of Entropy Operators

3.1. Entropy Operator $\mathbf{K}\to X$

Consider the constrained maximization problem for entropy (1) and (4) and construct the corresponding Lagrange function

$$L_M(X,\lambda )=H_M(X)+\sum _{n=1}^N{\lambda }_n({\alpha }_n{K}_n(t)-\sum _{i=1}^N{x}_{ni}),$$

(10)

where $\lambda =\{{\lambda }_1,\dots ,{\lambda }_N\}$ are the Lagrange multipliers. The optimality conditions have the form

$$\begin{array}{c}-\left(ln\frac{x_{ni}}{a_{ni}}+1\right)-{\lambda }_n=0,(n,i)=\overline{1,N};\hfill \\ \sum _{i=1}^N{x}_{ni}-{\alpha }_n{K}_n(t)=0,n=\overline{1,N}.\hfill \end{array}$$

(11)

The solution of these equations, i.e., the migration flows from region n to region i ($i\ne n$) are given by

$$x_{ni}^{\ast }=\frac{a_{ni}}{{\sum }_{l=1}^N{a}_{nl}}{\alpha }_n{K}_n(t),(n,i)=\overline{1,N},$$

(12)

and form the matrix $X_{\ast }$. In this case, the mapping $(\mathbf{K}\in R_{+}^N\to X\in R_{+}^{N^2})$ (the entropy operator) can be written in the analytic form (12).

The transposed matrix $X_{\ast }^{⊺}$ consists of the elements

$$x_{in}^{\ast }=\frac{a_{in}}{{\sum }_{l=1}^N{a}_{ln}}{\alpha }_i{K}_i(t),(n,i)=\overline{1,N}.$$

(13)

They represent the immigration flows from region i to region n ($i\ne n$).

Hence, for region n the net migration flow is

$$S_n(t)=\frac{{\sum }_{i=1}^N{a}_{in}{\alpha }_i{K}_i(t)}{{\sum }_{l=1}^N{a}_{ln}}-{\alpha }_n{K}_n(t),n=\overline{1,N}.$$

(14)

3.2. Entropy Operator $\mathbf{K}\to Y$

Now, consider the constrained maximization problem for entropy (2) and (4). The corresponding Lagrange function is defined by

$$L_I(Y,\lambda )=H_I(Y)+\lambda \left(T(\mathbf{K}(t))-\sum _{k=1}^M\sum _{n=1}^N{c}_{kn}{y}_{kn}\right),$$

(15)

where $\lambda$ is the Lagrange multiplier and the normalized specific generalized cost has the form

$$c_{k_0,n_0}=c=1,0<c_{kn}<1.$$

(16)

Here, the optimality conditions are

$$\begin{array}{c}-\left(ln\frac{y_{kn}}{b_{kn}}+1\right)-\lambda c_{kn}=0,k=\overline{1,M},n=\overline{1,N},\hfill \\ -\sum _{k=1}^M\sum _{n=1}^N{c}_{kn}{y}_{kn}+T(\mathbf{K}(t))=0.\hfill \end{array}$$

(17)

These equations yield the entropy-optimal immigration flows from external regions to the system:

$$\begin{array}{c}{y}_{kn}^{\ast }={\tilde{b}}_{kn}{z}^{c_{kn}},k=\overline{1,M},n=\overline{1,N},\hfill \\ z=exp(\lambda )\ge 0,{\tilde{b}}_{kn}=e^{-1}{b}_{kn}.\hfill \end{array}$$

(18)

The exponential Lagrange multiplier z satisfies the equation

$$\sum _{k=1}^M\sum _{n=1}^N{c}_{kn}{\tilde{b}}_{kn}{z}^{c_{kn}}-T(\mathbf{K}(t))=0.$$

(19)

In this case, the mapping $\mathbf{K}\to Y$ (the entropy operator) is described by equalities (18) and Equation (19).

The total immigration flow from external regions to the system constitutes

$$I_n(t)=\sum ^M{y}_{kn}^{\ast }=\sum _{k=1}^M{\tilde{b}}_{kn}{z}^{c_{kn}},n=\overline{1,N}.$$

(20)

4. Analysis of Migratory Interaction Model of Regional Systems

Under the above assumptions, the system state evolves with the internal net migration flows and also the net immigration flows from external regions, i.e.,

$$\frac{d{K}_n(t)}{dt}=\sum _{i=1}^N[x_{in}^{\ast }(t)-x_{ni}^{\ast }(t)]+\sum _{k=1}^M{y}_{kn}^{\ast },n=\overline{1,N}.$$

(21)

Using the formulas of these flows, we obtain the following equations of the dynamic migratory interaction model of regional systems:

$$\begin{array}{c}\frac{d{K}_n(t)}{dt}=-{\alpha }_n{K}_n(t)+\sum _{i=1}^N\frac{a_{in}}{{\sum }_{l=1}^N{a}_{ln}}{\alpha }_i{K}_i(t)+\sum _{k=1}^M{\tilde{b}}_{kn}{z}^{c_{kn}},n=\overline{1,N},\hfill \\ \sum _{k=1}^M\sum _{n=1}^N{c}_{kn}{\tilde{b}}_{kn}{z}^{c_{kn}}-T(\mathbf{K}(t))=0,z\ge 0.\hfill \end{array}$$

(22)

4.1. Existence of Unique Singular Point

The existence problem of unique equilibrium in this model is associated with analysis of the equations

$$\begin{array}{c}(1-{\alpha }_n)K_n+\sum _{i=1,i\ne n}^N{a}_{in}{\alpha }_i{K}_i+\sum _{k=1}^M{b}_{kn}{z}^{c_{kn}}=K_n,n=\overline{1,N},\hfill \\ \sum _{n=1}^N{\tilde{\gamma }}_n{K}_n(t)+z-\sum _{k=1}^M\sum _{n=1}^N{c}_{kn}{\tilde{b}}_{kn}{z}^{c_{kn}}=z.\hfill \end{array}$$

(23)

Introduce the vector of variables

$$\mathbf{u}=\{u_1,\dots ,u_N,u_{(N+1)}\},u_n=K_n,n=\overline{1,N};u_{(N+1)}=z.$$

(24)

Then Equation (23) can be written as

$$A(\mathbf{u})=\mathbf{u},\mathbf{u}\ge \mathbf{0},$$

(25)

with the vector function

$$A(\mathbf{u})=\left(\begin{array}{c}(1-{\alpha }_1)u_1+\sum _{i=1,i\ne 1}^N{a}_{i1}{\alpha }_i{u}_i+\sum _{k=1}^M{\tilde{b}}_{k1}{u}_{(N+1)}^{c_{k1}}\\ \dots \dots \dots \dots \dots \dots \dots \dots \\ (1-{\alpha }_N)u_N+\sum _{i=1,i\ne N}^N{a}_{iN}{\alpha }_i{u}_i+\sum _{k=1}^M{\tilde{b}}_{kN}{u}_{(N+1)}^{c_{kn}}\\ \sum _{n=1}^N{\tilde{\gamma }}_n{u}_n+u_{N+1}-\sum _{k=1,k\ne k_0}^M\sum _{n=1,n\ne n_0}^N{\tilde{c}}_{kn}{\tilde{b}}_{kn}{u}_{(N+1)}^{c_{kn}}\end{array}\right).$$

(26)

The Jacobian of this function has the form

$$J(\mathbf{u})=\left(\begin{array}{cc}{J}_{11}& J_{12}\\ J_{21}& J_{22}\end{array}\right),$$

(27)

where

$$\begin{array}{ccc}\hfill J_{11}& =& \left(\begin{array}{cccc}1-{\alpha }_1& a_{21}{\alpha }_2& \dots & a_{N1}{\alpha }_N\\ a_{12}{\alpha }_1& 1-{\alpha }_2& \dots & a_{N2}{\alpha }_N\\ ⋮& ⋮& \ddots & ⋮\\ a_{1N}{\alpha }_1& a_{2N}{\alpha }_2& \dots & 1-{\alpha }_N\end{array}\right)>0,\hfill \\ \hfill J_{12}& =& {\left(\begin{array}{cccc}\sum _{k=1}^M{\tilde{b}}_{k1}{c}_{k1}{u}_{N+1}^{(c_{k1}-1)}& \sum _{k=1}^M{\tilde{b}}_{k2}{c}_{k2}{u}_{N+1}^{(c_{k2}-1)}& \dots & \sum _{k=1}^M{\tilde{b}}_{kN}{c}_{kN}{u}_{N+1}^{(c_{kN}-1)}\end{array}\right)}^{⊺}>0,\hfill \\ \hfill J_{21}& =& \left(\begin{array}{cccc}{\gamma }_1& {\gamma }_2& \dots & {\gamma }_N\end{array}\right)>0,\hfill \\ \hfill J_{22}& =& 1-\sum _{k=1}^M\sum _{n=1}^N{c}_{kn}^2{\tilde{b}}_{kn}{u}_{N+1}^{(c_{kn}-1)}.\hfill \end{array}$$

(28)

Theorem 1.

Let $J_{22}>0$. Then the function $A(\mathbf{u})$ is strictly monotonic over the space $R_{+}^{(N+1)}$.

Proof. 

Under the hypothesis of this theorem, all elements of the Jacobian are positive, which proves the desired result. ☐

Assume we know the population distribution among system regions at the initial time $t_0$, i.e., $\{K_1(t_0)=u_1^0,\dots ,K_N(t_0)=u_N^0\}$. Denote by $u_{N+1}^0>0$ the solution of the last equation in (25) and (26). Define the vector ${\mathbf{u}}^0=\{u_1^0,\dots ,u_N^0,u_{N+1}^0\}$. Suppose that, by an expert appraisal of immigration from external regions, the population size in system regions may increase by $\kappa >1$ times. This means that $\{K_1(t)<\kappa u_1^0={\tilde{u}}_1,\dots ,K_N(t)<\kappa u_N^0={\tilde{u}}_{N+1}\}$ for $t>t_0$. Designate as ${\tilde{u}}_{N+1}>u_{N+1}^0>0$ the solution of the last equation in (25) and (26) with the described upper estimates for regional population sizes. Construct the vector $\tilde{\mathbf{u}}=\{{\tilde{u}}_1,\dots ,{\tilde{u}}_N,{\tilde{u}}_{N+1}\}$ and define the vector segment $\mathcal{U}=\{{\mathbf{u}}^0,\tilde{\mathbf{u}}\}$.

Theorem 2.

For Equation (26), let

$$A({\mathbf{u}}^0)>{\mathbf{u}}^0,A(\tilde{\mathbf{u}})<\tilde{\mathbf{u}}.$$

(29)

Then there exists an leats one solution ${\mathbf{u}}^{\ast }$ of Equation (26) on the vector segment $\mathcal{U}$.

The proof of this result follows from ([15], Theorem 3.1 in p. 48). Moreover, by this theorem the iterative process

$$A({\mathbf{u}}^s)={\mathbf{u}}^{(s+1)},\mathbf{u}(0)\in \mathcal{U},$$

(30)

converges to the point ${\mathbf{u}}^{\ast }$.

4.2. Stability of Singular Point

For the stability analysis of a singular point, represent the system of Equation (22) in the form

$$\frac{d\mathbf{u}}{dt}=A(\mathbf{u})-\mathbf{u}.$$

(31)

Denote by $\mathbf{y}=\mathbf{u}-{\mathbf{u}}^{\ast }$ the deviation from the singular point. Then the standard linearization procedure yields the following differential equations in the deviation from this singular point:

$$\frac{d\mathbf{y}}{dt}=\tilde{J}({\mathbf{u}}^{\ast })\mathbf{y},\mathbf{y}\in R^{(N+1)},$$

(32)

where

$$\tilde{J}({\mathbf{u}}^{\ast })=J({\mathbf{u}}^{\ast })-E.$$

(33)

The system of differential Equation (32) is linear, and there exist many stability analysis methods for its equilibrium. We will described a method based on the localization procedure of the eigenvalues of the matrix $\tilde{J}({\mathbf{u}}^{\ast })$ using the Gershgorin circles [16]. In accordance with the Gershgorin circle theorem, on the complex plane any eigenvalue of the matrix $\tilde{J}({\mathbf{u}}^{\ast })$ belongs to at least one of the following circles with center $c_i$ and radius ${\varrho }_i$:

$$c_i=\left\{\begin{array}{cc}-{\alpha }_i,\hfill & i=\overline{1,N},\hfill \\ -\sum _{k=1}^M\sum _{n=1}^N{c}_{kn}^2{\tilde{b}}_{kn}{u}_{N+1}^{(c_{kn}-1)},\hfill & i=N+1.\hfill \end{array}\right.$$

(34)

$${\varrho }_i=\sum _{j\ne i}^{(N+1)}\left|d_{ij}\right|,i=\overline{1,(N+1)},$$

(35)

where

$$d_{ij}=\left\{\begin{array}{cc}{a}_{ij},\hfill & (i,j)=\overline{1,N},j\ne i,\hfill \\ \sum _{k=1}^M{\tilde{b}}_{ki}{c}_{ki}{\left[u_{N+1}^{(c_{ki}-1)}\right]}^{\ast },\hfill & i=\overline{1,N},j=N+1,\hfill \\ {\gamma }_j,\hfill & i=N+1,j=\overline{1,N},\hfill \\ -\sum _{k=1}^M\sum _{n=1}^N{c}_{kn}^2{\tilde{b}}_{kn}{\left[u_{N+1}^{(c_{kn}-1)}\right]}^{\ast },\hfill & (i,j)=N+1.\hfill \end{array}\right.$$

(36)

These equalities dictate that the centers are $c_i<0,i=\overline{1,(N+1)}$, while the radii are ${\varrho }_i>0,i=\overline{1,(N+1)}$.

Theorem 3.

Let

$$c_i+{\varrho }_i<0,i=\overline{1,(N+1)}.$$

(37)

The the singular point ${\mathbf{u}}^{\ast }$ of system (22) is stable in the small.

Proof. 

Under the hypotheses of this theorem, all eigenvalues of the matrix $\tilde{J}({\mathbf{u}}^{\ast })$ have negative real parts. ☐

5. Model of Migratory Interaction: An Example

The appearance of territories with low economic status always causes the growth of immigration. The early 2000s were remarkable for the formation of several such territories in the Northern and Central Africa, the Near East, Afghanistan, etc. As a result, tens of millions of migrants moved to the EU as the level of life in these territories dropped below the subsistence minimum. The EU countries have to allocate considerable financial resources for their filtering and accommodation, which are often unacceptable.

As an illustrative example, consider the migratory interactions between three EU countries (the system $\mathcal{GFI}$ composed of regions with index n, namely, Germany (1), France (2), and Italy (3)) and two sources of immigration (the system $\mathcal{SL}$ composed of regions with index k, namely, Syria (1) and Lybia (2)). In terms of the mathematical model (22), we have (see [2,4])

$$\begin{array}{c}\frac{d{K}_n(t)}{dt}=-{\alpha }_n{K}_n(t)+\sum _{i=1,i\ne n}^3\frac{a_{in}}{{\sum }_{l=1,l\ne n}^n{a}_{ln}}{\alpha }_i{K}_i(t)+\sum _{k=1}^2{\tilde{b}}_{kn}{z}^{c_{kn}},n=1,2,3;\hfill \\ \sum _{n=1}^3{\gamma }_n{K}_n(t)-\sum _{k=1}^2\sum _{n=1}^3{c}_{kn}{\tilde{b}}_{kn}{z}^{c_{kn}}=0.\hfill \end{array}$$

(38)

5.1. Data Arrays for Numerical Study of Model (38)

This model contains four groups of parameters as follows:

• ${\alpha }_1,{\alpha }_2,$ and ${\alpha }_3$ as the characteristics of population mobility in the system $\mathcal{GFI}$;
• $A=[a_{in},(i,n)=\overline{1,N},a_{nn}=0]$ as the matrix of the prior probabilities of individual migration in the system $\mathcal{GFI}$;
• $B=[b_{kn},k=1,2;n=1,2,3]$ as the matrix of the prior probabilities of individual immigration from the system $\mathcal{SL}$;
• $C=[c_{kn},k=1,2;n=1,2,3]$ as the matrix of normalized specific cost of the system $\mathcal{GFI}$ for maintaining the immigration from the system $\mathcal{SL}$.

Recall that the elements of the first three groups of parameters have values strictly smaller than 1. The maximal element of the matrix C is 1 while the other elements are strictly smaller than 1. The coefficients are ${\gamma }_1=2.00,{\gamma }_2=2.53,$ and ${\gamma }_3=1.65.$ (These values are defined by the immigration budgeting rules of the EU countries).

Introduce the four-dimensional attribute space $\mathcal{P}\subset R_{+}^4$ of the status variables: $\nu$ (mobility), $\pi$ (migration choice), $\mu$ (immigration choice), and T (cost scale). For each group, assign the following rating points for the parameters using the ten-point scale:

• mobility $(m):m_1=7,m_2=8,m_3=5$;
• migration choice $(h):h_{12}=3,h_{13}=3,h_{21}=5,h_{23}=2,h_{31}=6,h_{32}=4$;
• immigration choice $(q):q_{11}=6,q_{12}=5,q_{13}=4,q_{21}=4,q_{22}=6,q_{23}=6$;
• immigration cost $(e):e_{11}=5,e_{12}=6,e_{13}=5,e_{21}=5,e_{22}=6,e_{23}=5.$

These points are mostly determined by regional population sizes and the levels of economic development. Then the parameters in these groups can be written as follows:

• the characteristics of population mobility in the system $\mathcal{GFI}$ as

  $${\alpha }_n=\nu m_n,n=1,2,3;$$

  (39)
• the prior probabilities of individual migration in the system $\mathcal{GFI}$ as

  $$a_{in}=\pi h_{in},(i,n)=1,2,3;$$

  (40)
• the prior probabilities of individual immigration from the system $\mathcal{SL}$ as

  $${\tilde{b}}_{kn}=\mu q_{kn},k=1,2;n=1,2,3;$$

  (41)
• the normalized specific cost of the system $\mathcal{GFI}$ for maintaining the immigration from the system $\mathcal{SL}$ as

  $$c_{kn}=T{e}_{kn},k=1,2;n=1,2,3.$$

  (42)

Define the admissible domains $\mathcal{F}$ of the status variables in the form

$$\begin{array}{cc}\hfill & \mathcal{F}=\mathcal{N}\otimes \mathcal{P}\otimes \mathcal{M}\otimes \mathcal{T},\hfill \end{array}$$

$$\begin{array}{c}\nu \in \mathcal{N}=[{10}^{-3},2\times {10}^{-3}];\pi \in \mathcal{P}=[0.5\times {10}^{-1},1.5\times {10}^{-1}];\hfill \end{array}$$

(43)

$$\begin{array}{c}\mu \in \mathcal{M}=[0.5\times {10}^{-1},1.5\times {10}^{-1}];T\in \mathcal{T}=[0.1,0.5].\hfill \end{array}$$

(44)

Exhaustive search over a spatial grid will be used below. So divide each interval into four subintervals. Then we have exhaustive search on 256 nodes of the grid. The discrete analogs of these intervals have the form

$$\begin{array}{c}\tilde{\mathcal{N}}={10}^{(-1)}·[0.5;1.0;1.5;2.0],\tilde{\mathcal{P}}={10}^{-1}·[0.75;1.00;1.25;1.50],\hfill \\ \tilde{\mathcal{M}}={10}^{-1}[0.75;1.00;1.25;1.50],\tilde{\mathcal{T}}=[0.2;0.3;0.4;0.5].\hfill \end{array}$$

(45)

The grid represents is the direct product of these intervals, i.e.,

$$\tilde{\mathcal{F}}=\tilde{\mathcal{N}}\otimes \tilde{\mathcal{P}}\otimes \tilde{\mathcal{M}}\otimes \tilde{\mathcal{T}}.$$

(46)

5.2. Equilibrium Distributions of Regional Population Sizes in System $\mathcal{GFI}$

For the equilibrium analysis of the system $\mathcal{GFI}$, we have to solve the equations

$$\begin{array}{c}-\nu m_n{K}_n+\sum _{i=1,i\ne n}^3\frac{\pi h_{in}}{{\sum }_{l=1,l\ne n}^n\pi h_{ln}}\nu m_i{K}_i+\sum _{k=1}^2\mu q_{kn}{z}^{T{e}_{kn}}=0,n=1,2,3;\hfill \\ 2.0K_1+2.53K_2+1.65K_3-\sum _{k=1}^2\sum _{n=1}^{3}T{e}_{kn}\mu q_{kn}{z}^{T{e}_{kn}}=0.\hfill \end{array}$$

(47)

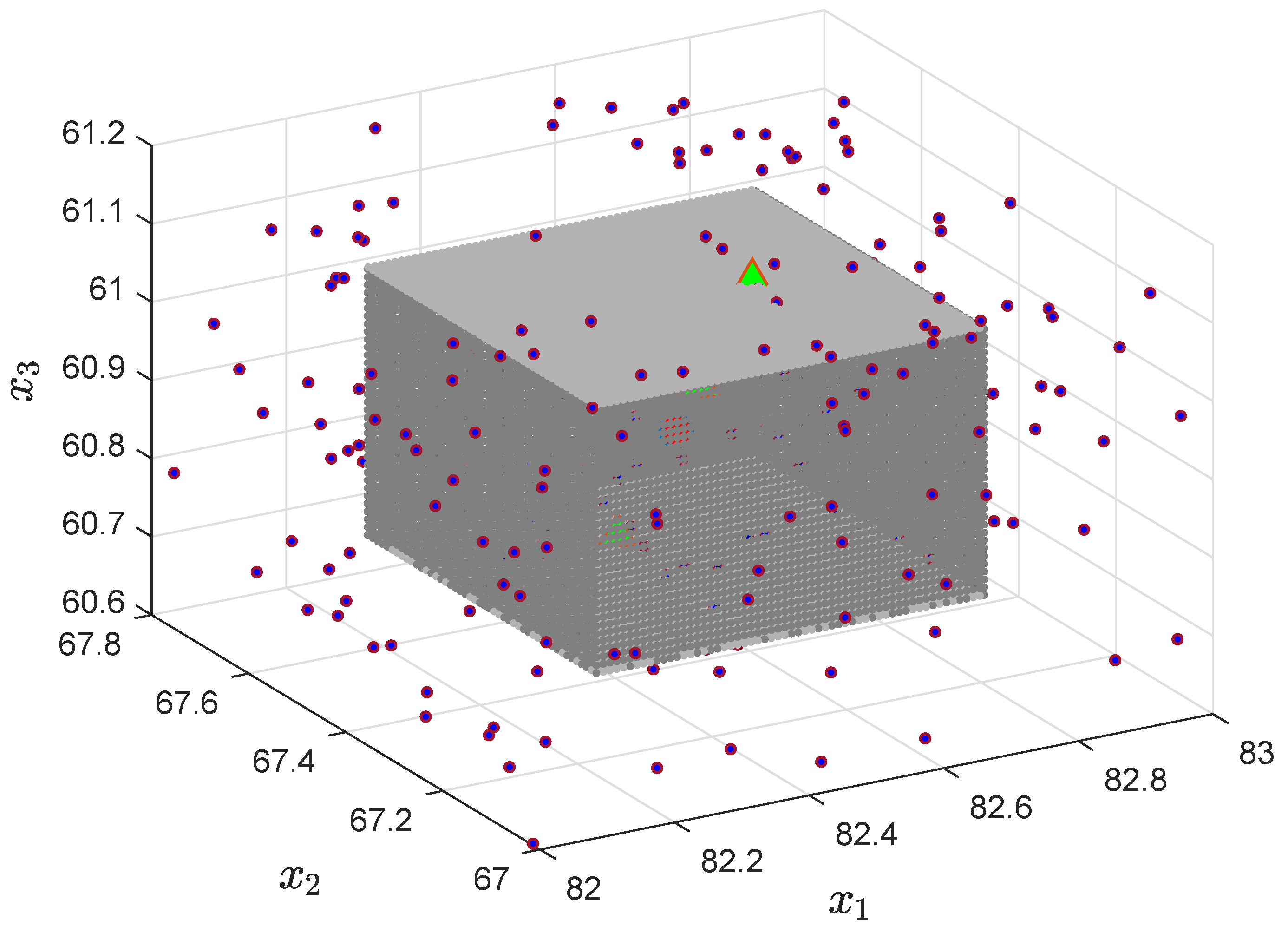
The initial values of the variables are $K_1^0=82,K_2^0=67,K_3^0=60,$ and $z^0=0.1$. Population size is measured in million people. Figure 1 shows the calculated equilibrium distributions $(K_1^{\ast },K_2^{\ast },K_3^{\ast })$ of regional population sizes for the systems $\mathcal{GFI}$ and $\mathcal{SL}$ over the grid $\tilde{\mathcal{F}}$ (46). The cloud $\mathcal{K}$ contains 256 points corresponding to the nodes of grid (46). The center of this cloud matches the average distribution of regional population sizes

$$\overline{\mathbf{K}}=\frac{1}{256}\sum _{i=1}^{256}{\mathbf{K}}^i=\{82.7;67.9;60.3\}.$$

(48)

A useful characteristic of the cloud is its variance core $\mathcal{R}$, i.e., the ball inside the cloud of radius

$$R=\frac{1}{256}\sum _{i=1}^{256}{(\mathbf{K}-\overline{\mathbf{K}})}^{⊺}(\mathbf{K}-\overline{\mathbf{K}})=1.17.$$

(49)

5.3. Stability of Equilibrium Distribution of Regional Population Sizes in System $\mathcal{GFI}$

The equilibrium distributions are stable in the small if and only if the real parts of the eigenvalues of the matrix $\tilde{J}$ (33) belong to intervals (37). On the strength of Theorem 3, we have the stability condition

$$\underset{i}{max}\left(c_{ii}^{\ast }+{\varrho }_i^{\ast }\right)\le 0,$$

(50)

where ${(}^{\ast })$ denotes the values of variables corresponding to the equilibrium distribution, ${\varrho }_i^{\ast }$ is defined by equality (35), and

$$c_{ii}^{\ast }=\left\{\begin{array}{cc}-{\nu }^{\ast }{m}_i,\hfill & i=\overline{1,3},\hfill \\ -{\left[T^2\mu \right]}^{\ast }\sum _{k=1}^M\sum _{n=1}^N{e}_{kn}^2{q}_{kn}{\left[z^{\ast }\right]}^{(T^{\ast }{e}_{kn}-1)},\hfill & i=4;\hfill \end{array}\right.$$

(51)

$$d_{ij}^{\ast }=\left\{\begin{array}{cc}{\pi }^{\ast }{h}_{ij},\hfill & (i,j)=\overline{1,3},j\ne i,\hfill \\ {\mu ]}^{\ast }\sum _{k=1}^M{q}_{ki}{e}_{ki}{\left[z^{\ast }\right]}^{(T^{\ast }{e}_{ki}-1)},\hfill & i=\overline{1,3},j=4,\hfill \\ {\gamma }_j,\hfill & i=4,j=\overline{1,3},\hfill \\ -{\left[T^2\mu \right]}^{\ast }\sum _{k=1}^M\sum _{n=1}^N{e}_{kn}^2{q}_{kn}{\left[z^{\ast }\right]}^{(T^{\ast }{e}_{kn}-1)},\hfill & (i,j)=4.\hfill \end{array}\right.$$

(52)

Figure 1 illustrates three equilibrium distributions (marked by triangles) with the coordinates

$$\begin{array}{c}{C}_1=\{82.6228;67.4256;61.0597\},C_2=\{82.5310;67.4051;60.9496\},\hfill \\ C_3=\{82.2856;67.2362;60.8639\},\hfill \end{array}$$

(53)

which satisfies the stability conditions. These stable in the small equilibrium distributions of regional population sizes are associated with the parameters of model (38) combined in

Table 1. Mobility coefficients.

Notations	${\mathit{\alpha }}_1$	${\mathit{\alpha }}_2$	${\mathit{\alpha }}_3$
$C_1$	0.0105	0.0120	0.0075
$C_2$	0.0070	0.0080	0.0050
$C_3$	0.0140	0.0160	0.0100

,

Table 2. Prior probabilities of regional mobility.

${\mathit{C}}_1$			${\mathit{C}}_2$			${\mathit{C}}_3$
0.000	0.375	0.375	0.000	0.300	0.300	0.000	0.450	0.450
0.625	0.000	0.250	0.500	0.000	0.200	0.750	0.000	0.300
0.750	0.500	0.000	0.600	0.400	0.000	0.900	0.600	0.000

,

Table 3. Prior probabilities of immigration.

${\mathit{C}}_1$			${\mathit{C}}_2$			${\mathit{C}}_3$
0.900	0.750	0.600	0.750	0.625	0.500	0.600	0.500	0.600
0.600	0.900	0.900	0.500	0.750	0.750	0.400	0.600	0.600

and

Table 4. Normalized specific cost.

${\mathit{C}}_1$			${\mathit{C}}_2$			${\mathit{C}}_3$
0.83	1.00	0.83	0.66	0.80	0.66	0.50	0.60	0.50
0.83	1.00	0.83	0.66	0.80	0.66	0.50	0.60	0.50

.

Therefore, using the known parameters of model (38), we may calculate its major dynamic characteristics, the stable equilibrium distributions of regional population sizes, which can be further used, e.g., for short-term forecasting.

6. Conclusions

In this paper, we have developed a dynamic entropy model of migratory interactions. Next, we have studied the entropy operators describing the distributions of migration and immigration flows as well as established the existence conditions of unique equilibrium distributions of regional population sizes and their stability conditions. The new model has been applied to analyze the equilibrium distributions of regional population sizes and their stability. The existence and stability conditions of these distribution both depend on the model parameters, which can be found using randomized machine learning procedures.