1. Introduction
Compressible flow has many applications some of which are of physics, mathematics and engineering interest. In general we have two types of flows, internal and external. Internal flows in ducts are important in industry and nozzles and diffusers used in engines are also an applied area for these types of flows. In general, density changes are related to temperature changes. External flows can be important for airplanes and projectiles where compressiblilty effects are important. The Navier Stokes equations have been dealt with extensively in the literature for both analytical [
1] and numerical solutions [
2,
3]. Some work converting the compressible Navier-Stokes equations to the Schrödinger equation in quantum mechanics by means of transformations has been carried out by Vadasz [
4]. General mathematical and computational methods for compressible flow have been outlined in [
5]. Methods in more general fluid mechanics are also addressed in [
6]. In the context of functional analysis it has been shown in [
7] that generally the motion of a compressible fluid with fixed initial velocity field and constant initial density converges to that of an incompressible fluid as its sound speed goes to infinity. Some analytical methods such as in [
8] have been successfully carried out for one and two dimensional isentropic unsteady compressible flow. In the present work I introduce a new procedure to write the compressible unsteady Navier Stokes equations with a general spatial and temporal varying density term in terms of an additive solution of the three principle directions in the radial, azimuthal and
z directions of flow. This procedure can be used in physics and engineering to simplify a complex system of PDE to a simpler one such as complex multiphase flows [
9] and other areas in physics using Geometric Algebra, such as for example the study of the Maxwell equations. In mathematics, the method leads to the present work which shows the necessary conditions for the full solution of the system of equations for compressible flow to blowup at a certain time for certain types of initial conditions and also implications of using assumptions for necessary and physically meaningful functional forms of density. Following the general procedure, a dimensionless parameter is introduced whereby in the large limit case a method of solution is sought for in the tube. It is concluded that the total divergence of the flow can be expressed as the integral with respect to time of the line integral of the dot product of inertial and azimuthal velocity. The line integral can be evaluated on a contour that is annular and traces the boundary layer as time increases in the flow. A reduction to a single partial differential equation is possible and integral calculus methods are applied for the case of a body force directed downwards with gravity to obtain an integral form of the Hunter-Saxton equation. A specific density function that is exponential in time and having characteristics of a pulse that propagates radially and axially in the tube and can be interpreted as having a large density gradient in time and in space is used.
2. A New Composite Velocity Formulation
The 3D compressible cylindrical unsteady Navier-Stokes equations are written in expanded form, for each component,
,
and
:
where
is the radial component of velocity,
is the azimuthal component and
is the velocity component in the direction along tube,
is density,
is dynamic viscosity,
,
,
are body forces on fluid. The total gravity force vector is expressed as
.
The following relationships between starred and non-starred dimensional quantities together with a non-dimensional quantity
are used:
c a constant is defined below,
as part of the continuity equation (Equation (
12)). The solution of this equation in terms of
is of the form
, for general function
, I first set
, which is a Dirac type pulse as
gets arbitrarily large. For the second type of density function of small amplitude,
, where
is a function of compact support on an interval
. For the second choice of
the density
is defined everywhere in tube when
is small for
large and in addition
solves the pde in
and
above for both types.This will eliminate two of the nonlinear terms in the Navier Stokes equations below for
sufficiently large and negative.
Using Equations (4)–(9),multiplying Equations (1)–(3) by cartesian unit vectors
,
and
respectively and adding Equations (1)–(3) gives the following equation, for the resulting composite vector
,
Furthermore one can take the cross product of Equation (
10) with
and
to form two equations respectively where in the second case multiplication by
to cancel squared nonlinear terms,
, leads to,
where
,
and continuity equation, Equation (
12) below has been used. Equation (
10) is sufficient to carry out the subsequent analysis.
3. A Solution Procedure for Arbitrarily Large in Quantity
Multiplication of Equation (
10) by
and Equation (
12) below by
, addition of the resulting equations [
9], and using the ordinary product rule of differential multivariable calculus a form as in Equation (
13) is obtained whereby I set
.
The continuity equation in cylindrical co-ordinates is
where
.
Taking the geometric product in the previous equation with the inertial vector term,
where
is defined, where in the context of Geometric Algebra, the following scalar and vector grade equations arise,
The geometric product of two vectors [
10], is defined by
.
Taking the divergence of Equation (
16) results in
Upon multiplication of Equation (
17) by,
the resulting equation is
which results upon using Equation (
15) in,
The continuity equation is written in terms of
as,
and
where the following compact expression is given,
Multiplying by
in Equation (
20) and, using properties of third derivatives involving the gradient and in particular the fact that the Laplacian of the divergence of a vector field is equivalent to the divergence of the Laplacian of a vector field, leads to the following form,
where
in Equation (
24) and,
This involves the vector projection of
onto
which is written in the conventional form,
Equation (
24) can be written compactly as
where
is the scalar projection for
,
,
(a differential operator defined by Equations (16) and (24)) and hence for a constant
,
with solution in terms of a function
,
If the rate of change of
with respect to
t is changing exponentially in time as
and
, where
is either of two density type functions defined in the beginning of this paper, it may be proven that
is written in terms of a separable function, if
is chosen to be negligible. and I obtain,
where
are the separable parts of the function,
,
,
, are arbitrary constants, and as
,
For
approaching zero and using the properties of the norm,
Furthermore using the property for a norm on a vector space of continuous functions (since away from
),
iff
, and Equation (
16) and the second line of Equation (
24) gives,
where
, for
, with
chosen such that
(here it can be proved that the viscosity is a function of density which is a Dirac pulse function, also in general it can be proven that Equation (
28) with viscosity as a function of small amplitude type density function can have a similar form as in Equation (
30)) for a new form of
. Next continuing with Equation (
33),
where
.
in Equation (
24) vanishes due to assumption on rate of change of density with respect to
t and
, and finally Equation (
22) has been used with a calculation done to show that the expression reduces in going from Equation (
33) to Equation (
34).
Also,
For large
r it can be proven that
is decaying as a
Bessel function and
is an increasing function radially in tube (
) with the following resulting upon taking the curl of Equation (
34),
where the conservative gravity force drops out.
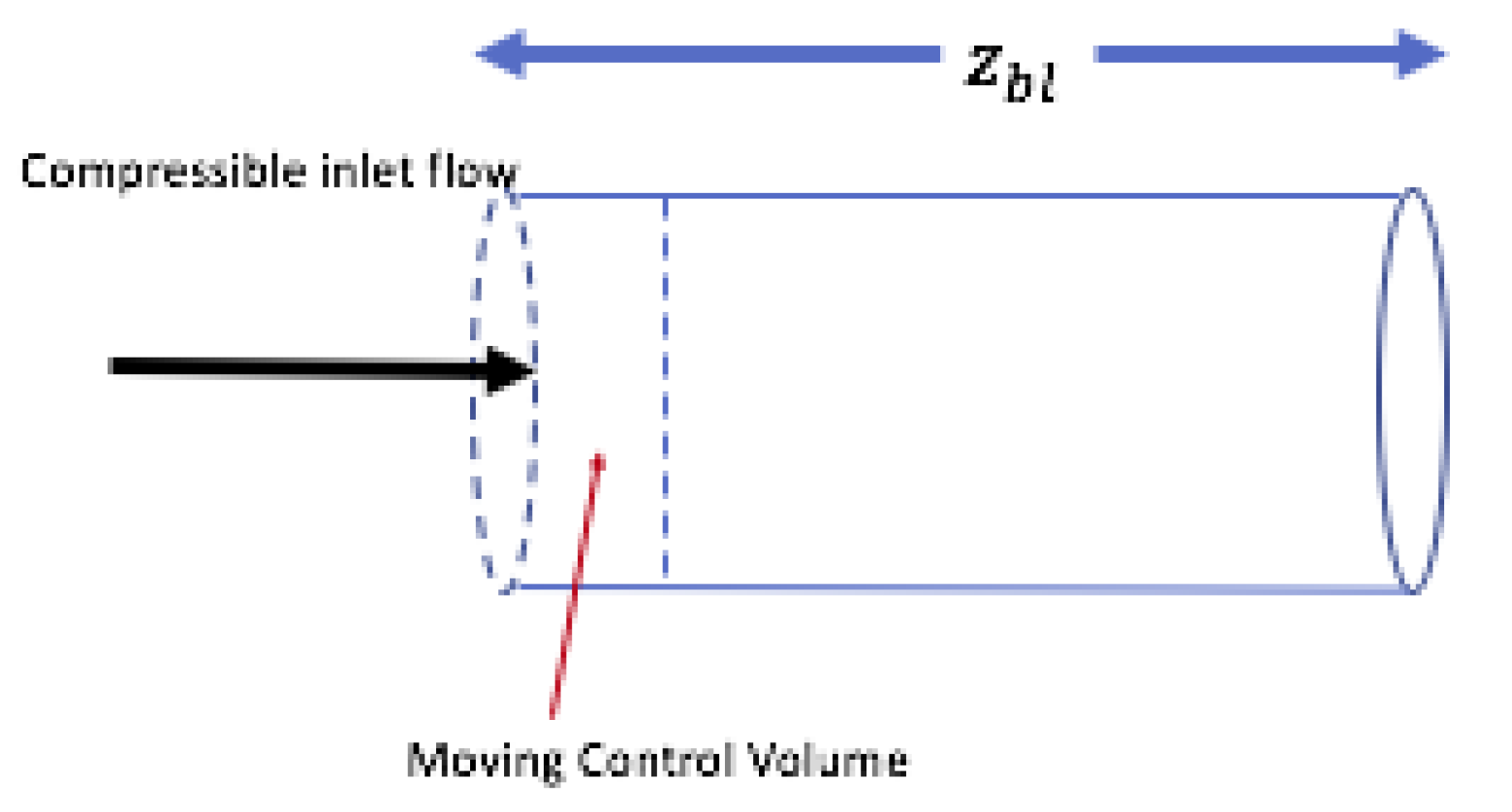
Multiply Equation (
35) by the normal vector
which is the normal component of
at wall of moving control volume (CV) in
Figure 1,
Recalling Divergence theorem and Stoke’s theorem, for general
,
where
C is the contour of a circle in control volume of tube and
S consists of all surfaces of control volume.
Defining the following vector field,
where
, and Stoke’s theorem has been used. Applying Stoke’s theorem to
, hence
.
where
is unit tangent vector to closed curve
C and
is arc length,
The third term in the parenthesis in Equation (
42) is integrated by parts for line integral and I obtain the following,
Parametrizing the circle as
in polar coordinates it can be proven that the line integral in Equation (
43) is,
The normal form of Green’s theorem can be used for the line integral in Equation (
44), setting first,
The line integral in Equation (
44) is equal to the following,
where
M and
N are given by Equations (45) and (46) respectively and
R is the open disk with boundary
C. The gravity force
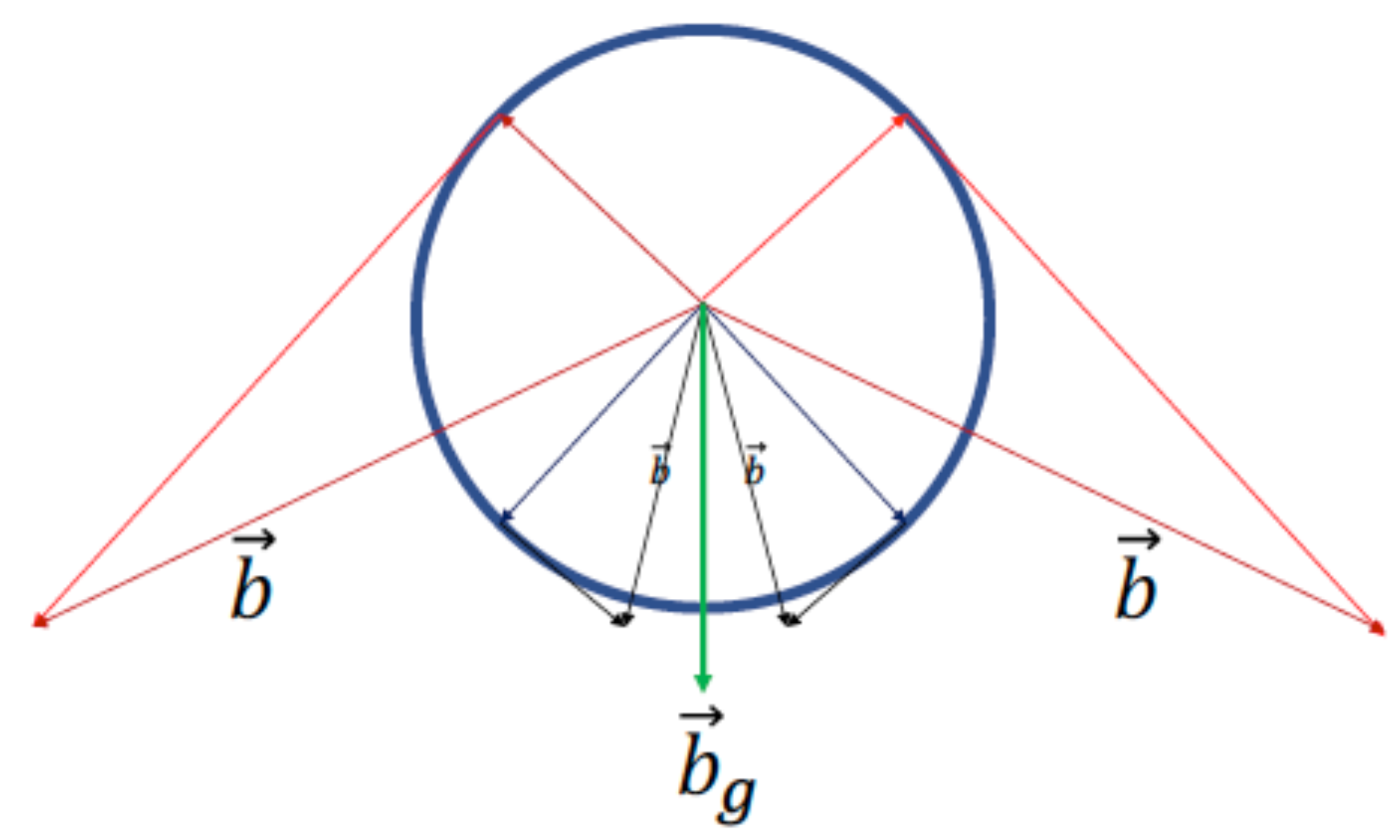
is expressed as follows,
where
is a potential function, h is the negative height in the direction of the vector
in
Figure 2,
T is a time constant and
g is gravity constant. Also
at the vertical vector
in
Figure 2. It follows that Equation (
47) becomes,
For
the function
and
, and thus for
small, integration in
r on the interval
, where
is near the wall in control volume,
In the above analysis I have integrated the second term in second line of Equation (
52) wiith respect to
r and have obtained,
where
A,
B and
C are constants. Letting
and
, I obtain a general non-zero constant
. Integrating the first term in Equation (
52) with respect to
r following the same procedure as in previous step, the result is that I obtain a general nonzero constant
. The same is true for the third term in Equation (
52) where I have a non-zero constant
.
Choosing constants in , and such that , and = 1, the resulting equation obtained is the Hunter-Saxton PDE.