Classifying Evolution Algebras of Dimensions Two and Three

Abstract

We classified evolution algebras of dimensions two and three. Evolution algebras of dimensions three were classified recently obtaining 116 non-isomorphic types of algebras. Herein, with a new approach, we classify these algebras into 14 non-isomorphic types of algebra, so that this new classification is easier to deal with.

1. Introduction

Mathematics and biology are intimately tied, and genetic algebras are an example of this link, as these are algebras with biological meanings. In this paper we are going to work with evolution algebras, kinds of genetic algebra introduced by Tian in [1] in 2008 that are used to model non-Mendelian genetics laws, although this is not their only application. In fact, they are strongly connected with group theory, Markov processes, the theory of knots, dynamic systems and graph theory. Due to the versatility of these algebras, the amount of literature studying them has grown immensely since 2008. In [2], the authors studied the relationship between evolution algebras and the spaces of functions defined by the Gibbs measure of a graph, which led into direct applications in biology, physics and mathematics itself. In works such as [3,4,5,6,7,8,9,10] they studied purely mathematical notions, such as nilpotency and solvency of evolution algebras, as well as the interpretation of these mathematical notions, relating, for example, the nilpotency of an element to gametes that go extinct after some generations. Chains of evolution algebras were studied in [11,12,13,14]. These are dynamic systems where the state of each system can be seen as an evolution algebra. Some derivatives of evolution algebras were studied in [1,15,16].

An important topic is the classification of evolution algebras of a given dimension up to isomorphism. There are several papers related with classification of evolution algebras, such as [17,18,19,20,21,22,23,24]. The first classification of evolution algebras of dimension two was given in [6], and some years later, in [17] (as part of a doctoral thesis [25]) another classification of these evolution algebras was provided, together with a classification of three dimensional evolution algebras into 116 non-isomorphic types.

Classifying a class of algebras consists of determining a classification criterion; i.e., defining different types of these algebras such that these different types are non-isomorphic to each other and such that each algebra belongs to exactly one of these types. In an intuitive way, we are constructing a cupboard with different drawers, in a such a way that each of the elements we are classifying belongs to one (and only one) of those drawers, but you can have more than one thing in each one. Nevertheless, if we change the shape of the drawers, the final cupboard will look completely different, even if it contains the same objects. As mentioned before, in [17] evolution algebras of dimension three were classified into 116 types of non-isomorphic evolution algebras. In this paper, we classify three-dimensional evolution algebras into 14 non-isomorphic types (Theorem 11). To do so, our classifying criteria are be based on distinguishing whether these algebras are degenerate or not and whether they are reducible or not. In the case of irreducible, non-degenerate algebras we differentiate three situations: when they have a basic ideal of dimension one and none of dimension two, when they have a two-dimensional basic ideal and they do not have a one dimensional basic ideal and when they have no basic ideals. According to the same criteria, we also obtain a classification of two-dimensional evolution algebras (Theorem 3). This shall be helpful for the classification of reducible three-dimensional evolution algebras. Since we reduce the study of evolution algebras of dimension three to 14 non-isomorphic types, this classification is much more practical than the classification provided in [17].

Note that every weighted digraph with three nodes is associated to an evolution algebra with dimension three in a one-to-one way. So, with this classification for evolution algebras we also have a classification of weighted digraphs with three vertices, particularly of discrete Markov processes with a state space of size three, as Markov processes are particular cases of evolution algebras. As a matter of fact, Markov processes are evolution algebras whose structure matrix is stochastic.

2. Basic Background

As the problem addressed in this paper is that of classifying evolution algebras of dimension two and three, in what follows we shall consider only evolution algebras of finite dimensions. Also, the algebras considered are defined over a field $\mathbb{K}$ (where $\mathbb{K}=\mathbb{R}$ or $\mathbb{C}$).

We recall that an evolution algebra is an algebra A that has a natural basis $B=\{e_1,\dots ,e_n\}$, which is a basis of A such that $e_i{e}_j=0$ if $i\ne j$. For a fixed natural basis B, the square of each element can be written as $e_i^2={\displaystyle \sum _{k=1}^n}{w}_{ki}{e}_k$, and so, we can define the structure matrix of A relative to B in the following way

$$M_B\left(A\right)=\left(\begin{array}{c}{w}_{11}\dots w_{1n}\\ ⋮\ddots ⋮\\ w_{n1}\dots w_{nn}\end{array}\right),$$

where the ith column is given by the coefficients of $e_i^2$ with respect to B. When the basis B is clear we shall refer to this matrix as the structure matrix of A, without any further specification to B. This matrix determines the product of $A.$ Indeed, given $a={\displaystyle \sum _{k=1}^n}{\alpha }_k{e}_k$ and $b={\displaystyle \sum _{k=1}^n}{\beta }_k{e}_k$ elements of A, it follows that $ab={\displaystyle \sum _{k=1}^n}{\gamma }_k{e}_k$, where

$$\left(\begin{array}{c}\hfill {\gamma }_1\\ \multicolumn{1}{c}{⋮}\\ \hfill {\gamma }_n\end{array}\right)=\left(\begin{array}{c}{w}_{11}\dots w_{1n}\\ ⋮\ddots ⋮\\ w_{n1}\dots w_{nn}\end{array}\right)\left(\begin{array}{c}\hfill {\alpha }_1{\beta }_1\\ \multicolumn{1}{c}{⋮}\\ \hfill {\alpha }_n{\beta }_n\end{array}\right).$$

The next definition shall be useful to understand whether the natural basis is essentially unique or not.

Definition 1.

Let A be an evolution algebra with dimension $n\in \mathbb{N}$, and let B and $\tilde{B}$ be two natural basis of A. We say that B and $\tilde{B}$ are related if $B=\{e_1,\dots ,e_n\}$ and $\tilde{B}=\{{\alpha }_1{e}_{\tau \left(1\right)},\dots ,{\alpha }_n{e}_{\tau \left(n\right)}\}$, where τ is a permutation of the set $\{1,\dots ,n\}$ and ${\alpha }_1,\dots ,{\alpha }_n$ are non-zero scalars.

In the next result, we shall see that, if the structure matrix of an evolution algebra A relative to one natural basis has non-zero determinant, then the natural basis is “essentially unique.”

Proposition 1.

Let A be an evolution algebra. Let $B=\{e_1,\dots ,e_n\}$ be a natural basis of A and $M_B\left(A\right)$ the corresponding structure matrix of A relative to B. Suppose that $det\left(M_B\left(A\right)\right)\ne 0$. Then any other natural basis $\tilde{B}$ of A is related to $B,$ and moreover, $det\left(M_{\tilde{B}}\left(A\right)\right)\ne 0.$

Proof. 

Since $A^2=lin\{e_1^2,\cdots ,e_n^2\},$ the condition $det\left(M_B\left(A\right)\right)\ne 0$ is equivalent to $dim{A}^2=n.$ Thus, if $\tilde{B}=\{u_1,\dots ,u_n\}$, since $A^2=lin\{u_1^2,\cdots ,u_n^2\}$ we obtain that $det\left(M_{\tilde{B}}\left(A\right)\right)\ne 0$, as $\{u_1^2,\cdots ,u_n^2\}$ must also be linearly independent. Now, consider ${\alpha }_{ij}\in \mathbb{K}$ for all $i,j\in \{1,\dots ,n\}$ such that

$$\begin{array}{c}{u}_1={\alpha }_{11}{e}_1+\dots +{\alpha }_{n1}{e}_n\\ ⋮\\ u_n={\alpha }_{1n}{e}_1+\dots +{\alpha }_{nn}{e}_n.\end{array}$$

Consider $\Lambda =\{{\alpha }_{ki}\ne 0:1\le k,i,\le n\}$, which has a maximum of $n\times n$ elements. Fix i in $\{1,\dots n\}.$ There must exist $k\in \{1,\dots ,n\}$ such that ${\alpha }_{ki}\ne 0$; otherwise, we would have $u_i=0$ (a contradiction). Thus, $|\Lambda |\ge n$. But as $u_i{u}_j=0$ for all $j\ne i$ we have that ${\sum }_{k=1}^n{\alpha }_{ki}{\alpha }_{kj}{e}_k^2=0$ and as $e_1^2$,..., $e_n^2$ are linearly independent; then, ${\alpha }_{ki}{\alpha }_{kj}=0$ whenever $i\ne j$. Thus, it must be ${\alpha }_{kj}=0$ for all $j\ne i$ as ${\alpha }_{ki}\ne 0$. Rephrasing what we just obtained, for each $1\le k\le n$ there is at most one sub-index i such that ${\alpha }_{ki}\ne 0$. Then, $|\Lambda |\le n$, which immediately implies that $|\Lambda |=n$. But as said before, each $u_i$ is non-zero, so we must have that there exists a unique $k\in \{1,\dots ,n\}$ such that $u_i={\alpha }_{ki}{e}_k$, and the result is clear. □

We shall now explain how to assign a graph to each evolution algebra. At first, it might depend on the natural basis selected, although we shall see that in some situations this graph is again “essentially unique.” For a discussion about this topic see [3].

Definition 2.

Let $B=\{e_i:i\in \Lambda \}$ be a natural basis of an evolution algebra A, and $M_B=\left(w_{ij}\right)$ its structure matrix. The graph associated to A with respect to $B$ is the graph $E_A^B$ whose set of vertices is B and the adjacency matrix is $M_B^t\left(A\right)$. The simplified graph associated to A with respect to $B,$ is defined as the associated graph but without taking into account the weights; i.e., just considering whether there is a link between two vertices or not. Again, whenever the basis is clear, we shall speak about the graph (respectively simplified graph) associated to A, without any further specification.

Example 1.

Let A be an evolution algebra with dimension 3, and consider a natural base $B=\{e_1,e_2,e_3\}$ being

$$\begin{array}{ccc}\hfill e_1^2& =& e_1-2e_2+3e_3,\hfill \\ \hfill e_2^2& =& -5e_2+e_3,\hfill \\ \hfill e_3^2& =& -2e_1.\hfill \end{array}$$

Then, the structure matrix is given by $M_B\left(A\right)=\left(\begin{array}{ccc}\hfill 1& \hfill 0& \hfill -2\\ \hfill -2& \hfill -5& \hfill 0\\ \hfill 3& \hfill 1& \hfill 0\end{array}\right),$ while the associated graph is

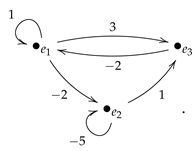
When we ignore the weigths $w_{ij}$ of the arrows of the graph we obtain the corresponding simplified graph:

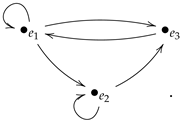
We shall see now how the structure matrix changes when we multiply the elements of the natural basis by non-zero scalars, and how it affects the associated graph.

Proposition 2.

Let A be an evolution algebra, $B=\{e_1,\dots ,e_n\}$ a natural basis, and $M_B\left(A\right)=\left(\begin{array}{c}{w}_{11}\dots w_{1n}\\ ⋮\ddots ⋮\\ w_{n1}\dots w_{nn}\end{array}\right)$ the structure matrix of A relative to B. If ${\alpha }_1,\dots ,{\alpha }_n$ are non-zero scalars, then $\tilde{B}=\{{\alpha }_1{e}_1,\dots ,{\alpha }_n{e}_n\}$ is a natural basis of A and its structure matrix is given by

$$M_{\tilde{B}}\left(A\right)=\left(\begin{array}{cccc}{\alpha }_1{w}_{11}\hfill & \frac{{\alpha }_2^2}{{\alpha }_1}{w}_{12}\hfill & \cdots \hfill & \frac{{\alpha }_n^2}{{\alpha }_1}{w}_{1n}\hfill \\ \frac{{\alpha }_1^2}{{\alpha }_2}{w}_{21}\hfill & {\alpha }_2{w}_{22}\hfill & \hfill & \frac{{\alpha }_n^2}{{\alpha }_2}{w}_{2n}\hfill \\ ⋮\hfill & \hfill & \hfill & ⋮\hfill \\ \frac{{\alpha }_1^2}{{\alpha }_n}{w}_{n1}\hfill & \frac{{\alpha }_2^2}{{\alpha }_n}{w}_{n2}\hfill & \cdots \hfill & {\alpha }_n{w}_{nn}\hfill \end{array}\right).$$

Thus, the corresponding simplified graphs of A with respect to B and $\tilde{B}$ coincide.

Proof. 

Taking into account that

$${\left({\alpha }_i{e}_i\right)}^2={\alpha }_i^2{e}_i^2=\sum _{k=1}^n{\alpha }_i^2{w}_{ki}{e}_k=\sum _{k=1}^n\frac{{\alpha }_i^2}{{\alpha }_k}{w}_{ki}\left({\alpha }_k{e}_k\right),$$

the conclusion is obtained straightforwardly. □

Corollary 1.

Let A be an evolution algebra and let B and $B^{\prime }$ be related natural basis. Then, the simplified graphs of A associated to B and $B^{\prime }$ respectively coincide, up to relabelling of the vertices.

Proof. 

The result follows from the above result together with the following fact: if $B=\{e_1,\dots ,e_n\}$ is a natural basis and $\tau$ is a permutation of the set $\{1,\dots ,n\}$, then $B^{\prime }=\{e_{\tau \left(1\right)},\dots ,e_{\tau \left(n\right)}\}$ is another natural basis whose associated graph coincides with the graph associated to B up to relabelling of the vertices if needed. □

Corollary 2.

Let $A_1$ and $A_2$ be two evolution algebras with finite dimensions. Let B be a natural basis of $A_1$ such that $\left|M_B\left(A_1\right)\right|\ne 0,$ and let $\theta :A_1\to A_2$ be an algebra isomorphism. Then:

(i)

$\theta \left(B\right)$ defines a natural basis of $A_2$ such that $\left|M_{\theta \left(B\right)}\left(A\right)\right|\ne 0.$

(ii)

Every two natural basis of $A_2$ (respectively of $A_1$) are related.

Proof. 

As $\theta$ is an algebra isomorphism, it is clear that $\theta \left(B\right)$ is a natural basis of $A_2$. Let $B=\{e_1,\dots ,e_n\}$. As $\{e_1^2,\dots ,e_n^2\}$ are linearly independent and $\theta \left(e_i^2\right)=\theta {\left(e_i\right)}^2$, we conclude that $\theta \left(e_i^2\right)$ are also linearly independent, and so $\left|M_{\theta \left(B\right)}\left(A\right)\right|\ne 0.$ Then, as a consequence of Proposition 1, we can conclude that any two natural bases of $A_2$ (respectively of $A_1$) are related. □

We see that whenever the structure matrix of an evolution algebra A associated to a natural basis B has non-zero determinant, then the basis as well as the associated graph are essentially unique (in fact, all the natural bases are related and the simplified associated graph is unique). This leads to a result which is useful to proving that two evolution algebras are non-isomorphic.

Corollary 3.

Let $A_1$ and $A_2$ be two evolution algebras with dimension $n\in \mathbb{N}.$ Let $B_1$ and $B_2$ be natural bases of $A_1$ and $A_2$ respectively. If $\left|M_{B_1}\left(A_1\right)\right|\ne 0$ and the simplified graph of $A_1$ associated to $B_1$ does not coincide with the simplified graph of $A_2$ associated to $B_2$ (up to relabelling the vertices), then $A_1$ and $A_2$ are non-isomorphic.

Proof. 

If there exists an isomorphism $\theta :A_1\to A_2$, then ${\theta }^{-1}\left(B_2\right)$ defines a natural basis on $A_1$ which is related to $B_1$ by Proposition 1. Thus, by Corollary 1, the simplified graphs with respect to these natural bases coincide, and therefore, the result follows. □

Definition 3.

An evolution algebra A is non-degenerate if

$$An\left(A\right)=\{b\in A:ab=0\forall a\in A\}=0,$$

and we say it is degenerate if $An\left(A\right)\ne 0$. As proven in ([3], Proposition 2.28), the latter is equivalent to the fact that any natural basis of A contains elements with zero square.

Definition 4.

Let A be an algebra. An idea l of A is a linear subspace I such that $AI\subseteq I$ and $IA\subseteq I$ (note that for commutative algebras $AI=IA$). This means that, the quotient linear space $A/I$ is an algebra with the canonical product $(a+I)(b+I)=ab+I,$ for $a,b\in I$.

We say that an ideal I is basic if there exists $B=\{e_1,..,e_n\}$ a natural basis of A such that $I=lin\{e_{j_1},\dots ,e_{j_k}\}$ where $\{e_{j_1},\dots ,e_{j_k}\}\subseteq B.$ This means that the ideal I is an evolution subalgebra provided with a natural basis that can be extended to a natural basis of $A.$

Note that if $B_I$ is a natural basis of I that is contained in $B_A$ a natural basis of A, and if $B_I^{\prime }$ is another natural basis of I, then $B_I^{\prime }\cup (B_A\backslash B_I)$ is a natural basis of A containing $B_I^{\prime }$.

In [17] basic ideals are called evolution ideals with the extension property; meanwhile, in [10] they are simply called ideals. Note that the image of a basic ideal by a homomorphism is a basic ideal. For a discussion about the above notions with explanatory examples, see [3].

Definition 5.

An evolution algebra A is reducible if there exists non-zero proper ideals I and J such that $A=I\oplus J.$ If A is not reducible then we say that it is irreducible.

The following result was proven in [3], where the problem of the reducibility of an evolution algebra was deeply studied.

Theorem 1.

Let A be a non-degenerate evolution algebra and $B=\{e_1,\dots ,e_n\}$ a natural basis of A. Then, A is reducible if and only if for some reorganisation $B^{\prime }$ of B the structure matrix $M_{B^{\prime }}$ is of the type

$$M_{B^{\prime }}:=\left(\begin{array}{cc}{W}_{m\times m}& 0_{m\times (n-m)}\\ 0_{(n-m)\times m}& Y_{(n-m)\times (n-m)}\end{array}\right),$$

with $m\in \mathbb{N}$, $m<n$ and $W_{m\times m}$, $Y_{(n-m)\times (n-m)}$ matrices with entries in $\mathbb{K}$.

In this case, we have that $A=I\oplus J$ where I and J are the ideals given by $I=lin\{e_i:i=1,\dots ,m\}$ and $J=lin\{e_i:i=m+1,\dots ,n\}$.

Note that the ideals I and J given in the above theorem are basic ideals, so that A is reducible as a direct sum of ideals if and only if A is reducible as a direct sum of basic ideals.

Before starting the study of the two-dimensional and three-dimensional evolution algebras, we need to clarify the notation we shall be using. From now on, a non-zero entry of a matrix shall be denoted by *. Note that two symbols * in the same matrix may represent different (non-zero) values.

3. Classification of Two-Dimensional Evolution Algebras

In this section, we make a classification of two-dimensional evolution algebras taking into account the following properties: whether they are irreducible or not and whether they are degenerate or not.

As we can see in the following result, the degenerate case is easy to study.

Theorem 2.

Let A be a two-dimensional degenerate evolution algebra. Then:

(i)

A is irreducible if and only if there exists a natural basis B of the evolution algebra A such that the structure matrix is $M_B\left(A\right)=\left(\begin{array}{cc}0& *\\ 0& 0\end{array}\right);$

(ii)

A is reducible if and only if there exists a natural basis B of A such that either $M_B\left(A\right)=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right)$ or $M_B\left(A\right)=\left(\begin{array}{cc}0& w\\ 0& *\end{array}\right),$

where * denotes a non-zero scalar and $w\in \mathbb{K}$.

Proof. 

Let $B=\{e_1,e_2\}$ be a natural basis of the evolution algebra A and denote by ${\pi }_i$ the canonical projection of A on the subspace $\mathbb{K}$ $e_i,$ for $i=1,2$. As A is degenerate, we know that $e_i^2=0$ for some $i\in \{1,2\}$ (according to [3], Proposition 2.28).

Case 1. $e_1^2=e_2^2=0$. Then $A=I\oplus J$ where $I=\mathbb{K}{e}_1$ and $J=\mathbb{K}{e}_2$ and

$$M_B\left(A\right)=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right).$$

Case 2. One of the elements of the natural basis has a zero square while the other has a non-zero square. We suppose that $e_1^2=0$ and $e_2^2\ne 0$ (which is not restrictive). Hence, $e_2^2=w_{12}{e}_1+w_{22}{e}_2$ where $w_{12}$, $w_{22}\in \mathbb{K}$ with at least one of those scalars being non-zero.

Case 2.1. Suppose that $w_{22}=0$. Then $e_2^2=w_{12}{e}_1$ with $w_{12}\ne 0$, so A is irreducible. In fact, assume the contradiction that I and J are non-zero proper ideals, such that $A=I\oplus J$. Then, we can suppose that ${\pi }_2\left(I\right)\ne 0$ (which is not restrictive, as it cannot be ${\pi }_2\left(I\right)={\pi }_2\left(J\right)=\left\{0\right\}$). It follows that $e_2^2\in I$, and so, $e_1=\frac{1}{w_{12}}{e}_2^2\in I$. Thus, $I=A$, a contradiction, as the decomposition $A=I\oplus J$ is non-trivial. Consequently, if $M_B\left(A\right)=\left(\begin{array}{cc}0& *\\ 0& 0\end{array}\right)$, then A is irreducible.

Case 2.2. Suppose that $w_{22}\ne 0.$ Then, as $e_1^2=0$, the structure matrix is $M_B\left(A\right)=\left(\begin{array}{cc}0& w\\ 0& *\end{array}\right)$ with $w=w_{12}$ and $e_2^2=w_{12}{e}_1+w_{22}{e}_2$. Then, $A=I\oplus J$ with $I=\mathbb{K}{e}_1$ and $J=\mathbb{K}{e}_2^2.$ □

In order to study the non-degenerate case, the following corollary is useful.

Lemma 1.

Let A be an evolutionary algebra, $B=\{e_1,e_2\}$ a natural basis and $M_B\left(A\right)=\left(\begin{array}{cc}{w}_{11}& w_{12}\\ w_{21}& w_{22}\end{array}\right)$ the corresponding structure matrix. Then the structure matrix of A related to the natural basis $B^{\prime }=\{e_2,e_1\}$ is given by $M_{B^{\prime }}\left(A\right)=\left(\begin{array}{cc}{w}_{22}& w_{21}\\ w_{12}& w_{11}\end{array}\right).$

Proof. 

If $B^{\prime }=\{v_1,v_2\}$ where $v_1=e_2,$ and $v_2=e_1,$ is clear that $v_1^2=w_{22}{v}_1+w_{12}{v}_2$ and $v_2^2=w_{21}{v}_1+w_{11}{v}_2$ as $e_1^2=w_{11}{e}_1+w_{21}{e}_2$ and $e_2^2=w_{12}{e}_1+w_{22}{e}_2.$ □

Corollary 4.

Let A be a non-degenerate evolution algebra, $B=\{e_1,e_2\}$ a natural basis and $M_B\left(A\right)=\left(\begin{array}{cc}{w}_{11}& w_{12}\\ w_{21}& w_{22}\end{array}\right)$ the corresponding structure matrix. Then A is reducible if and only if $w_{12}=w_{21}=0$, in which case $M_B\left(A\right)=\left(\begin{array}{cc}*& 0\\ 0& *\end{array}\right).$

Proof. 

Since the only possible reordination of B is $B^{\prime }=\{e_2,e_1\}$ and the corresponding structure matrix is $M_{B^{\prime }}\left(A\right)=\left(\begin{array}{cc}{w}_{22}& w_{21}\\ w_{12}& w_{11}\end{array}\right)$ from the above lemma, the result follows from Theorem 1, jointly with the fact that the columns of $M_B\left(A\right)$ cannot be zero because A is non-degenerate. □

Theorem 3.

Let A be a non-degenerate evolution algebra, with $dimA=2$. Then:

(i)

A is reducible if and only if there exists a natural basis B of A such that $M_B\left(A\right)=\left(\begin{array}{cc}*& 0\\ 0& *\end{array}\right);$

(ii)

A is irreducible if and only if there exists a natural basis B of A such that either $M_B\left(A\right)=\left(\begin{array}{cc}0& *\\ *& w\end{array}\right)$ or $M_B\left(A\right)=\left(\begin{array}{cc}w& \tilde{w}\\ *& *\end{array}\right),$ with $w,\tilde{w}\in \mathbb{K}$.

Proof. 

As A is a non-degenerate evolution algebra, by Corollary 4, we obtain that A is reducible if and only if the structure matrix of A respect any natural basis B is of the type

$$\left(\begin{array}{cc}*& 0\\ 0& *\end{array}\right).$$

Let us suppose now that A is irreducible and let $B=\{e_1,e_2\}$ be a natural basis. Then, by Corollary 4, and keeping in mind that A is non-degenerate, it is clear that $M_B\left(A\right)$ must be in one of the following cases:

$$\left(\begin{array}{c}\\ *\end{array}\right),\left(\begin{array}{cc}& *\\ \end{array}\right).$$

Moreover, as A is non-degenerate, we have that the structure matrix must be in one of the following cases:

$$M_1=\left(\begin{array}{cc}& *\\ *\end{array}\right),M_2=\left(\begin{array}{c}\\ *& *\end{array}\right),M_3=\left(\begin{array}{cc}*& *\\ \end{array}\right).$$

We can see that both $M_2$ and $M_3$ lead to the same evolution algebra. In fact, by switching if needed the elements of the basis (see Corollary 4) we obtain $\left(\begin{array}{cc}w& \tilde{w}\\ *& *\end{array}\right)$. The case $M_1$ produces the following situations:

$$\left(\begin{array}{cc}0& *\\ *& w\end{array}\right)\mathrm{and}\left(\begin{array}{cc}*& *\\ *& w\end{array}\right).$$

If in the situation $\left(\begin{array}{cc}*& *\\ *& w\end{array}\right)$ we switch the elements of the basis then we get $\left(\begin{array}{cc}w& *\\ *& *\end{array}\right)$, a matrix of the type $\left(\begin{array}{cc}w& \tilde{w}\\ *& *\end{array}\right)$ as desired. □

We can gather all this information in the following theorem, where we shall show, additionally, that he evolution algebras that we have found are not isomorphic.

Theorem 4.

Let A be a two-dimensional evolution algebra. Then, A is one of the following non-isomorphic ones, where $r,s\in \mathbb{K}\backslash \left\{0\right\}$ and $w,\tilde{w}\in \mathbb{K}.$

• $A_1$$=lin\{e_1,e_2\}$ is such that $e_1^2=e_2^2=0$ and $e_1{e}_2=0.$
• $A_2=lin\{e_1,e_2\}$ is such that $e_1^2=0$, $e_2^2=w{e}_1+r{e}_2$ and $e_1{e}_2=0.$
• $A_3=lin\{e_1,e_2\}$ is such that $e_1^2=r{e}_1$ and $e_2^2=s{e}_2$ and $e_1{e}_2=0.$
• $A_4=lin\{e_1,e_2\}$ is such that $e_1^2=0$ and $e_2^2=r{e}_1$ and $e_1{e}_2=0.$
• $A_5=lin\{e_1,e_2\}$ is such that $e_1^2=r{e}_2$ and $e_2^2=s{e}_1+w{e}_2$ and $e_1{e}_2=0.$
• $A_6=lin\{e_1,e_2\}$ is such that $e_1^2=w{e}_1+r{e}_2,$$e_2^2=\tilde{w}{e}_1+s{e}_2$ with $e_1{e}_2=0.$

As a matter of fact, we have the following classification:

	Degenerate	Non-Degenerate
Reducible	$A_1$, $A_2$	$A_3$
Irreducible	$A_4$	$A_5$, $A_6$

Proof. 

Let us consider the matrices

$$M_1=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right),M_2=\left(\begin{array}{cc}0& w\\ 0& *\end{array}\right),M_3=\left(\begin{array}{cc}*& 0\\ 0& *\end{array}\right),$$

$$M_4=\left(\begin{array}{cc}0& *\\ 0& 0\end{array}\right),M_5=\left(\begin{array}{cc}0& *\\ *& 0\end{array}\right),M_6=\left(\begin{array}{cc}w& \tilde{w}\\ *& *\end{array}\right).$$

The evolution algebras $A_i$ described above have a natural basis $B_i$ whose corresponding structure matrix is $M_i$ with $i=1,2,3,4,5,6$. By Theorem 2 we know that whenever A is degenerate, then A is reducible if and only if there exists a natural basis such that its corresponding structure matrix is like either $M_1$ or $M_2$. Meanwhile, A is irreducible if and only if A has a natural basis which structure matrix is like $M_4.$ If A is non-degenerate, A is reducible if and only if there exists a basis for which structure matrix is of the type $M_3$, as it is shown in Theorem 3. Moreover, by this last result, if A is non-degenerate, then A is irreducible if the structure matrix for some natural basis is either $M=\left(\begin{array}{cc}0& *\\ *& w\end{array}\right)$ or $\tilde{M}=\left(\begin{array}{cc}w& \tilde{w}\\ *& *\end{array}\right).$ If the structure matrix of A is of the type of $\tilde{M}$, then it is within $M_6$, whereas M can be identified with $M_5$ if $w=0$ or with $M_6$ if $w\ne 0.$

Now, we just need to prove that these evolution algebras are non-isomorphic. In order to do so, we need to take into account that the properties of being degenerate and being irreducible are maintained by algebra isomorphisms. Thus, $A_3$ and $A_4$ cannot be isomorphic to any of the others. To verify that $A_1$ and $A_2$ are non-isomorphic, we just need to realise that $A_1$ is a zero-product evolution algebra while $A_2$ is not. To check that $A_5$ and $A_6$ are not isomorphic, note that if $\left|M_6\right|=0$, then the conclusion follows from Corollary 2 as $\left|M_5\right|\ne 0$. Otherwise, we have $\left|M_5\right|\ne 0$ and $\left|M_6\right|\ne 0$, but then the simplified associated graphs do not coincide because the corresponding to $M_6$ has a loop and the given by $M_5$ does not have any loop, and Corollary 3 applies. □

4. Classification of Three-Dimensional Evolution Algebras

In order to start with this classification, we need to see the different structure matrices that we can obtain by just reordering the elements of a natural basis of a three-dimensional evolution algebra. As seen before, if $B=\{e_1,e_2,e_3\}$ is a natural basis of an evolution algebra, $A,$ and $\sigma$ is a permutation of the set $\{1,2,3\}$, then $\{e_{\sigma \left(1\right)},e_{\sigma \left(2\right)},e_{\sigma \left(3\right)}\}$ is a natural basis of A. We shall describe below the structure matrix associated to each possible reorganisation of a natural basis $B.$

Lemma 2.

Let A be an evolution algebra and $B=\{e_1,e_2,e_3\}$ a natural basis. Let σ be a permutation of the set $\{1,2,3\}$. If the structure matrix of A relative to B is given by $M_B\left(A\right)$, then the corresponding structure matrix of A relative to $B_{\sigma }=\{e_{\sigma \left(1\right)},e_{\sigma \left(2\right)},e_{\sigma \left(3\right)}\}$ is $M_{B_{\sigma }}\left(A\right)$ where

$$M_B\left(A\right)=\left(\begin{array}{ccc}{w}_{11}& w_{12}& w_{13}\\ w_{21}& w_{22}& w_{23}\\ w_{31}& w_{32}& w_{33}\end{array}\right)\mathit{and}{M}_{B_{\sigma }}\left(A\right)=\left(\begin{array}{ccc}{w}_{\sigma \left(1\right)\sigma \left(1\right)}& w_{\sigma \left(1\right)\sigma \left(2\right)}& w_{\sigma \left(1\right)\sigma \left(3\right)}\\ w_{\sigma \left(2\right)\sigma \left(1\right)}& w_{\sigma \left(2\right)\sigma \left(2\right)}& w_{\sigma \left(2\right)\sigma \left(3\right)}\\ w_{\sigma \left(3\right)\sigma \left(1\right)}& w_{\sigma \left(3\right)\sigma \left(2\right)}& w_{\sigma \left(3\right)\sigma \left(3\right)}\end{array}\right).$$

Proof. 

Straightforward. □

We can easily check that, for all permutation $\sigma$ of the set $\{1,2,3\}$ the corresponding associated graphs to $M_{B_{\sigma }}\left(A\right)$ are identical up to relabelling of the vertices (and coincide with the one associated to $M_B\left(A\right)$), as seen in Section 2.

From Theorem 1 (see also Remark 5.7 in [3]) we deduce the following result:

Corollary 5.

Let A be a non-degenerate evolution algebra and $B=\{e_1,e_2,e_3\}$ a natural basis. Then, A is reducible if an only if $M_B\left(A\right)$ is within one of the following types of matrices:

$$M_1:=\left(\begin{array}{ccc}{w}_{11}& 0& 0\\ 0& w_{22}& w_{23}\\ 0& w_{32}& w_{33}\end{array}\right),M_2:=\left(\begin{array}{ccc}{w}_{11}& 0& w_{13}\\ 0& w_{22}& 0\\ w_{31}& 0& w_{33}\end{array}\right),M_3:=\left(\begin{array}{ccc}{w}_{11}& w_{12}& 0\\ w_{21}& w_{22}& 0\\ 0& 0& w_{33}\end{array}\right),$$

with $w_{ij}\in \mathbb{K}$, $i,j=1,2,3.$

Proof. 

By the Theorem 1 we have that A is reducible if and only if the structure matrix of some reordenation of B is diagonal by blocks (that is like either $M_1$ or $M_3$). Taking into account the Lemma 2, the result follows. □

Proposition 3.

A three-dimensional evolution algebra A has a two-dimensional basic ideal if and only if there exists a natural basis B with respect to which the structure matrix $M_B\left(A\right)$ is of one of the following types of matrices:

$$M_1=\left(\begin{array}{ccc}& & \\ & & \\ 0& 0& \end{array}\right);M_2=\left(\begin{array}{cc}& \\ 0& & 0\\ & \end{array}\right)M_3=\left(\begin{array}{ccc}& 0& 0\\ & & \\ & & \end{array}\right).$$

(1)

Proof. 

If $B=\{e_1,e_2,e_3\}$ and if I is a basic ideal of dimension 2 associated to B then, either $I=I_1:=lin\{e_1,e_2\}$ or $I=I_2:=lin\{e_1,e_3\}$ or $I=I_3:=lin\{e_2,e_3\}.$ The result follows from the fact that $I_i$ is an ideal of A if and only $M_B\left(A\right)$ is like $M_i,$ for $i=1,2,3$, respectively. □

Finally, we shall see the relationship between two structure matrices $M_B\left(A\right)$ and $M_{\tilde{B}}\left(A\right)$ of an evolution algebra A associated to two different natural bases B and $\tilde{B}$. This can be seen in [1], but we shall also show the proof for completeness.

Proposition 4.

Let A be an evolution algebra; consider $B=\{e_1,e_2,e_3\}$ and $\tilde{B}=\{{\tilde{e}}_1,{\tilde{e}}_2,{\tilde{e}}_3\}$ two natural bases of A; and let $M_B\left(A\right)$ and $M_{\tilde{B}}\left(A\right)$ be the corresponding structure matrices. If ${\tilde{e}}_i=p_{1i}{e}_1+p_{2i}{e}_2+p_{3i}{e}_3$ for $i=1,2,3,$ then

$$P=\left(\begin{array}{ccc}{p}_{11}& p_{12}& p_{13}\\ p_{21}& p_{22}& p_{23}\\ p_{31}& p_{32}& p_{33}\end{array}\right)$$

is a nonsingular matrix such that $P{M}_{\tilde{B}}\left(A\right)=M_B\left(A\right)P^{\left[2\right]}$, where

$$P^{\left[2\right]}=\left(\begin{array}{ccc}{p}_{11}^2& p_{12}^2& p_{13}^2\\ p_{21}^2& p_{22}^2& p_{23}^2\\ p_{31}^2& p_{32}^2& p_{33}^2\end{array}\right).$$

Proof. 

Consider the structure matrices associated, respectively, to both basis:

$$M_B\left(A\right)=\left(\begin{array}{ccc}{\omega }_{11}& {\omega }_{12}& {\omega }_{13}\\ {\omega }_{21}& {\omega }_{22}& {\omega }_{23}\\ {\omega }_{31}& {\omega }_{32}& {\omega }_{33}\end{array}\right)\mathrm{and}{M}_{\tilde{B}}\left(A\right)=\left(\begin{array}{ccc}{\tilde{\omega }}_{11}& {\tilde{\omega }}_{12}& {\tilde{\omega }}_{13}\\ {\tilde{\omega }}_{21}& {\tilde{\omega }}_{22}& {\tilde{\omega }}_{23}\\ {\tilde{\omega }}_{31}& {\tilde{\omega }}_{32}& {\tilde{\omega }}_{33}\end{array}\right).$$

If ${\tilde{e}}_i=p_{1i}{e}_1+p_{2i}{e}_2+p_{3i}{e}_3$ for $p_{1i},p_{2i},p_{3i}\in \mathbb{K}$ and $i\in \{1,2,3\}$ then we have, ${\tilde{e}}_i^2=q_{1i}{e}_1+q_{2i}{e}_2+q_{3i}{e}_3$ where

$$\left(\begin{array}{c}{q}_{1i}\\ q_{2i}\\ q_{3i}\end{array}\right)=\left(\begin{array}{ccc}{\omega }_{11}& {\omega }_{12}& {\omega }_{13}\\ {\omega }_{21}& {\omega }_{22}& {\omega }_{23}\\ {\omega }_{31}& {\omega }_{32}& {\omega }_{33}\end{array}\right)\left(\begin{array}{c}{p}_{1i}^2\\ p_{2i}^2\\ p_{3i}^2\end{array}\right).$$

But also ${\tilde{e}}_i^2={\tilde{\omega }}_{1i}{\tilde{e}}_1+{\tilde{\omega }}_{2i}{\tilde{e}}_2+{\tilde{\omega }}_{3i}{\tilde{e}}_3$ and so

$$\left(\begin{array}{ccc}{p}_{11}& p_{12}& p_{13}\\ p_{21}& p_{22}& p_{23}\\ p_{31}& p_{32}& p_{33}\end{array}\right)\left(\begin{array}{c}{\tilde{\omega }}_{1i}\\ {\tilde{\omega }}_{2i}\\ {\tilde{\omega }}_{3i}\end{array}\right)=\left(\begin{array}{c}{q}_{1i}\\ q_{2i}\\ q_{3i}\end{array}\right).$$

Hence $P{M}_{\tilde{B}}\left(A\right)=M_B\left(A\right)P^{\left[2\right]}$ as desired. □

4.1. The Non-Degenerate Case

According to Theorem 1, if an evolution algebra A has no basic proper ideals then A is irreducible. In particular, if $dimA=3$ and A has no basic ideals of dimension two, then A is irreducible. In the following result we shall characterize this fact for a particular type of evolution algebra. Recall that two * symbols in the same matrix do not necessarily have the same non-zero value.

Lemma 3.

Let A be an evolution algebra with a natural basis $B=\{e_1,e_2,e_3\}$ with respect to which the structure matrix is like

$$M_B\left(A\right)=\left(\begin{array}{ccc}*& *& w\\ 0& *& *\\ 0& *& *\end{array}\right)$$

with $\left|M_B\left(A\right)\right|=0$. Then, A has a basic ideal with dimension 2 if and only if $M_B\left(A\right)=\left(\begin{array}{ccc}*& a& \lambda a\\ 0& b& \lambda b\\ 0& c& \lambda c\end{array}\right)$ with $a,b,c,\lambda \in \mathbb{K}\backslash \left\{0\right\}$ and $\lambda \ne -\frac{b^2}{c^2}.$

Proof. 

Suppose that I is a basic ideal of A with $dimI=2.$ Since it cannot be $I=\mathbb{K}{e}_1$ (as the ideal I has dimension 2), we obtain that $e_2^2=a{e}_1+b{e}_2+c{e}_3$ belongs to I. In fact, either ${\pi }_2\left(I\right)\ne 0$ or ${\pi }_3\left(I\right)\ne 0$. Thus, if $u\in I$ is such that ${\pi }_2\left(u\right)\ne 0$, then $e_{2}u=\mu e_2^2$$\in I$ for some $\mu \ne 0$, and hence, $e_2^2\in I$. Similarly if ${\pi }_3\left(u\right)\ne 0$ then $e_3^2\in I$ and if follows that $e_2^2\in I$ as $e_2{e}_3^2\in I$. Consequently $e_1^2=\frac{1}{a}{e}_1{e}_2^2\in I$. Therefore, $e_1\in I$ and $I=lin\{e_1,b{e}_2+c{e}_3\}$. Since I is a basic ideal, there exists $v=\alpha e_1+\beta e_2+\gamma e_3$ such that $\tilde{B}=\{e_1,b{e}_2+c{e}_3,v\}$ is a natural basis of $A.$ From $v{e}_1=0$ we obtain that $\alpha =0$, and hence, $v=\beta e_2+\gamma e_3$ where $\left|\beta \right|+\left|\gamma \right|\ne 0$. Since,

$$(b{e}_2+c{e}_3)v=(b{e}_2+c{e}_3)(\beta e_2+\gamma e_3)=b\beta e_2^2+c\gamma e_3^2=0,$$

it follows that $\beta \ne 0$ and $\gamma \ne 0$ simultaneously, as $e_2^2\ne 0$ and $e_3^2\ne 0.$ Hence, we obtain that $e_2^2$ and $e_3^2$ are proportional and non-zero. In fact, $e_3^2=\lambda e_2^2$ with $\lambda =-\frac{b\beta }{c\gamma }$. Moreover, as $b{e}_2+c{e}_3$ and $v=\beta e_2+\gamma e_3$ are linearly independent we obtain that $b\gamma -c\beta \ne 0.$ Thus, $\frac{\beta }{\gamma }\ne \frac{b}{c}$ and so $\lambda \ne -\frac{b^2}{c^2}.$

Conversely, if $e_3^2=\lambda e_2^2$ with $\lambda \ne -\frac{b^2}{c^2}$, then it follows that $B=\{e_1,b{e}_2+c{e}_3,e_2-\frac{b}{c\lambda }{e}_3\}$ is a natural basis of A and $I:=lin\{e_1,b{e}_2+c{e}_3\}$ is a proper two-dimensional basic ideal. □

Theorem 5.

Let A be a three-dimensional, irreducible, non-degenerate evolution algebra. Then, A has a one-dimensional basic ideal and has no two-dimensional basic ideals if and only if A has a natural basis B such that the structure matrix $M_B\left(A\right)$ is within the following types (non-isomorphic each other), where * denotes a non-zero scalar and $w,\tilde{w}\in \mathbb{K}:$

(i)

$M_1=\left(\begin{array}{ccc}*& *& 0\\ 0& w& *\\ 0& *& \tilde{w}\end{array}\right)$ with $\left|M_1\right|\ne 0.$

(ii)

$M_2=\left(\begin{array}{ccc}*& *& *\\ 0& w& *\\ 0& *& \tilde{w}\end{array}\right)$ with $\left|M_2\right|\ne 0.$

(iii)

$M_3=\left(\begin{array}{ccc}*& *& w\\ 0& *& *\\ 0& *& *\end{array}\right)$ with $\left|M_3\right|=0$ and either $M_3=\left(\begin{array}{ccc}*& a& -\frac{b^2}{c^2}a\\ 0& b& -\frac{b^2}{c^2}b\\ 0& c& -\frac{b^2}{c^2}c\end{array}\right)$ or $M_3$ having no proportional columns.

Proof. 

For the sufficient condition, suppose that A has a natural basis of type $M_1$, $M_2,$ or $M_3.$ Then A has a basic ideal with dimension 1 (namely $I=\mathbb{K}{e}_1$). Moreover, A does not have a basic ideal with dimension 2. In the case of $M_1$ and $M_2$ this last assertion follows from the fact that all the natural basis of A are related by Propositon 1, and from Lemma 2 none of the related natural basis of $M_1$ or $M_2$ are of the type

$$M_a=\left(\begin{array}{ccc}& & \\ & & \\ 0& 0& \end{array}\right),M_b=\left(\begin{array}{ccc}& & \\ 0& & 0\\ & & \end{array}\right),M_c=\left(\begin{array}{ccc}& 0& 0\\ & & \\ & & \end{array}\right),$$

(2)

which together with Proposition 3 shows that A does not have any two-dimensional basic ideals. In the case of $M_3$, it follows from Lemma 3 that A does not have any two-dimensional basic ideals.

For the necessary condition, suppose that A has a basic ideal of dimension one and does not have any two-dimensional basic ideals. Then, it is not restrictive to assume that $I=\mathbb{K}{e}_1$ is a one-dimensional basic ideal. On the other hand, by Proposition 3, we have that $M_B\left(A\right)$ is not in any of the situations of (2) (otherwise A has a two-dimensional basic ideal). As A is non-degenerate and $I=\mathbb{K}{e}_1$ is a basic ideal we have that

$$\left(\begin{array}{ccc}*& & \\ 0& & \\ 0& & \end{array}\right).$$

In order to not be in the cases of (2), we must have

$$\left(\begin{array}{ccc}*& & \\ 0& & *\\ 0& *& \end{array}\right).$$

Still, this matrix could be of the type $M_c$ in (2). Consequently we have the two following possibilities:

Case 1. $\left(\begin{array}{ccc}*& & 0\\ 0& & *\\ 0& *& \end{array}\right).$ Again because of (2) we must have $\left(\begin{array}{ccc}*& *& 0\\ 0& & *\\ 0& *& \end{array}\right)$. Therefore, $M_B\left(A\right)$ is of type $M_1$.

Case 2. $\left(\begin{array}{ccc}*& & *\\ 0& & *\\ 0& *& \end{array}\right).$ Here we have either $\left(\begin{array}{ccc}*& *& *\\ 0& & *\\ 0& *& \end{array}\right)$ or $\left(\begin{array}{ccc}*& 0& *\\ 0& & *\\ 0& *& \end{array}\right)$.

Case 2.1. $M_B\left(A\right)=\left(\begin{array}{ccc}*& *& *\\ 0& & *\\ 0& *& \end{array}\right).$ We consider the following situations:

Case 2.1.1. $M_B\left(A\right)$$=\left(\begin{array}{ccc}*& *& *\\ 0& & *\\ 0& *& \end{array}\right)$ with $\left|M_B\left(A\right)\right|\ne 0$ and we are within the type $M_2.$

Case 2.1.2. $M_B\left(A\right)$$=\left(\begin{array}{ccc}*& *& *\\ 0& & *\\ 0& *& \end{array}\right)=\left(\begin{array}{ccc}*& *& *\\ 0& w& *\\ 0& *& \tilde{w}\end{array}\right)$ with $\left|M_B\left(A\right)\right|=0$. Therefore we have that $\left|\left(\begin{array}{cc}w\hfill & *\hfill \\ *\hfill & \tilde{w}\hfill \end{array}\right)\right|=0$ so $w\ne 0$ and $\tilde{w}\ne 0.$ Consequently, $M_B\left(A\right)$$=\left(\begin{array}{ccc}*& *& *\\ 0& *& *\\ 0& *& *\end{array}\right)$ with $\left|M_B\left(A\right)\right|=0$, which is included in $M=\left(\begin{array}{ccc}*& *& w\\ 0& *& *\\ 0& *& *\end{array}\right)$ with $\left|M\right|=0.$ By Lemma 3 either $M_B\left(A\right)$$=\left(\begin{array}{ccc}*& *& w\\ 0& *& *\\ 0& *& *\end{array}\right)$ with no proportional columns or, $M_B\left(A\right)=\left(\begin{array}{ccc}*& a& -\frac{b^2}{c^2}a\\ 0& b& -\frac{b^2}{c^2}b\\ 0& c& -\frac{b^2}{c^2}c\end{array}\right)$ otherwise.

Finally, note that these three types of algebra are not isomorphic. In fact, if $A_i$ is an evolution algebra with a structure matrix of the type $M_i$ respectively, for $i=1,2,3,$ then obviously $A_i$ with $i=1,2$ is not isomorphic to $A_3$ because $|M_3|=0$ and $|M_i|\ne 0$ for $i=1,2$. Also, from Corollary 2 all the natural basis of $A_1$ are related, and from Lemma 2 we know that $A_1$ does not have a related structure matrix of the type $M_2.$ Therefore, $A_1$ and $A_2$ are not isomorphic. □

Theorem 6.

Let A be an irreducible, three-dimensional, non-degenerate evolution algebra. Then, A has a basic ideal of dimension two if and only if there exists a natural basis B such that the structure matrix associated $M_B\left(A\right)$ is within the following type, where * denotes a non-zero scalar and $\alpha ,\beta ,\gamma \in \mathbb{K}$:

$$M_B\left(A\right)=\left(\begin{array}{ccc}& \alpha & \gamma \\ \beta & & *\\ 0& 0\end{array}\right),\mathit{with}\left|\alpha \right|+\left|\beta \right|+\left|\gamma \right|\ne 0,\mathit{and}\mathit{no}\mathit{zero}\mathit{columns}.$$

Proof. 

As A has a two-dimensional basic ideal, there is a natural basis B such that the structure matrix is

$$M_B\left(A\right)=\left(\begin{array}{ccc}& & \\ & & \\ 0& 0& \end{array}\right).$$

Also, by Theorem 1, we have that the two first entries of the third column cannot be zero simultaneously (otherwise A is reducible). We have then two possibilities:

$$\left(\begin{array}{ccc}& & *\\ & & \\ 0& 0& \end{array}\right),\left(\begin{array}{ccc}& & \\ & & *\\ 0& 0& \end{array}\right).$$

(3)

In addition, we cannot have the following cases

$$\left(\begin{array}{ccc}& 0& \\ 0& & 0\\ & 0& \end{array}\right),\left(\begin{array}{ccc}& 0& 0\\ 0& & \\ 0& & \end{array}\right)$$

as in the first one $A=I\oplus J$ with $I=\mathbb{K}{e}_2$ and $J=lin\{e_1,e_3\}$, and in the second one $A=I\oplus J$ with $I=\mathbb{K}{e}_1$ and $J=lin\{e_2,e_3\}.$ Hence, applying this to (3) we have either

$$\left(\begin{array}{ccc}& \beta & *\\ \alpha & & \gamma \\ 0& 0& \end{array}\right)\mathrm{or}\left(\begin{array}{ccc}& \beta & \gamma \\ \alpha & & *\\ 0& 0& \end{array}\right)$$

(4)

with $\left|\alpha \right|+\left|\beta \right|+\left|\gamma \right|\ne 0.$ Nevertheless, if $B=\{e_1,e_2,e_3\}$ is such that $M_B\left(A\right)=\left(\begin{array}{ccc}& \beta & *\\ \alpha & & \gamma \\ 0& 0& \end{array}\right)$ and we consider $\tilde{B}=\{e_2,e_1,e_3\}$, then the structure matrix relative to the new natural basis is $M_{\tilde{B}}\left(A\right)=\left(\begin{array}{ccc}& \alpha & \gamma \\ \beta & & *\\ 0& 0& \end{array}\right).$ So in both cases we arrive (after reorganisation of the basis if needed) at a structure matrix of the type $\left(\begin{array}{ccc}& \alpha & \gamma \\ \beta & & *\\ 0& 0& \end{array}\right)\mathrm{with}\left|\alpha \right|+\left|\beta \right|+\left|\gamma \right|\ne 0$ and non-zero columns.

Reciprocally, if A is an evolution algebra and B a natural basis of A such that the structure matrix associated to it is $M_B\left(A\right)=\left(\begin{array}{ccc}& \alpha & \gamma \\ \beta & & *\\ 0& 0& \end{array}\right)$ without zero columns and with $\left|\alpha \right|+\left|\beta \right|+\left|\gamma \right|\ne 0$, then $I=lin\{e_1,e_2\},$ is a basic ideal of A and by Corollary 5 it is clear that A is irreducible. □

Lemma 4.

Let A be a non-degenerate evolution algebra such that $dim{A}^2=2.$ Then, $A^2$ is a basic ideal if and only if there exists a natural basis $B=\{e_1,e_2,e_3\}$ such that

$$M_B\left(A\right)=\left(\begin{array}{ccc}{\alpha }_1& {\beta }_1& {\gamma }_1\\ {\alpha }_2& {\beta }_2& {\gamma }_2\\ 0& 0& 0\end{array}\right),$$

(5)

with non zero columns and ${\alpha }_i,{\beta }_i,{\gamma }_i\in \mathbb{K}$, for $i=1,2.$

Proof. 

If $A^2$ is a proper basic ideal with $dim{A}^2=2$, then there exists a natural basis $B=\{e_1,e_2,e_3\}$ such that $A^2=lin\{e_1,e_2\}$. Thus, $e_{3}x=0$ for every $x\in A^2.$ As B is a natural basis, there exist ${\alpha }_i,{\beta }_i,{\gamma }_i\in \mathbb{K}$ for $i=1,2,3$ such that

$$\begin{array}{ccc}\hfill e_1^2& =& {\alpha }_1{e}_1+{\alpha }_2{e}_2+{\alpha }_3{e}_3,\hfill \\ \hfill e_2^2& =& {\beta }_1{e}_1+{\beta }_2{e}_2+{\beta }_3{e}_3,\hfill \\ \hfill e_3^2& =& {\gamma }_1{e}_1+{\gamma }_2{e}_2+{\gamma }_3{e}_3.\hfill \end{array}$$

Equivalently, the structure matrix of A relative to B is

$$M_B\left(A\right)=\left(\begin{array}{ccc}{\alpha }_1& {\beta }_1& {\gamma }_1\\ {\alpha }_2& {\beta }_2& {\gamma }_2\\ {\alpha }_3& {\beta }_3& {\gamma }_3\end{array}\right).$$

Since $e_3{e}_i^2=0$ for $i=1,2,3$ and $e_3^2\ne 0$ as A is non-degenerate, ${\alpha }_3={\beta }_3={\gamma }_3=0$. Thus,

$$M_B\left(A\right)=\left(\begin{array}{ccc}{\alpha }_1& {\beta }_1& {\gamma }_1\\ {\alpha }_2& {\beta }_2& {\gamma }_2\\ 0& 0& 0\end{array}\right)$$

and $A^2=lin\{e_1^2,e_2^2,e_3^2\}$ is such that $dim{A}^2=2$. Clearly, all columns are non-zero, as A is a non-degenerate algebra.

Conversely, suppose there exists a natural basis $B=\{e_1,e_2,e_3\}$ such that the structure matrix of A is given by (5). Then $A^2=lin\{e_1,e_2\}$ is a basic ideal with dimension 2, as desired. □

Lemma 5.

Let A be an evolution algebra and let $B=\{e_1,e_2,e_3\}$ be a natural basis such that the structure matrix of A relative to B is of the type

$$M_B\left(A\right)=\left(\begin{array}{ccc}& *& \\ \alpha & & *\\ \beta & \gamma & \end{array}\right)\mathit{with}\left|\beta \right|+\left|\alpha \gamma \right|\ne 0.$$

If $dim{A}^2=1$ then A has proper basic ideals.

Proof. 

If $\beta =0$ then $\alpha \ne 0$ and $\gamma \ne 0$, so $dim{A}^2=2$, a contradiction. Thus, $\beta \ne 0,$ and hence, since the columns of $M_B\left(A\right)$ are proportional, as $dim{A}^2=1,$ we have

$$M_B\left(A\right)=\left(\begin{array}{ccc}*& *& *\\ *& *& *\\ *& *& *\end{array}\right)=\left(\begin{array}{ccc}a& \lambda a& \mu a\\ b& \lambda b& \mu b\\ c& \lambda c& \mu c\end{array}\right),$$

with $a,b,c,\lambda ,\mu \in \mathbb{K}\backslash \left\{0\right\}.$ We shall split the proof in two cases:

Case 1. $\lambda b^2+\mu c^2\ne 0$. Then, $B=\{e_1,b{e}_2+c{e}_3,e_2-\frac{b\lambda }{c\mu }{e}_3\}$ is a natural basis of A and $I_1=lin\{e_1,b{e}_2+c{e}_3\}$ is a basic ideal of A.

Case 2. $\lambda b^2+\mu c^2=0$. Then, $\lambda =-\frac{\mu c^2}{b^2}$, so $e_2^2=-\frac{\mu c^2}{b^2}{e}_1^2$. Thus,

$$M_B\left(A\right)=M_1=\left(\begin{array}{ccc}*& *& *\\ *& *& *\\ *& *& *\end{array}\right)=\left(\begin{array}{ccc}a& -\frac{\mu c^2}{b^2}a& \mu a\\ b& -\frac{\mu c^2}{b^2}b& \mu b\\ c& -\frac{\mu c^2}{b^2}c& \mu c\end{array}\right).$$

Let us consider $\tilde{B}=\{{\tilde{e}}_1,{\tilde{e}}_2,{\tilde{e}}_3\}=\{e_1,\frac{b}{c}{e}_2,e_3\}.$ Then, by applying Proposition 2 with ${\alpha }_1=1,$${\alpha }_2=\frac{b}{c},$ and ${\alpha }_3=1$ we get that ${\alpha }_2^2\frac{c^2}{b^2}=1$ and

$$M_{\tilde{B}}\left(A\right)=\left(\begin{array}{ccc}{\alpha }_{1}a& -\frac{{\alpha }_2^2}{{\alpha }_1}\frac{\mu c^2}{b^2}a& \frac{{\alpha }_3^2}{{\alpha }_1}\mu a\\ \frac{{\alpha }_1^2}{{\alpha }_2}b& -{\alpha }_2\frac{\mu c^2}{b^2}b& \frac{{\alpha }_3^2}{{\alpha }_2}\mu b\\ \frac{{\alpha }_1^2}{{\alpha }_3}c& -\frac{{\alpha }_2^2}{{\alpha }_3}\frac{\mu c^2}{b^2}c& {\alpha }_3\mu c\end{array}\right)=\left(\begin{array}{ccc}a& -\mu a& \mu a\\ c& -\mu c& \mu c\\ c& -\mu c& \mu c\end{array}\right).$$

We shall consider two different cases again.

Case 2.1. $a^2+\mu c^2\ne 0$. Then, $B=\{{\tilde{e}}_2,a{\tilde{e}}_1+c{\tilde{e}}_3,c{\tilde{e}}_1-\frac{a}{\mu }{\tilde{e}}_3\}$ is a natural basis and $I_{e_2}=lin\{{\tilde{e}}_2,a{\tilde{e}}_1+c{\tilde{e}}_3\}$ is a basic ideal of dimension two.

Case 2.2. $a^2+\mu c^2=0$. Then,

$$M_{\tilde{B}}\left(A\right)=\left(\begin{array}{ccc}a& -\mu a& \mu a\\ c& -\mu c& \mu c\\ c& -\mu c& \mu c\end{array}\right)=\left(\begin{array}{ccc}a& \frac{a^2}{c^2}a& \frac{-a^2}{c^2}a\\ c& \frac{a^2}{c^2}c& -\frac{a^2}{c^2}c\\ c& \frac{a^2}{c^2}c& -\frac{a^2}{c^2}c\end{array}\right)=\left(\begin{array}{ccc}a& \frac{a^3}{c^2}& \frac{-a^3}{c^2}\\ c& \frac{a^2}{c}& -\frac{a^2}{c}\\ c& \frac{a^2}{c}& -\frac{a^2}{c}\end{array}\right).$$

Let us consider now $\widehat{B}=\{{\widehat{e}}_1,{\widehat{e}}_2,{\widehat{e}}_3\}=\{{\alpha }_1{\tilde{e}}_1,{\alpha }_2{\tilde{e}}_2,{\alpha }_3{\tilde{e}}_3\}=\{\frac{1}{a}{\tilde{e}}_1,-\frac{c}{a^2}{\tilde{e}}_2,-\frac{c}{a^2}{\tilde{e}}_3\}.$ By applying Proposition 2 with ${\alpha }_1=\frac{1}{a},$${\alpha }_2=-\frac{c}{a^2},$ and ${\alpha }_3=\frac{c}{a^2}$ we have,

$$M_{\widehat{B}}\left(A\right)=\left(\begin{array}{ccc}{\alpha }_{1}a& \frac{{\alpha }_2^2}{{\alpha }_1}\frac{a^3}{c^2}& -\frac{{\alpha }_3^2}{{\alpha }_1}\frac{a^3}{c^2}\\ \frac{{\alpha }_1^2}{{\alpha }_2}c& {\alpha }_2\frac{a^2}{c}& -\frac{{\alpha }_3^2}{{\alpha }_2}\frac{a^2}{c}\\ \frac{{\alpha }_1^2}{{\alpha }_3}c& \frac{{\alpha }_2^2}{{\alpha }_3}\frac{a^2}{c}& -{\alpha }_3\frac{a^2}{c}\end{array}\right)=\left(\begin{array}{ccc}\hfill 1& \hfill 1& \hfill -1\\ \hfill -1& \hfill -1& \hfill 1\\ \hfill 1& \hfill 1& \hfill -1\end{array}\right).$$

Thus, $B=\{{\widehat{e}}_1^2,u,v\}$, where ${\widehat{e}}_1^2={\widehat{e}}_1-{\widehat{e}}_2+{\widehat{e}}_3;$$u={\widehat{e}}_1+{\widehat{e}}_2;$$v={\widehat{e}}_1-{\widehat{e}}_2+2{\widehat{e}}_3$ is a natural basis of A and $A^2$ is the ideal generated by ${\widehat{e}}_1^2.$ Note that $A^2$ is a basic proper one-dimensional ideal. □

From Theorem 1 we can deduce that whenever a non-degenerate evolution algebra A has no basic ideals of dimension one or two, then A is irreducible. We shall obtain a necessary and sufficient condition for this property.

Lemma 6.

Let A be a non-degenerate three-dimensional evolution algebra with no proper basic ideals, and let $M_B\left(A\right)$ be the structure matrix of A with respect to a natural basis $B.$ Then $M_B\left(A\right)$ cannot be within any of the following types of matrices

$$\begin{array}{ccc}\hfill M_1& =& \left(\begin{array}{ccc}& & \\ 0& & \\ 0& & \end{array}\right);M_2=\left(\begin{array}{ccc}& 0& \\ & 0& \end{array}\right);M_3=\left(\begin{array}{ccc}& & 0\\ & & 0\\ & & \end{array}\right)\hfill \\ \hfill M_4& =& \left(\begin{array}{ccc}& & \\ & & \\ 0& 0& \end{array}\right);M_5=\left(\begin{array}{ccc}& & \\ 0& & 0\\ & & \end{array}\right);M_6=\left(\begin{array}{ccc}& 0& 0\\ & & \\ & & \end{array}\right).\hfill \end{array}$$

Proof. 

If $M_B\left(A\right)=M_i$ with $i=1,2,3$ then $\mathbb{K}{e}_i$ is a basic ideal of dimension 1 (with $i=1,2,3$ respectively). Similarly, by Proposition 3, the structure matrix of A has to be different from $M_i$ for $i=4,5,6$, as otherwise A has a basic ideal of dimension two (namely, $I_4=lin\{e_1,e_2\}$, $I_5=lin\{e_1,e_3\}$ and $I_6=lin\{e_2,e_3\}$ respectively). □

Theorem 7.

Let A be a non-degenerate three-dimensional evolution algebra with no proper basic ideals. Then, A has a natural basis $B=\{e_1,e_2,e_3\}$ such that

$$M_B\left(A\right)=\left(\begin{array}{ccc}& *& \\ \alpha & & *\\ \beta & \gamma & \end{array}\right)\mathit{with}\left|\beta \right|+\left|\alpha \gamma \right|\ne 0.$$

(6)

Moreover, B can be reordered in a way such that either

$$M_B\left(A\right)=M_1:=\left(\begin{array}{ccc}& *& \\ & & *\\ *& & \end{array}\right)\mathit{or}{M}_B\left(A\right)=M_2:=\left(\begin{array}{ccc}& *& 0\\ *& & *\\ 0& *& \end{array}\right).$$

Proof. 

First, we shall see that whenever $M_B\left(A\right)$ is like (6), then B can be reordered such that either $M_B\left(A\right)=M_1$ or $M_B\left(A\right)=M_2.$ Indeed, if $\beta \ne 0$ then $M_B\left(A\right)=M_1.$ Otherwise, $\beta =0$ and so

$$M_B\left(A\right)=\left(\begin{array}{ccc}& *& \\ *& & *\\ 0& *& \end{array}\right).$$

Then either $M_B\left(A\right)=M_2=\left(\begin{array}{ccc}& *& 0\\ *& & *\\ 0& *& \end{array}\right)\mathrm{or}{M}_B\left(A\right)=\left(\begin{array}{ccc}& *& *\\ *& & *\\ 0& *& \end{array}\right).$ But the latter case is gathered in $M_B\left(A\right)=\left(\begin{array}{ccc}& & *\\ *& & \\ & *& \end{array}\right).$ If we consider the reordering $B^{\prime }=\{e_1,e_3,e_2\}$ then, by Lemma 2, we have

$$M_B\left(A\right)=\left(\begin{array}{ccc}& & *\\ *& & \\ & *& \end{array}\right)\equiv M_{B^{\prime }}\left(A\right)=\left(\begin{array}{ccc}& *& \\ & & *\\ *& & \end{array}\right)=M_1,$$

(7)

which proves the claim.

We shall prove now that whenever A is non-degenerate and has no proper basic ideals, then A has a natural basis $B=\{e_1,e_2,e_3\}$ such that

$$M_B\left(A\right)=\left(\begin{array}{ccc}& *& \\ \alpha & & *\\ \beta & \gamma & \end{array}\right)\mathrm{with}\left|\beta \right|+\left|\alpha \gamma \right|\ne 0.$$

(8)

We shall split the proof into the following two cases: $\beta =0$ and $\beta \ne 0$ (Cases 1 and 2).

Case 1. $M_B\left(A\right)=\left(\begin{array}{ccc}& & \\ & & \\ 0& & \end{array}\right).$ By Lemma 6 we must have $\left(\begin{array}{ccc}& & \\ *& & \\ 0& *& \end{array}\right)$. Again by Lemma 6 the choices are the following:

Case 1.1 $\left(\begin{array}{ccc}& & *\\ *& & \\ 0& *& \end{array}\right)$ which is a particular case of $\left(\begin{array}{ccc}& & *\\ *& & \\ & *& \end{array}\right)$ which is equivalent to $M_1$ by (7).

Case 1.2 $\left(\begin{array}{ccc}& & 0\\ *& & \\ 0& *& \end{array}\right).$ Hence, again from Lemma 6, we have $\left(\begin{array}{ccc}& *& 0\\ *& & *\\ 0& *& \end{array}\right)$, so we arrive to $M_2.$

Case 2. $M_B\left(A\right)=\left(\begin{array}{ccc}& & \\ & & \\ *& & \end{array}\right).$ Here we consider the following situations:

Case 2.1 $\left(\begin{array}{ccc}& & 0\\ & & \\ *& & \end{array}\right).$ By Lemma 6 we have that $\left(\begin{array}{ccc}& *& 0\\ & & *\\ *& & \end{array}\right),$ but this is a particular case of $M_1$.

Case 2.2 $\left(\begin{array}{ccc}& & *\\ & & \\ *& & \end{array}\right).$ We have the following possibilities:

$$\left(\begin{array}{ccc}& & *\\ *& & \\ *& & \end{array}\right)\mathrm{and}\left(\begin{array}{ccc}& & *\\ 0& & \\ *& & \end{array}\right).$$

Case 2.2.1 $\left(\begin{array}{ccc}& & *\\ *& & \\ *& & \end{array}\right).$ Since by Lemma 6 we cannot have $\left(\begin{array}{ccc}& 0& \\ & & \\ & 0& \end{array}\right)$ then we get the cases $\left(\begin{array}{ccc}& & *\\ *& & \\ *& *& \end{array}\right)$ and $\left(\begin{array}{ccc}& *& *\\ *& & \\ *& & \end{array}\right).$

Case 2.2.1.1 $\left(\begin{array}{ccc}& & *\\ *& & \\ *& *& \end{array}\right)$. This is a particular case of $\left(\begin{array}{ccc}& & *\\ *& & \\ & *& \end{array}\right)$ that is equivalent to $M_1$ by (7).

Case 2.2.1.2 $\left(\begin{array}{ccc}& *& *\\ *& & \\ *& & \end{array}\right).$ Here we have either $\left(\begin{array}{ccc}& *& *\\ *& & \\ *& *& \end{array}\right)$ or $\left(\begin{array}{ccc}& *& *\\ *& & \\ *& 0& \end{array}\right).$ The matrix $\left(\begin{array}{ccc}& *& *\\ *& & \\ *& *& \end{array}\right)$ is gathered in $\left(\begin{array}{ccc}& & *\\ *& & \\ & *& \end{array}\right).$ For the case $\left(\begin{array}{ccc}& *& *\\ *& & \\ *& 0& \end{array}\right)$ the choices are

$$\left(\begin{array}{ccc}& *& *\\ *& & 0\\ *& 0& \end{array}\right)\mathrm{and}\left(\begin{array}{ccc}& *& *\\ *& & *\\ *& 0& \end{array}\right).$$

The first one is equivalent to $\left(\begin{array}{ccc}& *& 0\\ *& & *\\ 0& *& \end{array}\right)$ for $B^{\prime }=\{e_2,e_1,e_3\},$ and the second one is contained in the case $\left(\begin{array}{ccc}& *& \\ & & *\\ *& & \end{array}\right)$ and hence in $\left(\begin{array}{ccc}& & *\\ *& & \\ & *& \end{array}\right)$ by (7).

Case 2.2.2. $\left(\begin{array}{ccc}& & *\\ 0& & \\ *& & \end{array}\right).$ From Lemma 6, we arrive to $\left(\begin{array}{ccc}& & *\\ 0& & *\\ *& & \end{array}\right).$ Now the choices are either $\left(\begin{array}{ccc}& *& *\\ 0& & *\\ *& & \end{array}\right)$ or $\left(\begin{array}{ccc}& 0& *\\ 0& & *\\ *& & \end{array}\right).$ The first case is contained in $\left(\begin{array}{ccc}& & *\\ *& & \\ & *& \end{array}\right)$ for $B^{\prime }=\{e_1,e_3,e_2\}$. For the second one, by Lemma 6, we obtain $\left(\begin{array}{ccc}& 0& *\\ 0& & *\\ *& *& \end{array}\right)$ which is equivalent to $\left(\begin{array}{ccc}& *& 0\\ *& & *\\ 0& *& \end{array}\right)$ by considering $B^{\prime }=\{e_1,e_3,e_2\}$. □

Corollary 6.

Let A be a non-degenerate three-dimensional evolution algebra. Then the following assertions are equivalent:

(i)

A has no basic proper ideals;

(ii)

A has a natural basis B with respect to which,

$$M_B\left(A\right)=\left(\begin{array}{ccc}& *& \\ \alpha & & *\\ \beta & \gamma & \end{array}\right)\mathit{with}\left|\beta \right|+\left|\alpha \gamma \right|\ne 0,$$

(9)

and either $dim{A}^2=3$ or $dim{A}^2=2$, and there does not exist a nonsingular matrix P such that $P{M}_{\tilde{B}}\left(A\right)=M_B\left(A\right)P^{\left[2\right]}$ where $M_{\tilde{B}}\left(A\right)$ is a matrix of the type

$$M_{\tilde{B}}\left(A\right)=\left(\begin{array}{ccc}{\alpha }_1& {\beta }_1& {\gamma }_1\\ {\alpha }_2& {\beta }_2& {\gamma }_2\\ 0& 0& 0\end{array}\right).$$

Proof. 

$\left(i\right)⟹\left(ii\right)$ Let us suppose that A has no basic proper ideals. Then, by Theorem 7 there is a natural basis B such that its structure matrix is within the type (9). Also, by Lemma 5 we know that if $dim{A}^2=1$, A has basic ideals. If $dim{A}^2=3$ then A has no proper ideals. Indeed, as $\beta$ and $\gamma$ cannot be zero simultaneously, it follows that every non-zero ideal I contains $A^2.$ If $dim{A}^2=2$ the conclusion follows from Lemma 4 joint with Proposition 4 (In this last case, the entries of third row of $M_B\left(A\right)$ cannot be zero simultaneously).

$\left(ii\right)⟹\left(i\right)$ Whenever A has a structure matrix of the type (9), then any ideal contains $A^2$. Hence, if $dim{A}^2=3$ then the conclusion is clear, and if $dim{A}^2=2$, then by Lemma 4, A cannot have a proper ideal. □

The following result is nothing but Corollary 6 in the particular case that $dim{A}^2=2$: keep in mind Proposition 4 and the fact that the associated graph to a natural basis $B=\{e_1,e_2,e_3\}$ does not have a source in $e_i$ if and only if the ith row of the structure matrix associated to B is a zero row.

Corollary 7.

Let A be a non-degenerate evolution algebra with $dim{A}^2=2.$ Then A has no proper basic ideals if and only if A has a natural basis respect to which the structure matrix is of the type (9) and all the natural bases of A have an associated graph with no source vertices (this is a graph such that every vertex has some incoming edge).

We shall study now when a non-degenerate evolution algebra A is reducible. In this case, $A=I\oplus J$ where $dimI=1$ and it has no zero product (otherwise A is degenerate) and $dimJ=2$ with J a non-degenerate two-dimensional basic ideal. Therefore, by Theorem 4, J has a natural basis $\{e_2,e_3\}$ with respect to which the structure matrix is of the type $M_{J_1}=\left(\begin{array}{cc}*& 0\\ 0& *\end{array}\right),$$M_{J_2}=\left(\begin{array}{cc}0& *\\ *& 0\end{array}\right)$ or $M_{J_3}=\left(\begin{array}{cc}w& \tilde{w}\\ *& *\end{array}\right),$ being that these types are non-isomorphic. Thus, A has a natural basis $B=\{e_1,e_2,e_3\}$ with respect to which $M_B\left(A\right)$ is within the following types:

$$M_1=\left(\begin{array}{ccc}*& 0& 0\\ 0& *& 0\\ 0& 0& *\end{array}\right),M_2=\left(\begin{array}{ccc}*& 0& 0\\ 0& 0& *\\ 0& *& 0\end{array}\right),M_3=\left(\begin{array}{ccc}*& 0& 0\\ 0& w& \tilde{w}\\ 0& *& *\end{array}\right).$$

We shall see now that these algebras are non-isomorphic. In order to do so, the following Lemma shall be useful.

Lemma 7.

Let A be a three-dimensional evolution algebra such that $A=I\oplus J$ with $dimI=1$ and $dimJ=2.$ If J is irreducible, then the decomposition of A is unique.

Proof. 

Let us suppose that $A=I\oplus J=\widehat{I}\oplus \widehat{J}$ where $dimI=dim\widehat{I}=1.$ Then, $J\simeq A/I=(\widehat{I}\oplus \widehat{J})/I\simeq \widehat{I}/I\oplus \widehat{J}/I$. As J cannot be decomposed we have that $\widehat{I}/I=0;$ note that $dim\widehat{I}/I\le 1$. Then, $I=\widehat{I}$ as $dimI=dim\widehat{I}=1$, so $J\subseteq \widehat{J}$ or equivalently $J=\widehat{J}$, as they have the same dimension. □

Theorem 8.

Let A be a three-dimensional reducible and non-degenerate evolution algebra. Then, A has a natural basis B such that the structure matrix associated to it, $M_B\left(A\right)$, is within the following non-isomorphic types:

$$M_1=\left(\begin{array}{ccc}*& 0& 0\\ 0& *& 0\\ 0& 0& *\end{array}\right),M_2=\left(\begin{array}{ccc}*& 0& 0\\ 0& 0& *\\ 0& *& 0\end{array}\right),M_3=\left(\begin{array}{ccc}*& 0& 0\\ 0& w& \tilde{w}\\ 0& *& *\end{array}\right),$$

with $w,\tilde{w}\in \mathbb{K}.$

Proof. 

As said above, by Theorem 4 there exists a natural base B such that $M_B\left(A\right)$ has the form of $M_1$, $M_2$ or $M_3.$ Let us denote by $A_i$ the algebra given by the structure matrix $M_i$ with $i=1,2,3.$ By the above Lemma it follows that the decomposition of $A_2,$$A_3$ is unique, and so $A_i$ are non-isomorphic, for $i=2,3$, as $J_i$ are not isomorphic either. But similarly, neither $A_2$ nor $A_3$ can be isomorphic to $A_1$, as $J_1$ is reducible and $J_2$, $J_3$ are irreducible. □

4.2. The Degenerate Case

The following result describes whether an evolution algebra is reducible according with the number of elements in the natural basis having zero square.

Theorem 9.

Let A be a degenerate evolution algebra and let $B=\{e_1,e_2,e_3\}$ be a natural basis of A.

(i)

Suppose that $e_1^2=e_2^2=e_3^2=0$. Then, A has zero product and is reducible.

(ii)

Suppose that $e_1^2=e_2^2=0$ and $e_3^2\ne 0$. Then, A is reducible.

(iii)

Suppose that $e_1^2=0$, $e_2^2\ne 0$ and $e_3^2\ne 0$. Then we have one of the following situations

(a)

$e_2^2$ and $e_3^2$ are linearly dependent, and so $M_B\left(A\right)=\left(\begin{array}{ccc}0& \alpha & t\alpha \\ 0& \beta & t\beta \\ 0& \gamma & t\gamma \end{array}\right)$. Then:

(a.1)

A is reducible if and only if $\left|\beta \right|+\left|\gamma \right|\ne 0$.

(a.2)

A is irreducible if and only if $M_B\left(A\right)=\left(\begin{array}{ccc}0& *& *\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$.

(b)

$e_2^2$ and $e_3^2$ are linearly independent. Then:

(b.1)

A is reducible if and only if $M_B\left(A\right)=\left(\begin{array}{ccc}0& w_{12}& w_{13}\\ 0& w_{22}& w_{23}\\ 0& w_{32}& w_{33}\end{array}\right)$ with $w_{22}{w}_{33}-w_{32}{w}_{23}\ne 0.$

(b.2)

A is irreducible if and only if $M_B\left(A\right)=\left(\begin{array}{ccc}0& w& \tilde{w}\\ 0& \alpha & \alpha t\\ 0& \beta & \beta t\end{array}\right)$ with $\tilde{w}\ne wt$ and $\left|\alpha \right|+\left|\beta \right|\ne 0$.

Proof. 

(i) It is clear that if A has a zero product then A is reducible. Indeed, $A=I\oplus J$ where $I=lin\{e_1,e_2\}$ and $J=\mathbb{K}{e}_3$.

(ii) Suppose that $e_1^2=e_2^2=0$ and $e_3^2\ne 0.$ Consider $e_3^2=w_{13}{e}_1+w_{23}{e}_2+w_{33}{e}_3$. We have the following possibilities:

Case (ii)(1) $w_{33}\ne 0.$ Then, $A=I\oplus J$ where $I=lin\{e_1,e_2\}$ and $J=\mathbb{K}{e}_3^2.$

Case (ii)(2) $w_{33}=0$. We shall consider the following situations.

Case (ii)(2.1) $w_{23}\ne 0.$ Then $A=I\oplus J$ being $I=lin\{e_3,e_3^2\}=lin\{e_3,w_{13}{e}_1+w_{23}{e}_2\}$ and $J=\mathbb{K}{e}_1$.

Case (ii)(2.2) $w_{23}=0$, which immediately implies $w_{13}\ne 0$. Then $A=I\oplus J$ with $I=lin\{e_1,e_3\}$ and $J=\mathbb{K}{e}_2$.

(iii) Let assume that $e_1^2=0$, $e_2^2\ne 0$ and $e_3^2\ne 0$. We shall split the proof of this assertion in two cases (a) and (b).

Case (iii)(a) $e_2^2$ and $e_3^2$ are linearly dependent. Hence, there exists $t\in \mathbb{K}\backslash \left\{0\right\}$ such that $t{e}_2^2=e_3^2\ne 0.$ We claim that whenever A is reducible then one of the ideals is $\mathbb{K}{e}_1.$ To prove the claim suppose that $A=I\oplus J.$ Since it cannot be ${\pi }_2\left(I\right)={\pi }_2\left(J\right)=0$ (as ${\pi }_2\left(A\right)\ne 0$), it is not restrictive to assume that ${\pi }_2\left(I\right)\ne 0.$ But ${\pi }_2\left(I\right)\ne 0$ implies that ${\pi }_2\left(J\right)=0$, as otherwise $e_2^2\in I\cap J$. Also, whenever ${\pi }_2\left(I\right)\ne 0$ then ${\pi }_3\left(I\right)\ne 0$. Indeed, if ${\pi }_3\left(I\right)=0$, then ${\pi }_3\left(J\right)\ne 0$ (otherwise ${\pi }_3\left(A\right)=0$). Thus, $e_2^2=t{e}_3^2\in I\cap J=\left\{0\right\}$, a contradiction. Therefore ${\pi }_2\left(I\right)\ne 0$ and ${\pi }_3\left(I\right)\ne 0$ while ${\pi }_2\left(J\right)={\pi }_3\left(J\right)=0$ (as $I\cap J=\left\{0\right\}$ and $e_2^2=t{e}_3^2\ne 0$). Thus, we obtain $J=\mathbb{K}{e}_1$, as desired to prove the claim.

We shall consider two different situations:

Case (iii)(a.1) $e_3^2=t{e}_2^2\in \mathbb{K}{e}_1$, with $t\ne 0$. Then, from the former claim it follows that A is not reducible. Indeed, let us assume that $A=I\oplus J$. Then, $J=\mathbb{K}{e}_1$ and ${\pi }_2\left(I\right)\ne 0$ as shown above. Hence, $e_2^2=t{e}_3^2\in I\cap J$, and thus, $e_1\in I\cap J\ne \left\{0\right\}$, a contradiction. Thus, whenever the structure matrix of A is of the type

$$M_B\left(A\right)=\left(\begin{array}{ccc}0& *& *\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$$

the evolution algebra is irreducible.

Case (iii)(a.2) $e_3^2=t{e}_2^2\notin \mathbb{K}{e}_1$, with $t\ne 0$. Then $e_2^2=\alpha e_1+\beta e_2+\gamma e_3$ with $\left|\beta \right|+$$\left|\gamma \right|\ne 0$. We consider the following possibilities:

Case (iii)(a.2.1) $\alpha =0$. Then $A=I\oplus J$ with $I=lin\{e_2,e_3\}$ and $J=\mathbb{K}{e}_1.$

Case (iii)(a.2.2) $\alpha \ne 0$. Then, as $\left|\beta \right|+\left|\gamma \right|\ne 0$, we have the following possibilities:

Case (iii)(a.2.2.1) $\beta \ne 0$. Then $A=I\oplus J$ with $I=lin\{e_2^2,e_3\}=lin\{\alpha e_1+\beta e_2,e_3\}$ and $J=\mathbb{K}{e}_1$.

Case (iii)(a.2.2.2) $\beta =0.$ Then, $\gamma \ne 0$ and so $A=I\oplus J$ where $J=\mathbb{K}{e}_1$ and $I=lin\{e_2,e_2^2\}=lin\{\alpha e_1+\gamma e_3,e_2\}$.

Case (iii)(b) $e_2^2$ and $e_3^2$ are linearly independent. We claim that A is reducible if and only if $e_1\notin lin\{e_2^2,e_3^2\}$. To prove the claim, suppose that $e_1\notin lin\{e_2^2,e_3^2\}$. Then, A is reducible since $A=I\oplus J$ with $I=lin\{e_2^2,e_3^2\}$ and $J=\mathbb{K}{e}_1$. In this case, the structure matrix is

$$M_B\left(A\right)=\left(\begin{array}{ccc}0& w_{12}& w_{13}\\ 0& w_{22}& w_{23}\\ 0& w_{32}& w_{33}\end{array}\right)$$

with $w_{22}{w}_{33}-w_{32}{w}_{23}\ne 0.$ To finish the proof of the claim, suppose now that $e_1\in lin\{e_2^2,e_3^2\}$ and let us show that A is irreducible. Assume towards contradiction that $A=I\oplus J$ is a non-trivial decomposition and suppose that ${\pi }_2\left(I\right)\ne 0$ while ${\pi }_2\left(J\right)=0$, which is not restrictive. Let $e_2^2=\sum _{i=1}^3{w}_{i2}{e}_i$ and $e_3^2=\sum _{i=1}^3{w}_{i3}{e}_i.$ From the fact that $e_1\in lin\{e_2^2,e_3^2\}$ it follows that

$$\left|\left(\begin{array}{cc}{w}_{22}& w_{23}\\ w_{32}& w_{33}\end{array}\right)\right|=0.$$

Therefore, there exists $t\in \mathbb{K}$ such that

$$\left(\begin{array}{cc}{w}_{22}& w_{23}\\ w_{32}& w_{33}\end{array}\right)=\left(\begin{array}{cc}{w}_{22}& t{w}_{22}\\ w_{32}& t{w}_{32}\end{array}\right).$$

We are going to distinguish between two cases:

Case (iii)(b.1) $w_{32}\ne 0.$ Then, since $e_2^2\in I$ (because ${\pi }_2\left(I\right)\ne 0$) we deduce that $e_3^2\in I,$ and hence, $e_1\in I$ as $e_1\in lin\{e_2^2,e_3^2\}.$ Also, we have that ${\pi }_3\left(J\right)=0$ (otherwhise $e_3^2\in I\cap J$) and similarly ${\pi }_2\left(J\right)=0$. Thus, $J=\mathbb{K}{e}_1$ and $e_1\in I\cap J,$ a contradiction.

Case (iii)(b.2) $w_{32}=0.$ Then:

Case (iii)(b.2.1) If ${\pi }_3\left(I\right)\ne 0$ then, since ${\pi }_2\left(I\right)\ne 0$, we have that $I=lin\{e_2^2,e_3^2\}$, and hence, $e_1\in I$, and, as in the case (b.1), we get $e_1\in I\cap J,$ a contradiction.

Case (iii)(b.2.2) Suppose ${\pi }_3\left(I\right)=0$, and recall that ${\pi }_2\left(I\right)\ne 0$. Consequently, ${\pi }_3\left(J\right)\ne 0$ and ${\pi }_2\left(J\right)=0$. It follows that $w_{23}=w_{32}=0$ as $e_2^2=\sum _{i=1}^3{w}_{i2}{e}_i\in I$ with ${\pi }_3\left(I\right)=0$ and $e_3^2=\sum _{i=1}^3{w}_{i3}{e}_i\in J$ with ${\pi }_2\left(J\right)=0$. Therefore

$$\left(\begin{array}{cc}{w}_{22}& w_{23}\\ w_{32}& w_{33}\end{array}\right)=\left(\begin{array}{cc}{w}_{22}& t{w}_{22}\\ w_{32}& t{w}_{32}\end{array}\right)=\left(\begin{array}{cc}0& 0\\ 0& 0\end{array}\right)$$

which contradicts the fact that $e_2^2$ and $e_3^2$ are linearly independent.

Hence, we conclude that if $e_2^2$ and $e_3^2$ are linearly independent, then A is irreducible if and only if $e_1\in lin\{e_2^2,e_3^2\}$; i.e., if and only if $\left(\begin{array}{c}{w}_{22}\\ w_{23}\end{array}\right)$ and $\left(\begin{array}{c}{w}_{32}\\ w_{33}\end{array}\right)$ are proportional but $\left(\begin{array}{c}{w}_{21}\\ w_{22}\\ w_{23}\end{array}\right)$ and $\left(\begin{array}{c}{w}_{31}\\ w_{32}\\ w_{33}\end{array}\right)$ are not as $e_2^2$ and $e_3^2$ are linearly independent. This is equivalent to

$$M_B\left(A\right)=\left(\begin{array}{ccc}0& w& \tilde{w}\\ 0& \alpha & \alpha t\\ 0& \beta & \beta t\end{array}\right)$$

with $\tilde{w}\ne wt,$ and $\left|\alpha \right|+\left|\beta \right|\ne 0$. The rest is clear. □

Theorem 10.

Let A be a three-dimensional degenerate evolution algebra. Then we have the following:

(i)

A is reducible if and only if there exists a natural basis B of A whose structure matrix is within the following types:

(a)

$M_B\left(A\right)=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$.

(b)

$M_B\left(A\right)=\left(\begin{array}{ccc}0& 0& \alpha \\ 0& 0& \beta \\ 0& 0& \gamma \end{array}\right)$ with $\left|\alpha \right|+\left|\beta \right|+\left|\gamma \right|\ne 0$, $\alpha ,\beta ,\gamma \in \mathbb{K}$.

(c)

$M_B\left(A\right)=\left(\begin{array}{ccc}0& \alpha & t\alpha \\ 0& \beta & t\beta \\ 0& \gamma & t\gamma \end{array}\right)$ with $\left|\beta \right|+\left|\gamma \right|\ne 0$ and $t\ne 0,$$\alpha ,\beta ,\gamma \in \mathbb{K}$.

(d)

$M_B\left(A\right)=\left(\begin{array}{ccc}0& w& \tilde{w}\\ 0& \alpha & \beta \\ 0& \gamma & \delta \end{array}\right)$ with $w,\tilde{w},\alpha ,\beta ,\gamma ,\delta \in \mathbb{K}$ and $\alpha \delta -\gamma \beta \ne 0.$

(ii)

A is reducible if and only if there exists a natural basis B of A whose structure matrix is within the following types:

(e)

$M_B\left(A\right)=\left(\begin{array}{ccc}0& *& *\\ 0& 0& 0\\ 0& 0& 0\end{array}\right)$.

(f)

$M_B\left(A\right)=\left(\begin{array}{ccc}0& w& \tilde{w}\\ 0& \alpha & \alpha t\\ 0& \beta & \beta t\end{array}\right)$ with $\tilde{w}\ne wt$ and $\left|\alpha \right|+\left|\beta \right|\ne 0$.

The former type of evolution algebras are non-isomorphic to each other.

Proof. 

We obtained this classification because of Theorem 9. Let us check that they are non-isomorphic. First of all, none of the algebras in the group (i) can be isomorphic with any of the algebras in the group (ii), as those in the former group are reducible while those in the latter group are not. In the group (i), the algebra (a) is clearly non-isomorphic to any of the others, as its product is zero. On the other hand, (b) cannot be isomorphic to (c) or (d) because its annihilator has two-dimensional, while (c) and (d) and have a one-dimensional annihilator. To verify that (c) is not isomorphic with (d), we just point out that in (c), $dim{A}^2=1$, while in (d), $dim{A}^2=2$. In the group (ii), finally, (e) cannot be isomorphic to (f), as in (e) we have $dim{A}^2=1$; meanwhile, in (f) we have $dim{A}^2=2.$ □

4.3. The Main Result

To sum up, we gather Theorems 5 and 6, Corollary 6, Theorems 8 and 10 in the theorem below, showing that when we classify three-dimensional evolution algebras according to their degeneracy and their reducibility we obtain 14 non-isomorphic types of evolution algebras.

Theorem 11.

Let A be an evolution algebra with $dimA=3$ and let us consider $t,a,b,c\in \mathbb{K}\backslash \left\{0\right\}$ and $\alpha ,\beta ,\gamma ,\delta ,w,\tilde{w}\in \mathbb{K}$. Then:

(i)

Suppose that A is degenerate and reducible. Then, there exists a natural basis B such that the structure matrix of A relative to B is like $M_1$, $M_2$, $M_3$ or $M_4$, where:

• $M_1=\left(\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right);$
• $M_2=\left(\begin{array}{ccc}0& 0& \alpha \\ 0& 0& \beta \\ 0& 0& \gamma \end{array}\right)\mathit{with}\left|\alpha \right|+\left|\beta \right|+\left|\gamma \right|\ne 0;$
• $M_3=\left(\begin{array}{ccc}0& \alpha & t\alpha \\ 0& \beta & t\beta \\ 0& \gamma & t\gamma \end{array}\right)\mathit{with}\left|\beta \right|+\left|\gamma \right|\ne 0;$
• $M_4=\left(\begin{array}{ccc}0& w& \tilde{w}\\ 0& \alpha & \beta \\ 0& \gamma & \delta \end{array}\right)\mathit{with}\alpha \delta -\gamma \beta \ne 0.$

(ii)

Suppose that A is degenerate and irreducible. Then, there exists a natural basis B of A whose structure matrix is like $M_5$ or $M_6$, where:

• $M_5=\left(\begin{array}{ccc}0& *& *\\ 0& 0& 0\\ 0& 0& 0\end{array}\right);$
• $M_6=\left(\begin{array}{ccc}0& w& \tilde{w}\\ 0& \alpha & \alpha t\\ 0& \beta & \beta t\end{array}\right)\mathit{with}\tilde{w}\ne wt\mathit{and}\left|\alpha \right|+\left|\beta \right|\ne 0.$

(iii)

Suppose that A is non-degenerate and reducible. Then, there exists a natural basis B of A which structure matrix is like $M_7$, $M_8$ or $M_9$, where:

• $M_7=\left(\begin{array}{ccc}*& 0& 0\\ 0& *& 0\\ 0& 0& *\end{array}\right);$
• $M_8=\left(\begin{array}{ccc}*& 0& 0\\ 0& 0& *\\ 0& *& 0\end{array}\right);$
• $M_9=\left(\begin{array}{ccc}*& 0& 0\\ 0& w& \tilde{w}\\ 0& *& *\end{array}\right).$

(iv)

Suppose that A is non-degenerate and irreducible. Then, there exists a natural basis B of A such that the structure matrix associated to it is like $M_{10}$, $M_{11}$, $M_{12}$, $M_{13}$ or $M_{14}$, where:

• $M_{10}=\left(\begin{array}{ccc}*& *& 0\\ 0& w& *\\ 0& *& \tilde{w}\end{array}\right)\mathit{with}\left|M_{10}\right|\ne 0;$
• $M_{11}=\left(\begin{array}{ccc}*& *& *\\ 0& w& *\\ 0& *& \tilde{w}\end{array}\right)\mathit{with}\left|M_{11}\right|\ne 0;$
• $M_{12}=\left(\begin{array}{ccc}*& *& w\\ 0& *& *\\ 0& *& *\end{array}\right)$ with $\left|M_{12}\right|=0$ and either $M_{12}=\left(\begin{array}{ccc}*& a& -\frac{b^2}{c^2}a\\ 0& b& -\frac{b^2}{c^2}b\\ 0& c& -\frac{b^2}{c^2}c\end{array}\right)$ or $M_{12}$ has no proportional columns;
• $M_{13}=\left(\begin{array}{cc}\alpha & \gamma \\ \beta & *\\ 0& 0\end{array}\right)\mathit{with}\left|\alpha \right|+\left|\beta \right|+\left|\gamma \right|\ne 0,\mathit{and}\mathit{no}\mathit{zero}\mathit{columns};$
• $M_{14}=\left(\begin{array}{c}*\\ \alpha & *\\ \beta & \gamma \end{array}\right)\mathit{with}\left|\beta \right|+\left|\alpha \gamma \right|\ne 0$, range of $M_{14}$ greater than 1, and such that it does not exist a nonsingular matrix P such that $PX=M_{14}{P}^{\left[2\right]}$, where $X=\left(\begin{array}{ccc}{\alpha }_1& {\beta }_1& {\gamma }_1\\ {\alpha }_2& {\beta }_2& {\gamma }_2\\ 0& 0& 0\end{array}\right).$

Moreover, if A has a basic ideal of dimension 1 and has no basic ideals with dimension 2, then $M_B\left(A\right)$ is given by either $M_{10},$$M_{11}$ $or$ $M_{12}$. If A has basic ideals of dimension 2 then $M_B\left(A\right)$ is like $M_{13}$ and if A has no proper basic ideals then $M_B\left(A\right)$ is like $M_{14}.$

In fact, for $1\le i\le 14$, denote by $A_i$ an evolutionary algebra having a natural basis of the type $M_i$ described above. Then, these algebras are not isomorphic and we obtain the following classification of evolution algebras with three dimensions:

	Degenerate	Non-Degenerate
Reducible	$A_1$, $A_2$, $A_3$, $A_4$	$A_7$, $A_8$, $A_9$
Irreducible	$A_5$, $A_6$	$A_{10}$, $A_{11}$, $A_{12},$$A_{13},$$A_{14}$

Therefore, we have obtained 14 non-isomorphic types of evolution algebras of dimension 3.

This means that an algebra of the type $A_i$ is not isomorphic to an algebra of the type $A_j$ whenever $i\ne j$, $1\le i,j\le 14$. Nevertheless, we found several non-isomorphic evolution algebras that belong to the same type. As a matter of fact, by considering the 116 types of non-isomorphic three-dimensional evolution algebras described in [17], we have reclassified them into the 14 different types $A_i$ described above. It is easy to check when one of the algebras stated in [17] belongs to one of the types obtained in this paper by just considering the properties:

(a)

Being reducible or not;

(b)

Being degenerate or not,

(c)

Having a basic ideals of dimension 1 and no basic ideals of dimension 2;

(d)

Having a basic ideal of dimension 2;

(e)

Having no proper basic ideals.

References