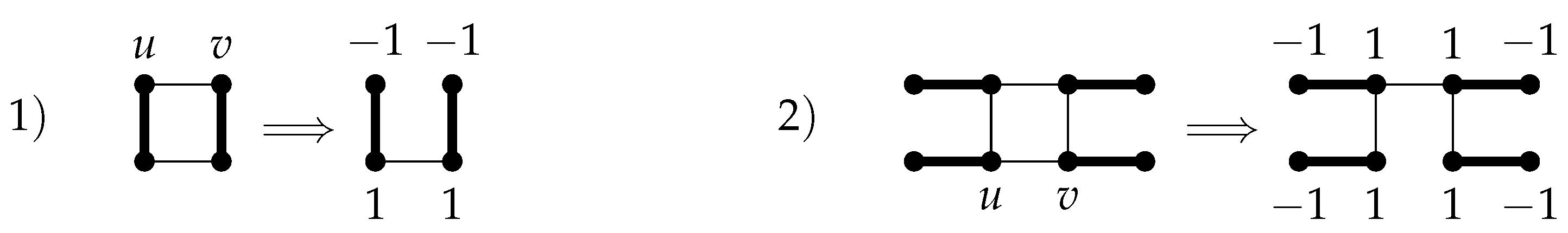Some Bicyclic Graphs Having 2 as Their Laplacian Eigenvalues

Abstract

If G is a graph, its Laplacian is the difference between the diagonal matrix of its vertex degrees and its adjacency matrix. A one-edge connection of two graphs $G_1$ and $G_2$ is a graph $G=G_1{\odot }_{uv}{G}_2$ with $V\left(G\right)=V\left(G_1\right)\cup V\left(G_2\right)$ and $E\left(G\right)=E\left(G_1\right)\cup E\left(G_2\right)\cup \{e=uv\}$ where $u\in V\left(G_1\right)$ and $v\in V\left(G_2\right)$. In this paper, we study some structural conditions ensuring the presence of 2 in the Laplacian spectrum of bicyclic graphs of type $G_1{\odot }_{uv}{G}_2$. We also provide a condition under which a bicyclic graph with a perfect matching has a Laplacian eigenvalue 2. Moreover, we characterize the broken sun graphs and the one-edge connection of two broken sun graphs by their Laplacian eigenvalue 2.

1. Introduction

All graphs in this paper are finite and undirected with no loops or multiple edges. Let G be a graph with n vertices. The vertex set and the edge set of G are denoted by $V\left(G\right)$ and $E\left(G\right)$, respectively. The Laplacian matrix of G is $L\left(G\right)=D\left(G\right)-A\left(G\right)$, where $D\left(G\right)=diag(d\left(v_1\right),\dots ,d\left(v_n\right))$ is the diagonal matrix and $d\left(v\right)$ denotes the degree of the vertex v in G and $A\left(G\right)$ is the adjacency matrix of G. Denoting its eigenvalues by ${\lambda }_1\left(G\right)\ge \cdots \ge {\lambda }_n\left(G\right)=0$, we shall use the notation ${\lambda }_k\left(G\right)$ to denote the kth Laplacian eigenvalue of the graph G. Also, the multiplicity of the eigenvalue $\lambda$ of $L\left(G\right)$ is denoted by $m_G\left(\lambda \right)$. For any $v\in V\left(G\right)$, let $N\left(v\right)$ be the set of all vertices adjacent to v. A vertex of degree one is called a leaf vertex. A matching of G is a set of pairwise disjoint edges of G. The matching number of G, denoted ${\alpha }^{{}^{\prime }}\left(G\right)$, is the maximum possible cardinality for a matching in G. Clearly, $n\ge 2{\alpha }^{{}^{\prime }}\left(G\right)$. In particular, if $n=2{\alpha }^{{}^{\prime }}\left(G\right)$, then G has a perfect matching.

Connected graphs in which the number of edges equals the number of vertices are called unicyclic graphs. Therefore, a unicyclic graph is either a cycle or a cycle with some attached trees. Let ${\mathfrak{U}}_{n,g}$ be the set of all unicyclic graphs of order n with girth g. Throughout this paper, we suppose that the vertices of the cycle $C_g$ are labeled by $v_1,\dots v_g$, ordered in a natural way around $C_g$, say in the clockwise direction. A rooted tree is a tree in which one vertex has been designated as the root. Furthermore, assume that $T_i$ is a rooted tree of order $n_i\ge 1$ attached to $v_i\in V\left(T_i\right)$, where ${\sum }_{i=1}^{i=g}{n}_i=n$. This unicyclic graph is denoted by $C(T_1,\dots ,T_g)$. The sun graph of order $2n$ is a cycle $C_n$ with an edge terminating in a leaf vertex attached to each vertex. A broken sun graph is a unicyclic subgraph of a sun graph.

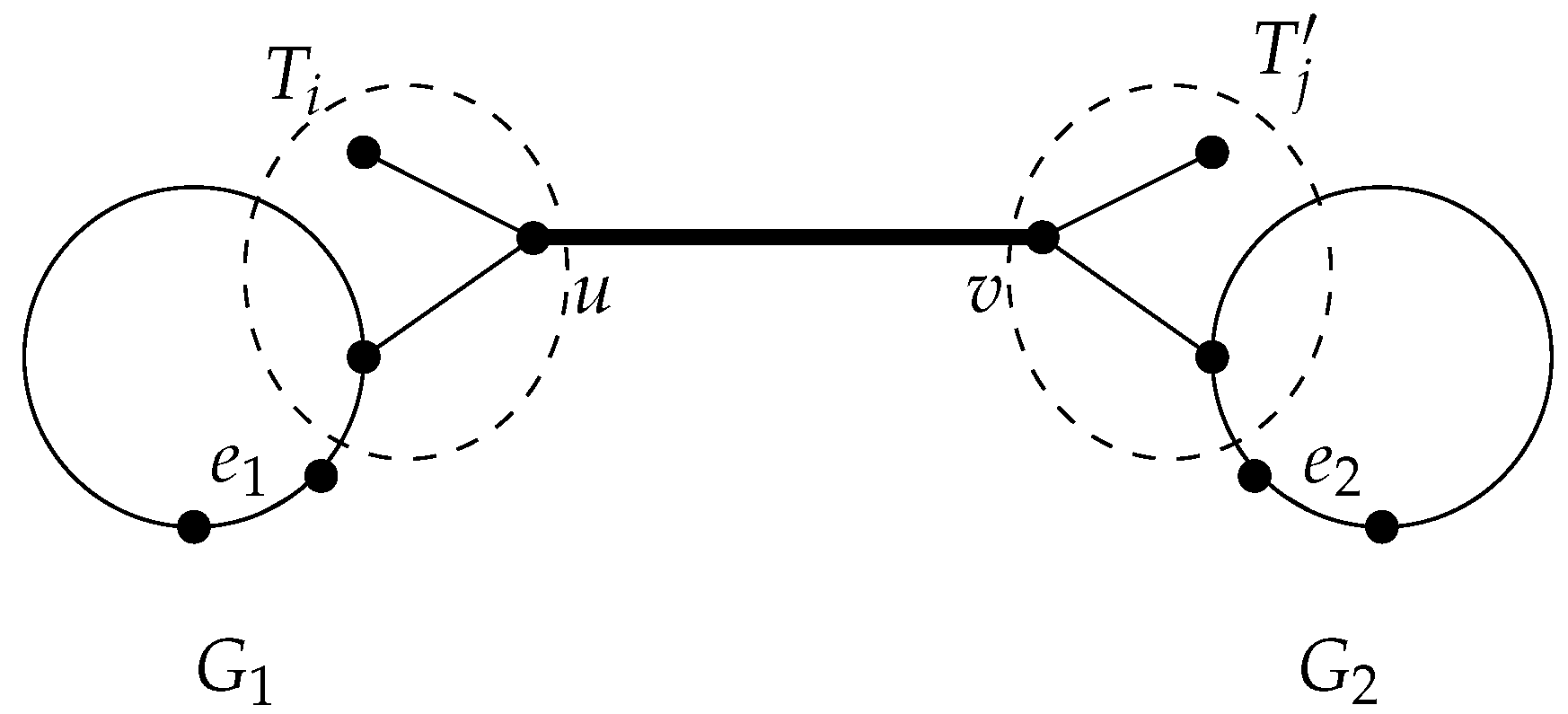
A one-edge connection of two graphs $G_1$ and $G_2$ is a graph G with $V\left(G\right)=V\left(G_1\right)\cup V\left(G_2\right)$ and $E\left(G\right)=E\left(G_1\right)\cup E\left(G_2\right)\cup \{e=uv\}$, where $u\in V\left(G_1\right)$ and $v\in V\left(G_2\right)$. We denote it by $G=G_1{\odot }_{uv}{G}_2$. In this manuscript, we would like to study the eigenvalue 2 in bicyclic graphs with just 2 cycles. We provide a necessary and sufficient condition under which a bicyclic graph with a perfect matching has 2 as its Laplacian eigenvalue, for more see [1]. For more about Laplacians of some parameters of graphs we refer to [2,3,4,5]. In the last couple of years there has been a renewed interest toward the Laplacian spectral properties of bicyclic graphs (see [6,7]), and it is very likely that many techniques employed in this paper could be also helpful to solve the correspondent problems in the context of signed graphs.

2. Preliminary Results

By [8] (Theorem 13) due to Kelmans and Chelnokov, the Laplacian coefficient, ${\xi }_{n-k}$, can be expressed in terms of subtree structures of G, for $0\le k\le n$. Suppose that F is a spanning forest of G with components $T_i$ of order $n_i$, and $\gamma \left(F\right)={\Pi }_{i=1}^k{n}_i$. The Laplacian characteristic polynomial of G turns out to be $L_G\left(x\right)=det(xI-L\left(G\right))={\Sigma }_{i=0}^n{(-1)}^i{\xi }_i{x}^{n-i}$.

Theorem 1

([9], Theorem 7.5). The Laplacian coefficient ${\xi }_{n-k}$ of a graph G of order n is given by ${\xi }_{n-k}={\sum }_{F\in {\mathfrak{F}}_k}\gamma \left(F\right)$, where ${\mathfrak{F}}_k$ is the set of all spanning forest of G with exactly k components.

In particular, we have ${\xi }_0=1$, ${\xi }_1=2m$, ${\xi }_n=0$, and ${\xi }_{n-1}=n\tau \left(G\right)$, in which $\tau \left(G\right)$ denotes the number of spanning trees of G.

Let G be a graph with n vertices. It is convenient to adopt the following terminology from [10]: for a vector $X={(x_1,\dots ,x_n)}^t\in {\mathbb{R}}^n$, we say that X gives a valuation of the vertex of V, and to each vertex $v_i$ of V, we associate the number $x_i$, which is the value of the vertex $v_i$; that is, $x\left(v_i\right)=x_i$. Then $\lambda$ is an eigenvalue of $L\left(G\right)$ with the corresponding eigenvector $X=(x_1,\dots ,x_n)$ if and only if $X\ne 0$ and

$$(d\left(v_i\right)-\lambda )x_i=\sum _{v_j\in N\left(v_i\right)}{x}_j\mathrm{for}\mathrm{all}i=1,\dots ,n.$$

(1)

It has been shown that if T is a tree containing a perfect matching, then T has 2 among its Laplacian eigenvalues and ${\lambda }_{{\alpha }^{{}^{\prime }}\left(T\right)}\left(T\right)={\lambda }_{n/2}\left(T\right)=2$, [11] (Theorem 2). In [12] (Theorem 2) the author proved that, if T is a tree with a perfect matching, M, a vector $X\ne 0$ is an eigenvector of $L\left(T\right)$ corresponding to the eigenvalue 2 if and only if X has exactly two distinct entries $-1$ and 1. Moreover, $x\left(u\right)=-x\left(v\right)$ for each $uv\in M$, and $x\left(u\right)=x\left(v\right)$ for each $uv\notin M$.

3. The Eigenvector of the Laplacian Eigenvalue 2

In what follows, we study some results on broken sun graphs and unicyclic graphs. Furthermore, we establish the eigenvector of these types of graphs that have two among their Laplacian eigenvalues. First, we cite a theorem from [13].

Theorem 2

([13], Theorem 3.2). Let G be a graph on n vertices and e be an edge of G. Let ${\lambda }_i\left(G\right),(1\le i\le n)$ be the eigenvalues of $L\left(G\right)$. Then the following holds:

$${\lambda }_1\left(G\right)\ge {\lambda }_1(G-e)\ge {\lambda }_2\left(G\right)\ge {\lambda }_2(G-e)\ge \cdots \ge {\lambda }_n\left(G\right)\ge {\lambda }_n(G-e).$$

Remark 1.

Let T be a tree of order $n\ge 3$ with a perfect matching, and let X be a Laplacian eigenvector of T corresponding to the eigenvalue 2. Then, by [12] (Theorem 2), T has $\frac{n}{2}$ vertices with value 1 and $\frac{n}{2}$ vertices with value $-1$ given by X. Let $V_1$ and $V_2$ be the sets of the former $\frac{n}{2}$ and the latter $\frac{n}{2}$ vertices, respectively. By [14] (Theorem 3.1), if we add edges between any two non-incident vertices in $V_1$ or $V_2$, then 2 is also an eigenvalue of the result graph. Hence, if u and v belong to $V_1$ (or $V_2$), then $G=T\cup \left\{uv\right\}$ has 2 among its Laplacian eigenvalues and $X={(x_1,\dots ,x_n)}^t$ is an eigenvector of $L\left(G\right)$ corresponding to the eigenvalue 2 where $x_i\in \{-1,1\}$.

Let $n_i\left(G\right)$ be the number of vertices of degree i in G. Now we have the following Theorem.

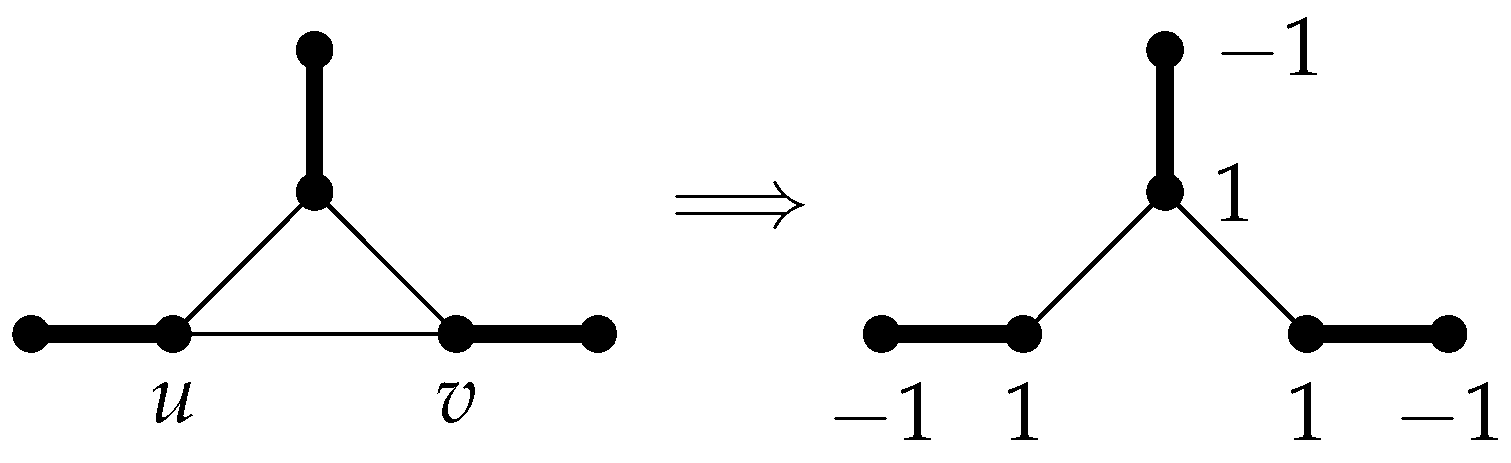
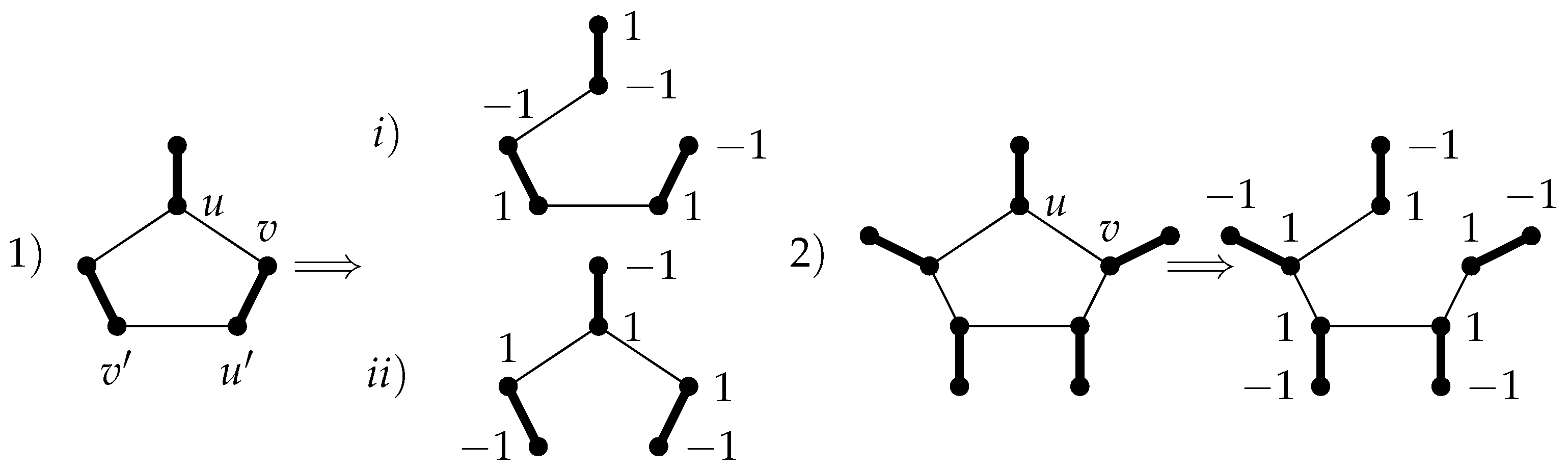
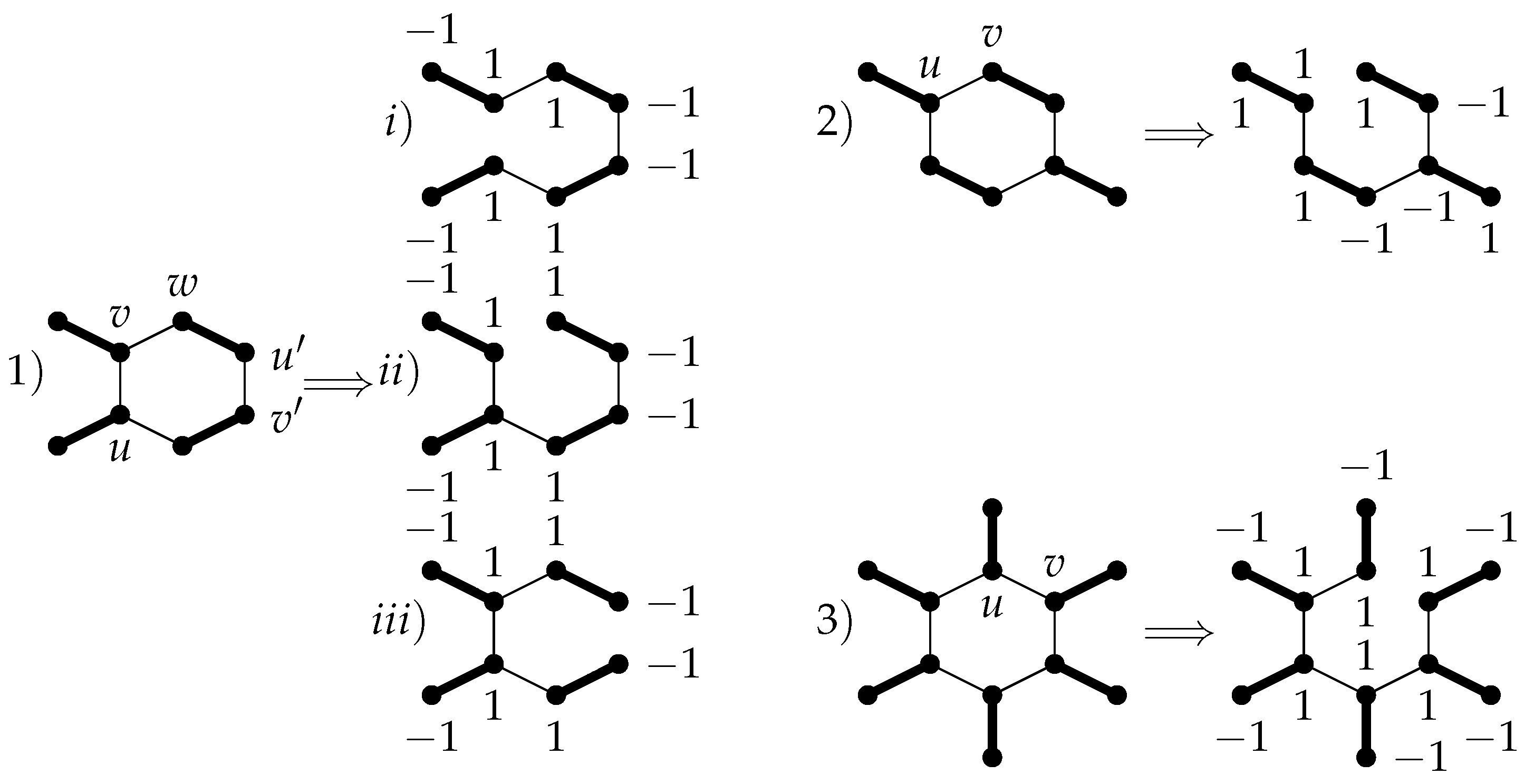
Theorem 3.

Let G be a broken sun graph containing a perfect matching which has 2 among its Laplacian eigenvalues. Thus, there exists an eigenvector corresponding to the eigenvalue 2, like $X={(x_1,\dots ,x_n)}^t$ such that $x_i\in \{-1,1\}$.

Proof. 

By induction on g and using Remark 1, we prove that $x\left(u\right)=x\left(v\right)$ for $uv\notin M$, where X is an eigenvector of $L\left(G\right)$ corresponding to the eigenvalue 2. Assume that M is a perfect matching in G. The following Figure 1, Figure 2, Figure 3 and Figure 4 show that for all broken sun graphs with $3\le g\le 6$, that contain a perfect matching and have 2 among their Laplacian eigenvalues, for each arbitrary edge $e=uv\notin M$, by removing e, we have a tree $T=G-e$ with a perfect matching. Thus, assume that $X={(x_1,\dots ,x_n)}^t$ be an eigenvector of $L\left(T\right)$ corresponding to the eigenvalue 2 such that $x_i\in \{-1,1\}$, by [12] (Theorem 2) and $x_T\left(u\right)=x_T\left(v\right)$. Also X is an eigenvector of $L\left(G\right)$ corresponding to the eigenvalue 2, by Remark 1.

Now assume that $g\ge 7$. We can find two pairs of adjacent vertices of degree 2 in G, because of G has a perfect matching. Also $n_2\left(G\right)\ge 4$, by [2] (Theorem 8). We suppose that $u_k,u_{k+1}$ and $u_l,u_{l+1}$ are these vertices. Suppose that $G^{{}^{\prime }}$ obtained from G by identifying three vertices $u_{k-1},u_k,u_{k+1}$ as one vertex $u_{k-1}$ and also by identifying three vertices $u_l,u_{l+1},u_{l+2}$ as one vertex $u_{l+2}$, where $l\ge k+2$. Obviously, $G^{{}^{\prime }}$ is a broken sun graph with a perfect matching $M^{{}^{\prime }}$ whose girth is $g-4$ and $n_2\left(G^{\prime }\right)\equiv 0\left(mod4\right)$. Thus, using induction hypothesis in $G^{{}^{\prime }}$ by removing $e=uv\notin M^{{}^{\prime }}$, $x\left(u\right)=x\left(v\right)$. So $G^{{}^{\prime }}$ has 2 among its Lapalcian eigenvalues with the eigenvector $X={(x_1,\dots ,x_{k-1},x_{k+2},x_{k+3},\dots ,x_{l-1},x_{l+2},\dots ,x_n)}^t\in {\mathbb{R}}^{n-4}$ such that $x_i\in \{-1,1\}$. If $l\ge k+3$, then we define the vector $Y={(y_1,\dots ,y_n)}^t\in {\mathbb{R}}^n$ as

$$y_i=\left\{\begin{array}{cc}{x}_i,\hfill & \mathrm{if}1\le i\le k-1;\hfill \\ x_{k+2},\hfill & \mathrm{if}i=k;\hfill \\ -x_{k-1},\hfill & \mathrm{if}i=k+1;\hfill \\ -x_i,\hfill & \mathrm{if}k+2\le i\le l-1;\hfill \\ -x_{l+2}\hfill & \mathrm{if}i=l;\hfill \\ x_{l-1}\hfill & \mathrm{if}i=l+1;\hfill \\ x_i\hfill & \mathrm{if}l+2\le i\le n;\hfill \end{array}\right.$$

also assign to each leaf vertex the negative value of its neighbor. If $l=k+2$, then we define the vector $Y={(y_1,\dots ,y_n)}^t\in {\mathbb{R}}^n$ as

$$y_i=\left\{\begin{array}{cc}{x}_i,\hfill & \mathrm{if}1\le i\le k-1;\hfill \\ x_{k+4},\hfill & \mathrm{if}i=k;\hfill \\ -x_{k-1},\hfill & \mathrm{if}i=k+1;\hfill \\ -x_{k+4},\hfill & \mathrm{if}i=k+2=l;\hfill \\ x_{k-1}\hfill & \mathrm{if}i=k+3=l+1;\hfill \\ x_i\hfill & \mathrm{if}k+4\le i\le n;\hfill \end{array}\right.$$

also assign to each leaf vertex the negative value of its neighbor. One may check that in both cases, the vector Y satisfies in Equation (1). Therefore, Y is an eigenvector of $L\left(G\right)$ corresponding to the eigenvalue 2 such that $y_i\in \{-1,1\}$ and the proof is complete. □

In what follows, we wish to prove the correspondence of Theorem 3 to any unicyclic graphs containing a perfect match for which the Theorem 3 plays as an induction basis.

Theorem 4.

Let $G=C(T_1,\dots ,T_g)$ be a unicyclic graph containing a perfect matching which has 2 among its Laplacian eigenvalues. It holds that there exists the eigenvector corresponding to the eigenvalue 2 like $X={(x_1,\dots ,x_n)}^t$, such that $x_i\in \{-1,1\}$.

Proof. 

First note that, for broken sun graphs, the proof is clear by Theorem 3. So, let $\left|V\right(T_i\left)\right|\ge 3$, for some i, $1\le i\le g$. We prove the theorem by induction on $n=\left|V\right(G\left)\right|$. Let $d(u,v_i)=ma{x}_{x\in V\left(T_i\right)}d(x,v_i)$, where $v_i$ is the root of $T_i$. Since G has a perfect matching, u is a leaf vertex and its neighbor, say v, has degree 2. Thus $G=(G⧹\{u,v\}){\odot }_{uv}{S}_2$, where $S_2$ is a star on 2 vertices. $G⧹\{u,v\}$ has 2 among its Laplacian eigenvalues because $m_G\left(2\right)=m_{(G⧹\{u,v\left\}\right)}\left(2\right)$, by [15] (Theorem 2.5). So, by the induction hypothesis, $X={(x_1,\dots ,x_{n-2})}^t$ is the eigenvector of $L(G⧹\{u,v\left\}\right)$ corresponding to the eigenvalue 2 such that $x_i\in \{-1,1\}$ for all $i=1,\dots ,n-2$. Let $w\ne u$ be a neighbor of v. $Z={(z_1,\dots ,z_n)}^t={(X,x\left(w\right),-x\left(w\right))}^t$ is an eigenvector of $L\left(G\right)$ corresponding to the eigenvalue 2, where $z_i\in \{-r,r\}$ for all $i=1,\dots ,n$. This is because

$$\begin{array}{cc}\hfill & (d_{G⧹\{u,v\}}\left(w\right)-2)x_{G⧹\{u,v\}}\left(w\right)=\sum _{v_i\in N_{G⧹\{u,v\}}\left(w\right)}x\left(v_i\right)\hfill \\ \hfill & (d_{G⧹\{u,v\}}\left(w\right)-2)x_{G⧹\{u,v\}}\left(w\right)+x\left(w\right)=\sum _{v_i\in N_{G⧹\{u,v\}}\left(w\right)}x\left(v_i\right)+x\left(w\right)\hfill \\ \hfill & (d_G\left(w\right)-2)z_G\left(w\right)=\sum _{v_i\in N_G\left(w\right)}z\left(v_i\right),\hfill \end{array}$$

and for vertex v

$$d_G\left(v\right)=2\Rightarrow \left\{\begin{array}{c}(d_G\left(v\right)-2)z\left(u\right)=0\hfill \\ \sum _{v_j\in N_G\left(v\right)}z\left(v_j\right)=z\left(w\right)+z\left(u\right)=x\left(w\right)-x\left(w\right)=0\hfill \end{array}\right..$$

Additionally, for the vertex u

$$d_G\left(u\right)=1\Rightarrow \left\{\begin{array}{c}(d_G\left(u\right)-2)z\left(u\right)=-z\left(u\right)=x\left(w\right)\hfill \\ \sum _{v_j\in N_G\left(u\right)}z\left(v_j\right)=z\left(v\right)=x\left(w\right)\hfill \end{array}\right..$$

By noting the fact that $d_G\left(p\right)=d_{G⧹\{u,v\}}\left(p\right)$ for the other vertices of G, we have

$$(d_G\left(v\right)-2)z_G\left(v\right)=\sum _{v_j\in N_G\left(v\right)}z\left(v_j\right),\mathrm{for}\mathrm{all}v\in V\left(G\right),$$

and the proof is complete. □

4. The Laplacian Eigenvalue 2 of Bicyclic Graphs

In this section, we study the multiplicity of the Laplacian eigenvalue 2 of a bicyclic graphs G with just two cycles $C_1$ and $C_2$. Let $g_i$ be the girth of $C_i$ ($i=1,2$).

Lemma 2.

Let G be a bicyclic graph and $\lambda >1$ be an integral eigenvalue of $L\left(G\right)$. It holds that $m_G\left(\lambda \right)\le 3$.

Proof. 

On the contrary, if $m_G\left(\lambda \right)\ge 4$, then using Theorem 2, for every unicyclic subgraph $G^{\prime }$ of G we have $m_{G^{\prime }}\left(\lambda \right)\ge 3$. This contradicts [2] (Lemma 4) and the result follows. □

Theorem 5.

Let G be a bicyclic graph of odd order n. It holds that $m_G\left(2\right)\le 2$. In particular, if $g_1$ and $g_2$ are odd, then $m_G\left(2\right)=0$.

Proof. 

On the contrary, suppose that $m_G\left(2\right)\ge 3$. Let $C_1$ and $C_2$ be two cycles of G. Let $G^{\prime }=G-e$, where $e\in E\left(C_1\right)$. Then, $G^{\prime }$ is a unicyclic graph. So $m_{G^{\prime }}\left(2\right)\ge 2$, by Theorem 2. If $m_{G^{\prime }}\left(2\right)>2$, this contradicts [2] (Lamma 4). Thus, $m_{G^{\prime }}\left(2\right)=2$. Let T be a spanning tree of $G^{{}^{\prime }}$. Therefore T has 2 among its Laplacian eigenvalues, by Theorem 2. By applying [15] (Theorem 2.1), we conclude that $2\mid n$ is a contradiction. Therefore, $m_G\left(2\right)\le 2$. Moreover, Theorem 1 implies that ${\xi }_{n-2}={\sum }_{F\in {\mathfrak{F}}_2}\gamma \left(F\right)$. Since n is odd, for each $F\in {\mathfrak{F}}_2$, the value of $\gamma \left(F\right)$ is even. So, ${\xi }_{n-2}$ is an even number. Thus, if G has 2 among its Laplacian eigenvalues, then $4\mid {\xi }_{n-1}=n\tau \left(G\right)=2n{g}_1{g}_2$, and hence, $2\mid n{g}_1{g}_2$. Therefore, $2\mid g_1{g}_2$, a contradiction, and the proof is complete. □

Remark 3.

Let $G=G_1{\odot }_{uv}{G}_2$ be a bicyclic graph such that $G_1$ and $G_2$ contain a perfect matching. It is obvious that G has a perfect matching.

Theorem 6.

Let $G_1=C(T_1,\dots ,T_{g_1})$ and $G_2=C(T_1^{\prime },\dots ,T_{g_2}^{{}^{\prime }})$ be unicyclic graphs containing a perfect matching. Let M be the perfect matching of a one-edge connected graph $G=G_1{\odot }_{uv}{G}_2$ that has 2 as Laplacian eigenvalue. It holds that $G-e$ has 2 among its Laplacian eigenvalues such that $e\in C_{g_1}$ or $e\in C_{g_2}$ and $e\notin M$.

Proof. 

Let $|V\left(G_1\right)|=n_1$ and $|V\left(G_2\right)|=n_2$. Without loss of generality, we can assume that $e\in C_{g_1}$ and ${\lambda }_k\left(G\right)=2$. So, by Theorem 2, we have,

$${\lambda }_{k-1}\left(G\right)\ge {\lambda }_{k-1}(G-e)\ge {\lambda }_k\left(G\right)\ge {\lambda }_k(G-e)⟹2\ge {\lambda }_k(G-e).$$

Now, let $e^{\prime }\in C_{g_2}$. Therefore, by Theorem 2, we have,

$$2\ge {\lambda }_k(G-e)\ge {\lambda }_k(G-e-e^{\prime }).$$

Assume that $n=n_1+n_2=2k^{\prime }$. Since $G-e-e^{\prime }$ has a perfect matching, ${\lambda }_{k^{\prime }}(G-e-e^{\prime })=2$, and hence, $2={\lambda }_{k^{\prime }}(G-e-e^{\prime })\ge {\lambda }_k(G-e-e^{\prime })$ and $k\ge k^{\prime }$ by Theorem 2. If $k=k^{\prime }$, then $2\ge {\lambda }_k(G-e)\ge 2$ so ${\lambda }_k(G-e)=2$ and the proof is complete. On the other hand, if $k>k^{\prime }$, then ${\lambda }_k(G-e-e^{\prime })\ne 2$. So we have,

$$2={\lambda }_{k^{\prime }}(G-e-e^{\prime })\ge {\lambda }_{k^{\prime }+1}(G-e-e^{\prime })\ge {\lambda }_{k-1}(G-e)\ge {\lambda }_k\left(G\right)=2,$$

and therefore, ${\lambda }_{k^{\prime }+1}(G-e-e^{\prime })=2$. This is a contradiction, by [15] (Theorem 2.1) and the result holds. □

As an immediate result we have the following corollary.

Corollary 4.

Let $G_1=C(T_1,\dots ,T_{g_1})$ and $G_2=C(T_1^{\prime },\dots ,T_{g_2}^{{}^{\prime }})$ be unicyclic graphs containing a perfect matching. Let $G=G_1{\odot }_{uv}{G}_2$ and ${\lambda }_k\left(G\right)=2$. Thus ${\lambda }_k\left(G\right)={\lambda }_k(G-e)={\lambda }_k(G-e-e^{\prime })=2$, where $e\in C_{g_1}$ and $e^{\prime }\in C_{g_2}$ and $\{e,e^{\prime }\}\cap M=\varnothing$.

In what follows, we state the condition under which the bicyclic graphs have 2 among their Laplacian eigenvalues.

Theorem 7.

Let $G_1=C(T_1,\dots ,T_{g_1})$ and $G_2=C(T_1^{{}^{\prime }},\dots ,T_{g_2}^{{}^{\prime }})$ be unicyclic graphs containing a perfect matching which have 2 among their Laplacian eigenvalues and $G=G_1{\odot }_{uv}{G}_2$ be a bicyclic graph. Let $s_1$ and $s_2$ be the number of $T_i$ and $T_j^{\prime }$ of odd orders of $G_1$ and $G_2$, respectively. It holds that $s_1\equiv s_2\equiv 0\left(mod4\right)$ if and only if G has 2 among its Laplacian eigenvalues.

Proof. 

Assume X and Y are eigenvectors of $L\left(G_1\right)$ and $L\left(G_2\right)$ corresponding to the eigenvalue 2, respectively. So vectors X and Y satisfy Equation (1). Let u and v be two vertices of $V\left(G_1\right)$ and $V\left(G_2\right)$ with $uv\in E\left(G\right)$. Now let $X^{\prime }=(X,\frac{x\left(u\right)}{y\left(v\right)}Y)$. We show that $X^{\prime }$ satisfies Equation (1) for $\lambda =2$. First, note that $d_G\left(p\right)=d_{G_1}\left(p\right)$ for all $p\in V\left(G_1\right)-\left\{u\right\}$ and $d_G\left(q\right)=d_{G_2}\left(q\right)$ for all $q\in V\left(G_2\right)-\left\{v\right\}$. So Equation (1) holds for all vertices $V\left(G\right)-\{u,v\}$. Also,

$$(d_G\left(u\right)-2)x^{\prime }\left(u\right)=(d_{G_1}\left(u\right)-2)x^{\prime }\left(u\right)+x^{\prime }\left(u\right)$$

$$\begin{array}{cc}\hfill & =(d_{G_1}\left(u\right)-2)x\left(u\right)+x\left(u\right)\hfill \\ \hfill & =\sum _{v_j\in N_{G_1}\left(u\right)}x\left(v_j\right)+x\left(u\right)\hfill \\ \hfill & =\sum _{v_j\in N_{G_1}\left(u\right)}{x}^{\prime }\left(v_j\right)+\frac{x\left(u\right)}{y\left(v\right)}y\left(v\right)\hfill \\ \hfill & =\sum _{v_j\in N_{G_1}\left(u\right)}{x}^{\prime }\left(v_j\right)+x^{\prime }\left(v\right)\hfill \\ \hfill & =\sum _{v_j\in N_G\left(u\right)}{x}^{\prime }\left(v_j\right)\hfill \end{array}$$

and

$$(d_G\left(v\right)-2)x^{\prime }\left(v\right)=(d_{G_2}\left(v\right)-2)x^{\prime }\left(v\right)+x^{\prime }\left(v\right)$$

$$\begin{array}{cc}\hfill & =(d_{G_2}\left(v\right)-2)\frac{x\left(u\right)}{y\left(v\right)}y\left(v\right)+y\left(v\right)\frac{x\left(u\right)}{y\left(v\right)}\hfill \\ \hfill & =\frac{x\left(u\right)}{y\left(v\right)}\sum _{v_j\in N_{G_2}\left(u\right)}y\left(v_j\right)+x\left(u\right)\hfill \\ \hfill & =\sum _{v_j\in N_{G_2}\left(v\right)}(y\left(v_j\right)\frac{x\left(u\right)}{y\left(v\right)})+x^{\prime }\left(u\right)\hfill \\ \hfill & =\sum _{v_j\in N_{G_2}\left(u\right)}{x}^{\prime }\left(v_j\right)+x^{\prime }\left(u\right)\hfill \\ \hfill & =\sum _{v_j\in N_G\left(u\right)}{x}^{\prime }\left(v_j\right).\hfill \end{array}$$

Thus, the proof of the “only if” part of the theorem is complete.

Conversely, assume that G has 2 among its Laplacian eigenvalues. Suppose $e=uv$ is a joining edge of G with $u\in V\left(T_i\right)$ and $v\in V\left(T_j^{\prime }\right)$. The unicyclic graph $G-e_1$ has 2 among its Laplacian eigenvalues, where $e_1\in C_{g_1}$ or $e_1\in C_{g_2}$ and $e_1$ is not in the perfect matching M of G, by Theorem 6. Without loss of generality, let $e_1\in C_{g_1}$. Then $s\equiv 0\left(mod4\right)$, where s is the number of trees of odd orders in $G-e_1=C(T_1^{\prime },\dots ,T_{j-1}^{\prime },T_j^{\prime }\cup \left\{e\right\}\cup \{G_1-e_1\},T_{j+1}^{\prime },\dots ,T_{g_2}^{\prime })$, by [2] (Theorem 9). If $\left|V\right(T_j^{\prime }\left)\right|$ is an even number, then $T_j^{\prime }\cup \left\{e\right\}\cup \{G_1-e_1\}$ is an even number. So the trees of odd orders in $G_2$ are the same as the trees of odd orders in $G-e_1$, and hence, $s_2\equiv 0\left(mod4\right)$. If $\left|V\right(T_j^{\prime }\left)\right|$ is an odd number, then $T_j^{\prime }\cup \left\{e\right\}\cup \{G_1-e_1\}$ is an odd number. So the trees of odd orders in $G_2$ are $T_j^{\prime }$ and all trees of odd orders in $G-e_1$ except $T_j^{\prime }\cup \left\{e\right\}\cup \{G_1-e_1\}$ (see Figure 5). Therefore, $s_2\equiv 0\left(mod4\right)$ and this completes the proof. □

As an immediate result from Theorems 3 and 7, we have the following corollary.

Corollary 5.

Let $G_1$ and $G_2$ be broken sun graphs containing perfect matchings and $G=G_1{\odot }_{uv}{G}_2$ be a bicyclic graph. Then, $n_2\left(G_1\right)\equiv n_2\left(G_2\right)\equiv 0\left(mod4\right)$ if and only if G has 2 among its Laplacian eigenvalues.

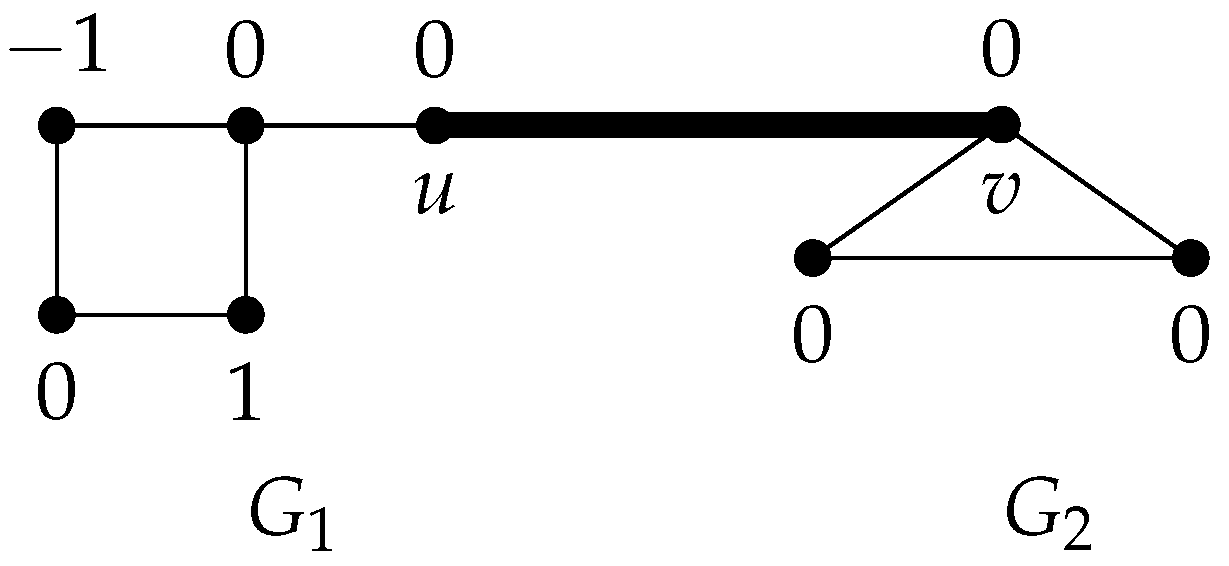
Let $G_1$ and $G_2$ be two unicyclic graphs. Assume $L\left(G_1\right)$ ($L\left(G_2\right)$) has 2 among its eigenvalues and $G=G_1{\odot }_{uv}{G}_2$. Even if $L\left(G\right)$ has 2 as eigenvalue, the same thing does not necessarily happen for $L\left(G_2\right)$ ($L\left(G_1\right)$).

Example 6.

Let $G_1$ and $G_2$ be the unicyclic graphs in Figure 6. Then $G_1$ and G have 2 among their Laplacian eigenvalues, but $G_2$ has not 2 as a Laplacian eigenvalue.

Here we establish some conditions on the degree of vertices of some bicyclic graphs having 2 as Laplacian eigenvalues.

Theorem 8.

Let $G_1$ and $G_2$ be broken sun graphs of orders $n_1$ and $n_2$ with no perfect matching. If $g_1\equiv g_2\equiv 0\left(mod4\right)$ and there are odd numbers of vertices of degree 2 between any pair of consecutive vertices of degree 3, then $G=G_1{\odot }_{uv}{G}_2$ has 2 among its Laplacian eigenvalues.

Proof. 

Assume that $g_1\equiv g_2\equiv 0\left(mod4\right)$ and there are odd numbers of vertices of degree 2 between any pair of consecutive vertices of degree 3 in $G_1$ and $G_2$; therefore, $G_1$ and $G_2$ have 2 among their Laplacian eigenvalues, by [2] (Theorem 10). Let the edge of G joining $G_1$ and $G_2$ be $e=uv$, where $v\in V\left(G_1\right)$ and $u\in V\left(G_2\right)$. We can assign $\{-1,0,1\}$ to the vertices of $C_{g_1}$ and $C_{g_2}$, by the pattern $0,1,0,-1$ consecutively, starting with a vertex of degree 3, and assign to each leaf vertex the negative of value of its neighbor to obtain eigenvectors X and Y of $L\left(G_1\right)$ and $L\left(G_2\right)$ corresponding to the eigenvalues 2, respectively. If u and v are two leaf vertices or two vertices of degree 3 or 1 of them is a leaf vertex and the other is of degree 3, then $Z=(X,Y)$ is an eigenvector of $L\left(G\right)$ corresponding to the eigenvalue 2 (note that Equation (1) is satisfied). If u is a vertex of degree 1 or degree 3 and v is a vertex of degree 2, $Z=(X,\overrightarrow{0})$ is an eigenvector of $L\left(G\right)$ corresponding to the eigenvalue 2 (note that Equation (1) is satisfied). If u and v are two vertices of degree 2, and consequently, if $x\left(u\right)=y\left(v\right)$, then $Z=(X,Y)$. If $x\left(u\right)=0$ and $y\left(v\right)\ne 0$, $Z=(X,\overrightarrow{0})$. If $x\left(u\right)\ne y\left(v\right)$ and both of them are other than 0, $Z=(X,-Y)$. Therefore, Z satisfies Equation (1) for $\lambda =2$ and G has 2 among its Laplacian eigenvalues. Therefore, the result follows. □

Theorem 9.

Let $G_1$ be a broken sun graph of orders $n_1$ with no perfect matching and $G_2$ be a unicyclic graph of order $n_2$ with a perfect matching. If $G_1$ and $G_2$ have 2 among their Laplacian eigenvalues, then $G_1{\odot }_{uv}{G}_2$ has 2 as a Laplacian eigenvalue.

Proof. 

It is proven like Theorem 8, by a similar method. □