Modulation Equation for the Stochastic Swift–Hohenberg Equation with Cubic and Quintic Nonlinearities on the Real Line
Abstract
1. Introduction
2. Space and Mild Solution
3. Derivation of Cubic–Quintic Ginzburg–Landau Equation
4. General Bounds on OU Process
5. Main Results
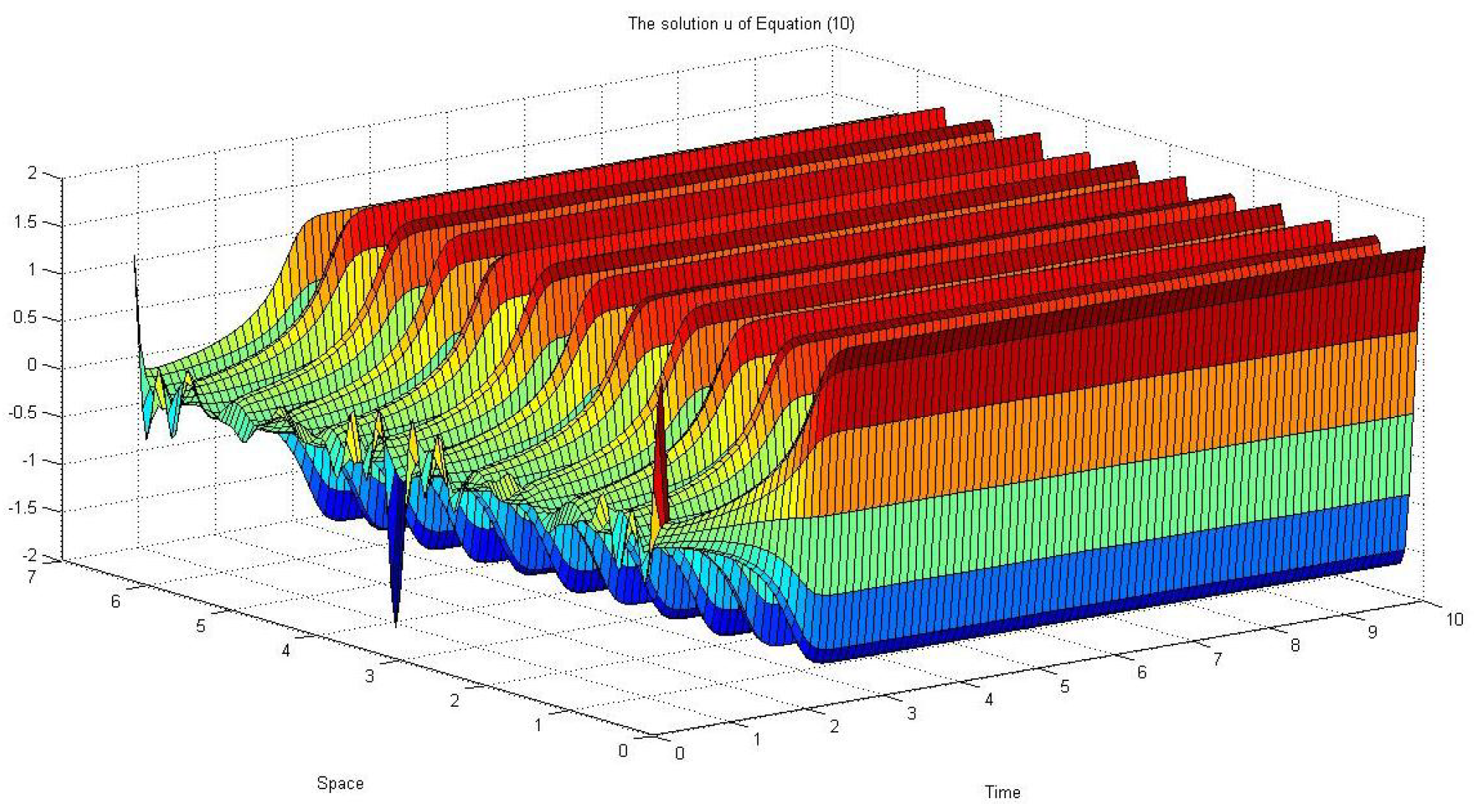
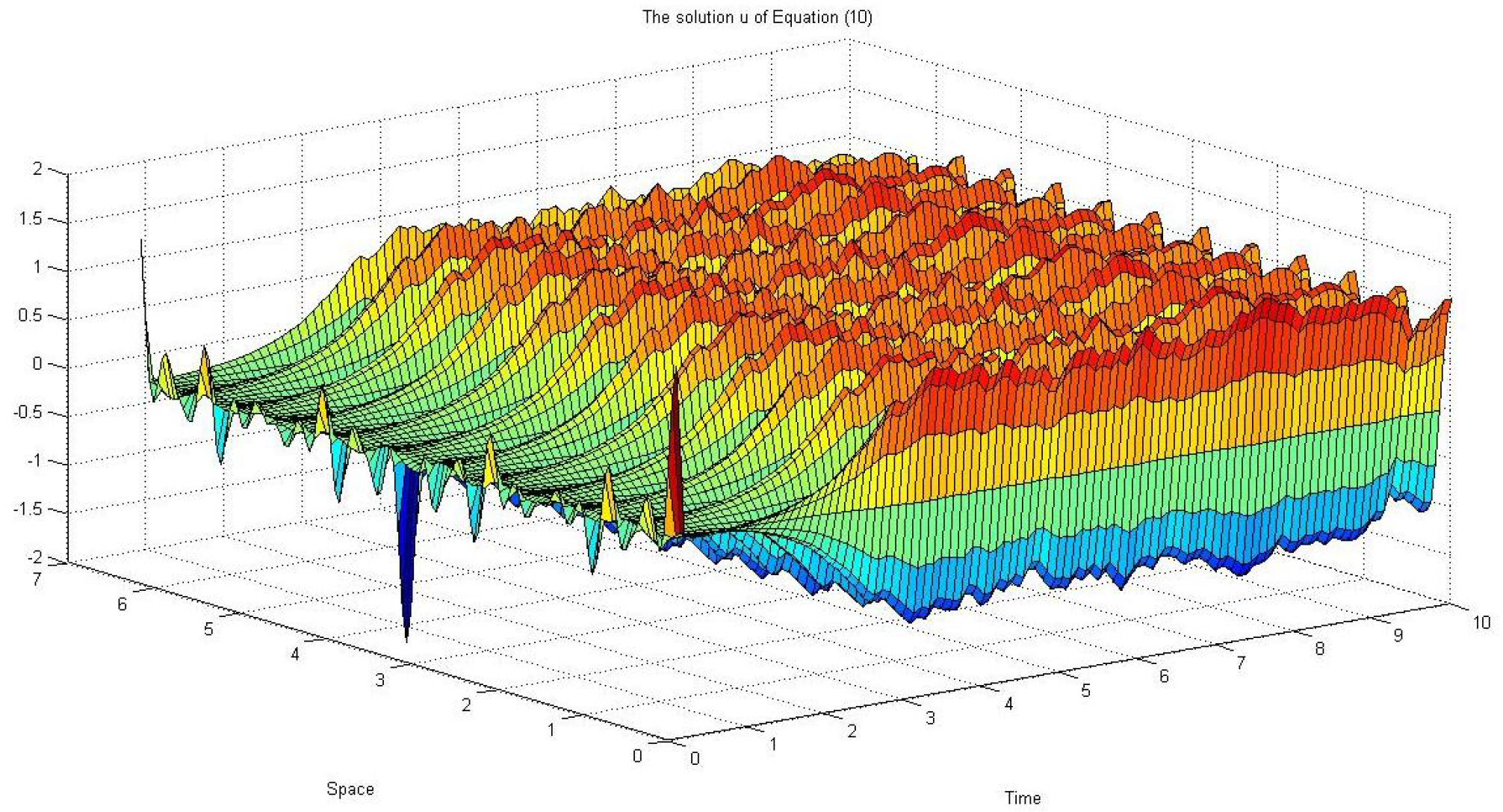
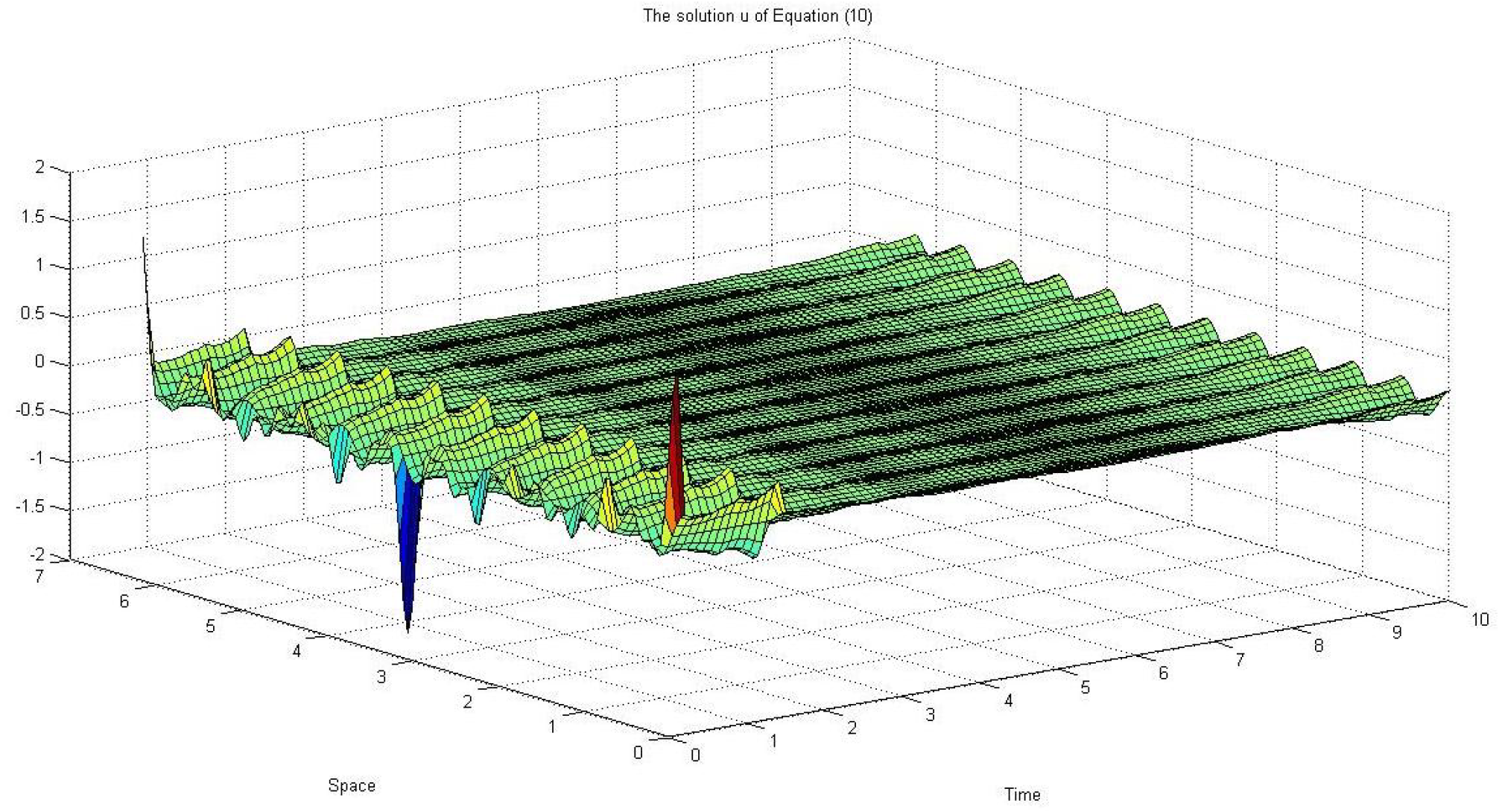
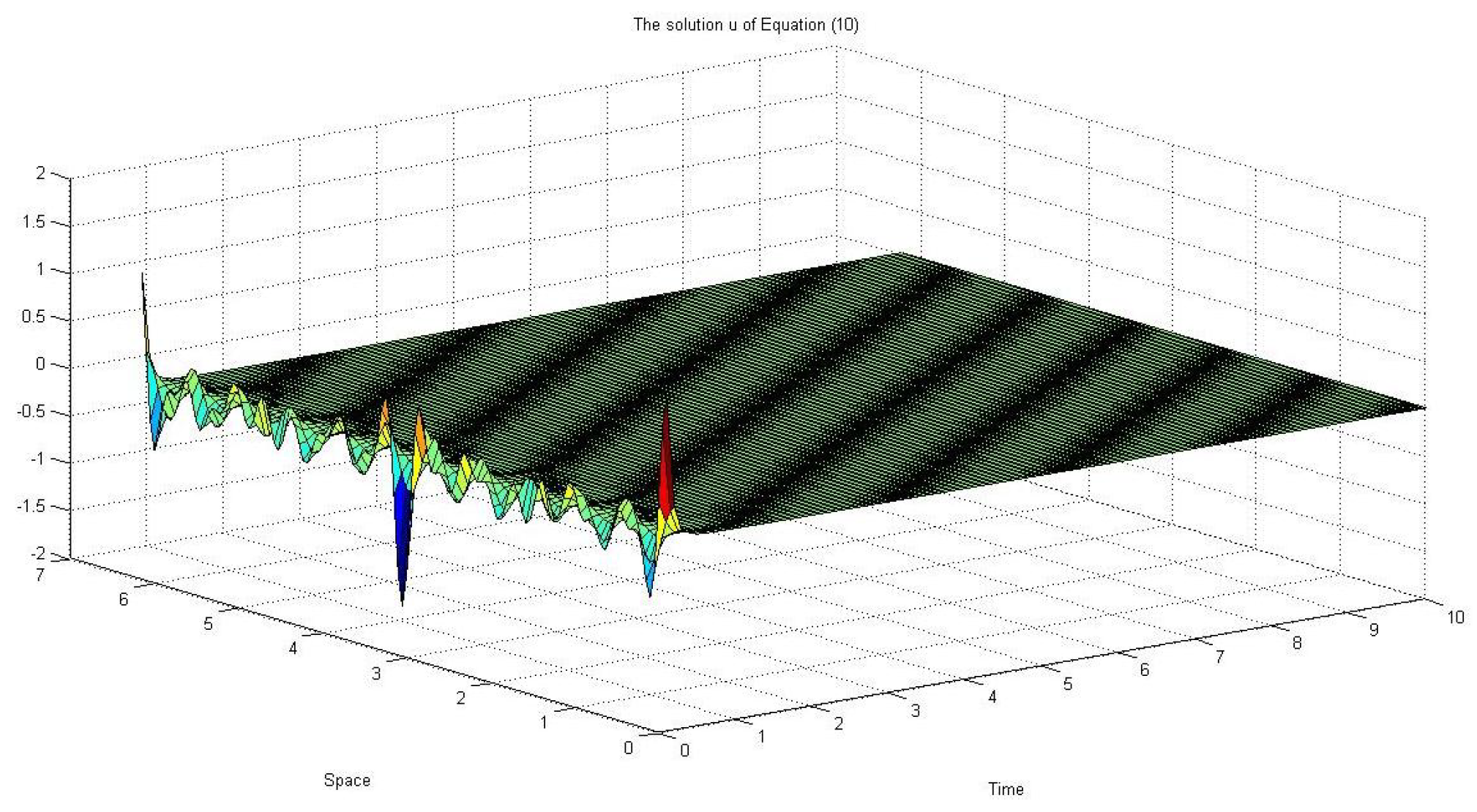
6. The Effect of Degenerate Additive Noise
- The coefficient of the cubic term is positive for and is a non-positive otherwise,
- The coefficient of the linear term is positive for if or if and is a non-positive otherwise.
7. Conclusions
Funding
Acknowledgments
Conflicts of Interest
References
- Swift, J.B.; Hohenberg, P.C. Hydrodynamic fluctuations at the convective instability. Phys. Rev. A 1977, 15, 319–328. [Google Scholar] [CrossRef]
- Cross, M.C.; Hohenberg, P.C. Pattern formation outside of equilibrium. Rev. Mod. Phys. 1993, 65, 536–1112. [Google Scholar] [CrossRef]
- Kirrmann, P.; Schneider, G.; Mielke, A. The validity of modulation equations for extended systems with cubic nonlinearities. Proc. R. Soc. Edinb. Sect. A 1992, 122, 85–91. [Google Scholar] [CrossRef]
- Batiste, O.; Knobloch, E.; Alonso, A.; Mercader, I. Spatially localized binary fluid convection. J. Fluid Mech. 2006, 560, 149–158. [Google Scholar] [CrossRef]
- Lo Jacono, D.; Bergeon, A.; Knobloch, E. Spatially localized binary fluid convection in a porous medium. Phys. Fluids 2010, 22, 073601. [Google Scholar] [CrossRef]
- Mercader, I.; Batiste, O.; Alonso, A.; Knobloch, E. Convectons, anticonvectons and multiconvectons in binary fluid convection. J. Fluid Mech. 2011, 667, 586–606. [Google Scholar] [CrossRef]
- Mercader, I.; Batiste, O.; Alonso, A.; Knobloch, E. Traveling convections in binary fluid convection. J. Fluid Mech. 2013, 722, 240–266. [Google Scholar] [CrossRef]
- Beaume, C.; Bergeon, A.; Knobloch, E. Homoclinic snaking of localized states in doubly diffusive convection. Phys. Fluids 2011, 23, 094102. [Google Scholar] [CrossRef]
- Burke, J.; Knobloch, E. Snakes and ladders: Localized states in the Swift–Hohenberg equation. Phys. Lett. A 2007, 360, 681–688. [Google Scholar] [CrossRef]
- Dawes, J.H. Modulated and localised states in a finite domain. SIAM J. Appl. Dyn. Syst. 2009, 8, 909–930. [Google Scholar] [CrossRef][Green Version]
- Hiraoka, Y.; Ogawa, T. Rigorous numerics for localized patterns to the quintic Swift–Hohenberg equation. Jpn. J. Indust. Appl. Math. 2005, 22, 57–75. [Google Scholar] [CrossRef]
- Sakaguchi, H.; Brand, H.R. Stable localized solutions of arbitrary length for the quintic Swift–Hohenberg equation. Physica D 1996, 97, 274–285. [Google Scholar] [CrossRef]
- Avitabile, D.; Lloyd, D.J.; Burke, J.; Knobloch, E.; Sandstede, B. To snake or not to snake in the planar Swift–Hohenberg equation. SIAM J. Appl. Dyn. Syst. 2010, 9, 704–733. [Google Scholar] [CrossRef]
- Mohammed, W.W.; Blömker, D.; Klepel, K. Modulation equation for stochastic Swift–Hohenberg equation. SIAM J. Math. Anal. 2013, 45, 14–30. [Google Scholar] [CrossRef]
- Blömker, D.; Hairer, M.; Pavliotis, G.A. Modulation equations: Stochastic bifurcation in large domains. Commun. Math. Phys. 2005, 258, 479–512. [Google Scholar] [CrossRef]
- Hutt, A. Additive noise may change the stability of nonlinear systems. Europhys. Lett. 2008, 84, 1–4. [Google Scholar] [CrossRef]
- Hutt, A.; Longtin, A.; Schimansky-Geier, L. Additive global noise delays Turing bifurcations. Phys. Rev. Lett. 2007, 98, 230601. [Google Scholar] [CrossRef] [PubMed]
- Klepel, K.; Blömker, D.; Mohammed, W.W. Amplitude equation for the generalized Swift Hohenberg equation with noise. Zeitschrift für Angewandte Mathematik und Physik ZAMP 2014, 65, 1107–1126. [Google Scholar] [CrossRef][Green Version]
- Adams, R.A. Sobolev Spaces; Academic Press: New York, NY, USA, 1975. [Google Scholar]
- Blömker, D.; Mohammed, W.W. Amplitude equations for SPDEs with cubic nonlinearities. Int. J. Probab. Stoch. Process. 2013, 85, 181–215. [Google Scholar] [CrossRef][Green Version]

© 2019 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammed, W.W. Modulation Equation for the Stochastic Swift–Hohenberg Equation with Cubic and Quintic Nonlinearities on the Real Line. Mathematics 2019, 7, 1217. https://doi.org/10.3390/math7121217
Mohammed WW. Modulation Equation for the Stochastic Swift–Hohenberg Equation with Cubic and Quintic Nonlinearities on the Real Line. Mathematics. 2019; 7(12):1217. https://doi.org/10.3390/math7121217
Chicago/Turabian StyleMohammed, Wael W. 2019. "Modulation Equation for the Stochastic Swift–Hohenberg Equation with Cubic and Quintic Nonlinearities on the Real Line" Mathematics 7, no. 12: 1217. https://doi.org/10.3390/math7121217
APA StyleMohammed, W. W. (2019). Modulation Equation for the Stochastic Swift–Hohenberg Equation with Cubic and Quintic Nonlinearities on the Real Line. Mathematics, 7(12), 1217. https://doi.org/10.3390/math7121217




