The Dirichlet Problem of the Constant Mean Curvature in Equation in Lorentz-Minkowski Space and in Euclidean Space

Abstract

We investigate the differences and similarities of the Dirichlet problem of the mean curvature equation in the Euclidean space and in the Lorentz-Minkowski space. Although the solvability of the Dirichlet problem follows standards techniques of elliptic equations, we focus in showing how the spacelike condition in the Lorentz-Minkowski space allows dropping the hypothesis on the mean convexity, which is required in the Euclidean case.

1. Introduction

In this paper, we investigate the differences and similarities in the study of the solvability of the Dirichlet problem for the constant mean curvature equation in the Euclidean space and in the Lorentz-Minkowski space. Firstly, we introduce the following notation. Let $ϵ\in \{-1,1\}$. Denote by ${\mathbb{R}}_{ϵ}^{n+1}$ the vector space ${\mathbb{R}}^{n+1}$ equipped with the metric

$$\langle ,\rangle ={(d{x}_1)}^2+{(d{x}_2)}^2+\dots +{(d{x}_n)}^2+ϵ{(d{x}_{n+1})}^2,$$

where $(x_1,\dots ,x_{n+1})$ are the canonical coordinates of ${\mathbb{R}}^{n+1}$. If $ϵ=1$ (respectively, $ϵ=-1$), the space is the Euclidean space ${\mathbb{E}}^{n+1}$ (respectively, the Lorentz-Minkowski space ${\mathbb{L}}^{n+1}$). We consider the Dirichlet problem for the constant mean curvature equation in ${\mathbb{R}}_{ϵ}^{n+1}$. Let $\Omega \subset {\mathbb{R}}^n$ be a bounded domain with smooth boundary $\partial \Omega$ and let H be a real number. The Dirichlet problem asks for existence and uniqueness of a function $u\in C^2(\Omega )\cap C^0(\partial \Omega )$ such that

$$\{\begin{array}{}\hfill \mathrm{(1)}& (1+\epsilon {|Du|}^2)\Delta u+\epsilon D_{i}u+D_{j}u{D}_{ij}u=2H{(1+\epsilon {|Du|}^2)}^{3/2}\hfill & \mathrm{in}\Omega \hfill \hfill \mathrm{(2)}& u=1\hfill & \mathrm{on}\partial \Omega \hfill \hfill \mathrm{(3)}& |Du|<1\hfill & \mathrm{in}\Omega . (\mathrm{if} \epsilon =-1)\hfill \end{array}$$

Here, D is the gradient operator, $D_i$ is the derivative with respect to the variable $x_i$, and the summation convention is used. A solution of Equations (1) and (2) describes a hypersurface with constant mean curvature H in ${\mathbb{R}}_{ϵ}^{n+1}$ whose boundary is contained in the hyperplane $x_{n+1}=0$. If $ϵ=-1$, the extra condition $|Du|<1$ in $\Omega$ means that the hypersurface is spacelike. A hypersurface in ${\mathbb{E}}^{n+1}$ (respectively, in ${\mathbb{L}}^{n+1}$) with zero mean curvature ($H=0$) is called a minimal (respectively, maximal) hypersurface.

The example that shows the differences of the theory of constant mean curvature hypersurfaces in both ambient spaces is the Bernstein problem which we now formulate. Suppose that the domain $\Omega$ is ${\mathbb{R}}^n$. A graph on ${\mathbb{R}}^n$ is called an entire graph. Let $H=0$. The Bernstein problem asks if, besides linear functions, there are other entire solutions of Equation (1) with zero mean curvature. In the case $n=2$, Bernstein proved that planes are the only entire minimal surfaces [1]. In arbitrary dimension, this result holds if $n\le 7$. A famous theorem of Bombieri, De Giorgi and Giusti asserts that there are other entire minimal graphs if $n\ge 8$ [2]. In contrast, in n-dimensional Lorentz-Minkowski space, Cheng and Yau proved, extending previous works of Calabi, that spacelike hyperplanes are the only entire maximal hypersurfaces [3].

The interest of the study of constant mean curvature (cmc) hypersurfaces has its origin in physics. In the Euclidean space ${\mathbb{E}}^3$, cmc surfaces are mathematical models of the shape of a liquid in capillarity problems and of a interface that separates two medium of different physical properties. In Lorentz-Minkowski ${\mathbb{L}}^{n+1}$, cmc spacelike hypersurfaces have been used in General Relativity to prove the positive mass theorem or analyze the space of solutions of Einstein equations [4,5].

We review briefly the state of the art of the Dirichlet problem for the constant mean curvature equation in both spaces. Assume that u takes arbitrary continuous boundary values $u=\phi$ on $\partial \Omega$. In the Euclidean space and for the minimal case $H=0$, the Dirichlet problem in Equation (1) was solved for $n=2$ by Finn [6] and in arbitrary dimension by Jenkins and Serrin [7] proving that the mean convexity of the domain $\Omega$ yields a necessary and sufficient condition of the solvability of the Dirichlet problem for all boundary values $\phi$: a domain $\Omega$ is said to be mean convex if the mean curvature ${\kappa }_{\partial \Omega }$ of $\partial \Omega$ with respect to the inner normal is non-negative. If $H\ne 0$, a stronger assumption is needed on $\Omega$ relating H and ${\kappa }_{\partial \Omega }$ and the answer appears in the seminal paper [8], where proved the following result.

Theorem 1.

The Dirichlet problem in Equation (1) in the Euclidean space has a unique solution for any boundary values φ if and only if

$${\kappa }_{\partial \Omega }\ge \frac{n|H|}{n-1}on \partial \Omega .$$

(4)

It is expected that, if we assume $\phi =0$ on $\partial \Omega$, the assumption in Equation (4) may be relaxed. Indeed, if $\phi =0$ and $n=2$, the Dirichlet problem in Equations (1) and (2) has a unique solution if ${\kappa }_{\partial \Omega }\ge |H|$ ([9]): see other results in the Euclidean case. If we drop the convexity assumption of $\partial \Omega$, it is possible to derive existence results if one assumes smallness on the domain $\Omega$ and certain uniform exterior sphere conditions: see [10,11,12].

The theory in ${\mathbb{L}}^{n+1}$ is shorter. The solvability of Equations (1)–(3) with arbitrary boundary values was initially investigated in the maximal case $H=0$ assuming the mean convexity of $\partial \Omega$ [13,14]. However, the groundbreaking result is due to Bartnik and Simon in 1982 where the counterpart to Theorem 2 in ${\mathbb{L}}^{n+1}$ is surprisingly simple because there is not any assumption on $\partial \Omega$ [15].

Theorem 2.

The Dirichlet problem in Equations (1)–(3) in the Lorentz-Minkowski space has a unique solution for any spacelike boundary values φ if and only if φ has a spacelike extension to Ω.

This result was later generalized in other Lorentzian manifolds: [16,17,18,19,20]. The method employed in the proof of Theorems 1 and 2 follows the Leray–Schauder fixed point theorem for elliptic equations because Equation (1) is a quasilinear elliptic differential equation: if $ϵ=-1$, this is assured by the spacelike condition in Equation (3). To apply standard methods in the solvability of the Dirichlet problem, we need to ensure a priori estimates of the height and the gradient for the prospective solutions. Throughout this paper, we refer to the reader to [11] as a general guide.

The purpose of this work is twofold. Firstly, we give an approach to the results in Lorentz-Minkowski space comparing with the ones of Euclidean space and show how the spacelike condition $|Du|<1$ makes completely different the method of obtaining the a priori estimates. The second objective is to provide geometric proofs to derive these estimates. For example, Serrin used the distance function to $\partial \Omega$ as a barrier for the desirable estimates [8], and similarly Flaherty in the solvability in the Lorentzian case when $H=0$ [14]. This distance function is defined in $\Omega$ but loses its geometric sense if we look the graph of u in ${\mathbb{E}}^3$ or ${\mathbb{L}}^3$. In our case, the a priori estimates is obtained by a comparison argument between the solutions of Equation (1) and known cmc surfaces, such as rotational surfaces. To simplify the notation and arguments, we consider the Dirichlet problem for the two-dimensional case, thus we work with surfaces in ${\mathbb{E}}^3$ and spacelike surfaces in ${\mathbb{L}}^3$. In such a case, the mean convexity of the curve $\partial \Omega$ is merely the convexity of $\partial \Omega$.

This paper is organized as follows. After Section 2 devoted to fix some definitions and notations, we derive the constant mean curvature equation in Section 3 obtaining some properties of the solutions showing differences in both ambient spaces. Section 4 describes the method of continuity to solve the Dirichlet problem in Equation (1). In Section 5, we obtain the height estimates for solutions of Equation (1) and we prove that the boundary gradient estimates imply global (interior) gradient estimates. In Section 6, we analyze the solvability of the Dirichlet problem in the Euclidean case showing that a strong convexity hypothesis is necessary to solve the problem. Finally, in Section 7, we solve the Dirichlet problem in Lorentz-Minkowski space for arbitrary domains and we show the role of the cmc rotational surfaces in the solvability of the problem.

2. Preliminaries

We need to recall some definitions in Lorentz-Minkowski space. In ${\mathbb{L}}^3$, the metric $\langle ,\rangle$ is non-degenerate of index 1 and classifies the vectors of ${\mathbb{R}}^3$ in three types: a vector $v\in {\mathbb{L}}^3$ is said to be spacelike (respectively, timelike and lightlike) if $\langle v,v\rangle >0$ or $v=0$ (respectively, $\langle v,v\rangle <0$, $\langle v,v\rangle =0$, and $v\ne 0$). The modulus of v is $|v|=\sqrt{|\langle v,v\rangle |}$. A vector subspace $U\subset {\mathbb{R}}^3$ is called spacelike (respectively, timelike and lightlike) if the induced metric on U is positive definite (respectively, non-degenerate of index 1, degenerate, and $U\ne \left\{0\right\}$). Any vector subspace belongs to one of the above three types. For two-dimensional subspaces, U is spacelike (respectively, timelike and lightlike) if its orthogonal subspace $U^{\perp }$ is timelike (respectively, spacelike and lightlike). A curve or a surface immersed in ${\mathbb{L}}^3$ is said to be spacelike if the induced metric is positive-definite.

The spacelike property is a strong condition. For example, any spacelike surface M is orientable. This is due because a unit vector orthogonal to M is timelike and in ${\mathbb{L}}^3$, the scalar product of any two timelike vectors is not zero. Thus, if we fix $e_3=(0,0,1)$, which is a timelike vector, it is possible to define a unit orthogonal vector field N on M so $\langle N,e_3\rangle$ is negative (or positive) on M, determining a global orientation. Another consequence is that there do not exist closed spacelike surfaces in ${\mathbb{L}}^3$; in particular, any compact spacelike surface has non-empty boundary. Similarly, if a plane contains a closed spacelike curve, the plane must be spacelike.

Let M be an orientable surface immersed in ${\mathbb{R}}_{ϵ}^3$. In case $ϵ=-1$, we also assume that the immersion is spacelike. Let ${\nabla }^0$ and ∇ be the Levi–Civita connections in ${\mathbb{R}}_{ϵ}^3$ and M, respectively. The Gauss formula is ${\nabla }_X^{0}Y={\nabla }_{X}Y+ϵ\sigma (X,Y)$ for any two tangent vector fields X and Y on M, where $\sigma$ is the second fundamental form. The mean curvature H of M is defined as

$$H=\frac{1}{2}\mathrm{trace}(\sigma ).$$

(5)

Let us choose N a unit normal vector field on M with $\langle N,N\rangle =ϵ$. Let $A={\nabla }_N^0$ stand for the Weingarten endomorphism with respect to N. Then, the Gauss formula is ${\nabla }_X^{0}Y={\nabla }_{X}Y+ϵ\langle A(X),Y\rangle N$ and A is a diagonalizable map. If ${\kappa }_1$ and ${\kappa }_2$ are the principal curvatures, we have

$$H=ϵ\frac{1}{2}\mathrm{trace}(A)=ϵ\frac{1}{2}({\kappa }_1+{\kappa }_2).$$

Remark 1.

In case of timelike surfaces of ${\mathbb{L}}^3$, the mean curvature is defined as in Equation (5). However, although A is self-adjoint with respect to the induced metric $\langle ,\rangle$, this metric is Lorentzian and it may occur that A is not real diagonalizable.

Example 1.

1. 

Planes of ${\mathbb{E}}^3$ and spacelike planes of ${\mathbb{L}}^3$ have zero mean curvature.

2. 

Round spheres ${\mathbb{S}}^2(r)$ in ${\mathbb{E}}^3$ and hyperbolic planes ${\mathbb{H}}^2(r)$ in ${\mathbb{L}}^3$ of radius $r>0$ can be described up to a rigid motion as

$$\{p\in {\mathbb{L}}^3:\langle p,p\rangle =ϵr^2\}.$$

If $ϵ=-1$, we also assume $\langle p,e_3\rangle <0$, where $e_3=(0,0,1)$. With respect to the Gauss map $N(p)=p/r$, the mean curvature is $H=-ϵ/r$.

3. 

Right circular cylinders of ${\mathbb{R}}_{ϵ}^3$ have constant mean curvature. To be precise, let $a\in {\mathbb{R}}_{ϵ}^3$ be a unit vector with $\langle a,a\rangle =1$ (in ${\mathbb{L}}^3$, the vector a is spacelike). Up to a rigid motion, the circular cylinder of axis a and radius $r>0$ is

$$C(r)=\{p\in {\mathbb{R}}_{ϵ}^3:\langle p,p\rangle -{\langle p,a\rangle }^2=ϵr^2\}.$$

For the orientation $N(p)=(p-\langle p,a\rangle a)/r$, the mean curvature is $H=-ϵ/(2r)$.

4. 

Let $u=u(x_1,x_2)$ be a smooth function defined in an open domain $\Omega \subset {\mathbb{R}}^2$ and let M be the graph of u. Suppose that M is endowed with the induced metric from ${\mathbb{R}}_{ϵ}^3$. If $ϵ=-1$, we also assume that M is spacelike, that is, $|Du|<1$ in Ω. The mean curvature H of M satisfies

$$(1+ϵ{(D_{2}u)}^2)D_{11}u-2ϵD_{1}u{D}_{2}u{D}_{12}u+(1+ϵ{(D_{1}u)}^2)D_{22}u={2H(1+ϵ|Du|}^2{)}^{3/2}$$

(6)

with respect to the orientation

$$N=\frac{(-ϵD_{1}u,-ϵD_{2}u,1)}{\sqrt{1+{ϵ|Du|}^2}}=\frac{(-ϵDu,1)}{\sqrt{1+{ϵ|Du|}^2}}·$$

(7)

Let us notice that Equation (6) coincides with Equation (1).

3. The Constant Mean Curvature in Equation

In this section we derives some properties on the solutions of the cmc in Equation (1). The mean curvature in Equation (1) (or Equation (6)) can be expressed in the divergence form

$$\mathrm{div}\left({\displaystyle \frac{Du}{\sqrt{1+{ϵ|Du|}^2}}}\right)=2H\mathrm{in} \Omega ,$$

(8)

with the observation that, if $ϵ=-1$, we assume the spacelike condition $|Du|<1$ in $\Omega$. For instance, spheres and hyperbolic planes of Example 1 are graphs of the functions

$$u(x_1,x_2)=-ϵ\sqrt{r^2-ϵ(x_1^2+x_2^2)},\left\{\begin{array}{cc}{x}_1^2+x_2^2<r^2\hfill & ϵ=1\hfill \\ (x_1,x_2)\in {\mathbb{R}}^2\hfill & ϵ=-1.\hfill \end{array}\right.$$

For $ϵ=1$, $x_3=u(x_1,x_2)$ is defined in a disc and describes a hemisphere in ${\mathbb{S}}^2(r)$, and, for $ϵ=-1$, $x_3=u(x_1,x_2)$ is the hyperbolic plane ${\mathbb{H}}^2(r)$. On the other hand, a cylinder $C(r)$ with axis $a=(0,1,0)$ and radius $r>0$ is the graph of the function

$$u(x_1,x_2)=-ϵ\sqrt{r^2-ϵx_1^2},\left\{\begin{array}{cc}|x_1|<r\hfill & ϵ=1\hfill \\ (x_1,x_2)\in {\mathbb{R}}^2\hfill & ϵ=-1.\hfill \end{array}\right.$$

Equation (8) (with Equation (3) if $ϵ=-1$) is of quasilinear elliptic type, hence we can apply the machinery for these equations. It is easily seen that the difference of two solutions of Equation (1) satisfies the maximum principle. Consequently, we give a statement of the comparison principle in our context. We define the operator

$$Q\left[u\right]={(1+ϵ|Du|}^2)\Delta u-ϵD_{i}u{D}_{j}u{D}_{ij}{u-2H(1+ϵ|Du|}^2{)}^{3/2}.$$

(9)

The comparison principle asserts ([11], Th. 10.1).

Proposition 1

(Comparison principle). If $u,v\in C^2(\overline{\Omega })$ satisfy $Q\left[u\right]\ge Q\left[v\right]$ in Ω and $u\le v$ on $\partial \Omega$, then $u\le v$ in Ω. If we replace $Q\left[u\right]\ge Q\left[v\right]$ by $Q\left[u\right]>Q\left[v\right]$, then $u<v$ in Ω. In particular, the solution of the Dirichlet problem, if it exists, is unique.

An immediate consequence is the touching principle.

Proposition 2

(Touching principle). Let $M_1$ and $M_2$ be two surfaces in ${\mathbb{R}}_{ϵ}^3$ with the same constant mean curvature and with possibly non-empty boundaries $\partial M_1$, $\partial M_2$. If $M_1$ and $M_2$ have a common tangent interior point and $M_1$ lies above $M_2$ around p, then $M_1$ and $M_2$ coincide at an open set around p. The same statement is also valid if p is a common boundary point and the tangent lines to $\partial M_i$ coincide at p.

A first difference of the Dirichlet problem for the constant mean curvature in Equation (1) is that in the Euclidean space ${\mathbb{E}}^3$ the value H is not arbitrary and depends on the size of $\Omega$, whereas in ${\mathbb{L}}^3$ the value H may be arbitrary. Indeed, from Equation (8), the divergence theorem yields

$$2|H|\mathrm{area}(\Omega )=\left|{\int }_{\partial \Omega }\langle \frac{Du}{\sqrt{1+{ϵ|Du|}^2}},\overrightarrow{n}\rangle \right|,$$

where $\overrightarrow{n}$ is the outward unit normal vector along $\partial \Omega$. The idea is to estimate the right-hand side from above. If $ϵ=1$, we have

$$2|H|\mathrm{area}(\Omega )=\left|{\int }_{\partial \Omega }\langle \frac{Du}{\sqrt{1+{|Du|}^2}},\overrightarrow{n}\rangle \right|\le {\int }_{\partial \Omega }\frac{|Du|}{\sqrt{1+{|Du|}^2}}<{\int }_{\partial \Omega }1=\mathrm{length}(\partial \Omega ),$$

Proposition 3.

A necessary condition for the solvability of the Dirichlet problem in Equation (1) in ${\mathbb{E}}^3$ is

$$|H|<\frac{length(\partial \Omega )}{2area(\Omega )}·$$

(10)

Let us notice that this upper bound for H does not depend on the boundary values $\phi$. In fact, there are explicit examples where all values between 0 and the upper bound in Equation (10) are attained. Indeed, let $\Omega$ be a disc of radius $\rho$ and $\phi =0$. Then, the value of $\mathrm{length}(\partial \Omega )/(2\mathrm{area}(\Omega ))$ is $1/\rho$. On the other hand, for each $0<H<1/\rho$, take the spherical cap of radius $1/|H|$

$$u(x_1,x_2)=-\sqrt{\frac{1}{H^2}-x_1^2-x_2^2},x_1^2+x_2^2<{\rho }^2.$$

Then, u is a graph on $\Omega$ with constant mean curvature H for every H going from 0 until $1/\rho$. The limit case $H=1/\rho$ corresponds with a hemisphere of radius $1/|H|$.

The same computations in ${\mathbb{L}}^3$ do not provide the same conclusion because $|Du|/\sqrt{1-{|Du|}^2}$ may be arbitrarily large. Thus, for the hyperbolic planes

$$u(x_1,x_2)=\sqrt{\frac{1}{H^2}+x_1^2+x_2^2},$$

(11)

the value

$$\frac{|Du|}{\sqrt{1-{|Du|}^2}}=|H|\sqrt{x_1^2+x_2^2}$$

is arbitrary large and the function u is defined in any domain of the plane ${\mathbb{R}}^2$ and for any H.

A second difference is the question of the existence of entire solutions of Equation (1) with non-zero mean curvature H: recall that the case $H=0$ (Bernstein problem) is discussed in the Introduction. In ${\mathbb{L}}^3$, the hyperbolic planes in Equation (11) show that, for any H, there are solutions of Equation (1) defined in the plane ${\mathbb{R}}^2$. In addition, the cylinders $u(x_1,x_2)=\sqrt{1/H^2+x_1^2}$ are other examples of entire solutions of Equations (1)–(3). However in the Euclidean space, we have

Proposition 4.

Let Ω be a domain of ${\mathbb{R}}^2$. If u is a solution of Equation (1) with $H\ne 0$ in ${\mathbb{E}}^3$, then Ω does not contain the closure of a disk of radius $1/|H|$.

Proof. 

We proceed by contradiction. Assume that D is an open disk of radius $1/|H|$ such that $\overline{D}\subset \Omega$. Let x be the center of D. Without loss of generality, we suppose that the sign of H is positive: recall that the mean curvature is computed with respect to the orientation in Equation (7). Let $r=1/H$ and ${\mathbb{S}}^2(r)$ be a sphere of radius r whose center lies on the straight-line through x and perpendicular to the $(x_1,x_2)$-plane. Here, and in what follows, ${\mathbb{S}}^2(r)$ denotes a sphere of radius r whose center may be changing. We orient ${\mathbb{S}}^2(r)$ by the inward orientation. With this choice of orientation, the mean curvature is H and the orthogonal projection of ${\mathbb{S}}^2(r)$ on ${\mathbb{R}}^2$ is $\overline{D}$.

Let M be the graph of u. Lift ${\mathbb{S}}^2(r)$ vertically upwards until ${\mathbb{S}}^2(r)$ is completely above M. Then, let us descend ${\mathbb{S}}^2(r)$ until the first point p of contact with M. Since $\overline{D}\subset \Omega$ and M is a graph on $\Omega$, the contact point p must be interior in both surfaces. By the touching principle, the surfaces M and ${\mathbb{S}}^2(r)$ agree on an open set around p, hence M is included in a sphere of radius $1/H$: this is a contradiction because the orthogonal projection onto ${\mathbb{R}}^2$ would give $\Omega \subset \overline{D}$.  □

4. The Solvability Techniques of the Dirichlet Problem

In this section, we present the method for solving the Dirichlet problem in Equations (1) and (2), which holds in the Euclidean and Lorentzian contexts. We establish the solvability of the Dirichlet problem by applying the method of continuity ([11] Sec. 17.2). The matrix of the coefficients of second order of Equation (1) is

$$\left(\begin{array}{cc}1+ϵ{(D_{2}u)}^2\hfill & -ϵD_{1}u{D}_{2}u\hfill \\ -ϵD_{1}u{D}_{2}u\hfill & 1+ϵ{(D_{1}u)}^2\hfill \end{array}\right).$$

The minimum and maximum eigenvalues of this matrix are $\lambda =1$ and $\Lambda =1+{|Du|}^2$ if $ϵ=1$ and $\lambda =1-{|Du|}^2$ and $\Lambda =1$ if $ϵ=-1$. Thus, if $ϵ=-1$, Equation (1) is uniformly elliptic provided $|Du|<1$ uniformly in $\Omega$.

For $t\in [0,1]$, define the family of Dirichlet problems

$$\left\{\begin{array}{cc}{Q}_t\left[u\right]=0\hfill & \mathrm{in} \Omega \hfill \\ u=0\hfill & \mathrm{on} \partial \Omega ,\hfill \\ |Du|<1\hfill & \mathrm{on} \Omega (\mathrm{if} ϵ= -1)\hfill \end{array}\right.$$

where

$$Q_t\left[u\right]={(1+ϵ|Du|}^2)\Delta u-ϵD_{i}u{D}_{j}u{D}_{ij}{u-2tH(1+ϵ|Du|}^2{)}^{3/2}.$$

A solution u of $Q_t\left[u\right]=0$ describe a surface with constant mean curvature $tH$. As usual, let

$$\mathcal{A}=\{t\in [0,1]:\mathrm{there} \mathrm{exists}{u}_t\in C^{2,\alpha }(\overline{\Omega }),Q_t\left[u_t\right]=0,{u_t}_{|\partial \Omega }=0\}.$$

The existence of solutions of the Dirichlet problem in Equations (1)–(3) is established if $1\in \mathcal{A}$. For this purpose, we prove that $\mathcal{A}$ is a non-empty open and closed subset of $[0,1]$. We analyze these three issues.

• The set $\mathcal{A}$ is not empty. This is because $u=0$ solves the Dirichlet problem for $t=0$.
• The set $\mathcal{A}$ is open in $[0,1]$. Given $t_0\in \mathcal{A}$, we need to prove that there exists $\eta >0$ such that $(t_0-\eta ,t_0+\eta )\cap [0,1]\subset \mathcal{A}$. Define the map $T(t,u)=Q_t\left[u\right]$ for $t\in \mathbb{R}$ and $u\in C^{2,\alpha }(\overline{\Omega })$. Then, $t_0\in \mathcal{A}$ if and only if $T(t_0,u_{t_0})=0$. If we show that the derivative of $Q_t$ with respect to u, say ${(D{Q}_t)}_u$, at the point $u_{t_0}$ is an isomorphism, the Implicit Function Theorem ensures the existence of an open set $\mathcal{V}\subset C^{2,\alpha }(\overline{\Omega })$, with $u_{t_0}\in \mathcal{V}$ and a $C^1$ function $\psi :(t_0-\eta ,t_0+\eta )\to \mathcal{V}$ for some $\eta >0$, such that $\psi (t_0)=u_{t_0}>0$ and $T(t,\psi (t))=0$ for all $t\in (t_0-\eta ,t_0+\eta )$: this guarantees that $\mathcal{A}$ is an open set of $[0,1]$.
  The map ${(D{Q}_t)}_u$ is one-to-one if, for any $f\in C^{\alpha }(\overline{\Omega })$, there is a unique solution $v\in C^{2,\alpha }(\overline{\Omega })$ of the linear equation $L\left[v\right]:={(D{Q}_t)}_u(v)=f$ in $\Omega$ and $v=0$ on $\partial \Omega$. The computation of L is done in Theorem 6, obtaining

  $$L\left[v\right]={(D{Q}_t)}_{u}v=a_{ij}{D}_{ij}v+b_i{D}_{i}v,$$

  where $a_{ij}=a_{ij}(Du)$ is symmetric, $b_i=b_i(Du,D^{2}u)$, and L is a linear elliptic operator whose term for the function v is zero. Therefore, the existence and uniqueness is assured by standard theory ([11], Th. 6.14).
• The set $\mathcal{A}$ is closed in $[0,1]$. Let $\left\{t_k\right\}\subset \mathcal{A}$ with $t_k\to t\in [0,1]$. For each $k\in \mathbb{N}$, there is $u_k\in C^{2,\alpha }(\overline{\Omega })$ such that $Q_{t_k}\left[u_k\right]=0$ in $\Omega$ and $u_k=0$ in $\partial \Omega$. Define the set

  $$\mathcal{S}=\{u\in C^{2,\alpha }(\overline{\Omega }):\mathrm{there} \mathrm{exists}t\in [0,1]\mathrm{such} \mathrm{that}{Q}_t\left[u\right]=0 \mathrm{in} \Omega ,u_{|\partial \Omega }=0\}.$$
  Then, $\left\{u_k\right\}\subset \mathcal{S}$. If we see that the set $\mathcal{S}$ is bounded in $C^{1,\beta }(\overline{\Omega })$ for some $\beta \in [0,\alpha ]$, and since $a_{ij}=a_{ij}(Du)$ in Equation (9), the Schauder theory proves that $\mathcal{S}$ is bounded in $C^{2,\beta }(\overline{\Omega })$, in particular, $\mathcal{S}$ is precompact in $C^2(\overline{\Omega })$ (Th. 6.6 and Lem. 6.36 in [11]). Hence, there is a subsequence $\left\{u_{k_l}\right\}\subset \left\{u_k\right\}$ converging to some $u\in C^2(\overline{\Omega })$ in $C^2(\overline{\Omega })$. Since $T:[0,1]\times C^2(\overline{\Omega })\to C^0(\overline{\Omega })$ is continuous, we obtain $Q_t\left[u\right]=T(t,u)={lim}_{l\to \infty }T(t_{k_l},u_{k_l})=0$ in $\Omega$. Moreover, $u_{|\partial \Omega }={lim}_{l\to \infty }{u_{k_l}}_{|\partial \Omega }=0$ on $\partial \Omega$, so $u\in C^{2,\alpha }(\overline{\Omega })$ and, consequently, $t\in \mathcal{A}$. The set $\mathcal{S}$ is bounded in $C^{1,\beta }(\overline{\Omega })$ if it is bounded in $C^1(\Omega )$, where the norm is defined by

  $${\parallel u_t\parallel }_{C^1(\Omega )}=\underset{\Omega }{sup}|u_t|+\underset{\Omega }{sup}|D{u}_t|.$$
  Usually, the a priori estimates for $|u|$ are called height estimates and gradient estimates for $|Du|$.
  Definitively, $\mathcal{A}$ is closed in $[0,1]$ provided we find two constants M and C independent on $t\in \mathcal{A}$, such that

  $$\underset{\Omega }{sup}|u_t|<M,\underset{\Omega }{sup}|D{u}_t|<C.$$

  (12)
  Here, we make the observation that whereas in the Euclidean space, the constant C can take an arbitrary value, the spacelike condition in the Lorentz-Minkowski space implies that C may be chosen to be $C=1$. However, during the above process of the method of continuity, we require that $Q_t$ is uniformly elliptic; in particular, we have to ensure that $|Du|<<1$ in $\Omega$. Definitively, in ${\mathbb{L}}^3$, the constant C in Equation (12) has to satisfy the condition $C<1$.

Remark 2.

In the Euclidean case, the smoothness of the solution on $\partial \Omega$ is guaranteed if the graph close to the boundary point does not blow-up at infinity, that is, $|Du|\cancel{\to }\infty$. In the Lorentzian case, we have to prevent the possibility that $|Du|\to 1$ as we go to $\partial \Omega$. The existence of the constant C shows that the surface cannot “go null” in the terminology of Marsden and Tipler [5], (p. 124).

5. Height and Gradient Estimates

Consider the Dirichlet problem for the cmc equation and arbitrary boundary values

$$\left\{\begin{array}{cc}\mathrm{div}\left({\displaystyle \frac{Du}{\sqrt{1+{ϵ|Du|}^2}}}\right)=2H\hfill & \mathrm{in} \Omega \hfill \\ u=\phi \hfill & \mathrm{on} \partial \Omega ,\hfill \end{array}\right.$$

(13)

where, in addition, if $ϵ=-1$, we suppose $|Du|<1$ in $\Omega$. In this section, we investigate the problem of finding estimates of $|u|$ and $|Du|$ for a solution u of Equation (13) in terms of the initial conditions. In Theorems 3–5, we derive the estimates for $|u|$. For the gradient estimates, we prove that the supremum of $|Du|$ in $\Omega$ is attained at some boundary point (Theorem 6).

We begin with the height estimates. The main difference between both ambient spaces is that in ${\mathbb{E}}^3$ there exist estimates of ${sup}_{\Omega }|u|$ depending only on H and $\phi$, whereas in ${\mathbb{L}}^3$ the size of the domain $\Omega$ appears in these estimates, such as shown in the hyperbolic planes in Equation (11).

The height estimates for cmc graphs in the Euclidean space are obtained with the functions

$$f(p)=\langle p,a\rangle ,g(p)=\langle N(p),a\rangle ,p\in M,$$

where a is a fixed unit vector of ${\mathbb{R}}^3$ and N is the Gauss map of M. Firstly, we need to compute the Beltrami–Laplacian ${\Delta }_M$ of the functions f and g. The following result holds for cmc surfaces in ${\mathbb{E}}^3$ and in ${\mathbb{L}}^3$ without necessarily being graphs: we refer the reader to [21] for a proof.

Lemma 1.

Let M be an immersed surface in ${\mathbb{R}}_{ϵ}^3$. Then,

$${\Delta }_M\langle p,a\rangle =2H\langle N,a\rangle .$$

(14)

If, in addition, the immersion has constant mean curvature, then

$${\Delta }_M\langle N,a\rangle +ϵ{|\sigma |}^2\langle N,a\rangle =0,$$

(15)

where $|\sigma |$ is the norm of the second fundamental form.

Consider u to be a solution of Equation (13) and let $M=\mathrm{graph}(u)$. If we take $a=e_3=(0,0,1)$, the functions $\langle p,e_3\rangle$ and $\langle N,e_3\rangle$ inform about u and $Du$ because

$$\langle p,e_3\rangle =ϵu,\langle N,e_3\rangle =\frac{ϵ}{\sqrt{1+{ϵ|Du|}^2}}.$$

(16)

In particular, $\mathrm{sign}(g)=\mathrm{sign}(ϵ)$. Suppose $H\ge 0$. Then, ${\Delta }_{M}f\ge 0$ (respectively, $\le 0$) in ${\mathbb{E}}^3$ (respectively, ${\mathbb{L}}^3$) and the maximum principle implies $\langle p,e_3\rangle \le {max}_{\partial \Omega }\langle p,e_3\rangle$ in ${\mathbb{E}}^3$ (respectively, $\langle p,e_3\rangle \ge {min}_{\partial \Omega }\langle p,e_3\rangle$ in ${\mathbb{L}}^3$). Thus, $u\le {max}_{\partial \Omega }u$ in both ambient spaces. On the other hand,

$${\Delta }_M(Hf+ϵg)=(2H^2-{|\sigma |}^2)g\left\{\begin{array}{cc}\le 0\hfill & ϵ=1\hfill \\ \ge 0\hfill & ϵ=-1.\hfill \end{array}\right.$$

Since ${|\sigma |}^2={\kappa }_1^2+{\kappa }_2^2\ge 2H^2$, the maximum principle yields

$$Hf+ϵg\left\{\begin{array}{cc}\ge \underset{\partial \Omega }{min}Hf+g\hfill & ϵ=1\hfill \\ \le \underset{\partial \Omega }{max}Hf-g\hfill & ϵ=-1.\hfill \end{array}\right.$$

In case $ϵ=1$, we have

$$Hu+\langle N,e_3\rangle \ge H\underset{\partial \Omega }{min}u+\underset{\partial \Omega }{min}\langle N,e_3\rangle \ge H\underset{\partial \Omega }{min}u$$

because $\langle N,e_3\rangle \ge 0$. Since $\langle N,e_3\rangle \le 1$, we deduce $u\ge -1/H+{min}_{\partial \Omega }\phi$.

Theorem 3.

A solution u of Equation (13) in the Euclidean space satisfies

$$\underset{\partial \Omega }{min}\phi -\frac{1}{H}\le u\le \underset{\partial \Omega }{max}\phi ,if H>0$$

$$\underset{\partial \Omega }{min}\phi \le u\le \underset{\partial \Omega }{max}\phi -\frac{1}{H},if H<0.$$

We analyze the same argument in ${\mathbb{L}}^3$. The reverse Cauchy–Schwarz inequality for timelike vectors yields $\langle N,e_3\rangle \le -1$ [22]. Then, the same computation gives

$$-Hu+\langle N,e_3\rangle \le H\underset{\partial \Omega }{max}(-u)+\underset{\partial \Omega }{max}\langle N,e_3\rangle \le -H\underset{\partial \Omega }{min}u-1,$$

but it is not possible to bound from below because of the function $\langle N,e_3\rangle$. This makes a key difference with the Euclidean case and concludes that the argument done in the Euclidean space is not valid in ${\mathbb{L}}^3$. If $H=0$, from Equation (14), we deduce:

Corollary 1.

In both ambient spaces, if u is a solution of Equation (13) for $H=0$, then

$$\underset{\partial \Omega }{min}\phi \le u\le \underset{\partial \Omega }{max}\phi .$$

As expected, in the Lorentz-Minkowski space there does not exist height estimates depending only on H and $\phi$. An example is the following. For $r>0$ and $m>r$, let $u^m(x_1,x_2)=\sqrt{r^2+x_1^2+x_2^2}-m$ be defined in the round disc ${\Omega }_{\sqrt{m^2-r^2}}=\{(x_1,x_2)\in {\mathbb{R}}^2:x_1^2+x_2^2<m^2-r^2\}$. The graph of $u^m$ is a piece of the hyperbolic plane ${\mathbb{H}}^2(r)$ which has been displaced vertically downwards a distance equal to m. Then, $u^m$ is a solution of Equation (13) in ${\Omega }_{\sqrt{m^2-r^2}}$ with $\phi =0$ and the height on $u^m$, namely $|u^m|=m-r$, goes to ∞ as $m\nearrow \infty$.

Motivated by these examples, we deduce height estimates for a solution of Equation (13) in terms of the size of $\Omega$ (see [23] for a height estimate in terms of the area of the surface). The estimates that we deduce are of two types: the first ones are given in terms of the diameter of $\Omega$ and the second ones depend on the width of narrowest strip containing $\Omega$.

Theorem 4.

If u is a solution of Equation (13) in ${\mathbb{L}}^3$, then

$$\underset{\partial \Omega }{min}\phi -\frac{1}{|H|}\left(\sqrt{1+\frac{diam{(\Omega )}^2{H}^2}{4}}-1\right)\le u\le \underset{\partial \Omega }{max}\phi +\frac{1}{|H|}\left(\sqrt{1+\frac{diam{(\Omega )}^2{H}^2}{4}}-1\right)$$

(17)

and equality holds if and only if the graph of u describes a hyperbolic cap. In the particular case $\phi =0$, we have

$$\underset{\Omega }{sup}|u|\le \frac{1}{|H|}\left(\sqrt{1+\frac{diam{(\Omega )}^2{H}^2}{4}}-1\right).$$

Proof. 

The inequalities are obtained by comparing $M=\mathrm{graph}(u)$ with hyperbolic caps with mean curvature $|H|$ coming from below and from above. There is no loss of generality in assuming that $\Omega$ is included in the closed disk $D_{\rho }$ of center the origin and radius $\rho =\mathrm{diam}(\Omega )/2$. Consider the hyperbolic plane ${\mathbb{H}}^2(r)$ defined by the function $u(x_1,x_2)=\sqrt{r^2+x_1^2+x_2^2}$, where $r=1/|H|$.

Let us take ${\mathbb{H}}^2(r;s)$ the compact part obtained when we intersect ${\mathbb{H}}^2(r)$ with the horizontal plane of equation $x_3=s$. Then, $\partial {\mathbb{H}}^2(r;s)$ is a circle of radius $\rho$, with $s=\sqrt{{\rho }^2+r^2}$ and

$${\mathbb{H}}^2(r;s)=\{(x_1,x_2,x_3)\in {\mathbb{H}}^2(r):x_3\le s\}.$$

Move vertically down ${\mathbb{H}}^2(r;s)$ until it is disjoint from M. Next, move upwards ${\mathbb{H}}^2(r;s)$ until that ${\mathbb{H}}^2(r;s)$ touches M the first time. If the contact between both surfaces occurs at some common interior point, the comparison principle and then the touching principle implies that u describes part of the hyperbolic plane ${\mathbb{H}}^2(r;s)$. In such a case, the left inequality of Equation (17) holds trivially.

In the case that the first contact occurs between a point of ${\mathbb{H}}^2(r;s)$ with a boundary point of M, we can arrive until the value $s={min}_{\partial \Omega }\phi$, hence

$$\underset{\partial \Omega }{min}\phi -\sqrt{r^2+{\rho }^2}+\sqrt{r^2+x_1^2+x_2^2}\le u\mathrm{in} \Omega .$$

Evaluating at the origin,

$$\underset{\partial \Omega }{min}\phi -\frac{1}{|H|}-\sqrt{\frac{1}{H^2}+{\rho }^2}\le u\mathrm{in} \Omega ,$$

which coincides with the left inequality in Equation (17) because $\rho =diam(\Omega )/2$.

The right hand inequality in Equation (17) is proved with a similar argument by taking the hyperbolic planes $u(x_1,x_2)=-\sqrt{r^2+x_1^2+x_2^2}$. □

A second height estimate can be deduced by comparing u with spacelike cylinders. We need to introduce the following notation. Given a bounded domain $A\subset {\mathbb{R}}^2$, consider the set $\mathcal{L}$ of all pairs of parallel straight-lines $(L_1,L_2)$ in ${\mathbb{R}}^2$ such that A is included in the planar strip determined by $L_1$ and $L_2$. Set

$$\Theta (A)=min\{\mathrm{dist}(L_1,L_2):(L_1,L_2)\in \mathcal{L}\}.$$

Observe that the domain A is included in a strip of width $\Theta (\Omega )$ and this strip is the narrowest one among all strips containing A in its interior. Notice also that $\Theta (A)\le \delta (A)$.

Theorem 5.

If u is a solution of Equation (13) in ${\mathbb{L}}^3$, then

$$\underset{\partial \Omega }{min}\phi -\frac{1}{2|H|}\left(\sqrt{1+\Theta {(\Omega )}^2{H}^2}-1\right)\le u\le \underset{\partial \Omega }{max}\phi +\frac{1}{2|H|}\left(\sqrt{1+\Theta {(\Omega )}^2{H}^2}-1\right).$$

(18)

In the particular case $\phi =0$, we have

$$\underset{\Omega }{sup}|u|\le \frac{1}{2|H|}\left(\sqrt{1+\Theta {(\Omega )}^2{H}^2}-1\right).$$

Notice that the estimates Equations (17) and (18) are not comparable.

Proof. 

The argument is similar to the proof of Theorem 4 by replacing the role of the hyperbolic planes by cylinders. After a rigid motion if necessary, assume that $\Omega$ is included in the strip $|x_1|<\Theta (\Omega )/2$. Consider the cylinder $C(r)$

$$u(x_1,x_2)=\sqrt{r^2+x_1^2},$$

where $r=1/(2|H|)$. Consider the value s such that the intersection of $C(r)$ with the plane of equation $x_3=s$ is formed by two parallel straight-lines separated a distance equal to $\Theta (\Omega )$: this occurs when the value s is

$$s=\sqrt{r^2+\frac{\Theta {(\Omega )}^2}{4}}.$$

Denote by $C(r;s)$ the part of $C(r)$ below the plane of equation $x_3=s$, which is a graph on a strip of width $\Theta (\Omega )$. Let us move down the cylinders $C(r;s)$ until that do not intersect $M=\mathrm{graph}(u)$. After, we move upwards $C(r;s)$ until the first touching point with M. If this point is a common interior point, then M is included in the cylinder $C(r)$ and the left inequality in Equation (18) is trivially satisfied. If the point is not interior, we can arrive until the height $x_3=s$ where $s={min}_{\partial \Omega }\phi$. Then,

$$\underset{\partial \Omega }{min}\phi -\sqrt{r^2+\frac{\Theta {(\Omega )}^2}{4}}+\sqrt{r^2+x_1^2}\le u\mathrm{in} \Omega .$$

At the points $x_1=0$, we deduce

$$\underset{\partial \Omega }{min}\phi +r-\sqrt{r^2+\frac{\Theta {(\Omega )}^2}{4}}\le u\mathrm{in} \Omega .$$

This inequality is just the left inequality in Equation (18). The right inequality in Equation (18) is proved by comparing with the cylinders $u(x_1,x_2)=-\sqrt{r^2+x_1^2}$. □

We finish this section investigating how to derive the a priori estimates Equation (12) of $|Du|$ in $\Omega$. Recall that we have to find a constant C depending only on the initial data such that $|Du|\le C$ in $\Omega$, with the observation that if $ϵ=-1$, we require that $C<1$. We prove that it suffices to find this estimate only in boundary points. We present two proofs of this result which hold in both ambient spaces.

Theorem 6.

If u is a solution of Equation (13), then

$$\underset{\Omega }{sup}|Du|=\underset{\partial \Omega }{max}|Du|.$$

(19)

Proof 1.

For each $i=1,2$, define the functions $v^i=D_{i}u$. Differentiate Equation (9) with respect to the variable $x_k$, $k\in \{1,2\}$. After some computations, we obtain

$$\left({(1+ϵ|Du|}^2){\delta }_{ij}-ϵD_{i}u{D}_{j}u\right)D_{ij}{v}^k+2\left(ϵD_i{u\Delta u+3H(1-|Du|}^2)D_{i}u-ϵD_{j}u{D}_{ij}u\right)D_i{v}^k=0.$$

(20)

Hence, $v^k$ satisfies a linear elliptic equation of type

$$a_{ij}{D}_{ij}{v}^k+b_i{D}_i{v}^k=0,$$

where $a_{ij}=a_{ij}(Du)$ and $b_i=b_i(Du,D^{2}u)$. By the maximum principle, $|v^k|$ does not have a maximum at some interior point. Consequently, the maximum of $|Du|$ on the compact set $\overline{\Omega }$ is attained at some boundary point. □

Proof 2.

Estimates of $|Du|$ are obtained by means of the function $\langle N,e_3\rangle$ because Equation (16). From Equation (15).

$${\Delta }_M\langle N,e_3\rangle =-ϵ{|\sigma |}^2\langle N,e_3\rangle =\frac{{|\sigma |}^2}{\sqrt{1+{ϵ|Du|}^2}}\le 0,$$

and the maximum principle implies

$$\underset{\Omega }{inf}\langle N,e_3\rangle =\underset{\partial \Omega }{min}\langle N,e_3\rangle .$$

Thus,

$$\underset{\Omega }{inf}\frac{ϵ}{\sqrt{1+{ϵ|Du|}^2}}=\underset{\partial \Omega }{min}\frac{ϵ}{\sqrt{1+{ϵ|Du|}^2}},$$

which is equivalent to Equation (19). □

To summarize, the problem of finding gradient estimates of $|Du|$ in $\Omega$ is passing to a problem of estimates along the boundary, exactly, finding a constant C depending only on the initial data such that

$$\underset{\partial \Omega }{max}|Du|<C.$$

(21)

In the proofs of the existence results in the following sections, the method to obtain the constant C in Equation (21) is by an argument of super- and subsolutions and then we apply the next result.

Lemma 2.

Let $x_0\in \partial \Omega$ be a boundary point. Suppose that there is a neighborhood $\mathcal{U}$ of $x_0$ and two functions $w^{+},w^{-}\in C^2(\overline{\Omega \cap \mathcal{U}})$ such that

$$\begin{array}{cc}Q\left[w^{+}\right]\le 0\le Q\left[w^{-}\right]\hfill & in \Omega \cap U\hfill \\ w^{-}\le u\le w^{+}\hfill & in \partial (\Omega \cap U)\hfill \\ w^{-}(x_0)=u(x_0)=w^{+}(x_0)\hfill \\ |D{w}^{-}|,|D{w}^{+}|\le C.\hfill \end{array}$$

Then, $|Du|\le C$.

Proof. 

The comparison principle yields $w^{-}\le u\le w^{+}$ in $\Omega \cap U$, concluding that $|Du|\le \{|D{w}^{-}|,|D{w}^{+}|\}$. □

6. The Dirichlet Problem with Zero Boundary Values: The Euclidean Case

In this section, we address the Dirichlet problem in Equation (1) in the Euclidean space. By Theorem 3, we know that the value H is not arbitrary. Without assuming convexity on $\partial \Omega$, there are results of existence assuming some smallness on the value H and on the size of $\Omega$ [10,11]. Thanks to this smallness on initial data, it is possible to obtain height and boundary gradient estimate of the solution. If we assume convexity, there are different hypothesis that ensure the solvability of the Dirichlet problem and relate the size or the convexity of $\Omega$ with the value H [9,12,24,25,26,27,28].

Theorem 1 solves the Dirichlet problem in the Euclidean space for arbitrary boundary values. If we now suppose that $u=0$ on $\partial \Omega$, the hypothesis in Equation (4) can be weakened assuming ${\kappa }_{\partial \Omega }\ge |H|$. We give two proofs of this result. The first one is proved in arbitrary dimension and, although the idea appears generalized in other ambient spaces [29,30,31,32], as far as we know, in the literature, there is not specifically a statement in the Euclidean space. Here, we follow [32].

Theorem 7.

Let $H\ne 0$. If the mean curvature of $\partial \Omega$ satisfies ${\kappa }_{\partial \Omega }>|H|$, then the Dirichlet problem

$$\left\{\begin{array}{cc}div\left({\displaystyle \frac{Du}{\sqrt{1+{|Du|}^2}}}\right)=nH\hfill & in \Omega \hfill \\ u=0\hfill & on \partial \Omega \hfill \end{array}\right.$$

(22)

in arbitrary dimension has a unique solution.

Proof. 

Firstly, we observe that the solutions $u_t$ of the method of continuity (Section 4) are ordered in decreasing sense according the parameter t. Indeed, if $t_1<t_2$, then $Q_{t_1}\left[u_{t_1}\right]=0$ and

$$Q_{t_1}\left[u_{t_2}\right]=(t_2-t_1)(1+|D{u}_{t_2}{|}^2)>0=Q_{t_1}\left[u_{t_1}\right].$$

Since $u_{t_1}=0=u_{t_2}$ on $\partial \Omega$, the comparison principle yields $u_{t_2}<u_{t_1}$ in $\Omega$. Thus, $u_1\le u_t<0$ for all t, where for the value $t=1$, $u_1$ is the solution u of Equation (1). By using Lemma 2, this implies that it suffices to find a priori height and gradient estimates for the prospective solution u of Equation (1).

If u is a solution of Equation (22), then $-u$ is a solution of Equation (22) for the value $-H$. Thus, without loss of generality, we suppose $H>0$. Let M be the graph of u. By the height estimates of Theorem 3, we know $-1/H<u<0$ in $\Omega$. This gives the a priori height estimates. According to Theorem 6, we need to find a priori boundary gradient estimates. However, we can find the gradient estimates on the domain $\Omega$.

We use again the function $Hf+g$ as in Theorem 3. Since ${\Delta }_M(Hf+g)\le 0$ and $u=0$ on $\partial \Omega$, the maximum principle ensures the existence of a boundary point $q\in \partial \Omega$ where $Hf+g$ attains its minimum, thus

$$H\langle p,e_3\rangle +\langle N,e_3\rangle \ge \underset{\partial \Omega }{min}\langle N,e_3\rangle =\langle N(q),e_3\rangle .$$

(23)

Furthermore, the maximum principle on the boundary implies

$$H\langle \nu (q),e_3\rangle +\langle d{N}_q\nu ,e_3\rangle \ge 0,$$

where $\nu$ is the inward unit conormal vector along $\partial \Omega$. If $\sigma$ is the second fundamental form, this inequality can be written as

$$\left(H-\sigma (\nu (q),\nu (q))\right)\langle \nu (q),e_3\rangle \ge 0.$$

Since $u<0$ in $\Omega$, the boundary condition $u=0$ on $\partial \Omega$ yields $\langle \nu (q),e_3\rangle <0$, hence $H-\sigma (\nu (q),\nu (q))\le 0$. If $\{v_1,\dots ,v_{n-1}\}$ is a orthonormal basis of the tangent space to $\partial \Omega$ at the point q, the above inequality implies

$$\sum _{i=1}^{n-1}\sigma (v_i,v_i)=nH-\sigma (\nu (q),\nu (q))\le (n-1)H.$$

(24)

Denote by ${\nabla }^{\partial \Omega }$ and ${\sigma }^{\partial \Omega }$ the Levi–Civita connection and second fundamental form of $\partial \Omega$ as submanifold of $\Omega$, respectively. Let $\eta$ be the unit normal vector field of $\partial \Omega$ in $\Omega$. The Gauss formula gives

$${\nabla }_{v_i}^0{v}_i={\nabla }_{v_i}{v}_i+\sigma (v_i,v_i)N(q)={\nabla }_{v_i}^{\partial \Omega }{v}_i-{\sigma }^{\partial \Omega }(v_i,v_i)\eta (q)+\sigma (v_i,v_i)N(q).$$

Then, $\sigma (v_i,v_i)={\sigma }^{\partial \Omega }(v_i,v_i)\langle N(q),\eta (q)\rangle$. From Equation (24),

$$\langle N(q),\eta (q)\rangle \sum _{i=1}^{n-1}{\sigma }^{\partial \Omega }(v_i,v_i)\le (n-1)H.$$

Since ${\sum }_{i=1}^{n-1}{\sigma }^{\partial \Omega }(v_i,v_i)=(n-1){\kappa }_{\partial \Omega }$, we have

$$\langle N(q),\eta (q)\rangle {\kappa }_{\partial \Omega }(q)\le H,$$

thus

$${\langle N(q),\eta (q)\rangle }^2{\kappa }_{\partial \Omega }{(q)}^2\le H^2.$$

Since ${\langle N(q),e_3\rangle }^2+{\langle N(q),\eta (q)\rangle }^2=1$, we deduce

$$\langle N(q),e_3\rangle \ge \sqrt{1-\frac{H^2}{{\kappa }_{\partial \Omega }^2(q)}}=\frac{\sqrt{{\kappa }_{\partial \Omega }^2(q)-H^2}}{{\kappa }_{\partial \Omega }(q)}:=C.$$

From Equation (23) and because $H\langle p,e_3\rangle \le 0$ in M, we find

$$\langle N,e_3\rangle \ge C\mathrm{in} \Omega .$$

Finally, we conclude from Equation (16)

$$|Du|\le \frac{\sqrt{1-C^2}}{C}\mathrm{in} \Omega$$

obtaining the desired gradient estimates in $\Omega$. □

The second proof is done in the two-dimensional case, where the mean convexity is now the convexity in the Euclidean plane. The proof uses spherical caps to find the boundary gradient estimates in Equation (21).

Theorem 8.

Let $H\ne 0$. If the curvature of $\partial \Omega$ satisfies ${\kappa }_{\partial \Omega }\ge |H|$, then the Dirichlet problem in Equation (22) has a unique solution.

Proof. 

We start as in the proof of Theorem 7 and we follow the same notation. We only need to find the a priori boundary gradient estimates. Set

$${\kappa }_0=\underset{q\in \partial \Omega }{min}{\kappa }_{\partial \Omega }(q)>0$$

and $r=1/{\kappa }_0$.

Firstly, we prove Theorem 4 in the case of strict inequality ${\kappa }_{\partial \Omega }>H$. Let $x\in \partial \Omega$ be a fixed but arbitrary boundary point. Consider $D_r$ a disc of radius r such that $x\in C_r\cap \partial \Omega$ and $\Omega \subset D_r$ where $C_r$ is the boundary of $D_r$. This is possible because ${\kappa }_0>H$. Consider $C_{1/H}$ a circle of radius $1/H$ and concentric to $C_r$. Notice that $r<1/H$. After a translation we suppose that the center of $D_r$ is the origin of coordinates.

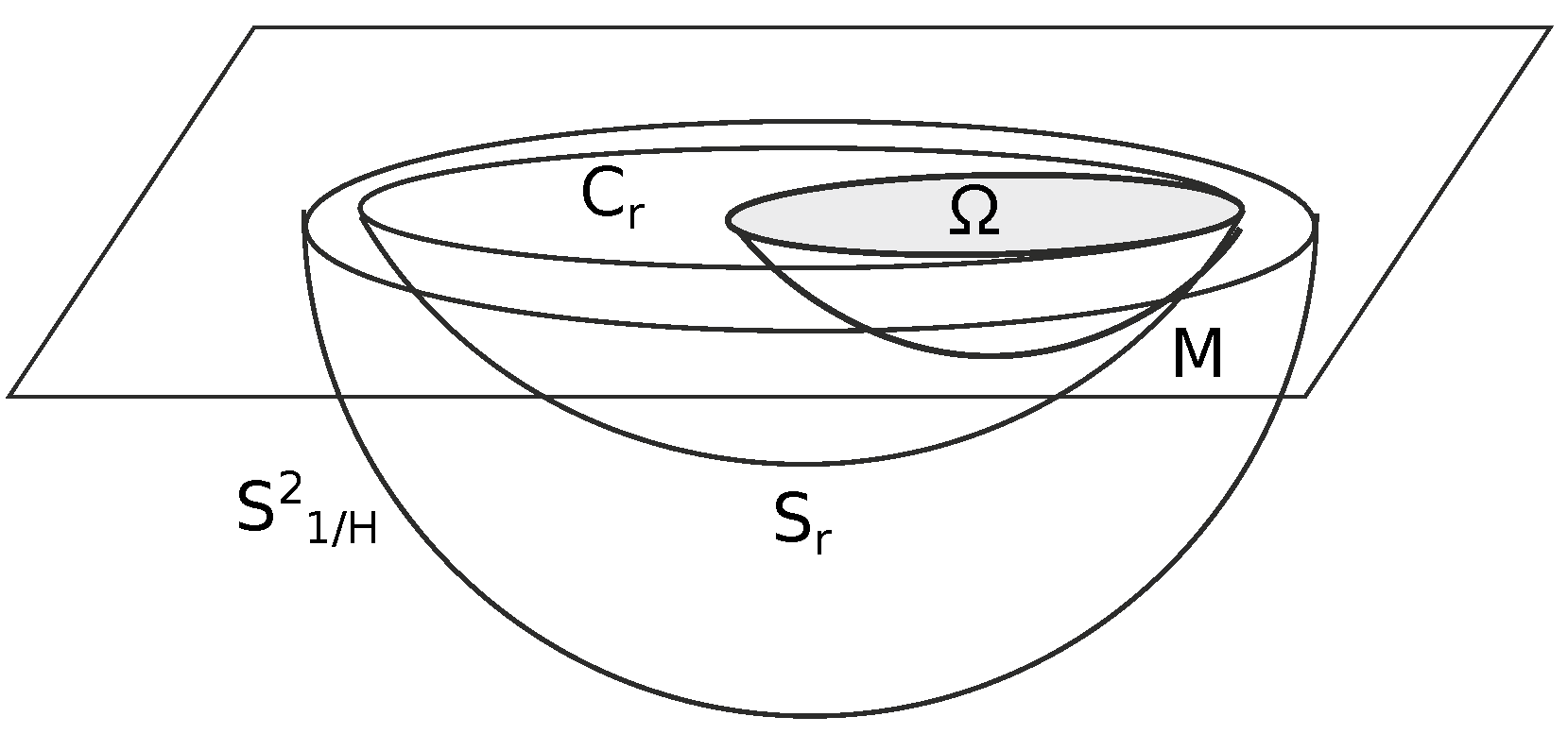
Let ${\mathbb{S}}^2(1/H)$ be the hemisphere of radius $1/H$ whose boundary is $C_{1/H}$ and below the plane $\Pi$ of equation $x_3=0$. Let us lift up ${\mathbb{S}}^2(1/H)$ until its intersection with $\Pi$ is $C_r$. Denote by $S_r$ the piece of ${\mathbb{S}}^2(1/H)$ below $\Pi$ at this position. See Figure 1. The surface $S_r$ is a small spherical cap which is the graph of

$$w^{-}(x_1,x_2)=-\sqrt{\frac{1}{H^2}-x_1^2-x_2^2},x_1^2+x_2^2\le r^2.$$

We prove now that M lies in the bounded domain determined by $S_r\cup D_r$. For this, we move down $S_r$ by vertical translations until $S_r$ does not intersect M and then, move upwards $S_r$ until the initial position. Since the mean curvature of $S_r$ is H and $\Omega \subset D_r$, the touching principle implies that there is not a contact before that $S_r$ arrives to its original position. Once we have arrived to the original position, in a neighborhood of the point x, the surface M lies sandwiched between $S_r$ and $\Pi$. Then,

$$Q\left[w^{+}\right]=-2H<0=Q\left[w^{-}\right]=Q\left[u\right]$$

and consequently by Lemma 2

$$\underset{\partial \Omega }{max}|Du|<\underset{\partial S_r}{max}\{|D{w}^{-}|,|D{w}^{+}|\}=\underset{\partial S_r}{max}|D{w}^{-}|=\frac{Hr}{\sqrt{1-H^2{r}^2}},$$

where this constant depends only on r and H.

Until here, we have obtained the existence of a solution for each $0<H<{\kappa }_0$. Moreover, since the gradient is bounded from above in $\overline{\Omega }$ depending only on the initial data, the solution obtained is smooth in $\overline{\Omega }$. Now, we proceed by proving the existence of a solution of Equation (1) in the case $H={\kappa }_0$: in case that $\Omega$ is a round disk of radius r (and ${\kappa }_0=1/r$), the solution is $u(x_1,x_2)=r-\sqrt{r^2-x_1^2-x_2^2}$.

Let us consider an increasing sequence $H_n\to H$ and $u_n$ the solution of (1) for the value $H_n$ for the mean curvature: the solution exists because ${\kappa }_0>H_n$. By the monotonicity of $H_n$ and the comparison principle, the sequence $\left\{u_n\right\}$ is monotonically increasing and converges uniformly on compact sets of $\Omega$. Let $u=lim{u}_n$. Standard compactness results involving Ascoli–Arzelá theorem guarantee that $u\in C^2(\Omega )$ and $Q\left[u\right]=0$. It remains to check that $u\in C^0(\overline{\Omega })$ and $u=0$ on $\partial \Omega$. Let $x\in \partial \Omega$ and $\left\{x_m\right\}\subset \Omega$ with $x_m\to x$. Consider the hemisphere ${\mathbb{S}}^2(r)$ as above and let $D_r$ be the open disk of radius $r=1/H$ such that ${\mathbb{S}}^2(r)=\mathrm{graph}(v)$, with $v\in C^{\infty }(D_r)\cap C^0(\overline{D_r})$. Place $D_r$ such that $x\in \partial D_r$. We know that $\overline{\Omega }\subset D_r$ and, by the touching principle, $0<u_n<v$ on $\Omega$. For each $n\in \mathbb{N}$, $0<u_n(x_m)<v(x_m)$. Then, $0\le u(x_m)\le v(x_m)$. Letting $m\to \infty$, $0\le u(x)\le 0$. This proves the continuity of u up to $\partial \Omega$ and that $u=0$ on $\partial \Omega$. □

7. The Dirichlet Problem with Zero Boundary Values: The Lorentzian Case

In this section, we address the Dirichlet problem in ${\mathbb{L}}^3$ following the ideas of the Euclidean case in the above section. The first result that we present is motivated by Theorem 8, where we assume a strong convexity of $\partial \Omega$ comparing with the value H, namely, ${\kappa }_{\partial \Omega }\ge |H|$. In contrast, in Lorenz–Minkowski space, this convexity assumption changes by merely the convexity ${\kappa }_{\partial \Omega }\ge 0$ of $\partial \Omega$.

Theorem 9.

If ${\kappa }_{\partial \Omega }\ge 0$, then the Dirichlet problem

$$\left\{\begin{array}{cc}div\left({\displaystyle \frac{Du}{\sqrt{1-{|Du|}^2}}}\right)=2H\hfill & in \Omega \hfill \\ u=0\hfill & on \partial \Omega \hfill \end{array}\right.$$

(25)

has a unique solution.

Proof. 

With a similar argument as in Theorem 8, the solutions $u_t$ of the method of continuity are ordered by $u_{t_1}<u_{t_2}$ if $t_2<t_1$, thus it suffices to get the a priori estimates for the solution u of Equation (25). Without loss of generality, we suppose $H>0$. The height estimates are proved in Theorem 4 (or Theorem 5) and we show that there exists $K=K(\Omega ,H)>0$ such that

$$-K<u<0\mathrm{in} \Omega .$$

(26)

To find the a priori boundary gradient estimates, consider the cylinder $C(r)$ determined by $v(x_1,x_2)=\sqrt{r^2+x_1^2}$, where $r=1/(2H)$. For each $m>r$, let

$$C(r;m)=\{(x_1,x_2,x_3)\in C_r:x_3\le m\}.$$

This surface is a graph on the strip ${\Omega }_{r,m}=\{(x_1,x_2)\in {\mathbb{R}}^2:-\sqrt{m^2-r^2}\le x_1\le \sqrt{m^2-r^2}\}$. Take m sufficiently large so m fulfills the next two conditions:

$$v(x_1=\sqrt{m^2-r^2})-v(x_1=0)=m-r>K$$

(27)

$$\mathrm{diam}(\Omega )<\mathrm{width}({\Omega }_{r,m})=2\sqrt{m^2-r^2}.$$

(28)

Let us restrict v in the half-strip

$$\mathcal{U}=\{(x_1,x_2)\in {\Omega }_{r,m}:0<x_1<\sqrt{m^2-r^2}\}$$

and $\tilde{C}(r;m)$ denotes the graph of v on $\mathcal{U}$. The boundary of $\tilde{C}(r;m)$ is formed by two parallel straight-lines

$$L_1\cup L_2=\left\{v(x_1=0)\right\}\cup \{v(x_1=\sqrt{m^2-r^2}\},$$

where $L_1$ is contained in the plane $x_3=r$ and $L_2$ in the plane $x_3=m$, with $r<m$.

Let $x_0\in \partial \Omega$ be a fixed but arbitrary point of the boundary of $\Omega$. After a rotation about a vertical axis and a horizontal translation, we suppose $x_0=(\sqrt{m^2-r^2},0)$, $\Omega$ is contained in $\mathcal{U}$ (this is possible by Equation (28)) and the tangent line L to $\partial \Omega$ at $x_0$ is parallel to the $x_2$-line. By vertical translations, we displace vertically down $\tilde{C}(r;m)$ until it does not intersect $M=\mathrm{graph}(u)$. Then, we move vertically upwards until $\tilde{C}(r;m)$ intersects M for the first time.

We claim that the first time that $\tilde{C}(r;m)$ touches M occurs when $L_2$ arrives to the plane of equation $x_3=0$ and, consequently, $L=L_2$. Firstly, the touching principle prohibits an interior tangent point between M and $\tilde{C}(r;m)$. On the other hand, it is not possible that a boundary point of $C(r;m)$, namely a point of $L_1\cup L_2$, touches a point of M because Equations (26) and (27). Definitively, we can move $\tilde{C}(r;m)$ until $L_2$ coincides with L, in particular,

$$x_0\in L_2\cap \partial \Omega .$$

At this position, $\tilde{C}(r;m)$ is the graph of the function

$$w^{-}(x_1,x_2)=\sqrt{r^2+x_1^2}-m.$$

Thus, M is contained between $w^{-}$ and $w^{+}=0$ in $\Omega \cap \mathcal{U}$ with $w^{-}(x_0)=w^{+}(x_0)=u(x_0)=0$. We are in position to apply Lemma 2 because $Q\left[w^{+}\right]<0=Q\left[u\right]=Q\left[w^{-}\right]$ and $w^{-}\le u\le w^{+}$ in $\partial (\Omega \cap \mathcal{U})$. We conclude that $|Du|\le C$, where the constant C in Equation (21) is

$$C=|D{w}^{-}{|}_{|x_1=\sqrt{m^2-r^2}}=\frac{\sqrt{m^2-r^2}}{m}.$$

 □

The key in the above proof is that the pieces of cylinders $\tilde{C}(r;m)$ of ${\mathbb{L}}^3$ have arbitrary large height and are graphs on strips of arbitrary width (see Equation (28)). This gives a priori height estimates by choosing m sufficiently large in Equation (28). Furthermore, the same cylinders provide us the boundary gradient estimates.

With a similar argument, we can derive a priori boundary gradient estimates by using hyperbolic caps. The only difference is that we have to assume strictly convexity ${\kappa }_{\partial \Omega }>0$.

After Theorem 9, we can come back to Euclidean space asking if a similar argument is possible by replacing the pieces of cylinders $C(r,m)$ by Euclidean circular cylinders. Let $H>0$ and consider the circular cylinder $v(x_1,x_2)=-\sqrt{r^2-x_1^2}$, $r=1/(2H)$ whose mean curvature is H with the orientation given in Equation (7). The only caution is to assure that the width of any strip containing the (convex) domain $\Omega$ is less than $1/|H|$ as well as its height is less than $1/(2H)$. Again, this gives not only the height estimates but also the boundary gradient estimates. With the same ideas as in Theorem 9, we prove ([12]):

Theorem 10.

Let $H>0$ and $\Omega \subset {\mathbb{R}}^2$ be a bounded domain with ${\kappa }_{\partial \Omega }\ge 0$. If

$$dist(L_1,L_2)<\frac{1}{H},forall(L_1,L_2)\in \mathcal{L},$$

(29)

then the Dirichlet problem in Equation (22) has a unique solution.

Comparing this result with Theorem 8, the domain here is merely convex even can contain segments of straight-lines; in contrast, the domain $\Omega$ is small in relation to the value of $1/H$.

Proof. 

Compare $M=\mathrm{graph}(u)$ with the cylinders $C(r)=\mathrm{graph}(v)$. An argument as in Theorem 9 proved that the hypothesis Equation (29) ensures that $-1/(2H)<u<0$ in $\Omega$: in fact, for this estimate it suffices that Equation (29) holds for one pair of lines $(L_1,L_2)\in \mathcal{L}$. The boundary gradient estimates follow comparing with quarter of cylinders $C(r)$ defined in the strip $0\le x_1\le 1/(2H)$. □

The following result solves affirmatively the Dirichlet problem in the Lorentz-Minkowski space Equation (25) for arbitrary domains. For this, we use cmc rotational spacelike surfaces of ${\mathbb{L}}^3$ as barriers. We now describe the rotationally symmetric solutions of Equation (1).

Consider a rotational surface about the $x_3$-axis obtained by the curve $(r,0,w(r))$, $0\le a<r<b$. With respect to the orientation in Equation (7), the mean curvature H satisfies

$$\frac{w^{″}}{{(1-w^{\prime 2})}^{3/2}}+\frac{w^{\prime }}{r\sqrt{1-w^{\prime 2}}}=2H.$$

(30)

The spacelike condition is equivalent to $w^{\prime 2}<1$. Multiplying by r, a first integral is

$$H{r}^2+c=\frac{r{w}^{\prime }}{\sqrt{1-w^{\prime 2}}}$$

for a constant $c\in \mathbb{R}$, or equivalently

$$w^{\prime }=\pm \frac{H{r}^2+c}{\sqrt{r^2+{(H{r}^2+c)}^2}}·$$

(31)

If $c=0$, the solution is $w(r)=\sqrt{1/H^2+r^2}$, up to a constant, that corresponds with a hyperbolic plane ${\mathbb{H}}^2(1/H)$.

Let $H>0$ and $c<0$. Since $w^{\prime 2}<1$, the function w is defined in $(0,\infty )$. By Equation (31), $w^{″}>0$ and $w^{\prime }$ vanishes at a unique point, namely $r_0=\sqrt{-c/H}$. It is also clear that ${lim}_{r\to 0}{w}^{\prime }(r)=-1$. Consider $w=w(r;c)$ to be the solution of Equation (31) parameterized by the constant c assuming initial condition

$$w(r_0)=0,(so w^{\prime }(r_0)=0).$$

(32)

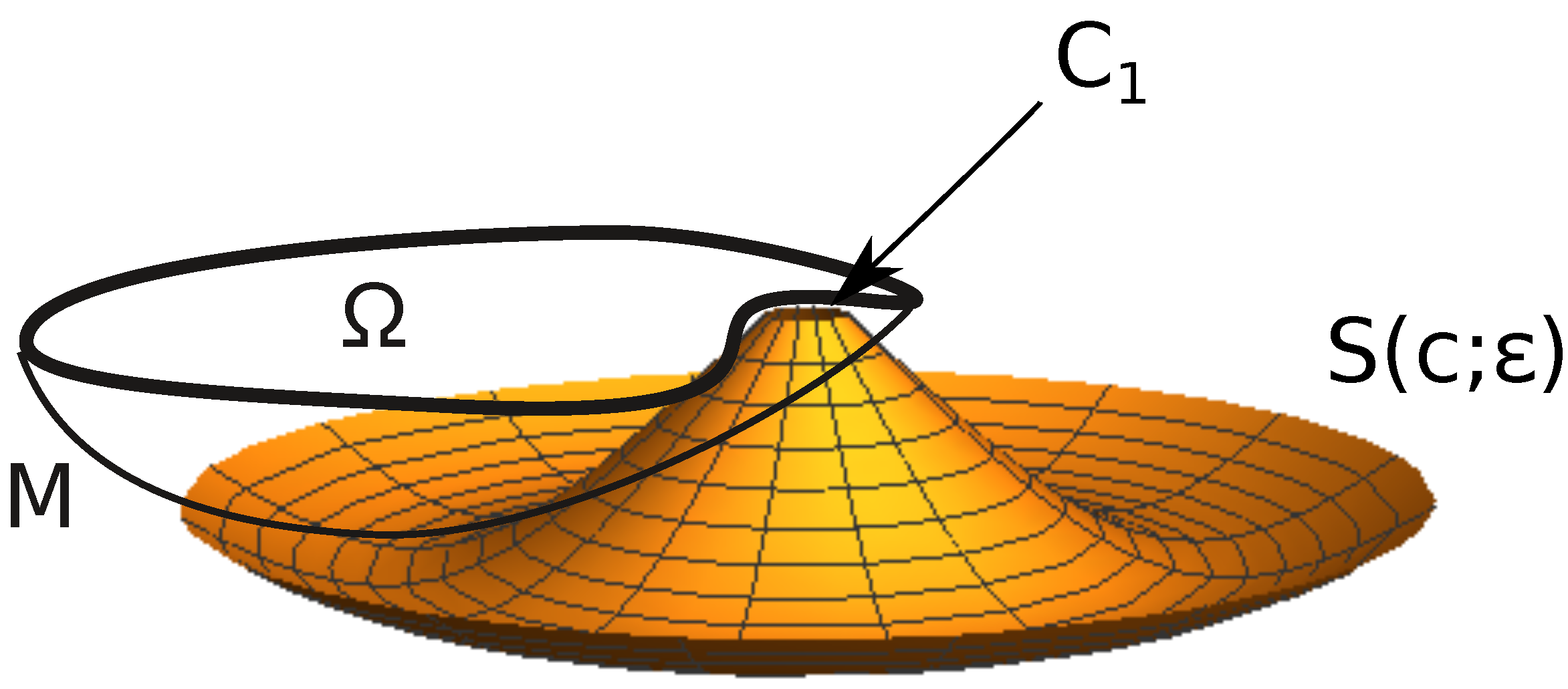
Let $S(c)$ denote the graph of $w(r;c)$ with $r^2=x_1^2+x_2^2$ (see Figure 2, left). Let ${\xi }_c={lim}_{r\to 0}w(r;c)$. The functions $w(r;c)$ have the following properties.

• $S(c)$ presents a singularity at the intersection point with the rotation axis (see Figure 2, right). At this point, the surface is tangent to the (backward) light-cone from $w(0;c)$, namely,

  $$x_1^2+x_2^2={(x_3-{\xi }_c)}^2,x_3<{\xi }_c.$$
• ${lim}_{c\to -\infty }{r}_0(c)=+\infty$ and ${lim}_{c\to -\infty }{\xi }_c=+\infty$.
• ${lim}_{c\to 0}{r}_0(c)=0$ and ${lim}_{c\to 0}{\xi }_c=0$.

The following result does not have a counterpart in the Euclidean space.

Theorem 11.

If Ω is a bounded smooth domain, then the Dirichlet problem in Equation (25) has a unique solution.

Proof. 

If $H=0$, the solution is the function $u=0$. Let $H\ne 0$. By changing u by $-u$ if necessary, without loss of generality, we suppose that $H>0$. We know by Theorem 4 that $u<0$ in $\Omega$. As in Theorem 9, it suffices to find a priori estimates for the solution u of Equation (1) which corresponds with the value $t=1$. Moreover, the function $w^{+}=0$ is an upper barrier because $Q\left[w^{+}\right]=-2H<0$ in $\Omega$ and $w^{+}=u$ along $\partial \Omega$. To find lower barriers for u, we take pieces of cmc rotational surfaces $S(c)$ for suitable choices of the parameter c depending only on the initial data.

Since $\Omega$ is smooth ($C^2$ is enough), $\Omega$ satisfies a uniform exterior circle condition. This means that there exists a small enough $\epsilon >0$ depending only on $\Omega$ with the following property: for any boundary point $x\in \partial \Omega$, there is a disc $D_{\epsilon }$ of radius $\epsilon$ and depending on x such that

$$D_{\epsilon }\cap \Omega =\varnothing ,\overline{D_{\epsilon }}\cap \overline{\Omega }=\left\{x\right\}.$$

Consequently, the same property holds for every ${\epsilon }^{\prime }>0$ with ${\epsilon }^{\prime }\le \epsilon$.

Fix the above $\epsilon$. Let $w=w(r;c)$ be a solution of Equations (31) and (32) defined only in the interval $[\epsilon ,r_0]$ and let $S(c;\epsilon )$ be its graph. Here, and in what follows, we identify the function $w=w(r)$ of one variable with the rotationally symmetric function of two variable $w=w(x_1,x_2)$ by setting $x_1^2+x_2^2=r^2$. Then, the boundary of $S(c;\epsilon )$ are the circles

$$\partial S(c;\epsilon )=C_1\cup C_2:=\{(x_1,x_2,w(\epsilon ;c)):x_1^2+x_2^2={\epsilon }^2\}\cup \{(x_1,x_2,0):x_1^2+x_2^2=r_0^2\}.$$

By the height estimates of Theorem 4, there exists a constant $K>0$ depending only on the initial data such that $-K<u<0$ in $\Omega$. Let $c<0$ be sufficiently small with the next two properties

$$r_0(c)>\mathrm{diam}(\Omega ),w(\epsilon ;c)>K.$$

(33)

Given $\epsilon$, the last inequality is a consequence of ${\xi }_c\to \infty$ as $r_0\to -\infty$. Let $w^{-}=w(r;c)$.

Let $x\in \partial \Omega$ be a boundary point and let $D_{\epsilon }$ be the disc given by the uniform exterior circle condition. We now prove that it is possible to choose a suitable $S(c;\epsilon )$ such that $S(c;\epsilon )$ is a lower barrier for u around the point x. In what follows, we denote by the same symbol $S(c;\epsilon )$ any vertical translation of this surface which corresponds with the functions $w(r;c)+k$ for different choices of the constant k.

After a horizontal translation, we suppose $x=(\epsilon ,0)$ and that the disc $D_{\epsilon }$ of the uniform exterior circle condition is $x_1^2+x_2^2<{\epsilon }^2$. We move vertically down the surface $S(c;\epsilon )$ until that it does not intersect $M=\mathrm{graph}(u)$. Then, we come back by lifting vertically upwards $S(c;\epsilon )$.

Claim. It is possible to move upwards $S(c;\epsilon )$ without touching M until we place $S(c;\epsilon )$ just at the position where the boundary circle $C_1$ coincides with $\partial D_{\epsilon }$ (see Figure 3).

This occurs because the touching principle forbids a first contact at some common interior point. The other possibility is that, during the vertical displacement, and before arriving at the final position, some boundary point of $S(c;\epsilon )$, namely a point of $C_2$, touches M: the circle $C_1$ does not touch M because $D_{\epsilon }\cap \Omega =\varnothing$. The other circle $C_2$ projects onto ${\mathbb{R}}^2$ in the circle $x_1^2+x_2^2=r_0^2$ which contains $\Omega$ inside by the first property of Equation (33). Finally, the circle $C_2$ does not touch M because the vertical distance between $C_1$ and $C_2$ is $w^{-}(\epsilon ;c)-w^{-}(0;c)=w(\epsilon ;c)>K$ by Equation (33).

Once we have placed $S(c;\epsilon )$ so that $C_1=\partial D_{\epsilon }$, the lower barrier is $w^{-}=w(r;c)-w(\epsilon ;c)$ defined in the annulus $\mathcal{U}=\{(x_1,x_2):{\epsilon }^2<x_1^2+x_2^2<r_0^2\}$. We deduce that $w^{-}<u$ in $\Omega \cap \mathcal{U}$. This proves that $|Du(x)|<|D{w}^{-}(x)|$ by Lemma 2 and this value depends only on the initial data, namely

$$|D{w}^{-}(x)|=-\frac{d}{dr}{|}_{r=\epsilon }w(r;c)=-\frac{H{\epsilon }^2+c}{\sqrt{{\epsilon }^2+{(H{\epsilon }^2+c)}^2}}·.$$

This gives the constant C in Equation (21). □