Generalized Abel-Grassmann’s Neutrosophic Extended Triplet Loop

Abstract

A group is an algebraic system that characterizes symmetry. As a generalization of the concept of a group, semigroups and various non-associative groupoids can be considered as algebraic abstractions of generalized symmetry. In this paper, the notion of generalized Abel-Grassmann’s neutrosophic extended triplet loop (GAG-NET-Loop) is proposed and some properties are discussed. In particular, the following conclusions are strictly proved: (1) an algebraic system is an AG-NET-Loop if and only if it is a strong inverse AG-groupoid; (2) an algebraic system is a GAG-NET-Loop if and only if it is a quasi strong inverse AG-groupoid; (3) an algebraic system is a weak commutative GAG-NET-Loop if and only if it is a quasi Clifford AG-groupoid; and (4) a finite interlaced AG-(l,l)-Loop is a strong AG-(l,l)-Loop.

1. Introduction

The concept of an Abel-Grassmann’s groupoid (AG-groupoid) was first given by Kazim and Naseeruddin [1] in 1972 and they have called it a left almost semigroup (LA-semigroup). In [2], the same structure is called a left invertive groupoid. In [3,4,5,6,7,8,9], some properties and different classes of an AG-groupoid are investigated.

Smarandache proposed the new concept of neutrosophic set, which is an extension of fuzzy set and intuitionistic fuzzy set [10]. Until now, neutrosophic sets have been applied to many fields such as decision making [11,12,13], forecasting [14], best product selection [15], the shortest path problem [16], minimum spanning tree [17], neutrosophic portfolios of financial assets [18], etc. Some new theoretical studies are also developed [19,20,21,22,23,24]. In [25], Xiaohong Zhang introduced the concept of Abel-Grassmann’s neutrosophic extended triplet loop (AG-NET-loop), and some properties and structure about AG-NET-loop are discussed. Recently, a new algebraic system, generalized neutrosophic extended triplet set, is proposed in [26].

In this paper, we combine the notions of generalized neutrosophic extended triplet set and AG-groupoid, introduce the new concept of generalized Abel-Grassmann’s neutrosophic extended triplet loop (GAG-NET-loop); that is, GAG-NET-loop is both AG-groupoid and generalized neutrosophic extended triplet set. We deeply analyze the internal connecting link between GAG-NET- loop and other AG-groupoid and obtain some important results.

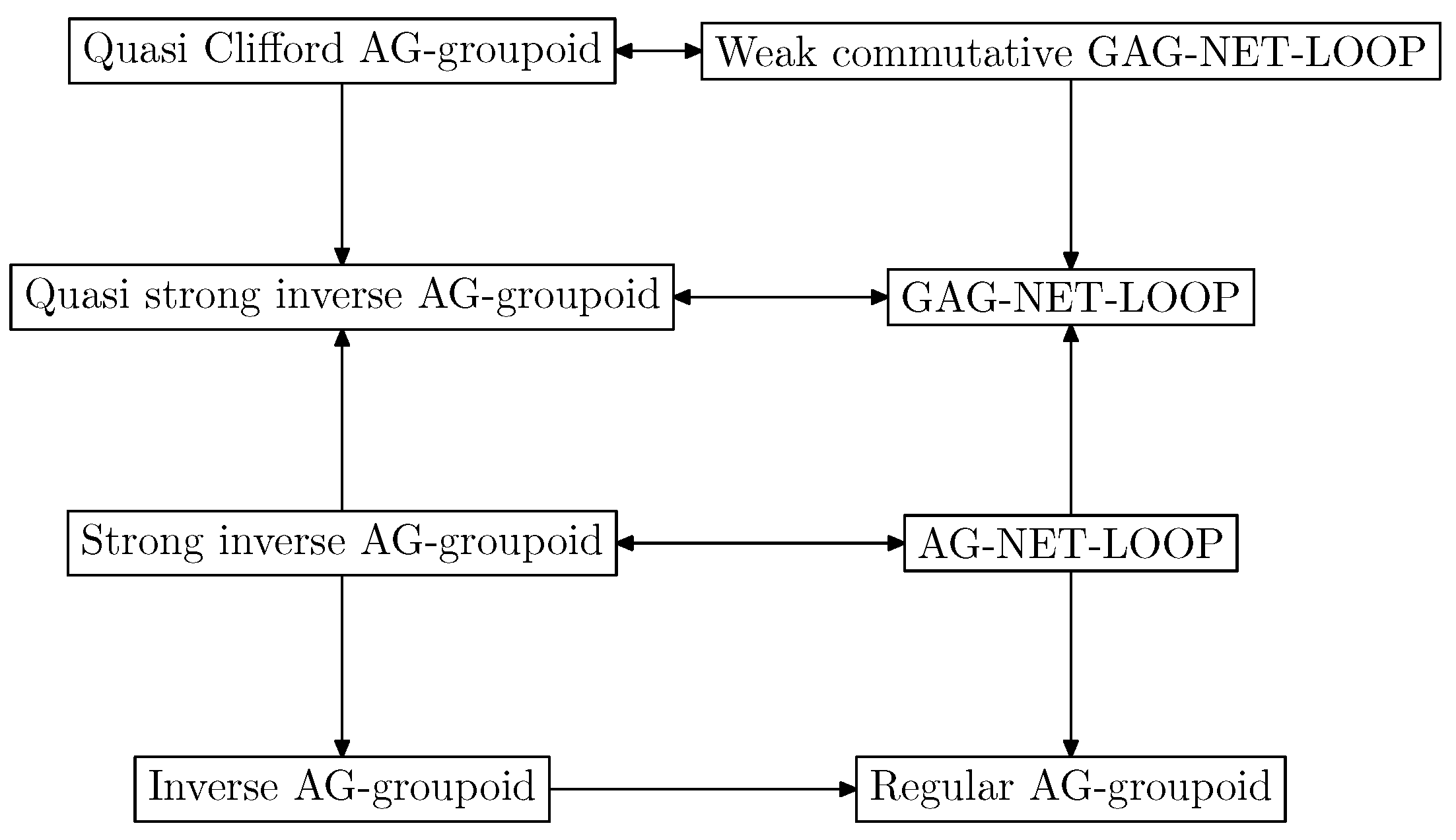
GAG-NET-loop is an extension of AG-NET-loop. Compared with AG-NET-loop, GAG-NET-loop relaxes the restriction on the elements in the AG-groupoid. According to our research, corresponding to the decomposition theorem of AG-NET-loop, some GAG-NET-loops can also be decomposed into smaller ones. This is also the embodiment of the research method of regular semigroups to quasi-regular semigroups in non-associative groupoid.

The paper is organized as follows. Section 2 gives the basic definitions. Some properties about finite interlaced AG-(l,l)-Loop and some structures about strong inverse AG-groupoid are discussed in Section 3. We proposed the GAG-NET-Loop and discussed its properties and structure in Section 4. Finally, the summary and future work are presented in Section 5.

2. Basic Definitions

In this section, the related research and results of the AG-NET-loop are presented. Some related notions are introduced first.

Let S be non-empty set, * is a binary operation on S. If $\forall a,b\in S$, implies $a*b\in S$, then $(S,*)$ is called a groupoid. A groupoid $(S,*)$ is called an Abel-Grassmann’s groupoid (AG-groupoid) [27,28] if it holds the left invertive law, that is, for all $a,b,c\in S$, $(a*b)*c=(c*b)*a$. In an AG-groupoid the medial law holds, for all $a,b,c,\in S$, $(a*b)*(c*d)=(a*c)*(b*d)$. In an AG-groupoid $(S,*)$, for all $a\in S$, $n\in Z^{+}$, the recursive definition of $a^n$ is as follows: $a^1=a,a^2=a*a,a^3=a^2*a=(a*a)*a,a^4=a^3*a,...,a^n=a^{n-1}*a$.

Definition 1

([29]). Let N be a non-empty set together with a binary operation *. Then, N is called a neutrosophic extended triplet set if for any $a\in N$, there exists a neutral of “a” (denoted by $neut\left(a\right)$), and an opposite of “a”(denoted by $anti\left(a\right))$, such that $neut\left(a\right)\in N$, $anti\left(a\right)\in N$ and:

$$a*neut\left(a\right)=neut\left(a\right)*a=a,$$

$$a*anti\left(a\right)=anti\left(a\right)*a=neut\left(a\right).$$

The triplet $(a,neut(a),anti(a\left)\right)$ is called a neutrosophic extended triplet.

Note that, for a neutrosophic triplet set $(N,*),a\in N,$ $neut\left(a\right)$ and $anti\left(a\right)$ may not be unique. In order not to cause ambiguity, we use the following notations to distinguish: $neut\left(a\right)$ denotes any certain one of neutral of a, $\left\{neut\right(a\left)\right\}$ denotes the set of all neutral of a, $anti\left(a\right)$ denotes any certain one of opposite of a, and $\left\{anti\right(a\left)\right\}$ denotes the set of all opposite of a.

Definition 2

([25]). Let $(N,*)$ be a neutrosophic extended triplet set. Then, N is called a neutrosophic extended triplet loop (NET-Loop), if $(N,*)$ is well-defined, i.e., for any $a,b\in N$, one has $a*b\in N$.

Definition 3

([25]). Let $(N,*)$ be a neutrosophic extended triplet loop (NET-Loop). Then, N is called an AG-NET-Loop, if $(N,*)$ is an AG-groupoid.

An AG-NET-Loop N is called a commutative AG-NET-Loop if for all $a,b\in N,a*b=b*a$.

Theorem 1

([25]). Let $(N,*)$ be an AG-NET-loop. Then, for any $x,y\in \left\{anti\right(a\left)\right\}$,

(1) 

$neut\left(a\right)*x=x*neut\left(a\right)=neut\left(a\right)*y$, that is,$\left|neut\right(a)*\{anti\left(a\right)\left\}\right|=1$.

(2) 

$(x*neut(a\left)\right)*a=\left(neut\right(a)*x)*a=neut\left(a\right)$.

(3) 

$a*(x*neut(a\left)\right)=a*\left(neut\right(a)*x)=neut\left(a\right)$.

(4) 

$\forall a\in N,neut\left(a\right)*neut\left(a\right)=neut\left(a\right)$.

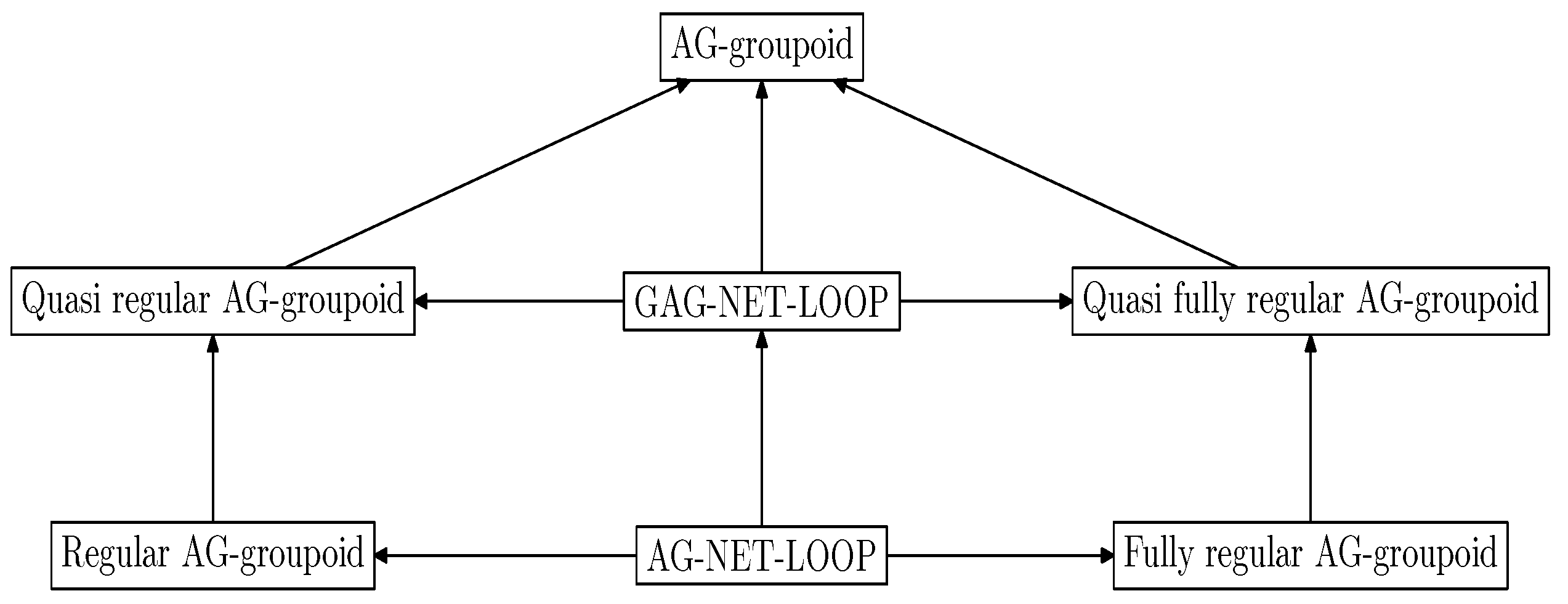
Definition 4

([5]).

An element a of an AG-groupoid $(S,*)$ is called a regular if there exists $x\in S$ such that $a=(a*x)*a$ and S is called regular if all elements of S are regular.

An AG-groupoid $(S,*)$ is called quasi regular if, for any $a\in S$, there exists a positive integer n such that $a^n$ is regular.

Definition 5

([6]).

An element a of an AG-groupoid $(S,*)$ is called a fully regular element of S if there exist some $p,q,r,s,t,u,v,w,x,y,z\in S$ ($p,q,...,z$ may be repeated) such that

$$\begin{array}{cc}\hfill a& =(p*a^2)*q=(r*a)*(a*s)=(a*t)*(a*u)\hfill \\ \hfill & =(a*a)*v=w*(a*a)=(x*a)*(y*a)\hfill \\ \hfill & =(a^2*z)*a^2.\hfill \end{array}$$

An AG-groupoid $(S,*)$ is called fully regular if all elements of S are fully regular.

An AG-groupoid $(S,*)$ is called quasi fully regular if for any $a\in S$, there exists a positive integer n such that $a^n$ is fully regular.

3. Strong Inverse AG-Groupoid and Finite Interlaced AG-Groupoid

Definition 6

([30]).

An AG-groupoid $(S,*)$ is called an inverse AG-groupoid if for each element $a\in S$, there exists an element x in S such that $a=(a*x)*a$ and $x=(x*a)*x$.

Definition 7.

An AG-groupoid $(S,*)$ is called a strong inverse AG-groupoid if for any $a\in S$, there exists a unary operation $a\to a^{-1}$ on S such that

$${\left(a^{-1}\right)}^{-1}=a,(a*a^{-1})*a=a*(a*a^{-1})=a,a*a^{-1}=a^{-1}*a.$$

The following example shows that an inverse AG-groupoid may not be a strong inverse AG-groupoid.

Example 1.

Let $S=\{1,2,3,4\}$, an operation * on S is defined as in

Table 1. The operation table of Example 1.

*	1	2	3	4
1	2	4	3	1
2	3	1	2	4
3	1	3	4	2
4	4	2	1	3

. Being $1=(1*3)*1,3=(3*1)*3,2=(2*4)*2,4=(4*2)*4$, from Definition 6, S is an inverse AG-groupoid. Being $(1*1)*1=3\ne 1,(1*2)*1=4\ne 1,(1*3)*1=1\ne 3=1*(1*3),(1*4)*1=2\ne 1$, from Definition 7, S is not a strong inverse AG-groupoid.

Proposition 1.

Let $(N,*)$ be an AG-NET-loop. Then, for any $a\in N$, $x\in \left\{anti\right(a\left)\right\}$,

$$neut\left(neut\right(a)*x)*anti\left(neut\right(a)*x)=a.$$

Proof. 

For any $x\in \left\{anti\right(a\left)\right\}$, we have

$$\begin{array}{cc}\hfill \left(neut\right(a)*x)*neut\left(a\right)& =\left(neut\right(a)*x)*(a*x)\hfill \\ \hfill & =\left(neut\right(a)*a)*(x*x)\left(applyingthemediallaw\right)\hfill \\ \hfill & =(a*neut(a\left)\right)*(x*x)\hfill \\ \hfill & =(a*x)*\left(neut\right(a)*x)\left(applyingthemediallaw\right)\hfill \\ \hfill & =neut\left(a\right)*\left(neut\right(a)*x),\hfill \end{array}$$

$$\begin{array}{cc}\hfill neut\left(a\right)*\left(neut\right(a)*x)& =(x*a)*\left(neut\right(a)*x)\hfill \\ \hfill & =(x*neut(a\left)\right)*(a*x)\left(applyingthemediallaw\right)\hfill \\ \hfill & =(x*neut(a\left)\right)*neut\left(a\right)\hfill \\ \hfill & =\left(neut\right(a)*neut(a\left)\right)*x\hfill \\ \hfill & =neut\left(a\right)*x,\left(byProposition\right(4\left)\right)\hfill \end{array}$$

we have $\left(neut\right(a)*x)*neut\left(a\right)=neut\left(a\right)*\left(neut\right(a)*x)=neut\left(a\right)*x.$

From Theorem 1 (2) and (3), we have

$$neut\left(neut\right(a)*x)=neut\left(a\right),a\in anti\left\{neut\right(a)*x\}.$$

From Theorem 1 (1) $neut\left(a\right)*x$ is unique, we have

$$neut\left(neut\right(a)*x)*anti\left(neut\right(a)*x)=neut\left(a\right)*a=a.$$

 □

Example 2.

Let $N=\{a,b,c\}$, an operation * on N is defined as in

Table 2. An AG-NET-Loop of Example 2.

*	a	b	c
a	a	b	c
b	b	c	a
c	c	a	b

. Since $neut\left(a\right)=a,anti\left(a\right)=a,neut\left(b\right)=a,anti\left(b\right)=c,neut\left(c\right)=a,anti\left(c\right)=b,$ so $(N,*)$ is an AG-NET-Loop. Being

$$neut\left(neut\right(a)*a)*anti\left(neut\right(a)*a)=a*a=a,$$

$$neut\left(neut\right(b)*c)*anti\left(neut\right(b)*c)=neut\left(c\right)*anti\left(c\right)=b,$$

$$neut\left(neut\right(c)*b)*anti\left(neut\right(c)*b)=neut\left(b\right)*anti\left(b\right)=c,$$

that is for any $a\in N$, $x\in \left\{anti\right(a\left)\right\}$, $neut\left(neut\right(a)*x)*anti\left(neut\right(a)*x)=a.$

Theorem 2.

Let $(N,*)$ be a groupoid. Then, N is an AG-NET-Loop if and only if it is a strong inverse AG-groupoid.

Proof. 

Necessity: Suppose N is an AG-NET-Loop, from Definition 3, for each $a\in N$, such that a has the neutral element and opposite element, denoted by $neut\left(a\right)$ and $anti\left(a\right)$, respectively. Set

$$a^{-1}=neut\left(a\right)*anti\left(a\right),$$

by Theorem 1 (1), $neut\left(a\right)*anti\left(a\right)$ is unique, so $a^{-1}$ is unique. By Proposition 1, we have

$${\left(a^{-1}\right)}^{-1}=neut(neut\left(a\right)*anti\left(a\right))*anti(neut\left(a\right)*anti\left(a\right))=a.$$

Being

$$a^{-1}*a=(neut\left(a\right)*anti\left(a\right))*a=(a*anti\left(a\right))*neut\left(a\right)=neut\left(a\right)*neut\left(a\right)=neut\left(a\right),$$

$$\begin{array}{cc}\hfill a*a^{-1}& =a*\left(neut\right(a)*anti(a\left)\right)\hfill \\ \hfill & =\left(neut\right(a)*a)*\left(neut\right(a)*anti(a\left)\right)\hfill \\ \hfill & =\left(neut\right(a)*neut(a\left)\right)*(a*anti(a\left)\right)\hfill \\ \hfill & =\left(neut\right(a)*neut(a\left)\right)*neut\left(a\right)\hfill \\ \hfill & =neut\left(a\right),\hfill \end{array}$$

$$(a*a^{-1})*a=neut\left(a\right)*a=a,$$

$$a*(a*a^{-1})=a*neut\left(a\right)=a,$$

we have

$$a^{-1}*a=a*a^{-1},$$

$$(a*a^{-1})*a=a*(a*a^{-1})=a.$$

From Definition 7, N is a strong inverse AG-groupoid.

Sufficiency: If N is a strong inverse AG-groupoid and $a^{-1}\in N$, such that $a*a^{-1}=a^{-1}*a$ and $(a*a^{-1})*a=a*(a*a^{-1})=a$. Set

$$neut\left(a\right)=a*a^{-1},$$

then $neut\left(a\right)*a=(a*a^{-1})*a=a*(a*a^{-1})=a*neut\left(a\right)=a,$ $a*{\left(a\right)}^{-1}={\left(a\right)}^{-1}*a=neut\left(a\right).$ From Definition 3, we have that N is an AG-NET-Loop and $a^{-1}\in \left\{anti\left(a\right)\right\}$. □

Example 3.

Apply $(S,*)$ in Example 2, we know that it is an AG-NET-Loop. We show that it is a strong inverse AG-groupoid in the following.

For b, there exists a inverse element $b^{-1}=c$, such that ${\left(b^{-1}\right)}^{-1}=b,(b*b^{-1})*b=b*(b*b^{-1})=b,b*b^{-1}=b^{-1}*b=a$, so b is strong inverse. a and c are strong inverse for the same reason, so $(S,*)$ is a strong inverse AG-groupoid by Definition 7.

An AG-groupoid (S, *) is called interlaced if it satisfies $(a*a)*b=a*(a*b)$, $a*(b*b)=(a*b)*b$ for all $a,b$ in S. An AG-groupoid (S, *) is called locally associative if it satisfies $(a*a)*a=a*(a*a)$ for all a in S.

Theorem 3.

Let $(D,*)$ be a locally associative AG-groupoid with respect to *. If D is finite, there is an idempotent element in D. That is, $\exists a\in D,a*a=a$.

Proof. 

Assume that D is a finite locally associative AG-groupoid with respect to *. Then, for any $a\in D$, $a,a*a=a^2,a*a*a=a^3,...,a^n,...\in D$. Since D is finite, there exists natural number m, k such that $a^m=a^{m+k}$.

Case 1: If $k=m$, then $a^m=a^{2m}$, that is, $a^m=a^m*a^m$, $a^m$ is an idempotent element in D.

Case 2: If $k>m$, then from $a^m=a^{m+k}$ we can get

$$a^k=a^m*a^{k-m}=a^{m+k}*a^{k-m}=a^{2k}=a^k*a^k.$$

This means that $a^k$ is an idempotent element in D.

Case 3: If $k<m$, then from $a^m=a^{m+k}$ we can get

$$a^m=a^{m+k}=a^m*a^k=a^{m+k}*a^k=a^{m+2k};$$

$$a^m=a^{m+2k}=a^m*a^{2k}=a^{m+k}*a^{2k}=a^{m+3k};$$

$$\dots \dots$$

$$a^m=a^{m+mk}.$$

Since m and k are natural numbers, then $mk\ge m$. Therefore, from $a^m=a^{m+mk}$, applying Case 1 or Case 2, we know that there exists an idempotent element in D. □

Definition 8

([31]).

Let $(N,*)$ be an AG-groupoid. Then, N is called an AG-(l, l)-Loop, if for any $a\in N$, there exist two elements b and c in N that satisfy the condition: $b*a=a$, and $c*a=b$. In an AG-(l,l)-Loop, a neutral of “a” denoted by $neu{t}_{(l,l)}\left(a\right)$.

Definition 9

([31]).

Let $(N,*)$ be an AG-(l, l)-Loop. Then, N is a strong AG-(l, l)-Loop if $neu{t}_{(l,l)}\left(a\right)*neu{t}_{(l,l)}\left(a\right)=neu{t}_{(l,l)}\left(a\right),\forall a\in N.$

Definition 10.

Let $(D,*)$ be an AG-(l,l)-Loop. Then, D is called an interlaced AG-(l,l)-Loop, if it satisfies $(a*a)*b=a*(a*b)$, $a*(b*b)=(a*b)*b$, for all $a,b$ in D.

Theorem 4.

Let $(D,*)$ be an interlaced AG-(l, l)-Loop with respect to *. If D is finite, there is an idempotent left neutral element in D. That is, $\forall a\in D,\exists s,p\in D,s*a=a,p*a=s,s*s=s$.

Proof. 

Assume that D is a finite interlaced AG-(l,l)-Loop with respect to *. Then, for any $a\in D$, $\exists s,p\in D,s*a=a,p*a=s,$ we have $s*a=(p*a)*a=(a*a)*p=a*(a*p)=a$,

$$\begin{array}{cc}\hfill a*s& =(a*(a*p\left)\right)*s\hfill \\ \hfill & =(s*(a*p\left)\right)*a\left(bytheleftinvertivelaw\right)\hfill \\ \hfill & =\left(\right(p*a)*(a*p\left)\right)*a\hfill \\ \hfill & =\left(\right((a*p)*a)*p)*a\left(bytheleftinvertivelaw\right)\hfill \\ \hfill & =(a*p)*\left(\right(a*p)*a)\left(bytheleftinvertivelaw\right)\hfill \\ \hfill & =\left(\right(a*p)*(a*p\left)\right)*a\left(bytheinterlacedlaw\right)\hfill \\ \hfill & =(a*(a*p\left)\right)*(a*p)\left(bytheleftinvertivelaw\right)\hfill \\ \hfill & =a*(a*p)=a,\hfill \end{array}$$

$$s^2*a=(s*s)*a=(a*s)*s=a,$$

$$s^3*a=(s^2*s)*a=(a*s)*s^2=a*s^2=a*(s*s)=(a*s)*s=a*s=a.$$

When $m>3,m\equiv 0\left(\mathrm{mod}2\right)$, we have

$$\begin{array}{cc}\hfill s^m*a& =(s^{m-2}*s^2)*a\hfill \\ \hfill & =(a*s^2)*s^{m-2}\hfill \\ \hfill & =a*s^{m-2}\hfill \\ \hfill & =a*(s^{(m-2)/2}*s^{(m-2)/2})\hfill \\ \hfill & =(a*s^{(m-2)/2})*s^{(m-2)/2}\left(bytheinterlacedlaw\right)\hfill \\ \hfill & =(s^{(m-2)/2}*s^{(m-2)/2})*a\left(bytheleftinvertivelaw\right)\hfill \\ \hfill & =s^{m-2}*a\hfill \\ \hfill & =......\hfill \\ \hfill & =s^2*a=a.\hfill \end{array}$$

When $m>3,m\equiv 1\left(\mathrm{mod}2\right)$, we have

$$\begin{array}{cc}\hfill s^m*a& =(s^{m-1}*s)*a\hfill \\ \hfill & =(a*s)*s^{m-1}\hfill \\ \hfill & =a*s^{m-1}\hfill \\ \hfill & =a*(s^{(m-1)/2}*s^{(m-1)/2})\hfill \\ \hfill & =(a*s^{(m-1)/2})*s^{(m-1)/2}\left(bytheinterlacedlaw\right)\hfill \\ \hfill & =(s^{(m-1)/2}*s^{(m-1)/2})*a\hfill \\ \hfill & =s^{m-1}*a\hfill \\ \hfill & =......\hfill \\ \hfill & =s^2*a=a.\hfill \end{array}$$

Thus, $s,s^2,s^3......s^m......$ are all left neutral element.

Applying Theorem 3, we know that there exists an idempotent left neutral element in D. □

Theorem 5.

Assume that $(N,*)$ is a finite interlaced AG-(l,l)-Loop. Then, for all a in N, if $neu{t}_{(l,l)}\left(a\right)$ is an idempotent element, then it is unique.

Proof. 

Assume that N is a finite interlaced AG-(l,l)-Loop with respect to *. Suppose that there exist $x,y\in \left\{neu{t}_{(l,l)}\left(a\right)\right\},a\in N$. By Definition 8, $x*a=a,y*a=a$, and there exist $p,q\in N$ which satisfy $p*a=x,q*a=y$. If $x*x=x,y*y=y$, we have

$$x=x*x=(p*a)*x=(x*a)*p=a*p,$$

$$y=y*y=(q*a)*y=(y*a)*q=a*q,$$

$$x*y=(p*a)*y=(y*a)*p=a*p=x,$$

$$y*x=(q*a)*x=(x*a)*q=a*q=y,$$

$$x=x*y=(x*x)*y=(y*x)*x=y*x=y.$$

We know that $x=y$, $neu{t}_{(l,l)}\left(a\right)$ is unique. □

Theorem 6.

Let $(N,*)$ be a finite interlaced AG-(l,l)-Loop. Then, N is a strong AG-(l,l)-Loop.

Proof. 

For any a in N, applying Theorem 4, we have $\exists s,p\in N,s*a=a,p*a=s,s*s=s$. From this and Definition 9, we know that N is a strong AG-(l,l)-Loop. □

Example 4.

Let $S=\{1,2,3\}$, an operation * on S is defined as in

Table 3. A finite interlaced AG-(l,l)-Loop of Example 4.

*	1	2	3
1	1	2	3
2	2	3	1
3	3	1	2

. Being $(1*1)*2=1*(1*2)=2,1*(2*2)=(1*2)*2=3,(1*1)*3=1*(1*3)=3,1*(3*3)=(1*3)*3=2,(2*2)*3=2*(2*3)=2,2*(3*3)=(2*3)*3=3$, and $1*1=1,1*2=2,3*2=1,1*3=3,2*3=1$, we have S is a finite interlaced AG-(l,l)-Loop by Definition 10. Being $neu{t}_{(l,l)}\left(1\right)=neu{t}_{(l,l)}\left(2\right)=neu{t}_{(l,l)}\left(3\right)=1$, 1*1=1, we have S is a strong AG-(l,l)-Loop by Definition 9.

The following example shows that a strong AG-(l,l)-Loop may not be an interlaced AG-(l,l)-Loop.

Example 5.

Let $S=\{1,2,3\}$, an operation * on S is defined as in

Table 4. A strong AG-(l,l)-Loop of Example 5.

*	1	2	3
1	1	2	3
2	3	1	2
3	2	3	1

. Being $1*1=1,1*2=2,2*2=1,1*3=3,3*3=1$, we have S is a strong AG-(l,l)-Loop by Definition 9. However, it is not an interlaced AG-(l,l)-Loop because $2*(3*3)=3\ne 2=(2*3)*3$.

4. GAG-NET-Loop

Definition 11

([26]). Let N be a non-empty set together with a binary operation *. Then, N is called a generalized neutrosophic extended triplet set if for any $a\in N$, at least exists a positive integer n, $a^n$ exists neutral element ( denoted by $neut\left(a^n\right)$) and opposite element (denoted by $anti\left(a^n\right)$), such that $neut\left(a^n\right)\in N,anti\left(a^n\right)\in N$ and

$$a^n*neut\left(a^n\right)=neut\left(a^n\right)*a^n=a^n,a^n*anti\left(a^n\right)=anti\left(a^n\right)*a^n=neut\left(a^n\right).$$

The triplet $(a,neut\left(a^n\right),anti\left(a^n\right))$ is called a generalized neutrosophic extended triplet with degree n.

Definition 12.

Let $(N,*)$ be a generalized neutrosophic extended triplet set. Then, N is called a generalized Abel-Grassmann’s neutrosophic extended triplet loop (GAG-NET-Loop), if the following conditions are satisfied: for all $a,b,c\in N$, $(a*b)*c=(c*b)*a$.

A GAG-NET-Loop N is called a commutative GAG-NET-Loop if for all $a,b\in N,a*b=b*a$.

Example 6.

Let $S=\{a,b,c\}$, an operation * on S is defined as in

Table 5. A GAG-NET-Loop of Example 6.

*	a	b	c
a	a	a	a
b	a	a	c
c	a	b	a

. We can see that $(a,a,a),(a,a,b)$, and $(a,a,c)$ are neutrosophic extended triplets, but b and c do not have the neutral element and opposite element. Thus, S is not an AG-NET-Loop. Moreover, $b^2=c^2=a$ has the neutral element and opposite element, thus $(S,*)$ is a GAG-NET-Loop. $(b,a,a)$ and $(c,a,a)$ are generalized neutrosophic extended triplets with degree 2. We can infer that $(S,*)$ is a GAG-NET-Loop but not an AG-NET-Loop. Moreover it is not a commutative GAG-NET-Loop being $b*c\ne c*b$.

The algebraic system $(Z_n,\otimes )$, ⊗ is the classical mod multiplication, where $Z_n=\{\left[0\right],\left[1\right],\cdots ,[n-1]\}$ and $n\in Z^{+},n\ge 2$.

Example 7.

Consider $(Z_4,\otimes )$, an operation ⊗ on $Z_4$ is defined as in

Table 6. The operation table of $Z_4$.

⊗	[0]	[1]	[2]	[3]
$\left[0\right]$	$\left[0\right]$	[0]	[0]	[0]
$\left[1\right]$	$\left[0\right]$	[1]	[2]	[3]
$\left[2\right]$	$\left[0\right]$	[2]	[0]	[2]
$\left[3\right]$	$\left[0\right]$	[3]	[2]	[1]

. We have:

(1) 

$\left[0\right],\left[1\right]$ and $\left[3\right]$ have the neutral element and opposite element.

(2) 

$\left[2\right]$ does not have the neutral element and opposite element, but we can see that ${\left[2\right]}^2=\left[0\right]$ has the neutral element and opposite element.

Thus, $Z_4$ is a generalized neutrosophic extended triplet set, but it is not a neutrosophic extended triplet set. Moreover, $(Z_4,\otimes )$ is a commutative GAG-NET-Loop.

Proposition 2.

Let $(N,*)$ be a GAG-NET-Loop, $a\in N$ and $(a,neut\left(a^n\right),anti\left(a^n\right))$ is a generalized neutrosophic extended triplet with degree n. We have:

(1) 

$neut\left(a^n\right)$ is unique.

(2) 

$neut\left(a^n\right)*neut\left(a^n\right)=neut\left(a^n\right)$.

Proof. 

Assume $c,d\in \left\{neut\left(a^n\right)\right\}$, so $a^n*c=c*a^n=a^n,a^n*d=d*a^n=a^n$, and there exists $x,y\in N$ such that

$$a^n*x=x*a^n=c,a^n*y=y*a^n=d.$$

We can obtain

$$c*d=(x*a^n)*d=(d*a^n)*x=a^n*x=c,$$

$$\begin{array}{cc}\hfill c*d& =(a^n*x)*(y*a^n)\hfill \\ \hfill & =(a^n*y)*(x*a^n)\hfill \\ \hfill & =(a^n*y)*c\hfill \\ \hfill & =(y*a^n)*c\hfill \\ \hfill & =(c*a^n)*y\hfill \\ \hfill & =a^n*y=d.\hfill \end{array}$$

We have $c=d=c*d$. Thus, $neut\left(a^n\right)$ is unique and $neut\left(a^n\right)*neut\left(a^n\right)=neut\left(a^n\right)$. □

Proposition 3.

Let $(N,*)$ be a GAG-NET-Loop, $a\in N$ and $(a,neut\left(a^n\right),anti\left(a^n\right))$ is a generalized neutrosophic extended triplet with degree n. Then,

(1) 

$(a^n*a^n)*a^n=a^n*(a^n*a^n)$.

(2) 

$neut\left(a^n\right)*x=neut\left(a^n\right)*y$, for any $x,y\in \left\{anti\left(a^n\right)\right\}$.

(3) 

$neut\left(neut\left(a^n\right)\right)=neut\left(a^n\right)$.

(4) 

$a^n*(x*neut\left(a^n\right))=(x*neut\left(a^n\right))*a^n=neut\left(a^n\right)$, for any $x\in \left\{anti\left(a^n\right)\right\}$.

(5) 

$a^n*(neut\left(a^n\right)*x)=(neut\left(a^n\right)*x)*a^n=neut\left(a^n\right)$, for any $x\in \left\{anti\left(a^n\right)\right\}$.

(6) 

$(neut\left(a^n\right)*x)*neut\left(a^n\right)=neut\left(a^n\right)*(neut\left(a^n\right)*x)=neut\left(a^n\right)*x$, for any $x\in \left\{anti\left(a^n\right)\right\}$.

(7) 

$neut(neut\left(a^n\right)*x)*anti(neut\left(a^n\right)*x)=a^n$, for any $x\in \left\{anti\left(a^n\right)\right\}$.

Proof. 

(1)

For $a\in N,neut\left(a^n\right)*a^n=a^n*neut\left(a^n\right)=a^n$, we have

$$(a^n*a^n)*a^n=(a^n*a^n)*(neut\left(a^n\right)*a^n)=(a^n*neut\left(a^n\right))*(a^n*a^n)=a^n*(a^n*a^n).$$

(2)

For any $x,y\in \left\{anti\left(a^n\right)\right\}$, we have $neut\left(a^n\right)*x=(y*a^n)*x=(x*a^n)*y=neut\left(a^n\right)*y$.

(3)

From Proposition 2, we have $neut\left(a^n\right)$ exists neutral element and opposite element. For any $x\in \left\{anti\left(a^n\right)\right\}$ and $y\in \left\{anti\left(neut\left(a^n\right)\right)\right\}$,

$$(y*x)*a^n=(a^n*x)*y=neut\left(a^n\right)*y=neut\left(neut\left(a^n\right)\right).$$

Moreover,

$$\begin{array}{cc}\hfill ((y*x)*a^n)*neut\left(a^n\right)& =(neut\left(a^n\right)*y)*neut\left(a^n\right)\hfill \\ \hfill & =(y*neut\left(a^n\right))*neut\left(a^n\right)\hfill \\ \hfill & =(neut\left(a^n\right)*neut\left(a^n\right))*y\hfill \\ \hfill & =neut\left(a^n\right)*y\hfill \\ \hfill & =neut\left(neut\left(a^n\right)\right).\hfill \end{array}$$

Thus, $neut\left(a^n\right)=neut\left(neut\left(a^n\right)\right)*neut\left(a^n\right)=((y*x)*a^n)*neut\left(a^n\right)=neut\left(neut\left(a^n\right)\right)$.

(4)

For any $x\in \left\{anti\left(a^n\right)\right\}$, from Definition 11 and Proposition 2, we have

$$\begin{array}{cc}\hfill a^n*(x*neut\left(a^n\right))& =(a^n*neut\left(a^n\right))*(x*neut\left(a^n\right))\hfill \\ \hfill & =(a^n*x)*(neut\left(a^n\right)*neut\left(a^n\right))\hfill \\ \hfill & =neut\left(a^n\right)*neut\left(a^n\right)\hfill \\ \hfill & =neut\left(a^n\right),\hfill \end{array}$$

$$(x*neut\left(a^n\right))*a^n=(a^n*neut\left(a^n\right))*x=a^n*x=neut\left(a^n\right).$$

Thus, $a^n*(x*neut\left(a^n\right))=(x*neut\left(a^n\right))*a^n=neut\left(a^n\right)$, for any $x\in \left\{anti\left(a^n\right)\right\}$.

(5)

For any $x\in \left\{anti\left(a^n\right)\right\}$, we have

$$\begin{array}{cc}\hfill (neut\left(a^n\right)*x)*a^n& =(neut\left(a^n\right)*x)*(neut\left(a^n\right)*a^n)\hfill \\ \hfill & =(neut\left(a^n\right)*neut\left(a^n\right))*(x*a^n)\hfill \\ \hfill & =neut\left(a^n\right)*neut\left(a^n\right)\hfill \\ \hfill & =neut\left(a^n\right),\hfill \end{array}$$

$$\begin{array}{cc}\hfill a^n*(neut\left(a^n\right)*x)& =(neut\left(a^n\right)*a^n)*(neut\left(a^n\right)*x)\hfill \\ \hfill & =(neut\left(a^n\right)*neut\left(a^n\right))*(a^n*x)\hfill \\ \hfill & =neut\left(a^n\right)*neut\left(a^n\right)\hfill \\ \hfill & =neut\left(a^n\right).\hfill \end{array}$$

Thus, $a^n*(neut\left(a^n\right)*x)=(neut\left(a^n\right)*x)*a^n=neut\left(a^n\right)$.

(6)

For any $x\in \left\{anti\left(a^n\right)\right\}$, we have

$$\begin{array}{cc}\hfill (neut\left(a^n\right)*x)*neut\left(a^n\right)& =(neut\left(a^n\right)*x)*(a^n*x)\hfill \\ \hfill & =(neut\left(a^n\right)*a^n)*(x*x)\hfill \\ \hfill & =(a^n*neut\left(a^n\right))*(x*x)\hfill \\ \hfill & =(a^n*x)*(neut\left(a^n\right)*x)\hfill \\ \hfill & =neut\left(a^n\right)*(neut\left(a^n\right)*x),\hfill \end{array}$$

$$\begin{array}{cc}\hfill neut\left(a^n\right)*(neut\left(a^n\right)*x)& =(x*a^n)*(neut\left(a^n\right)*x)\hfill \\ \hfill & =(x*neut\left(a^n\right))*(a^n*x)\hfill \\ \hfill & =(x*neut\left(a^n\right))*neut\left(a^n\right)\hfill \\ \hfill & =(neut\left(a^n\right)*neut\left(a^n\right))*x\hfill \\ \hfill & =neut\left(a^n\right)*x.\hfill \end{array}$$

Thus, $(neut\left(a^n\right)*x)*neut\left(a^n\right)=neut\left(a^n\right)*(neut\left(a^n\right)*x)=neut\left(a^n\right)*x$.

(7)

From (5) and (6), we have $neut(neut\left(a^n\right)*x)=neut\left(a^n\right)$, $a^n\in anti\{neut\left(a^n\right)*x\}$. From (2), $neut\left(a^n\right)*anti\left(a^n\right)$ is unique, we have

$$neut(neut\left(a^n\right)*x)*anti(neut\left(a^n\right)*x)=neut(neut\left(a^n\right)*x)*a^n=neut\left(a^n\right)*a^n=a^n.$$

 □

Example 8.

Let $S=\{a,b,c,d\}$, an operation * on S is defined as in

Table 7. A GAG-NET-Loop of Example 8.

*	a	b	c	d
a	a	a	a	d
b	a	a	c	d
c	a	b	a	d
d	d	d	d	a

. Since $neut\left(a\right)=a,\left\{anti\right(a\left)\right\}=\{a,b,c\},neut\left(d\right)=a,anti\left(d\right)=d$ and $b^2=a,c^2=a$, so $(S,*)$ is a GAG-NET-Loop. We can get that (Corresponding to the results of Proposition 3):

(1) 

Being $(b^2*b^2)*b^2=b^2*(b^2*b^2),(d^1*d^1)*d^1=d^1*(d^1*d^1)$, that is $(a^n*a^n)*a^n=a^n*(a^n*a^n)$.

(2) 

Being $a*a=a*b=a*c$, that is for any $x,y\in \left\{anti\left(c^2\right)\right\}$, $neut\left(c^2\right)*x=neut\left(c^2\right)*y$.

(3) 

Being $neut\left(neut\left(a^1\right)\right)=neut\left(a^1\right)=a$, $neut\left(neut\left(d^1\right)\right)=neut\left(d^1\right)=a$, $neut\left(neut\left(b^2\right)\right)=neut\left(b^2\right)=a$, $neut\left(neut\left(c^2\right)\right)=neut\left(c^2\right)=a$, that is $neut\left(neut\left(a^n\right)\right)=neut\left(a^n\right)$.

(4) 

Being $c^2*(a*neut\left(c^2\right))=a$, $(a*neut\left(c^2\right))*c^2=a=neut\left(c^2\right)$, $c^2*(b*neut\left(c^2\right))=a$, $(b*neut\left(c^2\right))*c^2=a=neut\left(c^2\right)$, $c^2*(c*neut\left(c^2\right))=a$, $(c*neut\left(c^2\right))*c^2=a=neut\left(c^2\right)$, that is $c^2*(x*neut\left(c^2\right))=(x*neut\left(c^2\right))*c^2=neut\left(c^2\right)$, for any $x\in \left\{anti\left(c^2\right)\right\}$. Being $d^1*(d*neut\left(d^1\right))=a$, $(d*neut\left(d^1\right))*d^1=a=neut\left(d^1\right)$, that is $d^1*(x*neut\left(d^1\right))=(x*neut\left(d^1\right))*d^1=neut\left(d^1\right)$, for any $x\in \left\{anti\left(d^1\right)\right\}$.

(5) 

Being $c^2*(neut\left(c^2\right)*a)=a$, $(neut\left(c^2\right)*a)*c^2=a=neut\left(c^2\right)$, $c^2*(neut\left(c^2\right)*b)=a$, $(neut\left(c^2\right)*b)*c^2=a=neut\left(c^2\right)$, $c^2*(neut\left(c^2\right)*c)=a$, $(neut\left(c^2\right)*c)*c^2=a=neut\left(c^2\right)$, that is $c^2*(neut\left(c^2\right)*x)=(neut\left(c^2\right)*x)*c^2=neut\left(c^2\right)$, for any $x\in \left\{anti\left(c^2\right)\right\}$. Being $d^1*(neut\left(d^1\right)*d)=a$, $(neut\left(d^1\right)*d)*d^1=a=neut\left(d^1\right)$, that is $d^1*(neut\left(d^1\right)*x)=(neut\left(d^1\right)*x)*d^1=neut\left(d^1\right)$, for any $x\in \left\{anti\left(d^1\right)\right\}$.

(6) 

Being $neut\left(c^2\right)*a=a$, $(neut\left(c^2\right)*a)*neut\left(c^2\right)=a$, $neut\left(c^2\right)*(neut\left(c^2\right)*a)=a$; $neut\left(c^2\right)*b=a$, $(neut\left(c^2\right)*b)*neut\left(c^2\right)=a$, $neut\left(c^2\right)*(neut\left(c^2\right)*b)=a$; $neut\left(c^2\right)*c=a$, $(neut\left(c^2\right)*c)*neut\left(c^2\right)=a$, $neut\left(c^2\right)*(neut\left(c^2\right)*a)=a$; that is $(neut\left(c^2\right)*x)*neut\left(c^2\right)=neut\left(c^2\right)*(neut\left(c^2\right)*x)=neut\left(c^2\right)*x$, for any $x\in \left\{anti\left(c^2\right)\right\}$. Being $neut\left(d^1\right)*d=d$, $(neut\left(d^1\right)*d)*neut\left(d^1\right)=d$, $neut\left(d^1\right)*(neut\left(d^1\right)*d)=d$, that is $(neut\left(d^1\right)*x)*neut\left(d^1\right)=neut\left(d^1\right)*(neut\left(d^1\right)*x)=neut\left(d^1\right)*x$, for any $x\in \left\{anti\left(d^1\right)\right\}$.

(7) 

Being $neut(neut\left(c^2\right)*a)*anti(neut\left(c^2\right)*a)=a=c^2$; $neut(neut\left(c^2\right)*b)*anti(neut\left(c^2\right)*b)=a=c^2$; $neut(neut\left(c^2\right)*c)*anti(neut\left(c^2\right)*c)=a=c^2$; that is $neut(neut\left(c^2\right)*x)*anti(neut\left(c^2\right)*x)=c^2$, for any $x\in \left\{anti\left(c^2\right)\right\}$. Being $neut(neut\left(d^1\right)*d)*anti(neut\left(d^1\right)*d)=d^1$, that is $neut(neut\left(d^1\right)*x)*anti(neut\left(d^1\right)*x)=d^1$, for any $x\in \left\{anti\left(d^1\right)\right\}$.

Proposition 4.

Let $(N,*)$ be a GAG-NET-Loop, then $\forall a,b\in N$, there are two positive integers n and m such that the following hold:

(1) 

$neut\left(a^n\right)*neut\left(b^m\right)=neut(a^n*b^m)$.

(2) 

$anti\left(a^n\right)*anti\left(b^m\right)\in \left\{anti(a^n*b^m)\right\}$.

Proof. 

Being $(N,*)$ be a GAG-NET-Loop, then for $a\in N$, there is a positive integer n, such that $a^n$ has the neutral element and opposite element, denoted by $neut\left(a^n\right)$ and $anti\left(a^n\right)$, respectively. For $b\in N$, there is a positive integer m, such that $b^m$ has the neutral element and opposite element, denoted by $neut\left(b^m\right)$ and $anti\left(b^m\right)$, respectively. Thus,

$$\begin{array}{cc}\hfill (neut\left(a^n\right)*neut\left(b^m\right))*(a^n*b^m)& =(neut\left(a^n\right)*a^n)*(neut\left(b^m\right)*b^m)\hfill \\ \hfill & =a^n*b^m.\hfill \end{array}$$

In the same way, we have $(a^n*b^m)*(neut\left(a^n\right)*neut\left(b^m\right))=a^n*b^m.$

That is,

$$(a^n*b^m)*(neut\left(a^n\right)*neut\left(b^m\right))=(neut\left(a^n\right)*neut\left(b^m\right))*(a^n*b^m)=a^n*b^m.$$

Moreover, for any $anti\left(a^n\right)\in \left\{anti\left(a^n\right)\right\}$ and $anti\left(b^m\right)\in \left\{anti\left(b^m\right)\right\}$, we can get

$$\begin{array}{cc}\hfill (anti\left(a^n\right)*anti\left(b^m\right))*(a^n*b^m)& =(anti\left(a^n\right)*a^n)*(anti\left(b^m\right)*b^m)\hfill \\ \hfill & =neut\left(a^n\right)*neut\left(b^m\right).\hfill \end{array}$$

Similarly, we have $(a^n*b^m)*(anti\left(a^n\right)*anti\left(b^m\right))=neut\left(a^n\right)*neut\left(b^m\right)$. That is:

$$(a^n*b^m)*(anti\left(a^n\right)*anti\left(b^m\right))=(anti\left(a^n\right)*anti\left(b^m\right))*(a^n*b^m)=neut\left(a^n\right)*neut\left(b^m\right).$$

Thus, we have

$$neut\left(a^n\right)*neut\left(b^m\right)\in \left\{neut(a^n*b^m)\right\}.$$

From this, by Proposition 2, we get $neut\left(a^n\right)*neut\left(b^m\right)=neut(a^n*b^m)$. Therefore, we get $anti\left(a^n\right)*anti\left(b^m\right)\in \left\{anti(a^n*b^m)\right\}$. □

Example 9.

Apply the $(S,*)$ in Example 8, since $neut\left(a\right)=a,\left\{anti\right(a\left)\right\}=\{a,b,c\},neut\left(d\right)=a,anti\left(d\right)=d$ and $b^2=a,c^2=a$, so $(S,*)$ is a GAG-NET-Loop, we can get:

(1)

Being $neut\left(c^2\right)*neut\left(d^1\right)=a$, $neut(c^2*d^1)=a$, that is $neut\left(c^2\right)*neut\left(d^1\right)=neut(c^2*d^1)$.

(2)

Being $a*d=b*d=c*d=d$, that is $anti\left(c^2\right)*anti\left(d^1\right)\in \left\{anti(c^2*d^1)\right\}$

Theorem 7.

Let $(N,*)$ be a GAG-NET-Loop. Then, N is a quasi regular AG-groupoid.

Proof. 

For any a in N, by Definition 11 we have $(a^n*anti\left(a^n\right))*a^n=neut\left(a^n\right)*a^n=a^n$. From this and Definition 4, we know that N is a quasi regular AG-groupoid. □

The following example shows that a quasi regular AG-groupoid may not be a GAG-NET-loop.

Example 10.

Apply the $(S,*)$ in Example 1, Being $1=(1*3)*1,2=(2*4)*2,3=(3*1)*3,4=(4*2)*4$, From Definition 4, S is a quasi regular AG-groupoid. However, it is not a GAG-NET-Loop.

Theorem 8.

Let $(N,*)$ be a GAG-NET-Loop. Then, N is a quasi fully regular AG-groupoid.

Proof. 

Suppose $a\in N$ and $(a,neut\left(a^n\right),anti\left(a^n\right))$ is a generalized neutrosophic extended triplet with degree n, then there exists $m\in \left\{anti\left(a^n\right)\right\},a^n*m=m*a^n=neut\left(a^n\right)$. Denote $p=m*neut\left(a^n\right),q=neut\left(a^n\right);r=m,s=neut\left(a^n\right);t=m,u=neut\left(a^n\right);v=m;w=m*neut\left(a^n\right);x=m,y=neut\left(a^n\right)$, then

$$\begin{array}{cc}\hfill (p*{\left(a^n\right)}^2)*q& =((m*neut\left(a^n\right))*{\left(a^n\right)}^2)*neut\left(a^n\right)\hfill \\ \hfill & =(({\left(a^n\right)}^2*neut\left(a^n\right))*m)*neut\left(a^n\right)\left(bytheleftinvertivelaw\right)\hfill \\ \hfill & =(((a^n*a^n)*neut\left(a^n\right))*m)*neut\left(a^n\right)\hfill \\ \hfill & =(((neut\left(a^n\right)*a^n)*a^n)*m)*neut\left(a^n\right)\left(bytheleftinvertivelaw\right)\hfill \\ \hfill & =((a^n*a^n)*m)*neut\left(a^n\right)\hfill \\ \hfill & =((m*a^n)*a^n)*neut\left(a^n\right)\left(bytheleftinvertivelaw\right)\hfill \\ \hfill & =(neut\left(a^n\right)*a^n)*neut\left(a^n\right)\hfill \\ \hfill & =a^n*neut\left(a^n\right)=a^n,\hfill \end{array}$$

$$(r*a^n)*(a^n*s)=(m*a^n)*(a^n*neut\left(a^n\right))=neut\left(a^n\right)*a^n=a^n,$$

$$(a^n*t)*(a^n*u)=(a^n*m)*(a^n*neut\left(a^n\right))=neut\left(a^n\right)*a^n=a^n,$$

$$(a^n*a^n)*v=(a^n*a^n)*m=(m*a^n)*a^n=neut\left(a^n\right)*a^n=a^n,$$

$$\begin{array}{cc}\hfill w*(a^n*a^n)& =(m*neut\left(a^n\right))*(a^n*a^n)\hfill \\ \hfill & =(m*a^n)*(neut\left(a^n\right)*a^n)\left(bythemediallaw\right)\hfill \\ \hfill & =(m*a^n)*a^n\hfill \\ \hfill & =neut\left(a^n\right)*a^n=a^n,\hfill \end{array}$$

$$(x*a^n)*(y*a^n)=(m*a^n)*(neut\left(a^n\right)*a^n)=neut\left(a^n\right)*a^n=a^n.$$

Moreover, from Proposition 4, we get:

$$neut\left(a^n\right)*neut\left(b^m\right)=neut(a^n*b^m),anti\left(a^n\right)*anti\left(b^m\right)\in \left\{anti(a^n*b^m)\right\}.$$

If $b^m=a^n$, we have $neut\left(a^n\right)*neut\left(a^n\right)=neut(a^n*a^n)$, $anti\left(a^n\right)*anti\left(a^n\right)\in \left\{anti(a^n*a^n)\right\}$, there exists $k\in \left\{anti(a^n*a^n)\right\}$. Denote $z=k*m$, then

$$\begin{array}{cc}\hfill ({\left(a^n\right)}^2*z)*{\left(a^n\right)}^2& =((a^n*a^n)*z)*{\left(a^n\right)}^2\hfill \\ \hfill & =((z*a^n)*a^n)*{\left(a^n\right)}^2\left(applyingtheleftinvertivelaw\right)\hfill \\ \hfill & =({\left(a^n\right)}^2*a^n)*(z*a^n)\left(applyingtheleftinvertivelaw\right)\hfill \\ \hfill & =({\left(a^n\right)}^2*a^n)*((k*m)*a^n)\hfill \\ \hfill & =({\left(a^n\right)}^2*a^n)*((a^n*m)*k)\left(bytheleftinvertivelaw\right)\hfill \\ \hfill & =({\left(a^n\right)}^2*a^n)*(neut\left(a^n\right)*k)(bym\in \left\{anti\left(a^n\right)\right\})\hfill \\ \hfill & =((a^n*a^n)*(neut\left(a^n\right)*a^n))*(neut\left(a^n\right)*k)\hfill \\ \hfill & =((a^n*neut\left(a^n\right))*(a^n*a^n))*(neut\left(a^n\right)*k)\left(applyingthemediallaw\right)\hfill \\ \hfill & =(a^n*{\left(a^n\right)}^2)*(neut\left(a^n\right)*k)\hfill \\ \hfill & =(a^n*neut\left(a^n\right))*({\left(a^n\right)}^2*k)\left(applyingthemediallaw\right)\hfill \\ \hfill & =a^n*neut(a^n*a^n)(bythedefinitionofk\in \left\{anti(a^n*a^n)\right\})\hfill \\ \hfill & =a^n*(neut\left(a^n\right)*neut\left(a^n\right))\hfill \\ \hfill & =a^n*neut\left(a^n\right)\left(byProposition\left(2\right)\right)\hfill \\ \hfill & =a^n.\hfill \end{array}$$

Therefore, combining above results, by Definition 5, we know that N is a quasi fully regular AG-groupoid. □

The following example shows that a quasi fully regular AG-groupoid may not be a GAG-NET-loop.

Example 11.

Applying the $(S,*)$ in Example 1, when $a=1$,$p=1,q=3,r=4,s=3,t=2,u=3,v=2,w=2,x=4,y=2,z=3$, we have $a^2=2$, and

$$\begin{array}{cc}\hfill 1& =(1*2)*3=(4*1)*(1*3)=(1*2)*(1*3)\hfill \\ \hfill & =(1*1)*2=2*(1*1)=(4*1)*(2*1)\hfill \\ \hfill & =(2*3)*2.\hfill \end{array}$$

When $a=4$,$p=1,q=3,r=4,s=4,t=3,u=2,v=3,w=3,x=4,y=4,z=2$, we have $a^2=3$, and

$$\begin{array}{cc}\hfill 4& =(1*3)*3=(4*4)*(4*4)=(4*3)*(4*2)\hfill \\ \hfill & =(4*4)*3=3*(4*4)=(4*4)*(4*4)\hfill \\ \hfill & =(3*2)*3.\hfill \end{array}$$

Being $2^2=1,3^3=1$, from Definition 5, S is a quasi fully regular AG-groupoid. However, it is not a GAG-NET-Loop.

Definition 13.

An AG-groupoid $(S,*)$ is called a quasi strong inverse AG-groupoid, if the following conditions are satisfied: for any $a\in S$, there exists a positive integer n, $a^n\in S$, and a unary operation $a^n\to {\left(a^n\right)}^{-1}$ on S such that

$${\left({\left(a^n\right)}^{-1}\right)}^{-1}=a^n,(a^n*{\left(a^n\right)}^{-1})*a^n=a^n*(a^n*{\left(a^n\right)}^{-1})=a^n,a^n*{\left(a^n\right)}^{-1}={\left(a^n\right)}^{-1}*a^n.$$

Theorem 9.

Let $(N,*)$ be a groupoid. Then, N is a GAG-NET-Loop if and only if it is a quasi strong inverse AG-groupoid.

Proof. 

Necessity: Suppose N is a GAG-NET-Loop, from Definition 12, for each $a\in N$, there exists a generalized neutrosophic extended triplet with degree n denoted by $(a,neut\left(a^n\right),anti\left(a^n\right))$. Set

$${\left(a^n\right)}^{-1}=neut\left(a^n\right)*anti\left(a^n\right),$$

by Proposition 3(2), $neut\left(a^n\right)*anti\left(a^n\right)$ is unique, so ${\left(a^n\right)}^{-1}$ is unique. By Proposition 3(7), we have

$${\left({\left(a^n\right)}^{-1}\right)}^{-1}=neut(neut\left(a^n\right)*anti\left(a^n\right))*anti(neut\left(a^n\right)*anti\left(a^n\right))=a^n.$$

Being

$${\left(a^n\right)}^{-1}*a^n=(neut\left(a^n\right)*anti\left(a^n\right))*a^n=(a^n*anti\left(a^n\right))*neut\left(a^n\right)=neut\left(a^n\right)*neut\left(a^n\right)=neut\left(a^n\right),$$

$$\begin{array}{cc}\hfill a^n*{\left(a^n\right)}^{-1}& =a^n*(neut\left(a^n\right)*anti\left(a^n\right))\hfill \\ \hfill & =(neut\left(a^n\right)*a^n)*(neut\left(a^n\right)*anti\left(a^n\right))\hfill \\ \hfill & =(neut\left(a^n\right)*neut\left(a^n\right))*(a^n*anti\left(a^n\right))\hfill \\ \hfill & =neut\left(a^n\right),\hfill \end{array}$$

we have

$${\left(a^n\right)}^{-1}*a^n=a^n*{\left(a^n\right)}^{-1},$$

$$(a^n*{\left(a^n\right)}^{-1})*a^n=neut\left(a^n\right)*a^n=a^n,$$

$$a^n*(a^n*{\left(a^n\right)}^{-1})=a^n*neut\left(a^n\right)=a^n,$$

$$(a^n*{\left(a^n\right)}^{-1})*a^n=a^n*(a^n*{\left(a^n\right)}^{-1})=a^n.$$

From Definition 13, N is a quasi strong inverse AG-groupoid.

Sufficiency: If N is a quasi strong inverse AG-groupoid, and ${\left(a^n\right)}^{-1}\in N$, such that $a^n*{\left(a^n\right)}^{-1}={\left(a^n\right)}^{-1}*a^n$ and $(a^n*{\left(a^n\right)}^{-1})*a^n=a^n*(a^n*{\left(a^n\right)}^{-1})=a^n$. Set

$$neut\left(a^n\right)=a^n*{\left(a^n\right)}^{-1},$$

then $neut\left(a^n\right)*a^n=(a^n*{\left(a^n\right)}^{-1})*a^n=a^n*(a^n*{\left(a^n\right)}^{-1})=a^n*neut\left(a^n\right)=a^n,$

$$a^n*{\left(a^n\right)}^{-1}={\left(a^n\right)}^{-1}*a^n=neut\left(a^n\right).$$

From Definition 12, we have that N is a GAG-NET-Loop and ${\left(a^n\right)}^{-1}\in \left\{anti\left(a^n\right)\right\}$.  □

Example 12.

Applying $(S,*)$ in Example 8, we know that it is a GAG-NET-Loop. We will show that it is a quasi strong inverse AG-groupoid in the following.

For d, there exists an inverse element $d^{-1}=d$, such that ${\left(d^{-1}\right)}^{-1}=d$, $(d*d^{-1})*d=d*(d*d^{-1})=d,d*d^{-1}=d^{-1}*d=a$, so d is quasi strong inverse. a is quasi strong inverse for the same reason. Moreover, being $b^2=a,c^2=a$, b and c are quasi strong inverse, thus $(S,*)$ is a quasi strong inverse AG-groupoid by Definition 13.

Definition 14.

Let $(N,*)$ be a GAG-NET-Loop. N is called a weak commutative GAG-NET-Loop if $\forall a,b\in N$, there exist a generalized neutrosophic extended triplet with degree n (denoted by $(a,neut\left(a^n\right),anti\left(a^n\right))$) and a generalized neutrosophic extended triplet with degree m (denoted by $(b,neut\left(b^m\right),anti\left(b^m\right))$), $n,m\in Z^{+}$, $a^n*neut\left(b^m\right)=neut\left(b^m\right)*a^n$.

Example 13.

Let $S=\{1,2,3,4,5,6,7\}$, an operation * on S is defined as in

Table 8. The operation table of Example 13.

*	1	2	3	4	5	6	7
1	1	2	3	4	5	6	7
2	2	2	2	2	2	2	2
3	4	2	1	3	5	6	7
4	3	2	4	1	5	6	7
5	5	2	5	5	2	2	2
6	6	2	6	6	2	6	6
7	7	2	7	7	2	6	6

. Since $(1,1,1),(2,2,2)$ and $(6,6,6)$ are neutrosophic extended triplets, but $3,4,5,7$ do not have the neutral element and opposite element, thus S is not an AG-NET-Loop. Moreover $3^2=1,4^2=1,5^2=2,7^2=6$ have the neutral element and opposite element, so $(S,*)$ is a GAG-NET-Loop. It is not a commutative GAG-NET-Loop being $3*1\ne 1*3$. We can show that it is a weak commutative GAG-NET-Loop.

For $1,2,3,4,5,6$ and 7, there exist positive integers $1,1,2,2,2,1$ and 2, respectively, thus $S^{\prime }=\{1^1,2^1,3^2,4^2,5^2,6^1,7^2\}=\{1,2,6\}$ being $3^2=1,4^2=1,5^2=2,7^2=6$. We know that $neut\left(1\right)=1,neut\left(2\right)=2,neut\left(6\right)=6$, thus $\{neut\left(1\right),neut\left(2\right),neut\left(6\right)\}\subseteq S^{\prime }$. In Table 8, we can get the sub algebra system $(S^{\prime },*)$ of $(S,*)$ as in

Table 9. The sub algebra system $S^{\prime }$ of S in Example 13.

*	1	2	6
1	1	2	6
2	2	2	2
6	6	2	6

, and $(S^{\prime },*)$ is commutative. Thus, $(S,*)$ is a weak commutative GAG-NET-Loop.

Example 14.

Let $S=\{1,2,3,4\}$, an operation * on S is defined as in

Table 10. The operation table of Example 14.

*	1	2	3	4
1	1	4	2	3
2	3	2	4	1
3	4	1	3	2
4	2	3	1	4

. Being $neut\left(1\right)*2=4\ne 3=2*neut\left(1\right)$, S is not a weak commutative GAG-NET-Loop. Moreover, it is not a commutative AG-NET-Loop.

Proposition 5.

Let $(N,*)$ be a GAG-NET-Loop. Then, $(N,*)$ is a weak commutative GAG-NET-Loop if and only if N satisfies the following conditions: $\forall a,b\in N$, there exist a generalized neutrosophic extended triplet with degree n (denoted by $(a,neut\left(a^n\right),anti\left(a^n\right))$) and a generalized neutrosophic extended triplet with degree m (denoted by $(b,neut\left(b^m\right),anti\left(b^m\right))$), $n,m\in Z^{+}$, $a^n*b^m=b^m*a^n.$

Proof. 

Necessity: If $(N,*)$ is a weak commutative GAG-NET-Loop, then there are two positive integers $n,m$, such that $a^n$ and $b^m$ have the neutral element and opposite element. Thus, from Definition 14, $\forall a,b\in N$, we have

$$\begin{array}{cc}\hfill a^n*b^m& =(neut\left(a^n\right)*a^n)*(b^m*neut\left(b^m\right))\hfill \\ \hfill & =(neut\left(a^n\right)*b^m)*(a^n*neut\left(b^m\right))\hfill \\ \hfill & =(b^m*neut\left(a^n\right))*(neut\left(b^m\right)*a^n)\hfill \\ \hfill & =(b^m*neut\left(b^m\right))*(neut\left(a^n\right)*a^n)\hfill \\ \hfill & =b^m*a^n.\hfill \end{array}$$

Sufficiency: If $(N,*)$ is a GAG-NET-Loop, then for $a\in N$, there is a positive integer n, such that $a^n$ has the neutral element and opposite element, denoted by $neut\left(a^n\right)$ and $anti\left(a^n\right)$, respectively. For $b\in N$, there is a positive integer m, such that $b^m$ has the neutral element and opposite element, denoted by $neut\left(b^m\right)$ and $anti\left(b^m\right)$, respectively. Suppose that $(N,*)$ satisfies the conditions $a^n*b^m=b^m*a^n$, From Proposition 2, we have $neut\left(b^m\right)$ exists neutral element and opposite element. We get $a^n*neut\left(b^m\right)=neut\left(b^m\right)*a^n$. From Definition 14, we know that $(N,*)$ is a weak commutative GAG-NET-Loop. □

Definition 15.

A GAG-NET-Loop $(S,*)$ is called a quasi Clifford AG-groupoid, if it is a quasi strong inverse AG-groupoid and for any $a,b\in S$, there are two positive integers $n,m$ such that

$$a^n*(b^m*{\left(b^m\right)}^{-1})=(b^m*{\left(b^m\right)}^{-1})*a^n.$$

Theorem 10.

Let $(N,*)$ be a groupoid. Then, N is a weak commutative GAG-NET-Loop if and only if it is a quasi Clifford AG-groupoid.

Proof. 

Necessity: Suppose that N is a weak commutative GAG-NET-Loop. By Theorem 9, we know that N is a quasi strong inverse AG-groupoid, then $\forall a,b\in N$ there are two positive integers $n,m$, such that $a^n$ and $b^m$ have the neutral element and opposite element. Set

$${\left(a^n\right)}^{-1}=neut\left(a^n\right)*anti\left(a^n\right).$$

For any $a,b\in N$, we have

$$a^n*(b^m*{\left(b^m\right)}^{-1})=a^n*neut\left(b^m\right)=neut\left(b^m\right)*a^n=(b^m*{\left(b^m\right)}^{-1})*a^n.$$

From Definition 15, we know that N is a quasi Clifford AG-groupoid.

Sufficiency: Assume that N is a quasi Clifford AG-groupoid, from Definition 15, it is a quasi strong inverse AG-groupoid. By Theorem 9, we know that N is a GAG-NET-Loop. Then, $\forall a,b\in N$ there are two positive integers $n,m$, such that $a^n$ and $b^m$ have the neutral element and opposite element, ${\left(a^n\right)}^{-1}\in N,{\left(b^m\right)}^{-1}\in N$. Set

$$neut\left(a^n\right)=a^n*{\left(a^n\right)}^{-1},neut\left(b^m\right)=b^m*{\left(b^m\right)}^{-1}.$$

From Definition 15, being $a^n*(b^m*{\left(b^m\right)}^{-1})=(b^m*{\left(b^m\right)}^{-1})*a^n,$ we have $a^n*neut\left(b^m\right)=neut\left(b^m\right)*a^n$. We can get that N is a weak commutative GAG-NET-Loop by Definition 14. □

Example 15.

Let $S=\{1,2,3,4,5,6,7,8\}$, an operation * on S is defined as in

Table 11. The operation table of Example 15.

*	1	2	3	4	5	6	7	8
1	1	2	3	4	5	6	7	8
2	2	2	2	2	2	2	2	2
3	4	2	1	3	5	6	7	8
4	3	2	4	1	5	6	7	8
5	5	2	5	5	2	2	2	2
6	6	2	6	6	2	6	6	6
7	7	2	7	7	2	6	6	6
8	8	2	8	8	2	6	6	6

. It is a weak commutative GAG-NET-Loop. We show that it is a quasi Clifford AG-groupoid. From Theorem 9, we can see that $(S,*)$ is a quasi strong inverse AG-groupoid. We just show for any $x,y\in S$, there are two positive integers n and m such that $x^n*(y^m*{\left(y^m\right)}^{-1})=(y^m*{\left(y^m\right)}^{-1})*x^n$.

In Example 15, $1,2,3,4,5,6,7$ and 8, there exist positive integers $1,1,2,2,2,1,2$ and 2, respectively, and set $1^{-1}=1,2^{-1}=2,{\left(3^2\right)}^{-1}=1,{\left(4^2\right)}^{-1}=1,{\left(5^2\right)}^{-1}=2,6^{-1}=6,{\left(7^2\right)}^{-1}=6,{\left(8^2\right)}^{-1}=6$. For any $x,y\in \{1^1,2^1,3^2,4^2,5^2,6^1,7^2,8^2\}$, without losing generality, let $x=1,y=2$, we can get $1^1*(2^1*{\left(2^1\right)}^{-1})=(2^1*{\left(2^1\right)}^{-1})*1^1=2$. We can verify other cases, thus $(S,*)$ is a quasi Clifford AG-groupoid.

Example 16.

Let $S=\{1,2,3,4,5\}$, an operation * on S is defined as in

Table 12. The operation table of Example 16.

*	1	2	3	4	5
1	1	4	2	3	1
2	3	2	4	1	3
3	4	1	3	2	4
4	2	3	1	4	2
5	1	4	2	3	5

. it is not a weak commutative GAG-NET-Loop. We show that there exist $x,y\in S$, for any two positive integers n and m such that $x^n*(y^m*{\left(y^m\right)}^{-1})\ne (y^m*{\left(y^m\right)}^{-1})*x^n$.

In Example 16, for any $n,m\in Z^{+}$, $1^n=1,2^m=2$ and ${\left(1^n\right)}^{-1}=1,{\left(2^m\right)}^{-1}=2$, but $1^n*(2^m*{\left(2^m\right)}^{-1})=4\ne 3=(2^m*{\left(2^m\right)}^{-1})*1^n$. That is, for $1,2\in S$, there are not two positive integers $n,m$ such that $1^n*(2^m*{\left(2^m\right)}^{-1})=(2^m*{\left(2^m\right)}^{-1})*1^n$. Thus, $(S,*)$ is not a quasi Clifford AG-groupoid.

5. Conclusions

We thoroughly study the GAG-NET-Loop from the perspective of the AG-groupoid theory and obtained some important results. Figure 1 and Figure 2 give the relations of the GAG-NET-Loop and other algebraic structures.

As can be seen in Figure 1, we prove that the AG-NET-Loop is equal to the strong inverse AG-groupoid, the GAG-NET-Loop is equal to the quasi strong inverse AG-groupoid, and the weak commutative GAG-NET-Loop is equal to the quasi Clifford AG-groupoid.

As can be seen in Figure 2, we prove that a GAG-NET-loop is a quasi regular AG-groupoid, but a quasi regular AG-groupoid may not be a GAG-NET-loop; a GAG-NET-loop is a quasi fully regular AG-groupoid, but a quasi fully regular AG-groupoid may not be a GAG-NET-loop.

Figure 3 can be used to further express the relationships among GAG-NET-Loop and some algebraic systems. Here, as shown in Example 2, A represents a commutative AG-NET-Loop; as shown in Example 15, B represents a weak commutative GAG-NET-Loop, but it is not an AG-NET-Loop; as i s shown in Example 14, C represents a non-commutative AG-NET-Loop; D represents a GAG-NET- Loop, but it is neither an AG-NET-Loop nor a weak commutative GAG-NET-Loop; as shown in Example 10, E represents a quasi regular AG-groupoid, but it is not a GAG-NET-Loop; and as shown in Example 11, F represents a quasi fully regular AG-groupoid, but it is not a GAG-NET-Loop. A+B represents a weak commutative GAG-NET-Loop, A+C represents an AG-NET-Loop, A+B+C+D represents a GAG-NET-Loop, A+B+C+D+E represents a quasi regular AG-groupoid, and A+B+C+D+F represents a quasi fully regular AG-groupoid.

All these results are interesting for the exploration of the structure characterization of GAG-NET-Loop. As the next research topics, we want to find some special GAG-NET-Loops which can be decomposed into some smaller GAG-NET-Loops, and explore the relationship between these special GAG-NET-Loops and the related AG-groupoids.