Modeling and Optimal Control on the Spread of Hantavirus Infection
Abstract
1. Introduction
2. The Optimal Control Model
3. Analyzing the Model
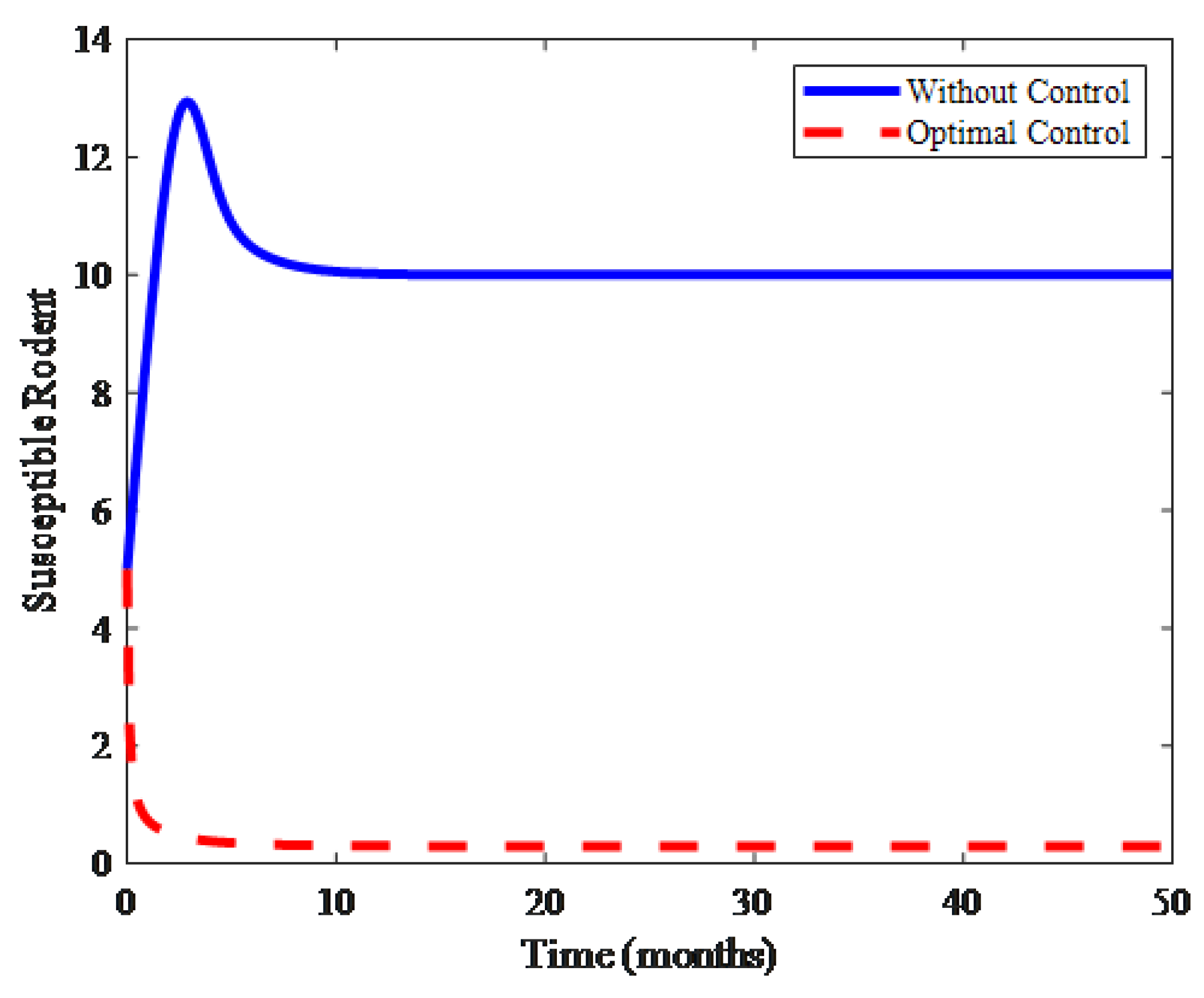
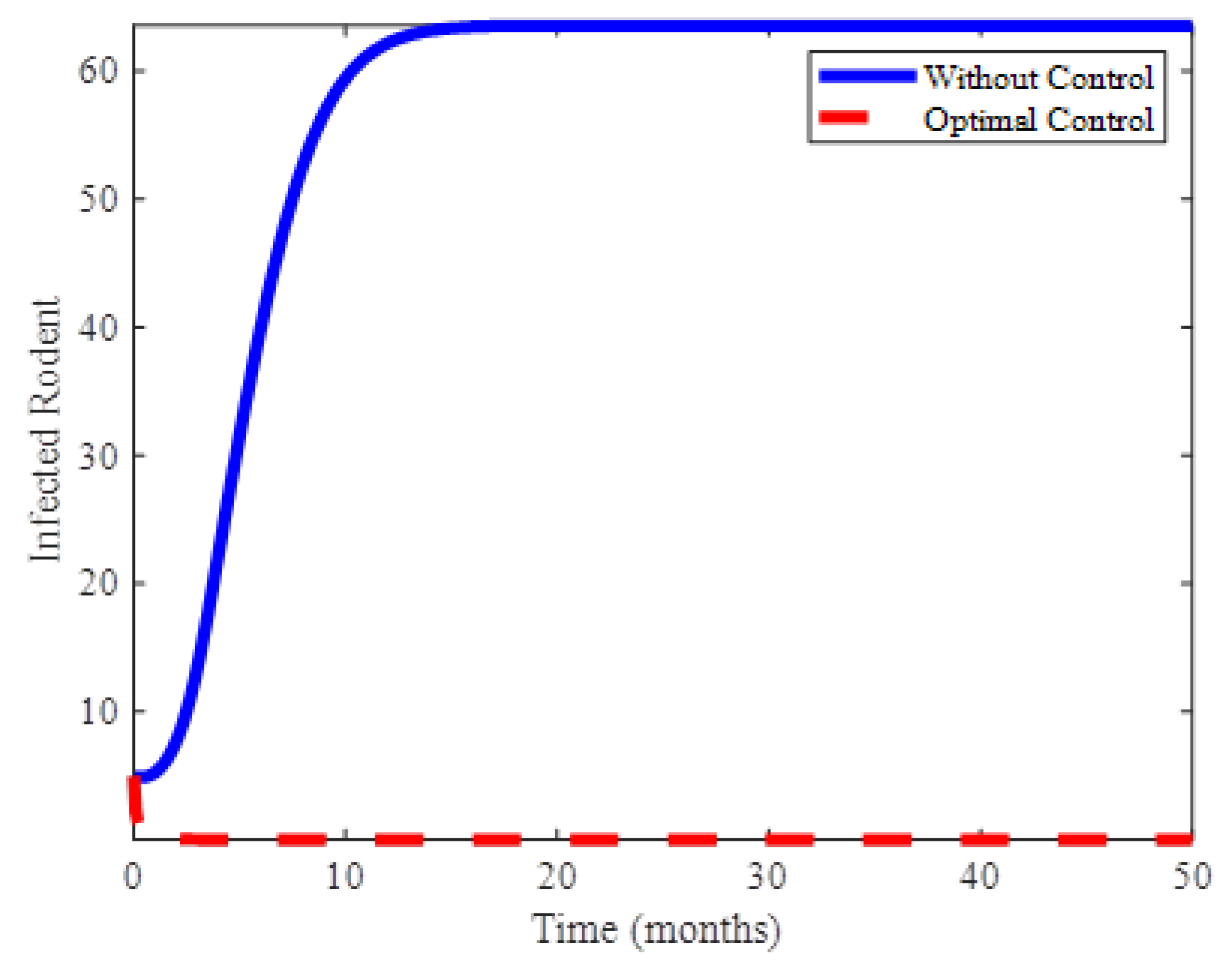
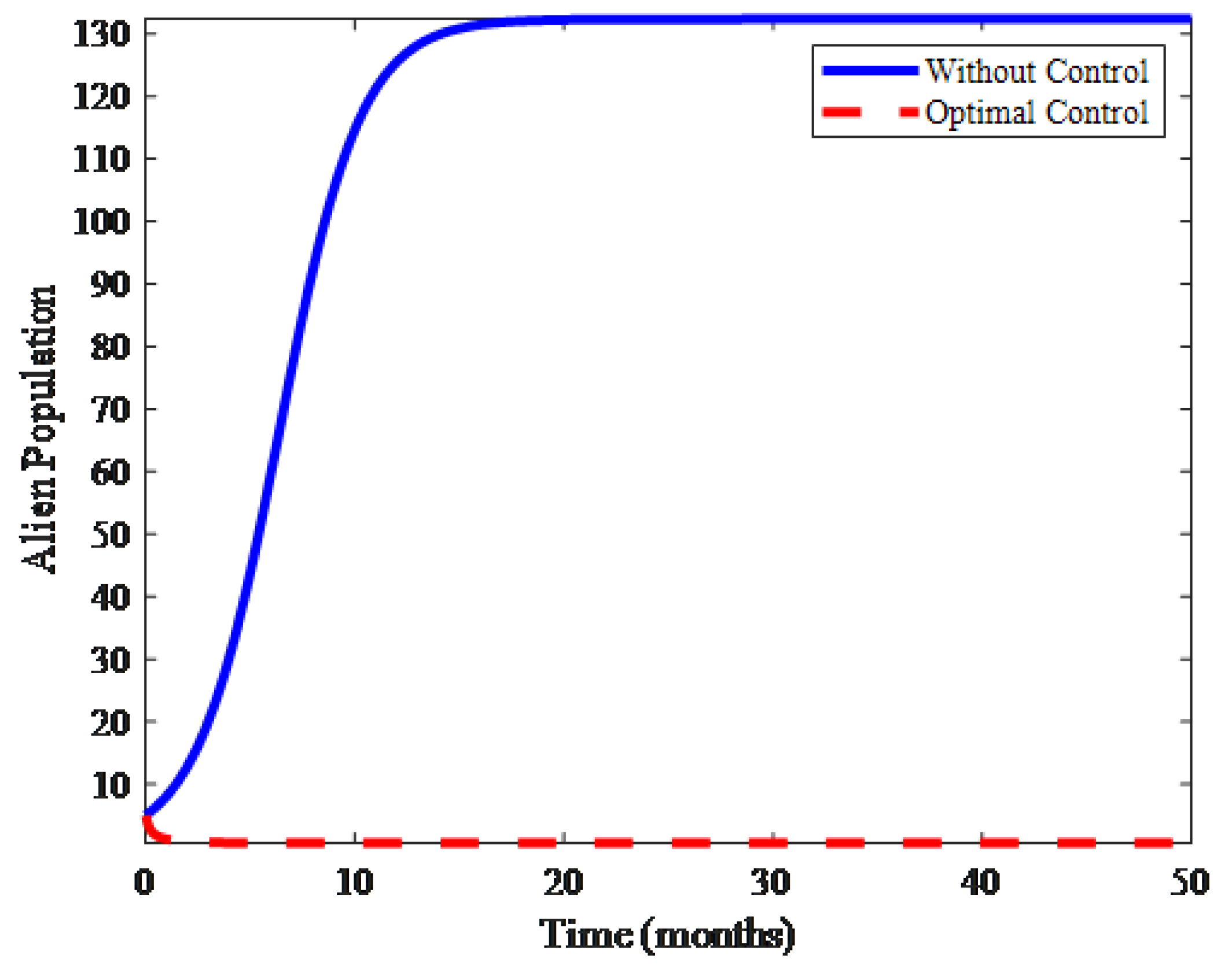
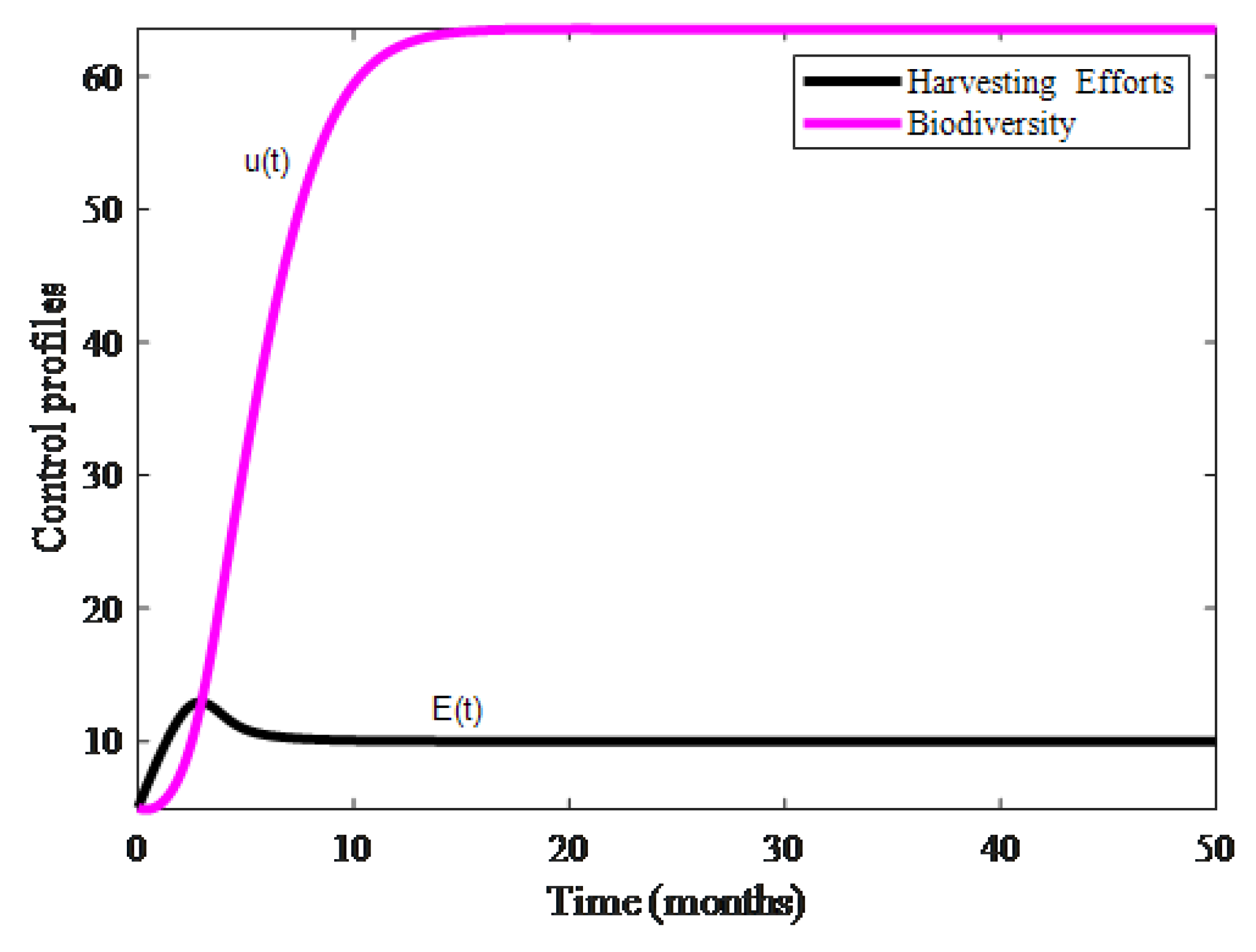
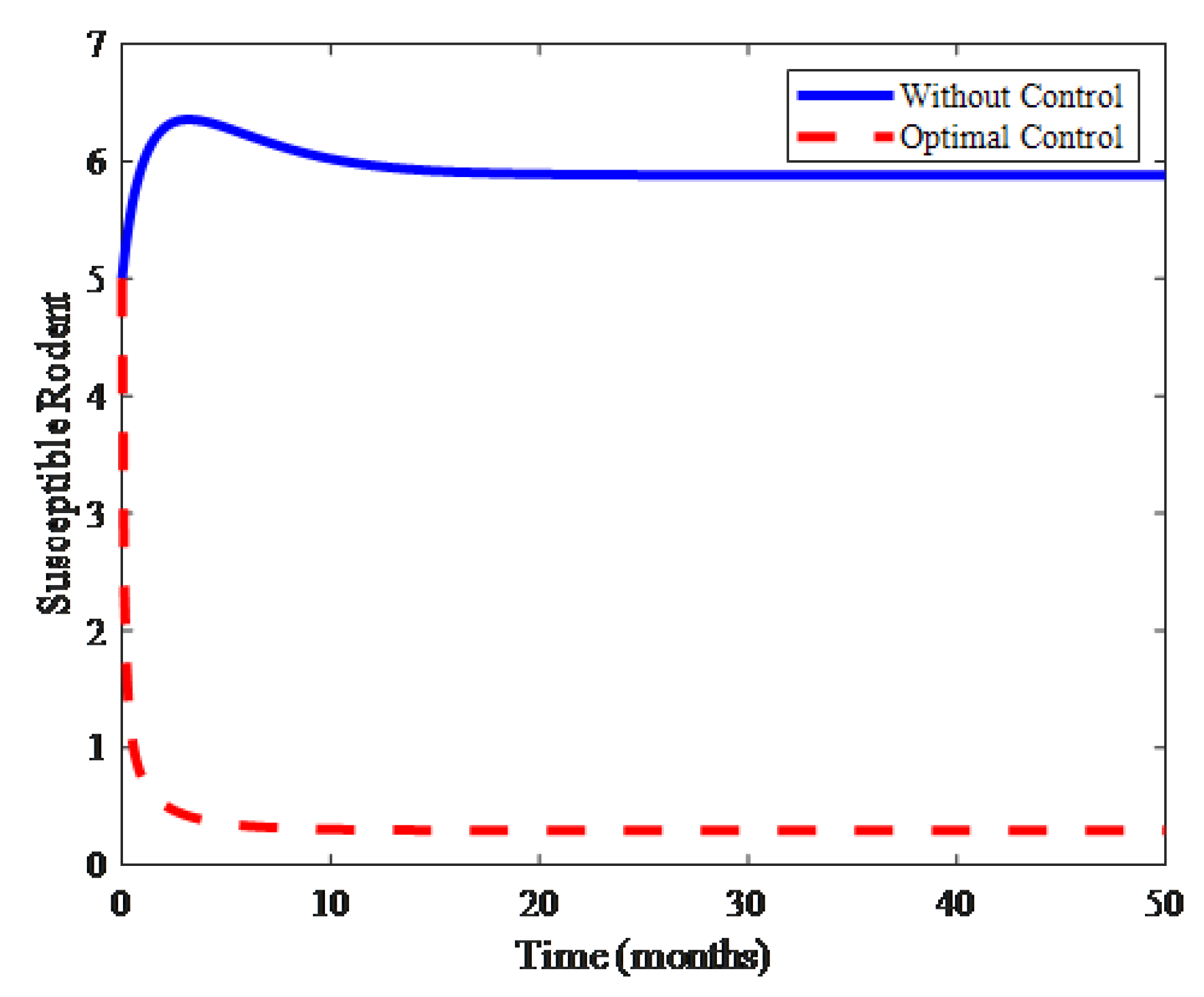
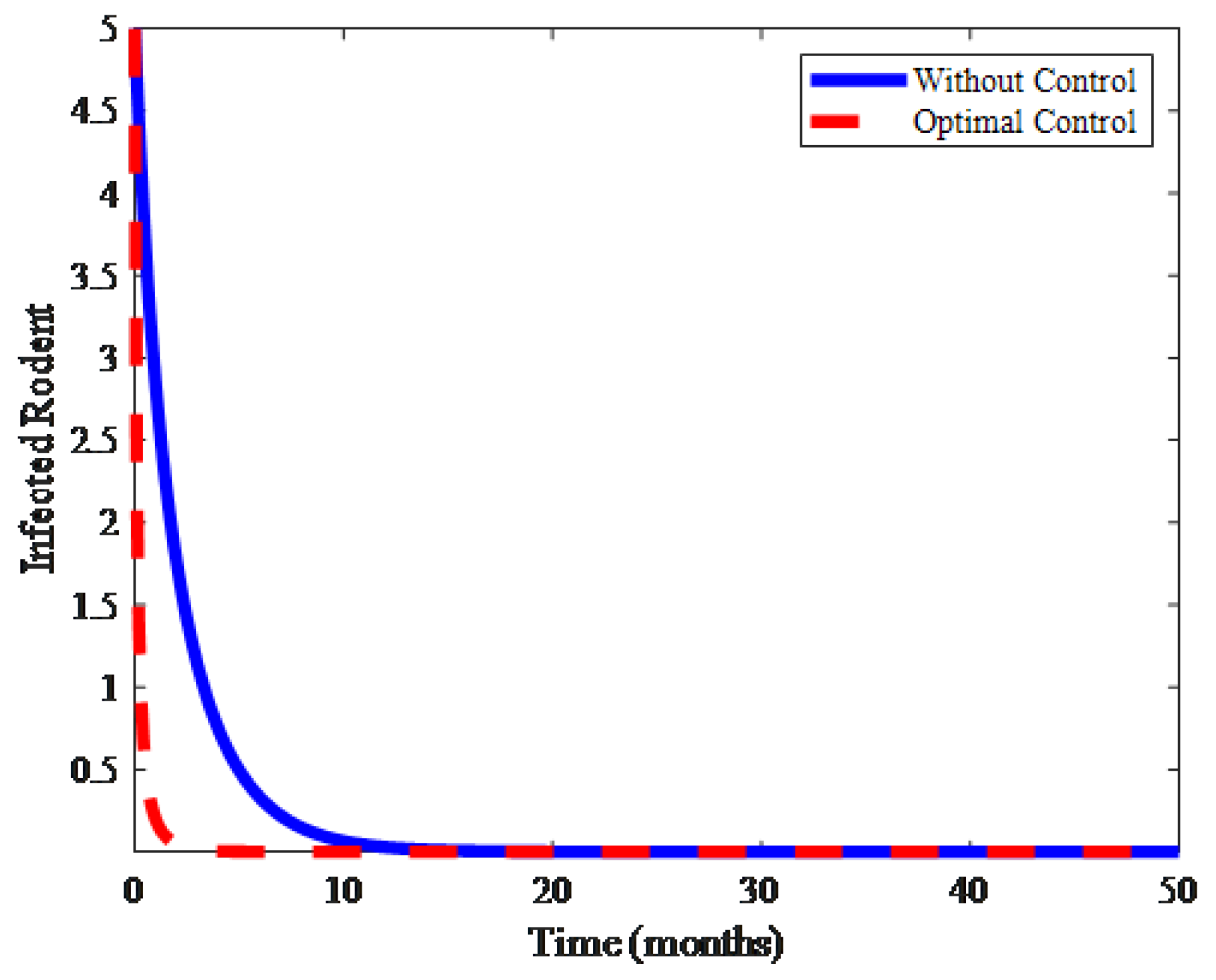
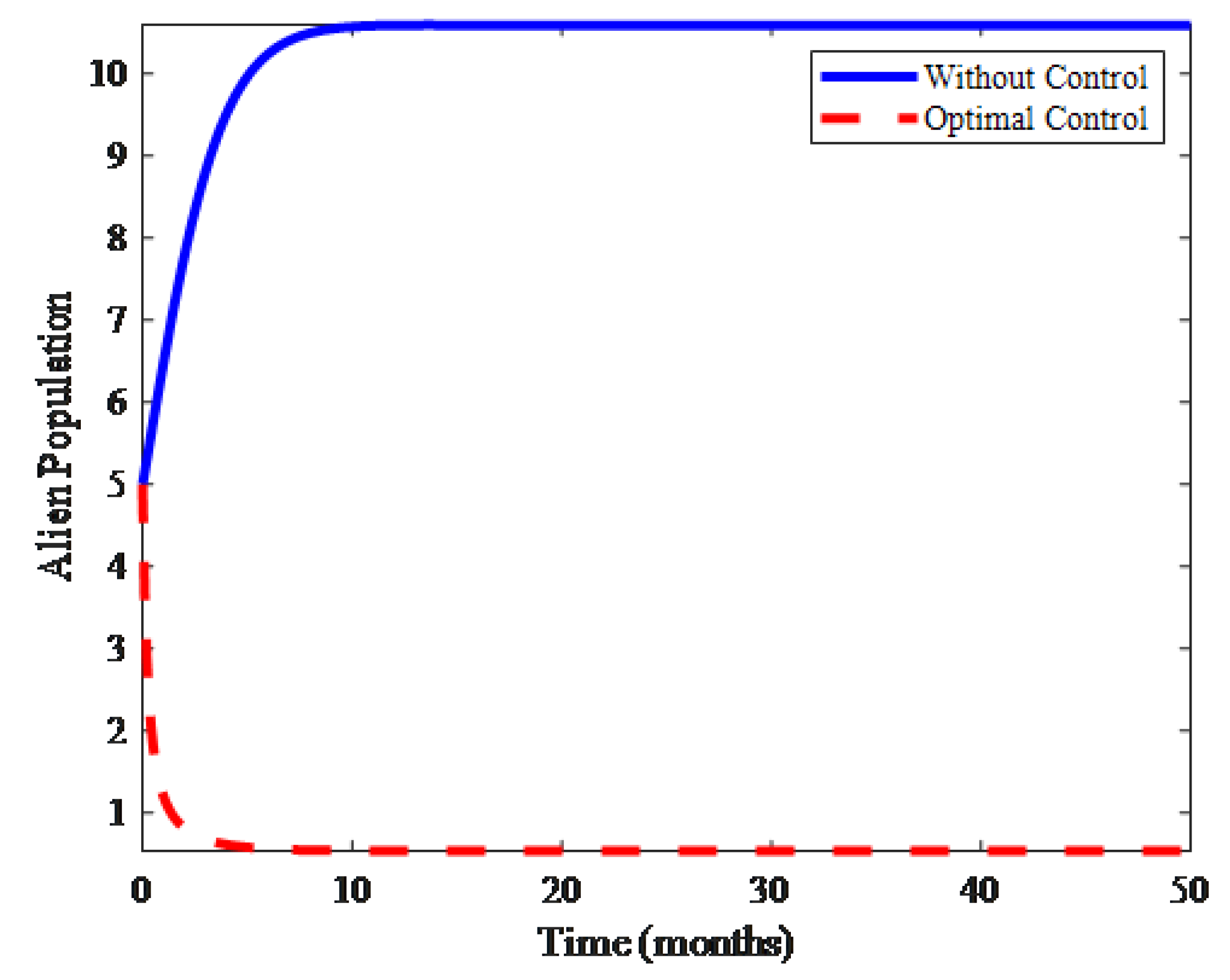
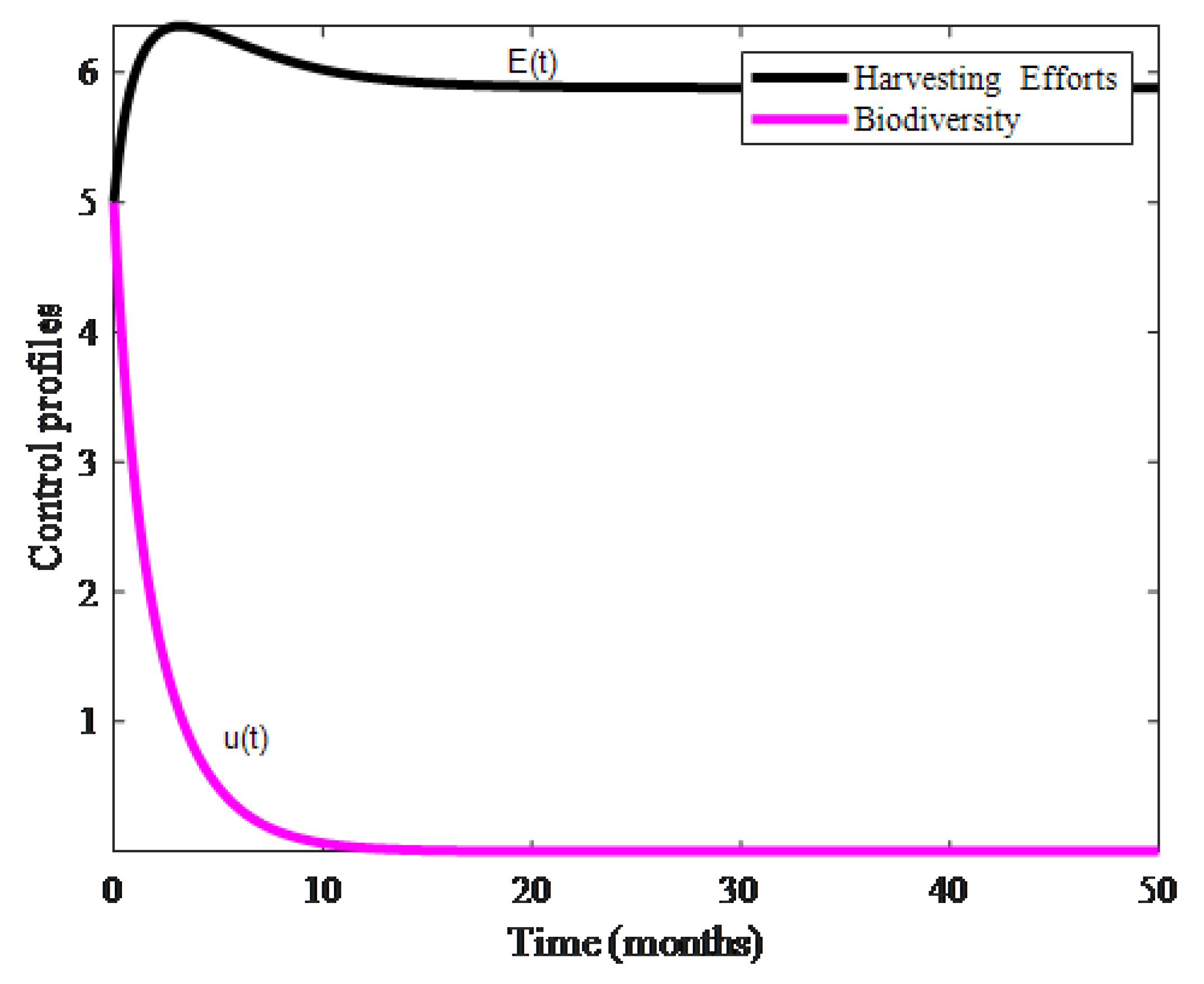
4. Numerical Results and Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Raharinosy, V.; Olive, M.-M.; Andriamandimby, S.F.; Filippone, C.; Heraud, J.-M. Geographical distribution of Hantivarus identified from small terrestrial mammals in Madagascar and evaluation of risk factors relating to the Hantivarus infection. Int. J. Infect. Dis. 2018, 73, 386. [Google Scholar] [CrossRef]
- Guterres, A.; Sampaio de Lemos, E.R. Hantaviruses and a neglected environmental determinant. One Health 2018, 5, 27–33. [Google Scholar] [CrossRef] [PubMed]
- Koishi, A.C.; Aoki, M.N.; Jorge, T.R.; Suzukawa, A.A.; Zanluca, C.; Levis, S.; Duarte dos Santos, C.N. Development and validation of a point-of-care test for detecting Hantavirus antibodies in human and rodent samples. Diagn. Microbiol. Infect. Dis. 2016, 85, 323–327. [Google Scholar] [CrossRef]
- Avšič-Županc, T.; Saksida, A.; Korva, M. Hantavirus infections. Clin. Microbiol. Infect. 2019, 21, e6–e16. [Google Scholar] [CrossRef] [PubMed]
- Abramson, G.; Kenkre, V.M. Spatiotemporal patterns in the Hantavirus infection. Phys. Rev. E 2002, 66, 1912. [Google Scholar] [CrossRef]
- Abramson, G.; Kenkre, V.M.; Yates, T.L.; Parmenter, B.R. Traveling waves of infection in the Hantavirus epidemics. Bull. Math. Biol. 2003, 65, 519–534. [Google Scholar] [CrossRef]
- Giuggioli, L.; Kenkre, V.M.; Abramson, G.; Camelo-Neto, G. Theory of Hantavirus infection spread incorporating localized adult and itinerant juvenile mice. Eur. Phys. J. B 2006, 55, 461–470. [Google Scholar]
- Peixoto, I.D.; Abramson, G. The effect of biodiversity on the Hantavirus epizootic. Ecology 2006, 87, 873–879. [Google Scholar] [CrossRef]
- Abramson, G. Mathematical modeling of Hantavirus: From the mean field to the individual level. In Progress in Mathematical Biology Research; Kelly, J.T., Ed.; Nova Science Publishers Inc.: New York, NY, USA, 2008; pp. 1–27. [Google Scholar]
- Goh, S.M.; Ismail, A.I.M.; Noorani, M.S.M.; Hashim, I. Dynamics of the Hantavirus infection through variational iteration method (VIM). Nonlinear Anal. Real World Appl. 2009, 10, 2171–2176. [Google Scholar] [CrossRef]
- Rida, S.Z.; Abdel Rady, A.S.; M Arafa, A.A.; Khalil, M. The effect of the environmental parameter on the Hantavirus infection through a fractional-order SI model. Int. J. Basic Appl. Sci. 2012, 1, 88–99. [Google Scholar] [CrossRef]
- Yusof, F.M.; Ismail, A.I.M.; Ali, N.M. Modeling population harvesting of rodents for the control of Hantavirus infection. Sains Malays. 2012, 39, 935–940. [Google Scholar]
- Jasrasaria, R.; Mitra, D. The Effects of Intraspecific and Interspecific Competition on Plant Growth. 2004. Available online: http: //88.198.249.35/d/Effect-of-plant-population-density-on-growth-and-yield-of.pdf (accessed on 20 January 2015).
- Yusof, F.M.; Ismail, A.I.M.; Ali, N.M. Effect of predators on the spread of hantavirus infection. Sains Malays. 2014, 43, 1045–1051. [Google Scholar]
- Yusof, F.M.; Ismail, A.I.M.; Hasan, Y.A. Implication of Predator Interaction of the Spread of Hantavirus Infection. Matematika 2018, 34, 205–226. [Google Scholar] [CrossRef]
- Yusof, F.M.; Azmi, A.; Mohd, M.H.; Ismail, A.I.M. Effect of Biodiversity on the Spread of Leptospirosis Infection. In Proceedings of the International Conference on Mathematical Sciences and Technology 2018 (MathTech 2018), The Hotel Equatorial Penang, Malaysia, 10–12 December 2018. [Google Scholar]
- Hale, B.M.; McCarthy, M.L. An Introduction to Population Ecology—Harvesting a Population with Logistic Growth. Available online: https://www.maa.org/press/periodicals/loci/joma/an-introduction-to-population-ecology-harvesting-a-population-with-logistic-growth (accessed on 20 January 2015).
- Kar, T.K.; Pahari, U.K. Modelling and analysis of a prey-predator system with stage-structure and harvesting. Nonlinear Anal. Real World Appl. 2007, 8, 601–609. [Google Scholar] [CrossRef]
- Sion, M.L.; Hatzitolios, A.I.; Armenaka, M.C.; Toulis, E.N.; Kalampalika, D.; Mikoudi, K.D. Acute renal failure caused by Leptospirosis and Hantavirus infection in an urban hospital. Eur. J. Intern. Med. 2002, 13, 264–268. [Google Scholar] [CrossRef]
- Bryson, A.E., Jr. Optimal control-1950 to 1985. Control Systems. IEEE Control Syst. Mag. 1996, 16, 26–33. [Google Scholar] [CrossRef]
- Khan, M.A.; Islam, S.; Khan, S.A.; Khan, I.; Shafie, S.; Gull, T. Prevention of Leptospirosis Infected Vector and Human Population by Multiple Control Variables; Hindawi Publishing Corporation: New York, NY, USA, 2014; pp. 1–9, Abstract and Applied Analysis. ID 619035. [Google Scholar]
- Okosun, K.O.; Mukamuri, M.; Makinde, D.O. Global stability analysis and control of Leptospirosis. Open Math. 2016, 14, 567–585. [Google Scholar] [CrossRef]
- Lenhart, S.; Workman, J.T. Optimal Control Applied to Biological Models; Mathematical and computational Biology Series; Chapman and Hall: London, UK, 2007. [Google Scholar]
- Bonyah, E.; Okosun, K.O. Mathematical modeling of Zika virus. Asian Pac. J. Trop. Dis. 2016, 6, 673–679. [Google Scholar] [CrossRef]
- Pontryagin, L.S.; Boltyanskii, V.G.; Gamkrelidze, R.V.; Mishchenko, E. The Mathematical Theory of Optimal Processes (Translated by D.E. Brown) A Pergamon Press Book; The Macmillan Company: New York, NY, USA, 1964; pp. 56–57. [Google Scholar]
- Momoh, A.; Fügenschuh, A. Optimal control of intervention strategies and cost effectiveness analysis for a Zika virus model. Oper. Res. Health Care 2018, 18, 99–111. [Google Scholar] [CrossRef]
- Khan, M.A.; Zaman, G.; Islam, S.; Chohan, M.I. Optimal Campaign in Leptospirosis Epidemic by Multiple Control Variables. Appl. Math. 2012, 3, 1655–1663. [Google Scholar] [CrossRef][Green Version]
- Lashari, A.A.; Zaman, G. Optimal control of a vector borne disease with horizontal transmission. Nonlinear Anal. Real World Appl. 2012, 13, 203–212. [Google Scholar] [CrossRef]
| Symbol | Description |
|---|---|
| b1 | The recruitment rate of human population |
| β1, β2 | The mediate transmission coefficients |
| λh | The immune human once again is susceptible at constant rate |
| μh | The natural mortality rate for human |
| δh | The disease related death rate from infected class occurs at human population |
| γh | The recovery rate for human from the infections |
| b2 | The recruitment rate for vector population |
| γv | The death rate of vector |
| β3 | The disease carrying of susceptible vector per host per unit time |
| δv | The disease death rate of vector populations |
| ∈1, ∈2 | The rate of positive constants. |
| u1(t) | Human should cover all cuts, water dry, full-cover boots, shoes and long sleeve shirts when handling animals |
| u2(t) | Wash hands thoroughly on a regular basis and shower after work |
| u3(t) | Clean up both work place and home |
| Symbol | Description | Parameter value |
|---|---|---|
| The birth rate of rodent species | 1 | |
| The death rate of rodent species | 0.6 | |
| The transmission rate of hantavirus | 0.1 | |
| The environmental parameter | Varied | |
| Competitive effect of rodents on alien species | 0.2 | |
| The birth rate of alien species | 1 | |
| The death rate of alien species | 0.5 | |
| Competitive effect of rodents on alien species | 0.1 | |
| The harvesting efforts | Varied | |
| The biodiversity | Varied |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohamed Yusof, F.; Abdullah, F.A.; Md. Ismail, A.I. Modeling and Optimal Control on the Spread of Hantavirus Infection. Mathematics 2019, 7, 1192. https://doi.org/10.3390/math7121192
Mohamed Yusof F, Abdullah FA, Md. Ismail AI. Modeling and Optimal Control on the Spread of Hantavirus Infection. Mathematics. 2019; 7(12):1192. https://doi.org/10.3390/math7121192
Chicago/Turabian StyleMohamed Yusof, Fauzi, Farah Aini Abdullah, and Ahmad Izani Md. Ismail. 2019. "Modeling and Optimal Control on the Spread of Hantavirus Infection" Mathematics 7, no. 12: 1192. https://doi.org/10.3390/math7121192
APA StyleMohamed Yusof, F., Abdullah, F. A., & Md. Ismail, A. I. (2019). Modeling and Optimal Control on the Spread of Hantavirus Infection. Mathematics, 7(12), 1192. https://doi.org/10.3390/math7121192





