Optimal Propagating Fronts Using Hamilton-Jacobi Equations

Abstract

The optimal handling of level sets associated to the solution of Hamilton-Jacobi equations such as the normal flow equation is investigated. The goal is to find the normal velocity minimizing a suitable cost functional that accounts for a desired behavior of level sets over time. Sufficient conditions of optimality are derived that require the solution of a system of nonlinear Hamilton-Jacobi equations. Since finding analytic solutions is difficult in general, the use of numerical methods to obtain approximate solutions is addressed by dealing with some case studies in two and three dimensions.

1. Introduction

Hamilton-Jacobi equations are well-know partial differential equations (PDEs) that have been successfully used to model moving interfaces. In fact, they are the basis of a widely-studied family of methods usually referred to as level set methods [1]. Hamilton-Jacobi equations are useful not only for the purpose of modeling dynamic fronts, but also to solve optimal control problems over finite and infinite horizons [2], with a number of different applications (see, e.g., [3,4,5]). In this paper, we propose a novel approach to construct optimal propagating fronts with propagation speed selected in order to minimize a suitable cost functional accounting for a desired front behavior. Sufficient conditions of optimality given by a system of nonlinear Hamilton-Jacobi equations are derived that can be numerically solved when it is difficult to find analytic solutions [6,7,8].

The propagation of fronts or boundaries separating two regions, either curves in two dimensions or surfaces in three dimensions, is a topic that has gained a lot of attention in the last decades. In fact, modeling the motion of fronts is crucial in different research areas such as, for instance, fluid dynamics and image processing (see, e.g., [9,10,11,12] and the references therein). The methods available in the literature for this task are usually catalogued as Lagrangian front tracking and Eulerian front capturing approaches. Front tracking ones are Lagrangian since they rely on the discretization of the front by means of a mesh. A number of points is positioned along the front, and such points are then moved by using ordinary differential equations (ODEs) [13,14]. Lagrangian methods turn out to be quite efficient and precise in applications with fronts characterized by small deformations, but their performances degrade in case of changes of topology, when they need re-meshing upon strong deformations of the boundary. Instead, front capturing methods are Eulerian since the boundary is represented implicitly on fixed grids. Level set methods are an important family of Eulerian approaches that overcome the aforementioned limits of Lagrangian techniques. In such methods, the front is described by the zero level set of a multidimensional function [9]. The possibility to easily account for changes of topology is one of their main features. The most known methods are those based on the normal flow equation (in which the propagation speed is directed towards the normal to the front) and the mean curvature flow equation (in which the speed is proportional to the curvature of the front in all points). In other words, they differ on the choice of the velocity field in the Hamilton-Jacobi equation.

The literature on the optimal control of infinite-dimensional systems (see [15] for an introduction) is vast and with a special emphasis on fluid flows [16,17,18], where the problems are addressed in abstract Banach spaces. By contrast, the literature regarding the control of moving fronts is at the very beginning. The control of level sets resulting from a two-phase Stefan problem is investigated in [19,20]. In [21], an original prey-predator model is presented with a predator front modeled as a curve that moves depending on the prey density. More recently, in [22,23,24], the problem of finding the normal velocity to the front described by level sets of a normal flow equation is attacked with the goal of minimizing a given performance index. After proving the existence of a solution to such a problem, the extended Ritz method is proposed to find suboptimal solutions [7,25]. Such solutions take on the structure of neural networks depending on neural weights, i.e., a set of parameters that need to be tuned. Then, the Gauss-Newton descent method can be used to find an optimal value for the weights, and the resulting algorithm may be viewed as neural learning based on the extended Kalman filter (EKF) [22,24].

As compared with such works, the present paper provides some advances. A new solution paradigm is proposed for the finite-horizon optimal control problem originally proposed in [23,24]. More specifically, sufficient conditions of optimality are rigorously established that require the solution of a system of Hamilton-Jacobi PDEs [26]. Similar conditions are proved for the extension of the same problem to an infinite horizon. Since analytic solutions of such problems are almost impossible to find, approximate solutions are searched for by using a numerical scheme based on the method proposed in [27]. The resulting approach is compared with that of [24,28] both in terms of computational time and ability to optimize the cost functional, thus highlighting the effectiveness of the proposed technique.

The rest of this paper is structured as follows. The main results concerning the considered problems are presented in Section 2. Section 3 describes the numerical results obtained in two case studies. Conclusions and prospect of future work are discussed in Section 4.

The following notation will be adopted throughout the paper. We define $(x,y):={[x^{\top },y^{\top }]}^{\top }$, where $x\in {\mathbb{R}}^n$ and $y\in {\mathbb{R}}^m$. Let $\mathcal{X}$ be a real linear normed space of functions with norm ${|·|}_{\mathcal{X}}$. Given a functional $F:\mathcal{X}\to \mathbb{R}$, F is Fréchet differentiable in $x\in \mathcal{X}$ if there exists a functional $F^{\prime }:\mathcal{X}\times \mathcal{X}\to \mathbb{R}$ such that

$$F(x+y)=F\left(x\right)+F^{\prime }(x,y)+r(x,y)$$

where $y\in \mathcal{X}$, $F^{\prime }(x,y)$ is the Fréchet derivative of $F\left(x\right)$, and $y\mapsto r(x,y)$ is a remainder of order higher than one, i.e.,

$$\underset{y\to 0}{lim}\frac{r(x,y)}{{\left|y\right|}_{\mathcal{X}}}=0.$$

Finally, let $\left|x\right|:={\left(x^{\top }x\right)}^{1/2}$ for any real vector x.

2. Optimal Moving Fronts

In this section, we focus on how moving fronts can be described by level set methods. Toward this end, let $\mathsf{\Omega }\subset {\mathbb{R}}^q$ and $t\in [0,T]$ be a compact space domain of dimension q and $T>0$ a given time horizon (in the case of infinite horizon problems, we consider the time domain $[0,+\infty )$). A moving front is a curve in two dimensions ($q=2$) or a surface in three dimensions ($q=3$) that separates two regions, associated to the zero level set of a function $\varphi :\mathsf{\Omega }\times [0,T]\to \mathbb{R}$. The boundary $x(t,s)$ is given at time t by the points such that $\varphi \left(x\right(t,s),t)=0$, where s is the arc-length parameter of the initial curve $x(0,s)$. 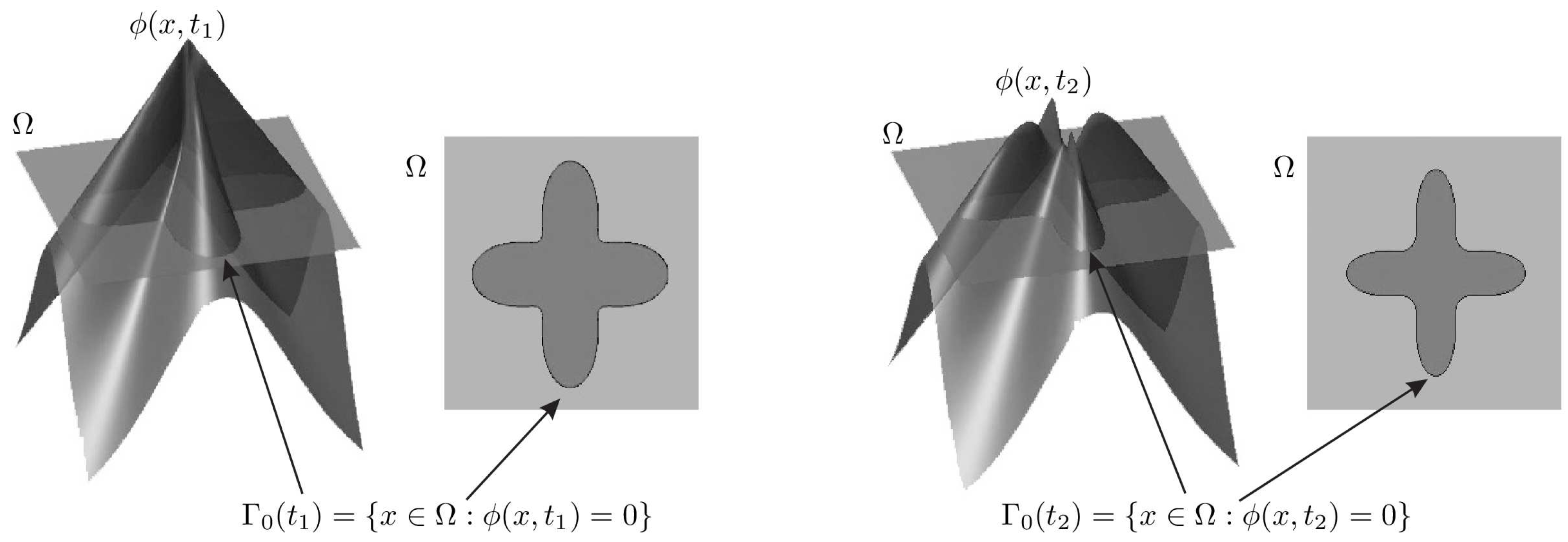Figure 1 displays fronts at time instants $t_1$ and $t_2$ together with the corresponding functions $\varphi$. After differentiating with respect to t, we obtain

$${\varphi }_t(x,t)+v(x,t)·\nabla \varphi (x,t)=0,$$

(1)

where $v(x,t):=\frac{d}{dt}x(t,s)$ is the Lagrangian particle velocity representing the direction of propagation of the front at the point $x(t,s)$, and ∇ is the gradient with respect to space. From now on, we refer only to the normal flow equation, in which $v(x,t)$ is chosen proportional to the normal to the front, i.e.,

$$v(x,t)=u\frac{\nabla \varphi (x,t)}{|\nabla \varphi (x,t\left)\right|},$$

(2)

where u is the propagation speed. After replacing (2) in (1), we obtain the normal flow equation:

$${\varphi }_t(x,t)+u|\nabla \varphi (x,t)|=0.$$

(3)

Equation (3) is associated to initial conditions ${\varphi }_0:\mathsf{\Omega }\to \mathbb{R}$, i.e., $\varphi (x,0)={\varphi }_0\left(x\right)$ for all $x\in \mathsf{\Omega }$. Usually, ${\varphi }_0$ is the signed distance to the initial front. The level set $l\in \mathbb{R}$ of the function $\varphi$ is a set-valued mapping ${\mathsf{\Gamma }}_l:[0,T]\rightrightarrows \mathcal{C}$, where ${\mathsf{\Gamma }}_l\left(t\right):=\left\{x\in \mathsf{\Omega }:\varphi (x,t)=l\right\}$.

We deal with the optimal control of (3) via a suitable choice of u. In other words, our aim is to drive the propagating front associated to a certain level set of $\varphi (x,t)$ as desired. In practice, the speed function u is considered as a control action depending on time and space, i.e., $u:\mathsf{\Omega }\times [0,T]\to \mathbb{R}$. Let us denote by $\mathcal{U}$ the set of admissible control functions, such as the set of measurable bounded functions. This set is made of the smooth functions $(x,t)\mapsto u(x,t)$ such that there exist solutions to the Cauchy problem for (3). Let $\mathcal{F}$ be the space of functions $(t,x)\mapsto \varphi (x,t)$ where such a problem is formulated.

The evolution over time and space of a level set of $\varphi$ may be related to a performance indicator depending on the interior or the boundary of the interface (see, e.g., [20]). In this respect, we focus on a cost functional quantifying performances of the control policy, as follows:

$$\begin{array}{cc}\hfill J(\varphi ,u)& ={\int }_0^T{\int }_{\mathsf{\Omega }}h(\varphi (x,t),u(x,t),t)dxdt+{\int }_{\mathsf{\Omega }}\overline{h}\left(\varphi (x,T)\right)dx,\hfill \end{array}$$

(4)

where $h:\mathbb{R}\times \mathbb{R}\times [0,T]\to \mathbb{R}$ and $\overline{h}:\mathbb{R}\to \mathbb{R}$ is a final penalty term, which we want to minimize subject to the normal flow equation in (3).

More generally, let us consider the running-time cost functional

$$J(t_0,\varphi ,u)={\int }_{t_0}^{T}L(\varphi (·,t),u(·,t))dt+K\left(\varphi \right),$$

with $t_0\in [0,T]$ and the functionals $L:\mathcal{F}\times \mathcal{U}\to \mathbb{R}$ and $K:\mathcal{F}\to \mathbb{R}$, which, in the case of (4), are given by

$$L(\varphi (·,t),u(·,t))={\int }_{\mathsf{\Omega }}h(\varphi (x,t),u(x,t),t)dx$$

and

$$K\left(\varphi \right)={\int }_{\mathsf{\Omega }}\overline{h}\left(\varphi (x,T)\right)dx$$

with a little abuse of notation. Such functionals are assumed to be continuous in their arguments, i.e., $\varphi$ and u for L as well as $\varphi$ for K. Our goal is to find the control policy $u\in \mathcal{U}$ that minimizes $J(t,\varphi ,u)$ with (3) as a constraint. Thus, we define

$$V(\varphi ,t)=\underset{u\in \mathcal{U}}{inf}J(t,\varphi ,u)$$

(5)

for $t\in [0,T]$.

Under mild conditions, the existence of viscosity solutions to (5) is shown ([24], Theorem 2, p. 905). Such a result is not constructive, but, by restricting the search to smooth solutions, the following holds.

Theorem 1.

Assume that there exists a continuously differentiable${\varphi }^{\circ }:\mathsf{\Omega }\times [0,T]\to \mathbb{R}$with${\varphi }^{\circ }(x,0)={\varphi }_0\left(x\right)$and$V:\mathbb{R}\times [0,T]\to \mathbb{R}$with$V(·,T)=K(·)$such that

$$V_t({\varphi }^{\circ },t)-u^{\circ }{V}_{\varphi }({\varphi }^{\circ },t)|\nabla {\varphi }^{\circ }|+L({\varphi }^{\circ },u^{\circ })=0$$

(6)

with

$$u^{\circ }\in arg\underset{u\in \mathcal{U}}{min}\left(L({\varphi }^{\circ },u)-u{V}_{\varphi }({\varphi }^{\circ },t)|\nabla {\varphi }^{\circ }|\right)$$

(7)

and${\varphi }_t^{\circ }+u^{\circ }|\nabla {\varphi }^{\circ }|=0$, where$V_{\varphi }(\varphi ,t)$is the Fréchet derivative of$V(\varphi ,t)$with respect to ϕ and$V_t(\varphi ,t)$is the partial time derivative of V. Then,

$$V({\varphi }^{\circ },0)=\underset{u\in \mathcal{U}:{\varphi }_t+u|\nabla \varphi |=0}{inf}J(0,\varphi ,u).$$

(8)

Proof. 

The proof is in line with [29], Theorem 1, p. 6. In more detail, using

$$\dot{V}(\varphi ,t)=V_t+V_{\varphi }{\varphi }_t=V_t-u{V}_{\varphi }|\nabla \varphi |,$$

since ${\varphi }_t+u|\nabla \varphi |=0$ and

$${\int }_0^T\dot{V}(\varphi (·,t),t)+L(\varphi (·,t),u(·,t))dt=V(\varphi ,T)-V(\varphi ,0)=K\left(\varphi \right)-V(\varphi ,0)+{\int }_0^{T}L(\varphi (·,t),u(·,t))dt$$

in general, from (6) and (7) we obtain

$$V(\varphi ,0)\le {\int }_0^{T}L(\varphi (·,t),u(·,t))dt+K\left(\varphi \right)$$

for all $u\in \mathcal{U}$, and hence (8) holds by choosing $\varphi ={\varphi }^{\circ }$. □

Let us focus on such a result by considering a simple example.

Example 1.

Consider a one-dimensional problem on the domain$\mathsf{\Omega }\times [0,T]$with$\mathsf{\Omega }=[1,2]$and$T=2$. For the sake of simplicity, we search for an optimal control policy that depends only on time, i.e.,$u:[0,T]\to \mathbb{R}$. Moreover, we focus on a quadratic cost

$$L(\varphi ,u)={\int }_{\mathsf{\Omega }}{\left(u\left(t\right)\right)}^{2}dx=u^2,K\left(\varphi \right)={\int }_{\mathsf{\Omega }}{\left(\varphi (x,T)\right)}^{2}dx.$$

According to Theorem 1, a sufficient condition of optimality is given by

$$V_t+\underset{u}{min}\left(u^2-u{V}_{\varphi }\left|{\varphi }_x\right|\right)=0$$

together with the related normal flow equation. Thus, we get

$$u^{\circ }=\frac{1}{2}{V}_{\varphi }\left|{\varphi }_x\right|$$

and

$$\left\{\begin{array}{c}{V}_t-\frac{1}{4}{\left(V_{\varphi }{\varphi }_x\right)}^2=0\hfill \\ {\varphi }_t+\frac{1}{2}{V}_{\varphi }{\left({\varphi }_x\right)}^2=0.\hfill \end{array}\right.$$

(9)

If${\varphi }_0\left(x\right)=x$and$K\left(\varphi \right)=1/3$, we can easily verify that the solution of (9) is given by$\varphi (x,t)=x-t/2$and$V(\varphi ,t)=\varphi +t/4$.

The finite-horizon problem considered so far can be extended to an infinite horizon setting by dealing with discounted cost functionals such as

$$J_{\infty }(\varphi ,u)={\int }_0^{+\infty }L(\varphi (·,t),u(·,t))exp(-\lambda t)dt,$$

(10)

where $\lambda >0$ and $L(\varphi ,u)$ is bounded for all $\varphi \in \mathcal{F},u\in \mathcal{U}$. The following result holds.

Theorem 2.

Assume that there exists a continuously differentiable${\varphi }^{\circ }:\mathsf{\Omega }\times [0,+\infty ]\to \mathbb{R}$with${\varphi }^{\circ }(x,0)={\varphi }_0\left(x\right)$and$V:\mathbb{R}\to \mathbb{R}$such that

$$-\lambda V\left({\varphi }^{\circ }\right)-u^{\circ }{V}_{\varphi }\left({\varphi }^{\circ }\right)|\nabla {\varphi }^{\circ }|+L({\varphi }^{\circ },u^{\circ })=0,$$

(11)

with

$$u^{\circ }\in arg\underset{u\in \mathcal{U}}{min}\left(L({\varphi }^{\circ },u)-u{V}_{\varphi }\left({\varphi }^{\circ }\right)|\nabla {\varphi }^{\circ }|\right)$$

(12)

and${\varphi }_t^{\circ }+u^{\circ }|\nabla {\varphi }^{\circ }|=0$, where$V_{\varphi }\left(\varphi \right)$is the Fréchet derivative of$V\left(\varphi \right)$with respect to ϕ. Then,

$$V\left({\varphi }_0\right)=\underset{\genfrac{}{}{0pt}{}{u\in \mathcal{U}:\varphi (·,0)={\varphi }_0}{{\varphi }_t+u|\nabla \varphi |=0}}{inf}{\int }_0^{+\infty }L(\varphi (·,t),u(·,t))exp(-\lambda t)dt,$$

(13)

with$\lambda >0$.

Proof. 

It is grounded on the theoretical framework reported in [2], which deals with the Hamilton-Jacobi-Bellman approach to the solution of infinite-horizon optimal control problems for systems described by ODEs. We will briefly sketch the demonstration by referring to [2] for details. Notice that

$$\begin{array}{cc}\hfill & \underset{u}{inf}\left({\int }_0^{+\infty }L(\varphi (·,t),u(·,t))exp(-\lambda t)dt\right)=\hfill \\ \hfill & \underset{u}{inf}\left({\int }_0^{t}L(\varphi (·,s),u(·,s))exp(-\lambda s)ds+{\int }_t^{+\infty }L(\varphi (·,s),u(·,s))exp(-\lambda s)ds\right)\hfill \end{array}$$

for all $t\ge 0$ and, after a simple change of integration variable,

$$V\left({\varphi }_0\right)=\underset{u}{inf}\left({\int }_0^{t}L(\varphi (·,s),u(·,s))exp(-\lambda s)ds+exp(-\lambda t)V\left(\varphi (·,t)\right)\right).$$

Following ([2], Proposition 2.5, p. 102), according to the principle of dynamic programming, the function

$$t\mapsto k\left(t\right):={\int }_0^{t}L(\varphi (·,s),u(·,s))exp(-\lambda s)ds+exp(-\lambda t)V\left(\varphi (·,t)\right)$$

is optimal if and only if the pair $(\varphi ,u)$ is optimal, i.e., $(\varphi ,u)=({\varphi }^{\circ },u^{\circ })$. If we perturb the optimal solution in the interval $[t,t+dt]$, it follows an increase of $k\left(t\right)$, i.e., $k(t+dt)\ge k\left(t\right)$. Using $k(t+dt)=k\left(t\right)+k^{\prime }\left(t\right)dt+o\left(dt\right)$ with $o(·)$ denoting the remainder of order higher than one, we obtain $k^{\prime }\left(t\right)\ge 0$ and, after computing the derivative of $k\left(t\right)$ and after multiplying for $exp\left(\lambda t\right)$, we get (11) with (12) for (13) to hold. □

Remark 1.

After selecting the desired shape in Ω as the zero level set${\mathsf{\Gamma }}_0^{\mathrm{ref}}\left(t\right)$of a given reference function${\varphi }_{\mathrm{ref}}(x,t)$, the goal is that of handling the zero level set${\mathsf{\Gamma }}_0\left(t\right)$associated to the solution$\varphi (x,t)$to match${\mathsf{\Gamma }}_0^{\mathrm{ref}}\left(t\right)$as much as possible. Thus, a convenient choice of the cost functional to minimize is the symmetric difference between such level sets, i.e.,

$$J={\int }_0^T\eta \left({\mathsf{\Gamma }}_0\left(t\right)\mathsf{\Delta }{\mathsf{\Gamma }}_0^{\mathrm{ref}}\left(t\right)\right)dt$$

(14)

where Δ stands for the symmetric difference operator, i.e.,${\mathsf{\Gamma }}_0\left(t\right)\mathsf{\Delta }{\mathsf{\Gamma }}_0^{\mathrm{ref}}\left(t\right):=({\mathsf{\Gamma }}_0\left(t\right)\cup {\mathsf{\Gamma }}_0^{\mathrm{ref}}\left(t\right))\backslash ({\mathsf{\Gamma }}_0\left(t\right)\cap {\mathsf{\Gamma }}_0^{\mathrm{ref}}\left(t\right))$, while η is an outer measure on${\mathbb{R}}^q$(see Figure 2). Though the proposed approach can deal with other performance indexes under the required assumptions (i.e., smoothness and, in the case of Theorem 2, the boundedness of$L(·,·)$), the choice of the cost strongly depends on the goal of matching the required shapes and thus it reduces to adopt a measure of the symmetric difference between level sets.

Unfortunately, it is difficult to find an expression for the minimizer in (7) or (12) (especially when we search for control laws that depend on both space and time) and obtain the exact analytic solution of (6) or (11) in general. Thus, numerical methods are well-suited to finding approximate solutions, as shown in the next section, where we deal with two case studies.

3. Numerical Results

In this section, we present the simulation results obtained in solving optimal control problems concerning the tracking of reference curves both in two and three dimensions (2D and 3D, for short). Specifically, we will search for a mapping $(x,t)\mapsto u(x,t)$ that drives the zero level set ${\mathsf{\Gamma }}_0\left(t\right)$ of the solution $\varphi (x,t)$ of (3) in order to match the zero level set ${\mathsf{\Gamma }}_0^{\mathrm{ref}}\left(t\right)$ of the function ${\varphi }_{\mathrm{ref}}(x,t)$ by using the cost functional

$$J={\int }_0^T{\int }_{\mathsf{\Omega }}{\left({\widehat{H}}_{\tau }\left(\varphi (x,t)\right)-{\widehat{H}}_{\tau }\left({\varphi }_{\mathrm{ref}}(x,t)\right)\right)}^{2}dxdt,$$

(15)

with ${\widehat{H}}_{\tau }$ denoting the approximate Heaviside step function, i.e.,

$${\widehat{H}}_{\tau }\left(\xi \right):=\frac{1}{2}+\frac{1}{2}tanh\left(\frac{\xi }{\tau }\right),$$

where $\tau >0$ modulates the smoothness of the approximation.

The solution of (6) with (7) was found by the approach presented in [27] (see also [30]), where the minimization in (7) was obtained by using the fmincon routine of the Matlab Optimization Toolbox. We refer to such a solution procedure as Guo-Sun numerical optimization (GSNO) method. For the purpose of comparison, we considered also the approach presented in [24], where the extended Ritz method is adopted to find parametrized approximate solutions by using a Gauss-Newton descent method. Such a method is treated by using a computationally efficient algorithm based on the extended Kalman filter (see [24] for details), thus it will be briefly referred to as EKF-based optimization (EKFO).

We considered two case studies in 2D and 3D. As regards the 2D example, we focused on a space domain $\mathsf{\Omega }=[-0.75,+0.75]\times [-0.5,+0.5]$, discretized using a regular grid of $75\times 50$ points for the numerical solution of (3). The time interval was fixed to $[0,1.5]$. The sampling time $\mathsf{\Delta }t$ was chosen equal to $0.03$, i.e., the simulation was completed after 50 time steps. Concerning the 3D case, we adopted a domain $\mathsf{\Omega }=[-1.5,1.5]\times [-1.0,1.0]\times [-1.0,1.0]$ sampled with a grid made of $90\times 60\times 60$ nodes. The time interval for the simulation was $[0,1.5]$ using a time step $\mathsf{\Delta }t=0.05$, i.e., the simulation was performed in 30 time steps. In both case studies, we fixed τ to 10⁻² in (15).

Concerning the EKFO, we chose one-hidden-layer feedforward neural networks with sigmoidal activation functions as parameterized approximating functions. In particular, we tested various numbers of basis functions, i.e., we considered n = 5, 10, and 15 neurons. Such numbers ensured sufficient accuracy with quite simple approximating structures. All the results were averaged on 50 randomly-chosen initial weights. Similarly, we randomly generated the initial points of the fmincon routine of the GSNO. We used a personal computer with a 2.6 GHz Intel Xeon CPU with 64 GB of RAM running Windows 10 to perform the simulations.

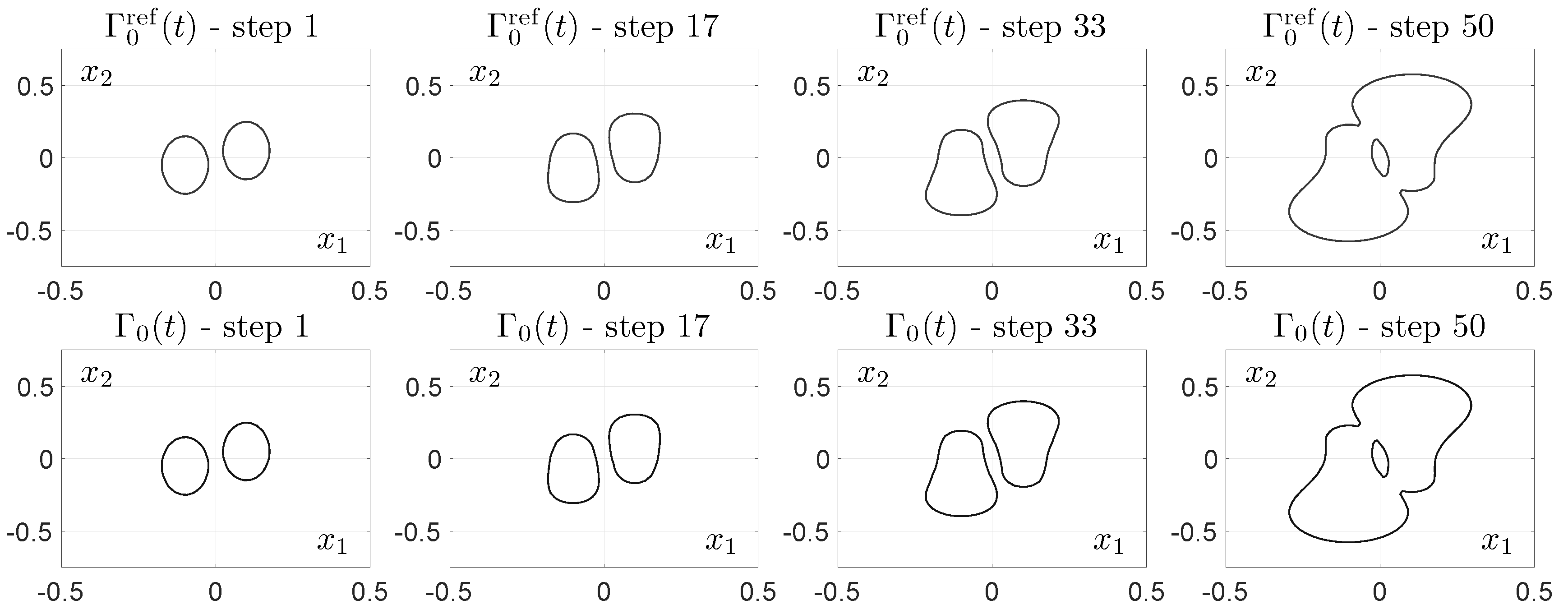
Figure 3 and Figure 4 show the results gained by using the GSNO with the reference and simulated fronts at different time instants.

Table 1. Summary of the means of optimal costs and optimization times over 50 simulation runs for the GSNO and EKFO.

	Mean of J°			Mean of $\stackrel{-}{\mathit{T}}$ (s)
	GSNO	EKFO	n	GSNO	EKFO	n
		$1.19\times {10}^{-4}$	5		$3.46\times {10}^2$	5
2D	$1.24\times {10}^{-3}$	$1.38\times {10}^{-4}$	10	$3.18\times {10}^2$	$5.19\times {10}^2$	10
		$3.77\times {10}^{-4}$	15		$8.41\times {10}^2$	15
		$5.87\times {10}^{-4}$	5		$1.39\times {10}^4$	5
3D	$8.57\times {10}^{-4}$	$4.52\times {10}^{-4}$	10	$6.08\times {10}^3$	$2.82\times {10}^4$	10
		$1.27\times {10}^{-4}$	15		$7.04\times {10}^4$	15

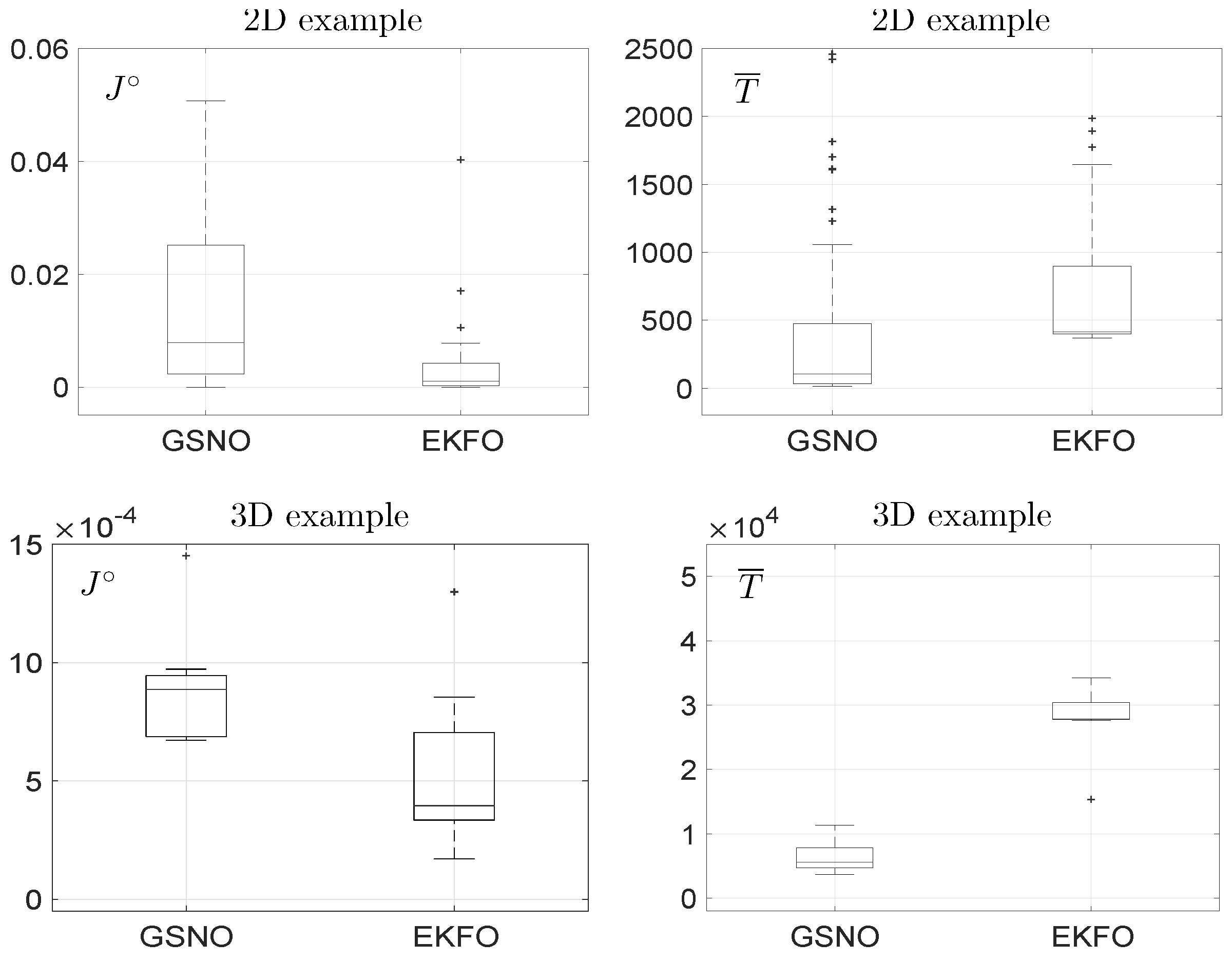
reports the means of the optimal cost J° and of the computational time $\overline{T}$ required to perform the computations with the GSNO and EKFO over 50 trials. Figure 5 displays the boxplots of the cost J° and of the computational time $\overline{T}$ obtained with 10 neurons. As compared with the EKFO, the GSNO is computationally much less demanding, especially in the 3D case study. In terms of resulting optimal cost, the results given by EKFO and GSNO are quite close.

4. Conclusions

We have addressed the problem of constructing propagating fronts by formulating optimal control problems with a front dynamics described by Hamilton-Jacobi equations such as the normal flow equations. Numerical solutions of such problems have been shown in two case studies and compared with previously-developed approaches. The results are quite satisfying and suggest the extension of the proposed approach to other kinds of Hamilton-Jacobi equations for front modeling such as the mean curvature flow equation. Another direction of research is the investigation of suitable stability conditions when dealing with infinite-horizon problems and the combination of level set methods with other complex phenomena in fluid dynamics such those described by Navier-Stokes equations [31].