Total and Double Total Domination Number on Hexagonal Grid
Abstract
1. Introduction
2. Preliminaries
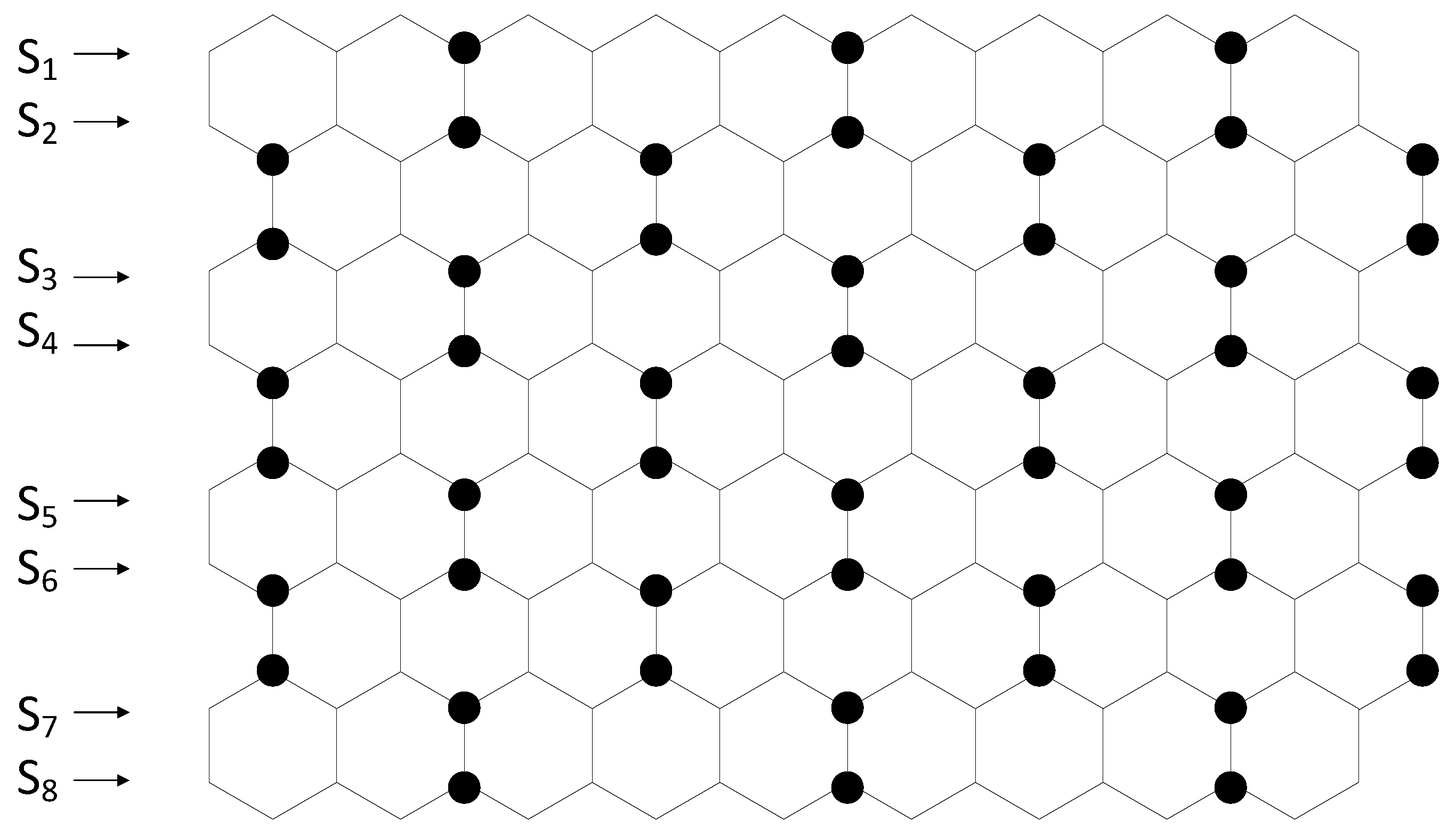
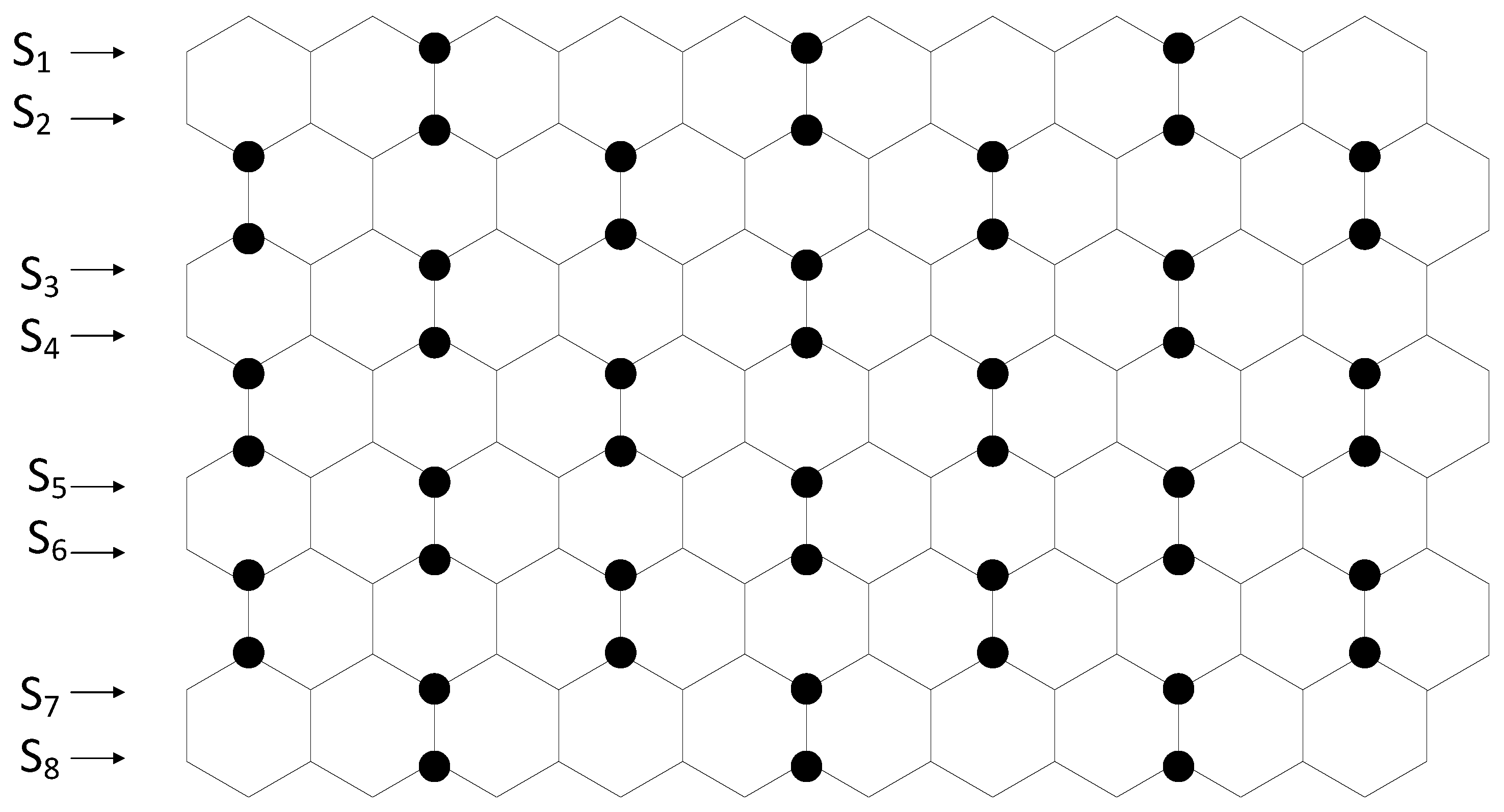
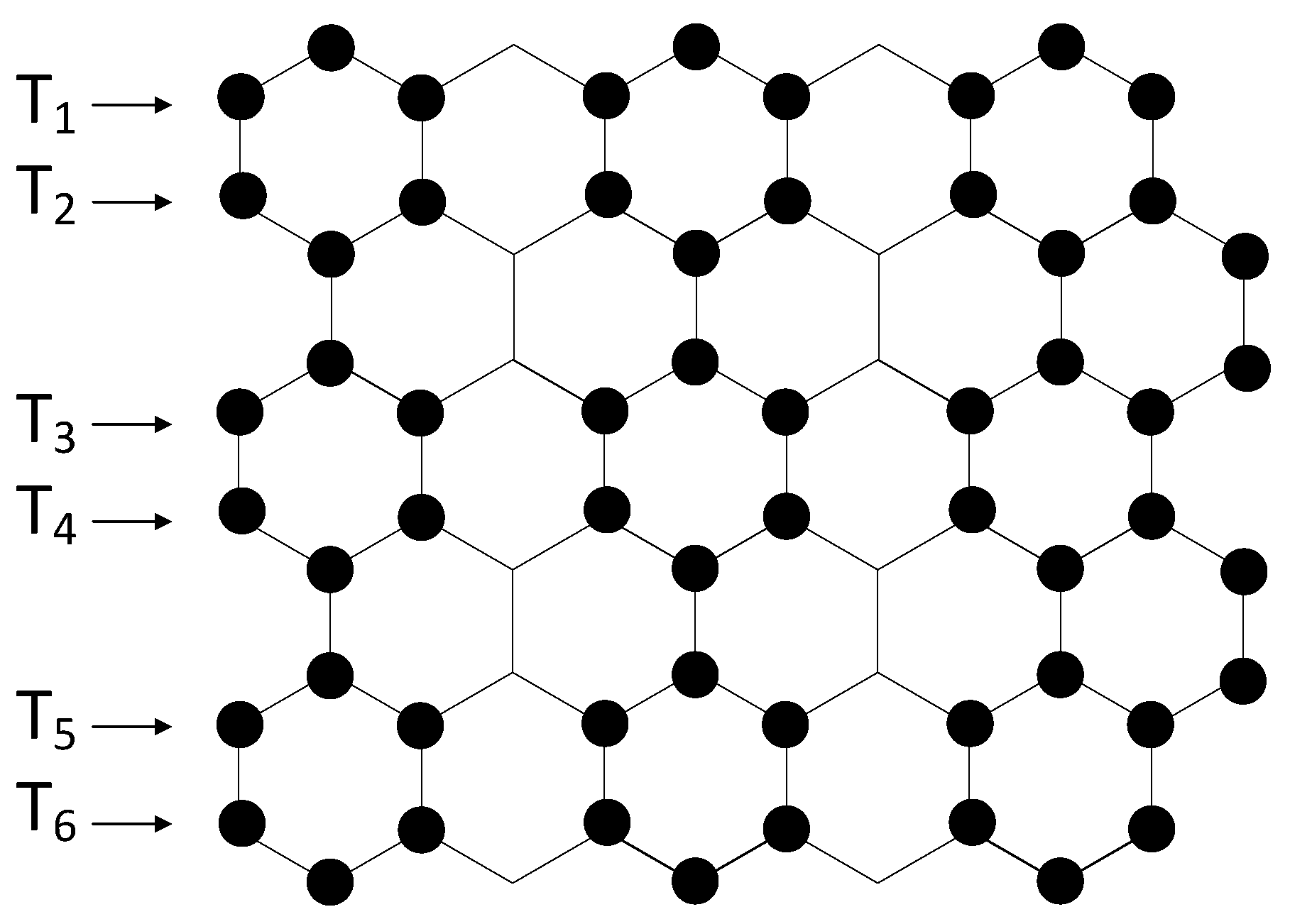
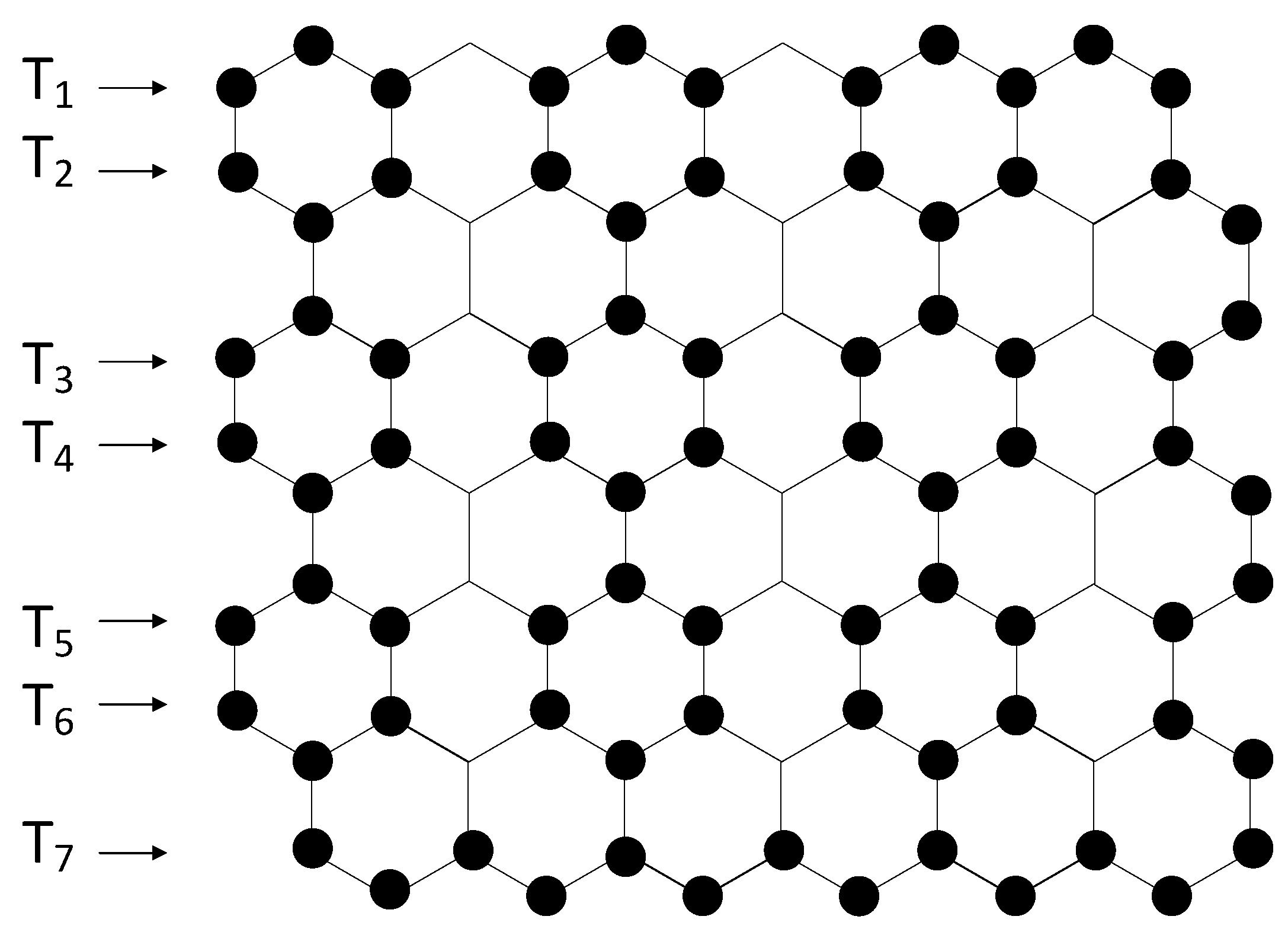
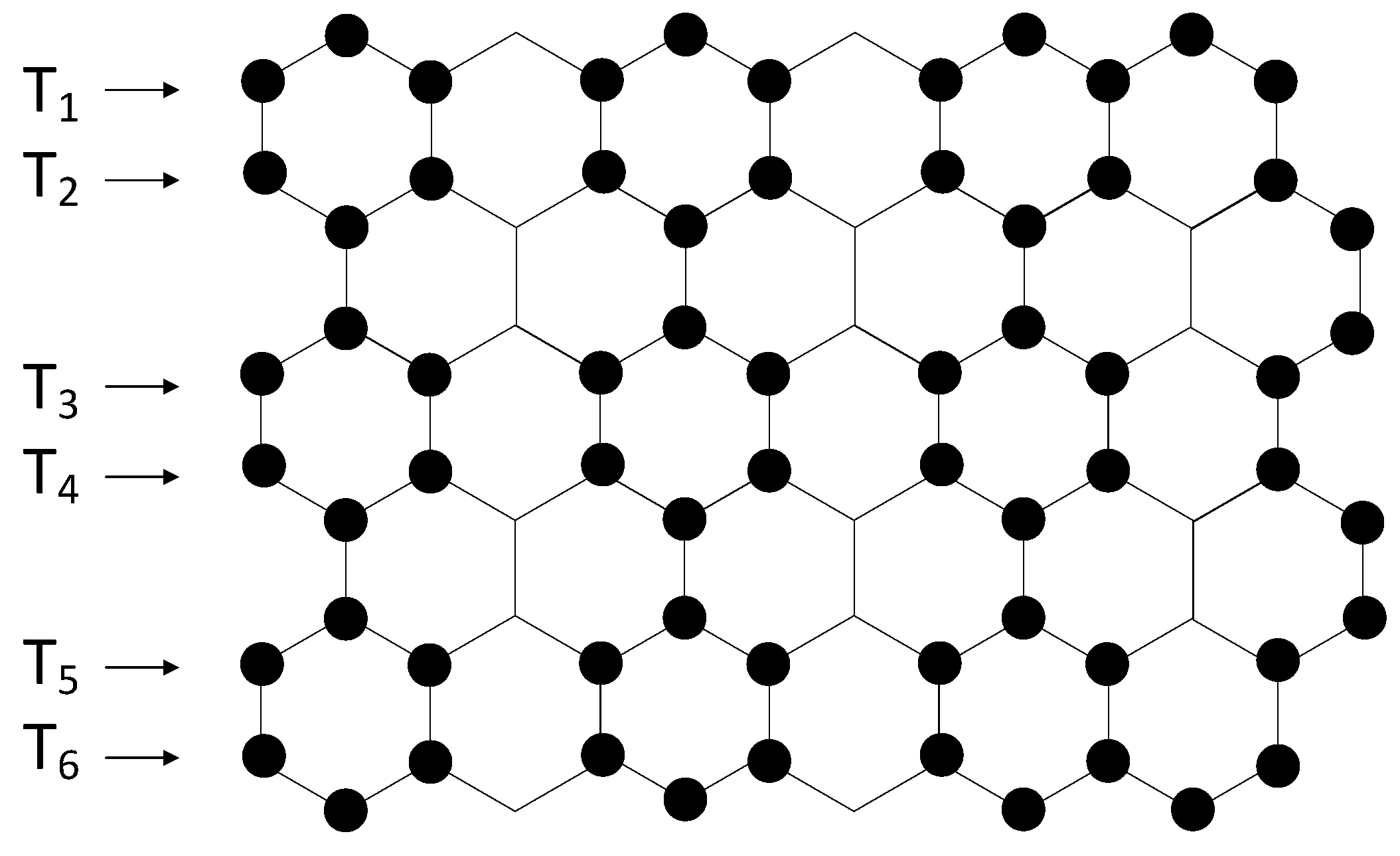
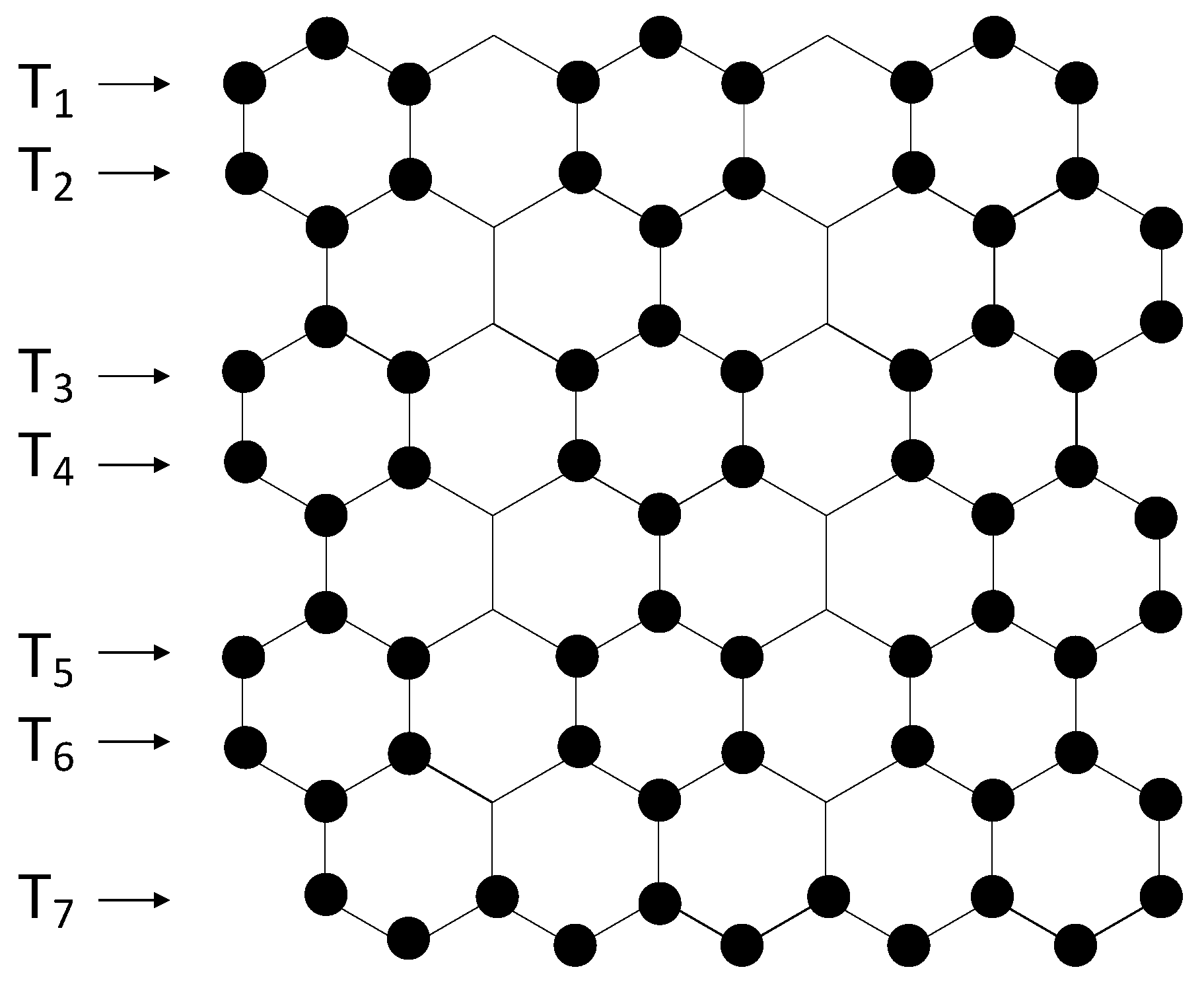
3. Total Domination Number of a Hexagonal Grid with Hexagons in a Row and Hexagons in a Column
4. Determining
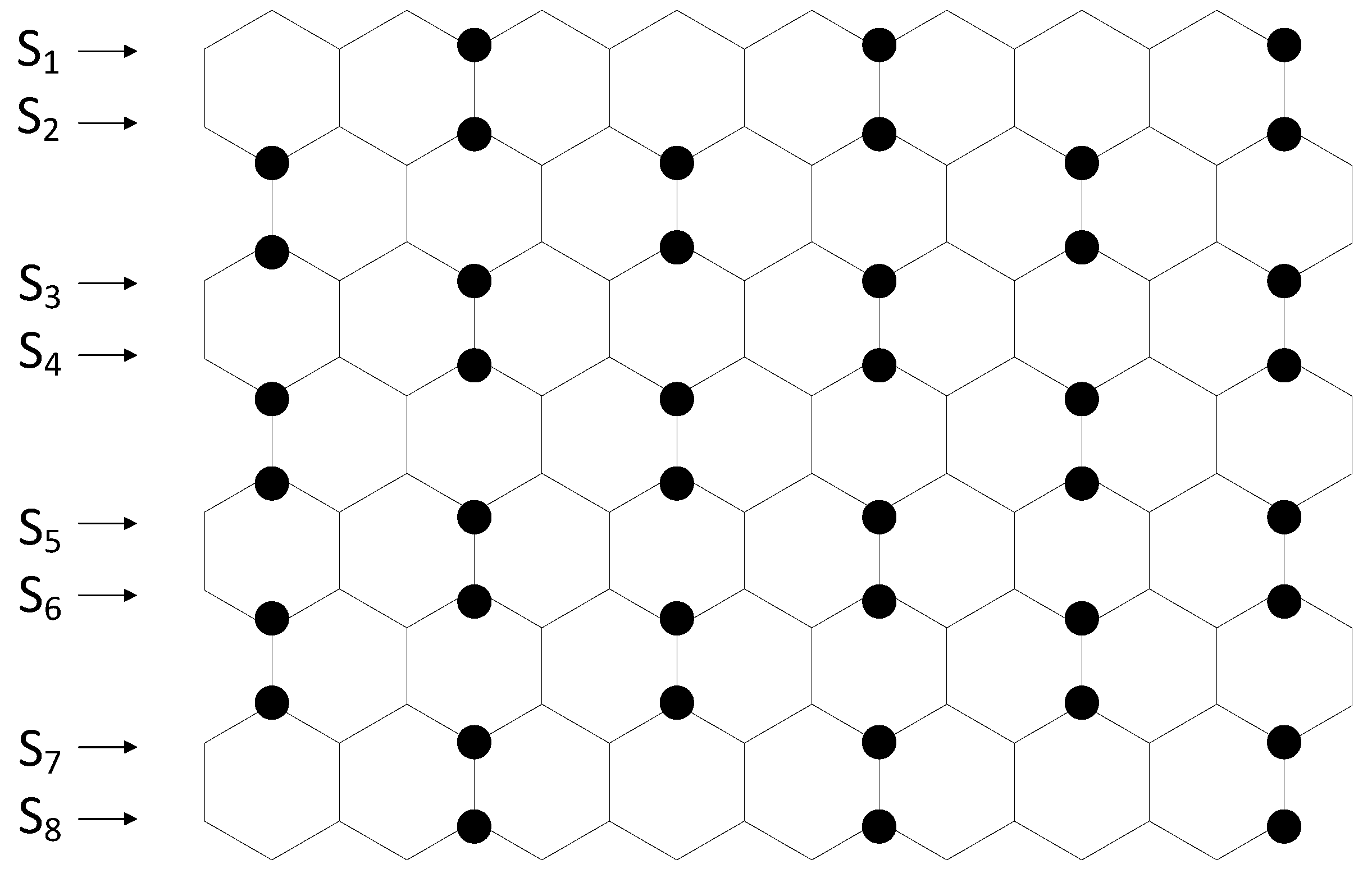
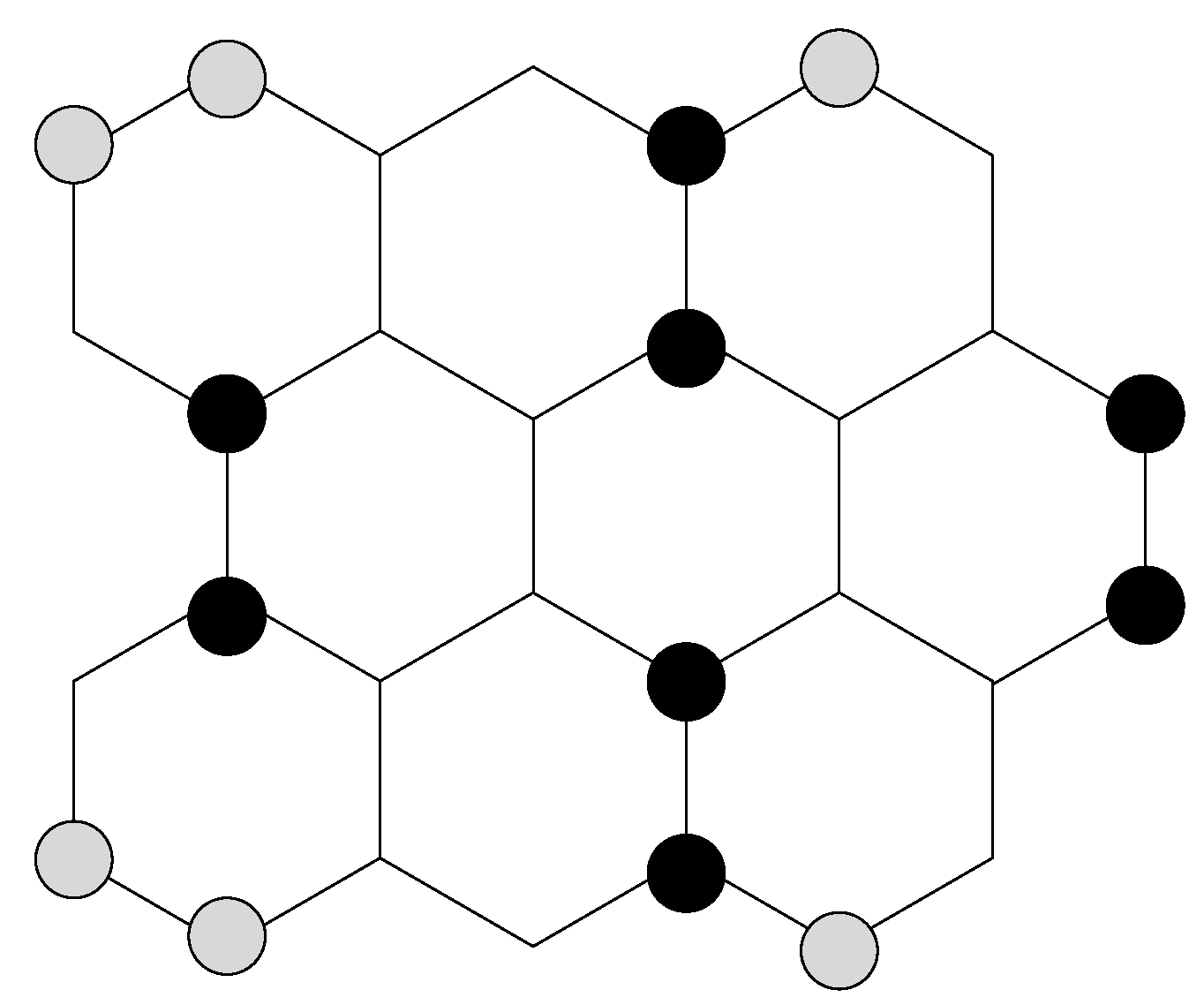
5. Double-Total Domination on a Hexagonal Grid
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Gao, Y.; Zhu, E.; Shao, Z.; Gutman, I.; Klobučar, A. Total domination and open packing in some chemical graphs. J. Math. Chem. 2018, 56, 1481–1493. [Google Scholar] [CrossRef]
- Henning, M.A.; Rautenbach, D.; Schäfer, P.M. Open packing, total domination and P3-Radon number. Discret. Math. 2009, 313, 992–998. [Google Scholar] [CrossRef]
- Majstorović, S.; Klobučar, A. Upper bound for total domination number on linear and double hexagonal chains. Int. J. Chem. Model. 2009, 3, 139–145. [Google Scholar]
- Mojdeh, D.A.; Habibi, M.; Badakhshian, L. Total and connected domination in chemical graphs. Ital. J. Pure Appl. Math. 2018, 39, 393–401. [Google Scholar]
- Vukičević, D.; Klobučar, A. K-Dominating sets on linear benzenoids and on the infinite hexagonal grid. Croat. Chem. Acta 2007, 80, 187–191. [Google Scholar]
- Bermudo, S.; Hernández-Gómez, J.C.; Sigarreta, J.M. On the total k-domination in graphs. Discuss. Math. Graph Theory 2018, 38, 301–317. [Google Scholar] [CrossRef]
- Cockayne, E.J.; Dawes, R.M.; Hedetniemi, S.T. Total domination in graphs. Networks 1980, 10, 211–219. [Google Scholar] [CrossRef]
- Henning, M.A.; Kazemi, A.P. k-tuple total domination in graphs. Discret. Appl. Math. 2010, 158, 1006–1011. [Google Scholar] [CrossRef][Green Version]
- Klobučar, A. Total domination numbers of Cartesian products. Math. Commun. 2004, 9, 35–44. [Google Scholar]
- Klobučar, A. Domination numbers of cardinal products. Math. Slovaca 1999, 49, 387–402. [Google Scholar]
- Gutman, I. Hexagonal systems, a Chemistry Motivated Excursion to Combinatorial Geometry. Teach. Math. 2007, 18, 1–10. [Google Scholar]
- Majstorović, S.; Došlić, T.; Klobučar, A. k-Domination on hexagonal cactus chains. Kragujev. J. Math. 2012, 36, 335–347. [Google Scholar]
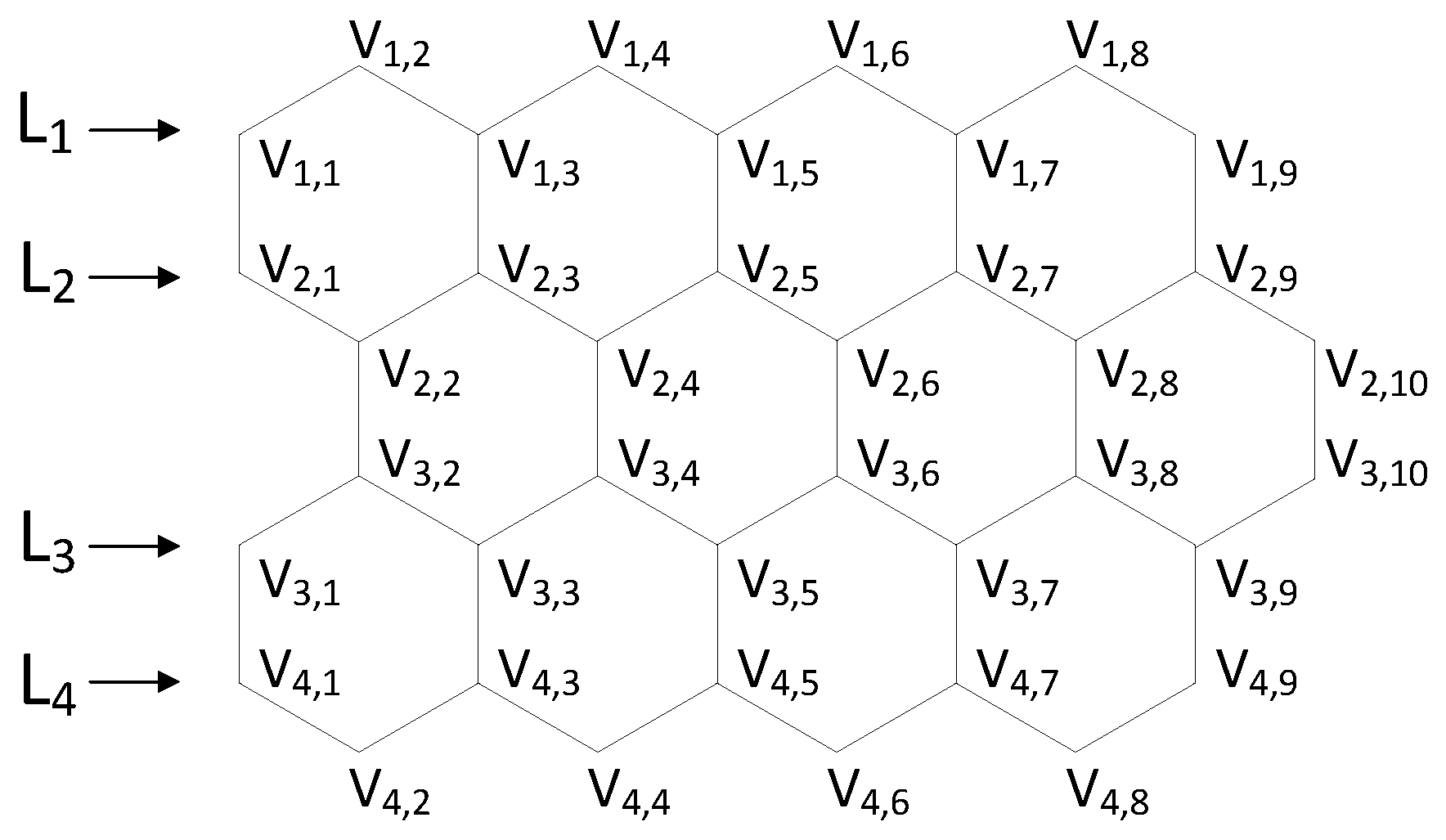
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Klobučar, A.; Klobučar, A. Total and Double Total Domination Number on Hexagonal Grid. Mathematics 2019, 7, 1110. https://doi.org/10.3390/math7111110
Klobučar A, Klobučar A. Total and Double Total Domination Number on Hexagonal Grid. Mathematics. 2019; 7(11):1110. https://doi.org/10.3390/math7111110
Chicago/Turabian StyleKlobučar, Antoaneta, and Ana Klobučar. 2019. "Total and Double Total Domination Number on Hexagonal Grid" Mathematics 7, no. 11: 1110. https://doi.org/10.3390/math7111110
APA StyleKlobučar, A., & Klobučar, A. (2019). Total and Double Total Domination Number on Hexagonal Grid. Mathematics, 7(11), 1110. https://doi.org/10.3390/math7111110



