Abstract
This paper analyzes Cournot duopoly games that are constructed based on Cobb–Douglas preferences. We introduce here two models whose dynamic adjustments depend on bounded rationality, dynamic adjustment, and tit-for-tat mechanism. In the first model, we have two firms with limited information and due to that they adopt the bounded rationality mechanism. They update their productions based on the changing occurred in the marginal profit. For this model, its fixed point is obtained and its stability condition is calculated. In addition, we provide conditions by which this fixed point loses its stability due to flip and Neimark–Sacker bifurcations. Furthermore, numerical simulation shows that this model possesses some chaotic behaviors which are recovered due to corridor stability. In the second model, we handle two different mechanisms of cooperation. These mechanisms are dynamic adjustment process and tit-for-tat strategy. The players who use the dynamic adjustment increase their productions based on the cooperative output while, in tit-for-tat mechanism, they increase the productions based on the cooperative profit. The local stability analysis shows that adopting tit-for-tat makes the model unstable and then the system becomes chaotic for any values of the system’s parameters. The obtained results show that the dynamic adjustment makes the system’s fixed point stable for a certain interval of the adjustment parameter.
1. Introduction
Back to 1838 where Cournot introduced the first mathematical model which describes the competition among firms, several studies of economic market structures have become in the foci of mathematicians and scientists. In [1], an excellent book of the theory of duopolistic market by Cournot appeared. In such competition, full rationality, cognitive and computational skills are important for those firms to identify the demand curve of the produced commodity and therefore they can expect the next step of the production by their competitors. According to the availability of such skills, firms may be able to solve a one period optimization problem. Recent studies have argued that reducing the rationality in terms of computational and informational capabilities leads to the appearance of dynamic adjustment processes such as bounded rationality and hence complex dynamic phenomena such as bifurcation and chaos can arise [2,3,4,5,6]. It is important to highlight Puu’s work in [7]. In [7], unimodel reaction functions have been incorporated with consumer’s Cobb–Douglas preferences to construct a duopolistic model. With these assumptions, Puu has shown that the behavior of the firms’ outputs is evolved through a chaotic scenario which in turn leads to chaos. Studies carried out by Puu have made researchers to investigate several decisional and adjustment mechanisms—as, for example, we mention bounded rationality, Puu’s incomplete information and tit-for-tat strategy. Players adopting bounded rationality use local knowledge to improve their output by marginal profit. This mechanism requires players not to have any knowledge about the demand and cost functions [8]. The players need only to check whether the market will respond to small changes in the quantities produced by estimating the marginal profit. This mechanism has been used by many authors in literature and mainly when a continuous time scenario was used [9]. It has been reported that production decisions may not be revised at every time instant and consequently discrete time decisions are more realistic than continuous one [8]. An alternative mechanism for the one discussed above is called Puu’s incomplete information. Puu has shown that this mechanism has a realistic advantage in that firms require to know only the profit and their quantities produced in the previous two time steps. They do not need the form of the profit to get estimation of the amount of production needed in the next time step. This mechanism has a serious problem related to the instability of the equilibrium point in the case of duopoly. Many authors have modified this mechanism to overcome this criticism—see, for example [10]. On the other hand, interaction between past decisions and market mechanisms has been investigated in literature. In [11], a monopolistic dilemma has been described due to unknown demand function. Indeed, when the demand function is unknown, a monopolistic player uses a gradient based rule in order to decide the amount of quantity produced in the next time step depending on the variation occurred in profits. Increasing demand may cause criticism to duopolistic players and this made Rotemberge and Saloner [12] introduce a cartel that may help to drop price in the case of increasing demand. In [13], we have shown that log-convex demand function can cause such an unusual behavior in the price. Cooperative cases among duopolistic firms have been studied in literature ([14,15]). In [14], a cooperation scenario among duopolistic firms under iso-elastic demand function has been introduced and studied. The tit-for-tat and adjustment mechanisms have been used to claim that complex dynamic behaviors of such games can be found even when cooperation is available. The main interest for researchers in those games is that whether Nash equilibrium or Cournot equilibrium is going to reflect rationality among cooperative firms or not. Here, we should differentiate among two important concepts which are rationality and Pareto optimality. Nash equilibrium appeared in duopolistic rational games is not Pareto optimal as rationality contradicts Pareto optimality in cooperative games. In other words, Pareto optimality can not be achieved by firm interest’s maximization. Recently, it has been reported in ([15,16]) that cooperative solution can be obtained. For instance, in a prisoner’s dilemma, which is a short game, Nash equilibrium is Pareto optimal because of the cooperation obtained. However, this may not be guaranteed in the case of Cournot repeated games as cooperation among competitors (firms) may be impossible to achieve. Recent studies have argued that the tit-for-tat strategy may achieve cooperation among firms in repeated games [14]. For more studies in this direction of research, readers are advised to see [17,18].
Literature reports an extensive consideration of Cournot duopoly games that were derived from Cobb–Douglas or other types of utility functions. For instance, in [19], the duopoly manufacturing game has been introduced and studied using the bounded rationality mechanism. The continuous delayed Bertrand game has been studied by Ma et al. in [20]. The complex dynamics of a Cournot duopoly game defined by a piecewise map have been investigated in [21]. In [22], two models of noncooperative oligopoly derived from Cobb–Douglas have been studied. It has been proved that Cobb–Douglas–Cournot–Nash equilibrium existed. The long-run equilibrium for an oligopoly model that is based on Cobb–Douglas has been investigated in [23]. There are other directions of research on the behavior of Cournot duopoly games that should be highlighted here. In [24], the synergies between evolutionary games and networks and their effects on cooperation between firms have been discussed. One of the factors that might affect the overall firm’s performance is the union members. This factor has been determined and studied in [25]. A decomposition mechanism with weighted degrees has been introduced in [26] to investigate the invaders impacts on cooperative communities.
The main purpose of this paper is to investigate the dynamic characteristics of Cournot duopoly games whose preferences are derived from Cobb–Douglas utility function. The firms in these games adhere different kind of mechanisms to modify their productions in a dynamic way. Those mechanisms are bounded rationality, dynamic adjustment process, and tit-for-tat mechanism. The current paper is divided into two parts. The first part handles a Cournot duopoly competition between firms on which bounded rationality is used and cooperation among competitors is disregarded. The system constructed due to adopting such mechanism is studied in detail focussing on its stability and other complex dynamic characteristics. In the second part, cooperation among firms is considered using dynamic adjustment process and the tit-for-tat mechanism and hence the characteristics of the cooperative systems are investigated in detail. A brief description of the paper is given as follows. Section 2 introduces the first model in this paper. The characteristics of this model are investigated in Section 3. In the Section 4, the cooperative models are presented and their complex characteristics are illustrated. Finally, conclusions are obtained in Section 5.
2. Model 1
In this section, we assume that the market structure consists of two firms whose preferences are based on Cobb–Douglas. It takes the form , where and denote the quantities produced by each firm. This unconstrained utility function is strictly concave if , and . It is concave when , and . Both firms want to maximize their preferences according to the budget constraint , where is a commodity price supplied by firm i. With these assumptions, the following maximization problem is given:
where is the solution of Equation (1). Now, the first step to build our dynamical model is to assume that both firms play in the market based on the variation occurred in their marginal profits. Profit is described by , where is a fixed marginal cost. According to this utility function, the profits take the following form:
Cournot duopoly competition has been intensively studied in literature ([27,28,29,30,31,32]). In literature, complex dynamic characteristics of such competition are the most highlighted ones. Here, we suppose that a dynamic competition is taken place between two firms according to discrete time scale, , Thus, the profits in Equation (2) can be rewritten in the form:
In such competition, information each player knows about its opponent is important. Each player may know some information so that he/she may expect the next decision of its opponent. For instance, knowing the profit function of your competitor or some knowledge about it makes you use some kinds of expectations against his/her decision. In literature [5,6,7,8], different kinds of those expectations have been studied. Naive expectations, rational expectations or adaptive expectations, or, alternatively, using weights of previous decisions to set the quantities at time are examples of those expectations. When there is a lack of information about profits, each player estimates the marginal profit in order to follow the steepest slope of the profit function. Considering such expectations helps to only get correct estimates of the slope (the partial derivatives of the profit computed at the current state of production) and does not help solving the optimization problem . This means that, if the marginal profit at time t is positive(or negative), the player will increase (or decrease) the quantity produced at time . Based on this discussion, the following adjustment mechanism is used:
where captures the speed at which firm i adjusts its quantity with respect to the consequent marginal change in its profit and . Therefore, the following dynamical model is given:
The system (5) admits a unique fixed point given by:
3. Local Analysis
Studying the complex behavior of system (5) requires investigation of the local stability of the fixed point (6). To do that, we get the following proposition.
Proposition 1.
The system (5) has a unique positive fixed point (6) that is locally asymptotically stable provided that: , .
Proof.
The proof of the above proposition is straightforward. We recall the Jacobian matrix of system (5),
where , . This matrix gives the following characteristic equation:
where
According to Jury conditions [28], the fixed point is locally stable provided that:
Substituting (9) in (10) gives
One can see that under the condition , the other two conditions, with simple calculations, yield and then the proof is completed. To confirm these results, the next subsection provides numerical simulation to validate the obtained results above and to investigate the complicated behavior of system (5). □
Proposition 2.
The fixed point (6) of system (5) loses its stability via period-doubling bifurcation (Flip bifurcation) only if .
Proof.
The Jacobian (7) has the following eigenvalues:
Using (6), the part under the square root of the above eigenvalues is reduced to
which is positive under the condition where . Therefore, both eigenvalues are real. Thus, if the second or the third condition of (11) is not satisfied, then the fixed point loses its stability via flip bifurcation. □
Proposition 3.
The fixed point (6) of system (5) loses its stability via Neimark–Sacker bifurcation only if .
Proof.
Similar to the above proof. □
Numerical Simulation and Global Analysis
Some simulations are carried out here to detect the regions identified by the conditions (11) on where the fixed point may lose its stability. By simulations, we investigate deeply the complex dynamic behavior of system (5) and in particular we illustrate the stabilization of the system’s fixed point. Such numerical simulations suggest to be cautioned when we try to make predictions on the future evolution of the economic competition and therefore global analysis should be performed. It is known that local stability analysis is discussed in some neighborhoods of the fixed point and therefore global analysis is necessary in order to get satisfied with the obtained trajectories. Let us set the parameter values to , and . At those parameter values, the fixed point (6) becomes and the Jacobian (7) takes the form:
and then the fixed point is locally stable if . This is clear in Figure 1a where the point is stable when varying the parameter k until k approaches the value of on where birth to period 2-cycle arises. After that high period, cycles exist and then a route to chaos appears, and the system becomes chaotic. This is observed from Lyapunov exponent diagram shown in Figure 1b.
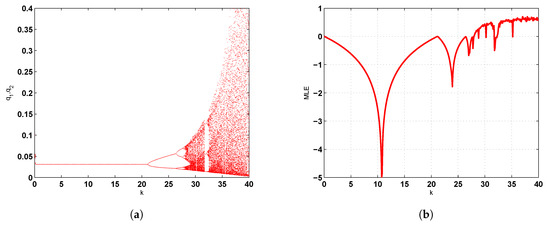
Figure 1.
(a) bifurcation diagram of and when varying k; (b) Lyapunov exponent with respect to k.
The stability analysis around the local fixed points doesn’t give any information about the size and shape of basin of attraction of different attractors of the corresponding system and therefore we here give some global analysis in order to explore some complex characteristics about those attractors. At the same parameter values but increasing the parameter k to , a stable period 2-cycle exists. Those period 2-cycles are and . This stable period cycles is given in Figure 2a where its basin of attraction and phase portrait are plotted together. This stable period 2-cycle appears near the fixed point until k goes to , where a stable period 4-cycle exists. Its basin of attraction with the phase portrait is given in Figure 2b.
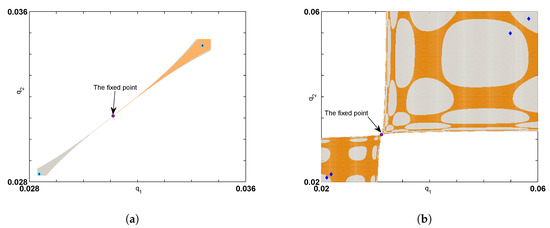
Figure 2.
(a) Basin of Attraction of period 2-cycle at ; (b) Basin of Attraction of period 4-cycle at .
Simulation shows that there are no stable cycles with period 6 and the system jumps instead to a stable period 8-cycle when varying the value of the parameter k to 27.74 with the other parameter values are fixed. This cycle is presented in Figure 3a with its basin. Increasing k slightly to gives birth to a stable period 16-cycle as shown in Figure 3b. After that, no other period cycles are obtained and the system starts to behave chaotically. To understand that, we increase the parameter and keep the other parameter values fixed. We get a chaotic behavior of the system around the fixed point as shown in Figure 4a. This chaotic behavior consists of an 8-band of chaotic attractors. This situation is called corridor stability which refers to small perturbations in nonlinear dynamic systems may be recovered as long as they are confined within a basin of attraction of the stable fixed point. Increasing k a little gives birth to a 4-band of chaotic attractors as shown in Figure 4b. This 4-band is reduced to only 2-band when k reaches . The phase portrait of this 2-band is given in Figure 4c. This 2-band of chaotic attractors is reduced to only one chaotic attractor as as given in Figure 4d. It continues to appear until and then the systems turn to a stable period 3-cycle at . The basin of attraction of these period cycles is given in Figure 5a. Then, the behavior of the system (5) will continue changing between a stable 3-cycle, and a one piece of chaotic attractor until k approaches 33; then, the behavior becomes entirely chaotic with only one piece of chaotic attractor. We give examples of those chaotic attractors in Figure 5b,c. Figure 5d gives the time series of the chaotic attractor given in Figure 5c.
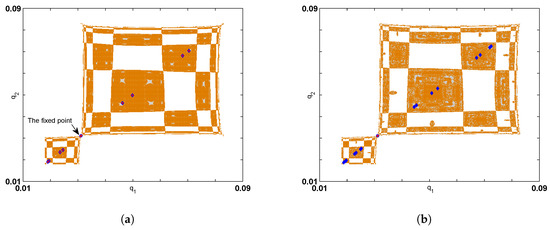
Figure 3.
(a) Basin of Attraction of period 8-cycle at ; (b) Basin of Attraction of period 16-cycle at .
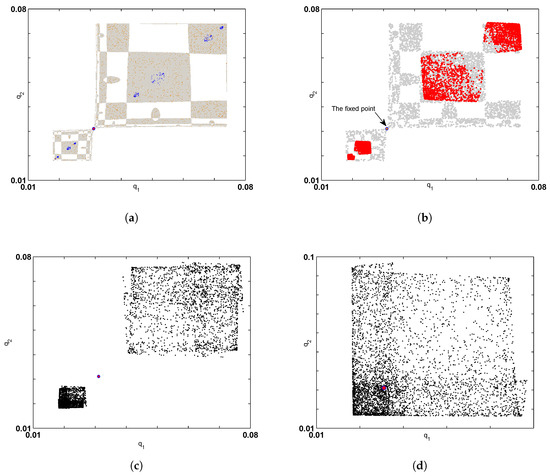
Figure 4.
(a) Basin of Attraction of 8-band chaotic attractors at ; (b) Basin of Attraction of 4-band chaotic attractors at ; (c) phase portrait of 2-band chaotic attractors at ; (d) phase portrait of 1-band chaotic attractor at .
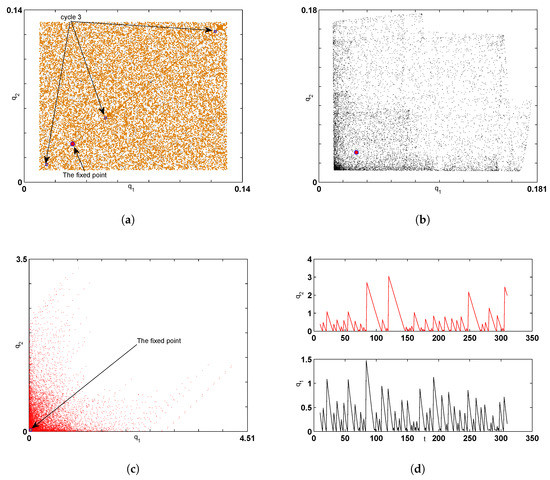
Figure 5.
(a) Basin of Attraction of period 3-cycle at ; (b) Basin of Attraction of chaotic attractor at ; (c) Basin of Attraction of chaotic attractor at ; (d) time series for both variables for the chaotic attractor in (c) at .
The readers should be aware that the above obtained results are for very small values of equal costs and for small parameter values of and . Now, we focus on the situation when the summation of and is almost close to 1. Let us set the parameter values to , and . Figure 6a shows that the fixed point becomes locally stable with respect to k, but, when k reaches , it becomes unstable due to Neimark–Sacker bifurcation. Increasing this parameter to 29 gives birth to two stable spirals around the fixed point. After that, these two stable spirals turn to a stable period 2-cycle when we increase k to , and the other parameter values are fixed. Figure 6c presents this cycle with its basin of attraction around the fixed point. In Figure 6d, we plot the time series for this stable period 2-cycle. One can observe from the numerical simulation that the system starts to form closed sets as k increases until it reaches , where we get a one piece chaotic attractor. Figure 7 gives some behaviors of the system at different values of k.
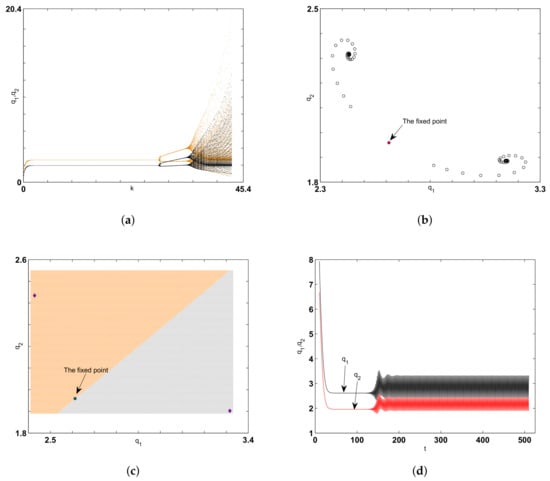
Figure 6.
(a) bifurcation diagram of and when varying k; (b) phase portrait of two spirals at ; (c) Basin of Attraction of period 2-cycle at ; (d) time series for both variables for the stable period 2-cycle in (c) at .
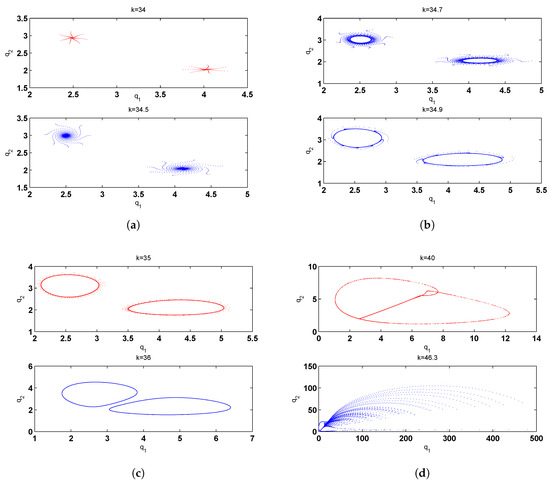
Figure 7.
(a) and ; (b) and ; (c) and ; (d) and .
To end this part of the analysis, several numerical simulation experiments are carried out to investigate more the complex behavior of system (5). We observe that, when gets near 1, the stability region of the fixed point becomes larger in comparison with summation near zero. In addition, the fixed point loses its stability via only two types of bifurcations that are flip and Neimark–Sacker bifurcations.
4. Model 2
In this section, we discuss a different case. We consider the cooperation that might occur between the two firms. Cooperation among firms can be carried out using several mechanisms. In [14], two important mechanisms have been used to identify the cooperation among firms. Those two mechanisms are adopted in this paper. Another important mechanism that has been used for that purpose is called the weighted mechanism [27]. This section is divided into two parts: the first part studies the cooperation between two firms who revise their beliefs due to the dynamic adjustment, which is described in the following subsection. The second part introduces a cooperation between two firms whose mechanisms are tit-for-tat strategies.
4.1. Dynamic Adjustment
Here, we assume that the two firms supply the market with quantities produced according to the following dynamical system:
where is an adjusting parameter and is the solution of the following optimization problem:
which is given as follows:
and we assume that both firms have the same marginal costs, . Using the profits (2), the cooperative profit is given by
Using the system (14) and the point (15), one can get the following system:
Proposition 4.
The system (17) has a unique fixed point , and it is locally asymptotically stable provided that .
The proof of the above proposition is straightforward. The Jacobian matrix takes the form:
It is easy to check that the conditions (10) give , which completes the proof.
Numerical Simulation
Here, we carry out some numerical simulation to validate the results given in Proposition 4. Let us assume that . Figure 8a shows the behavior of system (17) when varying the parameter k in the interval . The figure shows that the fixed point is locally stable for any value of k until k reaches the value on where the fixed point becomes unstable due to bifurcation occurred. Increasing the value of the parameter k above this point gives birth to fluctuations around the fixed point as shown in Figure 8b. Figure 8c shows the time series for the fluctuations given in Figure 8b.
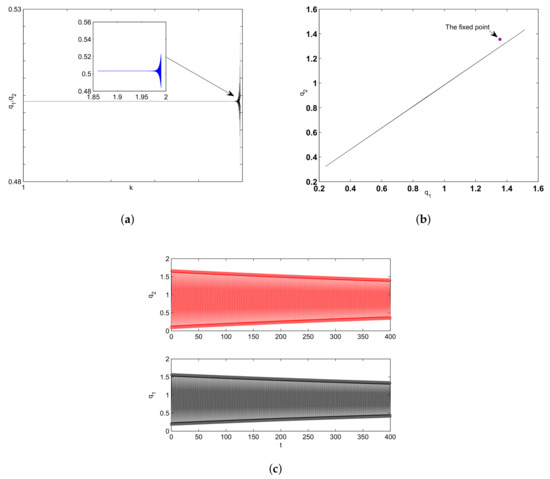
Figure 8.
(a) bifurcation diagram when varying the parameter k; (b) the fluctuations around the fixed point at ; (c) time series for the fluctuations in (b).
4.2. Tit-for-Tat Mechanism
With this mechanism, each firm agrees to cooperate as long as its profit does not contradict the cooperative profit. This means that, if , each firm will probably reduce its output to keep the cooperation between each other. On the other hand, cooperation cannot be achieved if because it indicates that one of the firms is non-cooperative. According to these thoughts, the following system is given:
Using the profits (3) and and the cooperative profit (16) in the matrix (19), the following dynamical system is obtained:
It is difficult to analytically calculate the fixed point of the above system and instead we do some numerical simulation to investigate its stability.
Numerical Simulation
Let us assume the following parameter values: . The simulation shows that the fixed point of system (20) is unstable as the parameter k varies and bifurcation is obtained. This is clear in Figure 9a and the phase space in Figure 9b at those values. Several numerical simulation experiments have been performed for different values of the parameter k. They show that any increase in this parameter yields negative values for the system’s variables which have no economic meanings. Setting the parameter values to also gives an instability situation of the fixed point of system (20). In addition, the positivity of the quantities’ trajectories can not be preserved and therefore negative trajectories appear. Figure 9c,d present this observation.
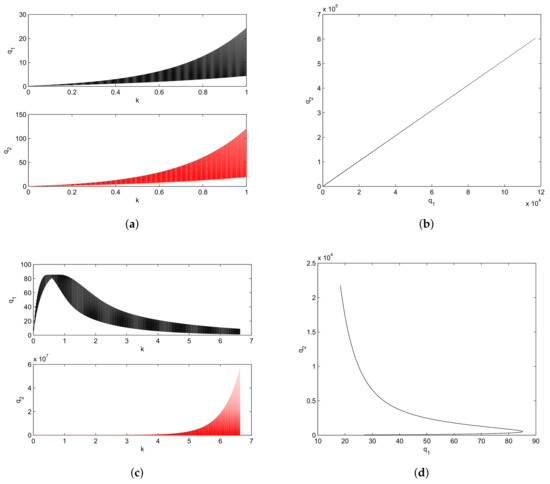
Figure 9.
(a) bifurcation diagram when varying the parameter k; (b) the phase portrait at , ; (c) bifurcation diagram when varying the parameter k; (d) the phase portrait at .
5. Conclusions
In this paper, we have recalled the Cobb–Douglas utility function to study three different Cournot duopoly models. Indeed, we have focused on the complex dynamic behaviors of those models and the influences their parameters can cause to destabilize their fixed points. As mentioned in the beginning of the paper, we have used bounded rationality for the non-cooperative game’s model and dynamic adjustment process and tit-for-tat mechanism for a cooperative game’s model. The obtained results have shown that the bounded rationality adopted by the competed firms in the first model gives a better stability region for the fixed point than those in the cooperative case. On the other hand, when cooperation may exist between firms as in the second model, the dynamic adjustment process gives better results for the fixed point than the tit-for-tat strategy. The fixed point for the tit-for-tat model was always unstable for any values for the model’s parameters. Finally, our obtained results may confirm that cooperation based on Cobb–Douglas preferences does not give any advantages for both firms, and still non-cooperative games based on Cobb–Douglas give better stability results.
Author Contributions
Concepualization: S.S.A. and A.A.-k.; methodology, S.S.A. and A.A.-k.; software, S.S.A. and A.A.-k.; validation, S.S.A. and A.A.-k.; formal analysis, S.S.A. and A.A.-k.; investigation, S.S.A. and A.A.-k.; resources, S.S.A. and A.A.-k.; data curation, S.S.A. and A.A.-k.; writing–original draft preparation, S.S.A. and A.A.-k.; writing–review and editing, S.S.A. and A.A.-k.; visualization, S.S.A. and A.A.-k.; supervision, S.S.A. and A.A.-k.; project administration, S.S.A. and A.A.-k.; funding acquisition, S.S.A. and A.A.-k.
Funding
This research was funded by the Deanship of Scientific Research at King Saud University No. RG-1435-054.
Acknowledgments
The authors would like to extend their sincere appreciation to the Deanship of Scientific Research at King Saud University for its funding this Research Group No. (RG-1435-054).
Conflicts of Interest
The authors declare that they have no conflict of interest.
References
- Cournot, A.A. Researches into the principles of the theory of wealth. In Classics in Economics; Augustus M Kelley Pubs.: New York, NY, USA, 1971. [Google Scholar]
- Cavalli, F.; Namizada, A.; Tramontana, F. Nonlinear dynamics and global analysis of a heterogeneous Cournot duopoly with a local monopolistic approach versus a gradient rule with endogenous reactivity. Commun. Nonlinear Sci. Numer. Simul. 2015, 23, 245–262. [Google Scholar] [CrossRef]
- Rand, D. Exotic phenomena in games and duopoly models. Math. Econ. 1978, 5, 173–184. [Google Scholar] [CrossRef]
- Poston, T.; Stewart, I. Catastrophe Theory and Its Applications; Pitman Ltd.: London, UK, 1978. [Google Scholar]
- Naimzada, A.; Sbragia, L. Oligopoly games with nonlinear demand and cost functions: Two boundedly rational adjustment processes. Chaos Solitons Fractals 2006, 29, 707–722. [Google Scholar] [CrossRef]
- Askar, S.S. Dynamic Cournot duopoly games with nonlinear demand function. Appl. Math. Comput. 2015, 259, 427–437. [Google Scholar] [CrossRef]
- Puu, T. Chaos in duopoly pricing. Chaos Solitons Fractals 1991, 1, 573–581. [Google Scholar] [CrossRef]
- Askar, S.S. The rise of complex phenomena in Cournot duopoly games due to demand functions without inflection points. Commun. Nonlinear Sci. Numer. Simul. 2014, 19, 1918–1925. [Google Scholar] [CrossRef]
- Matsumoto, A.; Szidarovszky, F. Complex dynamics of monopolies with gradient adjustment. Econ. Model. 2014, 42, 220–229. [Google Scholar] [CrossRef]
- Ahmed, E.; Elettreb, M.F.; Hegazi, A.S. On quantum team games. Int. J. Theor. Phys. 2006, 45, 907–913. [Google Scholar] [CrossRef]
- Clower, R.W. Some theory of an ignorant monopolist. Econ. J. 1959, 69, 705–716. [Google Scholar] [CrossRef]
- Rotemberg, J.; Saloner, G. A super game-theoretic model of price wars during booms. Am. Econ. Rev. 1986, 76, 390–407. [Google Scholar]
- Askar, S.S. Complex dynamic properties of Cournot duopoly games with convex and log-concave demand function. Oper. Res. Lett. 2014, 42, 85–90. [Google Scholar] [CrossRef]
- Askar, S.S.; Alshamrani, A.M.; Alnowibet, K. Analysis of nonlinear duopoly game: A cooperative case. Discret. Dyn. Nat. Soc. 2015, 2015, 528217. [Google Scholar] [CrossRef]
- Ding, Z.; Shi, G. Cooperation in a dynamical adjustment of duopoly game with incomplete information. Chaos Solitons Fractals 2009, 42, 989–993. [Google Scholar] [CrossRef]
- Cafagna, V.; Coccorese, P. Dynamical systems and the arising of cooperation in a Cournot duopoly. Chaos Solitons Fractals 2005, 25, 655–664. [Google Scholar] [CrossRef]
- Askar, S.S.; Al-Khedhairi, A. Analysis of nonlinear duopoly games with product differentiation: Stability, global dynamics, and control. Discrete Dyn. Nat. Soc. 2017, 2017, 1–15. [Google Scholar] [CrossRef]
- Askar, S.S.; Al-Khedhairi, A. The dynamics of a business game: A 2D-piecewise smooth nonlinear map. Phys. A Stat. Mech. Appl. 2020, 537, 122766. [Google Scholar] [CrossRef]
- Peng, Y.; Lu, Q.; Xiao, Y.; Wu, X. Complex dynamics analysis for a remanufacturing duopoly model with nonlinear cost. Phys. A Stat. Mech. Appl. 2019, 514, 658–670. [Google Scholar] [CrossRef]
- Ma, J.; Si, F. Complex Dynamics of a Continuous Bertrand Duopoly Game Model with Two-Stage Delay. Entropy 2016, 18, 266. [Google Scholar] [CrossRef]
- Agliari, A.; Gardini, L.; Puu, T. Global bifurcations in duopoly when the Cournot point is destabilized via a subcritical Neimark bifuraction. Int. Game Theory Rev. 2006, 8, 1–20. [Google Scholar] [CrossRef]
- Giulio, C.; Julien, L.A. Noncooperative Oligopoly in Markets with a Cobb–Douglas Continuum of Traders. Louvain Econ. Rev. 2013, 4, 75–88. [Google Scholar] [CrossRef]
- Kolberg, W.C. Long-Run Equilibrium in a Cournot Type Oligopoly Model with Cobb–Douglas Demand and Production. SSRN 2009. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, L.; Szolnoki, A.; Perc, M. Evolutionary games on multilayer networks: A colloquium. Eur. Phys. J. B 2015, 88, 124. [Google Scholar] [CrossRef]
- Kamal, S.M.; Al-Hadeethi, Y.; Abolaban, F.A.; Al-Marzouki, F.M.; Perc, M. An evolutionary inspection game with labour unions on small-world networks. Sci. Rep. 2015, 5, 8881. [Google Scholar] [CrossRef] [PubMed]
- Yang, G.; Benko, T.P.; Cavaliere, M.; Huang, J.; Perc, M. Identification of influential invaders in evolutionary populations. Sci. Rep. 2019, 9, 7305. [Google Scholar] [CrossRef]
- Askar, S.S. On Cournot-Bertrand competition with differentiated products. Ann. Oper. Res. 2014, 223, 81–93. [Google Scholar] [CrossRef]
- Askar, S.S.; Alshamrani, A.M. The dynamic of economic games based on product differentiation. J. Comput. Appl. Math. 2014, 268, 135–144. [Google Scholar] [CrossRef]
- Ahmed, E.; Elsadany, A.A.; Puu, T. On betrand duopoly game with differentiated goods. Appl. Math. Comput. 2015, 251, 169–179. [Google Scholar]
- Agiza, A.N.; Elsadany, A.A. Nonlinear dynamics in the Cournot duopoly game with heterogenous players. Physics A 2003, 320, 512–524. [Google Scholar] [CrossRef]
- Agiza, A.N.; Elsadany, A.A. Chaotic dynamics in nonlinear duopoly game with heterogeneous players. Appl. Math. Comput. 2004, 149, 843–860. [Google Scholar] [CrossRef]
- Askar, S.S.; Abouhawwash, M. Quantity and price competition in a differentiated triopoly: Static and dynamic investigations. Nonlinear Dyn. 2018, 91, 1963–1975. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).