Numerical Analysis, Circuit Simulation, and Control Synchronization of Fractional-Order Unified Chaotic System
Abstract
1. Introduction
2. Intege-Order Unified Chaotic System
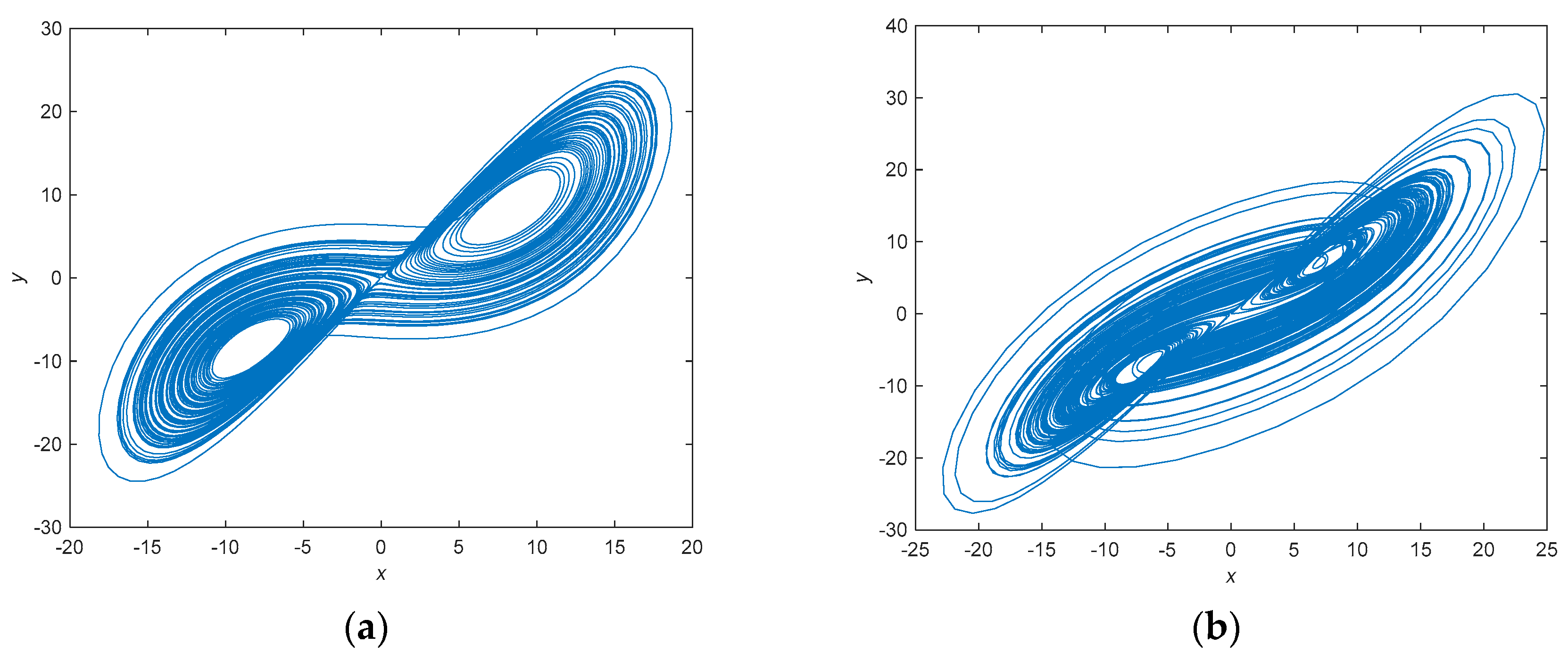
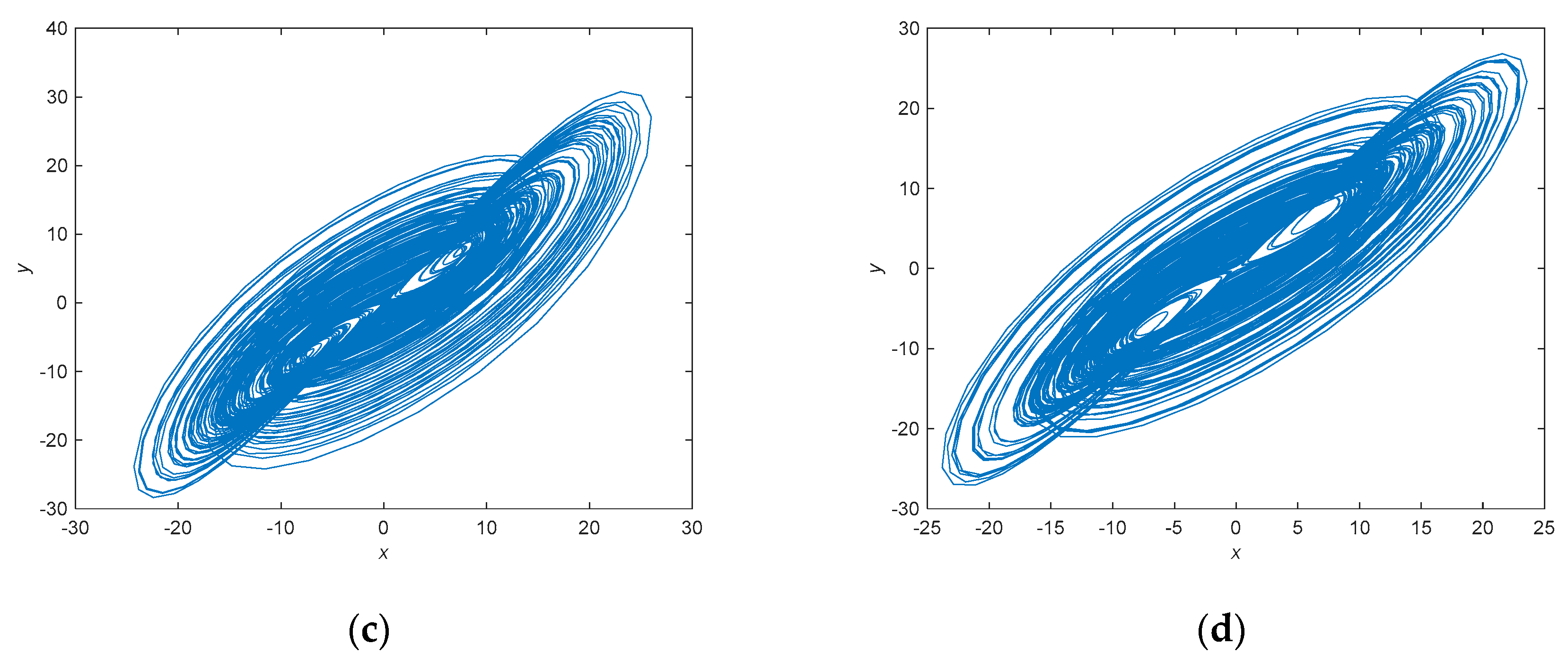
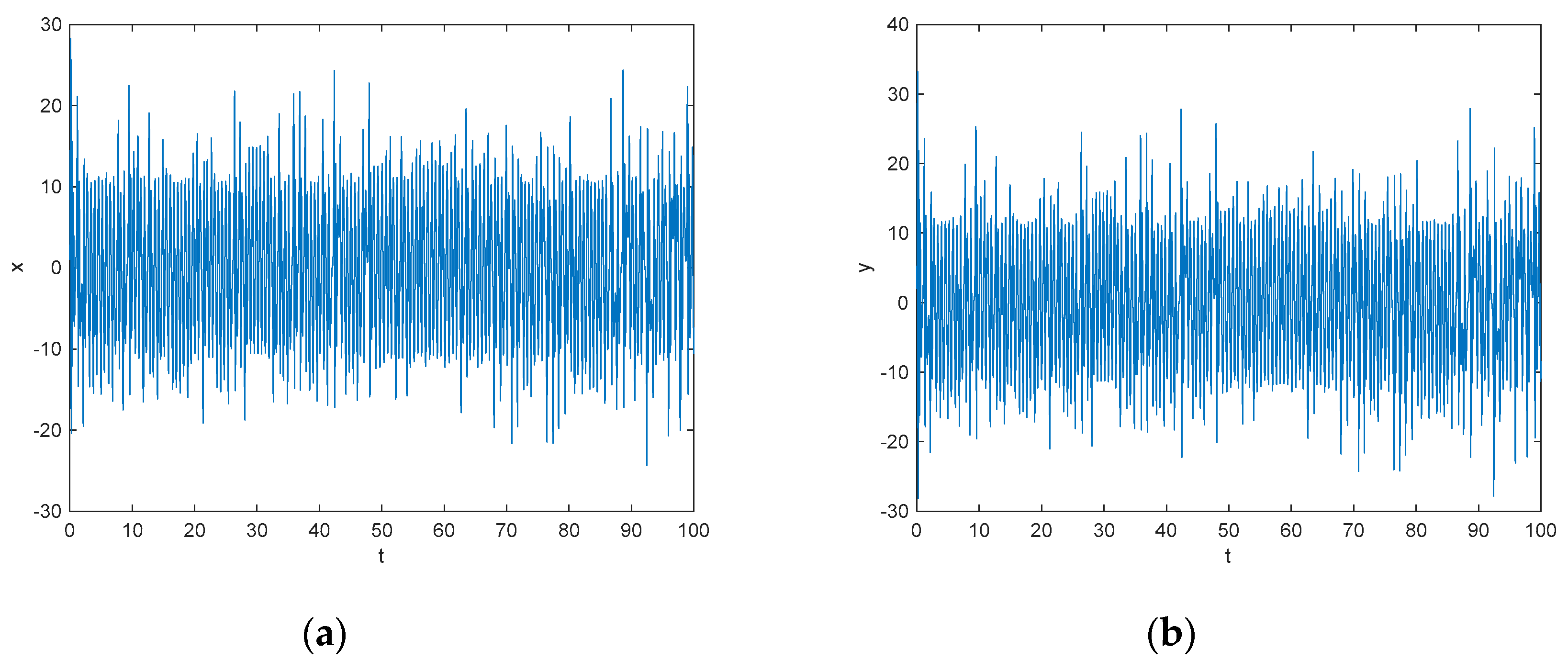
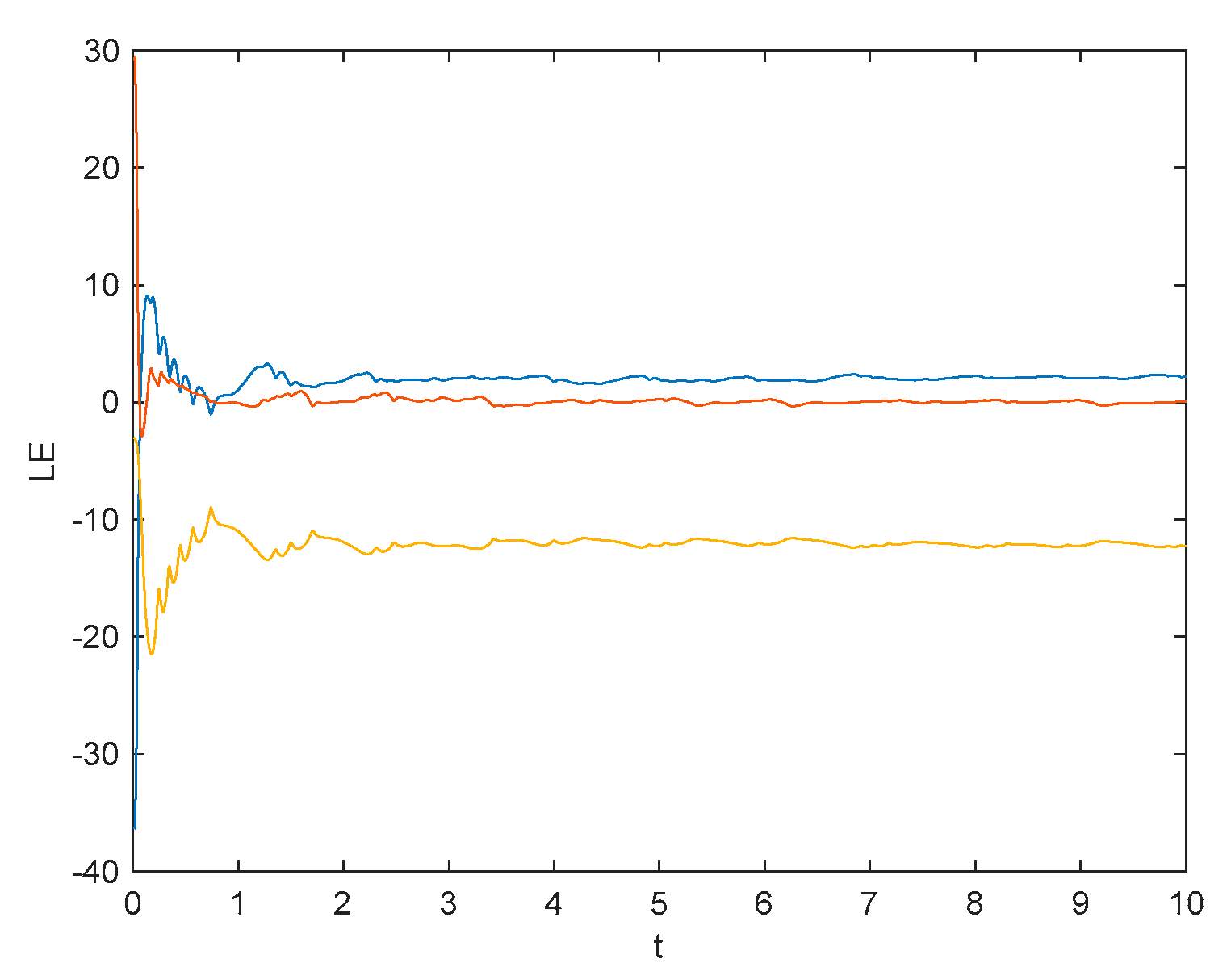
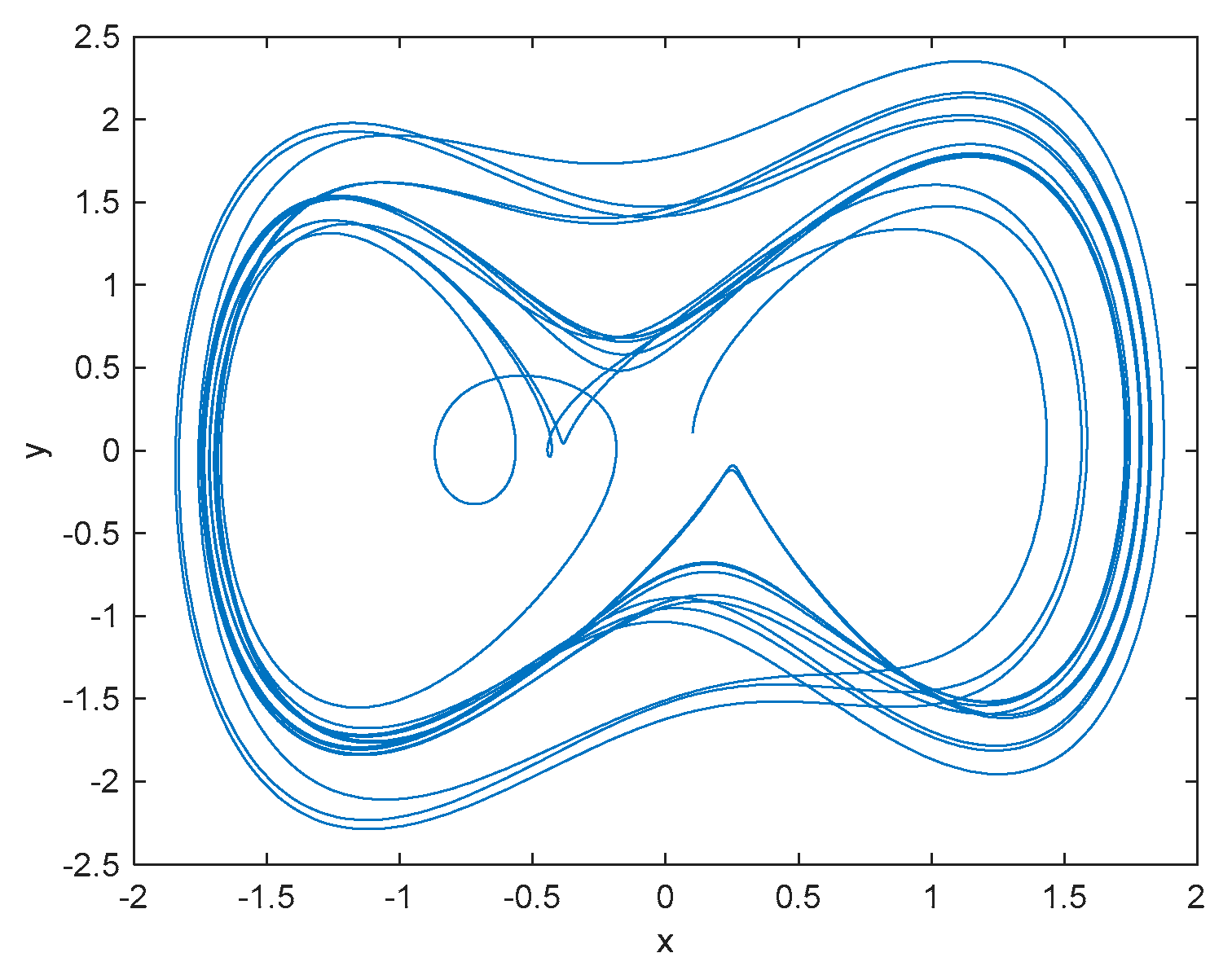
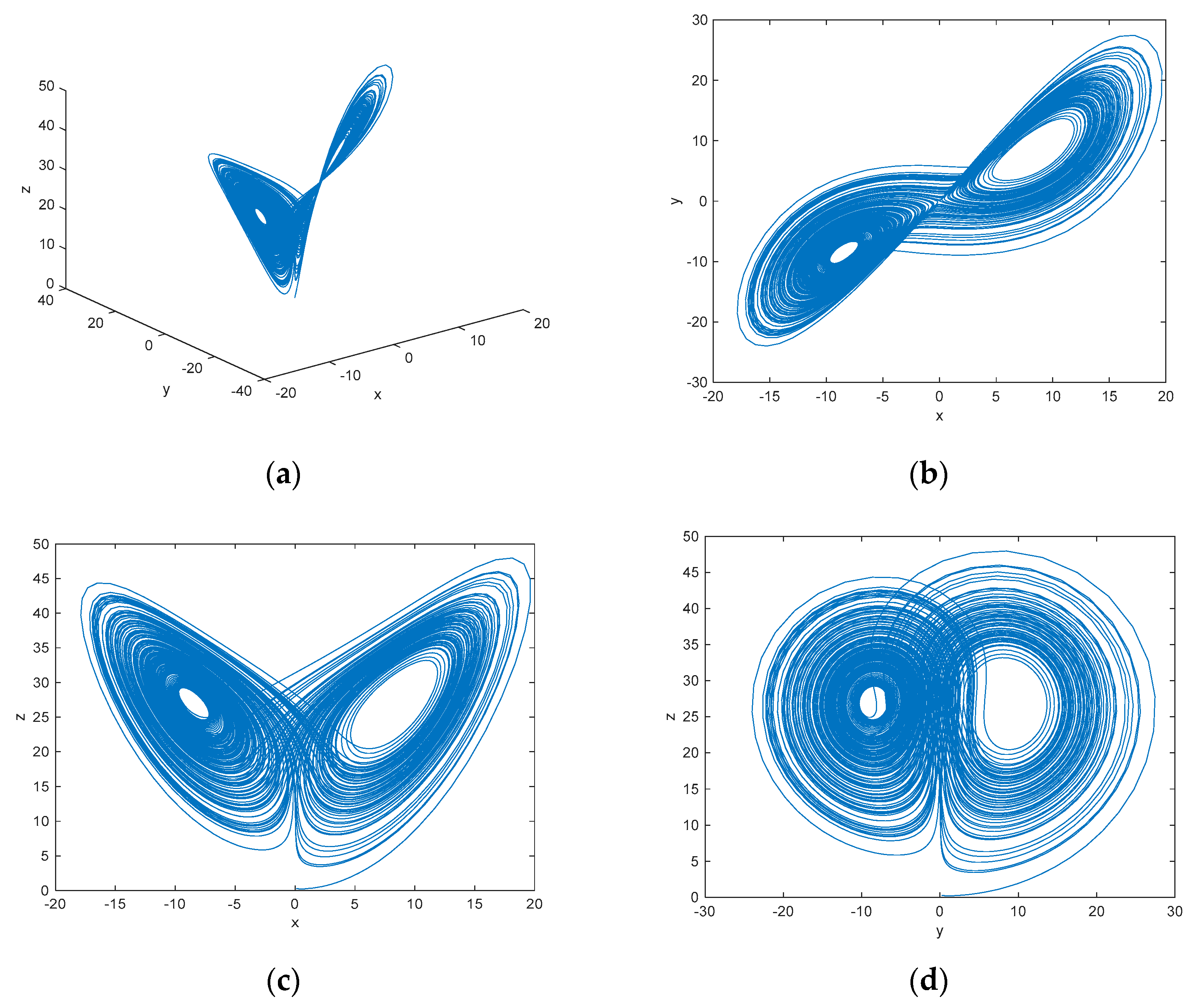
3. Fractional-Order Unified Chaotic System
3.1. Common Definitions of Fractional Calculus
3.2. The Calling Function Method
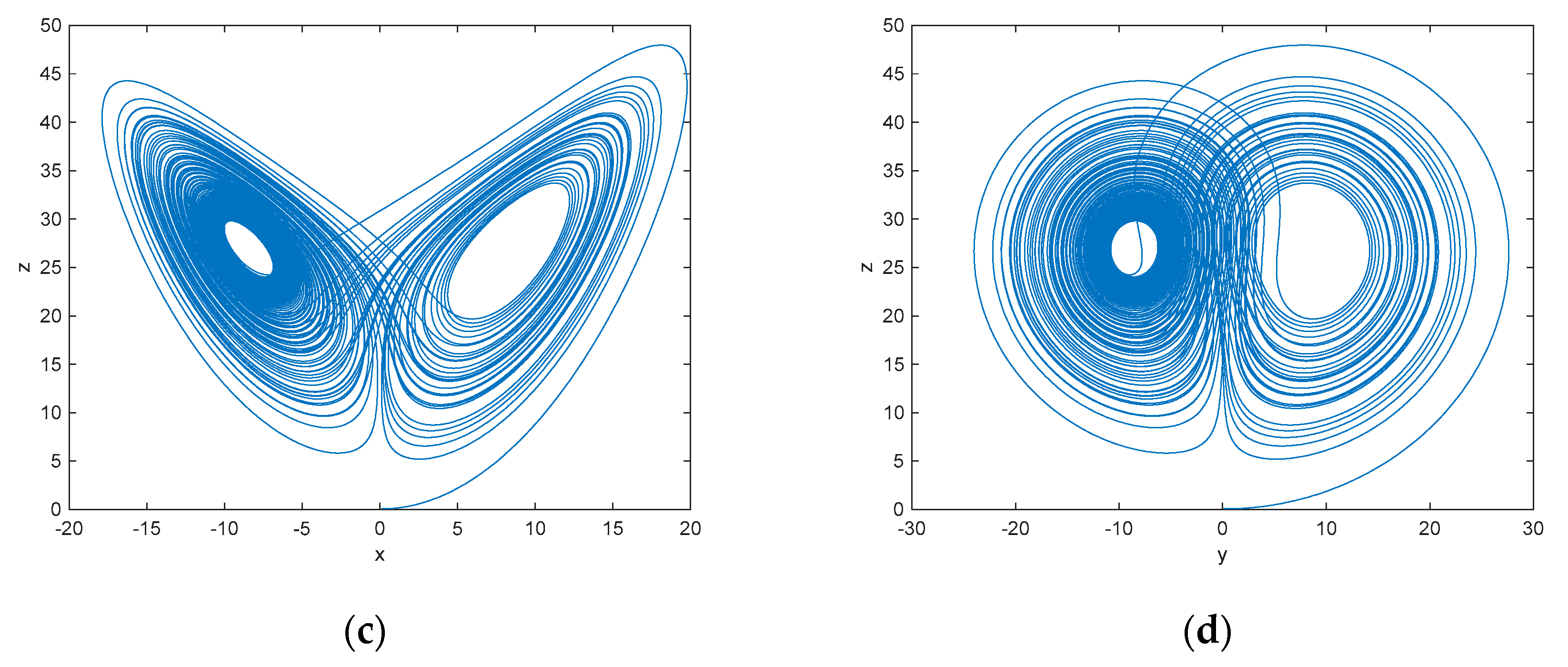
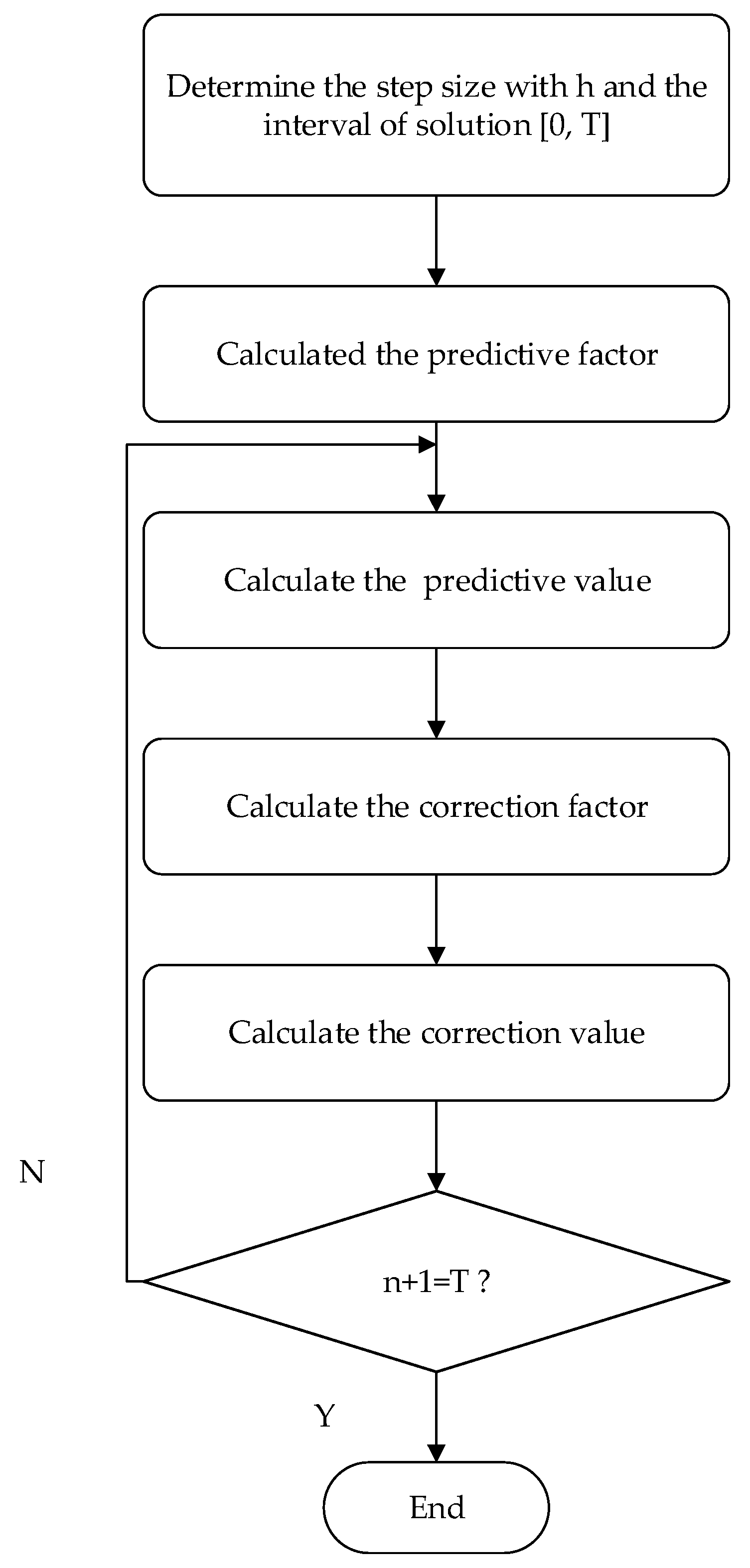
3.3. The Adams–Bashforth–Moulton Prediction–Correction Method [19]
- Step 1:
- Determine the step size and the interval of solution. Taking the fractional-order unified chaotic system as an example, the step size h = 0.01 is selected. The number of points is selected as N = 10,000, and the upper limit of integration is T = 100 (h = T/N).
- Step 2:
- Calculate the predictive factor.
- Step 3:
- Calculate the predictive value.
- Step 4:
- Calculate the correction factor.
- Step 5:
- Calculate the correction value.
- Step 6:
- Determine if the end condition is meet.
- Step 7:
- End the calculation if the condition is meet, or return to step 3.
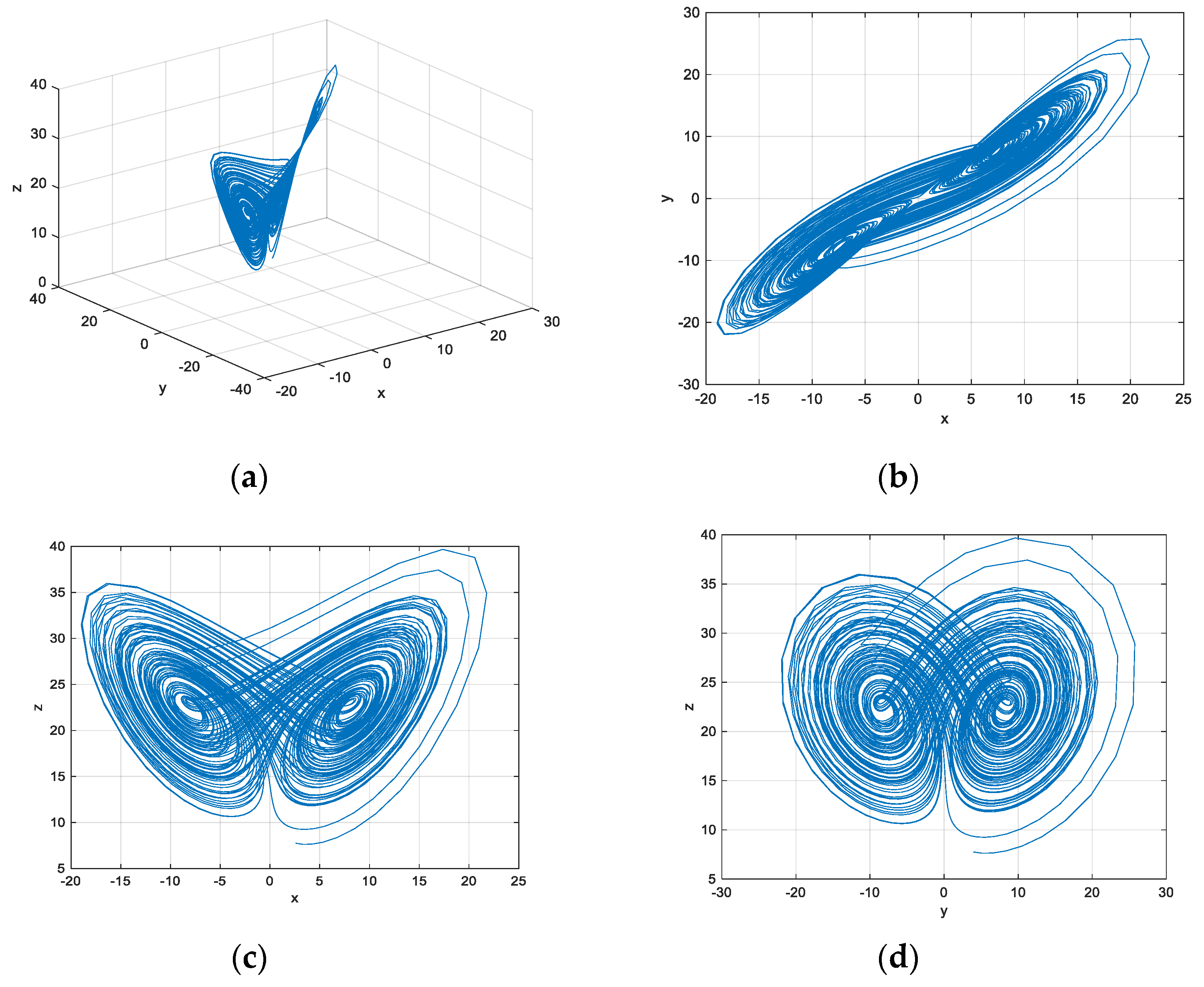
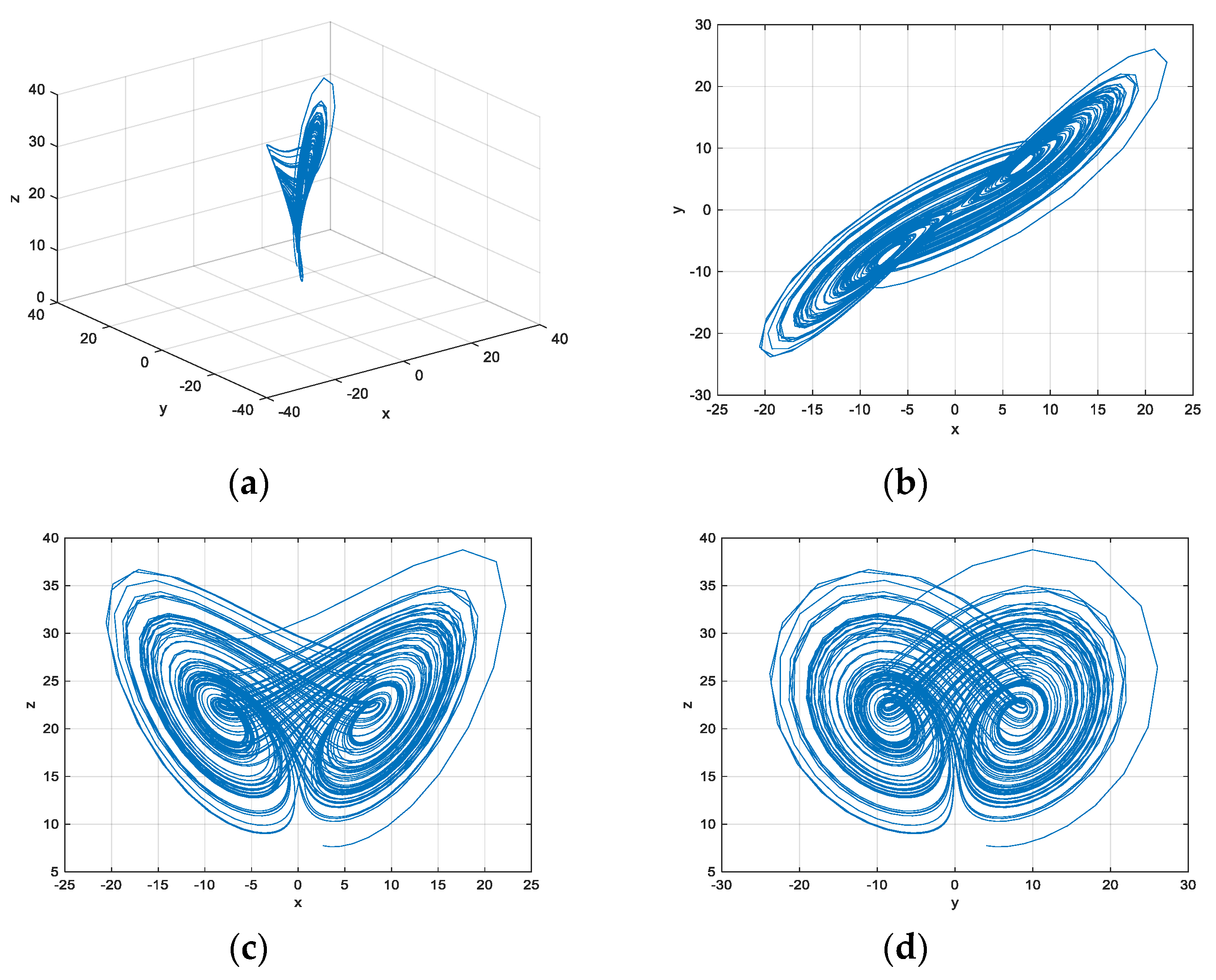
3.4. The Adomian Decomposition Method
3.5. The Improved Adomian Decomposition Method
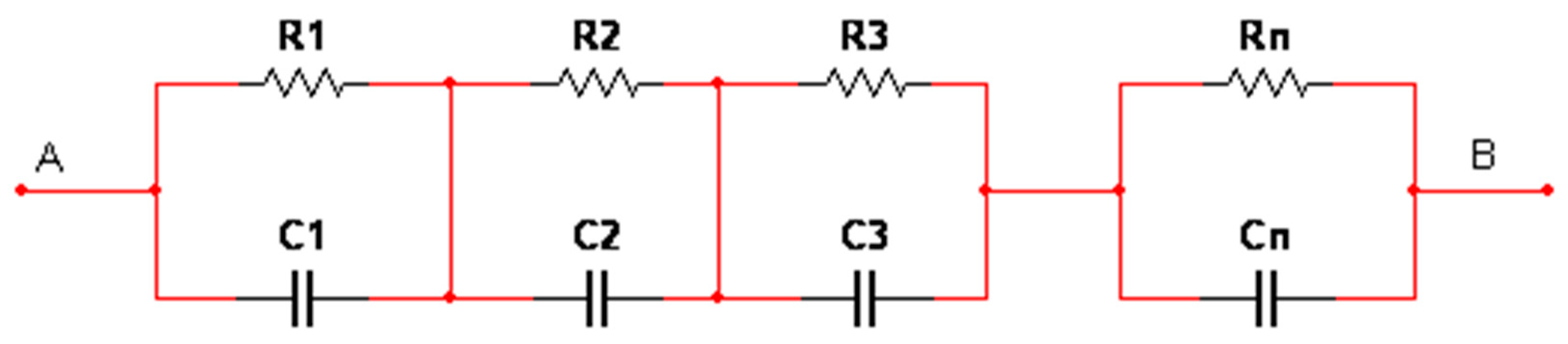
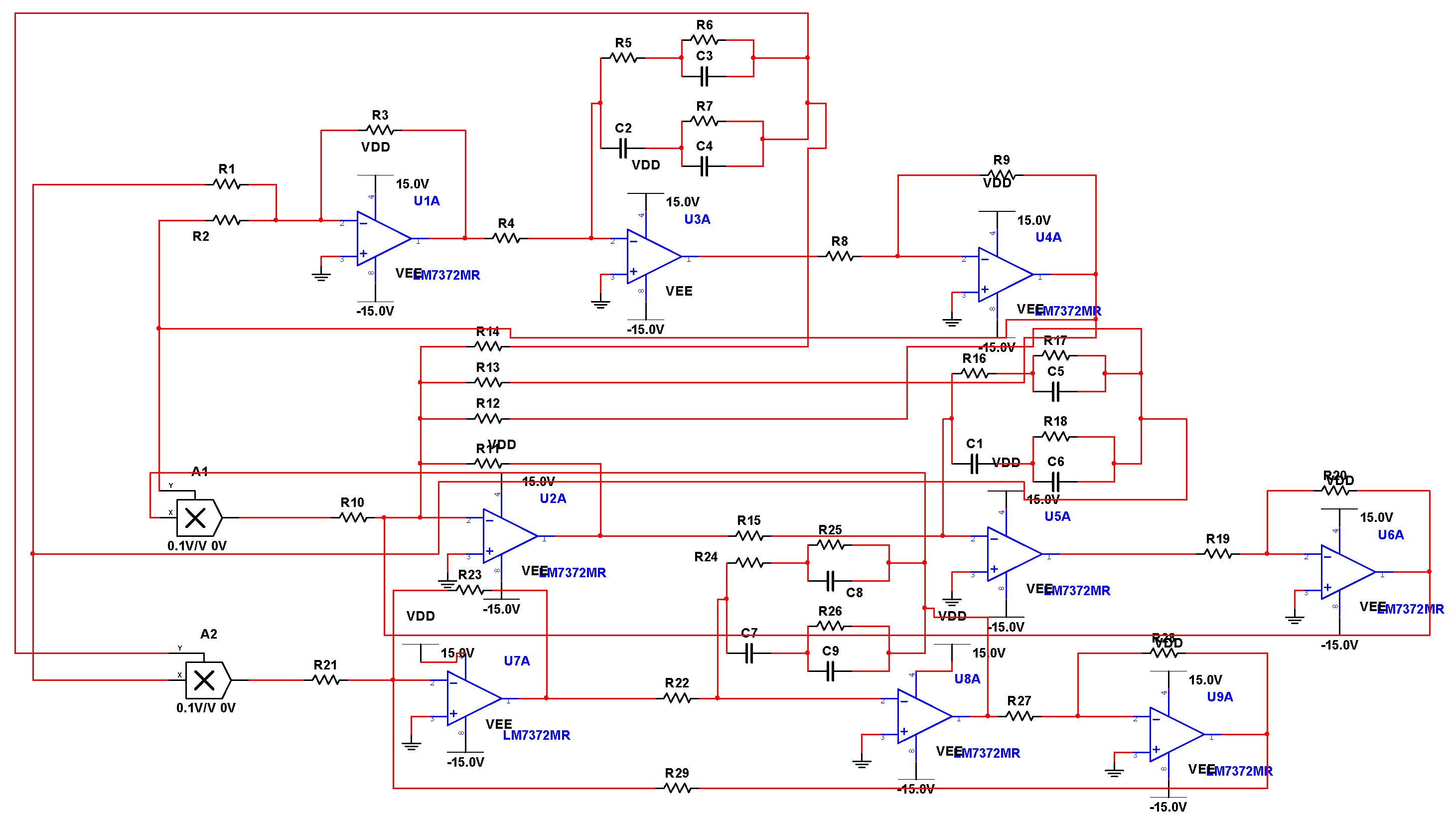
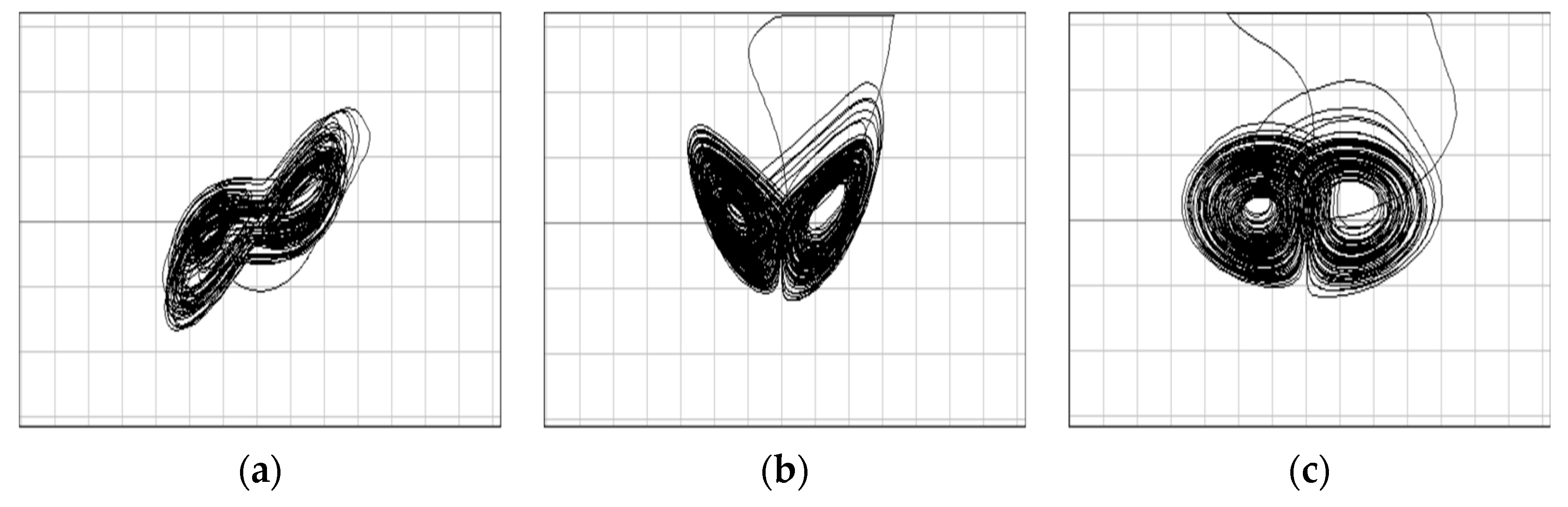
4. Circuit Simulation of Fractional-Order Unified Chaotic System
5. Control and Synchronization of Fractional-Order Unified Chaotic System
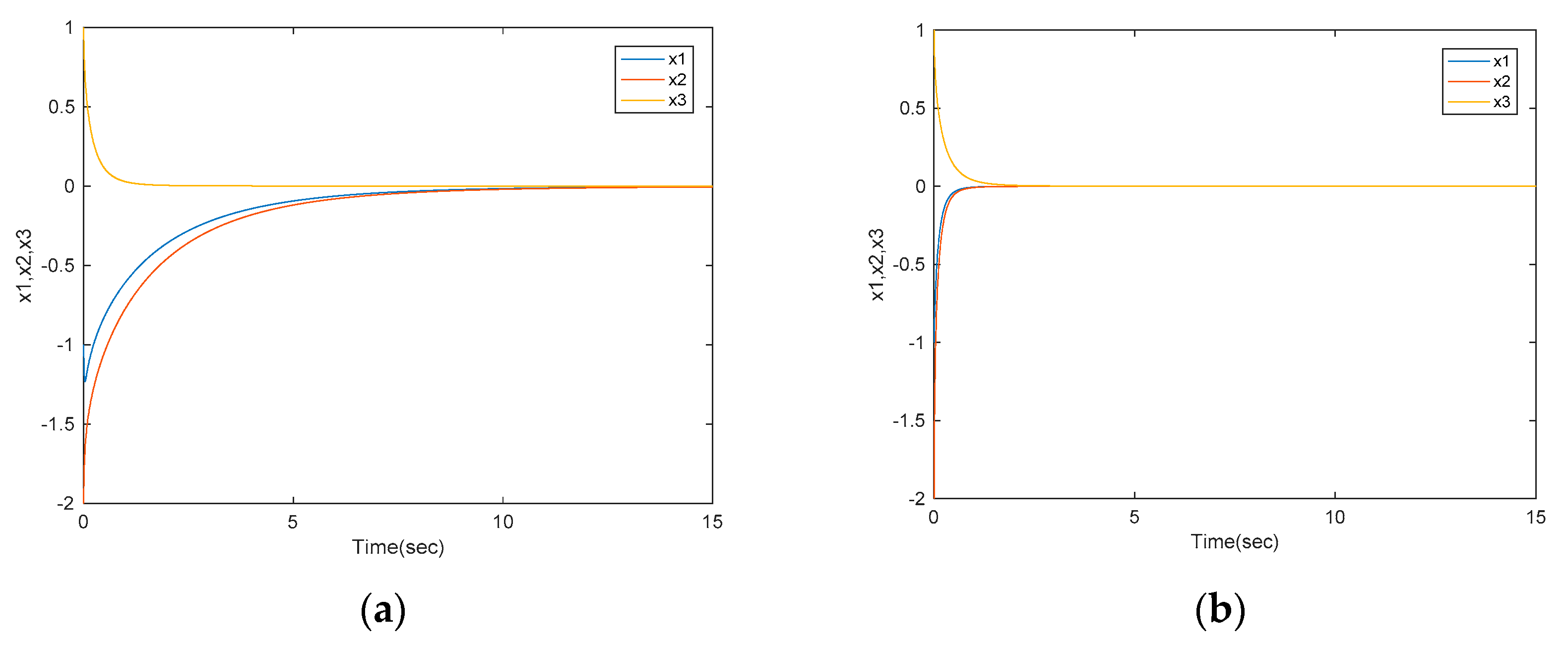
5.1. Control of Fractional-Order Unified Chaotic System
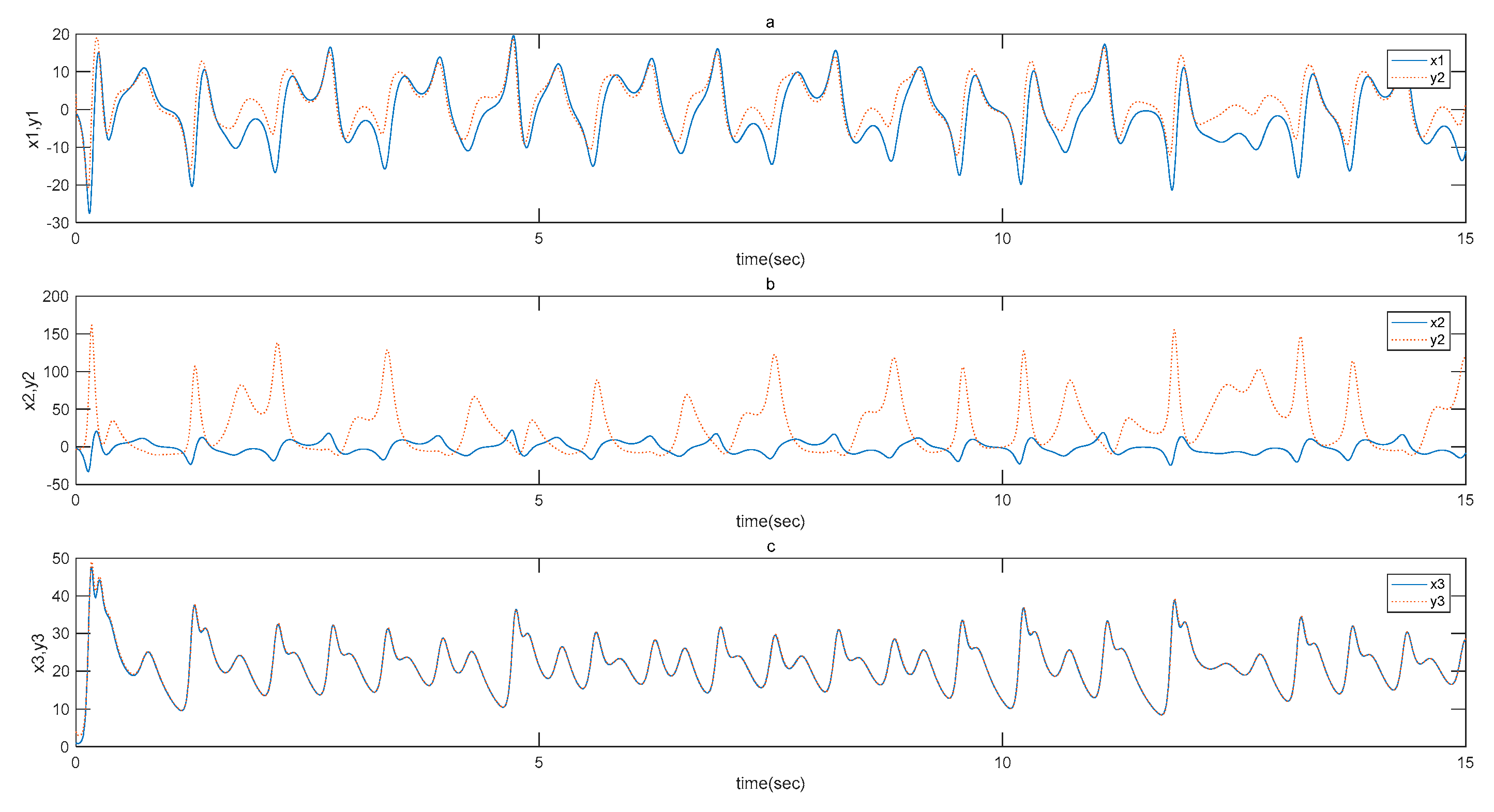
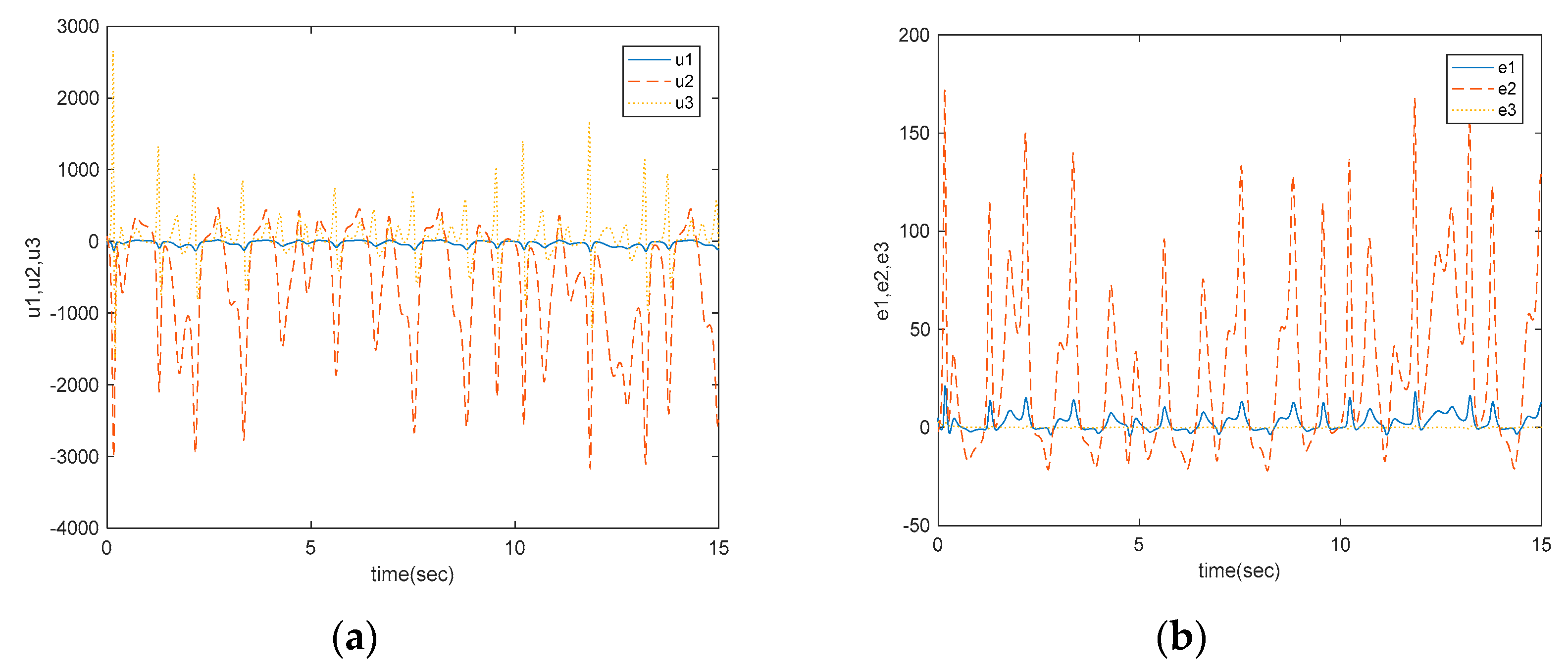
5.2. Synchronization of Fractional-Order Unified Chaotic System
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Chen, G.R.; Ueta, T. Yet another chaotic attractor. Int. J. Bifurc. Chaos 1999, 9, 1465–1466. [Google Scholar] [CrossRef]
- Lü, J.H.; Chen, G.R.; Zhang, S.C. Dynamical analysis of a new chaotic attractor. Int. J. Bifurc. Chaos 2002, 12, 1001–1015. [Google Scholar] [CrossRef]
- Rössler, O.E. An equation for continuous chaos. Phys. Lett. A 1976, 57, 397–398. [Google Scholar] [CrossRef]
- Lü, J.H.; Chen, G.R.; Cheng, D.Z. A new chaotic system and beyond: the generalized Lorenz-like system. Int. J. Bifurc. Chaos 2004, 14, 1507–1537. [Google Scholar] [CrossRef]
- Liu, W.B.; Chen, G.R. A new chaotic system and its generation. Int. J. Bifurc. Chaos 2003, 13, 261–267. [Google Scholar] [CrossRef]
- Liu, C.X.; Liu, T.; Liu, L.; Liu, K. A new chaotic attractor. Chaos Solitons Fractals 2004, 22, 1031–1038. [Google Scholar] [CrossRef]
- Qi, G.Y.; Chen, G.R.; Du, S.Z.; Chen, Z.Q.; Yuan, Z.Z. Analysis of a new chaotic system. Phys. A 2005, 352, 295–308. [Google Scholar] [CrossRef]
- Bao, B.C.; Liu, Z.; Xu, J.P. New chaotic system and its hyperchaos generation. J. Syst. Eng. Electron. 2009, 20, 1179–1187. [Google Scholar]
- Chen, X.R.; Liu, C.X.; Wang, F.Q.; Li, Y.X. Study on the fractional-order Liu chaotic system with circuit experiment and its control. Acta Phys. Sin. 2008, 57, 1416–1422. [Google Scholar]
- Wang, F.Q.; Liu, C.X. Study on the critical chaotic system with fractional order and circuit experiment. Acta Phys. Sin. 2006, 55, 3922–3927. [Google Scholar]
- Mao, X.X.; Sun, K.H.; Liu, W.H. Image encryption algorithm based on fractional order unified chaotic system. Transducer Microsyst. Technol. 2017, 36, 138–141. [Google Scholar]
- He, S.B.; Sun, K.H.; Wang, H.H. Solution of the fractional-order chaotic system based on Adomian decomposition algorithm and its complexity analysis. Acta Phys. Sin. 2014, 63, 030502. [Google Scholar]
- Wu, C.M. Linear feedback synchronization control method for fractional order chaotic systems. Control Eng. China 2019, 26, 898–902. [Google Scholar]
- Yan, X.M.; Shang, T.; Zhao, X.G. Synchronization of uncertain fractional-order chaotic systems based on the fractional-order sliding mode controller. Acta Math. Appl. Sin. 2018, 41, 765–776. [Google Scholar]
- Rabah, K.; Ladaci, S.; Lashab, M. Bifurcation-based fractional-order PIλDμ controller design approach for nonlinear chaotic systems. Front. Inf. Technol. Electron. Eng. 2018, 19, 180–191. [Google Scholar] [CrossRef]
- Rajagopal, K.; Karthikeyan, A.; Srinivasan, A. Bifurcation and chaos in time delayed fractional order chaotic memfractor oscillator and its sliding mode synchronization with uncertainties. Chaos Solitons Fractals 2017, 103, 347–356. [Google Scholar] [CrossRef]
- Tao, C.H.; Lu, J.A.; Lü, J.H. The feedback synchronization of a unified chaotic system. Acta Phys. Sin. 2002, 51, 1497–1501. [Google Scholar]
- Wu, Q.; Huang, J.H. Fractional Calculus; Tsinghua University Press: Beijing, China, 2016. [Google Scholar]
- Psihoyios, G.; Simos, T.E. Trigonometrically fitted Adams-Bashforth-Moulton methods for periodic initial value problems. Proceedings Second MIT Conference on Compurational Fluid and Solid Mechanics, Cambridge, MA, USA, 17–20 June 2003. [Google Scholar]
- Zhu, Y.G.; Chang, Q.S.; Wu, S.C. A new algorithm for calculating Adomian polynomials. Appl. Math. Comput. 2005, 169, 402–416. [Google Scholar] [CrossRef]
- Lei, T.F.; Zhang, X.; Zang, H.Y.; Xia, X.X. Experimental simulation of fractional Rabinovich hyperchaotic system based on improved Adomian decomposition method. Exp. Technol. Manag. 2018, 35, 137–140. [Google Scholar]
- Charef, A.; Sun, H.H.; Tsao, Y.Y.; Onaral, B. Fractal system as represented by singularity function. IEEE Trans. Autom. Control 1992, 37, 1465–1470. [Google Scholar] [CrossRef]
- Ahmad, W.M.; Sprott, J.C. Chaos in fractional-order autonomous nonlinear systems. Chaos Solitons Fractals 2003, 16, 339–351. [Google Scholar] [CrossRef]
- Zhang, X.H.; Sun, Q. Construction of heterogeneous fractional-order chaotic system and its multiple circuits simulation. J. Syst. Simul. 2014, 26, 1460–1466. [Google Scholar]
- Lei, T.F.; Fu, H.Y.; Zhang, X.; Wang, Z.L. Dynamics analysis and circuit implementation of a fractional-order chaotic systems based on adomian decomposition. Chin. J. Electron Devices 2019, 42, 193–200. [Google Scholar]
- Sun, K.H.; Yang, J.L.; Qiu, S.S. Circuit simulation and implement for fractional-order chaotic systems. Comput. Simul. 2011, 28, 117–119. [Google Scholar]
- Geng, Y.F.; Wang, L.Z. Function projective synchronization of fractional-order united chaotic system based on sliding mode control. J. Tianjin Norm. Univ. Nat. Sci. Ed. 2019, 39, 23–26. [Google Scholar]


| Calling Function Method | Adams Prediction–Correction Method | Adomian Decomposition Method | Improved Adomian Decomposition Method | |
|---|---|---|---|---|
| Time Complexity | O(), Slowly | O(), Slowly | O(n), Quickly | O(n), Quickly |
| Space Complexity | O(n), Complex | O(n), Complex | O(1), Simple | O(1), Simple |
| N = 1000 | 1.823s | 1.298s | 0.487s | 0.306s |
| N = 2000 | 5.032s | 4.680s | 0.510s | 0.403s |
| N = 5000 | 17.897s | 15.362s | 0.858s | 0.623s |
| N = 10,000 | 31.259s | 28.191s | 1.458s | 0.919s |
| 0.636 | 0.3815 | 0.5672 | ||||
| 1.130 | 0.6070 | 0.3500 | 0.425 | 0.2498 | ||
| 2.050 | 0.9380 | 0.4830 | 0.262 | 0.1430 | 0.106 | |
| 3.744 | 1.3920 | 0.6310 | 0.294 | 0.123. | 0.068 | |
| 6.824 | 1.9440 | 0.7440 | 0.296 | 0.0754 | 0.030 | |
| 12.330 | 2.44480 | 0.7380 | 0.233 | 0.0754 | 0.006 | |
| 21.900 | 2.6000 | 0.5260 | 0.113 | 0.0246 | ||
| 37.850 | 1.7540 | 0.1700 | 0.017 | 0.0018 | ||
| 62.840 | 0.2500 | 0.0025 |
| 15.720 | 0.1572 | 0.0006335 | ||||
| 27.990 | 2.9300 | 0.285 | 0.0132 | |||
| 22.640 | 5.5200 | 1.200 | 0.2460 | 0.029 | ||
| 15.020 | 5.9260 | 1.920 | 0.6050 | 0.183 | 0.036 | |
| 9.246 | 5.1450 | 2.129 | 0.8480 | 0.324 | 0.925 | |
| 5.527 | 4.0850 | 1.990 | 0.9260 | 0.420 | 0.156 | |
| 3.284 | 3.1390 | 1.700 | 0.8860 | 0.454 | 0.207 | |
| 1.980 | 2.4000 | 1.390 | 0.7800 | 0.420 | ||
| 1.232 | 1.8400 | 1.100 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Zhang, X.; Yang, H. Numerical Analysis, Circuit Simulation, and Control Synchronization of Fractional-Order Unified Chaotic System. Mathematics 2019, 7, 1077. https://doi.org/10.3390/math7111077
Li G, Zhang X, Yang H. Numerical Analysis, Circuit Simulation, and Control Synchronization of Fractional-Order Unified Chaotic System. Mathematics. 2019; 7(11):1077. https://doi.org/10.3390/math7111077
Chicago/Turabian StyleLi, Guohui, Xiangyu Zhang, and Hong Yang. 2019. "Numerical Analysis, Circuit Simulation, and Control Synchronization of Fractional-Order Unified Chaotic System" Mathematics 7, no. 11: 1077. https://doi.org/10.3390/math7111077
APA StyleLi, G., Zhang, X., & Yang, H. (2019). Numerical Analysis, Circuit Simulation, and Control Synchronization of Fractional-Order Unified Chaotic System. Mathematics, 7(11), 1077. https://doi.org/10.3390/math7111077





