1. Introduction
This paper deals with iterative methods for approximating the solutions of a nonlinear system of n equations and n unknowns, , where is a nonlinear vectorial function defined in a convex set D. The main aim of this work is to design iterative methods with memory for approximating the solutions of . An iterative method is said to have memory when the fixed point function G depends on more than one previous iteration, that is, the iterative expression is .
A classical iterative scheme with memory for solving scalar equations
,
, is the known secant method, whose iterative expression is
with
and
as initial estimations. This method can be obtained from Newton’s scheme by replacing the derivative by the first divided difference
. For
the secant method has the expression
where
is the divided difference operator, defined in [
1].
It is possible to design methods with memory starting from methods without memory by introducing accelerating parameters. The idea is to introduce parameters in the original scheme and study the error equation of the method to see if any particular values of these parameters allow to increase the order of convergence, see for example [
2,
3,
4] and the references therein. Several authors have constructed iterative methods with memory for solving nonlinear systems, by approximating the accelerating parameters by Newton’s polynomial interpolation of first degree, see for example the results presented by Petković and Sharma in [
5] and by Narang et al. in [
6]. As far as we know, in the multivariate case, higher-degree Newton polynomials have never been used. In this paper, we will approximate the accelerating parameters with multidimensional Newton’s polynomial interpolation of second degree.
In [
1], Ortega and Rheinboldt introduced a general definition of the order of convergence, called
R-order defined as follows
where
,
, and
is called
R-factor. The
R-order of convergence of an iterative method (IM) at the point
is
Let (
IM) be an iterative method with memory that generates a sequence
of approximations to the root
, and let us also assume that this sequence converges to
. If there exists a nonzero constant
and nonnegative numbers
,
such that the inequality
holds, then the R-order of convergence of (IM) satisfies the inequality
where
is the unique positive root of the equation
We can find the proof of this result in [
1].
Now, we introduce some notations that we use in this manuscript. Let
r be the order of an iterative method, then
where
tends to the asymptotic error constant of the iterative method when
. To avoid higher order terms in the Taylor series that do not influence the convergence order, we will use the notation used by Traub in [
2]. If
and
are null sequences (that is, sequences convergent to zero) and
where
C is a nonzero constant, we can write
Let
be a sequence of vectors generated by an iterative method converging to a zero of
F, with R-order greater than or equal to
r, then according to [
4] we can write
where
is a sequence which tends to the asymptotic error constant
of the iterative method when
, so
.
Accelerating Parameters
We illustrate the technique of the accelerating parameters, introduced by Traub in [
2], starting from a very simple method with a real parameter
This method has first order of convergence, with error equation
where
,
As it is easy to observe, the order of convergence can increase up to 2 if
. Since
is unknown, we estimate
by approximating the nonlinear function with a Newton polynomial interpolation of degree 1, at points
and
To construct the polynomial
, it is necessary to evaluate the nonlinear function
f in two points; so, two initial estimates are required,
and
. The derivative of the nonlinear function is approximated by the derivative of the interpolating polynomial, that is,
, and the resulting scheme is
substituting
in the iterative expression
we get the secant method [
7], with order of convergence
.
2. Modified Secant Method
A similar process can be done now using a Newton polynomial interpolation of second degree for approximating parameter
. As it is a better approximation of the nonlinear function, it is expected that the order of convergence of the resulting scheme is greater than the obtained in the case of a polynomial of degree 1. For the modified secant method, the approximation of the parameter is
, where
being
So,
and replacing this expression in
an iterative method with memory is obtained
Now, three initial points are necessary, , and , to calculate the value of parameter .
In the following result, we present the order of convergence of the iterative scheme with memory (
19).
Theorem 1. (Order of convergence of the modified secant method) Let ξ be a simple zero of a sufficiently differentiable function in an open interval D. Let , and be initial guesses sufficiently close to ξ. Then, the order of convergence of method (19) is at least , with error equation . Proof. By substituting the different terms of
by their Taylor expansions, we have
Now, from the error Equation (
13)
By Writing
and
in terms of
, we obtain
where
p denotes the order of convergence of method (
19). But, if
p is the order of (
19), then
. Therefore,
p must satisfy
. The unique positive root of this cubic polynomial is
and, by applying the result of Ortega and Rheinbolt, this is the order of convergence of scheme (
19). □
The efficiency index, defined by Ostrowski in [
8], depends on the number of functional evaluations per iteration,
d, and on the order of convergence
p, in the way
so, as in the modified secant method there is only one new functional evaluation per iteration, its efficiency index is
.
Nonlinear Systems
Method (
12) can be extended for approximating the roots of a nonlinear system
, where
is a vectorial function defined in a convex set
D,
It is easy to prove that this method has linear convergence, with error equation
being
,
In the multidimensional case, we can approximate the parameter
with a multivariate Newton polynomial interpolation. If we use a polynomial of first degree
then
and
is approximated by
, so the iterative resulting method is
that corresponds to the secant method for the multidimensional case.
To extend the modified secant method (
19) to this context, we need a multidimensional Newton polynomial interpolation of second degree
where
such that
, where
denotes the set of bi-linear mappings.
Moreover,
evaluating the derivative in
,
So, the iterative expression of the resulting method with memory is
The divided difference operator can be expressed in its integral form by using the Genocchi-Hermite formula for divided difference of first order [
9]
as
then
and, in general, the divided difference of
k-order can be calculated by [
10]
where
Theorem 2. (Order of Convergence of the Modified Secant Method in the Multidimensional Case) Let ξ be a zero of a sufficiently differentiable function in a convex set D, such that is nonsingular. Let , and be initial guesses sufficiently close to ξ. Then the order of convergence of que method (31) is at least 1.8393 with error equationbeing Proof. For the second order divided difference we write (
35) for
in the following way
where
and
. We can write
h and
k in terms of the errors as
and
. Substituting the approximation of
,
, in the error equation (
24), we obtain
Following the same steps as in the unidimensional case, the order of convergence
p of method (
31) must satisfy the equation
, which has the unique positive root
. □
3. Dynamical and Numerical Study
When a new method is designed, it is interesting to analyze the dynamical behavior of the rational function that appears when the scheme is applied on polynomials of low degree. For the secant method, this analysis has been made by different researchers, so we are going to study the behavior of the modified secant method. As this scheme would be accurate for quadratic polynomials, due to the approximation we make, we use 3rd degree polynomials in this analysis. In order to make a general study, we use four polynomials that combined can generate any third degree polynomial, that is, , , and , where is a free real parameter.
The rational operators obtained when our method (
31) is applied on the mentioned polynomials are:
In order to analyze the fixed points, we introduce the auxiliary operators
,
, defined as follows
So, a point
is a fixed point of
if
,
and
. We can prove that there are no fixed points different from the roots of the polynomials. So, the method is very stable. On the other hand, critical points are also interesting because a classical result of Fatou and Julia states that each basin of attraction of an attracting fixed point contains at least a critical point ([
11,
12]), so it is important to determine to which basin of attraction belongs each critical point. The critical points are determined by the calculation of the determinant of the Jacobian matrix
,
([
13]). For the polynomials
to
the critical points are the roots of the polynomials and the points
, such that
.
The bifurcation diagram ([
13]) is a dynamical tool that shows the behavior of the sequence of iterates depending on a parameter. In this case, we use parameter
from
. Starting from an initial estimation close to zero, we use a mesh of 500 subintervals for
in the
x axis and we draw the last 100 iterates. In
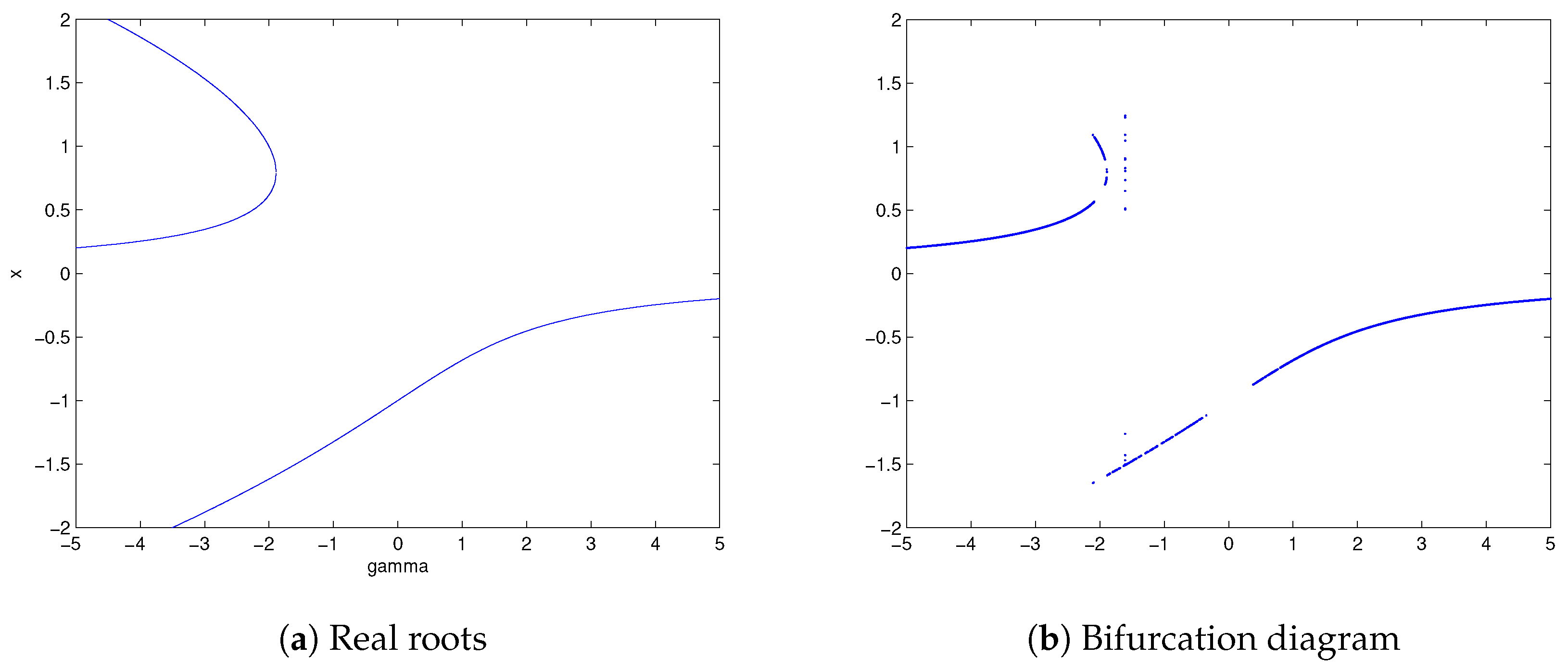
Figure 1a, we plot the real roots of
and in
Figure 1b we draw the bifurcation diagram. We can see how the bifurcation diagram always matches the solutions.
Now, we are going to compare Newton’s method and the secant and modified secant schemes on the following test functions, under different numerical characteristics, as well as the dynamical planes associated to them.
- (1)
,
- (2)
,
- (3)
,
- (4)
,
- (5)
,
- (6)
.
Variable precision arithmetics has been used with 100 digits of mantissa, with the stopping criterion
or
with a maximum of 100 iterations. That means the iterative method will stop when any of these conditions are met. These tests have been executed on a computer with 16GB of RAM using MATLAB 2014a version. As a numerical approximation of the order of convergence of the method, we use the
approximated computational order of convergence (
ACOC), defined as [
14]:
Let us remark that we use the same stopping criterium and calculation of ACOC in the multidimensional case, only replacing the absolute value by a norm. As we only use one initial point to be able to compare methods with memory with Newton’s method, to calculate the initial points needed for the methods with memory we use an initial estimation of . We take in the unidimensional case. In the multivariate case, we use the initial value for the secant method, and two different values for the two first iterations, and for the modified secant method, where I denotes the identity matrix of size . We have observed that, taking two different approximations of leads to a more stable behavior of the modified secant method.
On the other hand, for each test function we determine the associated dynamical plane. This tool of the dynamical analysis for methods with memory was introduced in [
15]. The dynamical plane is a visual representation of the basins of attraction of an specific problem. It is constructed by defining a mesh of points, each of which is taken as a initial estimation of the iterative method. The complex plane is created showing the real part of the initial estimate in the
x axis and the imaginary part on the
y axis ([
16]). In a similar way as before, we use an initial estimation of
to calculate the necessary initial points. This approach makes possible to draw the performance of iterative schemes with memory in the complex plane, thus allowing to compare the performance of methods with and without memory. To draw the dynamical planes we have used a mesh of
initial estimations, a maximum of 40 iterations and a tolerance of
. We used
to calculate the initial estimations. Each point used as an initial estimate is painted in a certain color, depending on the root to which the method converges. If it does not converge to any root, it is painted black.
In
Table 1, we show the results obtained by Newton’s method, secant and modified secant schemes for the scalar functions
,
and
. These tests confirm the theoretical results with a very stable ACOC when the method is convergent.
On the other hand, in
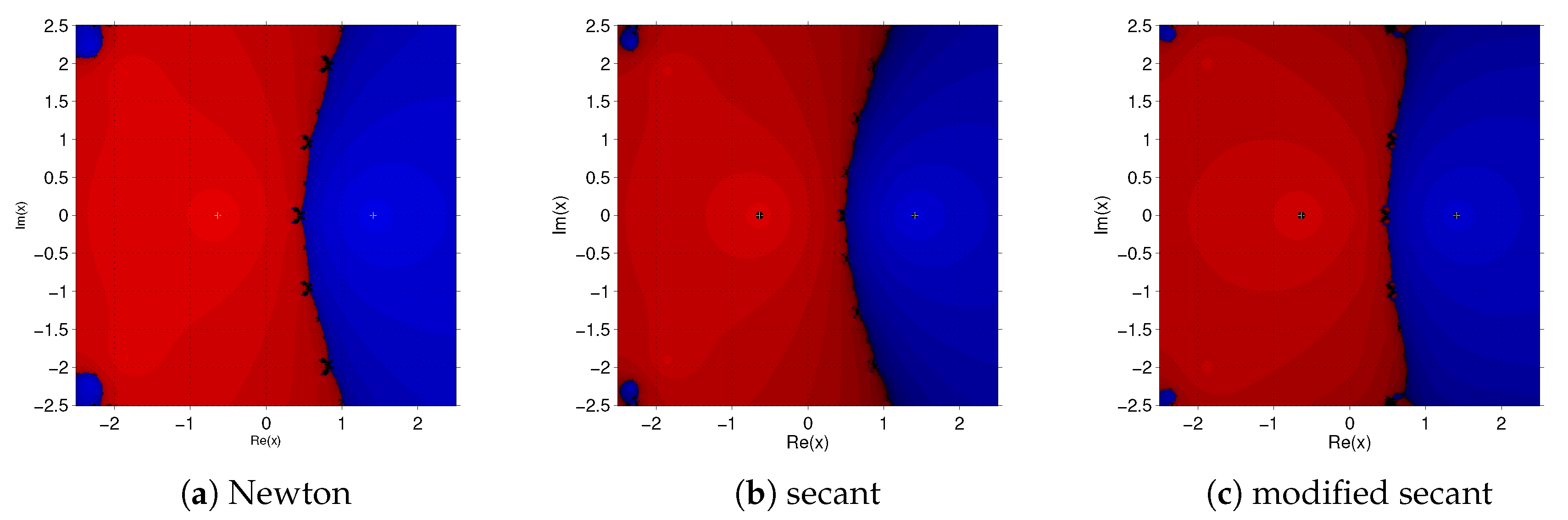
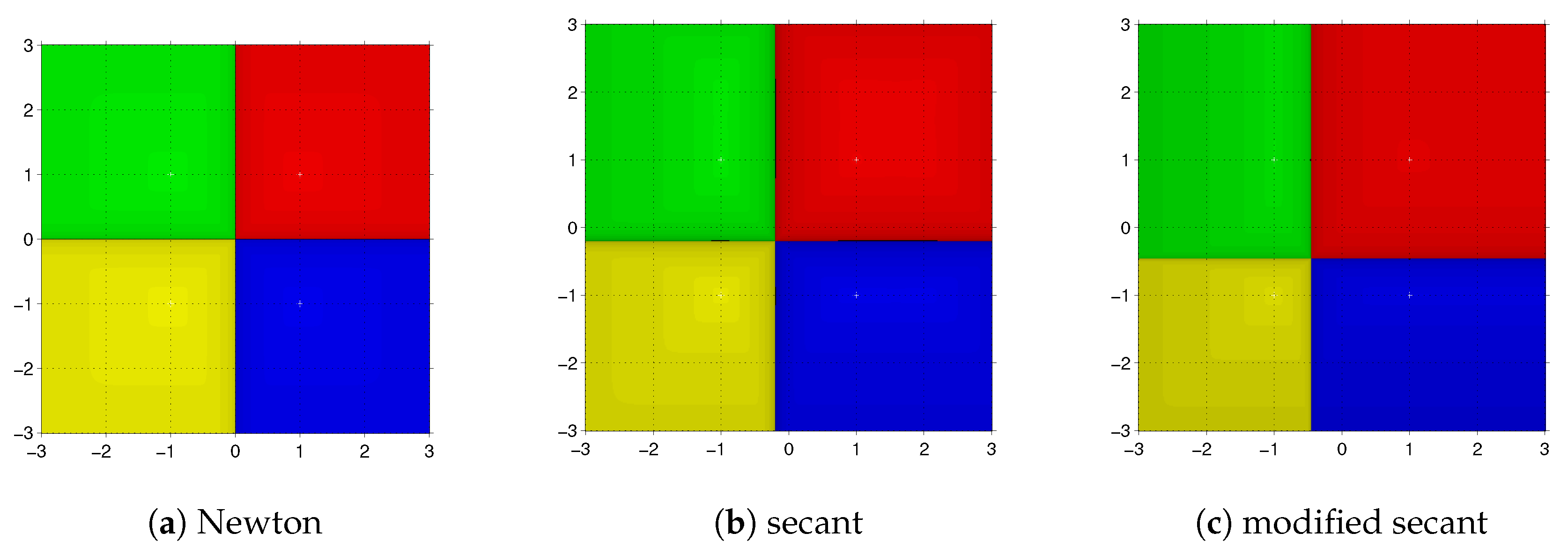
Figure 2 we see that the three methods behave well on function
, with no significant differences between their basins of attraction. In
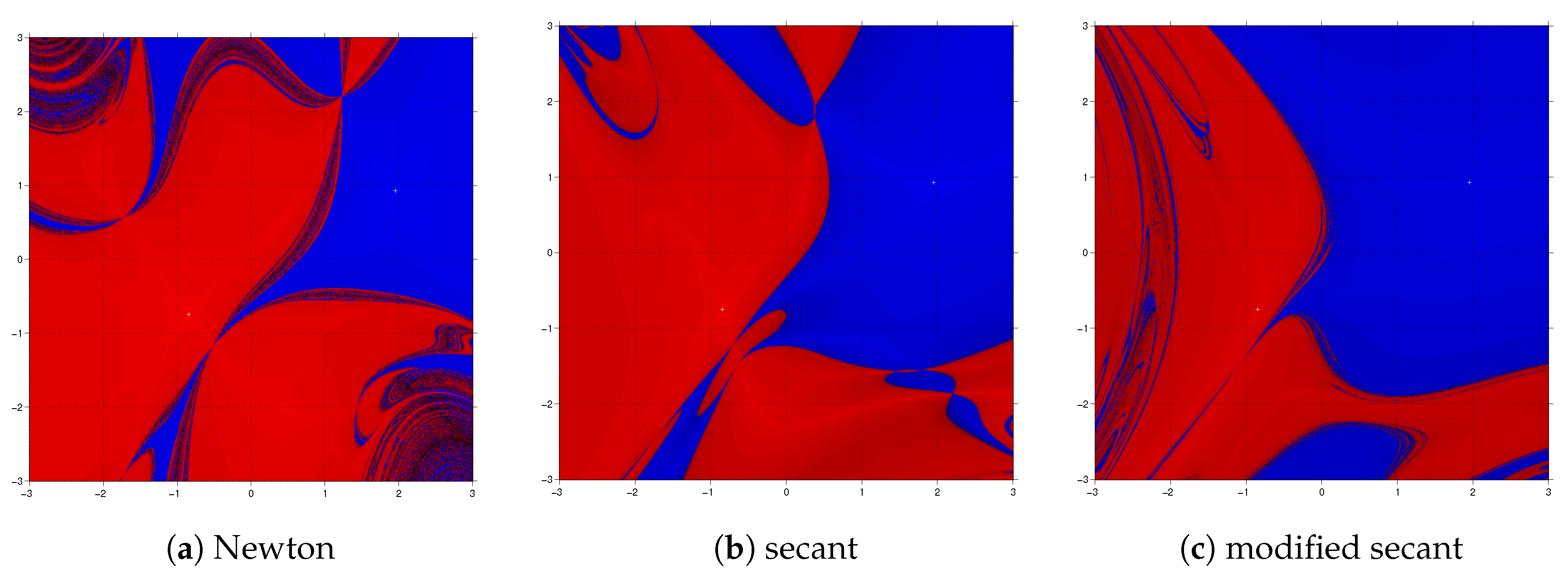
Figure 3, we see that in case of function
the dynamical plane of the modified secant is better than the secant and very similar to Newton’s one. The secant method presents black regions that, in this case, mean slow convergence. In
Figure 4, we see the basins of attraction of the methods on
. We observe that the wider basins of attraction correspond to the modified secant method. In this case, the black regions mean points where the methods are divergent.
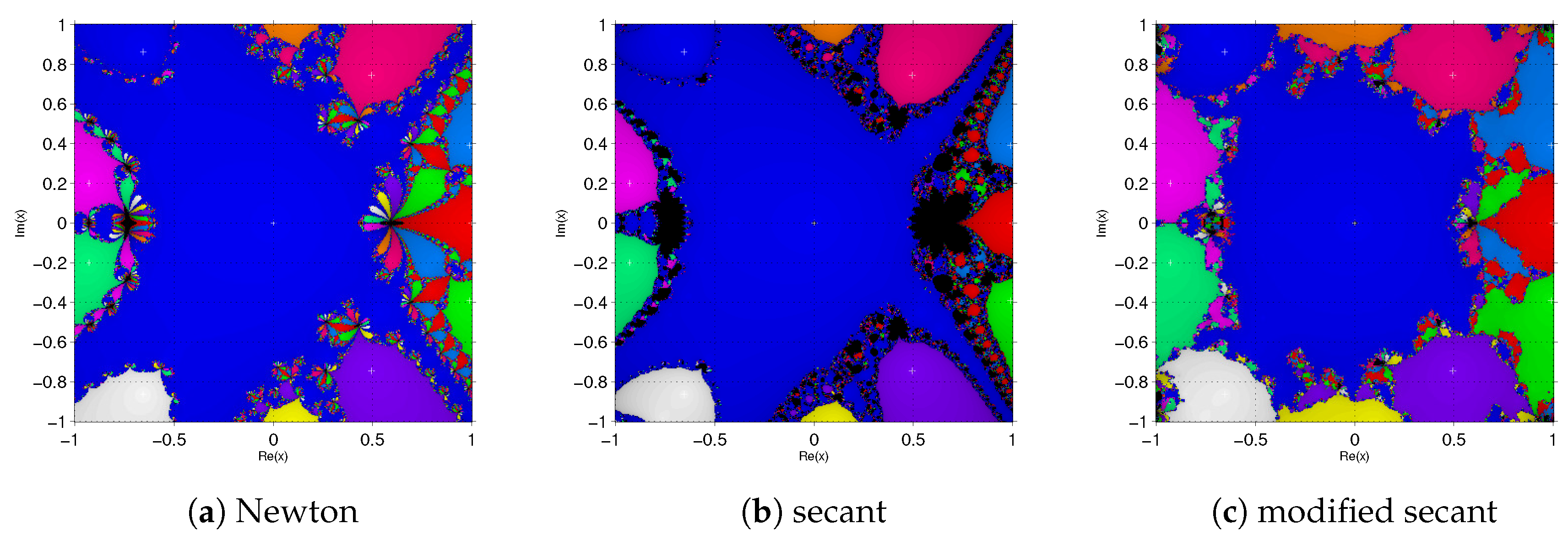
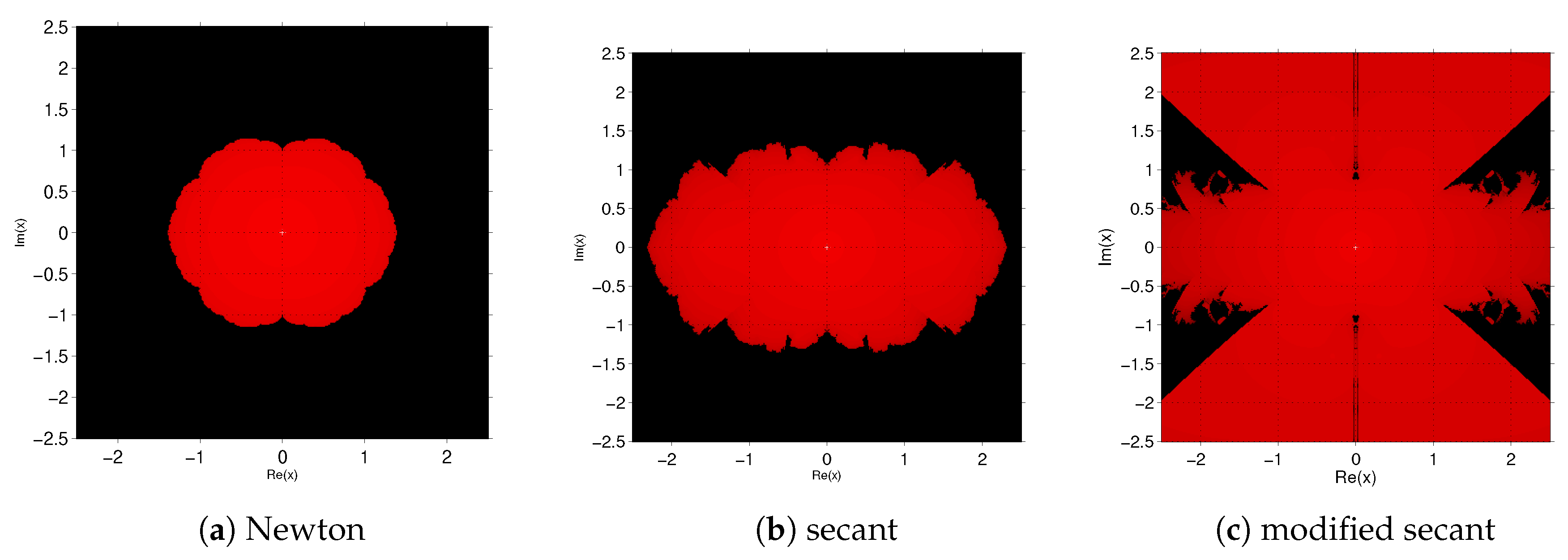
In
Table 2 the numerical results corresponding to the vectorial functions
,
and
are presented. There is nothing significant in these results, they are those expected taking into account the theoretical results. In this case, the definition of ACOC is the same as before, replacing the absolute value by the norm. For systems
and
, we show in
Figure 5 and
Figure 6 the basins of attraction of each root. In the first case, the three methods behave similarly, but in the second one, Newton’s scheme presents some black regions that do not appear in the modified secant method.