Compressible Navier-Stokes Equations in Cylindrical Passages and General Dynamics of Surfaces—(I)-Flow Structures and (II)-Analyzing Biomembranes under Static and Dynamic Conditions
Abstract
1. Introduction
1.1. Importance of Analyzing Biomembranes
- Finally, there is extensive literature on Bioelectromagnetic Dosimetry (BEM) and documenting its effects on cardiac function and thermal energy transfer; these results have been classically obtained by applying steady uni-directional electromagnetic fields in Human & Animal Models [23]. Information gleaned from such experiments are utilized to analyze biological tissue cultures under microwave electromagnetic frequencies.
1.2. Prominent Approaches and Shortcomings
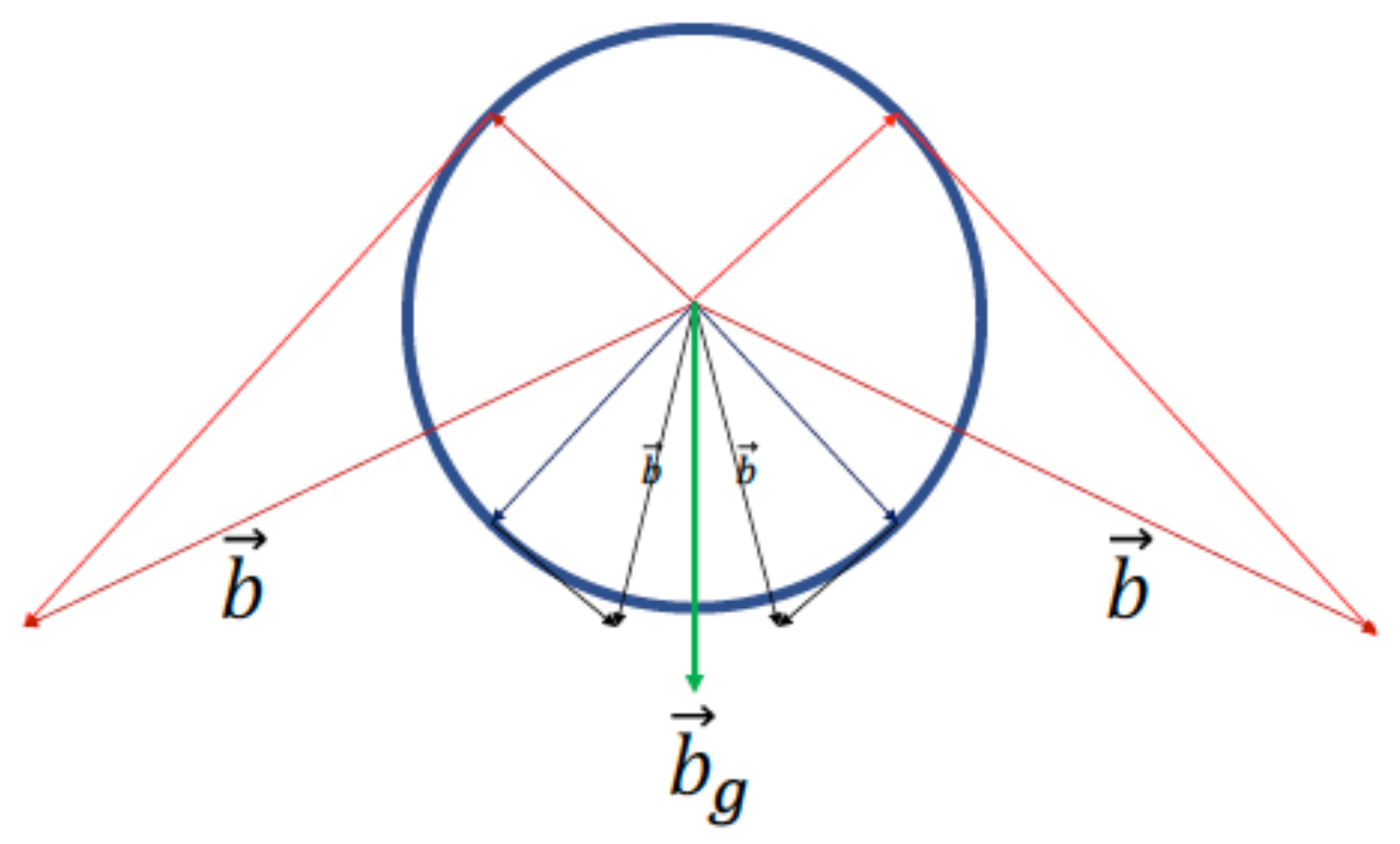
- A Variational Hamiltonian Approach: This method, drawing on inspiration from Statistical Mechanics attempts to derive a Hamiltonian-like expression of the Total Energy Density present on a surface, and variates this density with respect to the configuration of the surface [24,25]. This method has found application in explaining several steady microscopic morphological phenomena in cells, such as Terasaki Spiral Ramps [24], Rod Inclusions, and providing several Mechanochemical models for ‘Active Surfaces’
- -
- Shortcomings: While the approach is extremely effective in generating equilibrium conditions for biomembranes under a specific Energy Density using tensors in a coordinate-free manner, the framework simply does not contain the support to extend the analysis for Biomembranes which are not steady and stationary; in a biological context this dynamic nature of cells are of crucial importance.
- A “Calculus of Moving Surfaces” Approach: This method draws on inspiration from the recent Calculus of Moving Surfaces (CMS) [18]; CMS outlines a tensor framework which can be used to analyze surface membranes in motion denoted by . CMS demonstrates the perilous nature of several vector fields used to study dynamic membranes such as the velocity of the membrane, asserting that they are not proper tensors on with respect to coordinate changes. CMS proceeds to introduce operators and tensors on which do behave as tensors and can be used to analyze tensors and differential forms defined on . CMS has found application to Cellular Membranes in several papers [26,27] by tentatively proposing a CMS-derived method for modelling Membranes with no energy density on their surface, as well as being acted on by electromagnetic fields [28].
- -
- Shortcomings: While the above method has yielded valuable insight in the mechanics of dynamic surfaces providing several biomembrane models [26,27,28], the models are non-tensorial including several objects from classical mechanics such as and others which do not transform as tensors as per CMS [18]. Clearly, the mode obvious problem is that while formulated using CMS, it is difficult to identify symmetries and the significance of terms within the energy density which agree with classical physics, and also are CMS-tensorial. Thus, constants of motion cannot be readily obtained as can be in other more classical applied analysis methods.
2. Flow Structures
2.1. A New Composite Velocity Formulation
2.2. A Solution Procedure for Arbitrarily Small in Quantity
2.3. Characterization of the Sign of the Vorticity
2.4. Non-Linear Further Reduction
2.5. Stokes Theorem Applied to Dynamic Surfaces
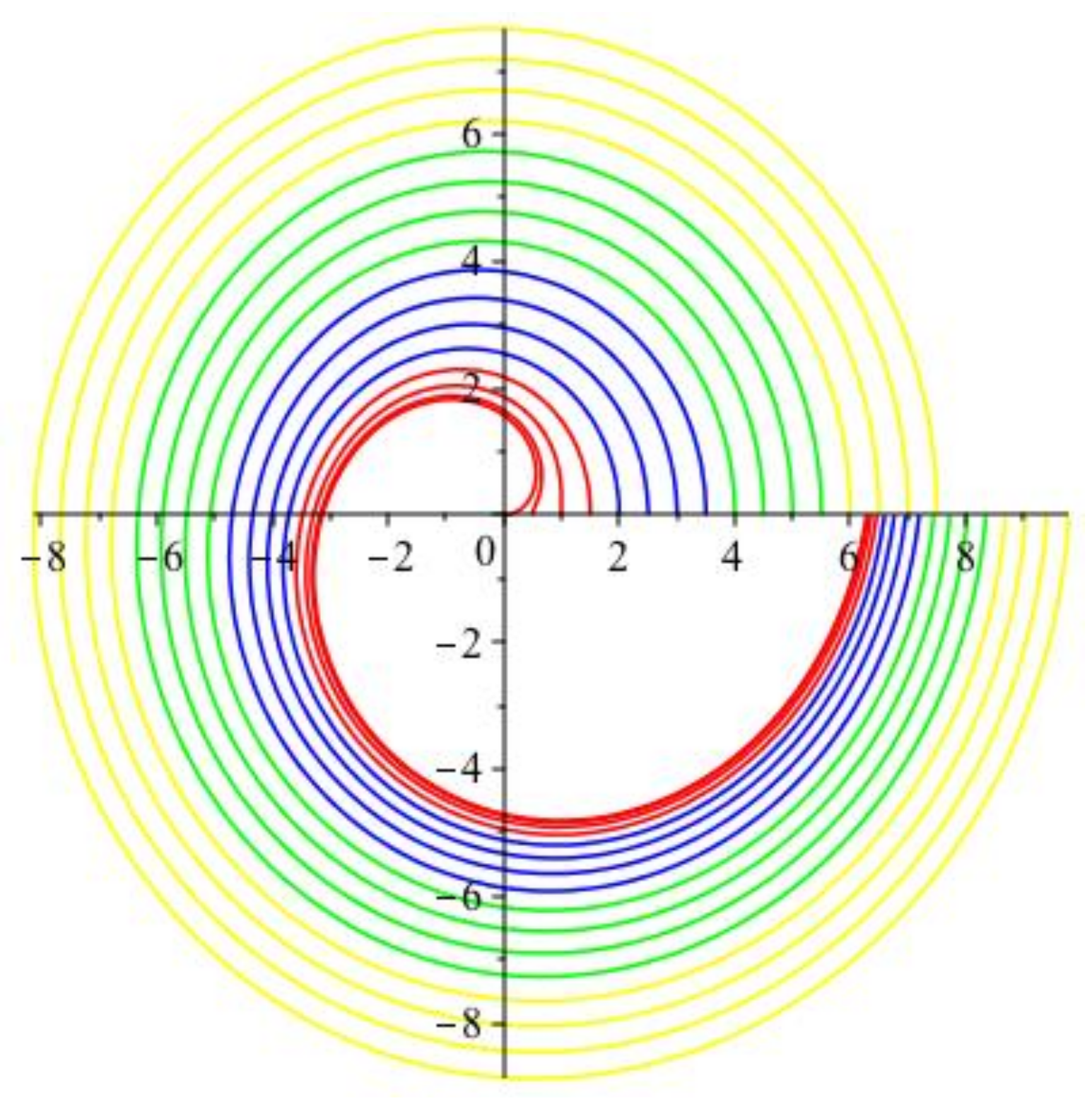
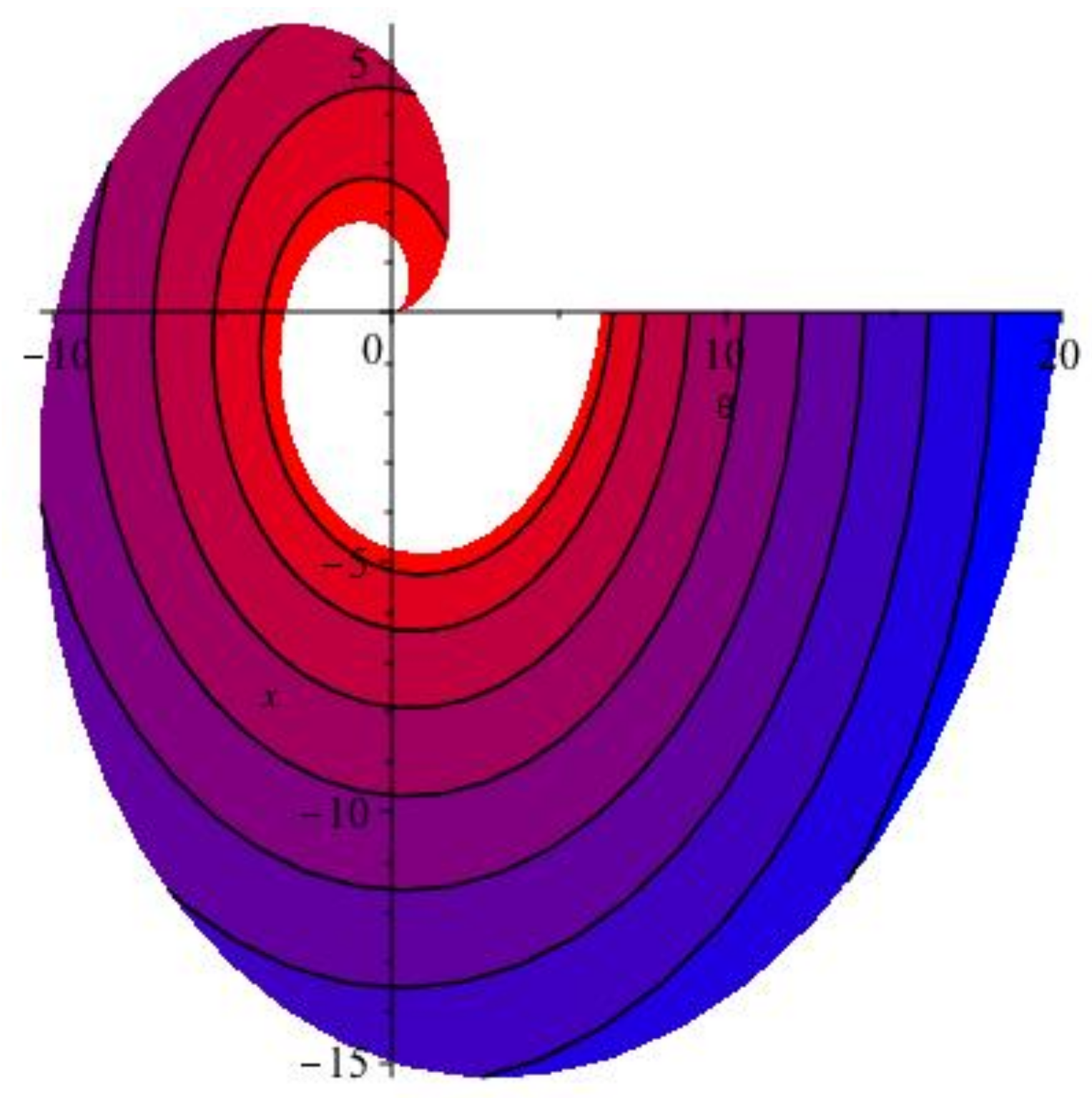
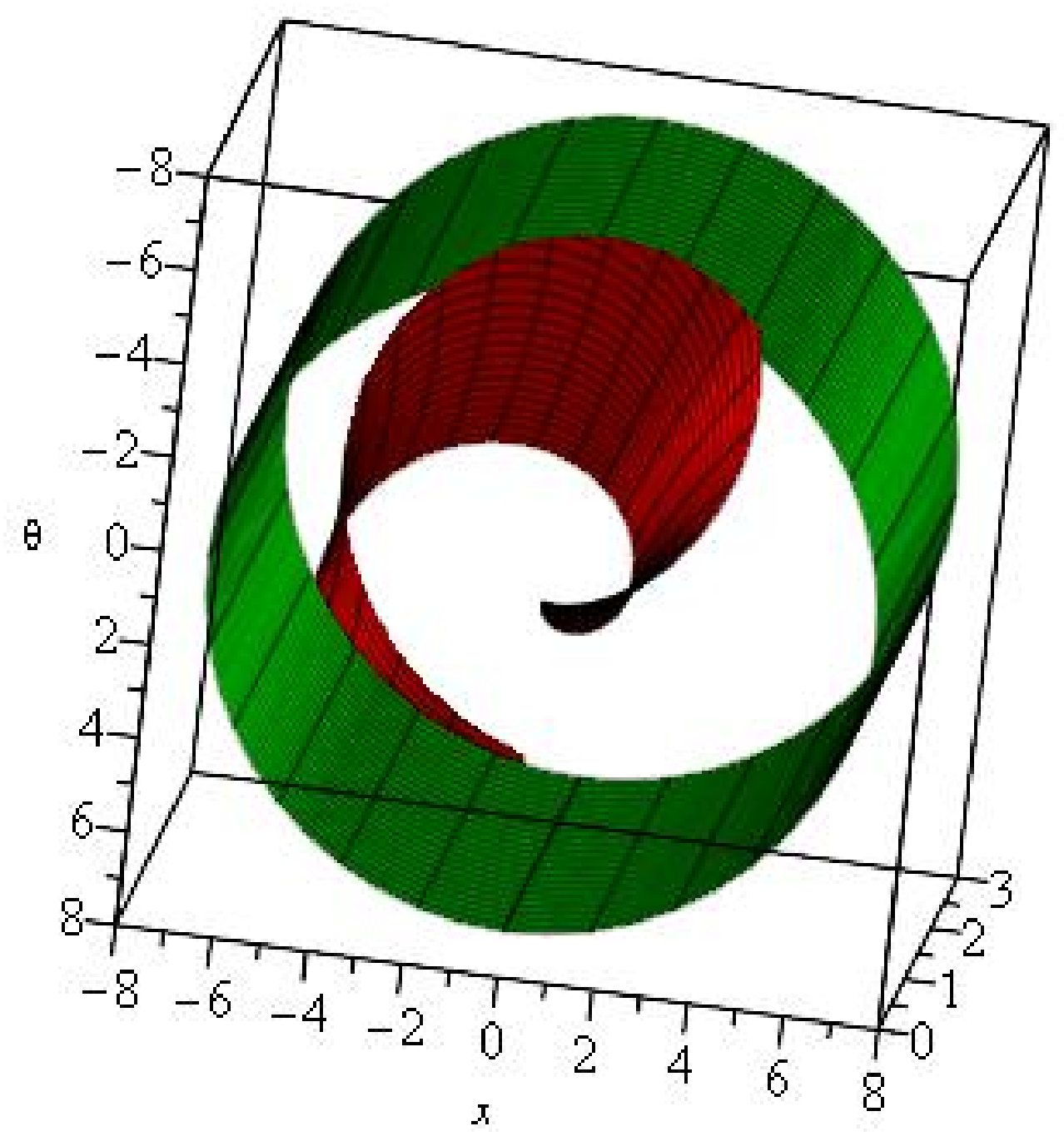
2.6. The Hunter-Saxton Equation
2.7. Non-Blowup Result
2.8. Geometrical and Variational Analysis of the Hunter-Saxton Equation
3. Analyzing Bio-Membranes under Steady and Dynamic Conditions
3.1. The Static Local Energy Density
3.1.1. Geometrical Preliminaries, Defining the Biomembrane Continuum
3.1.2. Introducing the Energy Density Action
3.1.3. Properties and Requirements of the Hamiltonian and Its variation
3.1.4. Stress Tensor
3.1.5. The Dynamic Alternative to the Static Hamiltonian
3.2. Invariant Scalars of Motion, Linear and Quadratic Invariants and Normal Speed Gradients
Temporal Curvature Trace Tensors
3.3. Developing a CMS-Invariant Hamiltonian, Variating the Hamiltonian and Divergence Form of the Variation
3.3.1. Defining a Surface Analog of ’Surface-Time’
3.3.2. Conservation Laws and the Stress Tensor
3.3.3. Specific Lagrangian: Quadratic Speed Lagrangian
- If the surface is not moving, .
- If the surface is only moving tangentially .
4. Work-Energy Theorem
5. Discussion
6. Conclusions
- Finally, the Dynamic Framework was utilized under a general Hamiltonian Energy Density to derive a constant of motion conserved with just the Normal Speed C contributing to the Hamiltonian Energy () and a general form of the Work-Energy Theorem that states that the rate of change of Kinetic Energy is equal to the Mechanical Power measured by on the Surface.
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Radial component of velocity of fluid | |
| Azimuthal component of velocity of fluid | |
| Axial component of velocity of fluid | |
| Dimensional radial coordinates | |
| Angular coordinate | |
| Dimensional axial coordinate | |
| density of fluid | |
| initial density of fluid- a constant | |
| viscosity of fluid | |
| P | pressure |
| gravitational force in radial direction | |
| gravitational force in azimuthal direction | |
| gravitational force in axial direction | |
| nondimensional parameter | |
| non-blowup function | |
| F | function of r, z and t |
| arbitrary constant | |
| arbitrary function of t | |
| arbitrary function of t | |
| G | arbitrary function of spatial variables and t |
| nondimensiional constant | |
| part of the density function | |
| constant part of blowup function | |
| constant part of blowup function | |
| unit vectors | |
| composite vector | |
| composite vector independent of | |
| velocity of fluid dependent on | |
| inertial vector term | |
| pressure gradient | |
| velocity of fluid, | |
| norm squared | |
| geometric product | |
| dot product | |
| cross product | |
| vorticity in direction | |
| vorticity in direction | |
| 3-d vorticity vector | |
| 3-d angular velocity | |
| new coordinate system for cylindrical function | |
| surface Jacobian | |
| radial velocity null-surface | |
| value at | |
| H | |
| vector projection of onto | |
| scalar projection for | |
| G | |
| non-dimensional constant | |
| Q | |
| c | constant equal to |
| vector field Equation (43) | |
| normal vector to surface | |
| S | surface of control volume |
| C | contour |
| unit tangent vector to closed curve C | |
| arclength | |
| differential operators acting on respectively | |
| R | open disk with boundary C |
| potential function | |
| g | gravity constant |
| A is , B is | |
| , , independent of | |
| defined according to | |
| R | radius of tube |
| Lagrangian | |
| energy density | |
| variation of energy density | |
| inner product | |
| tangent vector to | |
| Invariant time derivative | |
| differential of a function on | |
| takes 1-forms to corresponding 1-vector through metric tensor on | |
| normal on | |
| Lagrangian for static surfaces | |
| Lagrangian for dynamic surfaces | |
| tangential velocity of the surface | |
| boundary of cylindrical tube | |
| normal to boundary in direction | |
| ⋆ | Hodge star operator |
| ∧ | Exterior product |
| Energy density | |
| Riemannian 2-Manifold | |
| point on | |
| tangent space at | |
| cotangent space | |
| rank of Tensor | |
| space of Tensors of rank at at | |
| space of -Forms constructed from the Exterior product space of tangent space | |
| space of -Forms constructed from the Exterior product space of Dual of tangent space | |
| ⊗ | tensor product |
| surface 2-form | |
| components of Levi-Civita cotangent 2-form on | |
| Bilinear symmetric Tensor, metric tensor at | |
| exterior derivative | |
| co-differential | |
| nominal Laplace-DeRham operator | |
| insertion operator on | |
| S | Local Energy |
| components of curvature tensor on | |
| surface vector which points outwards at the boundary | |
| vector | |
| change of co-ordinates | |
| surface configuration | |
| orthonormal basis vectors | |
| variation of S | |
| stress tensor of the system | |
| surface Equilibrium configuration | |
| symmetric Tensor | |
| curvature Tensor | |
| 1-Tensor | |
| Canham-Helfrich Energy | |
| Mean-curvature density | |
| scalar field | |
| C | Normal speed of |
| commutator | |
| cotangent 1-form operator | |
| Temporal curvature tensor | |
| trace of Tensor | |
| cotangent 1-form | |
| Linear Invariant of Motion |
Appendix A. Time Derivative of Dynamic Line Integrals
Appendix B. Using Stokes Theorem on Dynamic Surfaces & Special Cases
Appendix C. Specific Density Formulation According to Theorem 1
References
- Pereira, L.M.; Perez Guerrero, J.S.; Cotta, R.M. Integral transformation of the Navier Stokes equations in cylindrical geometry. Comput. Mech. 1998, 21, 60–70. [Google Scholar] [CrossRef]
- Cai, R. Some Explicit analytical solutions of unsteady compressible flow. Trans. ASME J. Fluids Eng. 1998, 120, 760–764. [Google Scholar] [CrossRef]
- MacCormack, R.W. A Numerical Method for Solving the Equations of Compressible Viscous Flow. AIAA J. 1982, 20, 1275–1281. [Google Scholar] [CrossRef]
- Piquet, A.; Zebiri, B.; Hadjadj, A.; Safdari Shadloo, M. A parallel high-order compressible flows solver with domain decomposition method in the generalized curvilinear coordinates system. Int. J. Numer. Methods Heat Fluid Flow 2019. [Google Scholar] [CrossRef]
- Taylor, C.; Hughes, T.G. Finite element programming of the Navier Stokes equations. Z. Angew. Math. Mech. 1983. [Google Scholar] [CrossRef]
- Feistauer, M.; Felcman, J.; Straskraba, I. Mathematical and Computational Methods for Compressible Flow; Clarendon Press-Oxford Science Publications: Oxford, UK, 2003. [Google Scholar]
- Vadasz, P. Rendering the Navier-Stokes equations for a compressible fluid into the Schrödinger Equation for quantum mechanics. Fluids 2016, 1, 18. [Google Scholar] [CrossRef]
- Ebin, D.G. Motion of a Slightly Compressible Fluid. Proc. Natl. Acad. Sci. USA 1975, 72, 539–542. [Google Scholar] [CrossRef]
- Wang, Y.L.; Longwell, P.A. Laminar flow in the inlet section of parallel plates. AIChE J. 1964, 10, 323–330. [Google Scholar] [CrossRef]
- Harraga, H.; Yebdri, M. Attractors for a nonautonomous reaction-diffusion equation with delay. Appl. Math. Nonlinear Sci. 2018, 3, 127–150. [Google Scholar] [CrossRef]
- Vajravelu, K.; Li, R.; Dewasurendra, M.; Benarroch, J.; Ossi, N.; Zhang, Y.; Sammarco, M.; Prasad, K.V. Effects of second-order slip and drag reduction in boundary layer flows. Appl. Math. Nonlinear Sci. 2018, 3, 291–302. [Google Scholar] [CrossRef]
- Bazhenov, V.A.; Pogorelova, O.S.; Postnikova, T.G. Intermittent transition to chaos in vibroimpact system. Appl. Math. Nonlinear Sci. 2018, 3, 475–486. [Google Scholar] [CrossRef]
- Gibbs, J.W.; Wilson, E.B. Vector Analysis; Charles Scribner’s Sons: New York, NY, USA, 1901. [Google Scholar]
- Muralidhar, K. Algebra of complex vectors and applications in electromagnetic theory and quantum mechanics. Mathematics 2015, 3, 781–842. [Google Scholar] [CrossRef]
- Muller, C. Foundations of the Mathematical Theory of Electromagnetic Waves; Springer: New York, NY, USA, 1969; pp. 339–341. [Google Scholar]
- Lindell, I.V. Complex vector algebra in electromagnetics. Int. J. Electr. Eng. Educ. 1983, 20, 33–47. [Google Scholar] [CrossRef]
- Nelson, D.R. Statistical Mechanics of Membranes and Surfaces, 2nd ed.; World Scientific: London, UK, 2004. [Google Scholar]
- Grinfeld, P. Introduction to Tensor Analysis and the Calculus of Moving Surfaces; Springer: New York, NY, USA, 2010. [Google Scholar]
- McMullin, M.F. The molecular basis of disorders of the red cell membrane. J. Clin. Pathol. 1999, 52, 245. [Google Scholar] [CrossRef] [PubMed]
- Iolascon, A.; del Giudice Miraglia, E.; Camaschella, C. Molecular pathology of inherited erythrocyte membrane disorders: hereditary spherocytosis and elliptocytosis. Haematologica 1992, 77, 60–72. [Google Scholar] [PubMed]
- Falk, G.; Fatt, P. Linear electrical properties of striated muscle fibres observed with intracellular electrodes. Proc. R. Soc. Lond. Biol. 1964, 160, 69–123. [Google Scholar]
- Henszen, M.M.; Weske, M.; Schwarz, S.; Haest, C.W.; Deuticke, B. Electric field pulses induce reversible shape transformation of human erythrocytes. Mol. Membr. Biol. 1997, 14, 195–204. [Google Scholar] [CrossRef]
- Durney, C.H.; Johnson, C.C.; Barber, P.W.; Massoudi, H.; Iskander, M.F.; Allen, S.J.; Mitchell, J.C. Descriptive summary: Radiofrequency radiation dosimetry handbook-2nd Edition. Radio Sci. 1979, 14, 5–7. [Google Scholar] [CrossRef]
- Guven, J. Laplace pressure as a surface stress in fluid vesicles. J. Phys. A Math. Gen. 2006, 39, 3771–3785. [Google Scholar] [CrossRef]
- Capovilla, R.; Guven, J. Stresses in lipid membranes. J. Phys. A Math. Gen. 2002, 35, 6233–6247. [Google Scholar] [CrossRef]
- Svintradze, D.V. Two dimensional surface dynamics. arXiv 2018, arXiv:1802.07166. [Google Scholar]
- Svintradze, D.V. Micelles Hydrodynamics. arXiv 2016, arXiv:1608.01491. [Google Scholar]
- Svintradze, D.V. Moving manifolds in electromagnetic fields. Front. Phys. 2017, 5, 37. [Google Scholar] [CrossRef]
- Moschandreou, T. A Method of Solving Compressible Navier Stokes Equations in Cylindrical Coordinates Using Geometric Algebra. Mathematics 2019, 7, 126. [Google Scholar] [CrossRef]
- Doran, C.; Lasenby, A. Geometric Algebra for Physicists; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Beale, J.T.; Kato, T.; Majda, A. Remarks on the Breakdown of Smooth Solutions for the 3-D Euler Equations. Commun. Math. Phys. 1984, 94, 61–66. [Google Scholar] [CrossRef]
- Afas, K.C. Extending the Calculus of Moving Surfaces to Higher Orders. arxiv 2018, arXiv:1806.02335. [Google Scholar]
- Ivancevic, V.G.; Ivancevic, T.T. Undergraduate Lecture Notes in DeRham-Hodge Theory. arxiv 2011, arXiv:0807.4991v4. [Google Scholar]
- Deriglazov, A. Classical Mechanics; Springer: Berlin, Germany, 2010. [Google Scholar]
- Afas, K.C. Normal Calculus on Moving Surfaces. Preprints 2018. [Google Scholar] [CrossRef]
- Zhong-Can, O.-Y.; Helfrich, W. Instability and deformation of a spherical vesicle by pressure. Phys. Rev. Lett. 1987, 59, 2486–2488. [Google Scholar] [CrossRef]
- Bryant, R.L. A duality theorem for willmore surfaces. J. Differ. Geom. 1984, 20, 23–53. [Google Scholar] [CrossRef]
- Toda, M.; Athukoralage, B. Geometry of Biological Membranes and Willmore Energy; Simos, T., Psihoyios, G., Tsitouras, C., Eds.; American Institute of Physics Conference Series; American Institute of Physics Conference: New York, NY, USA, 2013; Volume 1558, pp. 883–886. [Google Scholar]
- Gonzalez, O.; Stuart, A.M. Kinematics; Cambridge Texts in Applied Mathematics; Cambridge University Press: Cambridge, UK, 2008; pp. 112–166. [Google Scholar]
- Grinfeld, P. A better calculus of moving surfaces. J. Geom. Symmetry Phys. 2012, 26, 61–69. [Google Scholar]
- Misner, C.W.; Thorne, K.S.; Wheeler, J.A. Gravitation, 1st ed.; Physics Series; W. H. Freeman: San Fransisco, CA, USA, 1973. [Google Scholar]
- Holton, G.; Brush, S.G.; Evans, J. Physics, the Human Adventure from Copernicus to Einstein and Beyond. Phys. Today 2001, 54, 69. [Google Scholar]
- Roura, P. Thermodynamic derivations of the mechanical equilibrium conditions for fluid surfaces: Young’s and Laplace’s equations. Am. J. Phys. 2005, 73, 1139–1147. [Google Scholar] [CrossRef]
- Laugier, A.; Garai, J. Derivation of the ideal gas law. J. Chem. Educ. 2007, 84, 1832. [Google Scholar] [CrossRef]
- Halliday, D.; Resnick, R.; Walker, J. Fundamentals of Physics, 9th ed.; Wiley: New York, NY, USA, 2011. [Google Scholar]
- Morisson, F.A. Compressible Fluids; Michigan Technological University: Houghton, MI, USA, 2004; pp. 94–98. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moschandreou, T.E.; Afas, K.C. Compressible Navier-Stokes Equations in Cylindrical Passages and General Dynamics of Surfaces—(I)-Flow Structures and (II)-Analyzing Biomembranes under Static and Dynamic Conditions. Mathematics 2019, 7, 1060. https://doi.org/10.3390/math7111060
Moschandreou TE, Afas KC. Compressible Navier-Stokes Equations in Cylindrical Passages and General Dynamics of Surfaces—(I)-Flow Structures and (II)-Analyzing Biomembranes under Static and Dynamic Conditions. Mathematics. 2019; 7(11):1060. https://doi.org/10.3390/math7111060
Chicago/Turabian StyleMoschandreou, Terry E., and Keith C. Afas. 2019. "Compressible Navier-Stokes Equations in Cylindrical Passages and General Dynamics of Surfaces—(I)-Flow Structures and (II)-Analyzing Biomembranes under Static and Dynamic Conditions" Mathematics 7, no. 11: 1060. https://doi.org/10.3390/math7111060
APA StyleMoschandreou, T. E., & Afas, K. C. (2019). Compressible Navier-Stokes Equations in Cylindrical Passages and General Dynamics of Surfaces—(I)-Flow Structures and (II)-Analyzing Biomembranes under Static and Dynamic Conditions. Mathematics, 7(11), 1060. https://doi.org/10.3390/math7111060




