Moisture Estimation in Cabinet Dryers with Thin-Layer Relationships Using a Genetic Algorithm and Neural Network
Abstract
1. Introduction
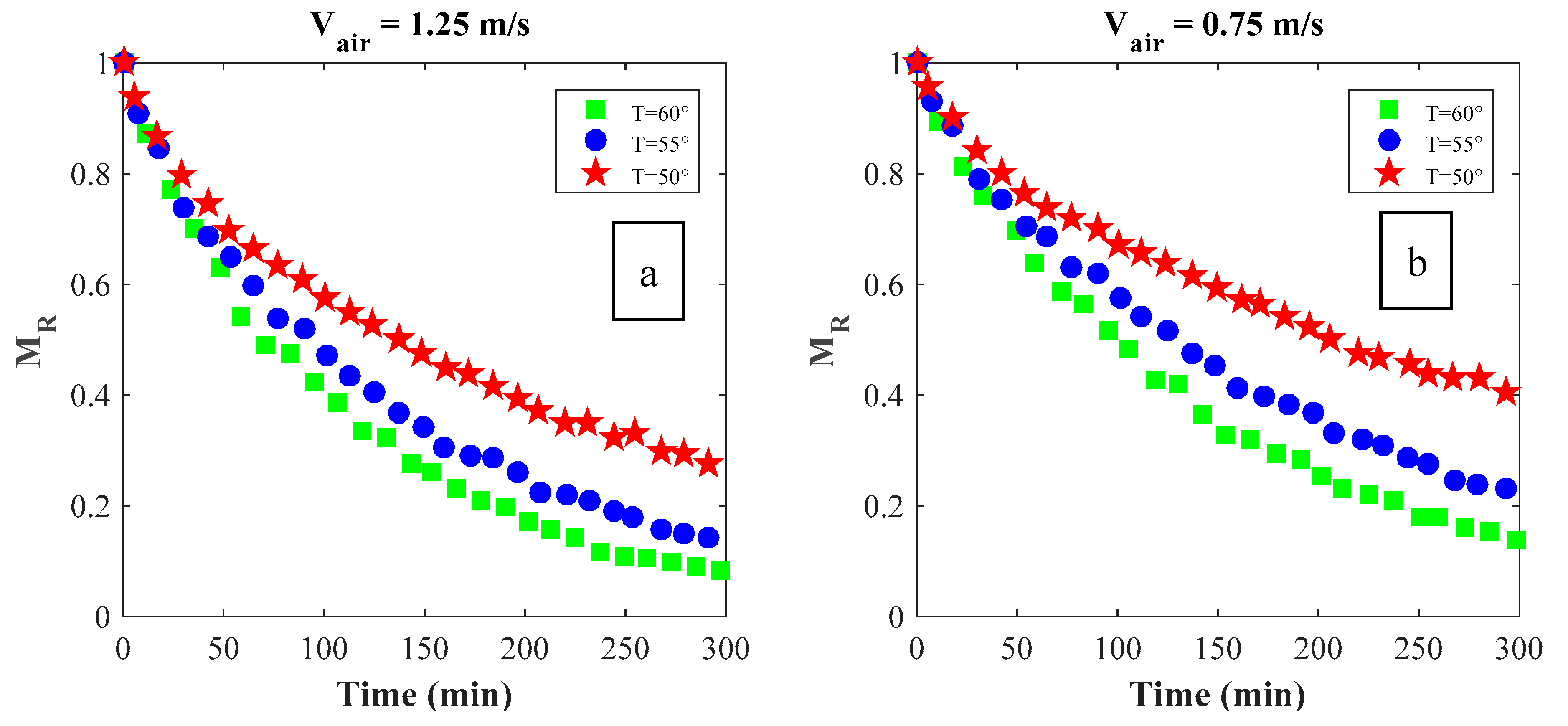
2. Study Procedure
3. Designing an Artificial Neural Network to Predict Instantaneous Moisture
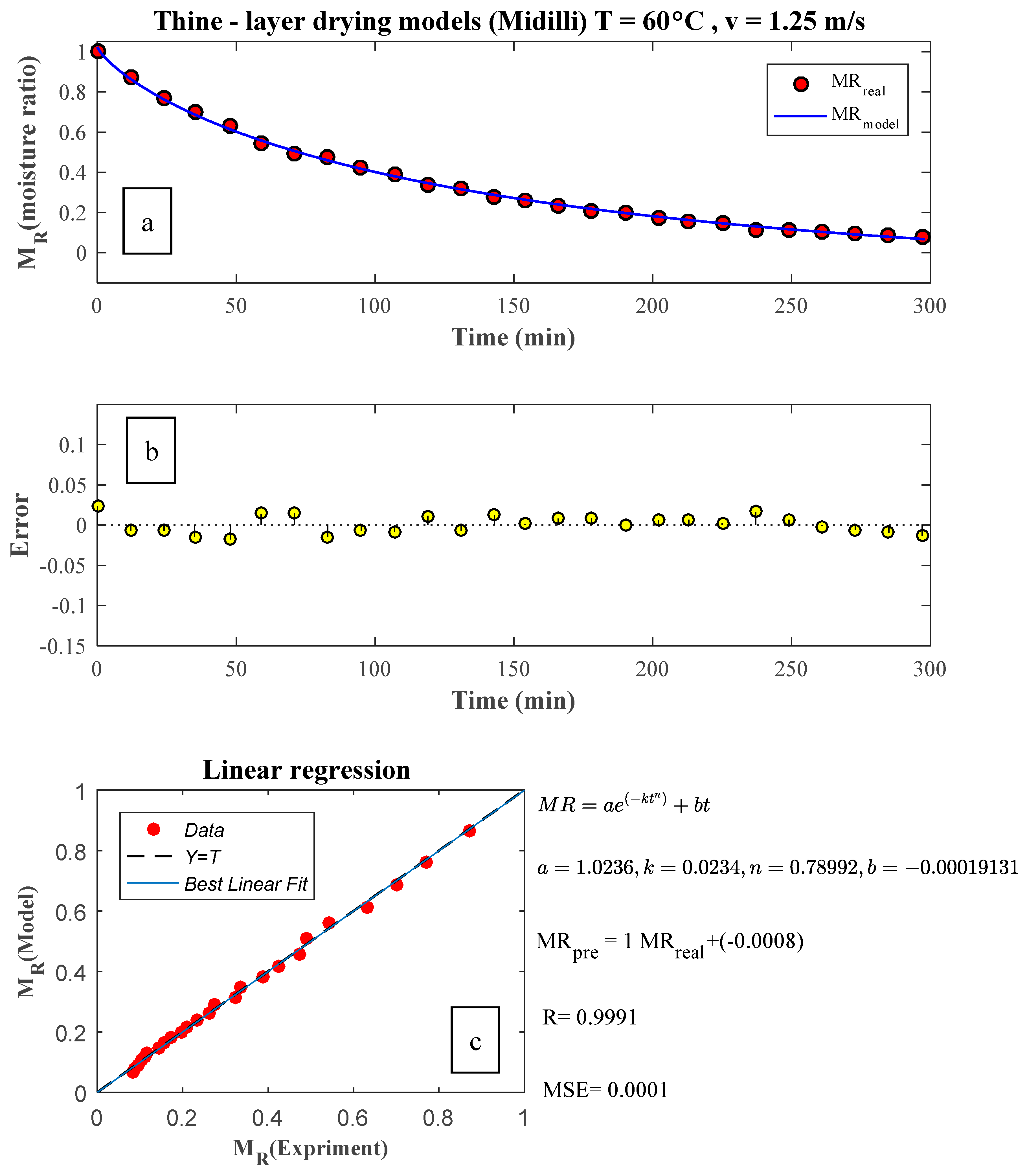
4. Calculating the Coefficients of the Thin Layer Drying Equations
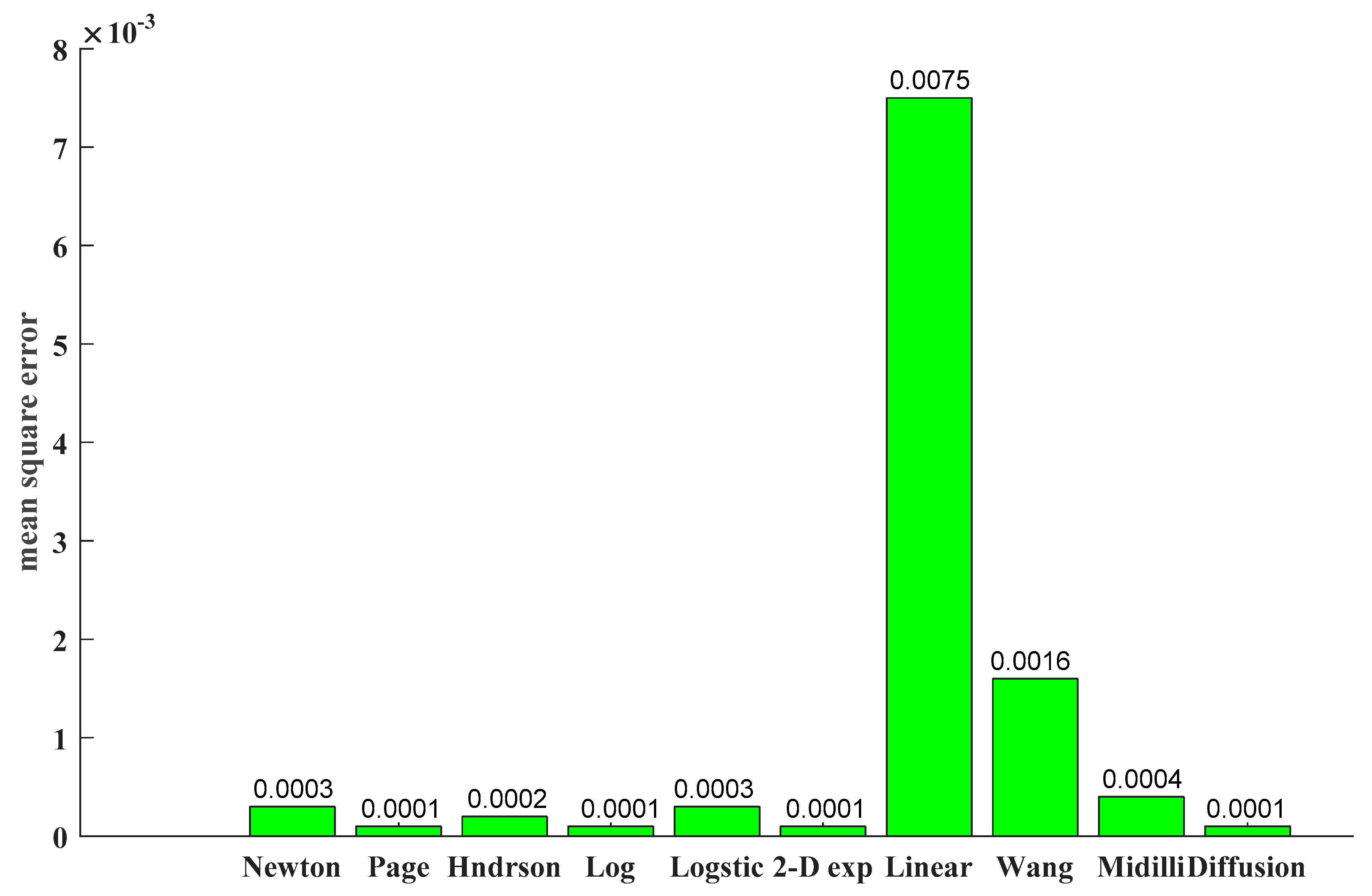
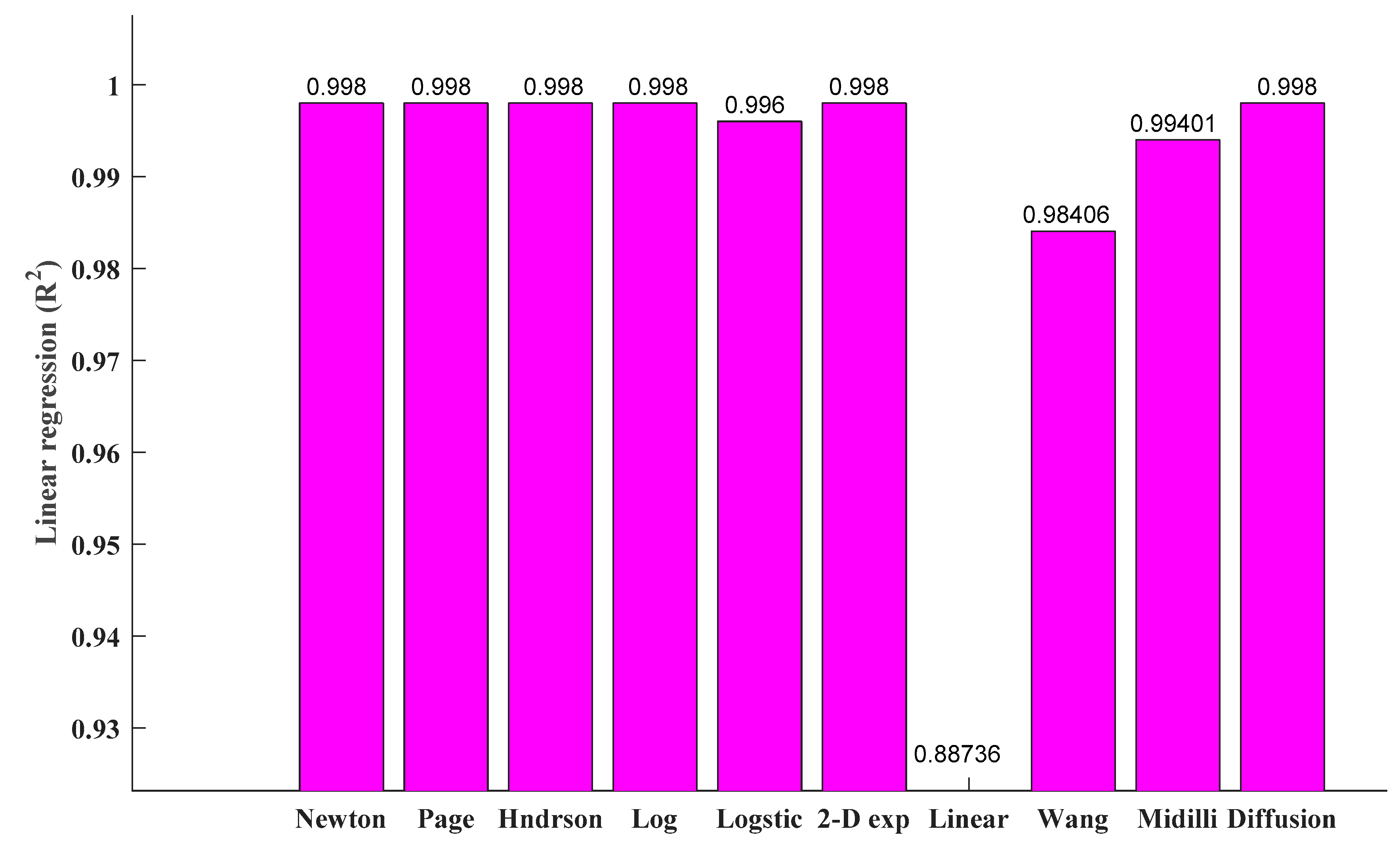
5. Comparison of the Accuracy Associated with Different Models of Thin-Layer Drying
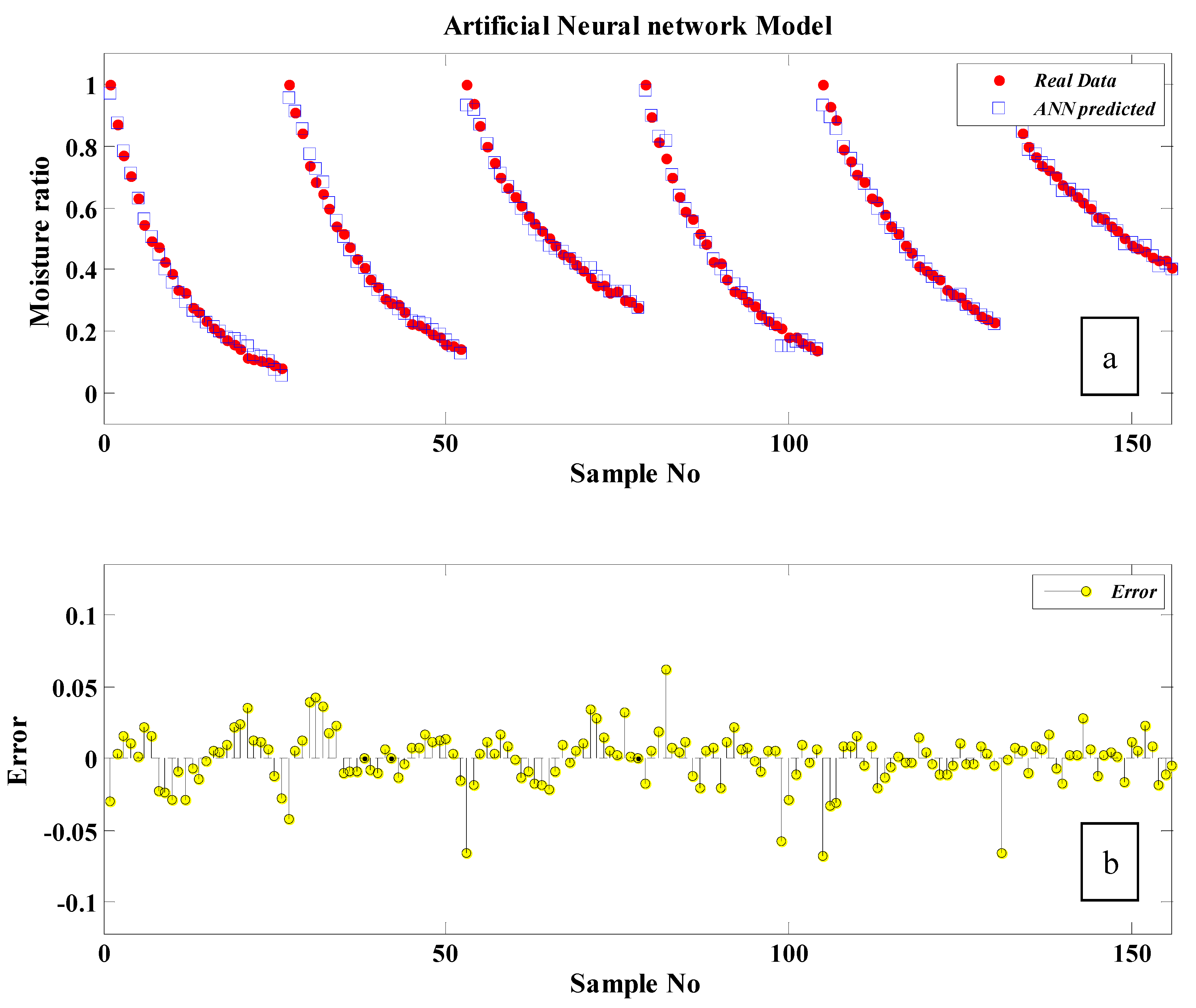
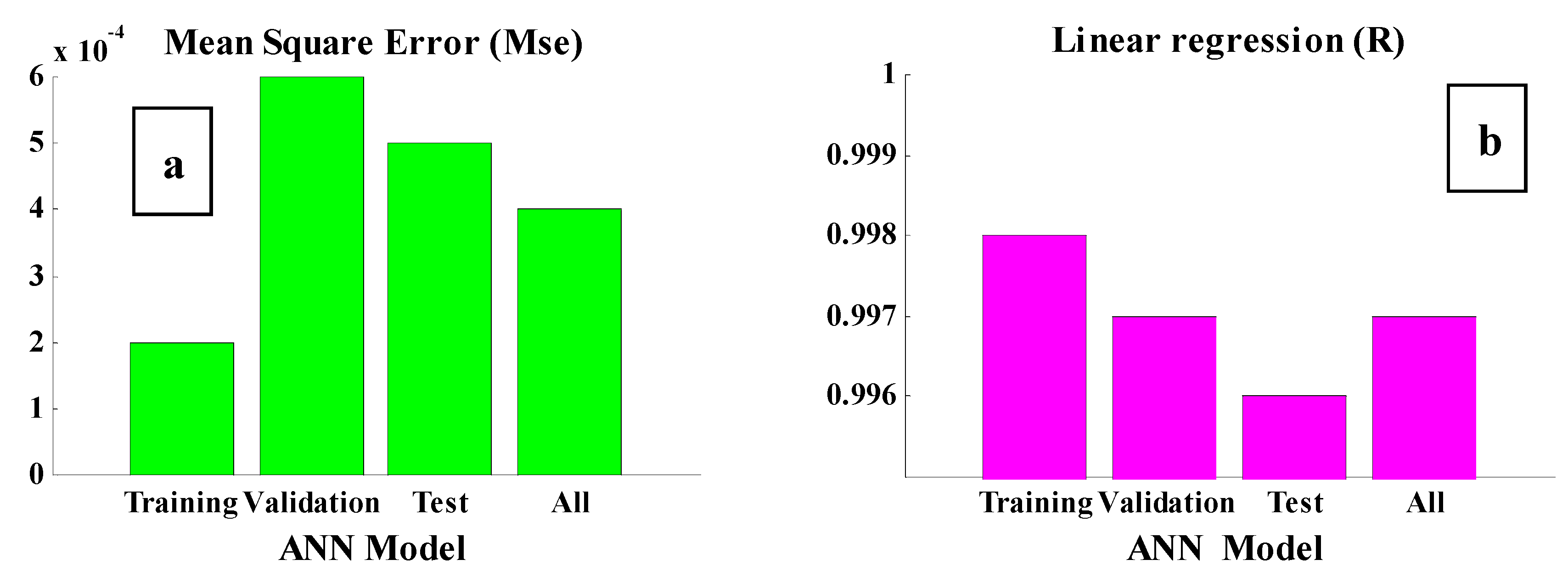
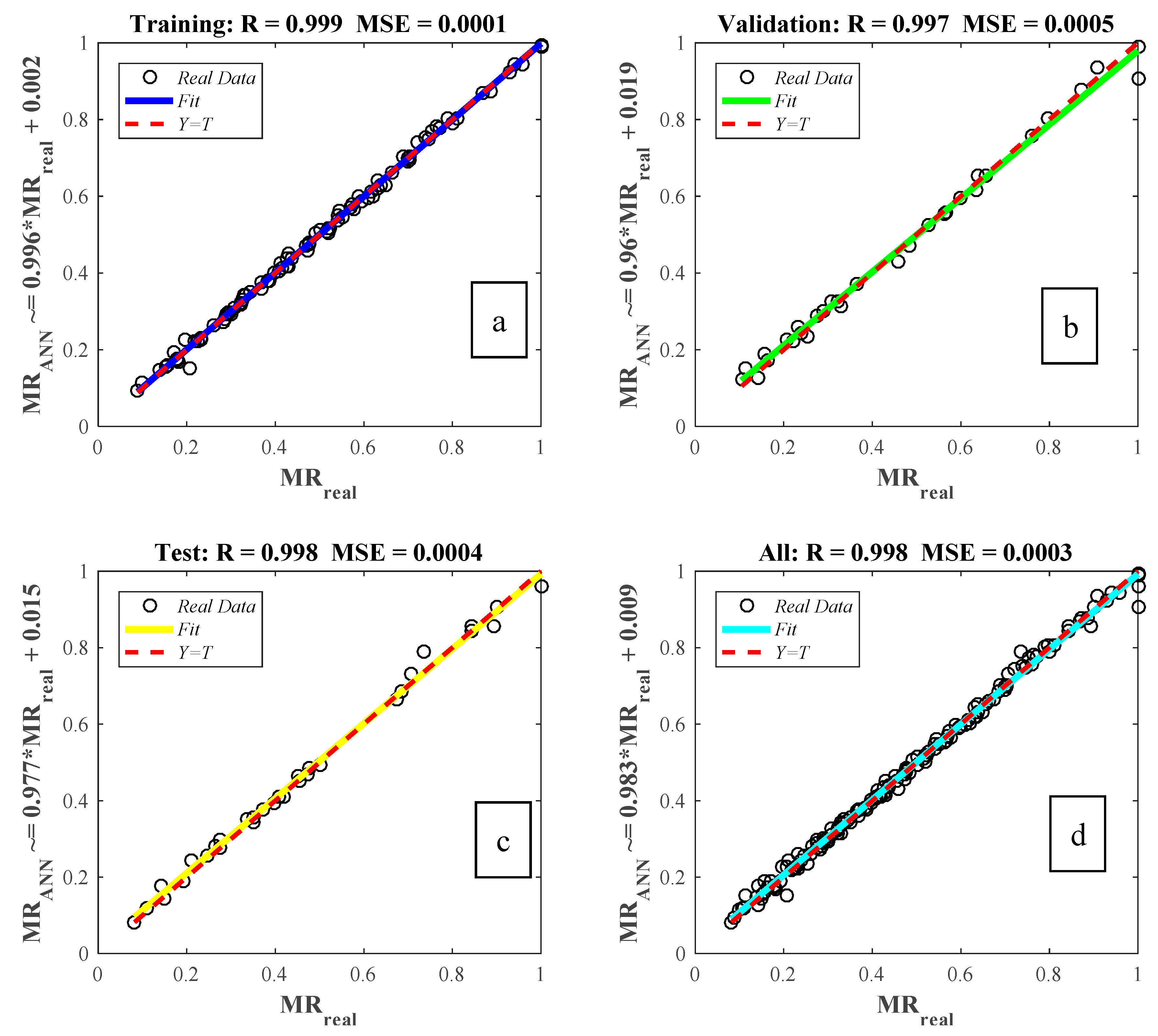
6. Neural Network Modeling
7. Discussions
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Rezaei, M.H.; Sadeghzadeh, M.; Alhuyi Nazari, M.; Ahmadi, M.H.; Astaraei, F.R. Applying GMDH artificial neural network in modeling CO2 emissions in four nordic countries. Int. J. Low Carbon Technol. 2018, 13, 266–271. [Google Scholar] [CrossRef]
- Aghayari, R.; Maddah, H.; Ahmadi, M.; Yan, W.-M.; Ghasemi, N. Measurement and Artificial Neural Network Modeling of Electrical Conductivity of CuO/Glycerol Nanofluids at Various Thermal and Concentration Conditions. Energies 2018, 11, 1190. [Google Scholar] [CrossRef]
- Zbiciński, I.; Strumiłło, P.; Kamiński, W. Hybrid neural model of thermal drying in a fluidized bed. Comput. Chem. Eng. 1996, 20, S695–S700. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Tatar, A.; Alhuyi Nazari, M.; Ghasempour, R.; Chamkha, A.J.; Yan, W.-M. Applicability of connectionist methods to predict thermal resistance of pulsating heat pipes with ethanol by using neural networks. Int. J. Heat Mass Transf. 2018, 126, 1079–1086. [Google Scholar] [CrossRef]
- Maddah, H.; Aghayari, R.; Ahmadi, M.H.; Rahimzadeh, M.; Ghasemi, N. Prediction and modeling of MWCNT/Carbon (60/40)/SAE 10 W 40/SAE 85 W 90 (50/50) nanofluid viscosity using artificial neural network (ANN) and self-organizing map (SOM). J. Therm. Anal. Calorim. 2018, 134, 2275–2286. [Google Scholar] [CrossRef]
- Ahmadi, M.H.; Tatar, A.; Seifaddini, P.; Ghazvini, M.; Ghasempour, R.; Sheremet, M.A. Thermal conductivity and dynamic viscosity modeling of Fe2O3/water nanofluid by applying various connectionist approaches. Numer. Heat Transf. Part A Appl. 2018, 74, 1301–1322. [Google Scholar] [CrossRef]
- Kahani, M.; Ahmadi, M.H.; Tatar, A.; Sadeghzadeh, M. Development of multilayer perceptron artificial neural network (MLP-ANN) and least square support vector machine (LSSVM) models to predict Nusselt number and pressure drop of TiO2/water nanofluid flows through non-straight pathways. Numer. Heat Transf. Part A Appl. 2018, 74, 1190–1206. [Google Scholar] [CrossRef]
- Maddah, H.; Ghazvini, M.; Ahmadi, M.H. Predicting the efficiency of CuO/water nanofluid in heat pipe heat exchanger using neural network. Int. Commun. Heat Mass Transf. 2019, 104, 33–40. [Google Scholar] [CrossRef]
- Dai, A.; Zhou, X.; Liu, X.; Liu, J.; Zhang, C. Intelligent control of a grain drying system using a GA-SVM-IMPC controller. Dry. Technol. 2018, 36, 1413–1435. [Google Scholar] [CrossRef]
- Aghbashlo, M.; Hosseinpour, S.; Mujumdar, A.S. Application of Artificial Neural Networks (ANNs) in Drying Technology: A Comprehensive Review. Dry. Technol. 2015, 33, 1397–1462. [Google Scholar] [CrossRef]
- Su, Y.; Zhang, M.; Mujumdar, A.S. Recent Developments in Smart Drying Technology. Dry. Technol. 2015, 33, 260–276. [Google Scholar] [CrossRef]
- Dufour, P. Control Engineering in Drying Technology: Review and Trends. Dry. Technol. 2006, 24, 889–904. [Google Scholar] [CrossRef]
- Freire, F.B.; Vieira, G.N.; Freire, J.T.; Mujumdar, A.S. Trends in Modeling and Sensing Approaches for Drying Control. Dry. Technol. 2014, 32, 1524–1532. [Google Scholar] [CrossRef]
- Wu, J.; Yang, S.X.; Tian, F. An adaptive neuro-fuzzy approach to bulk tobacco flue-curing control process. Dry. Technol. 2017, 35, 465–477. [Google Scholar] [CrossRef]
- Li, J.; Xiong, Q.; Wang, K.; Shi, X.; Liang, S. A recurrent self-evolving fuzzy neural network predictive control for microwave drying process. Dry. Technol. 2016, 34, 1434–1444. [Google Scholar] [CrossRef]
- Lutfy, O.F.; Selamat, H.; Mohd Noor, S.B. Intelligent Modeling and Control of a Conveyor Belt Grain Dryer Using a Simplified Type 2 Neuro-Fuzzy Controller. Dry. Technol. 2015, 33, 1210–1222. [Google Scholar] [CrossRef]
- Farkas, I. Use of Artificial Intelligence for the Modelling of Drying Processes. Dry. Technol. 2013, 31, 848–855. [Google Scholar] [CrossRef]
- Jumah, R.; Mujumdar, A.S. Modeling Intermittent Drying Using an Adaptive Neuro-Fuzzy Inference System. Dry. Technol. 2005, 23, 1075–1092. [Google Scholar] [CrossRef]
- Köni, M.; Yüzgeç, U.; Türker, M.; Dinçer, H. Adaptive Neuro-Fuzzy-Based Control of Drying of Baker’s Yeast in Batch Fluidized Bed. Dry. Technol. 2010, 28, 205–213. [Google Scholar] [CrossRef]
- Vahid, M.K.; Hamed, M.M.; Etemadi, A. Determination of Effective Diffusivity Coefficient and Activation Energy of Shelled Pistachio by Using Fluidized Bed Dryer. Arch. Sid 2008, 3, 1–12. [Google Scholar]
- Zhang, Q.; Yang, S.X.; Mittal, G.S.; Yi, S. AE—Automation and Emerging Technologies: Prediction of Performance Indices and Optimal Parameters of Rough Rice Drying using Neural Networks. Biosyst. Eng. 2002, 83, 281–290. [Google Scholar] [CrossRef]
- Islam, M.R.; Sablani, S.S.; Mujumdar, A.S. An Artificial Neural Network Model for Prediction of Drying Rates. Dry. Technol. 2003, 21, 1867–1884. [Google Scholar] [CrossRef]
- Erenturk, S.; Erenturk, K. Comparison of genetic algorithm and neural network approaches for the drying process of carrot. J. Food Eng. 2007, 78, 905–912. [Google Scholar] [CrossRef]
- Zubisinsky, I.; Ciesielski, K. Extension of the Neural Networks Operating Range by the Application of Dimensionless Numbers in Prediction of Heat Transfer Coefficients. Dry. Technol. 2000, 18, 649–660. [Google Scholar] [CrossRef]
- Mittal, G.S.; Zhang, J. Prediction of temperature and moisture content of frankfurters during thermal processing using neural network. Meat Sci. 2000, 55, 13–24. [Google Scholar] [CrossRef]
- Broyart, B.; Trystram, G. Modelling of Heat and Mass Transfer Phenomena and Quality Changes During Continuous Biscuit Baking Using Both Deductive and Inductive (Neural Network) Modelling Principles. Food Bioprod. Process. 2003, 81, 316–326. [Google Scholar] [CrossRef]
- Hernández-Pérez, J.A.; Garcı́a-Alvarado, M.A.; Trystram, G.; Heyd, B. Neural networks for the heat and mass transfer prediction during drying of cassava and mango. Innov. Food Sci. Emerg. Technol. 2004, 5, 57–64. [Google Scholar] [CrossRef]
- Poonnoy, P.; Tansakul, A.; Chinnan, M. Estimation of Moisture Ratio of a Mushroom Undergoing Microwave-vacuum Drying Using Artificial Neural Network and Regression Models. Chem. Prod. Process. Model 2007, 2. [Google Scholar] [CrossRef]
- Poonnoy, P.; Tansakul, A.; Chinnan, M. Artificial Neural Network Modeling for Temperature and Moisture Content Prediction in Tomato Slices Undergoing Microwave-Vacuum Drying. J. Food Sci. 2007, 72, E042–E047. [Google Scholar] [CrossRef]
- Cihan, A.; Kahveci, K.; Hacıhafızoğlu, O. Modelling of intermittent drying of thin layer rough rice. J. Food Eng. 2007, 79, 293–298. [Google Scholar] [CrossRef]
- O’Callaghan, J.R.; Menzies, D.J.; Bailey, P.H. Digital simulation of agricultural drier performance. J. Agric. Eng. Res. 1971, 16, 223–244. [Google Scholar] [CrossRef]
- Agrawal, Y.C.; Singh, R.P. Thin Layer Drying Studies for Short Grain Rice; ASAE Paper No: 3531; ASAE: St. Joseph, MI, USA, 1977. [Google Scholar]
- Manjeet, S.; Chhinnan, M.S. Evaluation of Selected Mathematical Models for Describing Thin-Layer Drying of In-Shell Pecans. Trans. ASAE 1984, 27, 610–615. [Google Scholar] [CrossRef]
- Chandra, P.K.; Singh, R.P. Applied Numerical Methods for Food and Agricultural Engineers; CRC Press: Boca Raton, FL, USA, 1995. [Google Scholar]
- Henderson, S.M. Progress in Developing the Thin Layer Drying Equation. Trans. ASAE 1974, 17, 1167–1168. [Google Scholar] [CrossRef]
- Wang, C.Y.; Singh, R.P. A single layer drying equation for rough rice. Am. Soc. Agric. Eng. 2016, 4, 115–124. [Google Scholar]
- Midilli, A.; Kucuk, H.; Yapar, Z. A New Model for Single-Layer Drying. Dry. Technol. 2002, 20, 1503–1513. [Google Scholar] [CrossRef]
- Kassem, A.S. Comparative studies on thin layer drying models for wheat. In Proceedings of the 13th International Congress on Agricultural Engineering, Rabat, Morocco, 2–6 February 1998. [Google Scholar]
- Shang, Y. Deffuant model of opinion formation in one-dimensional multiplex networks. J. Phys. A Math. Theor. 2015, 48, 395101. [Google Scholar] [CrossRef]
- Shang, Y. Limit of a nonpreferential attachment multitype network model. Int. J. Mod. Phys. B 2017, 31, 1750026. [Google Scholar] [CrossRef]
- Shang, Y. Resilient Multiscale Coordination Control against Adversarial Nodes. Energies 2018, 11, 1844. [Google Scholar] [CrossRef]
- Shang, Y. Resilient consensus of switched multi-agent systems. Syst. Control Lett. 2018, 122, 12–18. [Google Scholar] [CrossRef]
| Thin-Layer Drying Models | ||
|---|---|---|
| Name | Model Equation | References |
| Newton | MR = exp (−kt) | O’callaghanetal (1971), [31] |
| Page | MR = exp (−ktn) | Agrawal and Singh (1977), [32] |
| Henderson and Pabis | MR = aexp (−kt) | Chhinman (1984), [33] |
| Logarithmic (1995) | MR = a0 + aexp (−kt) | Chandra and Singh, [34] |
| Logistic (1995) | MR = a0/(1 + aexp (kt)) | Chandra and Singh, [34] |
| Two-term exponential | MR = a1exp (−k1t) + a2exp (−k2t) | Henderson (1974), [35] |
| Linear | MR = at + b | Chandra and Singh (1995), [34] |
| Wang and Singh | MR = 1 + a1t + a2t2 | Wang and Singh (1978), [36] |
| Midilli | MR = aexp (−ktn) + bt | Midilli et al. (2002), [37] |
| Diffusion approach | MR = aexp (−kt) + (1 − a) exp (−kbt) | Kassem (1998), [38] |
| Midili | ||||||
|---|---|---|---|---|---|---|
| Run No | Temp© | V (m/s) | A | K | n | B |
| Run 1 | 60 | 1.25 | 1.002705 | 0.015509 | 0.885033 | −4.11 × 10−5 |
| RUN 2 | 55 | 1.25 | 1.036377 | 0.034653 | 0.649945 | −0.00046 |
| RUN 3 | 50 | 1.25 | 1.020234 | 0.020321 | 0.729967 | 1.41 × 10−5 |
| RUN 4 | 60 | 0.75 | 1.012155 | 0.016581 | 0.805009 | −0.00024 |
| RUN 5 | 55 | 0.75 | 1.005385 | 0.014143 | 0.784523 | −0.00025 |
| RUN 6 | 50 | 0.75 | 1.024748 | 0.02253 | 0.621478 | −0.00021 |
| 0.996 | |
| 0.0005 | |
| Objective Function | MSE |
| Training Algorithm | LM |
| Transfer Function | tansig |
| Topology | 3-9-1 |
| Network Type | FF-BP |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maleki, B.; Ghazvini, M.; Ahmadi, M.H.; Maddah, H.; Shamshirband, S. Moisture Estimation in Cabinet Dryers with Thin-Layer Relationships Using a Genetic Algorithm and Neural Network. Mathematics 2019, 7, 1042. https://doi.org/10.3390/math7111042
Maleki B, Ghazvini M, Ahmadi MH, Maddah H, Shamshirband S. Moisture Estimation in Cabinet Dryers with Thin-Layer Relationships Using a Genetic Algorithm and Neural Network. Mathematics. 2019; 7(11):1042. https://doi.org/10.3390/math7111042
Chicago/Turabian StyleMaleki, Behzad, Mahyar Ghazvini, Mohammad Hossein Ahmadi, Heydar Maddah, and Shahaboddin Shamshirband. 2019. "Moisture Estimation in Cabinet Dryers with Thin-Layer Relationships Using a Genetic Algorithm and Neural Network" Mathematics 7, no. 11: 1042. https://doi.org/10.3390/math7111042
APA StyleMaleki, B., Ghazvini, M., Ahmadi, M. H., Maddah, H., & Shamshirband, S. (2019). Moisture Estimation in Cabinet Dryers with Thin-Layer Relationships Using a Genetic Algorithm and Neural Network. Mathematics, 7(11), 1042. https://doi.org/10.3390/math7111042





