Exact and Nonstandard Finite Difference Schemes for Coupled Linear Delay Differential Systems
Abstract
1. Introduction
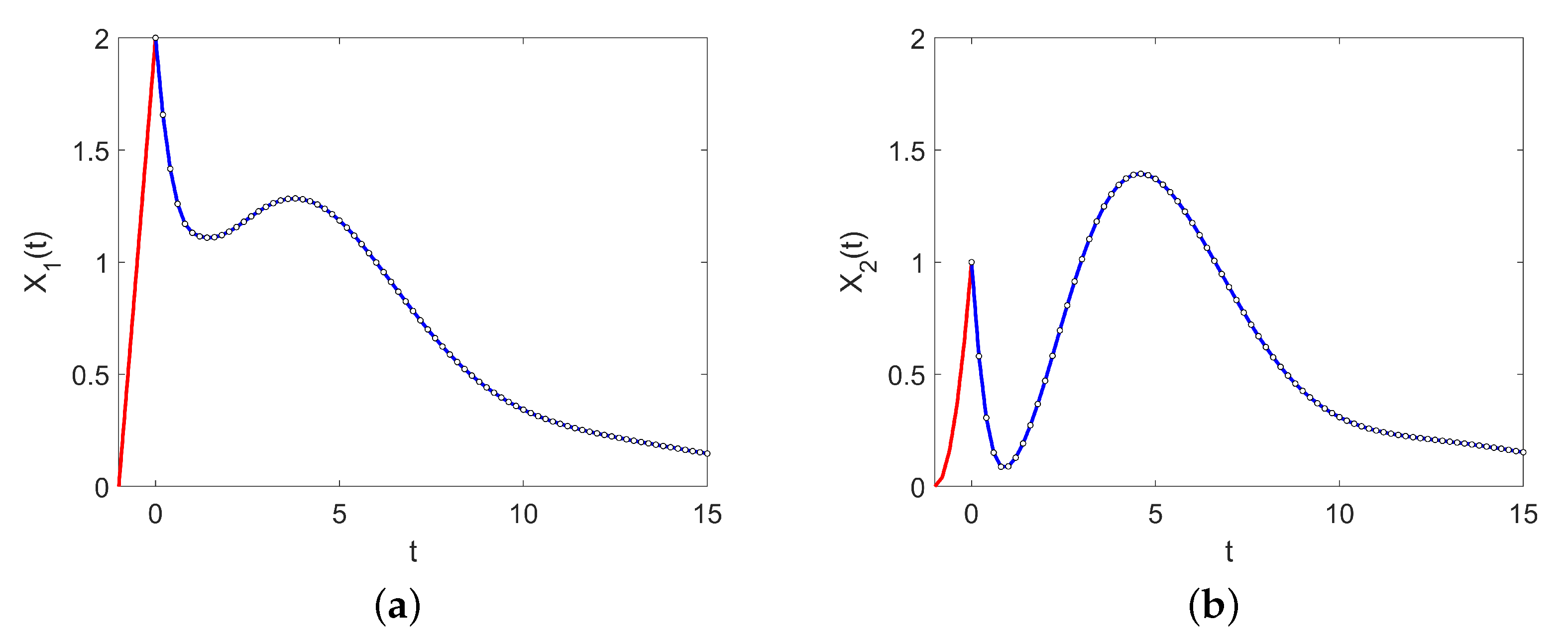
2. Exact Numerical Scheme
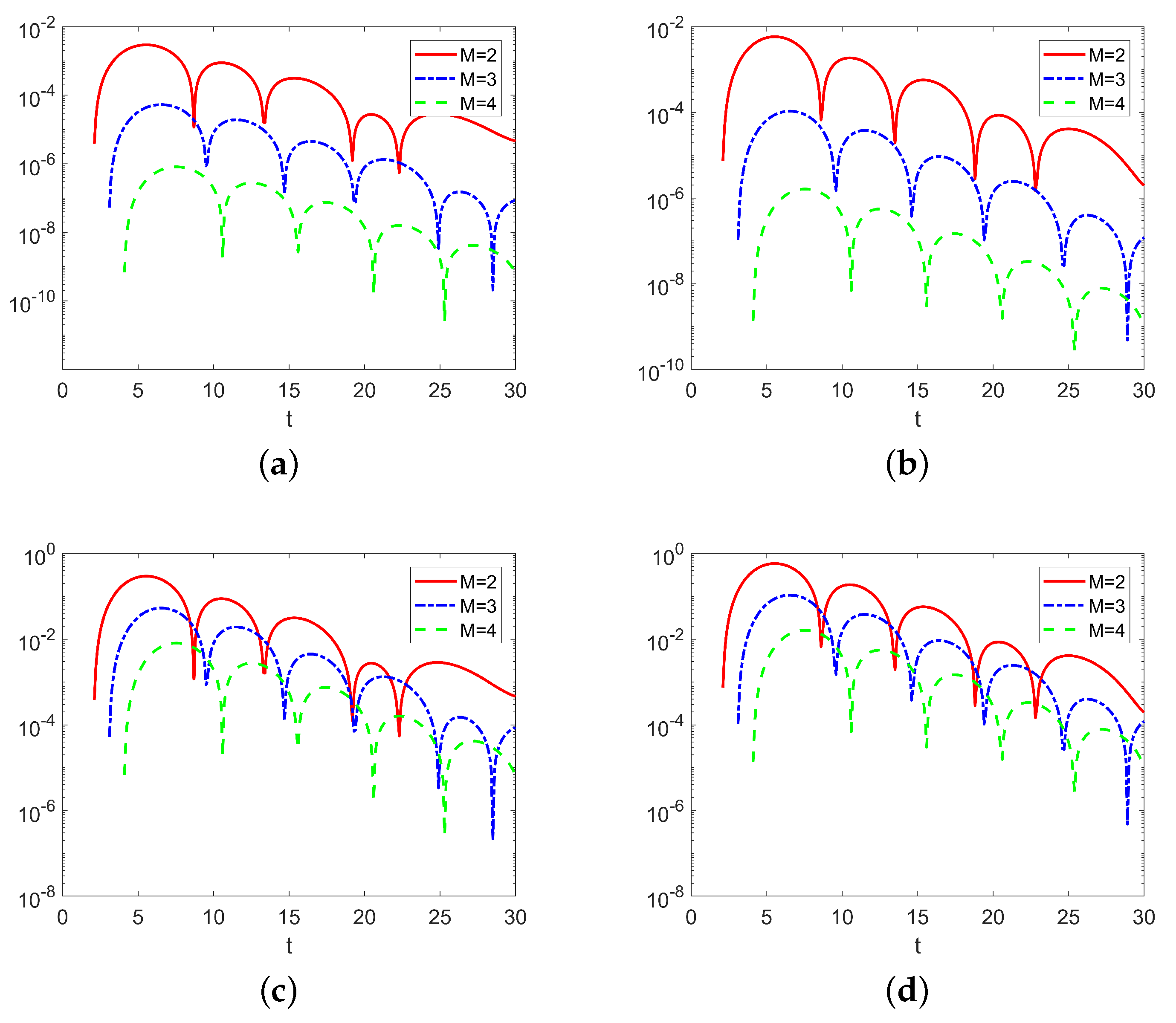
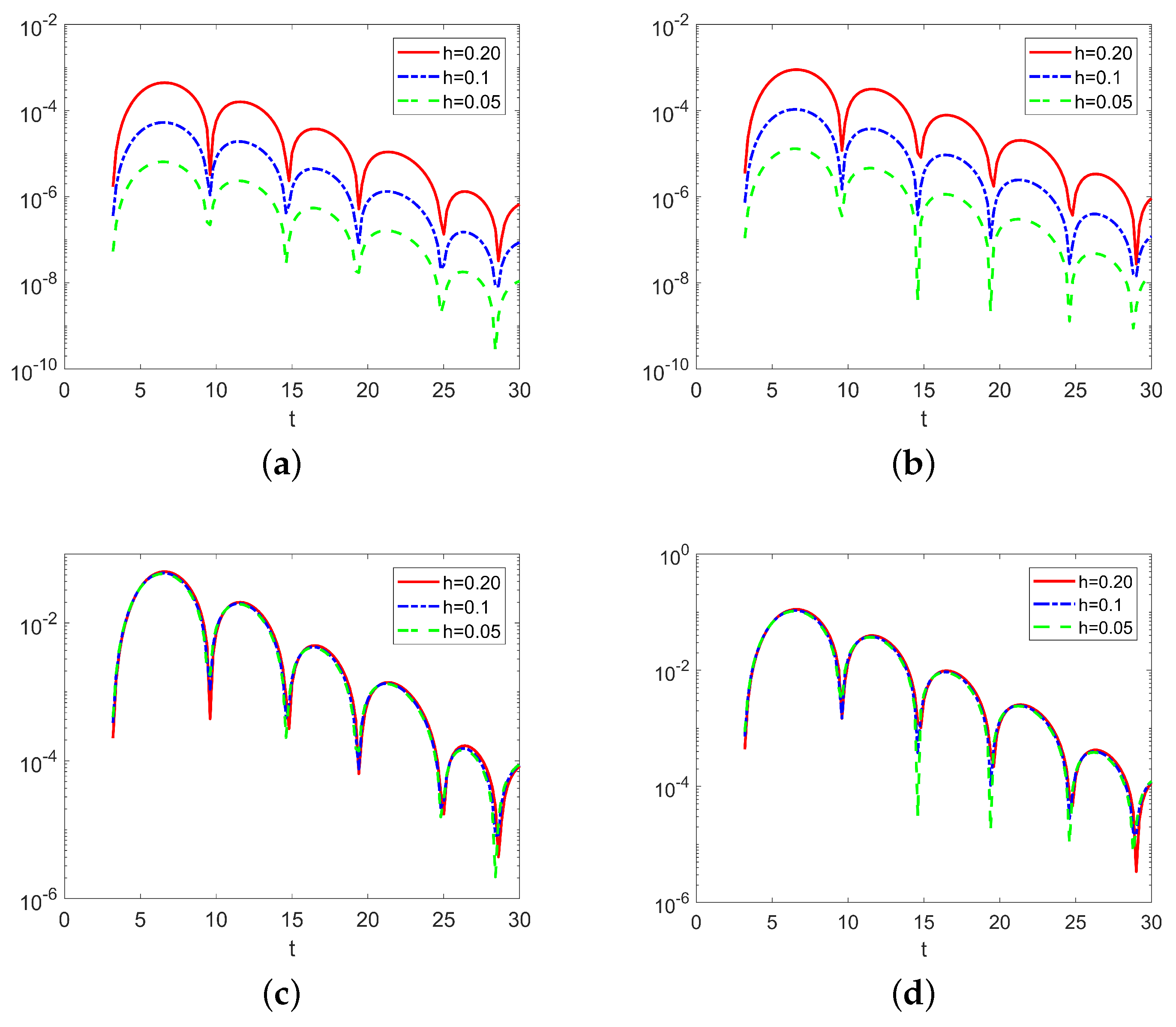
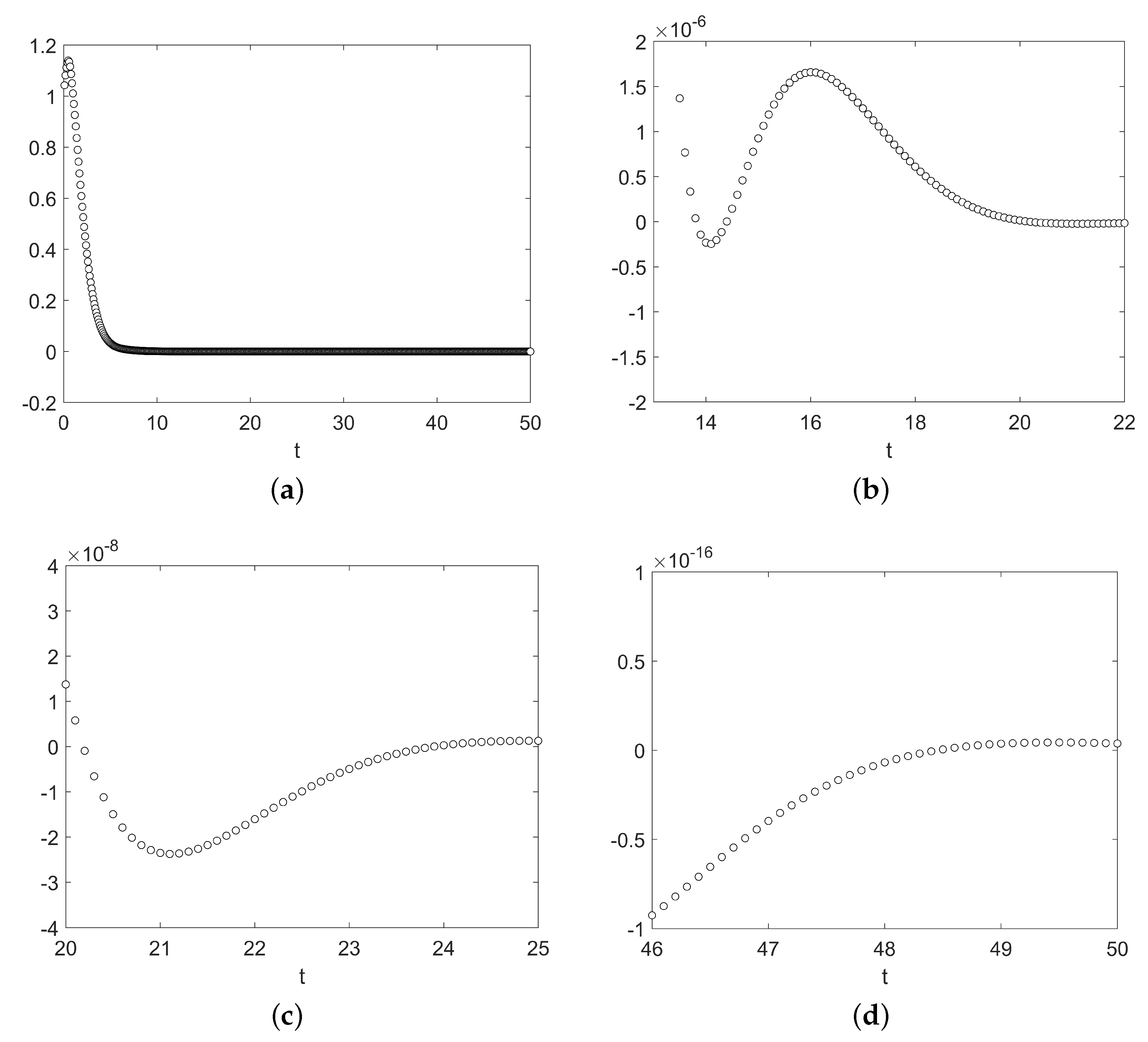
3. Nonstandard Finite Difference Methods of Increasing Orders
4. Dynamic Consistency Properties
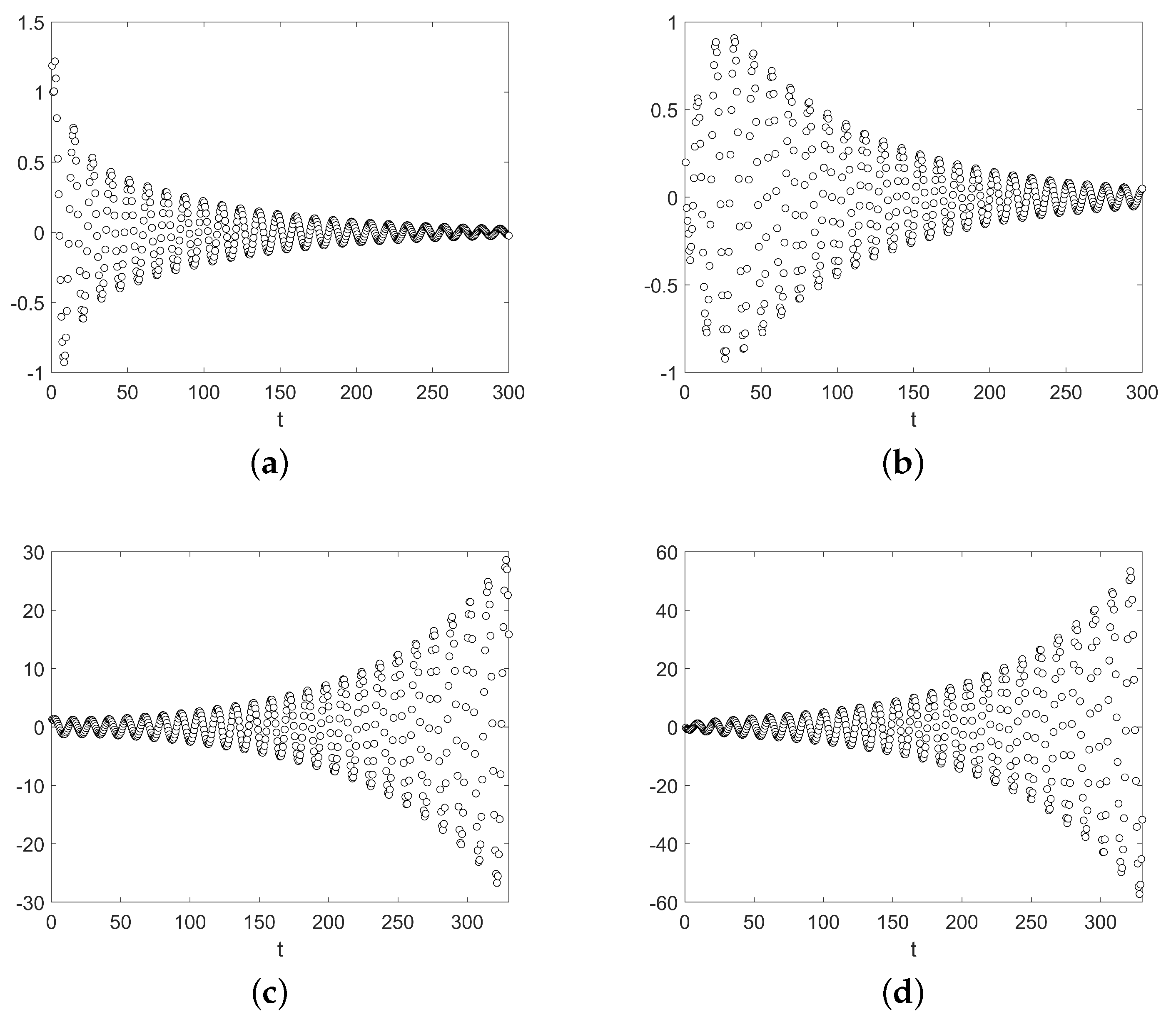
4.1. Asymptotic Stability
Delay Independent Stability
4.2. Oscillation and Positivity
Positivity
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kuang, Y. Delay Differential Equations. With Applications in Population Dynamics; Academic Press: San Diego, CA, USA, 1993. [Google Scholar]
- Kolmanovskii, V.; Myshkis, A. Introduction to the Theory and Applications of Functional Differential Equations; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1999. [Google Scholar]
- Smith, H. An Introduction to Delay Differential Equations with Applications to the Life Sciences; Springer: New York, NY, USA, 2011. [Google Scholar]
- Wu, M.; He, Y.; She, J.-H. Stability Analysis and Robust Control of Time-Delay Systems; Science Press: Beijing, China; Springer: Heidelberg, Germany, 2010. [Google Scholar]
- Chalishajar, D.N.; Kumar, A. Total controllability of the second order semi-linear differential equation with infinite delay and non-instantaneous impulses. Math. Comput. Appl. 2018, 23, 32. [Google Scholar] [CrossRef]
- Bellen, A.; Zennaro, M. Numerical Methods for Delay Differential Equations; Oxford University Press: Oxford, UK, 2003. [Google Scholar]
- Mickens, R.E. Nonstandard Finite Difference Models of Differential Equations; World Scientific: Singapore, 1994. [Google Scholar]
- Mickens, R.E. (Ed.) Advances on Applications of Nonstandard Finite Difference Schemes; World Scientific: Singapore, 2005. [Google Scholar]
- Patidar, K.C. Nonstandard finite difference methods: Recent trends and further developments. J. Differ. Equ. Appl. 2016, 22, 817–849. [Google Scholar] [CrossRef]
- Stuart, A.M.; Humphries, A.R. Dynamical Systems and Numerical Analysis; Cambridge University Press: Cambridge, UK, 1998. [Google Scholar]
- Jódar, L.; Villanueva, R.J.; Arenas, A.J.; González, G.C. Nonstandard numerical methods for a mathematical model for influenza disease. Math. Comput. Simul. 2008, 79, 622–633. [Google Scholar] [CrossRef]
- Arenas, A.J.; Moraño, J.A.; Cortés, J.C. Non-standard numerical method for a mathematical model of RSV epidemiological transmission. Comput. Math. Appl. 2008, 56, 670–678. [Google Scholar] [CrossRef]
- Arenas, A.J.; González-Parra, G.; Chen-Charpentier, B.M. A nonstandard numerical scheme of predictor–corrector type for epidemic models. Comput. Math. Appl. 2010, 59, 3740–3749. [Google Scholar] [CrossRef]
- Mickens, R.E.; Washington, T.M. NSFD discretizations of interacting population models satisfying conservation laws. Comput. Math. Appl. 2013, 66, 2307–2316. [Google Scholar] [CrossRef]
- Guerrero, F.; González-Parra, G.; Arenas, A.J. A nonstandard finite difference numerical scheme applied to a mathematical model of the prevalence of smoking in Spain: A case study. Comput. Appl. Math. 2014, 33, 13–25. [Google Scholar] [CrossRef]
- Sekiguchi, M.; Ishiwata, E. Global dynamics of a discretized SIRS epidemic model with time delay. J. Math. Anal. Appl. 2010, 371, 195–202. [Google Scholar] [CrossRef]
- Wang, Y. Dynamics of a nonstandard finite-difference scheme for delay differential equations with unimodal feedback. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 3967–3978. [Google Scholar] [CrossRef]
- Su, H.; Li, W.; Ding, X. Numerical dynamics of a nonstandard finite difference method for a class of delay differential equations. J. Math. Anal. Appl. 2013, 400, 25–34. [Google Scholar] [CrossRef]
- Xu, J.; Geng, Y. Stability preserving NSFD scheme for a delayed viral infection model with cell-to-cell transmission and general nonlinear incidence. J. Differ. Equ. Appl. 2017, 23, 893–916. [Google Scholar] [CrossRef]
- Zhou, J.; Yang, Y. Global dynamics of a discrete viral infection model with time delay, virus-to-cell and cell-to-cell transmissions. J. Differ. Equ. Appl. 2017, 23, 1853–1868. [Google Scholar] [CrossRef]
- Dang, Q.A.; Hoang, M.T. Lyapunov direct method for investigating stability of nonstandard finite difference schemes for metapopulation models. J. Differ. Equ. Appl. 2018, 24, 15–47. [Google Scholar] [CrossRef]
- Garba, S.M.; Gumel, A.B.; Hassan, A.S.; Lubuma, J.M.-S. Switching from exact scheme to nonstandard finite difference scheme for linear delay differential equation. Appl. Math. Comput. 2015, 258, 388–403. [Google Scholar] [CrossRef]
- García, M.A.; Castro, M.A.; Martín, J.A.; Rodríguez, F. Exact and nonstandard numerical schemes for linear delay differential models. Appl. Math. Comput. 2018, 338, 337–345. [Google Scholar] [CrossRef]
- Pospíšil, M. Representation and stability of solutions of systems of functional differential equations with multiple delays. Electron. J. Qual. Theory 2012, 54, 1–30. [Google Scholar] [CrossRef]
- Bellman, R.; Cooke, K.L. Differential-Difference Equations; Academic Press: New York, NY, USA, 1963. [Google Scholar]
- El’sgol’ts, L.E.; Norkin, S.B. Introduction to the Theory and Application of Differential Equations with Deviating Arguments; Academic Press: New York, NY, USA, 1973. [Google Scholar]
- Martín, J.A.; Rodríguez, F.; Company, R. Analytic solution of mixed problems for the generalized diffusion equation with delay. Math. Comput. Model. 2004, 40, 361–369. [Google Scholar] [CrossRef]
- Guglielmi, N. On the asymptotic stability properties of Runge–Kutta methods for delay differential equations. Numer. Math. 1997, 77, 467–485. [Google Scholar] [CrossRef]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 1985. [Google Scholar]
- Elaydi, S.N. An Introduction to Difference Equations; Springer: New York, NY, USA, 1996. [Google Scholar]
- Čermák, J.; Jánský, J.; Nechvátal, L. Exact versus discretized stability regions for a linear delay differential equation. Appl. Math. Comput. 2019, 347, 712–722. [Google Scholar] [CrossRef]
- Nishiguchi, J. On parameter dependence of exponential stability of equilibrium solutions in differential equations with a single constant delay. Discrete Contin. Dyn. Syst. 2016, 36, 5657–5679. [Google Scholar] [CrossRef]
- Györi, I.; Ladas, G. Oscillation Theory of Delay Differential Equations; Clarendon Press: Oxford, UK, 1991. [Google Scholar]
- Roeger, L.-I.W. Exact finite-difference schemes for two-dimensional linear systems with constant coefficients. J. Comput. Appl. Math. 2008, 219, 102–109. [Google Scholar] [CrossRef]
- Quang, A.D.; Tuan, H.M. Exact finite difference schemes for three-dimensional linear systems with constant coefficients. J. Vietnam J. Math. 2018, 46, 471–492. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Castro, M.Á.; García, M.A.; Martín, J.A.; Rodríguez, F. Exact and Nonstandard Finite Difference Schemes for Coupled Linear Delay Differential Systems. Mathematics 2019, 7, 1038. https://doi.org/10.3390/math7111038
Castro MÁ, García MA, Martín JA, Rodríguez F. Exact and Nonstandard Finite Difference Schemes for Coupled Linear Delay Differential Systems. Mathematics. 2019; 7(11):1038. https://doi.org/10.3390/math7111038
Chicago/Turabian StyleCastro, María Ángeles, Miguel Antonio García, José Antonio Martín, and Francisco Rodríguez. 2019. "Exact and Nonstandard Finite Difference Schemes for Coupled Linear Delay Differential Systems" Mathematics 7, no. 11: 1038. https://doi.org/10.3390/math7111038
APA StyleCastro, M. Á., García, M. A., Martín, J. A., & Rodríguez, F. (2019). Exact and Nonstandard Finite Difference Schemes for Coupled Linear Delay Differential Systems. Mathematics, 7(11), 1038. https://doi.org/10.3390/math7111038




