1. Introduction
This paper deals with a sharing economy platform with critical operational factors which include a status of the owners (contractors, suppliers) and seekers (subscribers, customers) under the sharing economy. Basically, the sharing economy platform makes the collaborative consumption by the activities of sharing, exchanging and rental of resources without owning the goods [
1]. Growing concerns about climate change have made the collaborative consumption an appealing alternative for consumers [
2]. This concept describes in a broader sense any sales transactions which are done in online market places, even in business-to-business (B2B). This sharing economy began to spread widely by sharing unused resources between individuals. Startup companies including Uber and AirBnB not only provide technological platforms to facilitate transactions but also become real-world companies, with the same responsibilities as transportation companies under the sharing economy platforms [
3,
4]. The constituent factors of a sharing economy business model could be largely divided into eight factors for the business operations—value proposition; financial profit and loss; resources; process; target customers; exterior cooperation; and logistical flow [
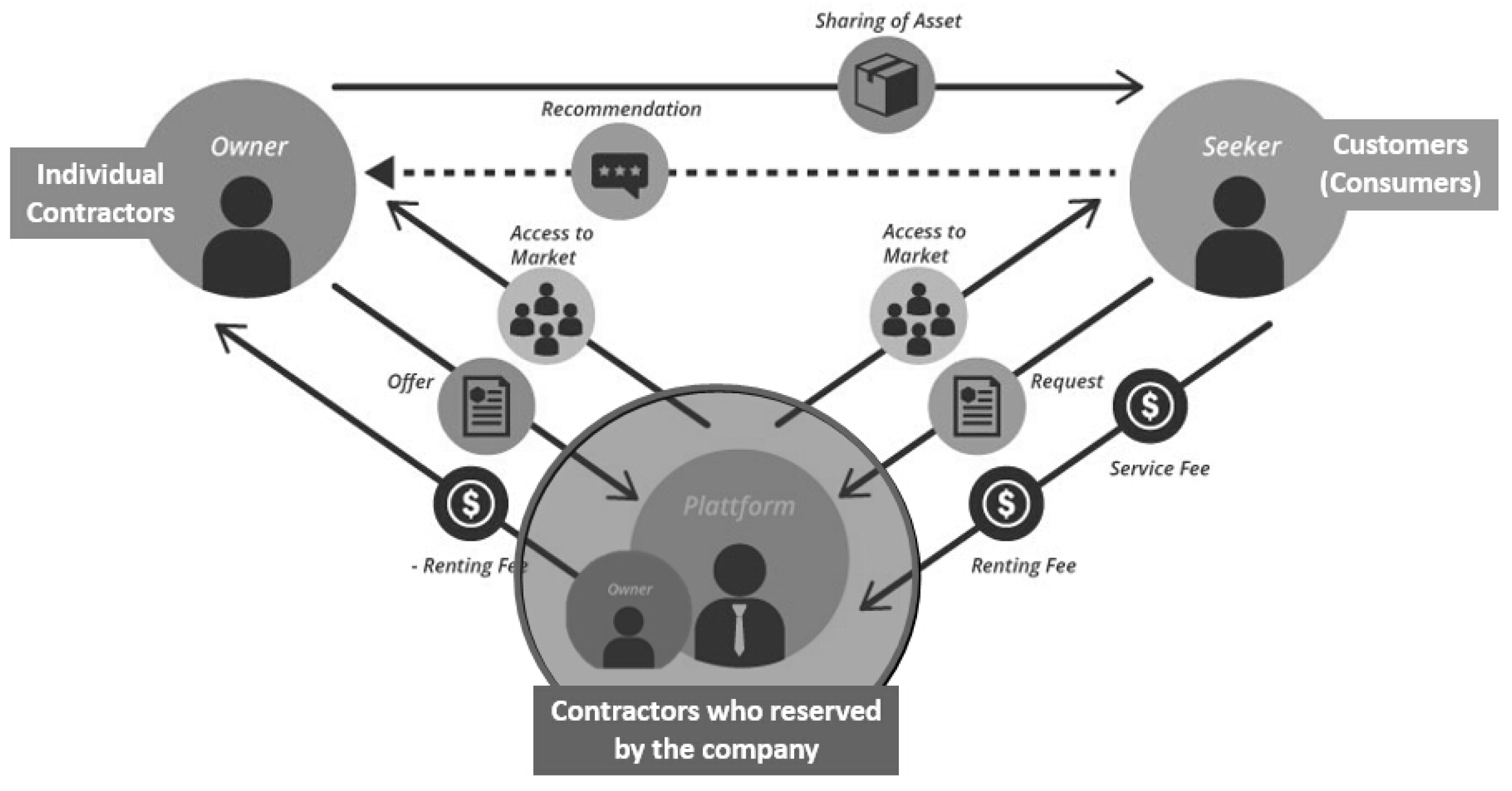
5]. The operations must evolve along with the new sharing business model and they should preserve the value created through innovation. This paper deals with modeling the business operations between resource owners (suppliers) and consumers (customers). As a platform provider, a manager should control the balance between them. This paper suggests that resource owners have two main types of contract in the sharing economy platform. Individual contractors are typical suppliers in the system which are independent and have fewer obligations but company contractors who are directly reserved by a platform provider have more obligations to support goods. The relationship between a platform provider and various types of suppliers in the sharing economy system is described in
Figure 1.
This type of a sharing economy system could be described as a classical G/M/1 type queueing model and its operations are critical for all companies in each section of the sharing economy. The main target of sharing economy operations is balancing conflicted goals such as keeping enough for various types of supplying resources (e.g., car drivers in Uber, room owners in AirBnB). The literature reviews of queueing research have contained massive studies regarding queues in various situations [
7,
8,
9,
10] and the
type queues have been not only theoretically studied [
11,
12] but also studied based on the algorithmic approach [
13].
The model in this paper considers two types of contracts for suppliers. The individual contractor is a typical resource owner in a sharing economy system. As mentioned, each contract is an individual which is similar to a part-time contract. The other contract is rather more permanent than the first and the contractors will be directly controlled by the service providers. In the terms of operating cost, the individual contract is cheaper but has the risk of being out of the service at the same time. Therefore, the contract type of resource owners should be balanced. Notably, valid suppliers are posted on the (online) platform as a bulk of suppliers after gathering and screening. The duration of gathering (and screening) resource owners is considered as a general inter-arrival time in a typical single channel queue and the service which is consumed by customers is based on the Markovian service time. This sharing economy model is well described as a
type queueing model rather than as a
type queue [
14]. Hence, this paper deals with a class of
queueing model with continuous time perspectives. More specifically, a
type system with a finite capacity
w is considered and each input (i.e., offering resources from the individual contractors) is stored as a fixed batch size
v. A basic
type queue has been well studied [
1,
15] in various areas including inventory controls [
10,
16] and manufacturing systems [
17] but it has never been adapted for sharing economy models. The “congruent properties” explored in this paper gives an explicit relationship between two models in terms of probabilities for the queueing processes. Explicit obtained formulas demonstrate a relatively effortless usage of functionals for the main stochastic characteristics and their objective function supports the optimization of the system. The main objective of this article is to analyze the random process describing the sharing economy system at any moment of time in equilibrium. Versatile scientific approaches using modern technologies, including an artificial intelligence and a complex information systems, have been adapted for resolving social and economic challenges [
18,
19]. The theoretical approach to find the optimization of a sharing economy platform might be a basic clue for analyzing social and economic challenges to understand vital factors of the problems before adapting complex intelligent systems.
The article is organized as follows:
Section 2 presents a “congruent model” which has the same characteristics as the principal model. Some expressions provide a very simple connection between the main and the congruent models. This section also includes mathematical formalism of two models and the congruent properties are further extended to a worthwhile relationship between Model 1 (
) and Model 2 (
).
Section 3 deals with the Markov processes and continuous time processes for Model 2 (which bring back to Model 1 via the stochastic congruence). In
Section 4, functions of the semi-regenerative process are introduced to demonstrate tractability of the main results, followed by optimization of a relevant objective function.
Section 5 deals with optimization of atypical sharing economy platform operation case, which is concluded with numerical examples.
2. Stochastically Congruent Models
The stochastically congruent model, referred to as Model 2, is introduced which is simpler than the main model (i.e., Model 1). The stochastic congruence is widely applied to solve a problem by using a well known model which is connected to the original problem. In this paper, Model 2 is similar to Model 1 and the analytical solutions of Model 2 are already well known [
15,
20]. According to the congruency, the states of Model 1 are equivalent to states of Model 2 which are simply flipped over and counted the other way around. In other words, Model 2 is directly connected to Model 1. Both the above models (Model 1 and 2) could be formally described.
Denote by
the total number of contracts from resource suppliers
w at time
t in Model 1. Once one batch of individual contracts
v from a supplier is ready, the resource is published for customers. As mentioned, this sharing economy model could be described as a
queueing model. Let
be the moment a batch contract is published on the system (the online platform) and let
be the duration for publishing bulk service suppliers. The random variables
are iid (independent and identically distributed) with a common CDF (Cumulative Density Function)
with the mean
. Each of the consuming services (or users getting the service from the contracted suppliers) is independent from each other and exponentially distributed with the parameter
. The summary of the related values are provided in the table (see
Table 1).
Model 2 describes the number of customers in a
queueing system which is a single sever process with the fixed batch size
v. It is like a single channel queue
except for the finite waiting room
w [
15]. Let
be the moment of contracted suppliers are published on the platform and it is assumed that the last action does not affect the status of the system in this particular problem setting. The random variables
(in Model 2) are stochastically equivalent to
of Model 1. It can be shown that
and
are sequences of stopping times of the processes
and
respectively and that these processes are regenerative relative to these sequences. Let us assign:
Consequently,
and
are embedded Markov Chains (MCs). Both Markov chains are stochastically congruent. Their limiting probabilities are expressed through the common invariant probability measure P
where
and P
where
. The states of the
queue are equivalent to the states of the flipped
queue.Therefore, the state
k in
queueing system “corresponds” to the state
in
queueing system which yields that
Since and are stochastically congruent, only one of them will be treated in the next section.
3. Embedded Processes and Continuous Parameters of Model 2
The embedded process
of Model 2 is a time-homogeneous Markov chain and
is the number of customers at time
and it has two types of transition matrices which depend on the relationship between the batch size
v and the system capacity
w. The transition probabilities could be changed because of these two factors but the method of solving stationary probabilities are essentially same. Let
be the number of completely processed customers during the period
when
. Then we have:
Two types of the transition probabilities
and
are as follows, if
(Type-1):
or, if
(Type-2):
where
Both TPMs (Transition Probability Matrices) of Model 2 (Type 1 and 2) repent a finite sub-matrix which occurs within the corresponding TPM of
queueing system. The embedded probabilities
Q of a
queue are as follows [
1]:
where
The generating function
converges inside the unit open disc centered at zero. Alternatively,
Q is also the solution of equations
Q = Q·M
and (
Q where M
is the TPM of the infinite queueing system. It is noted that M
is the
finite sub-matrix of M
. Let the vector
be the solution of the equation
M
. Because of the linearity of the equations
Q =
Q·
M and
M differ from
by the same constant respectively. It means a constant
A (proportionality) exists such that
Since we will use the probabilities
for the solutions of
, the constant
A will be determined from (P
, where P is the invariant probability measure of the embedded process in
system. The probabilities
were obtained [
21] from the expansion of the generating function (10). From (5) and (7)–(12), it follows that:
where
and
The next step is finding the continuous time parameter queueing process of Model 2. The below treatment is similar to that of Kim and Dshalalow [
22]. Let
be the counting process associated with the point process
and
.
gives the residual time from time
t to the next service completion
. The process
is weak Markov. Let
be the Markov semi-group associated with
. It is assumed to be absolutely continuous,, that is, if
then
Since all pertinent processes in equilibrium have been studied, the initial state is not considered. So the index
from
is dropped. To find the limiting distribution
of the process
, we will start with the Kolmogorov differential equations, assuming that
has the Radon-Nikodym density
, which, in addition, is pointless continuous. From (16), the Kolmogorov equations are as follows:
The process
is also semi-regenerative relative to the sequence
and its limiting distribution exists [
5,
8]. Let
Letting
in (17) and then applying the Laplace transformwe have:
Once,
are revealed,
could be found accordingly after calculating the invariant probability measure P
of
from the TPM of the system which is covered in the next section. To find the unknowns
when
. Denote
Note that
are the transition probabilities of the embedded MC
We use the natural assumption that
Let
and from the main convergence theorem,
By elementary probability arguments,
and then
When
in (30), due to (P
and (13a),
3.1. Process of Model 2 Type 1
The Type 1 of Model 2 is the case that the total number of services
w in the system is larger than double of the batch independent supplier size
v . In Type 1, the transition probability is determined from (8) and the TPM is constructed as follows:
and the invariant probability measure P
of
is determined from (P
and (13) and (14). From (23), summation over
in (23):
where
Summing up the equation of (24) and (25) in
j from
to
s then yields:
The continuous time parameter process of Type 1 (Model 2) could be analyzed from (31) and (33)–(35) and limiting distribution
is as follows:
and using
where
From (32), (35) and (36)–(38),
therefore,
For the process
the corresponding formulas yield for the limiting distribution
is as follows:
along with (6).
3.2. Process of Model 2 Type 2
Alternatively, the embedded process
of Model 2 is changed when
(Model 2 Type 2) and the TPM becomes as follows from (8b) and (9):
and the TPMs from (41) repent the same finite sub-matrix which occurs within the corresponding TPM of
queueing system (10). Similarly, the continuous time parameter process for Type-2 could be found from (23). From (23)–(26), summation over
in (24) and (25):
and summing up the equation of (24) and (25) in
j from
to
w then yields:
From (31), (34), (36) and (37), we finally arrive at the limiting distribution
with the different
:
For the process for Type 2 the corresponding formulas yield the same from (36), (39) and (40) but with different parameters from (44).
4. The Optimality of the Sharing Economy System
In this section, a class of optimization problem, from which arises a stochastic sharing business operation, is considered. Let us formalize a pertinent optimization problem. Let a strategy, say
, specify, ahead of time, a set of acts that are imposed on the queueing system such as the choice of the batch size of an individual contract
on the service platform, the total number of resource suppliers
and so on. Denote by
the expected costs within
, due to the strategy
and costs
C and define the expected cumulative cost rate over an infinite horizon:
Let
denote the cost function associated with holding the contract in the (service) platform for
n contractors which remain in the supplier pool. If
, a linear function, that is,
, then the expected holding cost for contractors in the supplier pool during the interval
is
(which by Fubini’s Theorem is)
Since
is the number of available suppliers on the service platform,
gives the number of suppliers which are reserved by the company (i.e., platform provider) for urgent cases (i.e., individual contractors are not enough to support all consumers). The expected cost for reserved suppliers in the interval
is
(which by Fubini’s Theorem is)
if
is a linear function (i.e.,
),
Since the Markov renewal function
represents the total number of services consumed by customers in the time interval
where 1
is the indicator function of a set
B. The functional
gives the set cost for posting the available suppliers on the service platform. The cumulative cost of the entire procedurs is involved in the sharing service operations in the interval
is
Now we turn to convergence theorems for Markov renewal and semi-Markov processes [
18],
- (i)
- (ii)
to arrive at the objective function
which gives the total expected rate of all processes over an infinite horizon. In light of Equations (i) and (ii) we have
With the cost functions being linear functions, we have
Recall that from (40) we have
With these attachments and (10) and (13b), Formula (50) for the objective function is complete.
5. Supplier Contract Optimization Case
In a special model of the sharing business operation situation, this section intends to demonstrate the tractability of our results in
Section 2,
Section 3 and
Section 4. We allow an exponential distribution of inter-arrival duration between an (individual) contract posting on the platform. Since the method involves operating with an embedded Markov process in a single channel open queue with a finite buffer, we get back to
Section 2 for some particular formulas.
5.1. M/M/1/w Sharing Business Operations
The pertinent special formulas of
Section 4 under these assumptions are as follows:
From Chaudhry and Templeton [
15],
where, from (55),
The remaining parameter such as from (34), from (38) (or (44)) and from (13) to get from (36) and (37) could be calculated accordingly. After finding , we can find from (51).
5.2. Optimization with the Two Types of Supplier Contracts
For our optimization example, we specify the remaining three primary cost functions are as follows:
where
is the holding cost per contract on the service platform,
is the supplier costs which are reserved by the company for urgent cases. From (49) and (57), we have
where
Finally, we arrive at the following expression for the objective function:
Here, we use Formulas (50), (51) and (38) for Type-1 (or (44) for Type-2). Notice that we have the parameter
v vary. We restrict the initial strategy of this model to one, which includes only the control level
v of the batch size of each arrival. In other words, we need to find a
v such that
As an illustration in
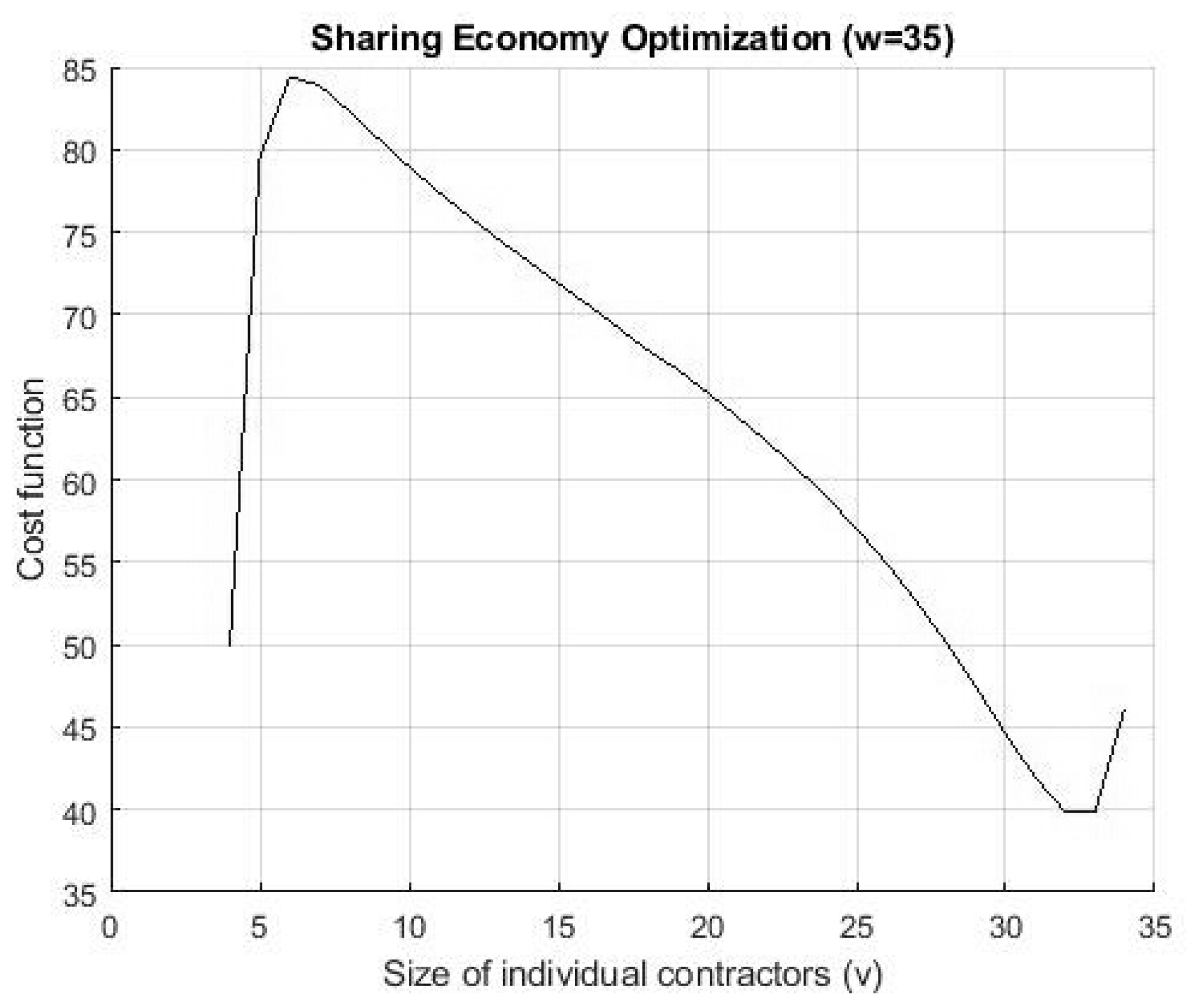
Figure 2, let us take
and
. The inter-duration between posting one bulk of contracts on the (online) platform is exponentially distributed with the mean
and the parameter of consuming services by customers is
. Take the maximum number of contracts (suppliers) as 35 and the maximal bulk size of the individual contracts must be smaller than the size of the total capacity
w . Now, we calculate
and
which gives a minimum for
. In other words, the control level
stands for the optimal batch size of the individual supplier contracts which minimizes the total operating cost of the sharing business. Below is a plot of
for
.
Our calculation yields that
for which the minimal cost equals
. When the total number of the allowed suppliers is 35, we obtain the threshold value
which gives us the decision point that is the number of bulk contracts for the individual suppliers to minimize the cost of the sharing economy system operations. It also indicates that only 2 suppliers are reserved by the platform provider (i.e.,
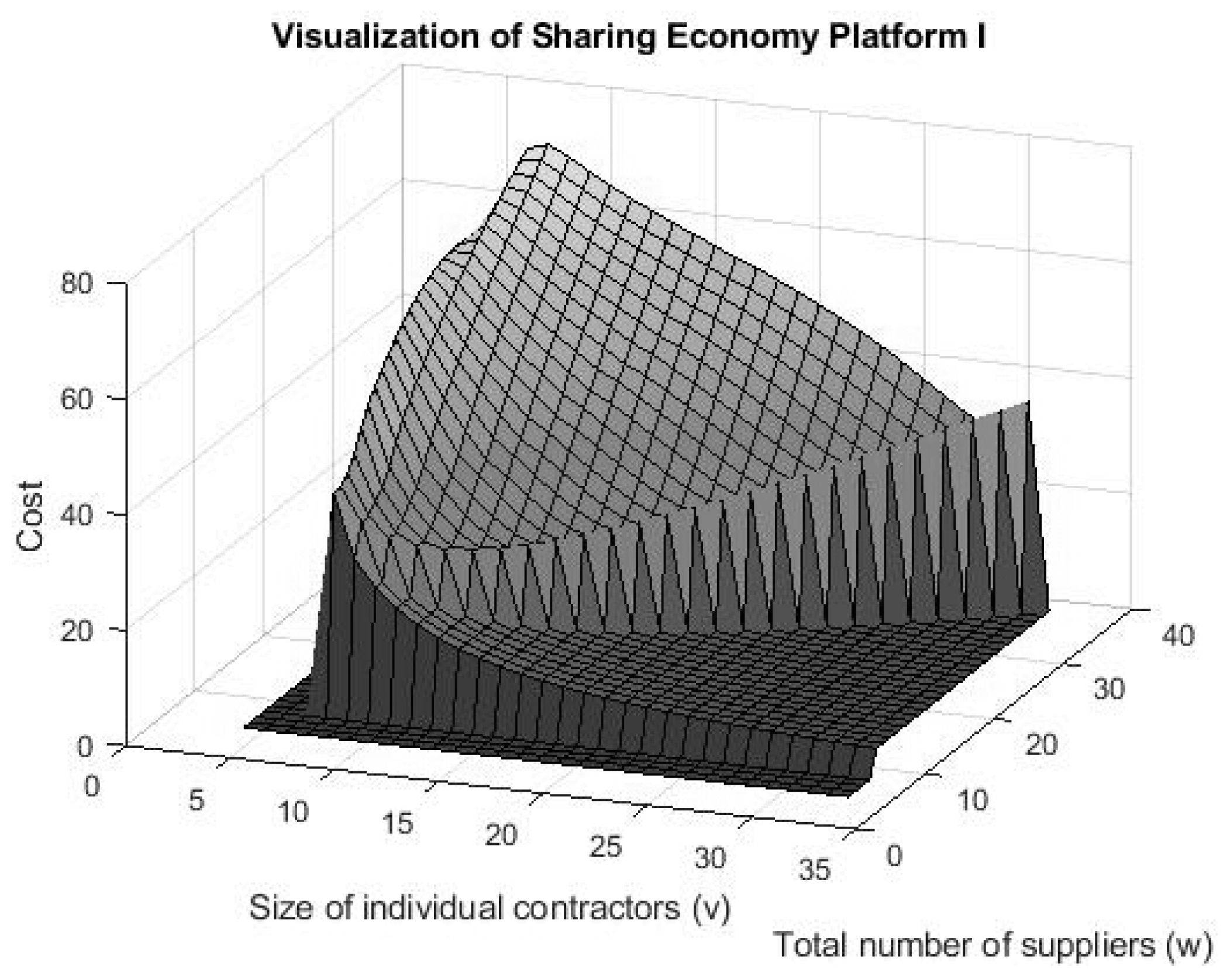
. In addition, it is also feasible to visualize the cost objective function with two variables in the platform (see
Figure 3).
As a part of reasonable performance measures, let us consider a capability factor
, which represents the estimated loss rate of the potential service (customers) at any moment of time in equilibrium:
In this particular case, this value is zero (i.e., ) and it indicates that there are no customer losses in the system. This value could not only be a performance measure but be also a constraint to optimize an objective function of the sharing economy platform.